ボーア模型(原子、分子) (13/10/19)
変分法 ( 微細構造定数, ゾンマーフェルト軌道, 相対性理論 ) (14/ 6/14 )
ベル不等式の破れ。 ( 遅延選択, 量子コンピューター ) (13/ 2/1)
場の量子論 ( ディラック方程式、量子電磁力学、ヒッグス粒子 ) (13/ 1/25)
物理の説明が難解な理由 (14/ 8/17)
Nature 誌 のボーア模型 (14/ 9/21) どこで科学が止まっている? (15/ 1/4)
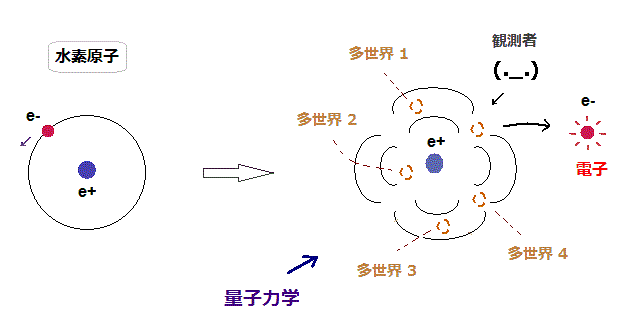
(Fig.1) 量子力学 = 多世界 = ファンタジー。

量子力学は 粒子の 曖昧な確率密度しか 示せない。
そして 粒子を観測した瞬間に、全空間に広がった 確率密度の波動関数が
1点 に 収束することになる。
不自然な 観測者による波束の収縮 (= コペンハーゲン解釈 ) を避けるには ファンタジックな 多世界解釈 しか残っていないのである。
なぜなら 量子力学では 実在的な解釈 (= ボーム解釈 ) が 不可能だからである。
そのため トップランクの 大学 ( ここも参照 ) や ジャーナルまでもが この現実離れした平行世界を 積極的に広めようとしている始末である。 もちろん この傾向は 現在の物理学の発展において 非常に 好ましくない ことは明白である。
結果的に ほとんどの物理学者達は 奇妙な波動関数の本当のメカニズムそのものを追及すること自体を避けるようになってしまった (= Shut up and calculate ! )。 しかし 目の前に分からないことがあるのに 追及を諦めることは、科学の根本的な精神に反する行為であることを言うまでもない。
(Fig.2) 陽子のスピンは OK. 電子スピンは 幻想である。
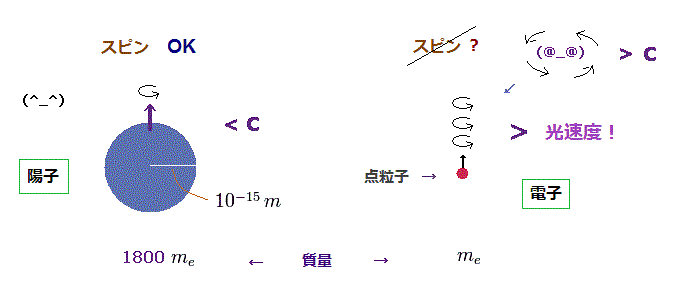
電子は 非常に軽くて小さい (= ほぼ点粒子 )。
このページに示したように、電子が陽子ほどの大きさと仮定したとしても、スピン角運動量の 1/2 ħ を出すには そのスピンスピードは 何と 光速の 100 倍以上 ( > 100c ) に到達しなければならない。
( 他の ウェブサイトも参照のこと ここ p.5, ここ, ここ など。 )
もちろん、実際には 電子は 陽子よりもはるかに小さいため、このスピンスピードは この結果よりも さらに 速くなる必要がある。
一方で、陽子は 電子に比して 非常に重くて かつ 大きい (= 0.84 fm )。
つまり この陽子のスピンスピードは 光速を 超えない ( < c )。
つまり この電子スピンという概念は どう転んでも現実的に あり得ない概念であり、スピン磁気モーメント (= ボーア磁子に等しい ) は ボーア軌道のような 軌道運動によって生じていると考えるのが自然である。
実際、同じ電荷量を持つにも関わらず、電子の磁気モーメント (= ボーア磁子 ) は 陽子のよりも 約 1000 倍も 強いのである。間違いなく 電子スピンは "スピン" によるものではない と言える。
(Fig.3) 360°回転後、 電子は まったくの別の物になってしまう。
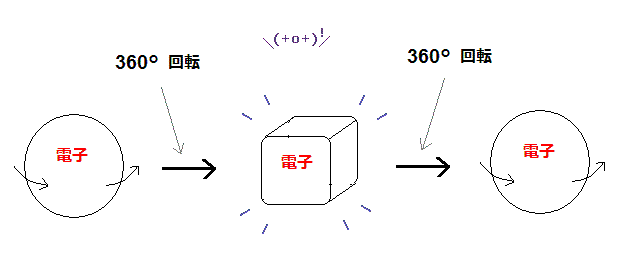
電子や中性子などのフェルミ粒子は 元に戻るには 1回転では不十分で 2回転 (= 720° = 4 π ) する必要があることが知られている。Wiki も参照。
この時点で あなたがたは これらフェルミ粒子という概念に リアリティーが まったく ない ことが 理解できると思われる。なぜなら この 現実の世界のものは 1回転で 元に戻るのが 当たり前だからである。
驚くことに、 このページに示したように、この奇妙な性質が 実際の中性子干渉による実験で 確認されているのである。このサイトも参照のこと。
もちろん、彼らは 中性子の回転 (= 歳差運動 ) を 直接 見ているわけではない。
スピン角運動量 1/2 ħ に基づいて それらの歳差運動角度を 推定しているだけにすぎない。
もし 通常のボーア軌道のように 角運動量として ħ ( 1/2 ħ の代わりに ) を採用したとすると、これらの実験結果の解釈は まったく変わってしまう。
例えば、コマの歳差運動 を思い浮かべてもらえると分かるが、 コマの回転する角運動量が 2倍になると ( 1/2 ħ → ħ ) この歳差運動の速度は 半分 ( 2 → 1 回転 ) に減る。これが 中性子を使った奇妙な実験結果の トリックである。
これらの実験は 単に ħ の角運動量を持つフェルミ粒子が 1回転で元に戻ったという 当たり前の結果を表しているにすぎない。
(Fig.4) シュレーディンガーの 2P の"動径" 波動関数 ( 角運動量 = 1 ).
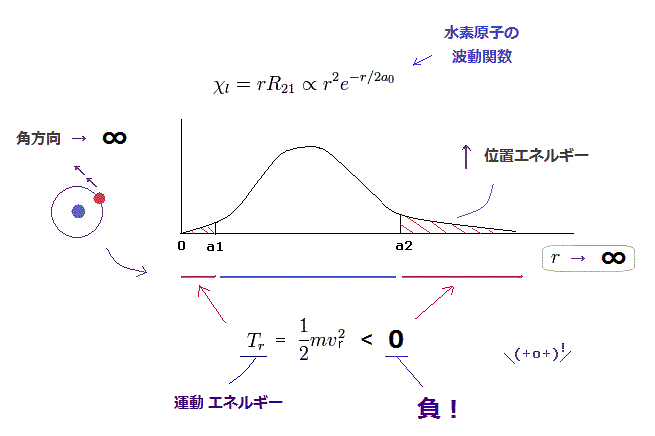
シュレーディンガーの水素原子は 2つ ( l > 0 ) の古典的に禁止された領域 (= 非実在的 ) を含んでいる。 ここ (p.2-) と ここ.を参照のこと。 Fig.4 (= 水素の 2p の波動関数 ) では、 動径方向の運動エネルギーが 2つの領域で 負 になってしまう (← あり得ない現象である )。
a2 の右側では、位置エネルギーが 全エネルギーよりも高くなってしまうため、それを打ち消すために 運動エネルギーが 負 になる必要がある。
そもそも 原子核に束縛された電子が r = 無限大のかなたまで行き来しているという考え自体 理不尽極まりない。
a1 の左側では、接線方向の運動エネルギーが急増するため、これをキャンセルするのに 動径方向の運動エネルギーが 負 にならなければならないという始末である。 この領域では 位置エネルギーは 全エネルギーよりも低いため、トンネル効果では説明できない。
この現実の世界で 動径方向 (= 負 ) と 接線方向 (= 角運動量のために 必ず 正 ) の 運動エネルギーの符号が異なる ということは考えられない現象である。つまりシュレーディンガーの水素原子に リアリティーがないことの明確な証拠と言える。
(Fig.5) ナトリウムの 3s 電子は 原子核と 内殻電子群を いつも貫いているのか?
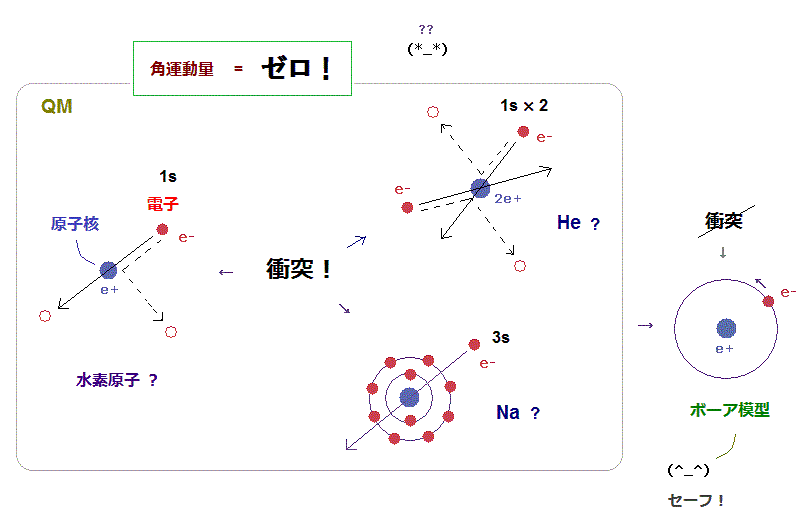
量子力学では、 "s" 軌道は 角運動量が ゼロ の状態である ( L = 0 )。 ここ や ここ を参照のこと。
つまり、水素原子や ヘリウム原子の 1s の電子は 原子に 衝突し続けているのだろうか? ( ← あり得ない状況である。 )
常識的に考えれば、ヘリウムの2つの電子間の反発力のために 各電子は 角運動量ゼロを保てないばかりか、度重なる衝突で 事実と異なる 非常に不安定なヘリウム原子になってしまう。
また ナトリウム (= 3s ) や カリウム (= 4s ) の最外殻電子も
ゼロ の 角運動量を持つことになる。
これはつまり これら最外殻電子が 継続的に 内殻 n = 1, 2 の電子群 と 原子核を
貫通 もしくは 跳ね返りし続けていることになるのだろうか?
これも あり得ない状況である。
一方で、ボーア模型の角運動量は 1 よりも 必ず 大きい ( L は ゼロに ならない ) ため、 原子核や 内殻の電子群に 衝突する必要が ない。非常に安定な原子模型と言える。
(Fig.6) 唯一の "万物の理論"、10 次元の超弦理論に リアリティーはなし。
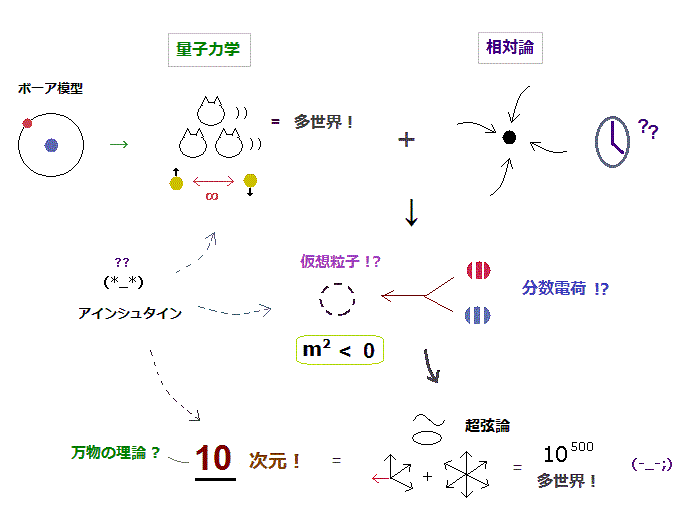
ここで 量子力学と 相対論が間違いだと主張する明白な理由の1つが 現在唯一存在する統一理論が 10 次元の 超弦理論だけだという事実である。 ここ や ここ も参照のこと。
ウィッテンが最近コメントしたように、ツイスター理論や ループ量子重力理論などは 統一理論として 完成された理論ではない。
つまり あなた方が もし物理の世界に入って 10 次元の超弦理論を信じなかったとしたら、まず間違いなく "教授" への出世街道は絶たれることになる。 要は 能力があるかどうかの問題でなくこの現実離れした概念を信じられるかという問題なのである。
ほぼすべての重要な役職と 最近創設された 3億円 の物理学賞などは この10 次元の超弦理論学者達で 独占されてしまっている。
これに続けとばかりに 11 次元の M 理論、や 12 次元の F 理論 が 新理論として次々に生まれてきてしまった。
もちろん、常識的に考えて この現実の世界が非実在的な 10 次元の世界を採用しているはずがない。
実は 相対論的な場の量子論では 特殊相対論に反する 仮想粒子というものが 必ずすべての反応過程に登場しなければならない。 (= タキオン, m2 < 0 ).
現在の物理は この矛盾した仮想粒子に 量子電磁力学 (QED) や 標準模型 ( ここ p.6 ) において 完全に依存しているのである。
つまり 自己矛盾であふれた現在の理論は 最初から 根本的な 欠陥を含んでいる。
(Fig.7) ディラックの水素 = ボーア・ゾンマーフェルト模型。
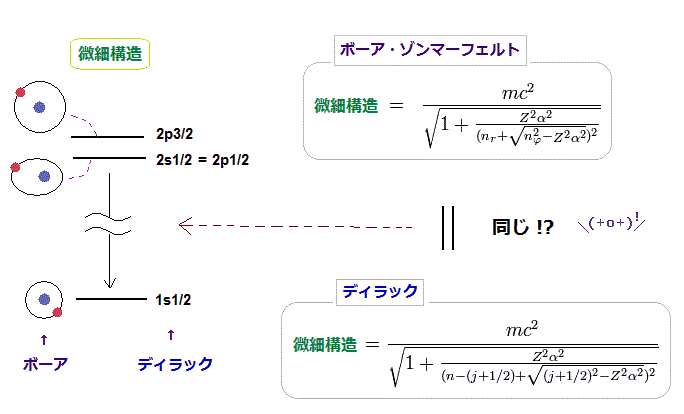
重要な点は 水素様原子の 微細構造は ボーア軌道に基づいて ゾンマーフェルトによって 最初に与えられたということである。
驚くことに、後に ディラック方程式による水素原子解も ボーア・ゾンマーフェルト模型の解と ちょうど 一致してしまったのである。 ( このページも参照のこと。 )
この ゾンマーフェルトとディラックの水素の偶然の一致は "ゾンマーフェルトのパズル" や "マジック" などと呼ばれた。他のウェブサイトも参照のこと ( ここ, ここ, ここ (p.12-), ここ (p.9), ここ )。
アインシュタインは 1916 年に 手紙の中で ゾンマーフェルト模型を次のように 称賛している。
"すばらしい。水素スペクトルに関する あなたの研究結果は 私が今まで経験してきたものの中で最高に美しい部類に入る。この理論によって ボーアの考えたモデルが 完全に 確実的なものになった。"
ゾンマーフェルトとディラックの式の導出に関しては、 ここ と ここ を参照のこと。
計算結果 と 実験値を比較すれば、ゾンマーフェルト模型の予測値が 実験値に ぴったりであることが理解できる。
(Fig.8) ディラック方程式は ゾンマーフェルト模型 ( n = 2 の場合 ) と一致する。
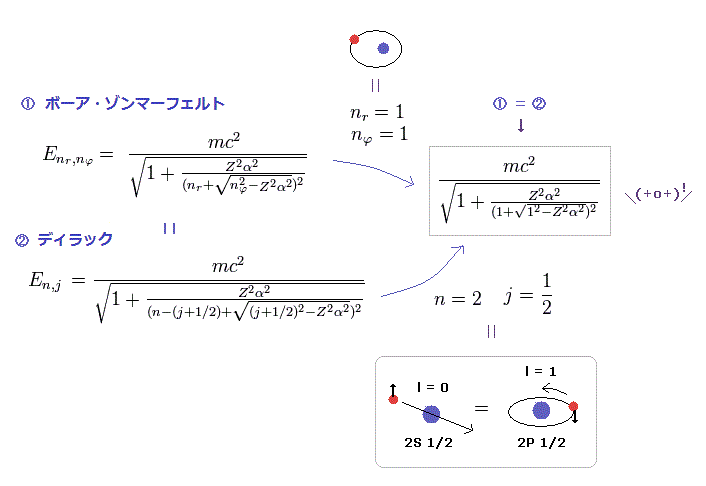
Fig.8 の上式は エネルギー準位 n = 2 ( ← nr + nφ = 2 ) の ゾンマーフェルトの楕円軌道 ( nr = 1, nφ = 1 ) である。
驚くことに、ディラック 2s1/2 と 2p1/2 のエネルギー準位は Fig.8 下図にあるように 起源が完全に異なるにも関わらず、ゾンマーフェルトの楕円軌道に 完全に
等しい。
( ディラックの水素は "スピン" を含むが、ゾンマーフェルト模型は 含まない。 )
なぜなら 例えば 2s1/2 と 2p1/2 は 共通の j = 1/2 だという理由で ディラックの水素では同じエネルギー準位に押し込められているからである。
これらまったく違う概念由来の数値が 完全に一致することを見れば、ディラックの水素原子が 先のゾンマーフェルトの式に倣って 解を導出したことは一目瞭然である。
(Fig.9) シュレーディンガーの水素、動径方向 = ドブロイ波の整数倍。
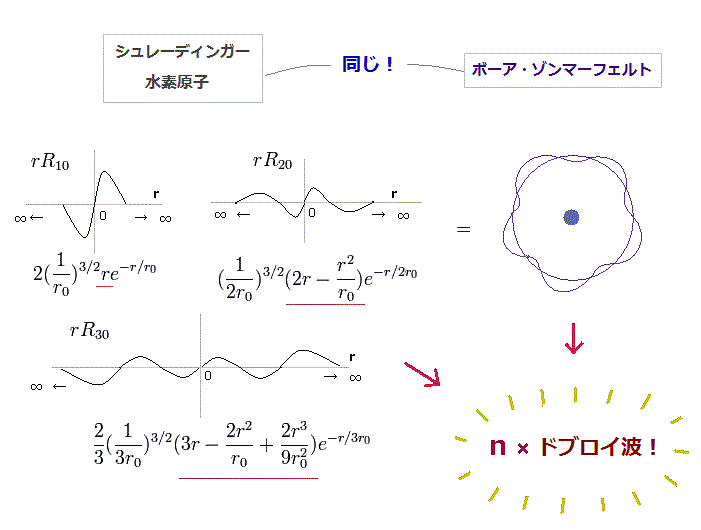
ボーア模型 が ドブロイ波長 に基づく理論であることは有名である。
このドブロイ波自体は ダヴィッソン-ガーマーの実験などにあるように、実験的に実証された 紛れもなくリアルな概念である。
つまり、シュレーディンガーの水素も ドブロイの関係式を用いることは必須条件である。
ということは このシュレーディンガーの水素原子の軌道も ボーア模型のように ドブロイ波の整数倍という条件を満足するのだろうか?
実は、この量子力学的な水素においても、ドブロイ波の整数倍の量子化条件を満たすのである。 このページも参照のこと。
Fig.9 は シュレーディンガーの水素の 動径方向の確率振幅 (= rR ) である。
他のウェブサイトも参照のこと ( 確率振幅 と 確率密度 ).
確率密度 (= (rR)2 ) は 確率振幅 (= rR ) の2乗で与えられる。
"rR10"、"rR20" と "rR30" は 1軌道が ちょうど 1 ×、2 ×、 3 × (= 整数倍 ) ドブロイ波長になっている。 角運動量 (= 接線方向 ) も量子化されているため、それらの和が 主量子数 (= n ) になる。
これらの結果は ボーア・ゾンマーフェルト模型のものと 完全に等しく、このことが 両者のエネルギー準位が すべて一致している要因である。
(Fig.10) 単純な古いボーアのヘリウム模型は 間違ったエネルギー (= -83.33 eV ) を与える。
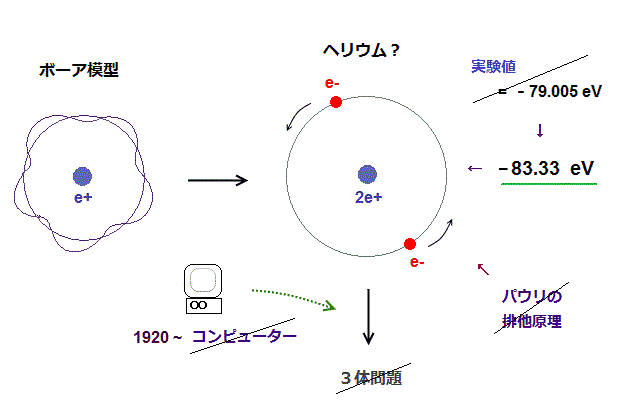
ボーア模型が棄却された最も決定的な要因は 水素以上の電子を持つヘリウム原子の説明の失敗にある。 このセクションにあるように、Fig.10 右 の単純なヘリウム模型は 間違った基底状態のエネルギー (= -83.33 eV ) を与える。
ヘリウム原子のエネルギーの実験値は -79.005147 eV (= 1st + 2nd イオン化エネルギー Nist, CRC ) である。
もちろん、1920 年代には ヘリウムのような 3体問題 (= 2つの電子 + 1つの原子核 ) を計算できる便利なコンピューターなんてものはなかった。
一方で、量子力学的な変分法は このサイトなどにあるように 実験値に近い計算結果を得られた。
なぜなら、最初に選ぶ変分関数がシンプルなものであれば、コンピューターなし の状況でも 近似的に 解を出せるからである。
(Fig.11) 計算結果は 最初に選んだ試行関数の”形”に依存する。
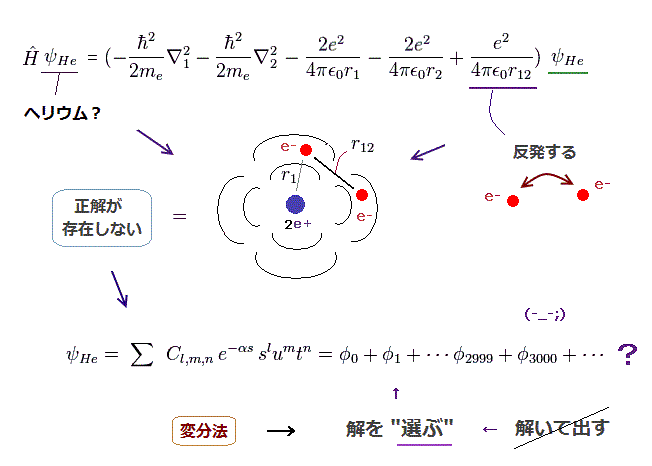
ヘリウム原子は2つの反発する電子を含んでいるため、シュレーディンガー方程式を解くことができない。
解けないということは、この方法では ヘリウムの真の基底状態エネルギーを知ることが不可能ということである。
変分法では、最初に ヘリウムの波動関数の形を選択することから始める。
この選ばれた波動関数の形の範囲内で 全エネルギーの 最も低い値をだすことができる。
もちろん、波動関数内の項 と 変分パラメーター ( 調節できる ) の 数が多ければ多いほど、より低い計算値を得ることができる。
しかしもちろん 無限の項とパラメーターを含む関数を用いて計算することは 不可能である。
つまり、無限の項と変分パラメーターを含んだときの この変分法の真の最低値を知ることができないため、そもそも 実験値と比較することができない。
このページにあるように、正確なヘリウムの基底状態を得るのに ある変分パラメーターを 人為的に 固定してしまっている ( ← つまり変分法でなくなっている )。
つまりこれらの方法は 第一原理ではない。
(Fig.12) 教科書の ボーア模型に関する説明は 間違い。
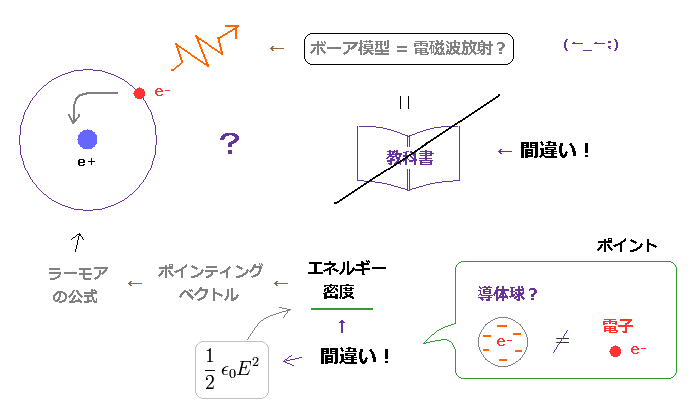
通常の教科書は 古典的なボーア軌道の 加速する電子 は エネルギー放射して 核に落ちて行くと くどいくらいに 述べている。ここ や ここ 参照。
残念ながら これらの説明は 完全に誤りであり、一般の多くの人達が 通常の教科書や ウェブサイトによって 誤った考えを 安易に吹き込まれていると言える。このページも参照のこと。
この主張は ポインティングベクトル (= E × H ) を エネルギーの流れとして用いている。
この ポインティングベクトルは 真空における 電場、磁場のエネルギーの変化を表している。 このサイトも参照のこと。
この真空における電場エネルギー (= 1/2εE2 ) は 中心の 導体球 に マイナスもしくはプラスの微小電荷を 集めるのに必要な ポテンシャルエネルギーを意味している
(= Fig.13 左、 このサイトも参照のこと )。
(Fig.13) ボーア模型の加速する単一電子が電磁波放射? ← 一種のマインドコンロトール。
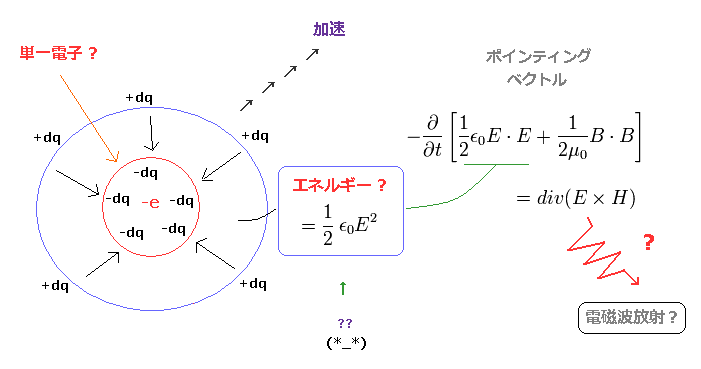
しかし 単一電子は それより 小さな電荷の集まりではない ( 単一電子は 最小の電荷である )。
これはつまり 真空の電場エネルギーというのは 単一電子においては エネルギーを 意味していないことになる。
すなわち ポインティングベクトルは 単一電子の場合は エネルギーの流れではないため、単なる円運動だけで エネルギーを失うことはないということになる。
この当たり前のように教科書で見かける間違った説明は ボーア模型に対する 一種のマインドコントロールとして作用していると言える。 困ったものである。
2つ以上の電荷が 関わっているときのみ、電磁波放射が可能と言える。
(Fig.14) 複雑なシュレディンガー方程式 + 行列式は 分子などで 使い物にならない。
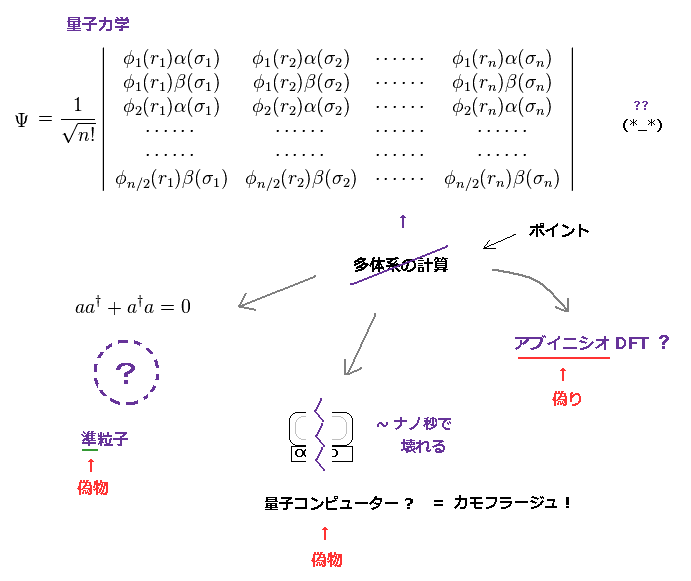
例えば、単純なヘリウム原子でさえ 電子が 互いに避け合うのに 量子力学では 3000 項以上もの項 ( ← 非現実的 ) を必要とする。 このサイト参照のこと。
つまり 現在の量子力学では 大きな分子などを 扱うこと自体が不可能なのである。
実際に 生物学などの 応用分野では 役に立たない量子化学は まったく姿形を見せない。
ある 非常に興味深い論文 (p.5- ) には 第一原理 (アブイニシオ) の量子化学計算は 実際は 第一原理ではなく 非常に多くの実験的に得られた経験的なパラメーターに依存している とある。
つまり 第一原理・密度汎関数法 ( DFT )
という呼び名は 完全に誤解を与えるもの以外何ものでもない。
これら 架空の準粒子、"偽の" アブイニシオ DFT、カモフラージュの量子コンピューターは すべて 量子力学の不都合な真実を 隠すために導入されたと言っていい。
このまったく使い物にならない量子化学のみに囲まれた厳しい状況においては、物理学者達が出来ることは、架空の準粒子 をこしらえることだけである。一覧も参照のこと。
また量子力学の不用性を隠すために、カモフラージュのターゲットとして登場したのが 所謂 量子コンピューターである。
この量子状態を保てる時間は 長年の研究にも関わらず 未だに マイクロ秒 という非実在的なレベルにも関わらず、様々な論文やニュースサイトを騒がせる存在としてのみ生き続けている。
(Fig.15) "架空"の準粒子は 1000 年後も "架空" のままである。
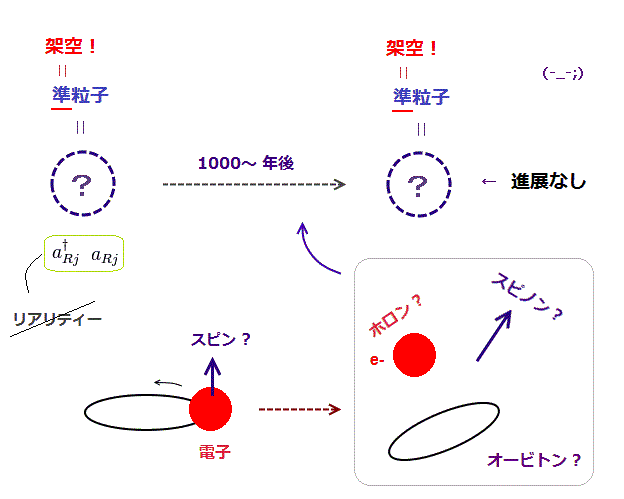
ネイチャー 科学誌 (
英サイト ) によれば、基本的な素粒子である電子が 何と 3つの成分に分離できたらしい。
3つの成分とは "スピノン" (= スピン ! )、ホロン (= 電荷 ! )、オービトン (= 軌道運動 ! ) のことらしい。 このサイトも参照のこと。
もちろん、これらの成分は 架空 (= 非実在 ) の準粒子 である。
つまり これらの準粒子は 物質の外では 独立した粒子として存在できないということである。 ここ や ここ も参照のこと。
ご覧の通り、現在の物性物理学は 物理の根本的なメカニズムの解明を避けて、 架空の準粒子をこしらえることだけに集中しているのである。 一覧 や 準電子 も参照のこと。
わざわざ架空の準粒子をこしらえるということは、物理学者達は 今後もずっと、これら準粒子をリアルな粒子で置き換えて説明する意志がまったくないことを示している。
要するに これら量子力学的な概念によって 現在の物性物理学 ( と言うことは その上の応用分野すべて ) の科学的進展が ストップしていることになる。
(Fig.16) 光子1つの大きさや形は? ← "黙れ !" ← 科学でない。

ある海外のインターネットの掲示板 ( ここ や ここ ) では、学生と思しき質問者が 基礎的な物理の質問をしている。
例えば、 " 光子に 形 や大きさがあるのか? " や " 電荷 の本当のメカニズムとは ? " などである。
なぜなら 現在の量子力学は これら非常に重要かつ根本的な質問を 完全に 避けまくっているからである。
案の定、この掲示板の mentor (= モデレーター ) は 光子や電子が何なのか答えることを避けて、 ややこしい 量子電磁力学 (= QED ) に逃げ込む姿勢をとっている。あまりしつこく聞くと コメント自体が削除される始末である。
場の量子論 や QED は 抽象的な 生成 (= a† ) 消滅 (= a ) 演算子 だけを提示するだけで、光子の具体的な描像に関しては まったく教えてくれない。
電荷に関しても、QED は 古典電磁気学と変わらず 単に 記号 "e" を示すだけで 根本的なメカニズムに関しては 何も答えてくれない。
これらの質問は 単なる氷山の一角にすぎず、現在の量子力学をベースとした物理学界が 結果として 好奇心旺盛な質問好きの学生達を 物理界から排除していることになる。
ということは 恐ろしいことに あなた方が 例え物理とは別の応用分野 (生物など) へ逃げ込んでも 根本的な機構が分からないままなので 進歩が止まっている悪影響を受けることに変わりはないのである。
(Fig.17) 光子は 波か粒子か? → 明確な回答を避ける → 永遠に未解決。
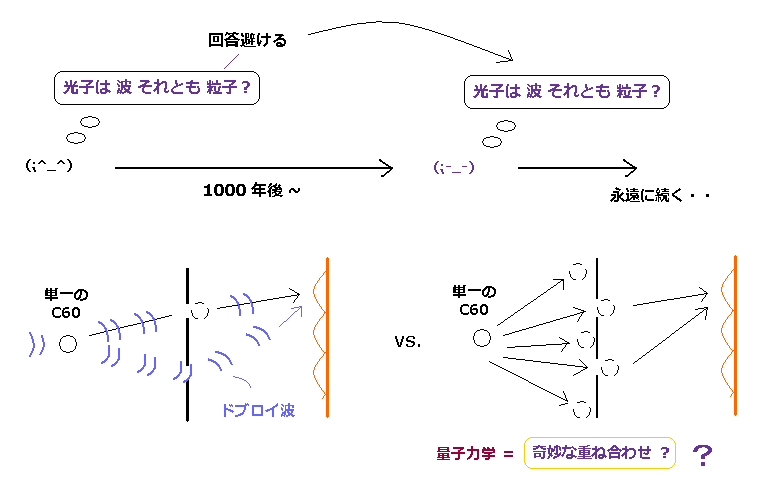
このサイト や Scientific american などを見ると分かるが、21世紀の今になっても 私達は 単純な2重スリット実験や "光は波か粒子か?" という 基本的な質問から永久に脱却できないでいる。
ということは、非実在的な量子力学を信奉している限り、 今から1000年後でさえも、"光は波か粒子か?" という質問 (+ 終わりのない解釈問題 ) を 現在と同じように 私達は 延々と ネットや論文などで 繰り返していることになってしまう。 恐ろしいことである。
基本的に このページに示したように、光子を扱うすべての実験は 光の 波動的な性質 (= 干渉、位相、偏光 ) に依存していると言っていい。
実際、 このサイト (= 最初のほう ) に載っているように、ノーベル賞受賞者である ラムシフトの ラムでさえ、"光子という粒子は存在しない" と断言しているくらいである。
(Fig.18) スピンホール、ベリー位相、トポロジカル絶縁体 はすべて 量子コンピューター !?
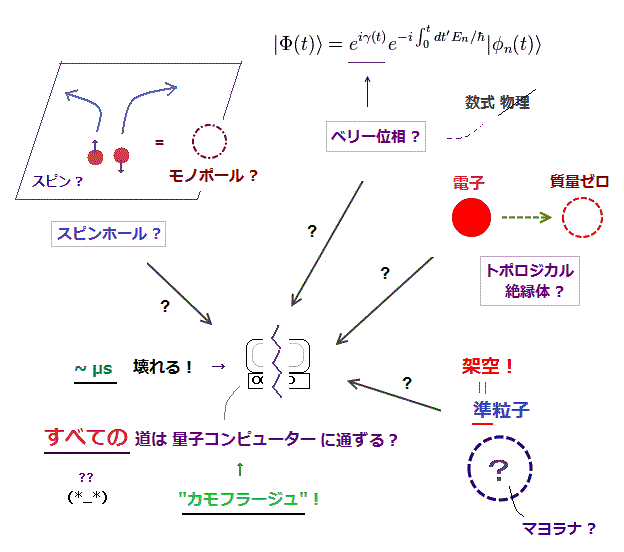
私達は よく "量子コンピュータ実現に向け 大きな一歩" というフレーズを 様々なニュースサイトや論文などで見かけるが、量子コンピュータの実験自体は 実質的に まったく進展していないのが実情である。
2013 年の時点で、量子コンピューターはたった数個の不安定な トラップされた イオン もしくは 超伝導ビットという有様であり、もちろん コンピューターと呼べるだけの姿形は どこにもない。
さらに それらの 平均して動く ( コヒーレント ) 時間と言うのは 今だに
マイクロ秒 という 非実用的なレベルにすぎない。
現在の量子力学は この明らかに非実用的 (← 永遠に ) な量子コンピューターを "架空" のターゲットとして持ち上げて あちこちで乱用している始末である。
つまり すべての道 (= スピンホール、 マヨラナ準粒子、 トポロジカル絶縁体、 ベリー位相 ) は 架空のターゲット 量子コンピューターに通ずるという具合である。
非常に弱いスピンホール効果は 今のところ まったく役に立たない。 この論文 (p.10) 参照のこと。
また 彼らは スピンそのものを観測したわけでなく、反射した光の変化で そう推定しているにすぎない。
また、 架空のモノポールを 式の形が"似ている" という理由だけで スピンホール効果の原理説明に適用した。 ここも参照のこと。
質量ゼロのディラック粒子は 光速度より はるかに遅く、明らかに 相対論と矛盾した存在である。
現在の物理は ベリー位相とはいったい本質的に何なのかという質問から目をそらし、 抽象的な 数式上の概念のみに 留まっている状況である。
(Fig.19) フラッシュメモリーでは 電荷は "古典電磁気学" に従って動く。
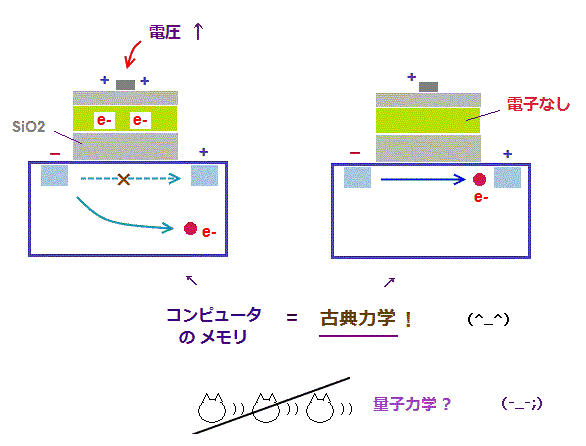
よく 量子力学のおかげで スマートフォン や 半導体メモリーなどの 最先端の技術が利用できるという話を聞くが、はっきり言ってこれは真実ではない。
実際、アップルの創業者、 スティーブ・ジョブズ は 大学を 中退したにも関わらず、ほぼ独力で コンピュータ事業を成功させた。
この成功例が教えてくれるのは 大学で習う 量子力学なんてものが 実社会には 何の役に立たっていないということである。
例えば、フラッシュメモリ などは 完全に 古典的な電磁気学 ( 非現実的な量子力学ではなく ) によって作動している。
しかし 多くの人々が 様々なマスメディアの影響で 量子力学が 役に立つテクノロジーだと 間違った情報を 信じこまされていると言える。
上部のゲートの電圧の高さに応じて、電子が中間部分に引き寄せられるかが決まり、これが コンピューターの"ビット" ( 0 もしくは 1 ) を表す。
この中間層の電子の量で、クーロン反発力が異なるため、続く電子が 右端のターゲットのゲートに入るかどうかが決まることになる。
よく物理学者達は 量子力学のおかげで 電子が SiO2 の層をトンネル効果で すり抜けると主張しているが、この絶縁体層は 電子を通すためには 非常に薄く (= ナノメートル ) なければ意味がない。
つまり 量子トンネル効果は 幽霊みたいな超常現象のようなものではなく 熱や 電子の非特異的な振動などによって生じる 現実的な現象である。
(Fig.20) 不確定性原理 → 場所と速度が同時に定められない !
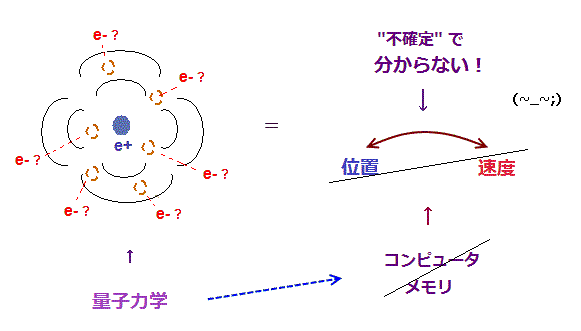
量子力学の不確定性原理によれば、各粒子の 位置と運動量 (= 速度 ) を 同時に 定めることができない。
常識的に考えて この物理の基本的性質が不確定な状況で 各粒子の動きを予測できるわけがないことは明らかである。
例えば日常のマクロの世界においてさえ、ある物を動かしたり、その運動を予測するには 当たり前の話だが その物体の位置と速度の両方の情報は必須である。
ましてや 目に見えない量子のミクロの世界で こんな不確定な状況では、 各粒子の動きの予測 や 制御など 何もできっこないのは当たり前の話である。
実際、Fig.19 のメモリにおいても、各電子は 電位の強さに応じて 指定された場所に移動し ( これがビットを表す )、もちろん その加速度 や 速度は 電位の場所や強さで細かく制御される。
この非常に小さな機械の内部で 場所と速度の情報がない曖昧な状況では どう転んでも 粒子制御の計画やら予測などは 不可能である。
つまり "量子力学のおかげ" でという 当たり前のように聞く誤ったフレーズは 一種のマインドコントロールとして 私達を惑わしていることになる。
(Fig.21) 光子 A が 偏光板 "a" を通過した瞬間に 光子 B の偏光が A のを模倣した ?
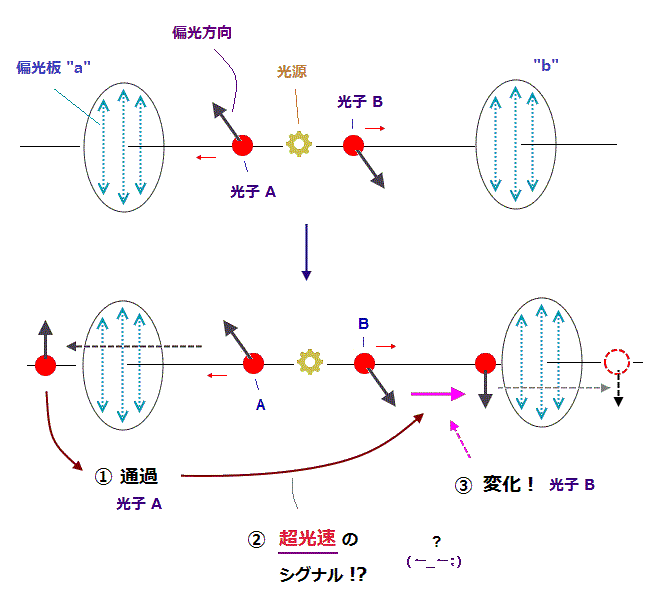
量子もつれによれば、光子 A が 偏光板 "a" を 通過した瞬間に 光子 B の 偏光状態が 偏光板 "a" の向きに平行になるらしい。 B と "a" がどんなに離れていようがである。
"瞬間" ということは、この光子 A から B へのシグナルは超光速で伝達するということである。
結論から言えば、この 非現実的な解釈は 光子という粒子が実在するという 間違った"思い込み" によって生じたと言っていい。
光子を 古典的な 分離可能な電磁波と考えれば このファンタジックな量子もつれは 自然に説明可能である。 このページも参照のこと。
そもそも この特別な存在 ? であるフィルターを通ったかどうかで 遠く離れた光子の運命が決定するといった考え自体が 不自然極まりない。
実際、このサイトの最後のほうにあるように すべてのループホール (= 実験における欠陥 ) は 同時には防がれておらず、すなわち 公式見解においても 量子もつれを完全に証明したことにはなっていない。
光子のケースでのみ、超光速のリンクが示されたとしている ( 144 km もの距離を隔てる必要あり ) が、この場合は 検出効率自体が低すぎて、都合のいい光子のみ記録したと言われても反論できない (= 検出のループホール ).
原子-光子、 イオン-イオンの量子もつれ実験では、超光速のリンク自体 実験的に証明することが 不可能である。 このサイト (p.4) 参照のこと。
(Fig.22) 交換相関汎関数の項は不明なため、自由に選べる。
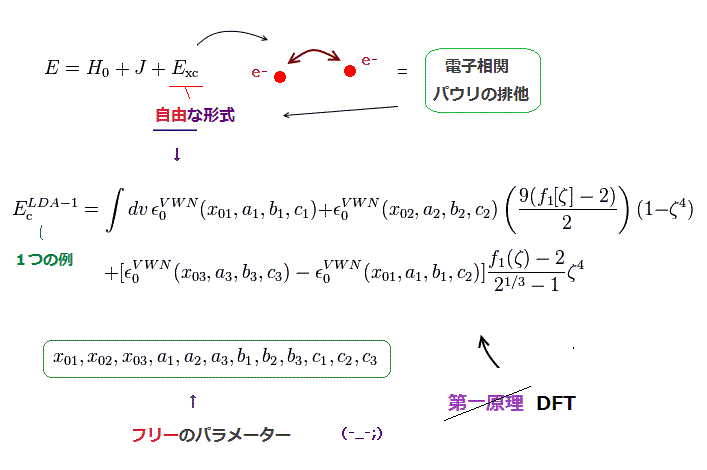
密度汎関数法は計算が簡便な方法とされているが、一番厄介な 電子相関やらパウリの排他原理を表す 交換相関汎関数部分の形が まったく未定であり、この部分に人為的な調節が入ることになる。 ここ、 ここ、ここ (p.11) など参照のこと。
ある状況でよく実験値を再現する汎関数は 別の分子などでは まったく再現性が悪いというように すべてに万能の 交換相関汎関数の形は 知られていない。 ここ (p.2) など参照のこと。
つまり、密度汎関数 ( DFT ) は 第一原理計算ではないのである。そう呼ばれることが多いが。
(Fig.23) 計算結果は 人為的に選んだ試行関数の形に依存する。

このページで述べたように、シュレーディンガー方程式は 多電子系では 解くことができない。
そのため 目的にあった試行関数の形を 人為的に選ぶことしかできない。
第一原理のハートリー・フォック法や 配置換相互作用法では まず最初に 基底関数セット (= 試行関数の形 ) を選ぶことから始まる。
ここ, ここ (p.3) 参照のこと。
選ぶということは これらの方法は 第一原理でもなんでもないことになる。ここ (p.6)、 など参照のこと。
また、調節パラメーターは 基本的に計算の間は 固定して動かさないため、DFT も含めたこれらの量子化学計算は 理論のみから 正確な実験値を 言い当てるといった類のものではないのである。
試行関数の形式やら、その中のパラメーター、基底関数の種類、数などは 目的の原子、分子に応じて 自由に選ぶため、第一原理計算という名前は誤解を与える以外何ものでもない。
(Fig.24) 量子力学的な水素原子は不安定すぎて非現実的である。
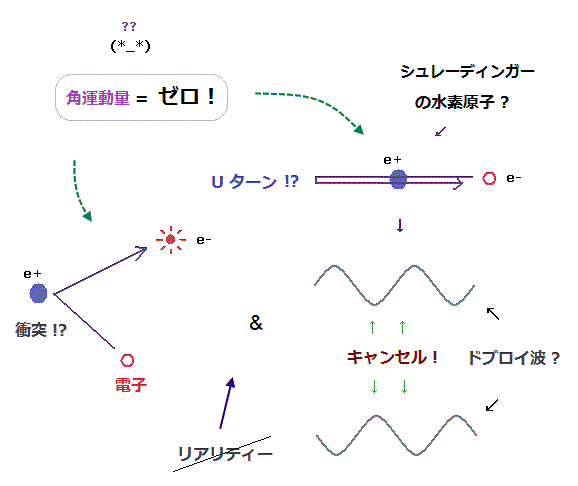
シュレーディンガーの水素原子では 軌道角運動量がゼロの基底状態 (= 1s ) などを含むため、 ボーム解釈で見られる 実在的な波という考え方が 不可能であることが容易に理解できる。
この状態では、電子が 原子核に常にぶつかったり、貫通したりすることになる。
すると、線上運動 (= 角運動量ゼロ ) のため この電子のドブロイ波内の 互いに逆位相の波同士が キャンセルし合って消えてしまうことになる。
( 1 × ドブロイ波長の波は ±の逆位相のペアで構成されている。 )
結果的に ドブロイ波の消失と共に、電子がはじき出されて不安定な状態になってしまう。
ダビッソン・ガーマーの干渉実験からこうなることが分かる。
さらに リアルな波のモデルは 両端の 負の 動径方向の運動エネルギーの状態を どう転んでも表現できない。
またもちろん、2重スリット実験や 原子構造をリアルなドブロイ波を用いて表そうとすると、相対論に反して 空間中に広がる エーテル様の物質の存在を認める必要が出てくる。
(Fig.25) 様々なメディア、大学、教科書などが 真のパラドックスをひたすら隠す !?
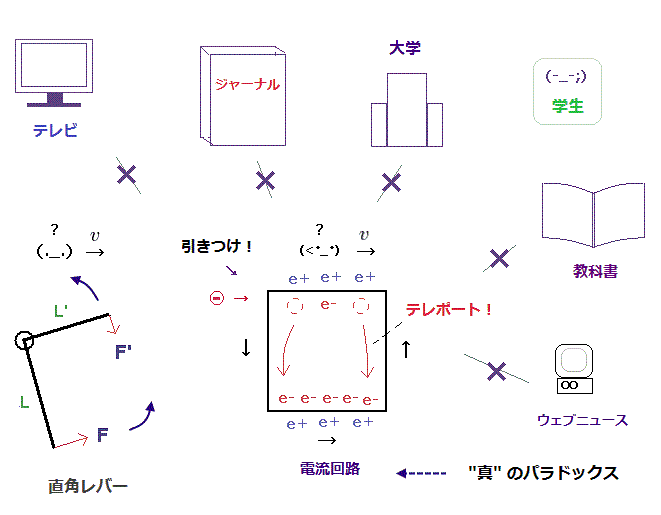
様々なメディアや教科書が 相対論は あらゆる検証試験を パスし、最も成功した理論の1つであると くどいぐらい主張しているが、残念ながら まったくの 大嘘である。
実際には ローレンツ力や直角レバーなどの致命的なパラドックスが存在し ( ここ、 ここ など参照 )、それらは 相対論が間違いであることを示している。
様々な サイトは これらのパラドックスが解決されたと主張しているが、架空の概念に頼るという理不尽な手段に頼らざるを得ない。
架空の回転中心 やら エネルギーの流れに頼らなければならないということは、これらのパラドックスは 現実的には解決されておらず、 相対論が 致命的な欠陥 (= 2方向の運動で露呈 ) を含有していることの証を示している。
特殊相対論は 様々な重要な理論 ( 場の理論、 QED、 ヒッグス ) の基礎を成している。
その圧倒的な影響力ゆえに 様々なメディアが これらの致命的なパラドックスを 一般の人々から隠し続けているのである ( 自信があるなら 堂々と紹介すればいいものを )。
実際、あなた方は これらの本当のパラドックスを教科書などで見たことは ほぼ皆無であろう。
超光速のニュートリノに対する辛辣な批判 ( ここ、ここ 参照 ) と、 BICEP2 のインフレーション発見の 誤報への甘さ を比較すれば、相対論者の 巨大すぎる既得権益が 科学的な事実を 捻じ曲げていることが 容易に理解できることだろう。
(Fig.26) 加速器内のすべての反応経路は "非実在の"仮想粒子を含まなければならない。
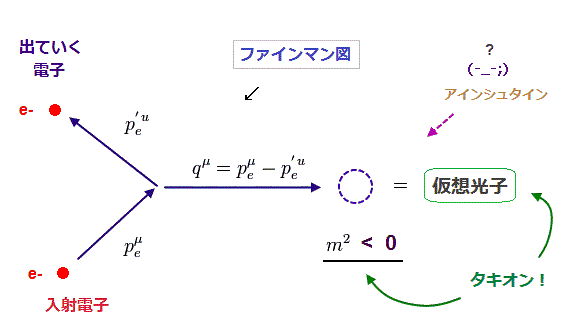
現在の標準模型は 非現実的な仮想粒子を その反応経路に含んでいなければならない。
これらの仮想粒子は 特殊相対論に従わない。
なんと その質量の2乗 m2 が マイナス になるのである。
ここ、 ここ (p.5-)、 ここ、ここ など参照のこと。
ほぼすべての教科書 ( ほとんどは仮想粒子自体触れてないが ) が このタキオン様の仮想粒子は 不確定性原理で解決できるから大丈夫と 簡単にコメントしているが、この論理は 明らかに 矛盾している。
例え、量子力学によって この 非現実的な仮想粒子を説明できたとしても、特殊相対論が破れているという事実に 何も変わりない。
また、反粒子の消滅でも 質量のある仮想光子 (= 本来質量ゼロ ) が生成されるのである。
要するに 標準模型、QED などの現在の相対論的な場の量子論は 根本的に自己矛盾を含んでおり、すなわち 間違っていることになる。
(Fig.27) ヒッグス、分数電荷クォーク、 W, Z ボソンは すべて "非実在"。
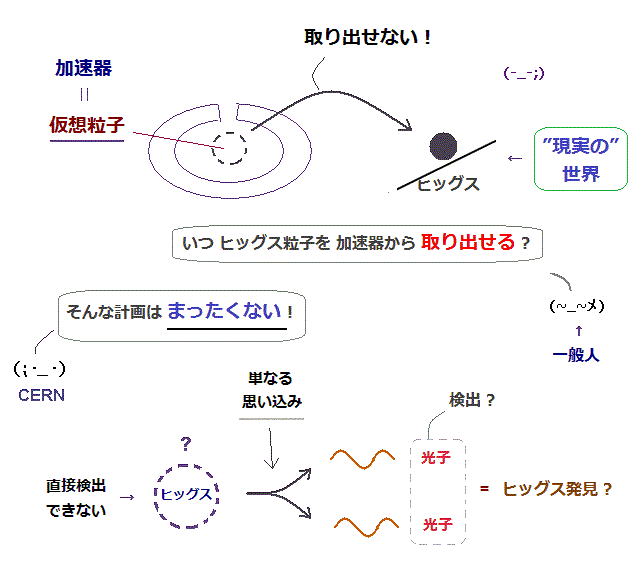
最近の興味深いニュースによれば、 ”ショッキング ! ヒッグス粒子は 発見されてなかった。 " というものがあった。ヒッグス粒子はすでに ノーベル賞を受賞しているのだが。
なぜなら そもそも ヒッグス粒子と断定するだけの実験的証拠は 公式上も 最初からないからである。 ここ や ここ, また BICEP2 ? 参照のこと。
このサイトにあるように ヒッグス自体は直接観測できず 2つの光子 (= 電磁波 ) のちょっとした過検出から ヒッグスだと推定しているにすぎない。
そもそも ヒッグスが これら2光子に分裂したと主張する実験的な証拠は何もない。
すなわち ヒッグス粒子は この強引な解釈による 何なる思い込みに過ぎないのである。
実際 もし ある予算調整をする役人が CERN の物理学者に 「 で、いつになったら 生成したヒッグス粒子を 加速器から取り出せるの? 」と質問したとしても、彼らは 「 ヒッグス粒子は 永遠に加速器から取り出せない。」 と答えるだけだろう。
なぜなら 加速器内でのみ生成された (← ? ) とされる非常に短時間の不安定な素粒子には リアリティーが何もないからである。
CERN の加速器 LHC は 私達の現実世界に広がっている (← ? ) とされる無数のヒッグス粒子の実在を証明してはいないのである。
実は 加速器内のカロリメーターは 各粒子の運動エネルギーや 光子の振動数を 測定できないのである ( 各電子を個別に異なる電場で止めることが この状況では不可能 )。 ここ、 ここ, ここ (p.5) など参照のこと。
つまり 分数電荷のクォークや 超対称性粒子の目安となる 消失エネルギーなどのデータにも 何の信頼性もないことが分かる。
(Fig.28) どうして ヒッグス、W ボソンは 通常の実験室で検出できない? ← リアルでないから。
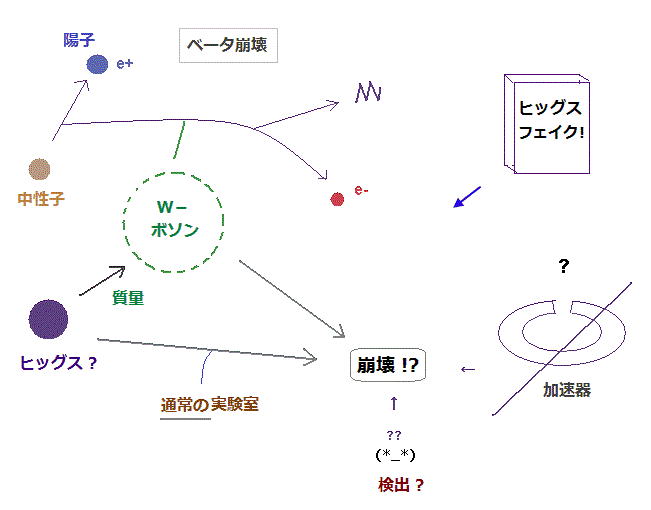
ノーベル賞発表直後に "Higgs fake" (= ヒッグス粒子は大嘘 ) という本まで出版された。
なぜなら ヒッグス粒子は 電子や陽子と異なり 実在性に 乏しいからである。
"火のないところに煙はたたず" である。
通常のベータ崩壊では、 W ボソン が 中性子が陽子に変化する過程で 生成されるとしている。
この時点で ヒッグス粒子が その場に 存在して、 W ボソンに 質量を与えなければならない。
もしそうだとすると、ヒッグスと W ボソン (= 陽子の 80倍 ! ) の両方とも 加速器外の通常の実験室のβ崩壊時に 観測されなければならない。
しかし 実際には、両者とも 通常のβ崩壊時には 観測できない。
これはつまり、加速器内で生成された ( ? ) とされる ヒッグスや W ボソンは 標準模型が主張する 無数のヒッグスや β崩壊時の W ボソンと 根本的に違う性質のものであることを示している。
つまり これらの曖昧な粒子には リアリティーが最初から ないことになる。
加速器内ですら、これら W ボソンは リアリティーのない仮想粒子である。
なぜなら エネルギー保存則を満たさないからである。
ヒッグス (= 125 GeV ) → 2 × W ボソン (= 80+80 = 160 GeV ! ) という反応は 常識的にはあり得ない現象である。
(Fig.29) 単なる変数変換で 結果が変わってしまった !? ← 意図的な間違い。
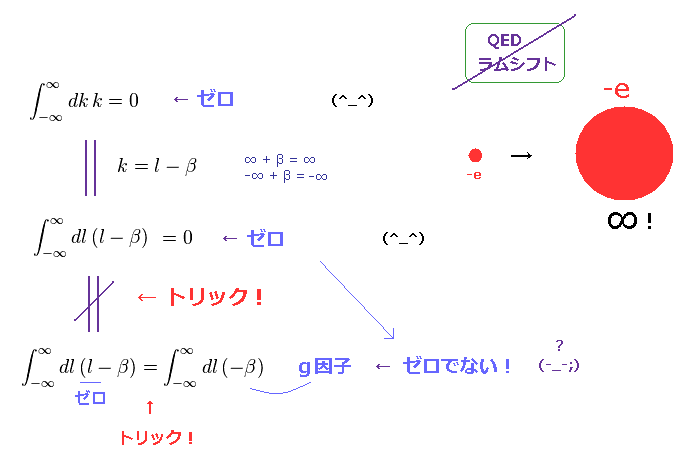
実は、量子電磁力学 (= QED ) による 異常磁気モーメント (= g因子 ) は 完全に
間違った 数学上のトリックに依存している。 このページを参照のこと。
Fig.15 では、"変数変換" ( k = l - β ) という 単なる計算手段にすぎないもので、 結果自体が 意図的に 変わってしまっている。あり得ない話である。
( これは 完全に 意図的な 計算ミス である。 )
ラムシフトも その一部分として この 間違った数学に基づく g因子の値を使用している
つまり QED ラムシフト も間違いということになる。
また 彼らは 実験結果に近づけるために 様々な意図的な効果を 付け足そうとしており、とてもじゃないが
自然な結果とは 言えない代物である。
もちろん、 特殊相対論 と ディラックの水素 が間違いならば、 QED ラムシフト は 他の解釈で 速やかに 置き換える必要がでてくる。
また、原子核を貫通することが 非常に小さな 超微細構造 に関与しているというのも不自然極まりない。
高次の補正になればなるほど ループが増え、自由に操作できる変数の種類が増加するため、より意図的な変更が可能になる。 つまり QED は人為的なトリックの宝庫と言える。
(Fig.30) ダークエネルギーの"密度" や 地球と太陽間の距離は 宇宙膨張でも 不変 !?

現在の物理学は 私達の目前の原子などの重要な現象 ( 例えば スピン ) などから 目を背け、はるかかなたの架空の 加速膨張宇宙などの研究に集中している傾向にある。
もし 宇宙膨張が加速しているとすると、その駆動力の物質 (= ダークエネルギー ? ) は、膨張によって まったく薄まらない ことになる。
そのため 物理学者達は はっきり言ってあり得ない "負の圧力" なるものをこしらえてしまった。
さらに どんなに高速で宇宙膨張しようとも 地球と太陽間の距離は まったく変化しないことになっている。 ここ や ここ (p.36) 参照のこと。
つまり この膨張宇宙という考え方は 非常に都合のいい 現実性を欠いた理論であることが理解される。
遠くからの光ほど 長い道中 コンプトン効果などで 自身のエネルギーを失い 波長が長くなる (= 赤方偏移 ) と考えるのが自然である。
(Fig.31) すべてのマイクロ波が 非常に長い期間 その一様性を保つことは不可能。
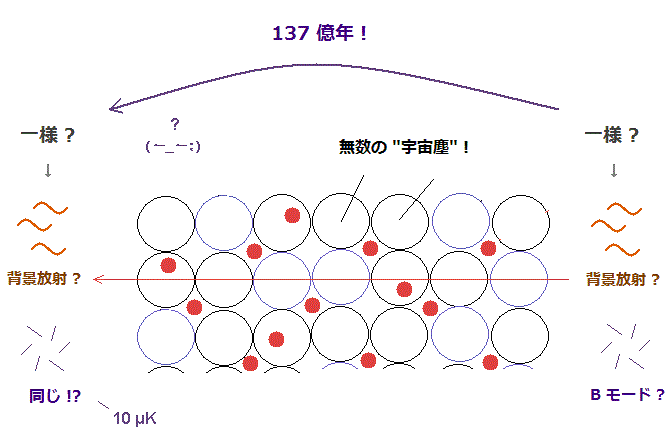
膨張宇宙の最も有力な証拠が 一様すぎる 宇宙マイクロ波背景放射 (= CMB ) であるとされる。
しかし 常識的に考えて この考えが非現実的であることが分かる。
彼らが言うのは 非常に小さいエリアの古代の光が 137 億年もかけて 宇宙膨張によって引き伸ばされて 一様な背景放射になったらしい。
しかし こんなに長い間に 常識的に 各光は 宇宙の様々な異なる塵などの散乱によって バラバラの波長 に変化してしまうことは明らかである。
つまり 背景放射の一様性を ビッグバン (= 膨張宇宙 ) で説明するには 余りにも無理であり、宇宙空間が何らかの 電磁波を伝える 一様なエーテル様物質で満たされていると考えるのが自然である。
実際、背景放射の若干の非等方性から 地球が 約 400 km/s の速度で 背景放射全体に対して運動していることが示されている。
さらに 元の狭い空間内の光の一様性に関しては 137億年前のビッグバン直後の 超光速のインフレーションによって 説明できるとされている。
しかしこのインフレーション ( 原子重力波 ) の証拠とされる 背景放射内のかすかな揺れは たったの 0.4 μK (= 0.4 × 10-6 K、 このサイト 参照 ) とされ、137 億年も長きの間に こんな弱すぎる光の偏光パターンが そのまま維持されるわけがないことは 明らかである。
多くの人為的な調節可能なパラメーターを持つインフレーション理論は 非常に 疑わしい と言わざるを得ない。 また 重力波も人為的な概念である。
(Fig.32) ブラックホールが 有限 (= 宇宙年齢 ) の時間内に形成されるのは不可能。
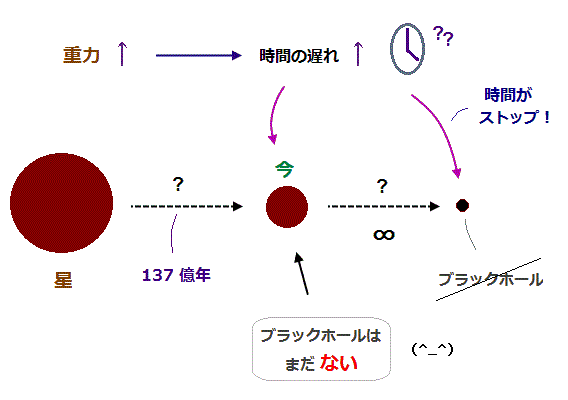
様々なジャーナルやメディアは ブラックホールの実在性を既成事実のように伝える傾向があるが、そもそも 光も含めてすべてを飲み込むブラックホールを直接観測することはできない。
彼らは ブラックホール周囲 (← ? ) から放射されたであろう X線 の観測から その存在を 推定しているだけにすぎない。
つまりブラックホールは 実験的に架空の存在であることが分かる。
実際 宇宙空間には 起源不明の 様々な x 線で溢れかえっている。 ここ、 ここ など参照のこと。
理論的にも ブラックホールが ”有限”の時間 (= 宇宙年齢 ) 内に形成されること自体 不可能である。
星が 重力崩壊 によって 収縮していき 密度が大きくなるにつれて 増大する重力によって 時間の遅れがエスカレートする。
ブラックホールを形成するには その表面である 地平線上の時間が ストップするくらい 収縮し 強力な重力を生み出す必要がある。
このサイトにあるように、外部 ( 例えば地球 ) から、このブラックホールの形成を観測したとしたら、重度の時間の遅れ (= というか 時間停止 ) のため 私達は ブラックホールが 有限の時間内に形成されるのを見ることは 絶対に不可能である。
(Fig.33) どのように "非実在的な"理論が 広まったのか?
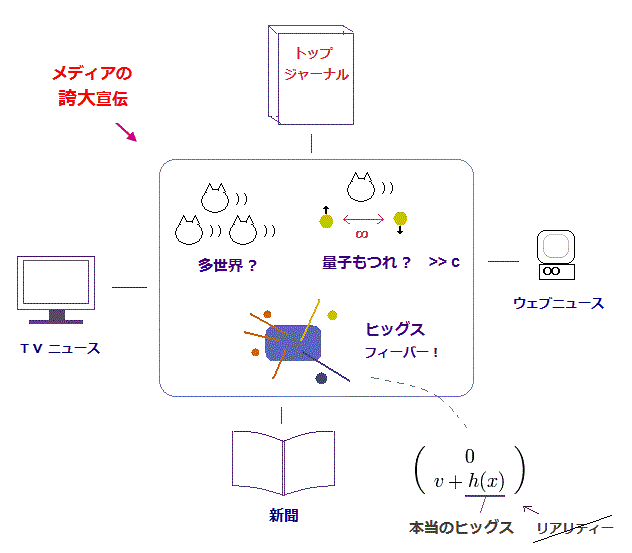
量子力学には リアリティーが存在しない。
それは 超光速の量子もつれや 平行宇宙 (= 多世界 ) などを認めている。
しかし 1920 年代に計算能力のあるコンピューターが存在しなかったがために 他の現実的な模型によって 様々な現象を説明できなかった。
根本的な理論に欠陥があることによる歪みは 物理の世界だけに留まらない。
トップジャーナル以外にも テレビ、新聞、ウェブニュースなどの様々なマスメディアが こぞって これらのファンタジーとしか言いようのない概念を 一般の人々に浸透させようと
報道し続けてしまった。
例えば オリジナルの ヒッグス粒子は 何の姿形もない 非常に抽象的な数式記号にすぎないのに、これらのメディアが 華やかな映像をこしらえて あたかも "神の粒子" が実在するかのごとく報道した。 ここ や ここ など参照のこと。
同じような傾向は 何年たっても実用化できない ( はっきり言って 研究者自体が実用化よりも論文投稿のことしか考えていない ) 架空の夢の技術、量子コンピューターに関しても見られる。 ここ、 ここ など参照のこと。
(Fig.34) 万物の理論 = 10 次元の超弦理論には 何の具体的なイメージもない。
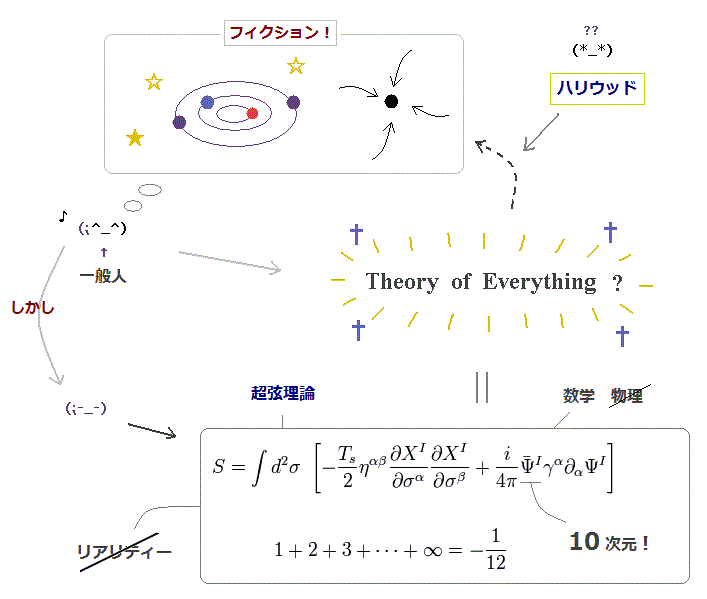
もちろん 100 年の物理理論の歪みの悪影響を 華やかな ハリウッド の世界が免れることができないのは 想像に難くない。
ニューヨークタイムズによれば、 映画 "
Theory of Everything " (= 万物の理論 ) がリリースされた。
これはつまり 物理と関係なかったハリウッドの世界まで 10 次元の 超弦理論 (= 現在唯一の万物の理論 ) を リアリティーがまったくないにも拘わらず、魅惑的な映像を持って一般人に広めようとしているわけである。
ハリウッドの役者達の演技や 映像技術は世界トップクラスのため、ここが本気で乗り出すと 何も知らない一般人を信じ込ますことは 非常に容易い。
実際の 超弦理論はというと ここ や ここ に示されたように 具体的な物理的な映像はいっさいない 単なる抽象的な数式の羅列なのである。
そればかりか、 超弦論は その理論の辻褄を合わせるのに 間違った数学 ( ここ、 ここ 参照 ) に頼っているのである。
メディアの伝えるイメージと 実際のもの (= 単なる数式の羅列 ) の間に これほどの 隔たり がある分野は 物理以外では まず考えられない。
(Fig.35) 2 × 1s 軌道の電子の角運動量は 共に L = 0 ← 不安定なヘリウム (= He )。
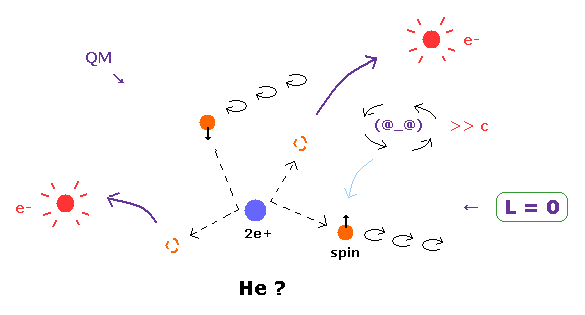
量子力学によれば、ヘリウムの基底状態の2つの電子は 角運動量がゼロ ( L = 0 ) の 1s 状態である。
もしそうだとすると、ヘリウムの2つの電子は たびたび 原子核に
衝突して そこから 跳ね返っては どこかに飛んで行っているのだろうか?
原子核や 他の電子との 無秩序な衝突を考慮すれば、2つの電子は 各々の軌道から 容易に 弾かれてしまうと考えられる。
さらに Fig.24 で述べた通り、1s 軌道のドブロイ波は 線状のため 逆位相同士が打ち消し合ってしまう。
つまり この 1s 軌道電子 2つで構成された 量子力学のヘリウム原子は 恐ろしく
不安定で 安定なヘリウムの実像とは 相当 かけ離れた ものになることが 容易に 理解される。
このページに示したように、リチウム原子における パウリの排他原理による 反発相互作用の大きさは 約 11 eV ほども大きい。
この非常に強い反発力は 弱すぎる スピン・スピン相互作用 (= 1.0 × 10-5 eV ) では 到底 説明することができない。
つまり 非現実的な "スピン" は 現実のヘリウムの安定性に関して まったくの 無意味な存在であることが分かる。
(Fig.36) スピン・スピン相互作用は たったの 10-6 eV、 これは 0.05 K で壊れてしまう。
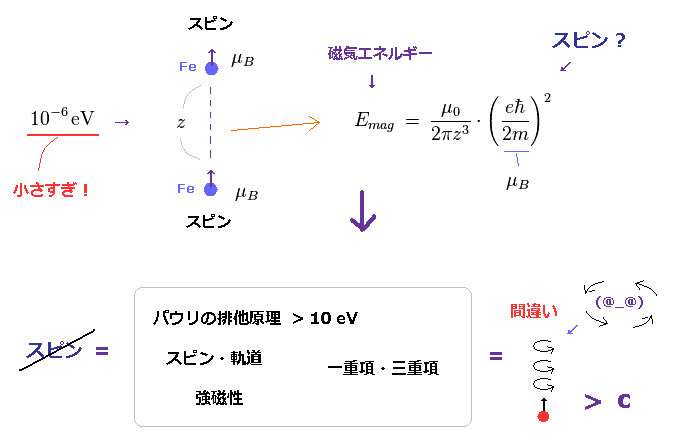
このページ や このサイト (p.7) にあるように、スピン・スピン磁気 (= ボーア磁子 ) 相互作用は 弱すぎて ( 0.05 K 温度換算で ) 実際の強磁性 ( 鉄は 1043 K まで強磁性を保持できる ) をまったく説明できない。
例えば、 Fe-Fe 間の平均的な距離は 約 2.8 Å (= 2.8 × 10-10 meter ) である。 このサイト (p.2) など。
このページ、 このサイト、 このサイト (p.6) などを用いれば、スピン・スピン磁気双極子作用というのが あまりにも 弱すぎることが分かる。 たったの 4.55 × 10-6 eV (= 0.05 K ) ほどである 。
パウリの排他原理も この弱すぎるスピン・スピン相互作用では まったく説明することが できない。
このサイトにあるように、 リチウムの3つの電子がすべて 1s 状態にあるとすると、そのエネルギー
(= 8.46 = -230 eV ) は 実験値 (= -203 eV ) よりも 低くなってしまう ( Hartree → eV 使って )。
この大きなエネルギー差 ( 27 eV = 230 - 203 eV ) は パウリの排他原理の反発力が ドブロイ波の干渉などの 他の強力な効果によることを示している。
さらに、ナトリウムの D 線 の分裂幅も スピン軌道相互作用で 説明するには 余りにも弱すぎる。
これら実験値と根本的に異なる概念 (= スピン ) にしがみつく限り、量子力学の "問わない" 姿勢が継続されて 真理の解明は 遅れることになる。
(Fig.37) ひも理論の失敗は 何を意味するのか?
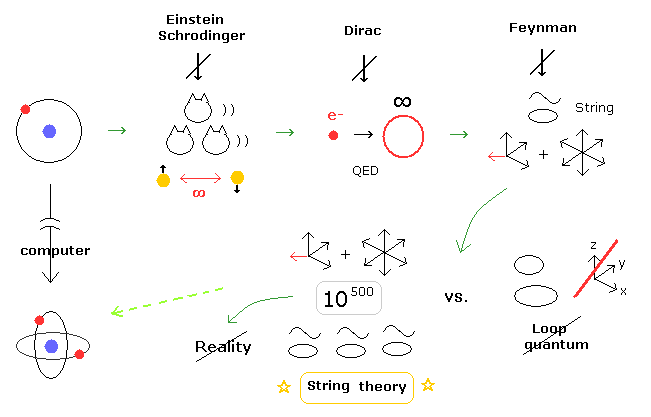
現在唯一の万物の理論である超弦論は 10 次元 を必要とし、かつ 10500 の異なった理論を内包し、実在性がないばかりか、何も予測することができない。
しかし ループ量子重力理論 などの 他の量子重力理論が 量子力学と一般相対論を統合することができないため ひも理論のみが生き残った。
ひも理論が誕生してから すでに 30年もの歳月が流れている。つまり 他の量子重力理論が 完全に排除されたという 十分な時間は経過したといっていい。
10次元なんて 現実的には あり得ないのに 超ひも理論のみが唯一の最終理論として残ってしまった。
奇妙な ひも理論の他にも 現在の量子論は 物理界の偉人達の承認を得られていないのである。
アインシュタイン や シュレディンガー 達は 非実在的な 量子力学に断固として反対した。
また ディラックは 無限大を人為的に除去する 量子電磁力学 (QED) に 非常に不満だった。
また ファインマンは 10 次元の超ひも理論を 嫌っていた。
このように次から次へと 物理界の大物達を巻き込んだトラブル続きの状況は 現在の物理理論の根幹に致命的な欠陥があることを示している。
辻褄のあった理論なら ( 例えばクーロン、マクスウェルの時代 ) ここまで"ぎくしゃく"することはなかったはずである。
(Fig.38) "ファンタジー"の量子力学は 本当のミクロ世界の解明を 阻害している。
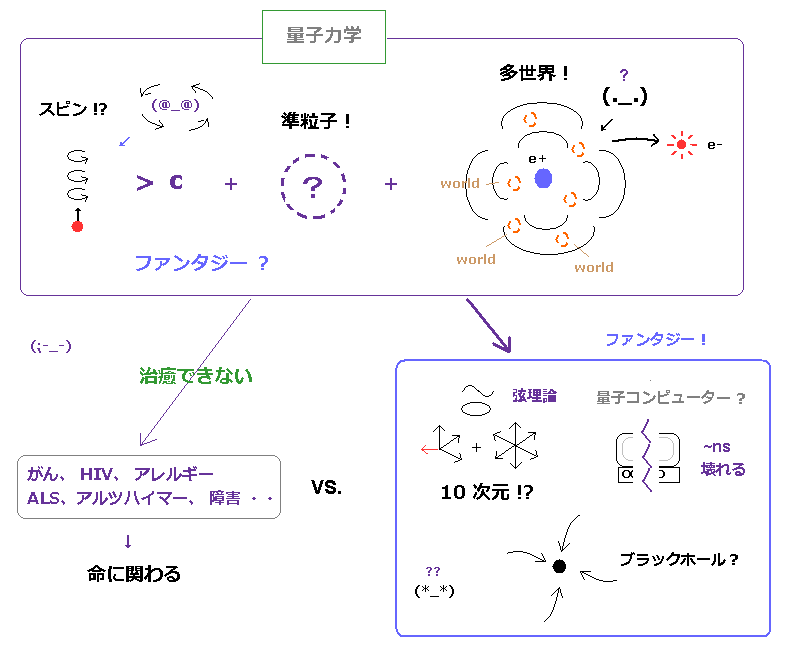
量子力学は 1920 年に導入されて以来、超光速の スピン や 多世界 (= シュレディンガーの猫 ) など 余りにも現実離れしていたため 様々な批判を招いた。
基本的に 量子力学は 非常に 曖昧な態度 をとり続け、ミクロの世界を明らかにすることを 意図的に避ける ことによって、生き残ってきたといっていい。
曖昧な波動関数が 多体粒子の具体的な ダイナミックな 動きを表現することが できなかったために、 仮想の準粒子 や 量子コンピューター (= わずか ナノ秒で壊れて非実用的 ) という 仮想の目標をこしらえて アピールしてきた節がある。
人間も含めた 地球上の生物の体は ミクロな微生物ですら 非常に高性能な ナノマシーンであり、今だに 私達の知識で 全然解明できていない部分が多い。
ミクロの世界を明らかにすることから逃げていれば、応用分野 ( 医療など ) で、がん、HIV、ALS、重度のアレルギー、認知症 などの 深刻な病気を 根本的に治療することが 永遠に "できない" ということになる。
(Fig.39) ダビッソン・ガーマーの実験は 電子がドブロイ波であることを示した。
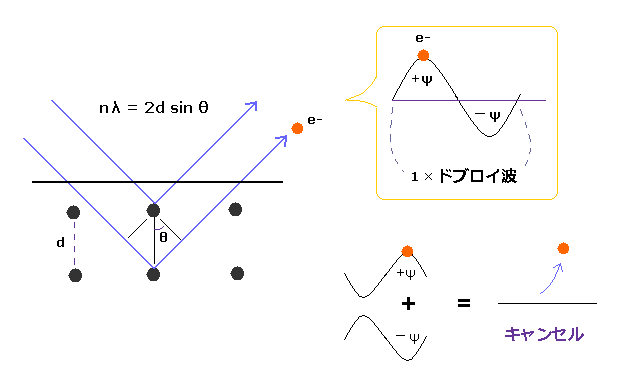
ダビッソン・ガーマー の実験では、電子を 電場によって加速し、それを ニッケル結晶で反射させた。
電子のドブロイ波長 は 単一電子の干渉パターンから得られるが、これと 電場の強さから計算したものと一致した。
この実験は 単一電子が ドブロイ波という 波動的性質 をもち、そこでは 互いに逆位相の電子波 ( ±ψ ) が キャンセルしあって 電子を追い出している (Fig.39)。
(Fig.40) ドブロイ波の両端が合う。
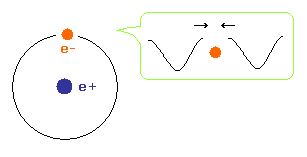
ドブロイ波が打ち消しあわないために、水素原子の電子波の両端の位相は ちょうどぴったりあう必要がある。
(Fig.41) 古いボーア模型の失敗。互いに逆位相のドブロイ波が打ち消し合う。
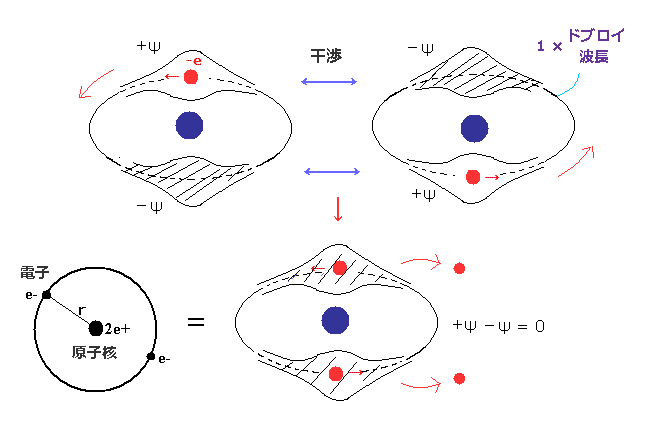
古いボーアのヘリウム (Fig.41) では、2つの電子は 同一円軌道上 (= 1ドブロイ波長 ) を 原子核を挟んで互いに正反対に位置しながら運動している。
Fig.39 と Fig.40 を考慮すると、古いボーア模型のヘリウムの2つの電子は 互いに逆位相のドブロイ波がキャンセルしあって、不安定になる。
実際に Fig.41 の 古いボーアのヘリウム模型は 間違ったヘリウムの基底状態のエネルギーを与える。
ヘリウムの円軌道において、遠心力をクーロン力に等しいとして、
(Fig.42) 古いボーア模型のヘリウム。
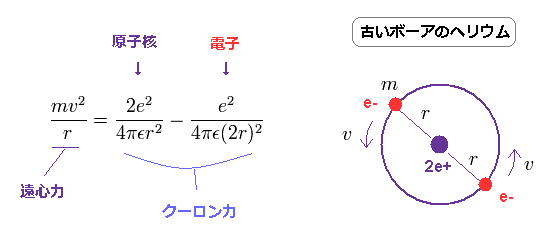
ここで r は 円軌道の半径 ( meter )、e は 電子の電荷である。
円軌道の軌道長は 電子のドブロイ波長の整数倍 (n) とする。
(Fig.43)
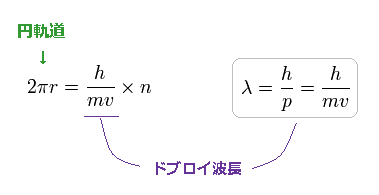
ここで h/mv は ドブロイ波長である。
ヘリウムの全エネルギー E は 2つの電子の運動エネルギーとクーロンポテンシャルエネルギーの和である。
(Fig.44) 古いボーア模型のヘリウムのエネルギー。
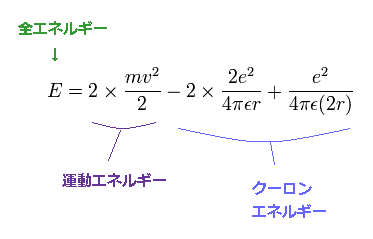
上の3つの式 (Fig.42-44) を解くと、基底状態のエネルギー (n=1) は - 83.33 eV となる。
この値は 実験値 -79.005 eV よりも 低くなってしまう。つまり間違いということになる。
(Fig.45) 古いボーア模型のヘリウムのエネルギー。

さらに 酸素などの他の原子が 古いボーアのヘリウムに近づくと、外場の力によって 容易に 2つのヘリウムの電子波がカオスの状態に乱れてしまう。
これは 実際のヘリウムの非常に強固な 安定性、閉殻性と一致しない。
(Fig.46) もう1つの電子が 同一軌道に入ると、全運動量は "2mv" に変化する。
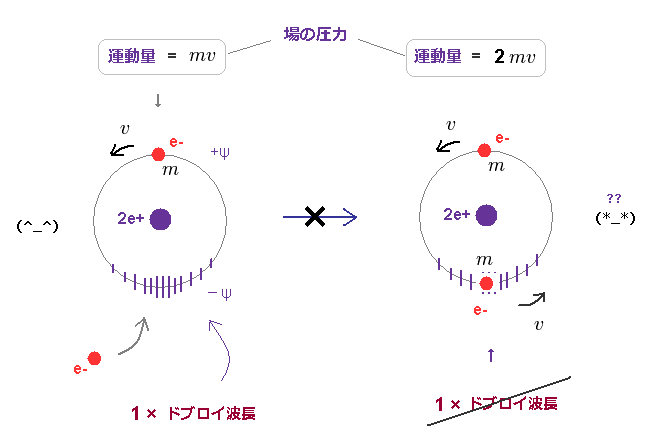
最初に、2つの電子が 同一軌道状の原子核の逆サイドで運動している 古いボーア模型のヘリウム について考える。
Fig.46 左図は ヘリウムイオン (= He+ ) で 電子の運動量 (= mv ) の圧力の下で 収縮 (= -ψ ) している。
その軌道長は ちょうど 1 × λ (= h/mv ) のときに 安定になる。
もう1つの電子が この同一軌道に入ると、周囲の場に与える圧力は 2倍 ( mv → 2mv ) になる。
なぜなら 軌道半径が変わらないとすると、この軌道上には トータルで "2mv" の運動量が含まれることになるからである。
場に加えれらる圧力が 2倍になると、その場は より収縮し、 ドブロイ波長を変化させる。
結果的に 元の関係式 ( 軌道長 = 1 × ドブロイ波長 ) が Fig.46 右 にあるように 保たれなくなってしまう。
ドブロイ波と電磁場の具体的な形 も参照のこと。
(Fig.47) 様々な古いボーア模型のヘリウム。
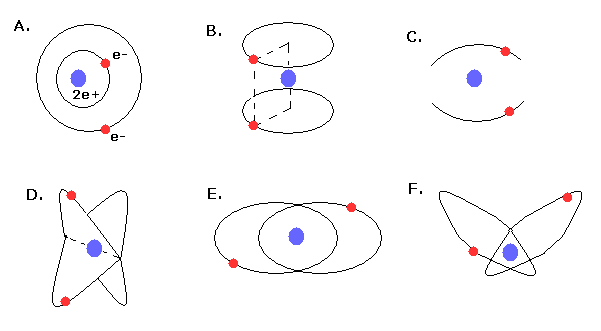
1910 - 1920 年代、 ランデ (= 外と内側の軌道、 Fig.47A ), ラングミュア (= 2つの平行軌道、 Fig.47B、 2つの線状の振動する軌道、 Fig.47C)、クラマース (= 120 度で交わる軌道、 Fig.47D )、ハイセンベルク (= 同一平面、傾いた面、 Fig.47E,F ) 等は より良いヘリウム模型を得ようと目指していた。
しかし どのヘリウム模型も 正確な基底状態のエネルギー、安定性、閉殻性を説明することができなかった。このページ参照のこと。
なぜなら 当時は 3体問題であるヘリウム原子を計算するためのコンピューターがなかったからである。
(Fig.48) 量子力学のヘリウム。
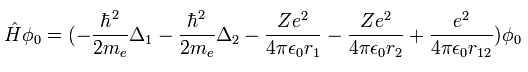
Z=2 のとき、 Fig.49 は ヘリウムのハミルトニアンを意味する ( Δ = ∇2 )。
ヘリウム原子の基底状態のエネルギーの正確な値を得ようとするとき、次のような 変分関数の 千以上もの項 を使用しなければならない。
(Fig.49) 量子力学のヘリウム。
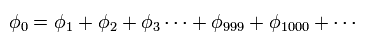
もちろん、これら単なる数式の羅列から ヘリウムの実際の形を思い浮かべることは不可能である。
この変分法の最新結果は -79.015 eV [9] であり、これは実験値 -79.0051 eV と少し異なる。
一方で、新しいボーアのヘリウム原子模型では 後の章で説明するが、-79.0035 eV という より正確な値を得ることに成功した。
( 79.0035 eV と 79.0051 eV のわずかな差は いわゆる "相対論的"効果であり、この値は極めて妥当である。 このページも参照のこと。)
(Fig.50) 量子力学のヘリウムは 確率密度すら示せない。
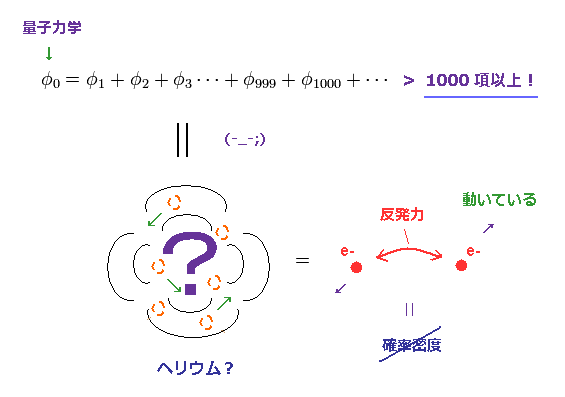
単純な水素原子と異なり、ヘリウムの2つの電子は 反発力のため 互いに避け合っている (= 動いている )。
そのため ヘリウムに関しては 量子力学は 定常な確率密度すら 示すことができない。
結果的に、何の粒子の情報も与えられない 1000 項以上にもわたる 量子力学のヘリウムの波動関数は まったくの無用の産物以外何者でもない。
他の原子、分子においても ( このページを参照のこと )、量子力学的手法は 具体的な電子状態を与えることができず、このことが ナノテクノロジーの発展の妨げになっている。
また 奇妙な多世界解釈が優勢になっている要因でもある。
(Fig.51) 安定で 互いに独立した ドブロイ波 (= 互いに垂直 )。
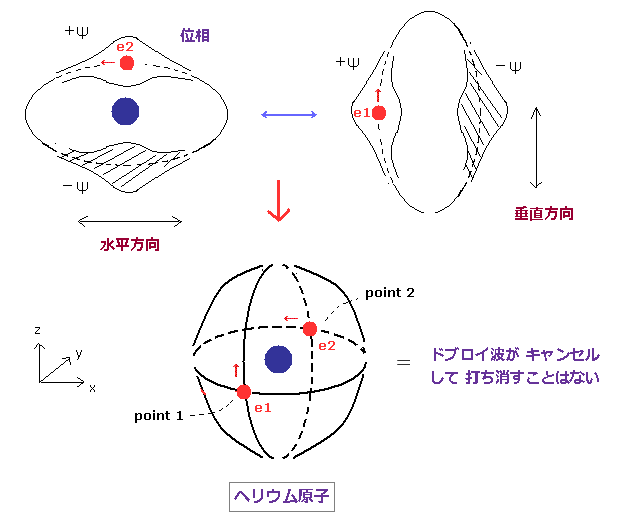
上のセクションにおける 消えるドブロイ波の問題を避けるために、Fig.51 の 新しい模型を考える。
Fig.51 に示すように、この新しいボーアのヘリウム模型は 互いに垂直な 2つの電子軌道によって成り立っている。
もし 2つの電子軌道が互いに垂直だと、それらの波の位相は 互いに 独立で 安定だからである。
もし 電子が クーロン反発力に完全に従って その軌道を倒して Fig.41 のようになったとすると、それらのドブロイ波の 逆位相どうしがキャンセルしあって 電子を追い出す。( もちろん これらの波の位相は カオス状態になり、不安定になる。)
このページも参照のこと。
(Fig.52) 古いボーアのヘリウム = 電子が弾かれる。 新しいヘリウムは安定。
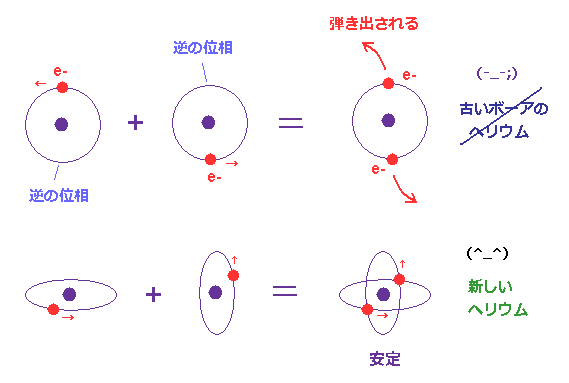
1 × ドブロイ波長においては、原子核を挟んだ反対側には 逆位相のドブロイ波が 含まれているため、もう一方の位相を 打ち消してしまう。
2つの電子のドブロイ波が ちょうど 互いに垂直になり ぎりぎりのところで 干渉による打ち消しを避けている。
つまり このヘリウム模型には 3番目の電子が 入っていくスペースは もう残っていないのである (= パウリの排他原理 も 正確に説明可能。)
(Fig.53) 新しいボーア模型のヘリウム (= A.) は 電気的に分極していない。
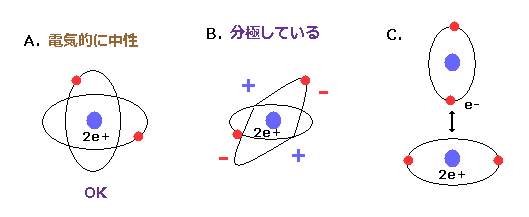
ご存じのとおり、ヘリウム原子は 他の原子と化合物を形成せず、かつ すべての原子の中で 最も低い 沸点を持つ。
残念ながら 量子力学的な電子スピンには 化合物の形成をストップさせるほどのパワーはない。
なぜなら スピンの磁気モーメントは クーロン力に比して 非常に弱いからである。
( スピン相互作用は 非常に弱い微細構造レベルである。)
つまり このヘリウムの非常に重要な性質を説明するものとして ドブロイ波しか残っていないのである。
Fig.53 左 に示すように、2つの電子軌道が互いに垂直だとすると、2e+ の原子核の周囲の空間は ちょうど電気的に中性になる。
( この状態だと 2つの負の電子が 2e+ の原子核の周囲に 垂直、水平方向に均等に分布している。)
また ドブロイ波の干渉による打ち消しのため、他の原子が近づいてきたとしても この状態は継続することになる。
他のヘリウム模型では、空間は 電気的に分極し、また 他の原子が近づくと それらのドブロイ波の位相は 容易に乱れて カオスの状態になる。
(Fig.54) 古いヘリウム、量子力学スピンは パウリの排他原理を説明できない。
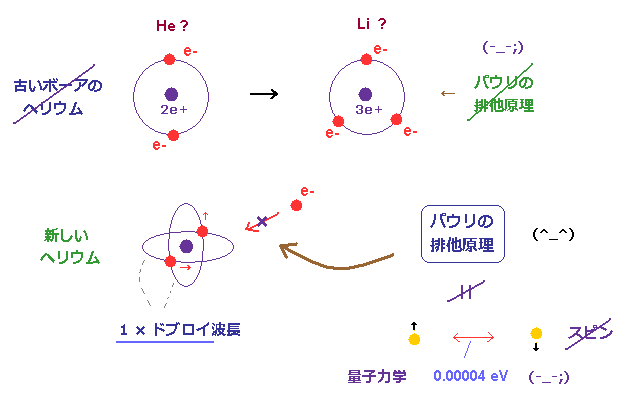
また、Fig.51 の状態には 3番目の電子が入っていくスペースは残っていない (= パウリの排他原理 )。
なぜなら 3番目の電子が 1 × ドブロイ波の軌道中へ入っていくと、それは 他の2つの両方の軌道と垂直になることができない。
一方で、古いボーア模型のヘリウムでは、Li の3番目の電子は この軌道中に入っていける。
なぜなら ドブロイ間の干渉による打ち消しに 頼っていないからである。
スピン・スピン磁気モーメントの相互作用は 弱すぎて パウリの排他原理を まったく説明できない。
例えば、水素の微細構造は たったの 0.000045 eV で、スピン・スピン結合は それよりも弱い。
結果的に パウリの排他原理を説明するのに ドブロイ波の干渉効果の機構しか残っていないのである。
(Fig.55) 2つの互いに垂直で対称的な軌道。
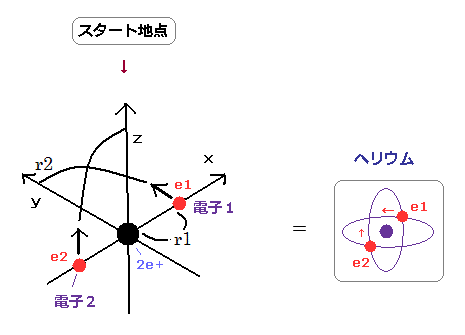
ドブロイ波同士は 波と山が異なる状態で重なると打ち消し合って消えてしまうため、それを回避するには 2つの電子軌道 ( ドブロイ波 ) が 互いに垂直に交わる必要がでてくる。
次に 簡単なコンピュータープログラムを使用して この新しいヘリウム模型の計算に移る。
Fig.55 は 軌道の 4分の1周を示している。
電子1は (r1, 0, 0) をスタートし、一方 電子2は (-r1, 0, 0) をスタートする。
(Fig.56) 2つの電子が 各軌道の 1/4 周を進んだ後。
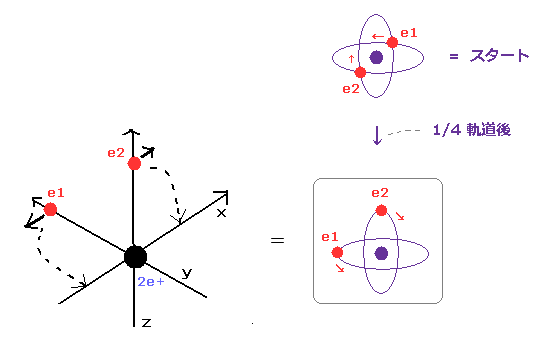
Fig.56 では、電子1は y 軌道を 垂直に横切り、電子2は z 軌道を横切っている。
2つの電子軌道が垂直に交わっているとき、Fig.55 と Fig.56 に示される運動パターンがもっとも ポテンシャルエネルギーが低い安定な状態である。
ここで ヘリウムの電子がどのように運動するかを 微小時間ごとに 2つの電子と原子核の間のクーロン力を計算して調べることにする。
JAVA ( version 1.5.0 )、 C言語、Python ( version 2.7 ) で書かれた コンピュータープログラム を次に示す。
サンプル JAVA プログラム。
サンプル C言語 プログラム。
サンプル Python プログラム。
Fig.55 と Fig.56 に示すように、ヘリウム原子核は 原点にある。
電子1は ( r1, 0, 0 ) を最初にスタートし、軌道を 1/4 周して ( 0, r2, 0 ) に進む。
その間、電子2は ( -r1, 0, 0, ) をスタートして ( 0, 0, r2 ) に進む。
meter と second は かなり大きな単位なので 次の新しい定義による単位を使用する。
(Fig.57) 時間と長さの新しい単位。
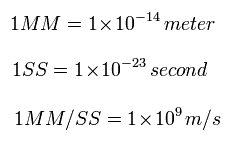
Fig.57 から、 加速度は、
(Fig.58)
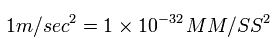
上のソースプログラムをそのままテキストエディタ(メモ帳など)にコピー and ペースト すれば、簡単にコンパイルと実行できる。
このサンプルプログラム ( 例えば、JAVA ) では、実行すると、次のようなメッセージが画面に表示される。
(Fig.59)

最初に 電子1 ( Fig.60 参照 ) の最初の x 座標 r1 = r ( MM 単位で ) を入力して "エンターキー" を押す。
Fig.59 では、"3060" を入力しており、これはつまり 電子1の スタート地点の x 座標が 3060 MM = 3060 × 10-14 meter であることを意味している。
電子2の x 座標は 自動的に -3060 MM になる。
次に ヘリウムの全エネルギーの絶対値 |E| を入力する。
Fig.59 では、"79.0" を入力して エンターキーを押したとき、ヘリウムの全エネルギーを -79.0 eV として計算する。
(Fig.60) "r" は 電子1の最初の x 座標。
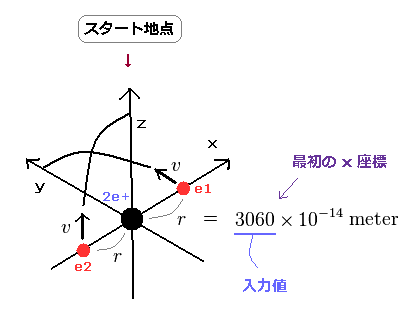
これら入力値から 電子1の 初期速度 ( 1 は y 方向、2 は z 方向 )を計算する。 Fig.60 の最初の状態での 全位置エネルギー (= V ) は、
(Fig.61) 最初の 全位置エネルギー V。

Fig.61 の右辺の最初の項は 電子と 2e+ の原子核間の位置エネルギーである。
2番目の項は 2つの電子間の反発位置エネルギーである。
(Fig.62) 最初の 速度 "v"。

2つの電子の 全運動エネルギーは 全エネルギー ( 例えば -79.0 eV ) − 位置エネルギー (= V ) で与えられる。
Fig.59 の入力値から 各電子の初期速度を出せる。
(Fig.63) 速度の単位の変更。
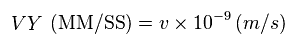
Fig.57 の新しい単位を用いて、このプログラムは 初期速度の単位を "m/s" から "MM/SS" に変更する。
なぜなら 1 SS (= 10-23 ) 秒ごとに 加速度などを計算するのに都合がいいからである。
(Fig.64) 2つの電子の位置。
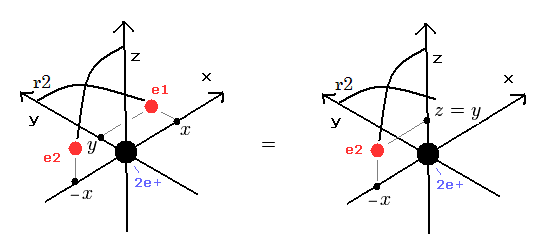
1 SS の時間間隔ごとに、2つの電子と原子核間のクーロン力を計算していく。
電子1が ( x, y, 0 ) にあるとき、 電子 2 は ( -x, 0, y ) にある。 ( Fig.55 と Fig.56 を参照のこと。)
つまり、電子1の 加速度の x 成分 ( m/sec2 ) は、
(Fig.65) 加速度の x 成分。
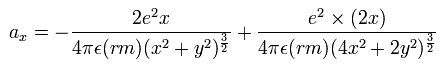
ここで 最初の項は 原子核と電子1の間のクーロン力、2番目の項は 2つの電子間のクーロン力である。
(Fig.66) 粒子間距離。
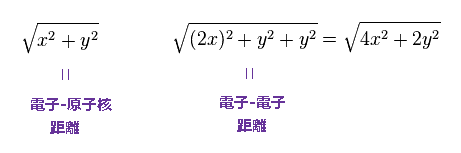
2つの電子の 対称的な位置関係より、電子1が ( x, y, 0 ) にあるとき、電子2は ( -x, 0, z ) にあり、 z = y である。
結果、電子1と原子核間の距離は Fig.66 の最初の式で与えられる。
2番目の式は 2つの電子間の距離である。
ヘリウム原子核 (= α粒子 ) の運動を考慮して、次の 換算質量 (= rm ) を 質量中心が原点にある場合を除いて使用することにする。
(Fig.67)
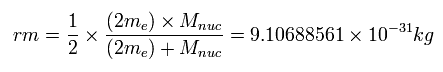
3体問題の換算質量も参照のこと。
同じように 加速度の y 成分 (m/sec2) は、
(Fig.68) 加速度の y 成分。
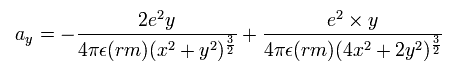
これらの計算値に基づいて、電子の速度ベクトルと位置を変えていく。
電子1は X-Y平面のみを動くとしているため z方向の加速度は考えていない。
もし、電子にはたらく力のすべての成分を考慮すると、電子の運動は Fig.41 ( 古いボーアのヘリウムを参照 ) に示すようになってしまう。
しかし、Fig.41 では、2つの電子が1つの1ド・ブロイ波長の 同一の円軌道におしこめられている。
そのため それらのドブロイ波が互いに打ち消しあってしまう。
(Fig.69) 各微小区間内の ドブロイ波。
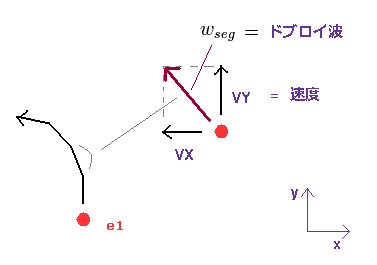
また、ここでは1 SS ごとに電子の速度からド・ブロイ波長 ( λ = h/mv ) を求めていく。
1 SS の間に電子が進む微小移動区間に含まれるド・ブロイ波 (1つの長さλ ) の数を次のように計算する(この合計が WN)。
(Fig.70)
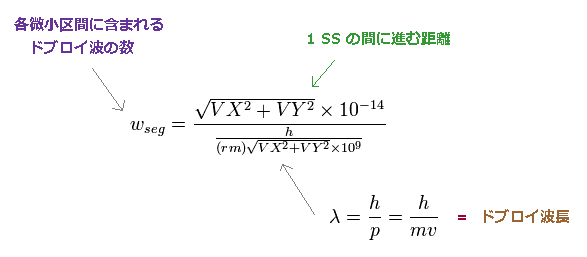
VX, VY は電子1の速度 (MM/SS) で、この式の分子は 1 SS に進む移動距離 (meter)、分母はド・ブロイ波の波長の長さ (meter) である。
ここでは、電子軌道をこのように100 万以上の微小区間 (1 SSごとに電子が進む微小移動距離)に分離している。
電子がその軌道の 1/4 進んで、その x 座標がゼロになったとき ( Fig.71 )、このプログラムはその地点での電子1の速度の y 成分をチェックする ( この y 速度成分 を last VY とする)。
もし、last VY がゼロの時、2つの電子は Fig.55 と Fig.56 に示す軌道を定期的に周回することになる。
(Fig.71) 計算結果。

1/4 周した後、このプログラムは画面上に r1, VY, preVY ( 1SS 前のVY ), (mid)WN ( 軌道の1/4 に含まれるド・ブロイ波の総数)を表示する。
(Fig.72) 全エネルギーが -79.00 eV のとき、1/4 軌道のドブロイ波は 0.25006
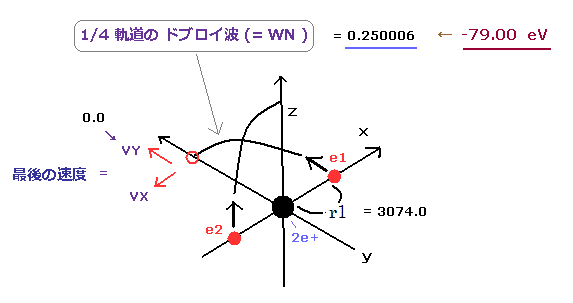
このプログラムでは r1 が入力値 ( 3060 )から r1+100 (= 3160 ) までのときの各計算結果を表示させる。
Fig.71 にあるように、r1 が 3074 MM のとき、電子1の最後の速度 VY は 最もゼロに近くなる ( VY = 0.000000 )。
つまり、初期 x 座標 r1 が 3074 × 10-14 meter のとき、これらの電子軌道は ちょうど対称的で 安定になる。
このとき、1/4 軌道に含まれるドブロイ波の数は 0.250006 になる。
よって 1軌道には 0.250006 × 4 = 1.000024 のドブロイ波が 含まれていることになる (← 1.000000 でない )。
Table 1 にあるように、入力値が -79.0037 eV のとき、ドブロイ波は ちょうど 1.000000 になる。
Table 1 は last VY が最もゼロに近いときの結果である。
この結果は 新しいボーア模型のヘリウムの全エネルギーが -79.0037 eV であることを示している。
| E (eV) | r1 (MM) | WN | WN x 4 |
|---|---|---|---|
| -78.80 | 3082.0 | 0.250323 | 1.001292 |
| -79.00 | 3074.0 | 0.250006 | 1.000024 |
| -79.003 | 3074.0 | 0.250001 | 1.000004 |
| -79.0037 | 3074.0 | 0.250000 | 1.000000 |
| -79.005 | 3074.0 | 0.249998 | 0.999992 |
| -79.01 | 3074.0 | 0.249990 | 0.999960 |
| -79.20 | 3067.0 | 0.249690 | 0.998760 |
WN × 4 は 軌道1周に含まれる ド・ブロイ波の数の総数。
ヘリウムの基底状態のエネルギーの実験値は -79.005147 eV ( Nist, CRC ) である。
この結果は エネルギーに対する相対論的な補正値が -79.005147 - (-79.0037) = -0.001447 eV であることを示している。
ヘリウムイオン (He+) の基底状態のエネルギーの理論値は 換算質量を用いて ボーア模型や シュレディンガー方程式から得ることが可能である。
この値は -54.41531 eV である。
また He+ の基底状態のエネルギーの実験値は -54.41776 eV ( Nist ) である。
そのため、He+ イオンにおける エネルギーの相対論的な補正値は -54.41776-(-54.41531) = -0.00245 eV となる。
水素原子 (H) の基底状態のエネルギーの理論値も 換算質量を用いて ボーア模型や シュレディンガー方程式から得ることが可能である。
この値は -13.5983 eV である。
また H の基底状態のエネルギーの実験値は -13.59844 eV (Nist) である。
そのため、H における エネルギーの相対論的な補正値は -13.59844-(-13.5983) = -0.00014 eV となる。
中性ヘリウムの電子速度は ヘリウムイオンよりも遅く、また 水素原子よりも速い。
そのため 中性ヘリウムにおける 相対論的な補正値は -0.00245 eV と -0.00014 eV の間になる必要がある。
上の計算結果は -0.001447 eV で 何とそれらのちょうど間にある。
コントロール群のプログラムとして 水素様原子 ( 水素原子、ヘリウムイオン ) のプログラムも下に示す。
上記のヘリウムと同じ計算方法をとっているので、一度試してほしい。
JAVA プログラム ( H、He+ )。
C言語 プログラム ( H, He+ )。
ここでは 新しい時間の単位 ( 1 SS = 1 × 10-23 second ) を用いて 1 SS ごとに各値を計算した。
もし この 1 SS の定義を変更させると、軌道長が ちょうど 1ドブロイ波長になるときの 全エネルギー (E) の計算結果は次のようになる。
| 1 SS = ? sec | Result of E(eV) |
|---|---|
| 1 × 10-22 | -79.00540 |
| 1 × 10-23 | -79.00370 |
| 1 × 10-24 | -79.00355 |
| 1 × 10-25 | -79.00350 |
これはつまり、軌道が滑らかになるにつれて、計算値は -79.00350 eV に 収束することを意味している。
他の 1 SS の定義の プログラムを次に示す。
サンプル JAVA プログラム 1 SS = 1 × 10-25 sec, 計算時間が少しかかります。
古いサンプル JAVA プログラム 1 SS = 1 × 10-22 sec--計算が速い。結果と Eq 番号が少し異なっています。
標準のヘリウム模型はスピンアップとスピンダウンの2つの電子を持っている。
それで磁場を生じないことになっている。
しかし正確には2つの電子は離れているため磁場は等距離の地点を除くすべての空間で生じることになる。
もし、それを打ち消すため電子が動くと磁場が変動し、電磁場を放出して不安定になってしまう。
つまり自己矛盾を含んでいることになる。
(Fig.73) 水素とヘリウム原子。
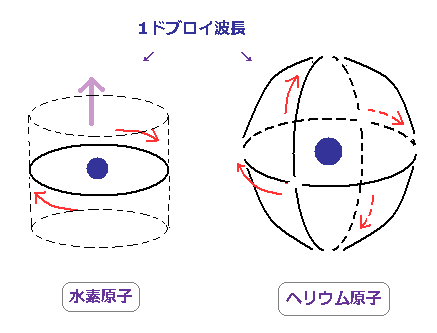
これらの軌道はすべて、ちょうど1ド・ブロイ波長である。
今回の新しいヘリウム模型では、2つの軌道は対称的で 互いに垂直に交わっており、それがヘリウム原子全体をすっぽり取り囲んでいる。
一方、水素原子は、軌道が1つしかないため、1つの方向が開放しているため、磁場が生じる。
これはヘリウムの高い安定性と閉殻性にちょうど一致した模型といえる。
(Fig.74) n × ドブロイ波長 → 何周後も安定。
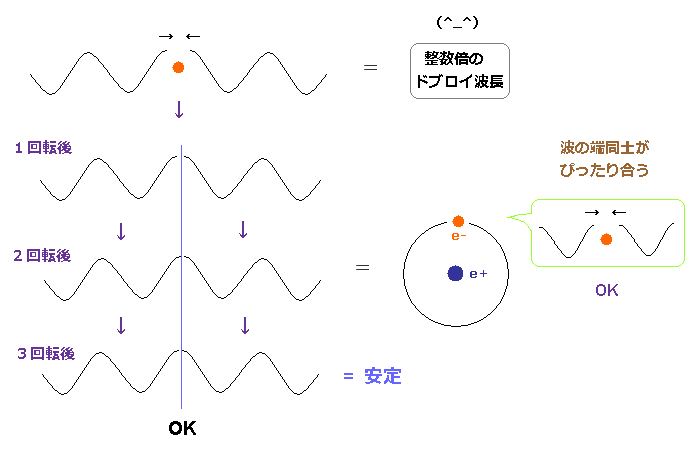
ご存じのとおり、水素のエネルギー準位は 量子化されている。なぜなら その軌道長は ドブロイ波長の整数倍 (= n ) だからである。
シュレディンガー方程式に関しても、このドブロイの関係式は 保たれている。
Fig.74 に示したように、軌道長が ちょうど n × ドブロイ波長のとき、その波の位相は どの地点においても 互いに フィットし合う。
つまり、任意の軌道運動後においても、これらドブロイ波は安定に その元の波形を 保つことができるわけである。
ドブロイ波の波形 (= 波長 ) は p = h/λ の関係式を介して 電子の運動量 (= p ) を表している。
つまり その波形を保つことは 電子の動きが 安定であることと等価である。
(Fig.75) ドブロイ波長の整数倍でない。 → 干渉によってキャンセルされる。
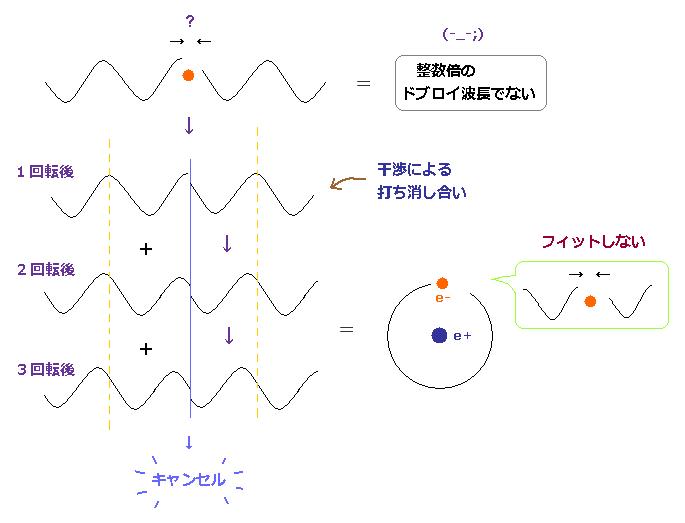
軌道長が ドブロイ波長の整数倍でないとき、それらの波の位相は スタート地点で 一致しなくなる。
このケースでは、電子が原子核の周りを 何周かする間に、同一の軌道の中に 異なった位相をもつ 多種類のドブロイ波が 重なり合ってしまい 干渉効果によって 互いを キャンセルしてしまう。
結果、電子の動きが不安定になって 原子状態を保てなくなる。
(Fig.76) ヘリウムの2つの軌道が 垂直でないとき・・
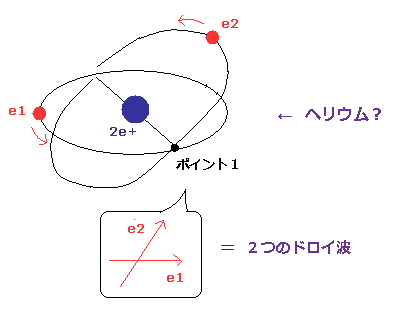
Fig.76 のヘリウムでは、2つの軌道は 完全には互いに垂直になることができない。
このケースでは、交差点 (= ポイント 1 ) のところで、2つの同じ向きのドブロイ波が 重なりあう。
すでに述べたように、ヘリウムの軌道は 1 × ドブロイ波長のため、これらの波の位相は 互いに逆位相どうしになる。
結果、それらの波の一部が 打ち消しあってしまう。
(Fig.77) 波がキャンセルされる → ドブロイ波の整数倍を保てない。
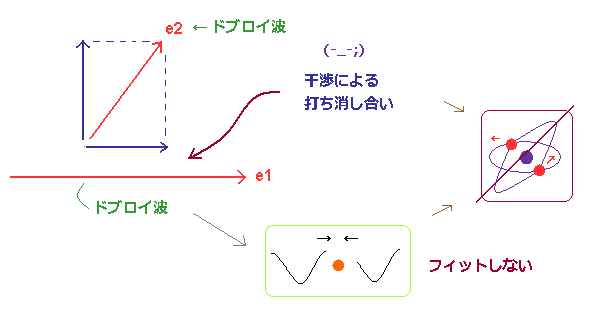
もし それらドブロイ波の一部が 逆位相の干渉のため 打ち消し合ってしまうと、厳密に ドブロイ波の整数倍が 保てなくなってしまう。
Fig.75 で述べたように、任意の軌道運動の後、多くの 異なった位相を含んだ波が重なり合って 互いを 打ち消し合ってしまうことになる。
このことが 安定なヘリウムの2つの軌道が 互いにちょうど垂直にならなければならない理由である。
驚くことに、この新しいボーアのヘリウムの原子構造は 他のすべての 2電子 もしくは 3電子原子(イオン)に適用できる。
| 原子 | r1 (MM) | WN x 4 | 同一円軌道 | 計算結果 (eV) | 実験結果 (eV) | 誤差 (eV) |
|---|---|---|---|---|---|---|
| He | 3074.0 | 1.000000 | -83.335 | -79.0037 | -79.0051 | 0.001 |
| Li+ | 1944.5 | 1.000000 | -205.78 | -198.984 | -198.093 | -0.89 |
| Be2+ | 1422.0 | 1.000000 | -382.66 | -373.470 | -371.615 | -1.85 |
| B3+ | 1121.0 | 1.000000 | -613.96 | -602.32 | -599.60 | -2.72 |
| C4+ | 925.0 | 1.000000 | -899.67 | -885.6 | -882.1 | -3.50 |
| N5+ | 788.0 | 1.000000 | -1239.8 | -1223.3 | -1219.1 | -4.20 |
| O6+ | 685.3 | 1.000000 | -1634.38 | -1615.44 | -1610.70 | -4.74 |
| F7+ | 607.3 | 1.000000 | -2083.3 | -2062.0 | -2057.0 | -5.00 |
| Ne8+ | 544.5 | 1.000000 | -2586.7 | -2563.0 | -2558.0 | -5.00 |
Table 4 は リチウムなどの 3電子原子の計算結果である。
| 原子 | r1 (MM) | WN x 4 | 計算結果 (eV) | 実験結果 (eV) | 誤差 (eV) |
|---|---|---|---|---|---|
| Li | 1949.0 | 1.000000 | -203.033 | -203.480 | 0.47 |
| Be+ | 1427.0 | 1.000000 | -388.785 | -389.826 | 1.04 |
| B2+ | 1125.0 | 1.000000 | -635.965 | -637.531 | 1.56 |
| C3+ | 928.0 | 1.000000 | -944.46 | -946.57 | 2.11 |
| N4+ | 790.5 | 1.000000 | -1314.25 | -1317.01 | 2.76 |
| O5+ | 688.0 | 1.000000 | -1745.70 | -1748.82 | 3.12 |
| F6+ | 609.4 | 1.000000 | -2237.60 | -2242.21 | 4.61 |
| Ne7+ | 546.0 | 1.000000 | -2791.15 | -2797.12 | 5.97 |
具体的な計算手法に関しては、 このページを参照のこと。
量子力学 の 標準的な模型では、電子は 電子雲として安定で 実際に動いていないとしている。
彼らは このことが 電子が エネルギー放射して原子核に落ちていかない原因だと主張している。
しかし もしそうだとすると、どのように 高速度の電子によって生じる相対論的補正や 換算質量の使用を説明できるのだろうか?
実際に、換算質量を使用すると、水素原子のエネルギー準位の計算結果は より正確になる。
これはつまり、電子や原子核は 実際に質量中心の周囲を運動していることを意味している。
つまり 量子力学的な模型は この部分においても明確な説明ができないでいる。
また もし ディラックの水素原子が間違いだとしたら、ラムシフトの解釈も当然変わる必要がある。
この非常に微小なラムシフトは 光子によって生じる 2S1/2 の準安定状態という仮定に頼っている。
しかし ラム自身が 後に 光子という粒子は存在しないと言い放っている。
ドブロイ波、 ビリアル定理、 ゼーマン効果 なども参照のこと。
中性のネオン (Ne) においては、8つの 外殻 軌道の電子(価電子) はどう動いているのだろうか?
またしても 量子力学は 具体的なイメージを何も示せない。
ネオンは、10の電子をもっており、そのうち、2つの 1S 軌道の電子は 原子核にとても近づいている。
つまり、近似的に、8つの外殻電子が +8e の中心核 (+10e-2e = +8e) の周りを周回している。
(Fig.78) 中性のネオン模型。
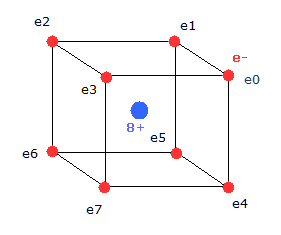
8つの価電子 ( e0 - e7 ) 間の クーロン反発力を考慮すると、これらの外殻電子は 正六面体のように分布していると考えられる。
この正六面体の構造が 8つの価電子が最も安定になる構造である。
しかし 炭素などの他の原子と異なり、Fig.78 模型では 上下部の価電子は 原子核の周囲を周っているときに 互いに衝突してしまう。
(Fig.79) 上下部の価電子の衝突。
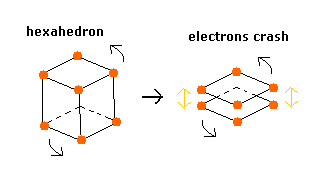
トップページに示したように、ミステリアスなパウリの排他原理は 互いに垂直な 2つの 1s 軌道によって生じる。
つまり ネオンのような希ガスにおいても このドブロイ波の性質が 自然に関係していると考えられる。
この衝突を回避し、ヘリウムの垂直なドブロイ波を用いると、8つの外殻電子の軌道は 次のようになると考えられる。
(Fig.80) 中性のネオンの 8つの外殻電子の軌道。
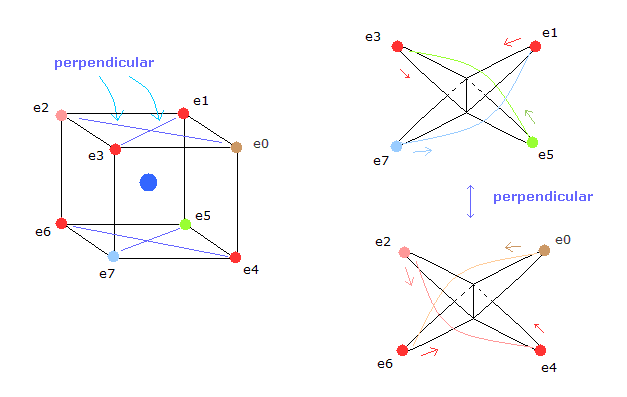
Fig.57 では、例えば 電子 3 と 5 ( e3 と e5 ) の軌道は 共通の頂点を持ち、次のように 互いに垂直である。
(Fig.81) 互いに垂直な軌道。
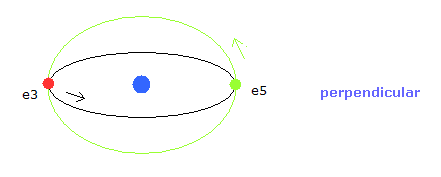
Fig.80 の模型では、8つの価電子は 互いに衝突しない。
また 8つの価電子は 互いに通過するとき 単一の共通の平面に 入る必要がない。
そして 共通の2つの頂点を共有する 2つの電子の軌道は 上のヘリウム模型のように 互いに垂直である。
( ペアは e1-e7、e3-e5、e2-e4、e0-e6 である。)
つまり 8つの価電子は 各自の異なった軌道を持っている。
多面体の対称的な構造と ドブロイ波の干渉を考慮すると、この8つの価電子が n = 2 (= 2ドブロイ波長 ) のエネルギー準位の限界であると考えられる (= パウリの排他原理 )。
n = 1 と異なり 動径方向のドブロイ波のために 軌道は長円形になり得る。
もちろん ネオンに関しての この模型はまだ推定の段階である。
そのため 誰か より良い かつ実在的な ネオン模型を示せると非常に喜ばしい。
このページのこのプログラムを実行すると、もう一方の原子側に 突き出た価電子 "e0" が 様々な共有結合長を決定する際の キーファクターであることが分かる。
すでに述べたように、これらの形を決定するのが クーロン力と ドブロイ波の2つである。
どちらも欠けても 無理である。
(Fig.82) C の電子に作用する力の比較。
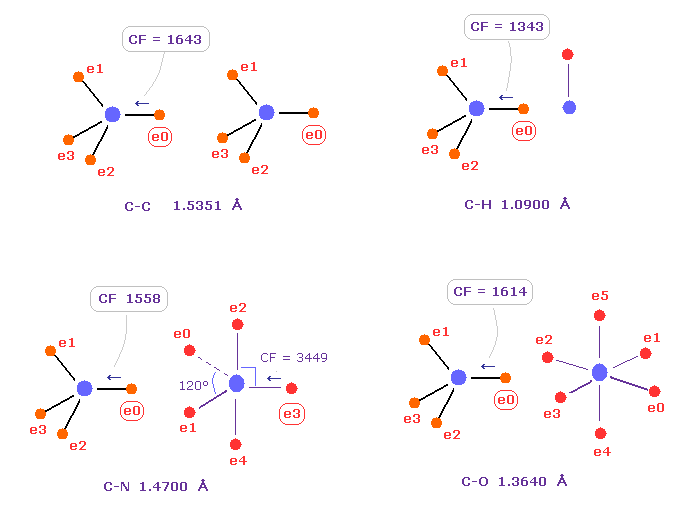
ここでは ボーア半径 離れた -e と +e の間に働く力を 1000 とする。
Fig.82 は C-C、 C-H、 C-N、 C-O のシングル結合における 炭素の電子 e0 に作用する力 CFを示したものである。
炭素が 様々な結合において 正四面体構造を 保っていることを考慮すると、炭素の電子に作用する力が 互いに ほぼ 等しくなるのが自然である。
実際に これらの力 (= CF ) は 異なった C-C、C-H、C-N、C-O 結合において それぞれ 1643, 1343, 1558, 1614 になる。
( これらの結合長は 実験値である、C-O の シングル結合は 酢酸からのものである。 )
| 分子結合 | 結合長 | e0 への力 |
|---|---|---|
| C - H | 1.0900 Å | CF = 1343 |
| C - C | 1.5351 Å | CF = 1643 |
| C - N | 1.4700 Å | CF = 1558 |
| C - O | 1.3640 Å | CF = 1614 |
| C - F | 1.3500 Å | CF = 1605 |
| C - Si | 1.8500 Å | CF = 1602 |
| C - P | 1.8400 Å | CF = 1584 |
| C - S | 1.8200 Å | CF = 1708 |
| C - Cl | 1.7700 Å | CF = 1626 |
Table 5 は 様々な結合における 炭素の電子 "ele 0" に作用する力 (= CF ) を示したものである。
驚くべきことに、異なった結合において、これらの力 (= CF ) は ほぼ 同じになる。
これはつまり 共通のメカニズムが働いて、炭素の正四面体の構造が 様々な結合において 保たれていることを示している。
"分離した" 電子の概念が重要なキーポイントである。なぜなら これらの結合長の違いは 明らかに 分離した電子概念がないと実現できないからである。
例えば、塩素では その原子核が 3ドブロイ波長のために より露出しているため、力 CF が 他の結合と同じになるためには 結合長が長くなる必要があると言える。
(Fig.83) どうやって 原子は立体障害と共有結合を区別するのか?
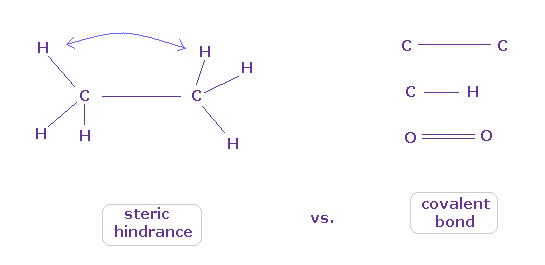
よく教科書で "エタンの6つの水素原子は 互いに避け合う配置をとる" とか "タンパク質の構造は その立体障害のために 非常に制限される " だとかの説明を見られるかもしれない。
これはつまり 各原子は 必ず 他の原子を避ける傾向があるということだろうか?
一方で 希ガス原子を除いて 様々な原子は 安定な共有結合を形成することができる。
各原子が 互いに"避け合う"のに、どうして それらは 安定で タイトな共有結合を形成することが可能なのだろうか?
(Fig.84) レナード・ジョーンズポテンシャルは 共有結合への移行を説明できない。
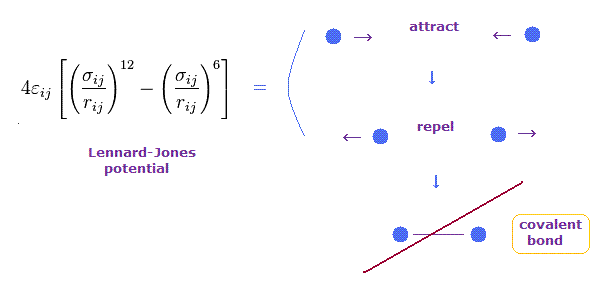
レナード・ジョーンズポテンシャルは ファンデル・ワールス力などの分子間力を表すのに よく使用される。
このポテンシャルでは、2つの粒子間の距離が 非常に 長いとき、それらは 互いに弱く引き合う。
一方で、2つの粒子が ある閾値の結合長よりも近づくとき、それらは 互いに避け合うことになる。
この反発力は 電子雲の衝突とパウリの排他原理によると 彼らは主張している。
しかし このレナード・ジョーンズポテンシャルは もっと短い結合長において どうして非常に安定かつ タイトな共有結合が形成されるのかを説明することができない。
(Fig.85) C-C = 1.5400 Å は 釣り合いのとれた長さである。
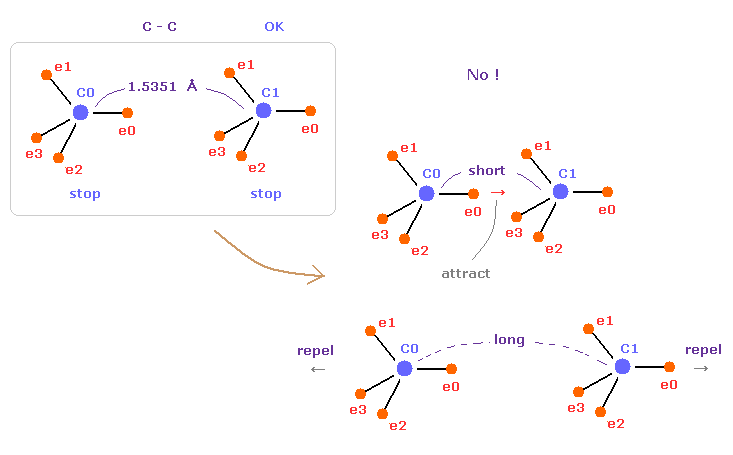
このページでは エタンの C-C 結合長 1.5351 Å が 両方の C 原子核の安定性にとって 必要不可欠なものであることを示した。
もし C-C 結合長が 1.5351 Å よりも短くなると、e0 と C1 間の引力が 強くなりすぎ、不安定になる (= 電子の周期運動も壊れる。 )。
そして もし C-C 結合長が これよりも長くなると、2つの C 原子核間の反発力が優勢になり 不安定になる (= 結合エネルギーが 負の値になる。)。
これが C-C 結合長を決定する 本当のメカニズムである。
(Fig.86) 結合長が "長い" か "短い" かにより その性質が決まる。
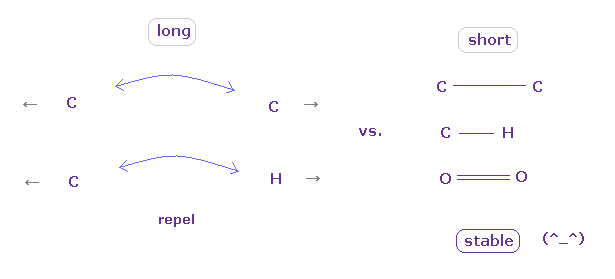
結論からして、このページに示したように、 安定な結合を形成するには、2つの原子が ある閾値の長さよりも 互いに 接近する必要があると言える。
その閾値の長さよりも 長いと、 電子間や核間の反発力 が 優勢になり、いわゆる 立体障害を引き起こす。
2つの原子が 互いに ある閾値よりも近づくと、突き出た電子 ( Fig.55 の "e0" ) の引きつけ力が強くなり 原子核間の反発力をキャンセルする。
また これらの短い共有結合長では、2つの原子の電子が 互いに周期的に避け合う傾向になり、これが 結合エネルギーの源になる。
( これらの 周期的に避け合う運動パターンは 非常に長い結合長では 形成しにくいと考えられる。)
通常のタンパク質では、2つの原子間の ほぼすべての距離は 共有結合長よりも 長いため、それらは 立体障害を引き起こす。
[1] N. Bohr, Philos. Mag. 26, 1 (1913).
[2] A. Sommerfeld, Ann. d. Physik 51, 125 (1916).
[3] P.A.M. Dirac, The Principles of Quantum Mechanics (Fourth Edition).
[4] C. Davisson, and L. H. Germer, Nature 119, 558 (1927).
[5] A. Tonomura, J. Endo, T. Matsuda, et al., Am. J. Phys., 57, 117 (1989).
[6] A. A. Svidzinsky, M. O. Scully and D. R. Herschbach, Proc. Natl. Acad. Sci. U.S.A. 102, 11985 (2005).
[7] A. A. Svidzinsky, M. O. Scully and D. R. Herschbach, Phys. Rev. Lett. 95, 080401 (2005).
[8] G. Chen, Z. Ding, S-B Hsu, M. Kim and J. Zhou, J. Math. Phys. 47, 022107 (2006).
[9] G.W.F. Drake, M. M. Cassar, and R. A. Nistor, Phys. Rev. A 65, 054051 (2002).
[10] G. E. Uhlenbeck and S. A. Goudsmit, Nature 117, 264 (1926).
[11] H. Rauch et al., Phys. Lett. 54A, 425 (1975).

2014/12/14 updated This site is link free.