トップページ (正確な新ボーア模型)
電子スピンは存在しない。。
繰り込みによる 電子g因子計算。
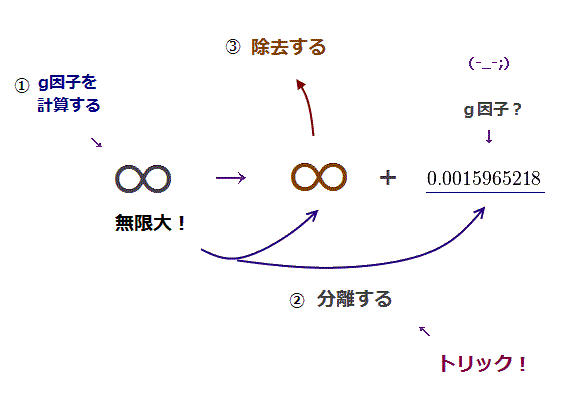
(Fig.1) 無限大を人為的に除去 (= 繰り込み ) して 小さなg因子を出す !?

量子電磁力学 (= QED ) は 異常磁気モーメント (= g因子 ) や ラムシフトを精密に予測できる 最も成功した理論と よく言われるが 実はこれは真実ではない。
QED とは 繰り込み という人為的な操作によって 計算で出た無限大を意図的に除去して 都合のいい 有限の値のみを残そうとする手段にすぎない。
つまり ある有限の物理量は 裸の電子の電荷、質量が 無限大のため、 計算で出た無限大を都合よく打ち消してくれるという解釈に頼っているわけである。
実際に、 デイラック は、QED が 無限大を任意の方法で 無視している状況に不満を抱いており、 ファインマンも この QED を "hocus-pocus" (= ごまかし ) にすぎないと はっきり明言しているのである。.
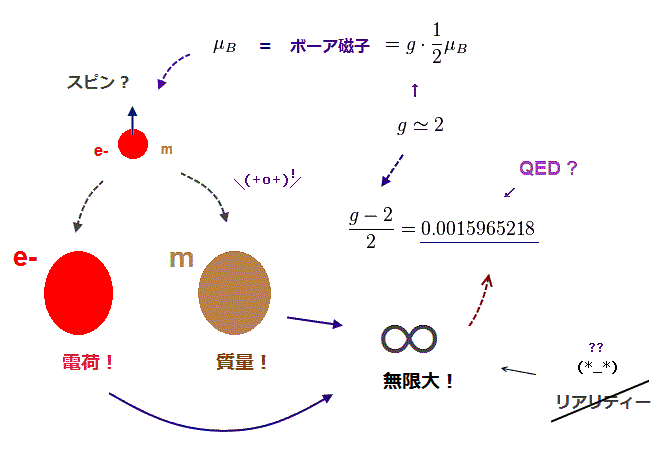
電子スピンの 磁気モーメントは 偶然にも ボーア磁子 (= μB ) に等しい。
なぜなら スピン角運動量を 古典的な "1 ħ" から 1/2 ħ に定義したと同時に、そのg因子を 2倍 ( 1 → 2 ) にしたからである。
すると、磁気モーメント (= g因子 × 角運動量 ) は ボーア軌道と電子スピンで 同じ になる。
なぜなら 磁気モーメント = 1 ħ × 1 (= ボーア軌道のg因子 ) = 1/2 ħ × 2 (= スピンg因子 ) だからである。
理想的なg因子の値 1 ( もしくは 2 ) と 実際の測定値の間に 若干の違いがあることは 極自然なことである。 現在の物理では、この小さな違い (= 0.001596 .. ) は 無限大しか出せない非現実的な QED によって説明できるとしている。
(Fig.2) QED の人為的なトリック = "便利な" 有限値のみ残す。
ファインマン図で QED を計算するとき "ループ" を含んでいると、計算結果は 必ず 無限大に 発散する。
もちろん、磁気モーメントなどの有限の物理量を得るには 何とかして これら無限大を 取り除かなければならない。
そのため 物理学者達は 無限大 = 無限大 + 有限値 という理不尽な方程式を正当化させ、1940 年代から 様々な重要な物理量を得るのに 乱用し始めた。
お気づきの通り、これらは 単なる人為的かつ "お粗末な" 数学的トリックにすぎず、デイラックが 最後まで反対していた理由が 良く理解できる。
つまるところ、 "無限大" というものは いかなる "有限" の値でも 吸収 ( もしくは 放出 ) して誤魔化すことができるからである。
"無限大"という 数学的に意味のない厄介な概念を 逆に悪用することが QED の最大のトリックだったわけである。
(Fig.3) 1ループのファインマン図の 繰り込み計算。
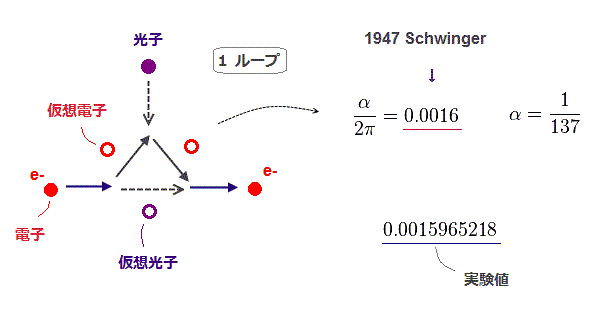
QED の ファインマン図は 1光子 (= 点線の両端 ) と2つの電子 (= 実線の両端 ) で構成される各頂点において 電子-電子、光子-光子を結合させてできる。
内線は 伝播関数 すなわち 相対論に反する 仮想粒子 である。
1947 年に シュウィンガーが 1ループ頂点補正で α/2π ( α = 微細構造定数 ) をだし、この結果は 実際の g - 2 の値に 近かった。
なぜなら このシュウィンガーの g因子の値は QED による最初の予測値であったため、QED の 伝播関数、ゲージ、繰り込みなどの 様々な新ルールを この計算に合わせて作ったからである。
この時点で QED の計算結果は 自然な帰結ではないが、さらにこれに加えて 間違った数学的手法 (= "偽"変数変換 ) を用いて 強引に実験結果に近づけようとしたのである。
(Fig.4) 2ループを含む7つのファインマン図の計算はミス?
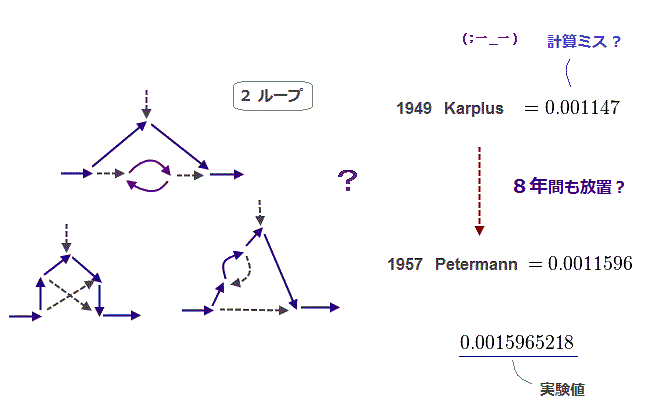
シュウィンガーのg因子の1ループ計算から1年もたたずして、Karplus と Kroll が 1949 年 に 7つのファインマン図からなる2ループ補正を計算した。
このサイトによれば、彼らの計算結果は 間違っており、 Petermann が 8年も後の 1957 年 に修正したことになっている。
しかし 世界中の物理学者達が この計算ミス (← ? ) を
8年もの長い期間 そのままに放置していたという事実は はっきり言って 不自然極まりない。
たかだか 7つのファインマン図の計算だけで 8年もかかるわけが ない からである。
なぜなら これら2ループ補正計算を シュウィンガーの1ループ補正と同じ方法で単純に行っただけでは 正しい結果は得られないからである。
満足のいく結果を得るには 他の新たな新ルールを こしらえる必要があったのである。
8年という長い期間は 単に計算だけでなく、これら 新たな人為的なルールの考案に要したものだと考えるとしっくりくる。
(Fig.5) "k" の積分範囲は -∞ から +∞ → 変数変換 → "l" も同じく -∞ から +∞。
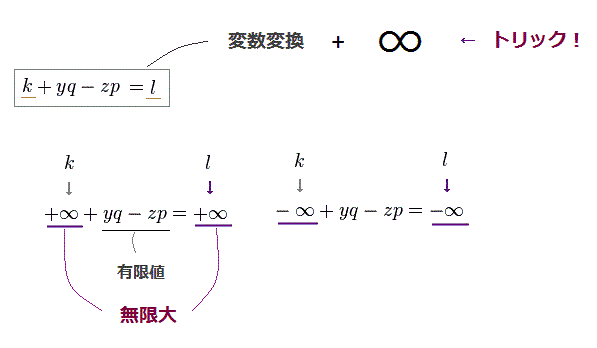
1ループ補正における最も重要なトリックは 変数 "k" から "l" への "変数変換である。
ここで "yq - zp" の部分は 有限な変数であり、また 元の 相対論的な運動量 "k" の積分範囲は -無限大 から +無限大 になる必要がある。
これら無限大を含む伝播関数は 紫外発散を起こす。 ここ や ここ (p.2) を参照のこと。
仮想の運動量 "k" の積分範囲は -∞ から +∞ である。
そのため、変数変換後の "l" の積分範囲も -∞ から +∞ になる。 なぜなら 有限の値は 無限大に 吸収されて 見えなくなってしまうからである。( 無限大 ± 有限値 = 無限大。 )
(Fig.6) "k" ( もしくは "l" ) による積分は "ゼロ" になる。
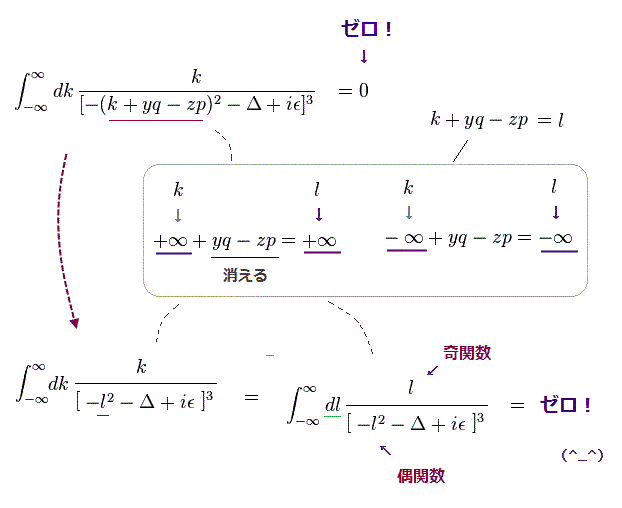
Fig.6 では、分母は "偶関数" になる。なぜなら ±∞ は 変数変換後 ( k → l ) でも ±∞ のままだからである。
そして 分子は "k" ( もしくは "l" ) に関して "奇関数" である。
結果的に この -∞ から +∞ の積分は "積分変換" にかからわず ゼロ になる。
これが 正しい数学である。 この結果は 部分積分すれば確かめられる。
(Fig.7) 変数変換 ( k → l ) が 結果を"変える" !? ( ゼロ → ゼロでない。 )
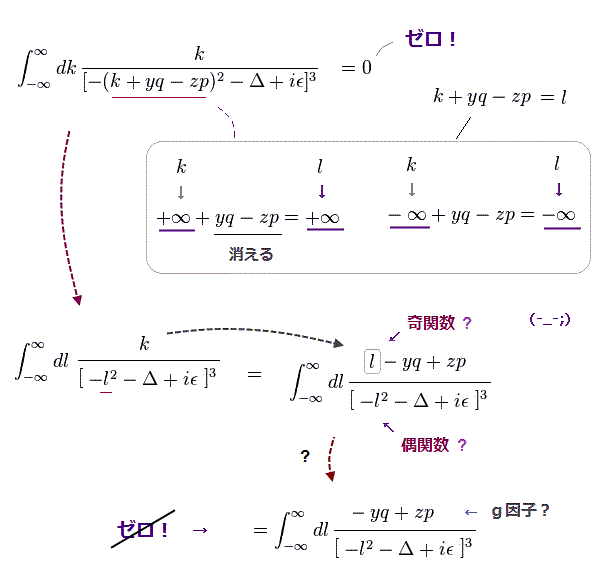
シュウィンガーが行った QED 計算では 完全に間違った数学を用いている。
変数変換 ( k → l ) の後、 分母のみ 正しい数学を用いている。
分子では k = "l" - yq + zq の中の "l" の部分のみ 奇関数として扱っており 完全に上記と矛盾した対応をしている。
結果的に ( -yq+zp ) という有限の値が 残り、これが 欲しかったg因子の一部になるという具合である。
元々は 分子の "k" 自体が 純粋な 奇関数 ( -∞ から +∞ までの ) であるため、この操作は 完全に意図的な計算間違いであることは明白である。
実際の計算に関しては ここ (= Eq.7, 14, 15 ) や ここ (p.98) や ここ など参照のこと。
(Fig.8) 単なる変数変換で 結果が変わってしまった !? ← 意図的な間違い。
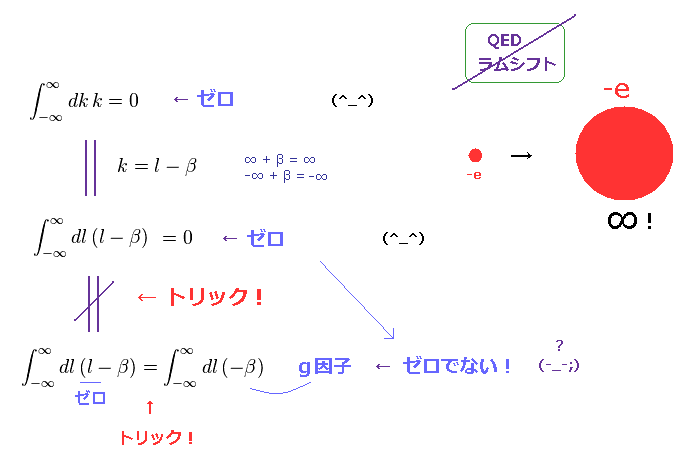
Fig.8 の簡単な例にあるように、"変数変換" ( k = l - β ) という 単なる計算手段にすぎないもので、 結果自体が 意図的に 変わってしまっている。あり得ない話である。
( これは 完全に 意図的な 計算ミス である。 )
ラムシフトも その一部分として この 間違った数学に基づく g因子の値を使用している つまり QED ラムシフトも間違いということになる。
QED によるラムシフト では 実験結果に近づけるために 様々な意図的な効果を 付け足そうとしており、とてもじゃないが
自然な結果とは 言えない代物である。
例えば 非相対論項における 仮想的な励起エネルギー などがそうである。
もちろん、 特殊相対論 と ディラックの水素 が間違いならば、 QED ラムシフト は 他の解釈で 速やかに 置き換える必要がでてくる。
(Fig.9) 新たなルール = "質量" と "伝播関数" の繰り込みが 2-ループ補正の人為的なトリック。
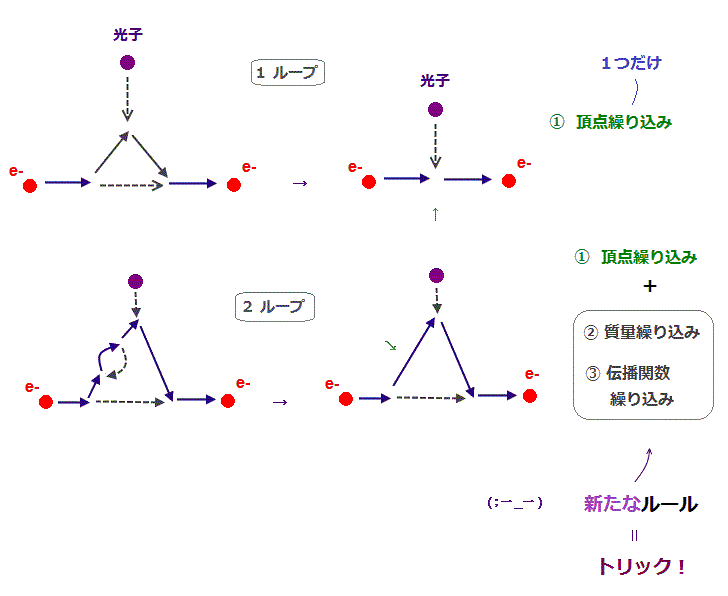
最初の 異常磁気モーメントの1ループ頂点補正では 間違った数学に頼ることによってα/2π の値を得ることができた。
この1ループ計算が QED における まさに最初の計算であったため、この計算手法全体が 言わば 新ルールだったといっていい。
g因子の2ループ補正では、質量 や 伝播関数の繰り込みという "新たな"ルールを導入して計算している。
また 新たなルールに頼るということは この2ループ補正の計算も 第一原理でなく 単なる 人為的なトリックということになる。
このサイトで "L7-KarpusKrollPhysRev.77" ボタンをクリックして 2ループ計算の 論文 (= Karplus、 Kroll ) を得られる。
この Karplus の論文の中の 質量、伝播関数の繰り込みの項 (= IId, IIe の図 )は 最新のPetermann の論文と同じ結果をだしている。
(Fig.10) "有限値" を "不用な部分" と "必要な部分" に分離するトリック。
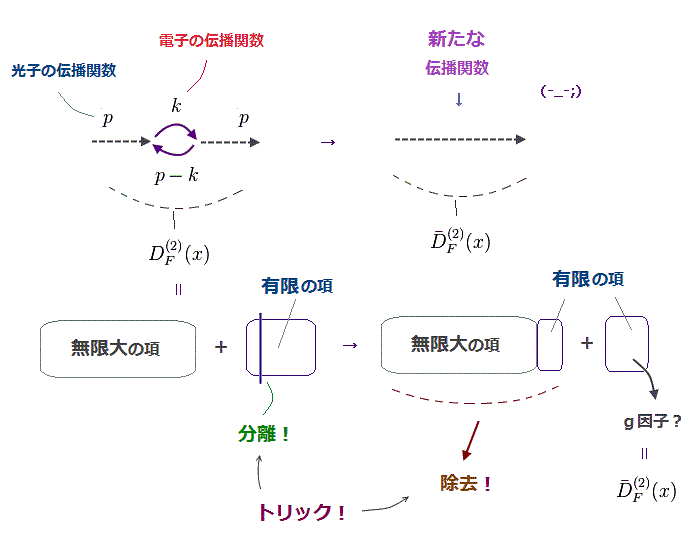
2ループ計算における最も重要なトリックは 伝播関数 ( 光子と電子 ) の
再定義 である。
この論文 (= Eq.11, 12, 13 ) にあるように、 彼らは オリジナルの光子の伝播関数 (= DF ) を 不都合な部分を 人為的に除去して 新たなものにすり替えてしまった。
問題は 無限大の部分だけでなく 有限の部分の一部も g因子を得るために 除去したところにある。
この除去方法に関する 決まった規則などはないため、好きな部分を除去できるわけである。
もちろん、この新たな手法は 元の1ループ補正のところでは使用されていないため、2ループ補正における 新トリックと言える。
(Fig.11) 電子の伝播関数 (= SF ) の "再定義" も 人為的なトリックの1つ。
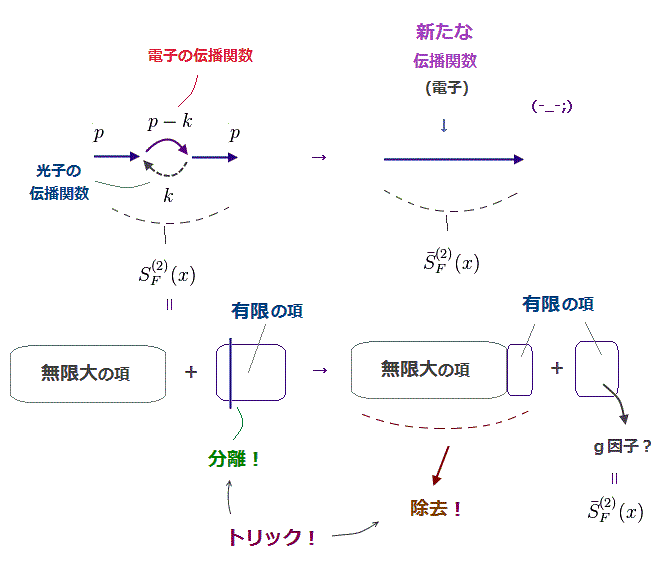
この論文 (= Eq.15-23) にあるように、 彼らは 電子の伝播関数 (= SF ) を 新しいものに置き換えてしまった。
この過程において、無限大の部分のみならず 不用な有限の部分も除去してしまった。
またもや この伝播関数における繰り込み (← ? ) も人為的なトリックである。
つまり これら異常磁気モーメントの計算は 第一原理でも何でもなく、QED の正当性を実証したことには まったくならないわけである。
(Fig.12) 光子の伝播関数の有限の部分から "不用な"数を意図的に除去。
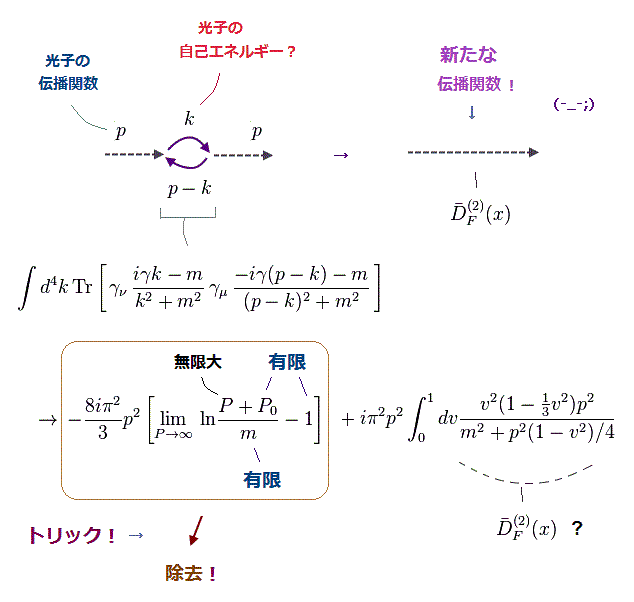
上記の論文 ( Eq.13, FIG.1 の図のFig.IIe ) では、無限大の部分 (= P ) のみならず 有限の値まで 光子の自己エネルギーの計算過程で 除去してしまった。
さらに 有限部分の "P0" 項 などの 中身 の詳細は不明のままである。
この分離・除去に関する絶対的なルールなどは存在しない。
具体的な計算に関しては このセクションを参照のこと。
(Fig.13) 不用な "有限部分" も除去。
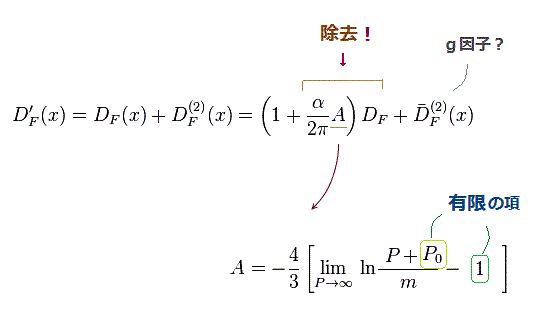
無限大を "無限大" の項と "有限" の項 に分離する手段は 本質的に 任意である。
要するに 欲しい有限値を得るために 無限大 (+ 不用な有限値 ) の繰り込みを 悪用しているのが QED の正体と言える。
(Fig.13') 人為的な光子の伝播関数 (= bar-DF(2) ) への置き換え。
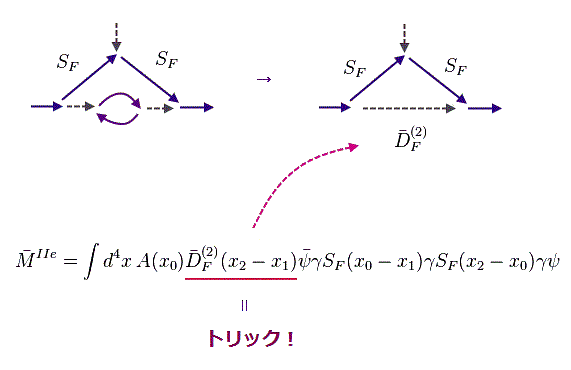
上記論文の Eq.36e にあるように、彼らは 1ループの光子の自己エネルギー部分 (= Fig.12 ) を 人為的な光子の伝播関数 (= bar-DF(2), Fig.13 ) に置き換えてしまった。
つまり 異常磁気モーメントの計算では 都合のいい"有限値"のみを 意図的に残す手法に依存していることが分かる。
(Fig.14) この論文の光子の伝播関数の形は 標準の形式と異なる。
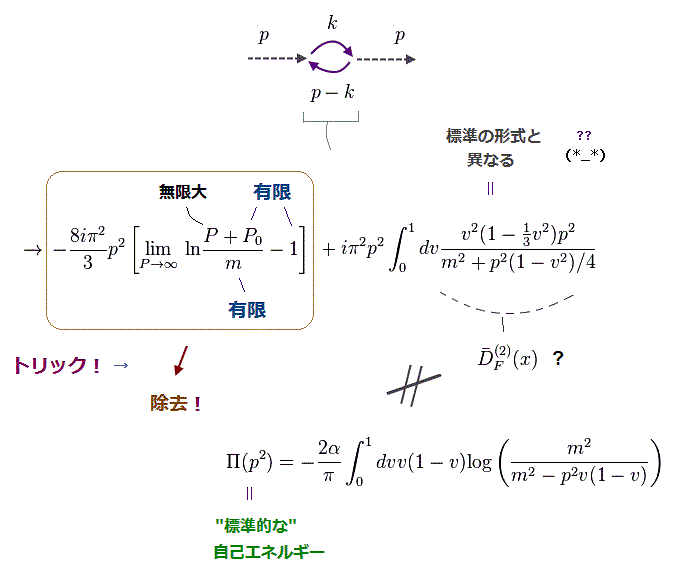
光子の自己エネルギーは 両側の2つの光子の伝播関数 (= 点線, p ) と 2つのループ状の電子の伝播関数 (= 実線、 k と p-k ).
標準的な光子の自己エネルギーは ここ (p.14) や ここ (p.199) で見られる。
この2ループ補正の計算で使用されている光子の自己エネルギーは 標準のものと まったく異なることが分かる。
つまり 繰り込みで どの部分を除去するかという決まったルールというのが存在しないということである。
これらの自由な規則によって 異常磁気モーメントの計算で 任意の調節が可能となっている。
(Fig.15) 電子の自己エネルギーのファインマン図。
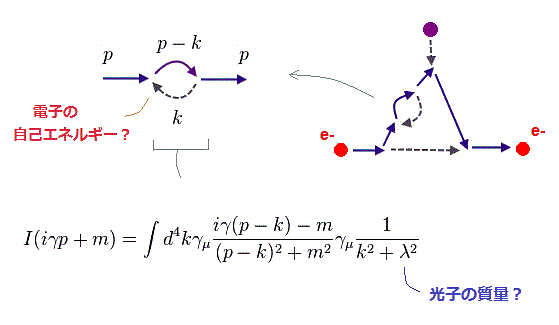
g因子の2ループ計算では 電子の自己エネルギーという 新たな概念も導入した。 上記の論文の Eq.15, 16、 IId 図 参照のこと。
電子の自己エネルギーのファインマン図は 両側の2つの電子の伝播関数 (= p ) とループ状の 電子 (= p-k ) と 光子 (= k ) の伝播関数ので成り立っている。
(Fig.16) ↓ 式の人為的な変形。
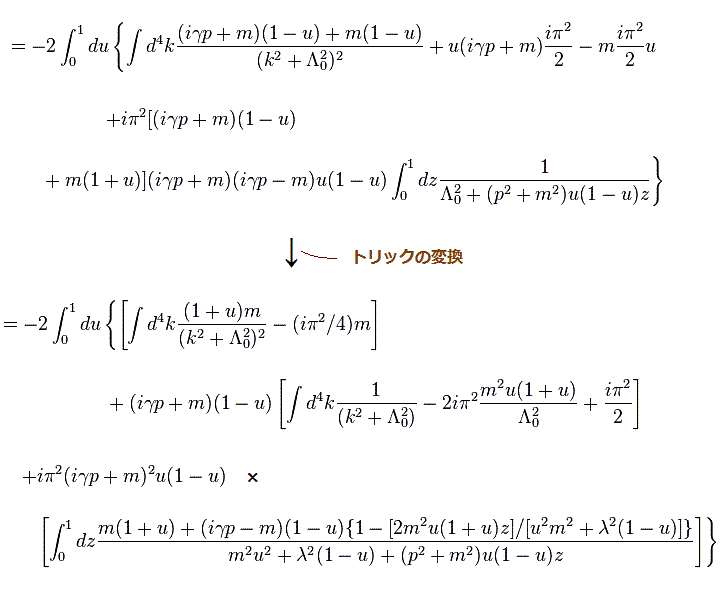
上記論文における 式 Eq.21 から Eq.22 の変換のとき、非標準的な手法を用いている。
Fig.26 にあるように この変換は 何らかの別の仮定を導入しない限り 普通では行えない。
つまり ここでも "無限大" などを利用して 不自然な式変形をしたと思われる。
(Fig.17)
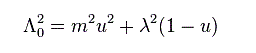
ここで Λ0 は "有限値" である。
"m" と "λ" は 電子と光子の質量で、 "u" は 0 から 1 の範囲の変数である。
この光子の質量 λ が ゼロになるとき、 赤外発散 という 新たな無限大が発生する。
高次の計算に現れるこの種の赤外発散の除去方法に関しては またもや決まった方法はなく、無限大をどこまでにするかに応じて 計算結果が変わる。
(Fig.18) 無限大のみならず "有限の"項 も除去。

上記の論文の Eq.22、 23 では、無限大のみならず 不用な有限値までも 人為的に除去してしまった。
Fig.18 の最初の項 (= "有限" ) は ”質量”の繰り込みという新たなルールによって除去して、2番目の項 (= "有限" ) は ”伝播関数”の繰り込みというもので除去した。
(Fig.19) ↓ 不用な "有限の"項 も除去 !?

Fig.19 にあるように "有限の項" の一部も 繰り込みと一緒に 除去していることが分かる。
(Fig.20) 有限値。
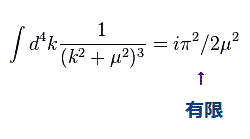
上記論文の Eq.19 にあるように Fig.20 の積分は "有限値"になる。
(Fig.20') 人為的な電子の伝播関数 (= bar-SF(2) ) への変換。
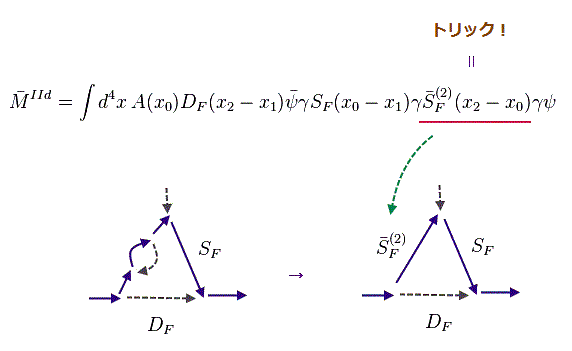
上記論文の Eq.36d にあるように、1ループの電子の自己エネルギー部分 (= Fig.15 ) を 人工的な電子の伝播関数 (= bar-SF(2), Fig.19 ) に置き換えてしまった。
ここでも 意図的に 欲しい値のみを残す操作が行われたことを示している。
(Fig.21) "質量" 繰り込み は 頂点繰り込みの 一部であり、無意味。
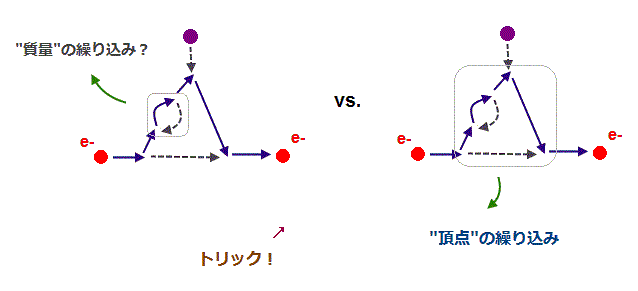
g因子の2ループ補正では 最初に 質量の繰り込みをして "都合のいい" 有限値のみを残す。
しかし 見ての通り、この "質量"繰り込みの区別は無意味である。
なぜなら この質量の繰り込み (= Fig.21 左 ) は もっと大きな 頂点の繰り込み (= Fig.21 右 ) の一部にすぎないからである。
つまり 小さな質量繰り込みと 大きな頂点繰り込みの区別は 人為的な選択に依存する。
私たちの自然界が このような 意図的に都合よく無限大を利用したトリックに依存していない ことは 明らかである。
つまり ”QED は最も成功した理論”という お馴染の謳い文句は 間違いであり、一種のマインドコントロールの役割を果たしているのである。
(Fig.22) 光子の自己エネルギーは "任意の"変換の影響を受ける。

上記の論文 (Eq.12)では シュウィンガーの自己エネルギーを 少し 修正したものを用いている。
"修正" ということは すなわち好きなように結果を 改変できることと等価であり、第一原理でないことは明白である。
シュウィンガーの論文は このサイト や ここ ( appendix p.25- を参照 ) から得られる。
この論文 (= Eq.25 の eq. A.13 in p.25 ) では、2つの電子の伝播関数 (= SF、p.7 の Eq.1.66 in p.7 ) を用いて、光子の自己エネルギー項 (= Gμν ) を定義している。
(Fig.23) 2つの ( 仮想の ) 電子の伝播関数。

Fig.23 は ( 仮想の ) 電子の伝播関数である。
k' と k'' は 各電子の 4元運動量であり、 電子質量として "κ" の代わりに "m" を用いている。
(Fig.24) "p" = 両端における 光子の運動量。
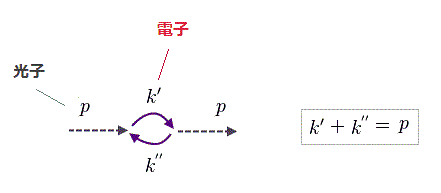
"p" は 両端の光子の運動量 (= "in" と "out" ) である。
つまり k' と k'' の和が "p" になる。
(Fig.25) "便利な" 変数変換を利用。

この論文 (= p.26 の eq. A.28 ) では、 人為的な "変数変換" を試行している。
ご存知の通り、 "変数変換" は 単なる "手段" にすぎず、 正しい数学によれば、これによって 結果自体が変わることはあり得ない。
ここでは "p" は 光子の運動量で、 "k" は 2つの電子の運動量の差によって生じた仮想の運動量である。 ( ここでは 上記論文の "p" と "k" を統一のため 交換した。 )
(Fig.26) 便利な "無限大" が "有限値" を吸収した。
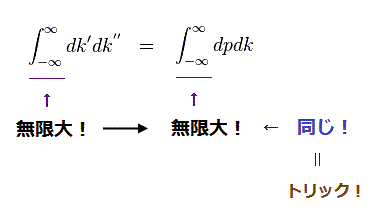
重積分の ヤコビアン行列式を用いれば、この変換によって 積分係数が変わらないことが分かる。
しかしもちろんのこと、この積分の 上限 (= +∞ ) と 下限 (= -∞ ) は 無限大でない限り 変化することは言うまでもない。
これはつまり このセクションにあるように 彼らは 無限大を乱用しているのである。
なぜなら "無限大" は 有限の値を 自由に 吸収、放出できるからである。
(Fig.27)
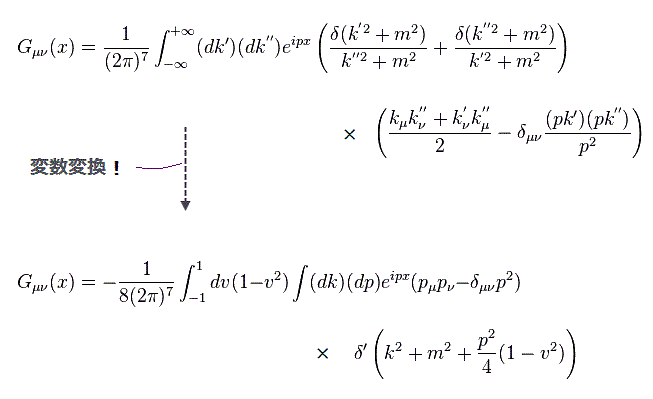
この論文 ( A.27 から A.29) では、この変数変換を用いて 式を変形した。
さらに A.32 で "v" に関して部分積分をして次を得た。
(Fig.28) 光子の自己エネルギー?
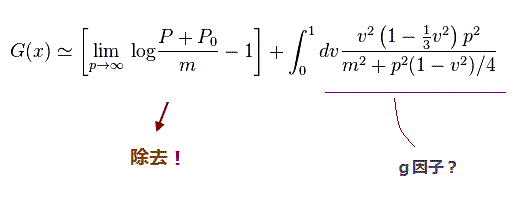
上記論文の Eq. A.32, A.33, A.35 を参照のこと。
この結果は 2ループ補正の Fig.12 の結果とほぼ同じである。
(Fig.29) 人為的な "変数変換"、 パート II。
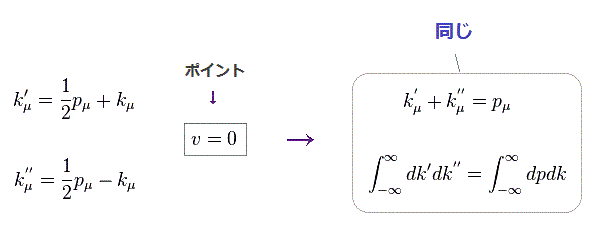
ここで 元の変数変換の代わりに Fig.29 の v = 0 の変換を用いる。
もちろん、 "v" は変数 ( -1 < v < 1 ) であるため、 "v = 0" としても 積分の形自体は変わらない。
(Fig.30) "変数変換" が 計算結果を変える !

しかし 変数変換のところで "v=0" にすると 光子の自己エネルギーの結果が Fig.28の代わりに ゼロ になってしまう。
つまり 変数変換という手段に過ぎないものが 結果自体を変えてしまったことになる。
これはつまり 異常磁気モーメント (= g因子 ) の結果は 人為的な 変数変換 に依存しており、まったくもって QED の自然の帰結ではないことが分かる。

2015/1/4 updated This site is link free.