トップページ ( 正確な新ボーア模型 )
標準模型は 間違っている。
超対称性変換の計算。
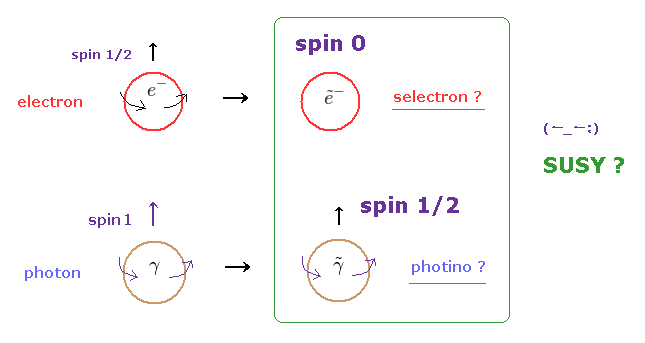
(Fig.1) 超対称性粒子 (= SUSY ) は 実在するのか?

超対称性理論によれば、各素粒子には 対になる パートナーが存在するらしい。
例えば、電子やクォークなどのフェルミ粒子には "ボソン" の パートナー である
スカラー電子 (= selectron ) や、 スクォーク が存在することになる。
Fig.1 や このサイトにあるように、 スカラー電子は スピン 0 のボソン、また フォティーノ (= 光子の超対称性粒子 ) は スピン 1/2 のフェルミ粒子である。
つまり、超対称性理論では、粒子の種類が 元の 約 2倍までに 増加してしまうことになる。
統一理論とは、本来 粒子の数を 減らすべきなのに、逆に急増してしまっている。
つまり、超対称性理論は 統一理論として 完全に 不適格な理論と言わざるを得ない。
(Fig.2) ダークマターは 超対称性粒子?
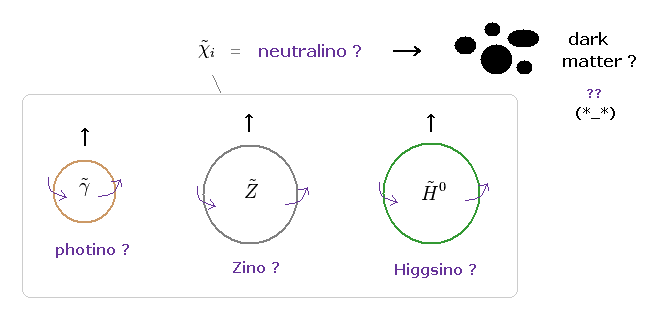
フォティーノ (← 光子 )、 ジーノ (← Z ボソン )、ヒグシーノ (← ヒッグス ) は スピン 1/2 と 中性の電荷を持つ。
超対称性理論によれば、これらの中性粒子は 重ね合わせを起こし、 "ニュートラリーノ" を形成するらしい。
もし、超対称性粒子 (= SUSY ) が 通常の粒子ほどの軽さだとすると、それらは すでに 加速器で発見されているはずである。
そのため、物理学者達は 超対称性粒子は 通常の粒子に比べて 非常に重い ( ~ 1000 GeV、陽子の約 1000 倍 ! ) から 見つかってないんだ と主張し始めた。
現在の理論によれば、 ダークマター (暗黒物質)は 全宇宙のエネルギーの 約 30 % も 占めると言われている。
通常のニュートリノとかでは この非常に重いダークマターを説明するには
軽すぎる。
つまり、このダークマターの候補としては、ニュートラリーノ や グラビティーノ などの "非実在的" な 超対称性粒子しか 残っていないのである。
(Fig.3) "超対称性の破れ" は 非常に便利な概念である。
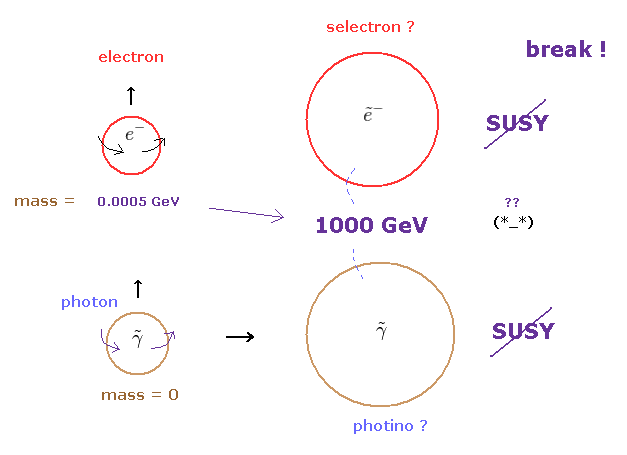
超対称性理論 (= supersymmetry, SUSY ) では、 各素粒子が それと 同じ質量と電荷を 持たなければならない。
しかしもしそうだとすると、私達は すでに 超対称性粒子 を発見していなければならないが、そういうことはない。
つまり このサイト (p.18) にあるように、超対称性粒子は 破れていなければならない。非常に便利な 対称性である。
SUSY 粒子が 1000 GeV ほどにも重ければ、まだ発見されていないことを説明できるわけである。
しかし 超対称性が 最初から破れているならば、そもそも 超対称性という仮定自体 無意味ということになる。
実は、現在の標準模型は "対称性" という 非常に 抽象的な概念に依存している。
相対論の厳しい制限のために、対称性という "人為的" な定義が 理論を発展させる 唯一の手段となっているのである。
このことが 超対称性に しがみつく要因となっている。
(Fig.4) 電子のみが安定? selectron、 陽電子、"spositron" は 不安定?

もし 電子のボソンのパートナー、 "selectron" が存在するとしたら、 陽電子のパートナー、"spositron" も存在することになる。
これらの素粒子の中で、電子のみが 安定ということになる。
お気づきの通り、この 超対称性粒子は 非常に多くの 不必要な粒子を導入しているのである。
素粒子とは 本来 長期間にわたって 安定でなければならないはずだが、不自然極まりない。
(Fig.5) "スピンストッパー" = 超対称性変換 ?
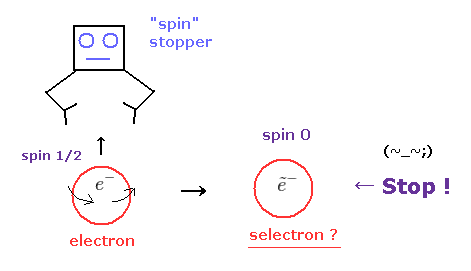
スピン ゼロ のヒッグス粒子が ( 間接的に ) 見つかったとされている。
これはつまり、ヒッグスは 永久に 回転が停止していることを意味しているのか?
もしそうだとしたら、いったい何が ヒッグスが 回転するのを 阻害しているのだろうか?
これは奇妙である。
もし、ゼロのスピン という概念がリアルだとしたら、超対称性変換は スピンを停止できる "スピンストッパー" によって なされなければならない。
それでは このスピンストッパーは 今現在 一体どこにいるのだろうか?
こういう現実的な質問に対しては 何も答えられないのである。
(Fig.6) スピン回転機は ヒグシーノ を生成するのか?
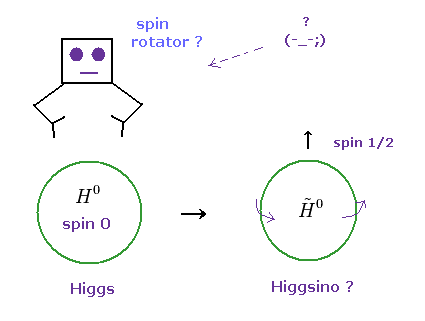
超対称性理論によれば、ヒグシーノは スピン 1/2 を持つ。
通常のフェルミ粒子に反して、 ヒッグスの場合、 "スピンゼロ" 粒子のほうが スピン 1/2 のヒグシーノよりも 安定である。なぜだろうか?
ということは、ヒグシーノを生成するには、スピンを加速させて生成する "スピン回転機" が どこからか飛んでくる必要がある。
これらの スピンストッパー や スピン回転機 は 一体 どのように 作られるのだろうか?
またもや 現在の理論は こういう根本的な質問に まったく 答えようとしない。
(Fig.7) 反粒子は 非常に便利な概念である。
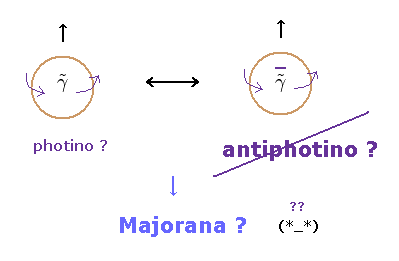
光子 は 中性であるため、そのフェルミ粒子のパートナーの フォティーノも中性ということになる。
電子や クォークなどのフェルミ粒子は 必ず その 反粒子 を持つ。
これはつまり フォティーノにも 反フォティーノが存在するということか?
奇妙なことに、超対称性理論によれば、これらフォティーノは 粒子と反粒子が 同じ マヨラナ粒子 らしい。
反粒子の有無までも人工的に設定してしまう 超対称性は 都合が良すぎの理論と言わざるを得ない。
(Fig.8) "カイラル対称性"、 "ゲージ対称性" とは何か? ← 物理?
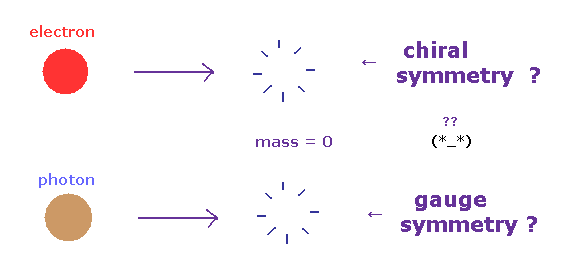
標準模型によれば、フェルミ粒子は 質量がゼロのとき、左巻き と 右巻き粒子に 分離できるらしい。
これを カイラル対称性 という ( このセクションも参照のこと )。
また ゲージ対称性のために、光子の質量は ゼロになると している。
ご覧のとおり、現在の素粒子理論は 非常に抽象的な 数学の"対称性" を 盲目的に信じている状況である。
(Fig.9) 超対称性は "軽い" ヒッグスにとって必要?
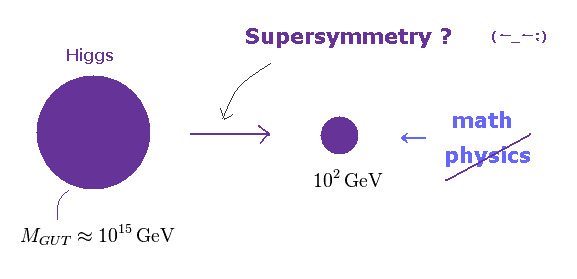
上で述べたように、 フェルミ粒子の質量は カイラル対称性のために ゼロになる。
光子などの ベクトルボソンの質量は ゲージ対称性のために ゼロになる。
問題は 現在の標準模型には ヒッグス粒子の質量が軽く ( 〜 126 GeV ほど ) なる 対称性が 存在しないということである。
そのため、 新たな 超対称性 という概念を導入して、ヒッグス粒子を 軽くする必要がでてきたわけである。 このサイト や このサイト を参照のこと。
なぜなら ヒッグスは スピンゼロの スカラーボソン であり、フェルミ粒子 や スピン 1 の ベクトルボソン とは 異なるものだからである。
しかし この理由は 実態とかけ離れた 単なる抽象的な数式に基づくもので、物理学とは 到底言えない代物である。
このセクション も参照のこと。
(Fig.10) 超対称性粒子は 加速器で 直接 検出できない。
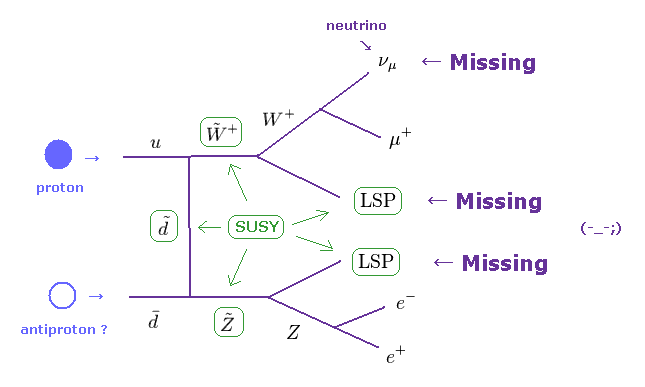
重要な点は 超対称性粒子 (= SUSY ) は 加速器で 直接 観測できない ということである。
R パリティー の保存則 ( これも人為的な規則であるが・・) によれば、超対称性粒子は 必ず 超対称性粒子に 崩壊することになる。
これはつまり、超対称性粒子は 最も軽くて 安定な LSP という粒子に 最終的に 崩壊することを意味する。
しかし、この LSP は ニュートリノのように 検出器に まったく 痕跡を残さないのである。
つまり、この超対称性粒子の存在は 消失エネルギー として 間接的に観測するしか他に方法がない。
問題は、この 消失 (= missing ) エネルギー を計測するには、それ以外のすべての 散乱されたエネルギーを かき集めなければならないということである。
もちろん、加速器内には ほぼ無数の バックグラウンド粒子が 飛び交っているため、この正確な測定は はっきり言って不可能である。
それに この曖昧な LSP 粒子の他にも、通常の ニュートリノも 消失エネルギーの主要な要因になるため、これとの区別も必須になる。
つまり、現在の 高エネルギー加速器の実験結果の解釈は 報道とは裏腹に相当 強引な 解釈に基づいてなされていることになる。
(Fig.11) "無数の" ヒッグスが 私達の周りに広がっており、質量を与えている?
このサイト や このサイト によれば、 無数ともいえる ヒッグス粒子が 空間中に広がって、すべての素粒子に 質量を与えているとされている。
通常の ニュースなどでは、 "ヒッグスは 空間中に広がっているが、それを検出するのは 非常に 難しい。" という説明を よく目にする。
あなた方も思われるように、この表現は 自己矛盾 している。
もし 無数のヒッグスが 空間中に広がっているとしたら、私達は容易に ヒッグスを 検出できて かつ 日常生活に利用 できているはずである。
しかし そういうことは 不可能であり、それをしようという計画すらない。非常におかしいと言わざるを得ない。
(Fig.12) 何兆回もの衝突で ヒッグス1つだけ? ← 本当に全空間中にあるの?
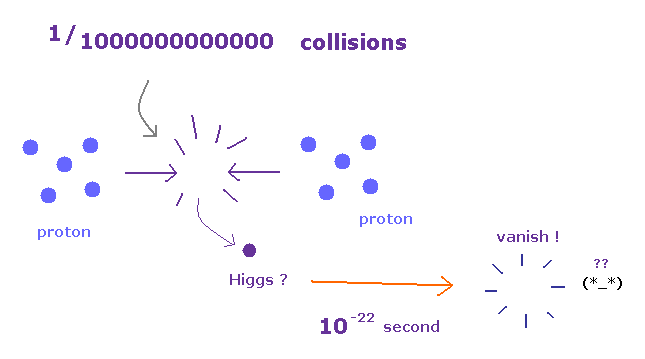
このサイト や このサイト にあるように、ヒッグス粒子1つを生成するには 1兆回以上もの 衝突が必要になるらしい。 まさに 干し草の山の中から 小さな針を見つけるかの如くである。
これらのコメントを見ると、この 非常に 稀にしか現れないヒッグス粒子が 全空間中に広がっているという 無数のヒッグスの定義と まったく 一致してない ことが分かる。
例えば、電子は 原子核と伴に すべての原子を形成するとされている。
実際、いかなる原子、分子においても、イオン化することによって、飛び出してきた電子を
容易に検出できる。
つまり、電子は 元の電子の定義と 一致し、すなわち リアルな存在であることがわかる。一方、ヒッグスのほうは 元の定義と 全然 一致していない。
また このサイトにあるように、ヒッグスの寿命は たったの 10-22 秒であり、非常に不安定な粒子である。
つまり、加速器内で見つかったとされるヒッグスは 本来の "無数"のヒッグス粒子の定義を
満たしていないのである。つまり、リアルな存在とは "言えない" ことになる。
(Fig.13) トップクォークは 金原子ほどの重さ でも素粒子 !?
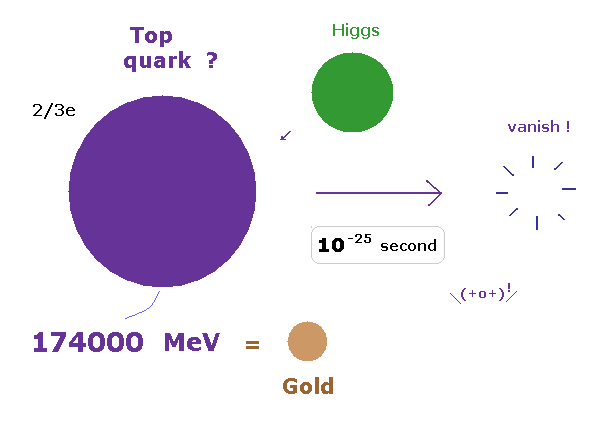
このサイトにあるように、トップクォークの質量は 174000 MeV ほどで、 金原子ほどの重さがある。
これだけ大きな質量にも関わらず、その寿命は たったの 10-25 秒しかないのである。
このサイトによれば、 6兆回もの衝突で たったの 40個 のトップクォークしか 生成できないとされている。
もちろん、 +2/3. -1/3 などの 分数電荷は 単離できないため、クォーク自体は 単なる "想像上の" 粒子にすぎない。
(Fig.14) 原子核の質量の 98% は QCD よるもので、 ヒッグスは たった 2% のみ。

このサイトにあるように、クォークの質量は 原子核の質量の たったの 数% を占めるにすぎない。
原子核質量の 98 % 以上は カイラル対称性の破れ ( グルーオンの相互作用 ) によるとされている。
"アップ"、"ダウン" クォーク の質量は QCD の自由に決められるパラメーターであり、自然な結果とは まったく言えないものである。
また 非常に重い トップクォークと 非常に軽い アップクォークが まったく同じ電荷量 (= +2/3e ) を持っていることも 不自然極まりない。
しかし、トップクォークは 原子核を 形成できず、その質量 (= 金原子ほど ) は ヒッグスのみ によって生じるとされている。
これらの 非常に強引な解釈を見れば、これらのクォークが 便利な 非現実的な概念であることが 理解できる。
(Fig.15) β崩壊 では 全エネルギー ( W ボソンの ) の保存則が破れている。 ← 非実在的な粒子。
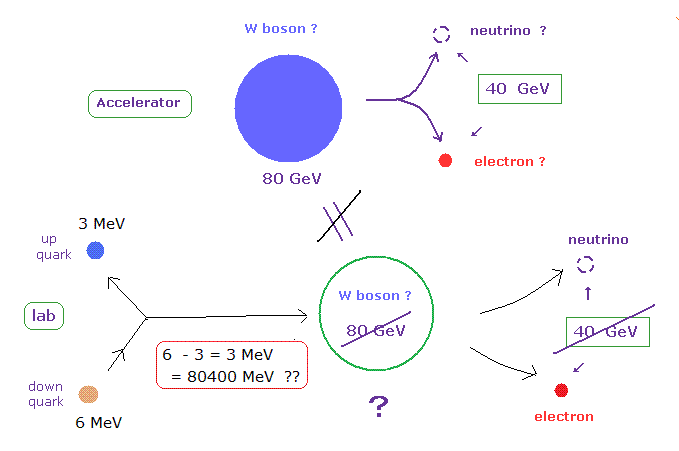
この 陽子の 80 倍もの 非常に重い W ボソン (= 80 GeV ) の質量は 高エネルギーの加速器でのデータを基に算出したものである。
つまり 加速器内での この W ボソンは 実験室内でのものをは まったくの 別物なのである。
通常の β 崩壊では、中性子内の ダウンクォーク が 負電荷の W ボソンを放出して 陽子内の アップクォークに変化するとされている。
しかし これら ダウンとアップクォーク間の質量エネルギーの違いは たったの 3 MeV であり、これは W ボソンの質量 (= 80 GeV = 80000 MeV ) よりも 比較にならないほど小さい。
つまり β崩壊の W ボソンが 高エネルギー加速器でのそれを等しいとすると、エネルギー保存則という 物理の基本的性質が 完全に破れていることになる。
これはつまり W ボソンとは 非常に非現実的な粒子なのである。
また W ボソンの寿命は たったの 10-25 秒であり、 このサイト にあるように 10 億もの衝突で せいぜい 10 個 ほどしかできないとされている。
そもそも このように 無数ともいえる 衝突を繰り返せば、 その中で 少しぐらい 欲しかったデータが あっても 不思議でも何でもない。
つまり 加速器は ヒッグス、クォーク、W ボソンの証明には まったくなっていないと言える。
(Fig.16) ヒッグス、クォーク、超対称性粒子が見つかっても その "次" がない。

例え、物理学者達が "ヒッグス、超対称性粒子、 4クォーク を見つけたと主張しても、はっきり言って 完全に 無意味以外何者でもない。
これらの不安定な粒子は 直接観測することが できない。
また、それらを生成するのに ほぼ無数の衝突を必要とする。
つまり、加速器内の 不安定な粒子の探索は 無用な長物という点で 初期宇宙 や ブラックホールの研究と 非常に似通っている。
例え、効果な加速器に 莫大な費用と時間を使ったとしても、私達は これら架空の粒子を 永遠に 利用することができない。
そもそも 非常に 稀にしか出現しないとされる ヒッグス粒子は 私達の周囲に無数に存在するとされる ヒッグスの元の定義と 完全に 異なっている。
直接的にも間接的にも 役に立たないということは、これらが 実存していないということと等価である。
(Fig.17) ハイパーチャージは 粒子の運動方向のみで 変わってしまう?
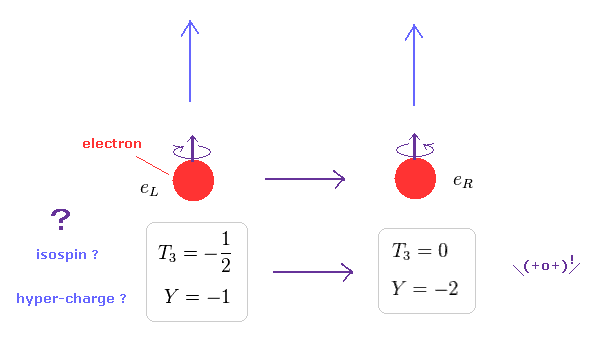
このサイトにあるように、 右巻きの粒子では、そのスピンと運動量の向きが 同じで、 左巻きの粒子では、それらの方向が 逆 である。
現在の標準模型は これら曖昧な ヘリシティー なるものを 最も重要な概念と 考えている。
驚くことに ウィークハイパーチャージ は このサイトにあるように、右巻きと左巻きの粒子で まったく異なるのである。
Fig.17 を見て分かるように、 電子が その移動方向を 変えるとき、 そのハイパーチャージ は "-2" から "-1" に変わってしまう。
つまり、このハイパーチャージとは 粒子に備わった 基本的な電荷とは まったく 異なるものということか? 非常に奇妙な概念である。
(Fig.18) "ハイパーチャージ" とは何か? → "黙って計算だけしてろ?"
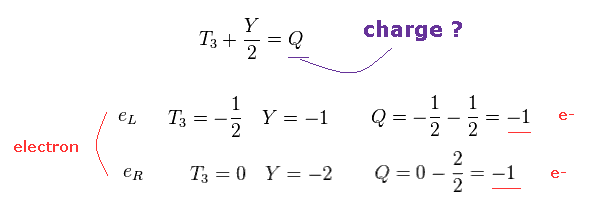
もちろん、電子では、左巻き (= eL ) も 右巻き (= eR ) も 同じ 負電荷 (= -1 ) を持つことは言うまでもない。
この事実に合わせるために、彼らは 各ウイークアイソスピン (= T3 ) と ハイパーチャージ (= Y ) の値を 都合のいい値に 調整した。
つまり これらの概念や数値は 非常に人工的に設定したものである。
また、これらのハイパーチャージが 粒子の移動方向のみで その値を変えてしまうことは 非常に 不自然である。
極めつけは、物理学者達は このハイパーチャージとは 一体全体何なのか これ以上 追及することを
諦めて 抽象的な概念のまま放置していることである。
(Fig.19) 陽電子は実在するのか ?
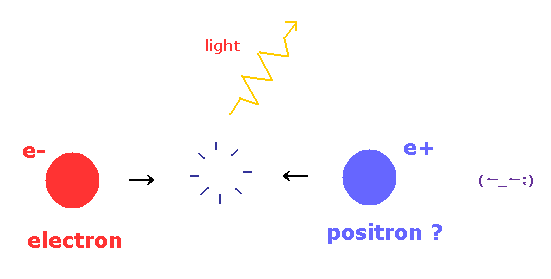
陽電子は 電子の反粒子である。
陽電子は 電子と 同じ質量で、かつ 反対の電荷 +e を持つ。
現在の量子論によれば、陽電子は 容易に 電子と 対消滅し、 γ 線 を形成する。
重要な点は、これから説明するが、この反粒子の存在は 物理の基本的な原理と 矛盾するということである。
これはつまり、反粒子には 最初から 実在性が ないのである。
(Fig.20) 陽電子は 光子から生成される。 なのに なぜ "原子核" が必要?
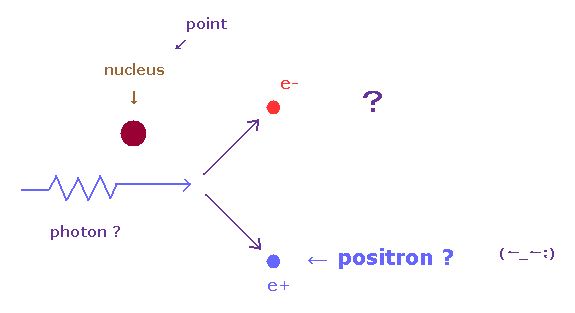
このサイトによれば、 高エネルギーの電子が 原子核の近くを 通るとき、光子を 放射し、 この光子が 電子・陽電子対に 変化する としている。
しかし、この説明が正しいとすると、原子核 (= 標的 ) は まったく 必要ない ことになってしまう。
なぜなら、強力な電磁場の条件さえあれば、各電子は 高エネルギーの光を放射できるからである。
では なぜ 陽電子を生成するのに 電子を 他の原子核に 衝突させる必要があるのだろうか?
実は この理由は 非常に 理不尽で 許されざるものである。
(Fig.21) 入射した光の運動量が 突然 ゼロになる ( p = 0 ) !?
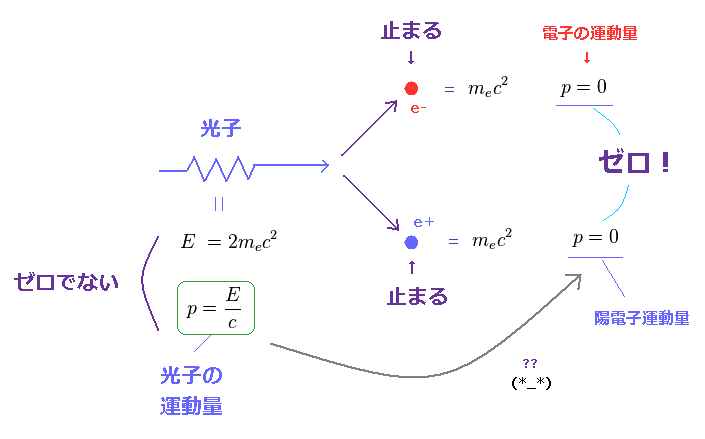
このウェブサイト には 次のような説明がある。
----------------------------
もし、光子が ちょうど 電子・陽電子対の質量エネルギーを生成するだけの エネルギー (= 2mc2 ) を持っているとき、生成された 電子と陽電子は 静止することになる。
このとき、 運動量の保存則 を 破ってしまう。
なぜなら 入射した光子には 運動量 ( p = E/c ) があるが、生成された 電子・陽電子は 静止しているため、運動量を 持たない からである ( p = 0 )。
これはつまり、この対生成は 原子核の近くで 起きなければならない。
なぜなら、この原子核に 光子の運動量を 吸収してもらう必要があるからである。
-----------------------------
実は、この説明は 自己矛盾を含んでいるのである。 このサイトも参照のこと。
なぜなら、原子核が (運動)エネルギーを吸収せずに、 運動量のみを 吸収することは 不可能だからである。
(Fig.22) 運動量のみが 保存されない !?
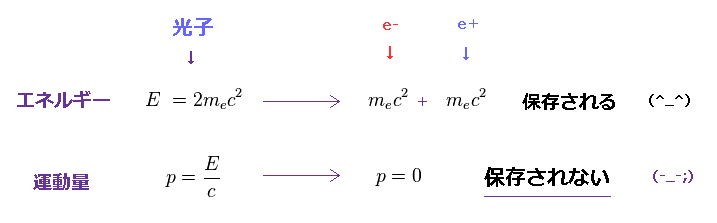
Fig.22 に示したように、入射した光子が ちょうど 2mc2 のエネルギーを持つとき、アインシュタインの質量公式によれば、1対の電子と陽電子が生成される。
しかしこのケースでは、生成された電子・陽電子は 静止しているため 運動エネルギーを 持っていない ことになる。
なぜなら、入射光のすべてのエネルギーが 質量エネルギーに 使われてしまうからである。
もちろん、入射光は 運動量 ( p = E/c ) を持つ。
しかし、生成された電子・陽電子は 運動量を 持っていないのである ( p = 0 )。
これは明らかに 致命的な矛盾である。
(Fig.23) 便利な原子核が "余分な" 運動量を吸収してくれる ?
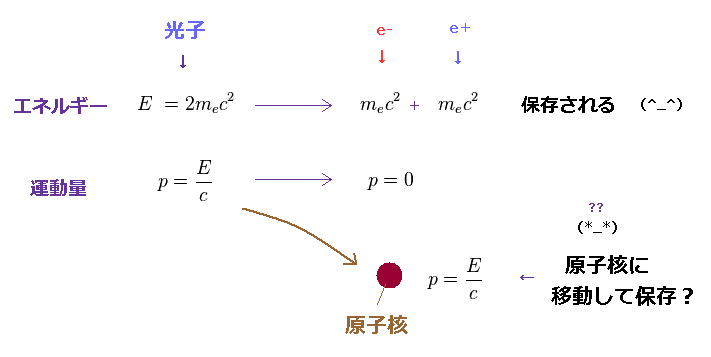
もちろん、全運動量 ( と エネルギー ) は 保存されなければならない。
この 物理の基本的なルールを満たすために、彼らは 光子の近くにある原子核が この余分な運動量を 吸収する と考えたわけである。
お気づきのとおり、この説明は 非常に理不尽である。
(Fig.24) この原子核は "運動量" があるが、運動エネルギーを持たない !?

奇妙なことに、この原子核は 運動量を持つのに、運動エネルギーを 持たない のである。
もちろん、この現実の世界では こんなことは 不可能である。
よって この事実は 電子・陽電子対の生成自体が あり得ない現象であることを示している。
つまり、陽電子は 単に 正電荷のイオン、陽子、もしくは 散乱された電子群 が混ざったものということになる。
事実、彼らは 陽電子発生のために、必ず 原子核との衝突 に頼っている。
(Fig.25) 陽電子・電子対消滅は リアルなのか?
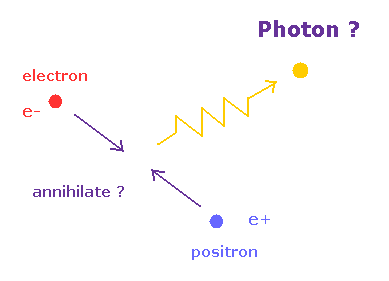
次に 電子・陽電子の対消滅について考える。
ファインマン則によれば、この粒子対は 新たな光子1つ を生成することになる。
(Fig.26) 重心系での 対消滅。
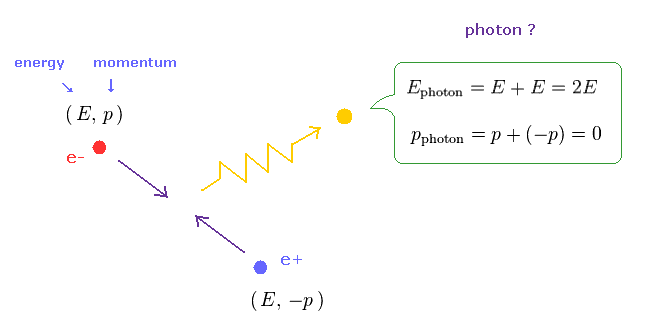
ここで、重心系での 対消滅を考える。
つまり 互いにちょうど逆方向の運動量を持つ 電子と陽電子が 衝突して 光子が形成されるケースである。
エネルギー・運動量の保存によれば、生成された光子のエネルギーは 元の粒子の2倍となる。
(Fig.27)
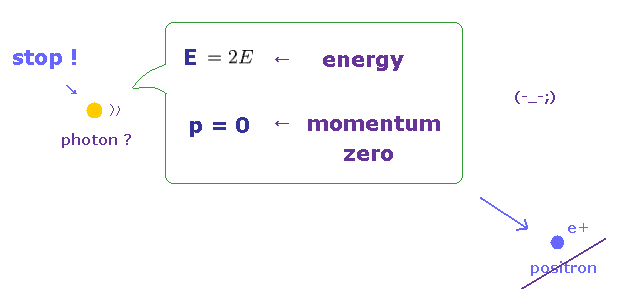
しかし 生成された光子の運動量は キャンセルされて ゼロ になってしまう。
これはつまり、この光子が ストップしてしまうことを意味している。 このサイト (p.2) も参照のこと。
もちろん、光子 (= 電磁波 ) は ストップすることは できない。
つまり この生成された光子は 相対論に反する 仮想光子 ということになる。
ファインマン図によれば、電子・陽電子対消滅では まず最初に 1つの光子のみ生成される必要がある。
ご覧のとおり、陽電子の存在は 相対論的な場の量子論において、自己矛盾を生みだす要因となっている。
(Fig.28) Na22 は 電子捕獲 と β+崩壊 の両方で 崩壊できる。

このサイト や このサイト (p.3) にあるように、 Na22 は β+ 崩壊 (90%) もしくは 電子捕獲 (10%) の どちらの経路でも Ne22 に崩壊できる。
そのどちらの経路でも、Na22 原子核の 正電荷は 1つ 減少する。
しかし実は 同種類の原子核において、これら2種類の異なる崩壊を し得ることは
不可能 である。
(Fig.29) 電子捕獲: Na 原子核が 1つの負の電子を "吸収"する。
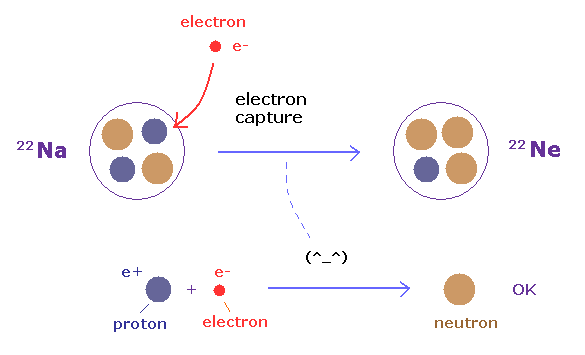
電子捕獲では、原子核は 1つの負の電子を吸収する。
そのため、 Na の原子番号 (= 11 ) は Ne (= 10 ) に変わる。
Na 原子核の内部では、陽子と電子が 結合して 中性子になる。
中性子は 陽子よりも 少し重いことを考えれば、この反応は 非常に 自然なものと言える。
(Fig.30) β+崩壊: Na 原子核は 1つの陽電子を放出する ?
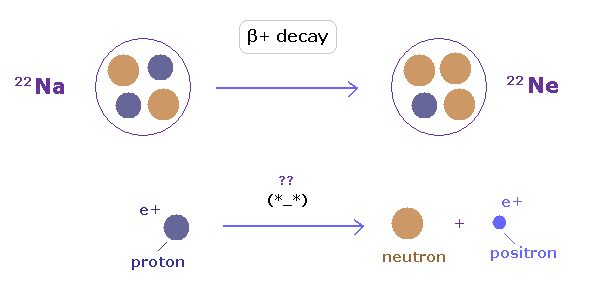
β+崩壊では、 Na 原子核は 1つの陽電子を放出する。
つまりこのケースでも、Na 原子核の正電荷 (= 原子番号 ) は 1つ減ることになる。
よって 電子捕獲と β+崩壊の両方の経路で 同一の Ne 原子核を生成できる というわけである。
しかし 電子捕獲では Na 原子核は 粒子を1つ 吸収するのに対し、 β+崩壊では、 Na 原子核は 粒子を 放出している。
要するに これらの反応は まったく違うものなのである。
(Fig.31) 陽子が 2つに分離して 陽電子を放出?
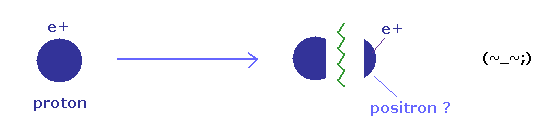
ご存じのとおり、原子核の正電荷は もともと 陽子 に由来している。
なぜなら 非常に不安定な陽電子が 原子核内部で 長期間 存在し続けることは 不可能だからである。
これはつまり、 β+崩壊では、 Na 原子核内の陽子が 2つに分離して、陽電子に 正電荷 を与えるという あり得ない現象が 起こることを前提にしている。
(Fig.32) エネルギーが どこから放出されるのか ? ← 自己矛盾。
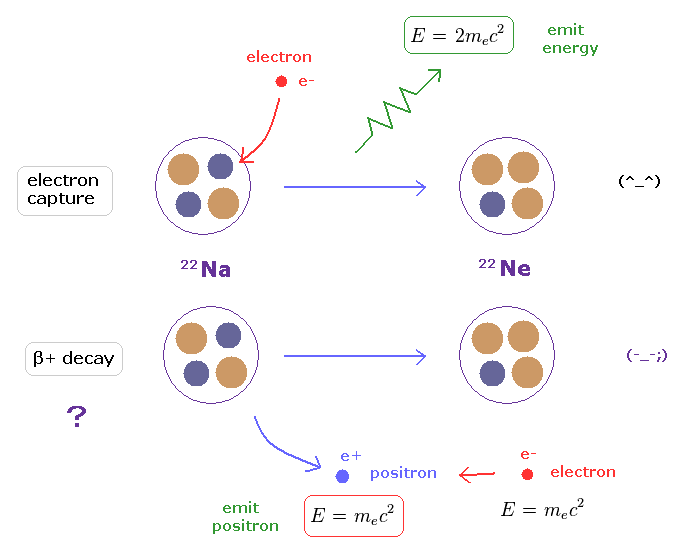
同じ Ne 原子核が 生成されるということは、電子捕獲と β+崩壊の両方において、 同じ量のエネルギーが 放出されることを意味している。
電子捕獲 ( Fig.32 上 ) では、このエネルギーは 吸収した Na 原子核そのものから 放出されることになる。
一方で、 β+崩壊 ( Fig.32 下 ) では、 Na 原子核は エネルギーの代わりに 陽電子を放出することになる。
そして、この陽電子は 外部の電子のどれかと消滅して、原子核とは別の場所で、 2me2 のエネルギーを放出することになる。
これはつまり、β+崩壊においては、放出されるべきエネルギーの一部 (= mc2 ) が まったく関係ない外部の電子のどれかに 予め テレポートされていることになる。
もちろん、こんなことは あり得ないため、 β+崩壊 (= 陽電子 ) 自体 非現実的な現象であることが理解される。
(Fig.33) Mg 原子核を破壊して、 Na22 陽電子源を生成。 ← 陽電子は 何の関係もなし。
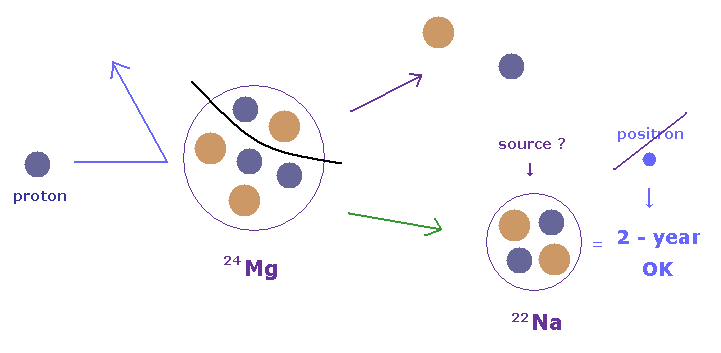
このサイトにあるように、陽電子源 Na22 を生成するには、 マグネシウムの標的に 高エネルギーの陽子ビームを 数週間にわたって 衝突させる。
これはつまり Na22 原子核は Mg 原子核から 陽子と中性子を1つずつ 除去することによって得られる。
この Na22 陽電子源の 寿命は 2年間ほどと長い。
そのため、最初の衝突で 陽電子が生成されたとしても 非常に不安定なため、Na 原子核内で その状態を保持できない。
この事実から、 Na22 陽電子源が "想像上"の陽電子とは 何の関係もないことが 容易に理解できると思われる。
この Na22 は 過剰の陽子を持ち、これが 電子捕獲を介して 電子を吸収することになる。
(Fig.34) 減速材は 陽電子を減速できる?
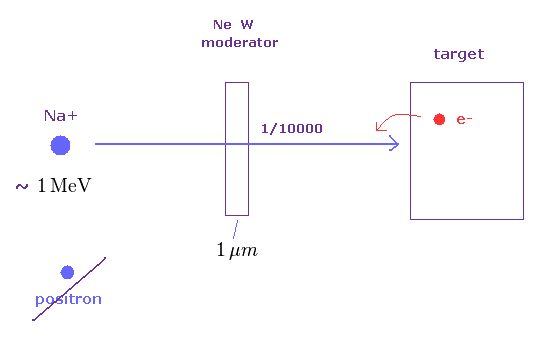
このサイトや
このサイトにあるように、減速材は 高エネルギーの陽電子の速度を 減少させると言われている。
この減速材は わずか 数 µm ほどの厚さで、タングステンや 固体ネオン などからできている。
この減速材を通過後は 陽電子の量は 元の 1/10000 ほどに減ってしまう。
そもそも 陽電子を減速させたいのなら 電場を逆方向にかければいいだけなのに、減少の危険を顧みず 減速材を用いるのは なぜなのだろうか?
電子や イオン (= Na+ ) などの 放射される粒子は 高エネルギー ( ~ 1 MeV = 106 eV ! ) 状態にある。
よって、固体内の 結合エネルギー (= 3 eV ) に打ち勝って、一部が 貫通して出てくることになる。
つまり、陽電子と称するものは 高エネルギーの 陽イオン ( Na+ )、電子などの ミックスしたものと 考えるのが自然である。
なぜなら、非常に少量の陽電子のみを 他の粒子から 分離することは 不可能だからである。
(Fig.35) 非常に少量の陽電子は 分離できる ?
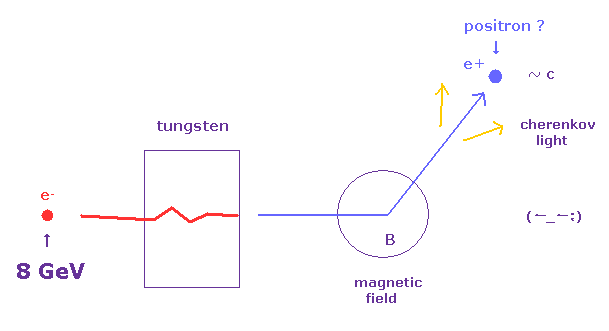
この論文では、高エネルギーの電子ビーム (= 8 GeV ) を タングステンの標的に 入射させて陽電子を発生させている。
磁場のかかった部分で、生成されたとされる陽電子は ローレンツ力によって その方向を変える。
検出装置の部分では、高速度の陽電子が 所謂 チェレンコフ光を放射し、その強度から 陽電子数を推定するとしている。
重要な点は、この種の加速器実験では 無数の荷電粒子間の クーロン散乱に関するコメントが ほとんどないことである。
(Fig.36) 磁気ローレンツ力は "運動量" の情報のみを与える。
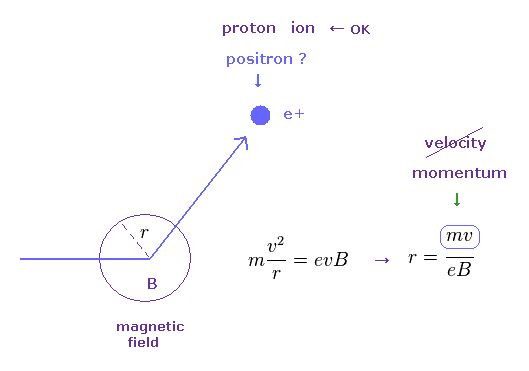
Fig.36 では、外磁場 (= B ) の下で、 遠心力が ローレンツ力に等しい。
このケースでは、回転半径 (= r ) が 運動量 (= mv ) の関数になっている。
つまり、この磁場のみの状況では、陽電子と 他の正の荷電粒子を 見分けることができない。
もし、粒子が 同一の運動量 ( = mv ) を持つとしたら、重い粒子ほど その速度は 遅くなることになる。
これらの区別のため、粒子を ある放射物質中に通して、ある閾値以上の高速度の荷電粒子 ( 例えば、軽い陽電子とか ) が チェレンコフ光 を発するのを検出する。
この方法で、果たして 陽電子を 正確に検出できるのだろうか?
(Fig.37) 多粒子間の "クーロン散乱" を もっと考慮すべき。
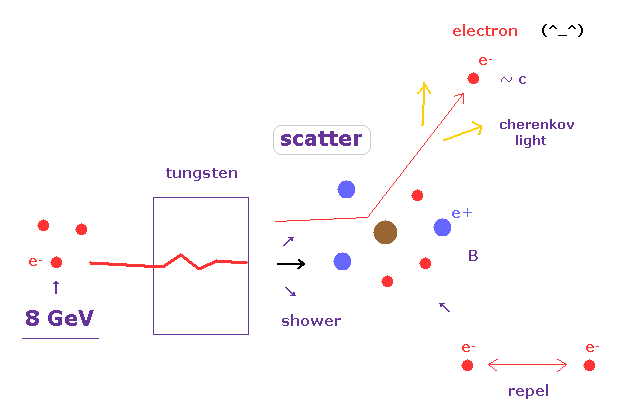
しかし、この解釈は 最も理想的な前提条件を想定している。
この装置内に 陽電子が 1つのみしか存在しなければ、この陽電子は ローレンツ磁気力で 正確に曲がれるだろう。
しかし、このケースでは 通路内は 高エネルギー衝突後の たくさんの 電子、陽子、壊れた原子核などの荷電粒子で 溢れ返っている。
つまり、入射する高エネルギーの電子は 容易に 他の粒子で 散乱されてしまう。
もしくは この高エネルギー電子が 装置内壁に衝突してできた
二次電子などが 検出器方向へ 飛んでいくことも 十分にあり得る。
8 GeV というエネルギーは 電子の質量エネルギー 0.5 MeV よりも はるかに巨大であるため、散乱後の電子なども 非常に 高速になる。
(Fig.38) クーロン散乱が 支配的。
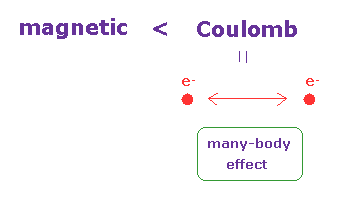
基本的に 高エネルギー加速器の研究者達は 多数の荷電粒子間のクーロン相互作用を 軽視する傾向にある 。
荷電粒子同士が 互いに近づくと、ローレンツ磁気力よりも クーロン相互作用のほうが
はるかに強くなる。
もちろん、無数の 高速の粒子が飛び交う空間での 正確な クーロン多体相互作用の計算は 実質的に不可能である。
このことが 高エネルギー物理における 最も重要な 弱点である。
(Fig.39) 少なすぎる反粒子は "誤差" だらけ。
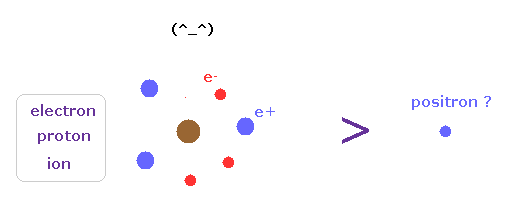
基本的に 反粒子の数の割合は 他の電子、陽子、イオンの数に比べて
非常に少ない。
つまり、容易に 反粒子を 他の荷電粒子と間違える原因になる。
(Fig.40) ATLAS 検出器は トラッカー、カロリメーター、ミューオン検出器 からなる。
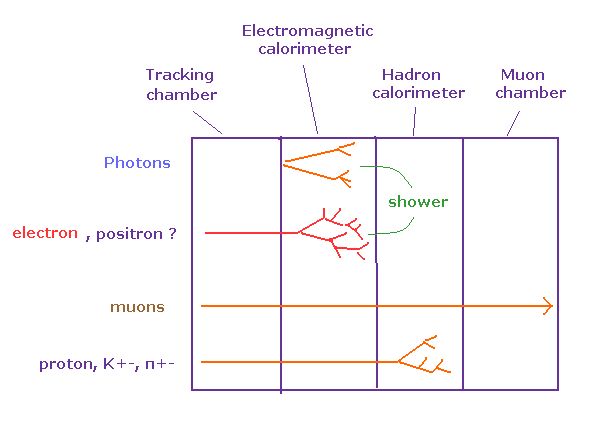
このサイトにあるように、加速器の検出器は 4つの主要な部分で構成されている。
飛跡検出器 (= tracker ) では、外磁場の中、飛んできた荷電粒子は 媒質中の電子を イオン化し、その電気信号を検出することによって、 粒子の位置、運動量情報を得ることができる。
カロリメーターでは、荷電粒子は 検出器の物質に衝突することによって、多数の2次粒子 のシャワーを発生させる。
この発生した 2次粒子の全荷電量もしくは 全光量 を測定することによって、元の粒子のエネルギーを推定するわけである。
現在の素粒子物理学によれば、ミューオンは 止まることなく これらのカロリメーターをすり抜けることができる。
そのため、ミューオン検出器は ATLAS 検出器の 最外層を覆っている。
(Fig.41) シリコン飛跡検出器 クーロン散乱だらけ。
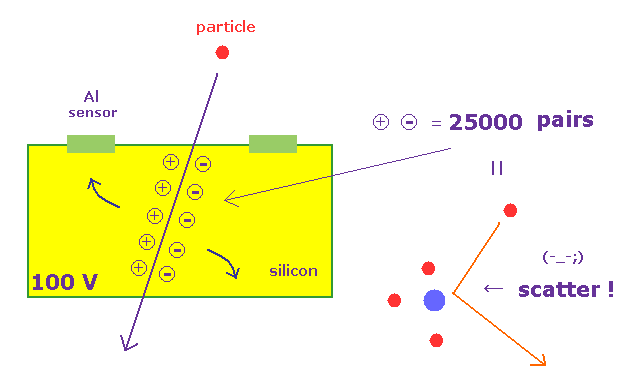
ATLAS の最内層は シリコン半導体トラッカーがあり、 このサイト (p.15) や このサイト にあるように、荷電粒子が通過すると、シリコン中の 多数の電子・ホール対をイオン化する。
この 正のホールが Al 検出器のほうへ ドリフトして、その電気信号を検出することによって、通過する粒子の位置情報を得るわけである。
このサイト (p.4) や このサイト (p.40) にあるように、荷電粒子が 1回通過するごとに 25000 もの 電子・ホール対が 生成される。
つまり、各粒子は これらシリコン検出器内で 明らかに クーロン力による 散乱 を受けることになる。
もちろん、このことは 磁場による運動量測定に
悪影響を与えることは 明白である。
(Fig.42) クーロン散乱は 磁気ローレンツ力よりも はるかに大きい。
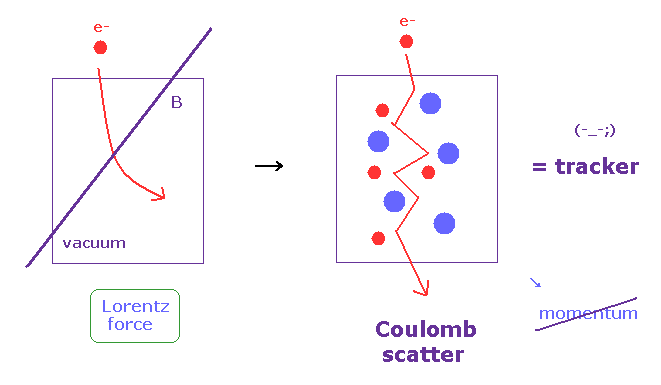
色んな検出機構を調べると分かるが、加速器の研究者達は これらの クーロン散乱の効果を 明らかに 軽視している ( 要するに 考察コメントが かなり ラフな推測に基づいている )。
それもそのはず、ほぼ無数の 粒子間の 多体クーロン相互作用を 正確に知ることは 不可能だからである。
トラッカーで 粒子の運動量を正確に知ることは 粒子の識別にとって 必須事項である。
各粒子は 上記のシリコン検出器を 少なくとも 4 層以上 通過しなければならない。
つまり 25000 × 4 = 100000 もの 電子・ホール対が、たった一個の入射粒子によって 生じることになる。
もちろん、このことによって 各粒子は そのエネルギーを 非特異的に消失することは 間違いなく、この消失エネルギーは 正確に 知り得ないため、間違った消失エネルギーの要因の1つになる。
(Fig.43) ATLAS の TRT 飛跡検出器。
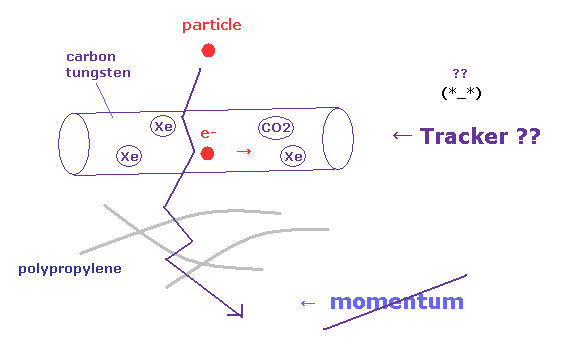
さらに、 このサイト (p.23, p.25 ) にあるように、各粒子は 30 もの TRT (= transition radiation tracker ) という飛跡検出器を通過しなければならない。
TRT は 直径 4 mm の 炭素と タングステンでできた ストローチューブを含んでいる。
このストロー間は ポリプロピレンで満たされ、この物質内で 電子が X 線を放射する。
この X 線は Xe ガスに吸収され、それが 多数の二次電荷を生成する。
見てのとおり、各粒子は その運動量の測定のために 真空どころか、非常に多くの固体物質の中を 通過しなければならない。
つまり 粒子識別のための こういった運動量測定というのは 磁場しか想定していないため 非常に疑わしいことが分かる。
(Fig.44) 電磁カロリメーター。
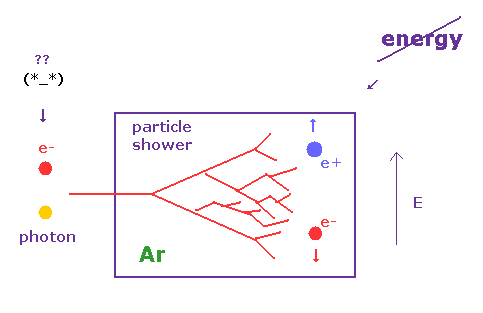
このサイト (p.4) や このサイトにあるように、光子や電子が カロリメーターの吸収層に衝突すると、 多数の2次粒子や イオン化された電子が 液体アルゴン中に放出される。
ここでは 外電場がかけられており、生じた電荷の全量を 電気信号として検出して 全エネルギー量を推定するわけである。
しかしもちろん、こういった検出器には 検出閾値の設定が 絶対に必要であるため、すべての生じた粒子を検出することは 不可能である。
さらに 単に全量を知るだけで、個々の 運動エネルギーの情報が分からず、これもまた 誤った消失 (= missing ) エネルギーの原因となる。
(Fig.45)
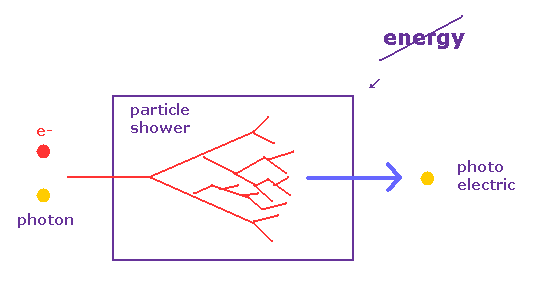
荷電粒子が これら物質を横切ると、そのエネルギーは だいたい イオン化と 放出光 の半々に分配される。
つまり 電荷シグナルと 放射光シグナルの 両方を同時に正確に知る検出器が本来は必要である。
しかし このサイト (p.39) にあるように、 技術的に 同一の装置で 光と電荷を見分けることは 実際には困難である。
(Fig.46) 移行した運動エネルギー ( や 光の振動数 ) は 分からない。
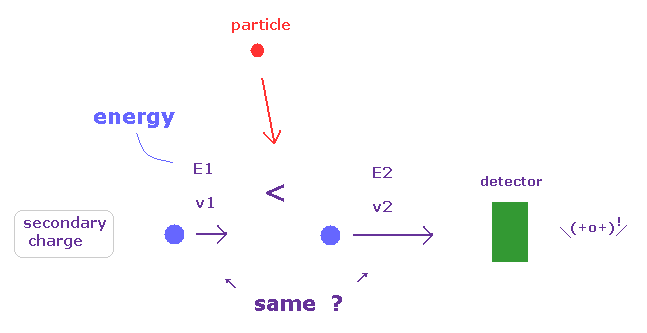
カロリメーターにおける 全エネルギーの測定は 非常に粗い推定に基づいている。
例え、2次粒子の全電荷量を測定しても それが全エネルギーを測定したことにはならない。
なぜなら、これらの検出器は 各粒子の 運動エネルギー や 光の振動数を 測定することができないからである。
つまり 加速器で得られる ニュートリノや LSP の存在に指標となる 消失エネルギーの値は 非常に
疑わしい と言わざるを得ない。
(Fig.47) ボソンと フェルミ粒子のループが 互いにキャンセルする?
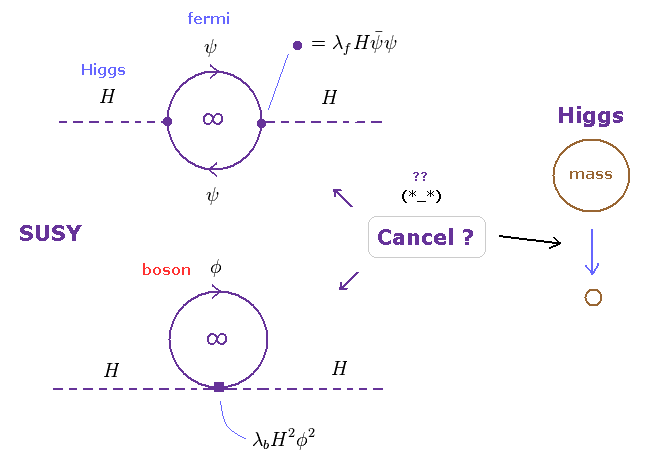
このサイトにあるように ヒッグスの質量の 1ループ補正は 無限大 に発散する。
この時点で、繰り込みに基づく 標準模型は 本当の物理とは 到底言えないことが分かる。
QED によれば、フェルミ粒子と ボソンは は 互いに逆符号の 無限大のループを与える。
逆符号は フェルミ粒子の反交換関係に起因している。
しかし 物理学者達は この反交換や 無限大ループの 物理的なメカニズムに関して まったく
答えようとしない。
つまり、標準模型と 超対称性は この時点から 決して 進歩することができない。
(Fig.48) フェルミ粒子の質量が軽い理由は "カイラル対称性" ? 本当に物理?
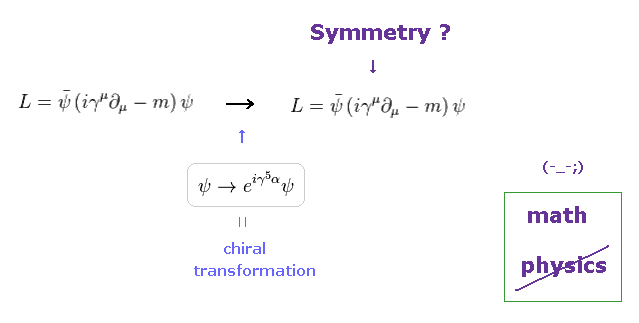
非常に厳しい相対論的な制限のために、物理学者達は 理論を発展させるのに人為的な対称性という概念に頼らざるを得ない。
例えば、 Fig.48 では ラグランジアンが カイラル変換の下で 不変のとき これを カイラル対称性と呼ぶ。
フェルミ粒子に質量があるとき、このカイラル対称性は 破れる。
( つまり 最初から破れていることになるので この対称性自体 無意味なものである。 )
見てのとおり、これらの抽象的な数式記号で 現実の複雑な世界を表現すること自体
不可能である。
(Fig.49) 124 ものフリーパラメーターを含む MSSM は 都合のいい理論である。

最小超対称標準模型 (= MSSM ) は、超対称性理論の 最も単純なモデルである。
現在の素粒子物理学者達は 超対称性を 最も重要な概念と考えている。
しかし これら超対称性粒子は 簡単には見つからないため、超対称性は 破れていなければならず、すなわち 超対称性粒子は 非常に重い と彼らは主張している。
この破れのために、MSSM は 124 もの 自由に設定できる パラメーター (= 質量や結合定数など ) を含むことになる。
このサイト (p.12) や
このサイト 参照のこと。
これはつまり 超対称性理論は 10500 もの異なった真空を含む 10 次元の超弦理論のように、何も予測する力がない ことを意味する。
(Fig.50) "ゲージ対称性" が 光子の質量ゼロの原因? 本当 ?
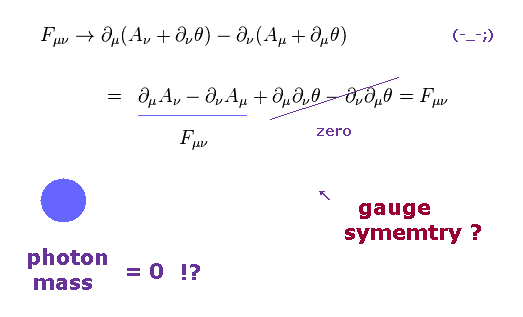
現在の標準模型では、 "ゲージ対称性" が 最も重要な概念である。
ラグランジアン (= Fμν ) が ゲージ変換で 不変のとき、これを "ゲージ対称性" という。
もし 光子に質量があるとき、この ゲージ対称性は 破れるため、光子には 質量がない と 彼らは主張しているわけである。
しかし ウィークボソンには 大きな質量があるため、このゲージ対称性は 最初から破れていることになる。
つまり 最初から "破れた" ゲージ対称性自体 無意味な概念であることが分かる。
彼らは 盲目的に この 単なる数式である 対称性を 信じることを止めるべきである。
(Fig.51) ヒッグス粒子と フェルミ粒子 (ボソン) 間の 相互作用ハミルトニアン。
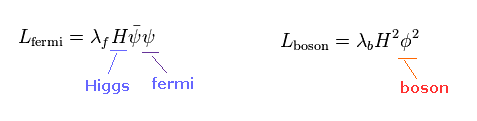
このサイトによれば、超対称性は ヒッグスの質量における 階層性問題を 解決できるとされている。
残念ながら、これらの概念は 単なる数式記号の話で、私達のリアルな世界とは
何の関係もない。
ヒッグスと フェルミ粒子 ( もしくは ボソン ) 間の相互作用は Fig.51 のように表せる。
ラグランジアン (= ハミルトニアン ) は 量子論において 非常に抽象的な概念である。
(Fig.52)
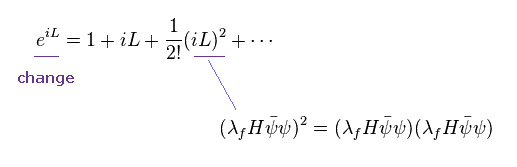
系の時間発展は ラグランジアン L を含む指数関数に依存する。
フェルミ粒子のケースでは、2次の項が 1ループの発散に関与している。
(Fig.53)
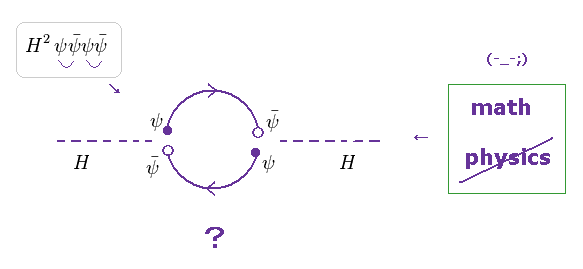
Fig.52 の2次の項を用いて 各関数を繋げると、ファインマンダイアグラムは 1ループを形成する。
"ループ" とは、この式が 無限大の (= 非現実的な ) 確率密度を与えることを意味する。
これは 単に QED における 数学的なルールにすぎない。
(Fig.54)
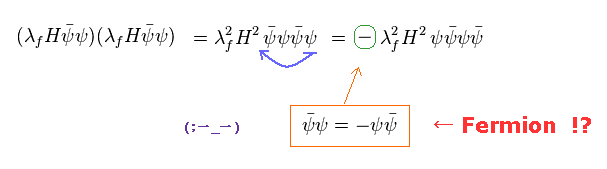
QED では、各関数の順番が 非常に重要である。
Fig.52 と Fig.53 を比べると、 右の ψ を 左側に移動させる必要があることが分かる。
フェルミ粒子の 反交換関係のために、2つの関数を交換すると、全符号にマイナスがつく。
もちろん、これは 単に 数学上 ( 物理でなく ) の理由にすぎない。
右の ψ を 左に移動するのに、関数を 3回 交換する必要がある。
"3" という数字は 奇数であるため、 (-1)3 = -1 となり、 負の符号が この式にくっつくというわけである。
(Fig.55)
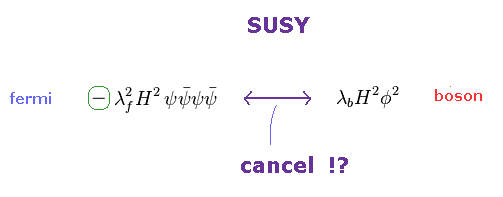
一方で、ボソンは 通常の交換関係に従う。
そのため、ボソンの関数を いくら交換しても 負の符号はつかない。
結果的に、フェルミ粒子のラグランジアンのみが 負になり、ボソンのほうは 正になる。
これらの逆符号の式同士が 互いに キャンセルし合うというわけである。
(Fig.56)
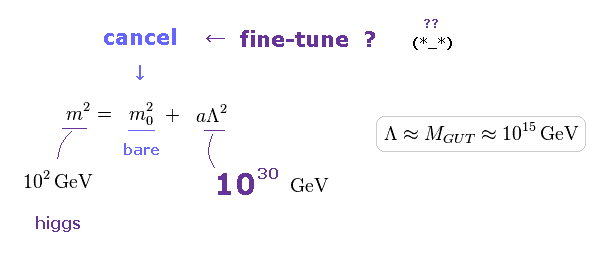
もし 超対称性が使えないと、 裸の (= bare ) ヒッグスの質量が この 2次の発散項 (= Λ2 ) を打ち消す必要がある。
二次の発散は 統一理論では 1030 GeV ほどの大きさになる。
本当のヒッグスの質量は 126 GeV ということになっているので、約 30 桁にもわたる 数を ちょうどキャンセルする必要がある (= 微調整問題 )。
残念ながら、この説明には まったくと言っていいほど 物理的実態を伴っていない。
まったく無意味な こじつけ である。
(Fig.57) フェルミ粒子とボソンは 互いにキャンセル ? 物理 ?
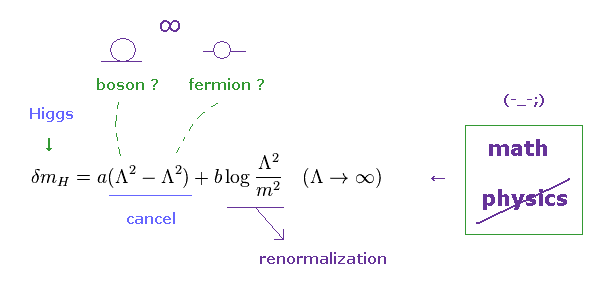
Fig.53、 Fig.55、 このページ などに基づいて、ループ関数を計算すると、 2次の発散項が フェルミ粒子の 負の発散項によって キャンセルできる。
そのため 彼らは フェルミ粒子とボソンによる 超対称性が ヒッグスの質量の 微調整問題を解決できると 主張しているわけである。
しかし 対数発散が まだ残っており、これは 無限大を与える。
結局、超対称性を導入しても、人為的な 繰り込みは 無限大の除去のために 使わなければならないのである。
(Eq.1)
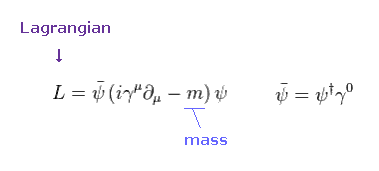
このセクションでは、 フェルミ粒子の質量が小さいことの原因とされる "カイラル対称性" について説明する。
残念ながら、一見して分かるとおり、この対称性という概念は 単なる抽象的な数式で "真の"物理とは 到底言えない代物である。
ディラック方程式のラグランジアンは Eq.1 のように表せる。 このサイト (p.42) も参照のこと。
4 × 4 の γ 行列では 次のような "カイラル表現" を用いる。
(Eq.2)
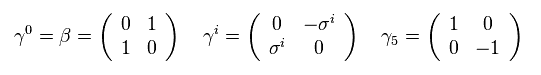
(Eq.2')
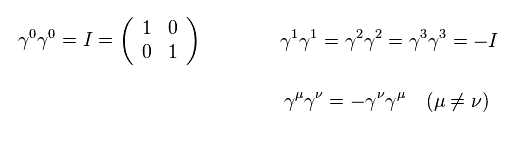
異なった γ 行列同士を交換すると、Eq.2' に示したように、負の符号がつく。
Eq.2 では、 σ は 2 × 2 のパウリ行列である。
(Pa.1)
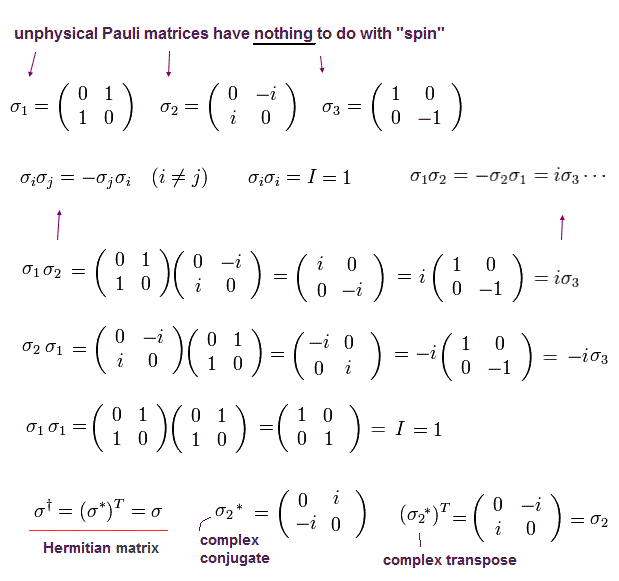
ここで Eq.2 の γ5 行列を用いて、次のような カイラル変換をする。
(Pa.2)
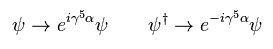
この変換の下で ラグランジアン (= L ) が 不変のとき、これを"カイラル対称性" と呼ぶ。
つまり、 "対称性" とは ローレンツ変換、ゲージ変換、超対称性変換などの 操作で ラグランジアン (= これは ハミルトニアンや 運動方程式を与える ) が 不変であるということである。
(Eq.3)

最初に、Eq.3 で フェルミ粒子の 質量 (= m ) が ゼロ のケースを考える。
結果、Eq.3 の最初の項 (= 運動エネルギー ) のみ残る。
(Eq.4)

"†" は 共役な転置行列の意味である。
Eq.3 のカイラル変換のもとで、Eq.4 のラグランジアンは 次のように変化する。
(Eq.5)
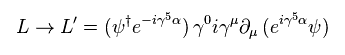
Eq.2 から、次を得る。
(Eq.6)
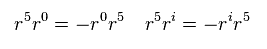
Eq.6 から、 γ5 が 2つの (異なる) γ 行列を移動すると、式の全符号は 同じままである。
(Eq.7)
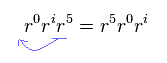
結果的に 次のように、Eq.5 は 元のラグランジアンと 同じままである ( L' = L )。
(Eq.8)

Eq.8 は フェルミ粒子の質量がゼロ のとき、カイラル対称性の下で そのラグランジアンは不変であることを意味している。
物理学者達は この状態を "カイラル対称性" と呼んでいるが、単なる 抽象的な数式記号にすぎず、物理とは 到底呼べないものである。
次に 有限の質量を持つフェルミ粒子について考える。
(Eq.9)
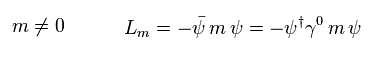
Eq.3 のラグランジアンの 2項目は 質量項 (= Eq.9 ) である。
カイラル変換の下で、この 質量項は 次のように 変化する。
(Eq.10)
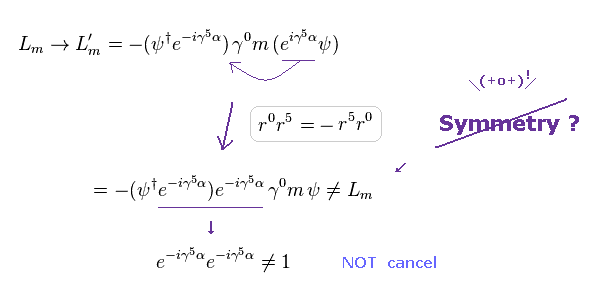
Eq.10 に示したように、2つの指数関数は この 質量項においては キャンセル されない。
そのため、フェルミ粒子に 質量 (= ラグランジアンの質量項 ) があると、 カイラル対称性が 破れると 彼らは主張し始めた。
残念ながら、ここには 何の物理的実態が ない。
これらは 単なる 人為的な数式のルールに過ぎず、自然の法則を 表わしたものでは ない。
(Eq.11) ゲージ対称性 → 光子の質量はゼロ !?
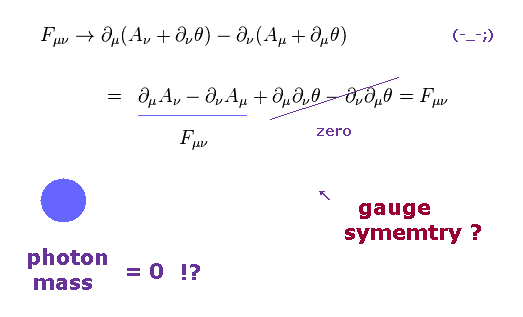
マクスウェル方程式のラグランジアンは 反対称テンソル (= Fμν ) を含む。 このサイト (p.10) や このサイトを参照のこと。 .
"Aμ" は ベクトルポテンシャルであり、これは 光子 ( もしくは W ボソン、グルーオン ) を表す。
もし ラグランジアンが ゲージ変換 (= Eq.13 ) の下で不変だと、これを "ゲージ対称性" という。
もし 光子のラグランジアンが 質量項を含んでいると、このラグランジアンは ゲージ変換の下で 同じ形を保てなくなる。
そのため、物理学者は このゲージ対称性のために、光子の質量がゼロになると主張しだした。
残念ながら、まったく物理的実態のない、抽象的な数式のみの理屈である。
(Eq.12)
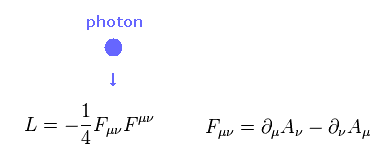
光子のラグランジアンの運動エネルギー項は Eq.12 のようになる ( このページも参照のこと )。
(Eq.13) ゲージ変換。

Eq.13 のゲージ変換の下で、Eq.12 の Fμν は 次のように変換する。
(Eq.14)
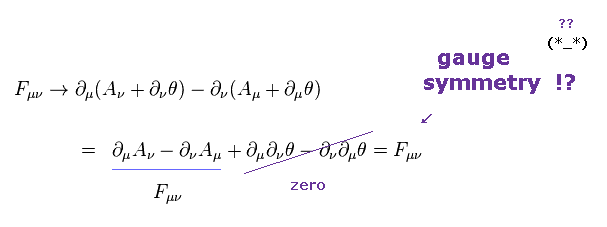
Eq.14 に示したように、ラグランジアン内の この Fμν は ゲージ変換の下で 不変である。
結果、全ラグランジアンも 同じ形式を保てる。
これを "ゲージ対称性" という。
(Eq.15) 光子の質量項。
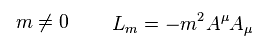
次に、ラグランジアン内の 光子の質量項 について考える。
Eq.13 のゲージ変換の下で、質量項 (= Eq.15 ) は 次のように変換する。
(Eq.16)
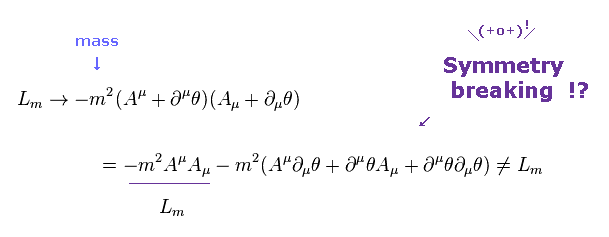
ご覧のとおり、Eq.16 の ラグランジアンの質量項は 元の形 (= Eq.15 ) を保てない。
そのため 物理学者達は ゲージ対称性を保つために 光子の質量がゼロであると 主張し始めた。
再び、これは 単なる抽象的な数学上の理由にすぎず、現実社会と 何の関係もない。
彼らは この ゲージ (= θ ) の 本当の意味を 速やかに 明らかにすべきである。
それができないのなら、物理的意味がないと言っているに等しい。
また W ゲージボソンは 非常に大きな質量をもつため、ゲージ対称性は 最初から破れていることになる。
つまり、元から破れている対称性を 信じること自体 無意味である。
(Eq.17) ボソンとフェルミ粒子と含む ラグランジアン。
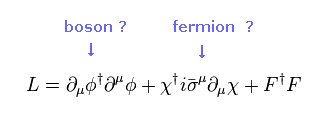
もし ボソンとフェルミ粒子が 超対称性 を介して "重ね合わせ"状態にあるとき、ヒッグスの質量は カイラル対称性を利用できるため 小さくなれる。
残念ながら、ここには 何の物理的な理由もない。
Eq.17 は 同じ質量 ( ex. m = 0 ) をもつ ボソンとフェルミ粒子のラグランジアンである。
(Eq.18) 超対称性変換 ?

このサイト や このサイトにあるように、 超対称性変換は ボソン (= φ ) と フェルミ粒子 (= χ ) を変換する。
ラグランジアンが この変換の下で 不変だと、これを "超対称性" と呼ぶ。
Eq.18 を見て分かるように、これらは 単なる 人為的な数式のルールにすぎず、 物理的実態を 何も表していない。
物理学者達は ”本当の”科学を発展させるために、この非現実的な超対称性や 10 次元の超弦理論を まず最初に 諦らめなければならない。
(Eq.19) "破れた" 超対称性は 対称性ではない。

重要な点は 超対称性粒子を 日常生活で まったく 発見できない ことである。
これはつまり、超対称性自体 最初から破れているということである。
つまり ”超対称性”という対称性を信じて追及すること自体が 無意味ということになる。
しかし 現在の標準模型では その理論を発展させていく手法において、 架空の対称性に頼る以外に方法がないので、今さら諦めることができないのである。
悲惨としか言いようがない。
(Eq.20) ボソンとフェルミ粒子の 質量単位。

ボソンとフェルミ粒子のラグランジアンは Eq.17 に示したように 異なった数の導関数を含んでいる。
そのため ボソン (= φ ) と フェルミ粒子 (= χ ) の (質量)単位は異なったものになる。
お気づきのとおり、もし ボソンとフェルミ粒子が 異なった単位を持つとしたら、そもそも 超対称性変換自体 不可能である。
そのため 理論家達は 人為的に "非実在" のフェルミ粒子 ξ を導入した。
この ξ も フェルミ粒子ではあるが、 真のフェルミ粒子 χ と 異なる質量単位を持つ。
もちろんのことだが、異なる単位を持つ2種類のフェルミ粒子が存在しているとしたら、その理論は
自己矛盾を含んでいることになる。
結果的に、超対称性という考え自体が 理不尽であることが分かる。
しかし 現在の "黙って計算だけしてろ !" の場の量子論の世界では 物理学者達は 黙々と 抽象的な対称性を信じて進むしか道がないのが現状である。
これもまた悲惨としか言いようがない。
計算の詳細については このページを参照のこと。
(Fig.58) 26 次元 → 10 次元の超弦理論 !? ファンタジー ?
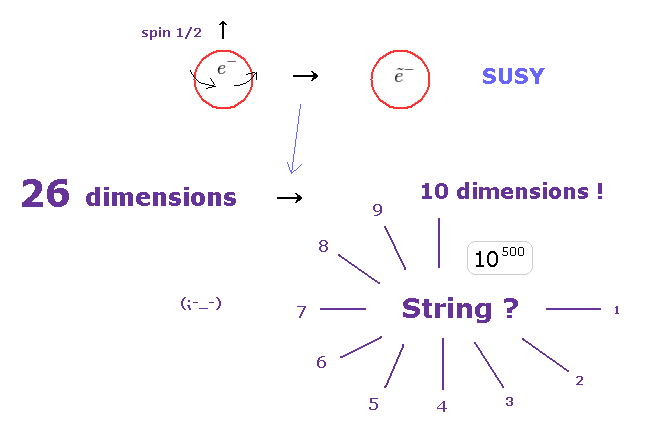
このサイトにあるように、元の弦理論は ボソンのみからなり 26 次元もの時空間を必要とした。
超弦理論の "超" の意味は 超対称性を表している。
そのため 超対称性理論が この 26 次元を 10 次元にするのに必須になってくる。
しかし残念ながら、 これらどちらの次元も 非現実的な ファンタジーであることには 変わりない。
相対論の 致命的なパラドックスを無視すれば、現在の物理界では。 "ファンタジー"の弦理論しか 勉強することがないのである。これもまた悲惨である。

2014/5/7 updated This site is link free.