トップページ
奇妙なスピン。
相対論は電磁気学で破綻。
解決策なし。
直角レバーの矛盾。
相対論は 本当に終わり。(14/7/23)
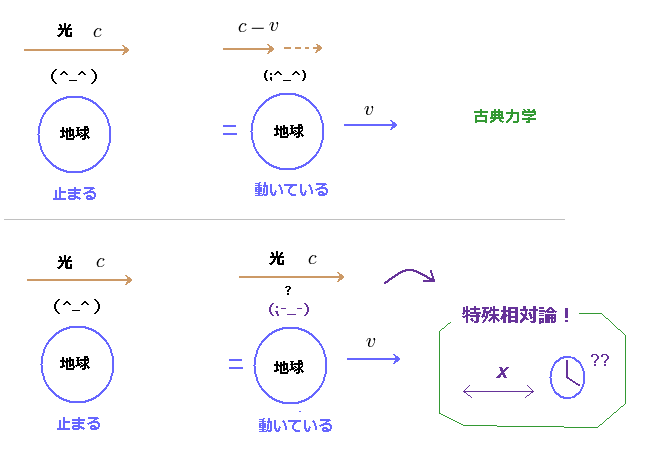
(Fig.1) 光速は すべての慣性系で "c"。 → 相対論。

特殊相対性理論 は 1905 年に アインシュタインによって提唱された 時空間の変換を表す理論である。
ただ 相対論は 非常に奇妙な性質に依存しているため 今までに多くの反対意見が存在する。
Fig.1 に示したように、相対論では、光速は 任意の速度で運動する観測者の視点から見て 必ず "c" という一定の値になる。
この 超自然的な条件を満足するために、時間と空間が ファンタジーの世界のように 遅れたり、縮んだりしてしまう。
(Fig.2) 観測者の速度に応じて ボールの速度が異なって見える。
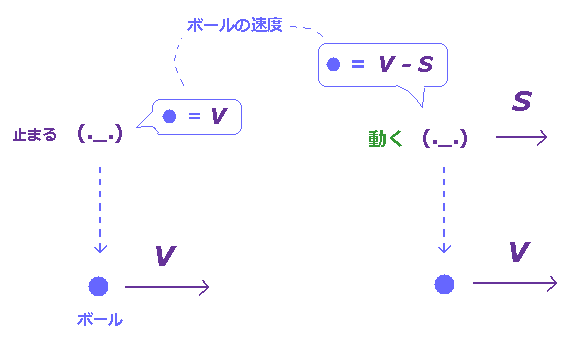
Fig.2 では、ボールが 速度 "V" で動いている。
通常の古典力学によれば、観測者が それと同じ方向に 速度 "S" で 動き出したら、ボールの速度は " V - S " に減速して見える。
(Fig.3) 光速は 観測者の速度によらず 常に "c" ?
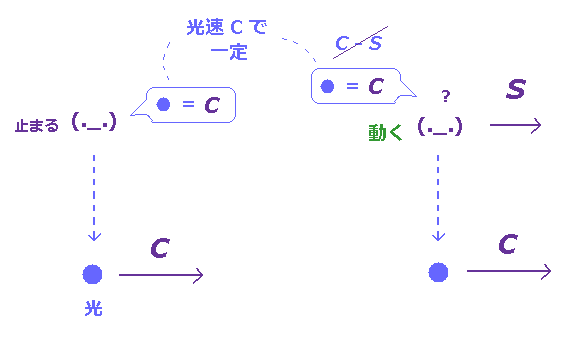
相対論によれば、光速は 観測者が静止しているか動いているかに関わらず すべて同じ "c" になる。
つまり、 Fig.3 の左右の状況で、観測者は 光の速度が 常に "c" と計測されることになる。
(Fig.4) K' 慣性系が x 軸上を 右方向へ 速度 "v" で運動している。
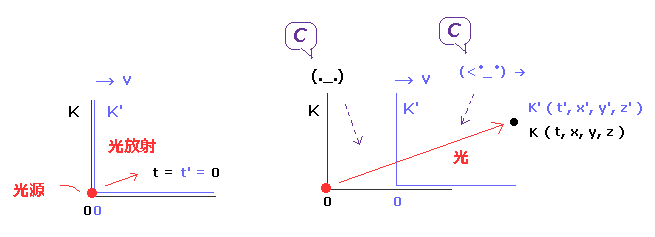
時刻 t = 0 ( t' = 0 ) に、 K と K' 慣性系の原点は 同地点にあるとし、そのとき、 原点にある光源から 光が 放射されるとする。
K' は K に対して 速度 "v" で x 方向へ進んでいるとする。
時刻t = t ( t' = t' ) に、両観測者が 光の先端の位置を 測定する。
相対論では、静止系、運動系問わず 両慣性系において 光速は 等しく "c" と観測されなければならない。
そうするには、次の2つの等式を同時に満足する必要がある。
(Fig.5) 両慣性系で、光速は 一定の "c"。
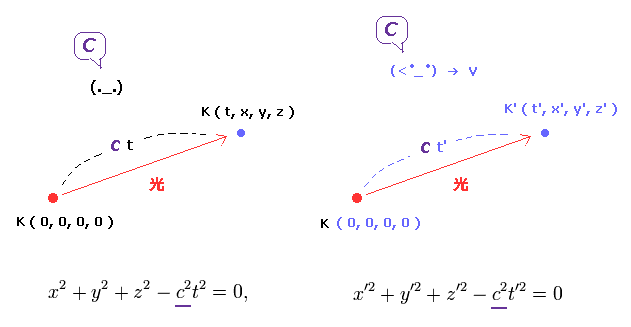
Fig.4 にあるように、 x' 座標系は x に対して動いている ( x' = x - vt )。
そのため 通常の古典力学に範囲では、Fig.5 の両式を同時に満たすことは 不可能である。
これをするには、 時間と空間が 観測者の速度に応じて 遅れたり縮んだりするという 奇妙な 考えを受け入れる必要がある (= ローレンツ変換 )。
(Fig.6) ローレンツ変換の下で 光速は 常に "c" である。

K と K' で 時間と空間座標が Fig.6 のように変換すると、Fig.5 の両式が成り立つことになる。
しかしもちろんのこと、時空間に対する根本的な概念を変えることは 他の基本的な法則も 捻じ曲げることになる。
計算に関しては このセクションを参照のこと。
(Fig.7) 致命的なパラドックス → 相対論は間違い。
このローレンツ変換は 電磁気 や
直角レバーなどで 深刻なパラドックスを引き起こす。
残念ながら、これらのパラドックスは まったく解決されていない。
一応様々な解決法なるものは提案されているが、 何かしらの おかしな定義を持ち出したりして 一目で 間違いであることが分かる。
(Fig.8) ジャーナル、大学、教科書・・ が "真のパラドックス" を隠している。
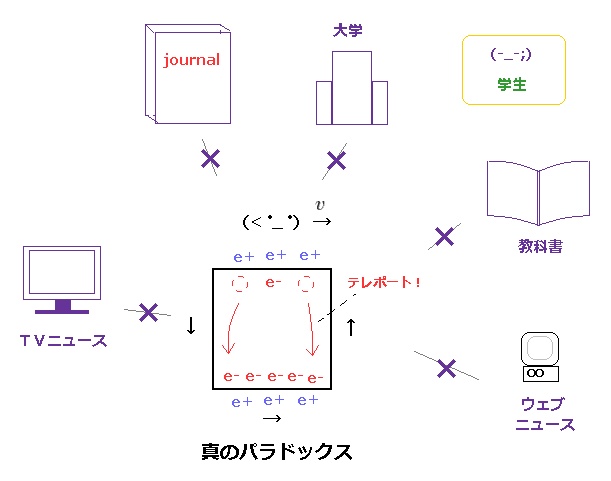
様々な相対論の教科書、 ジャーナル、大学などの学術機関のホームページ、他のメディア などを見れば分かるが、 "車とガレージ" のパラドックス や "双子のパラドックス" などの "ダミー"のパラドックスの情報しか 一般人に流していない。
ローレンツ力 や 直角レバーなどに関する 本当のパラドックスには まったくお目にかかることができない。
( もしくは それらは 非常に目立たない片隅に 小さく触れられているかいないかというぐらいである。 )
つまり、これらの真のパラドックスが隠され続けている限り、夢を描く学生、一般人が 誤った方向へ誘導され、貴重な人生が潰される人数が 単純に増えていってしまうことになる。
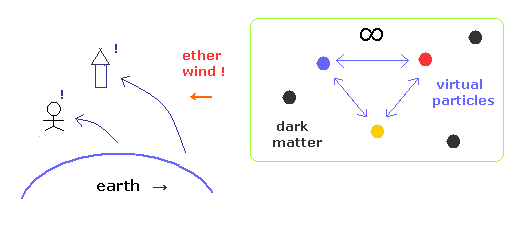
(Fig.9) エーテルは否定? → ダークエネルギー、マター、ヒッグス = エーテル !?

このサイトにあるように、特殊相対論は エーテルを否定したことになっている。
しかしその代わりに
ダークマター、ダークエネルギー、ヒッグス、仮想粒子などの 空間を埋め尽くす 別の種類のエーテル様物質を必要とする。
つまり、相対論では エーテルを否定したはずが、逆に エーテルの種類を 増加させてしまっているのである。
もし 1種類のエーテルを認めれば、ダークマター や 一様な 宇宙マイクロ波背景放射 などを自然に説明できる。相対論に反する仮想粒子に頼る必要もなくなる。
(Fig.10) 超光速のインフレーション = 特殊相対論 !?
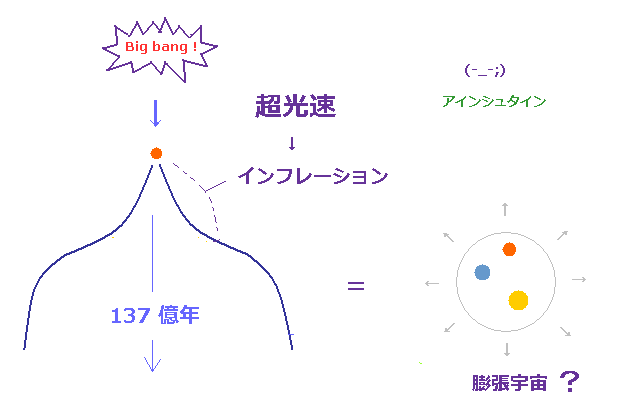
相対論は エーテルを否定したために、逆に 超光速の 宇宙インフレーション理論が必要不可欠になってくる。
超光速の領域にわたって 背景放射が 一様であることを説明するには、どうしても空間が 超光速の速度で 膨張しなければならないと 物理学者達は主張している。
しかし お気づきのとおり、これらの説明は 光速を超える存在を許さない相対論の核心とも言える部分に 完全に 違反している。
(Fig.11) 仮想光子 = タキオン !? → 相対論は間違い。

相対論的な場の量子論では、 仮想粒子が ファインマン図に 必ず現れる。
このサイト (p.5-6)にあるように、仮想粒子は 必ず特殊相対論に違反する。
しかし 一般人の方は この一番重要な矛盾した概念のことを まったく 知らず、 教科書や他の様々なメディアが提供する 歪曲された情報を信じ込まされている状況である。
特殊相対論では、クーロン力は これら仮想光子の交換によって 生じるとされている。
エネルギーと運動量が保存されるには、この仮想光子が このページにあるように タキオンのように振る舞う必要がでてくるのである。
結果的に、相対論は 最初から 自己矛盾を抱えていることになるため、 間違いということになる。
(Fig.12) 影響力のある相対論は 様々な分野の基礎理論になっている。

特殊相対論は 1905 年という大昔に アインシュタインによって導入された。
その長い歴史故に、この考えは 標準模型、量子電磁力学 (= QED )、ブラックホール、膨張宇宙、超弦理論 などの 様々な相対論的理論の基礎に使用されることになった。
もし特殊相対論が間違いならば、これらの理論は すべて棄却されることになる。
恐ろしい事実であるが、このことが 相対論の勢力が 非常に甚大である理由である。
また 超光速の宇宙インフレーションや 10 次元の 超弦理論が 明らかに ファンタジーの世界であるにも関わらず、現在も 物理学者達が それらを追い続けている 主要な要因になっている。
(Fig.13) 26 → 10 次元の ひも理論しか 統一理論として残らない。

深刻な悪影響として、物理学者達が 真のパラドックスを無視して、 特殊相対論を信じている限り、10次元の超弦理論しか 統一理論として残っていないのである。
これは深刻な状況である。
なぜなら 夢を持った新しい学生が 明らかに非現実的な ひも理論に 疑いを持った瞬間に 彼らの物理の人生は 非主流派として 終わってしまうからである。
(Fig.14) 変数変換 = 間違った数式のトリック QED は間違い。
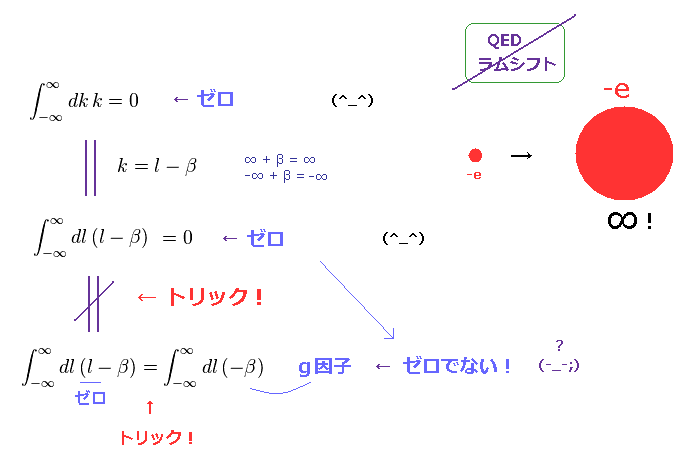
このページに示したように、異常磁気モーメント g-2 の 量子電磁力学 (= QED ) の計算は 完全に 間違った数学のトリックに依存している。
Fig.14 では、 "変数変換" ( k = l - β ) で 人為的に 結果自体が変わってしまっている。
この 1ループ補正は 紫外発散除去で 有限な値が得られる。
しかし 2ループ補正では、紫外発散 (= UV ) を 繰り込んだ後でも, やっかいな 赤外発散 (= IR ) が残っている。
このサイト (p.25-) にあるように、赤外発散の処理は 高次の補正においては 紫外発散よりも はるかに 難しい。
( この赤外発散を除去する 決まった方法が 存在しない。 )
1ループ補正の計算から 8年もの年月が流れて、 実験値に辻褄を合せるために、 人為的な新たな概念 ( 修正された伝播関数、 Yennieゲージ、 contact term ) が 次々に導入され利用された。
( "Particles. Sources, and Fields" vol 3, Schwinger に詳しく載っている。)
つまり 異常磁気モーメントの計算は 自然な帰結とは どう転んでも 言えない代物である。
(Fig.15) QED は ラムシフトの予測もできない。
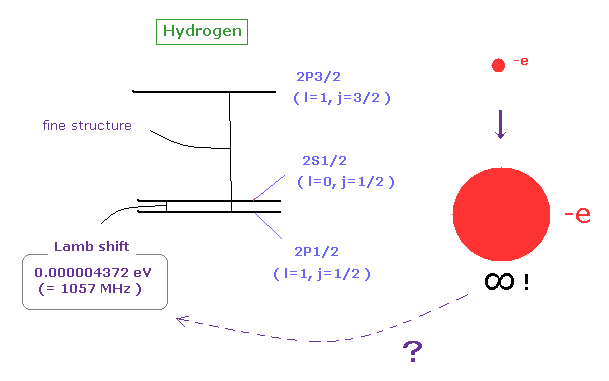
ラムシフトの計算では、 赤外発散を回避するために、人為的に 高エネルギーと低エネルギーの部分に式を分離した。
問題は 高エネルギー部分は 仮想光子を含み、一方、低エネルギー部分は実光子から成り立っていることである。
つまり、根本的に 相対論的、非相対論的部分の再結合自体 不可能なのである。 ( 上級量子力学 II 巻、サクライ 参照のこと。 )
さらに 最終的に 適切なラムシフトの値を出すには 解析的な式でなく 曖昧な 数値計算に頼るしかなく、ここでも 仮想の励起状態という 新たな概念に依存しているのである。
( このサイト (p.23) や、場の量子論 2巻 ワインバーグ p.401 参照のこと。 )
つまり、量子電磁力学による ラムシフト計算も 第一原理とは 到底言えない代物である。
(Fig.16) マイケルソン・モーリーの実験 = 地球と伴に動く "エーテル"?
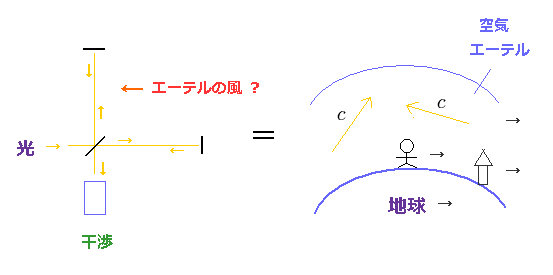
マイケルソン・モーリーの実験では、 電磁波の干渉の違いを観察しようとしていた。
( つまり 光速度 "c" というのは 光の波としての性質に完全に依存している。)
地球は太陽の周りを公転している。
よって もし 何らかの媒質 (= エーテル ) が 絶対空間を満たしているとしたら、"エーテルの風" が 地球の動きと逆方向に吹くことになり、光の干渉に変化が見られるだろう。
しかし この実験では 様々な方向を試したが 干渉の変化は見られなかった。
通常の相対論の教科書は しばしば この実験は "エーテル" (= エーテルの風 ) を否定したと説明している。
しかし お気づきだと思うが、これらの教科書は 地球とともに動く "エーテル" に関しては ほとんど触れていない。
(Fig.17) すべての荷電粒子は 地球とともに動いている。
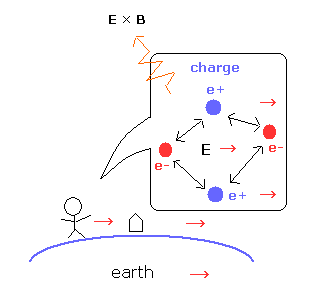
もし エーテルが 大気や 他のすべての物のように 地球とともに動いているとしたら、光速度は エーテルの風を生じることなく 必ず "c" になる。
また 私達の体も含めたすべての荷電粒子は 地球と一緒に動いており、それらの間の 電場 E も 地球と一緒に動いていると考えることは自然である。
電磁波の速度は 地球と一緒に動く大気や水などの媒質に完全に依存している。
(Fig.18) 相対論的な場の量子論は "エーテルの風" を受け入れている。
多くの人々は "エーテル" の言葉を聞くやいなや 特に深く考えることなく反射的に その考えを捨ててしまう。
しかし 実際は QED や 標準模型などの現在の場の量子論は 様々な種類の "エーテル"様の物質を使用しているのである。
もし あなた方が "エーテル"を否定したら、クーロン力や磁気力を表すのに 空間を埋め尽くす 無限の仮想粒子を使用しなければならない。
驚くことに これらの仮想粒子は 特殊相対論 (= アインシュタインの質量公式 ) に従っていないのである。
また ダークマター、ダークエネルギー、ヒッグス場などの 他の物質も 全空間を埋め尽くしている。
しかし 彼らは決して これら"エーテル様の物質"を エーテルと認めようとしない。なぜなら "相対論的"な場の量子論だからである。
そして 現在の素粒子物理では 肝心なところは "Shut up and calculate !" で 回答を避けているのである。
( これらの矛盾した曖昧な姿勢が 明らかに 私たち人類の科学の発展を阻害している。)
(Fig.19) 移動する物体は 収縮する。
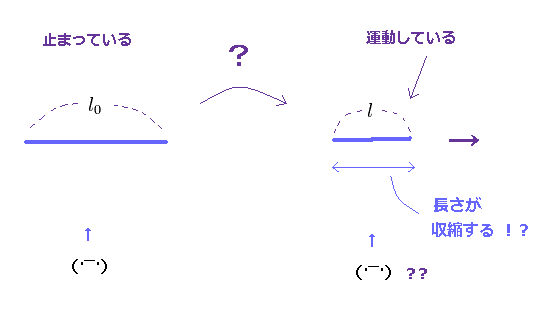
Fig.19 では、棒の元の静止長は " l0 " である。
それが動きだすと 静止した観測者の視点からは 棒は 収縮して見えることになる ( l < l0 )。
(Eq.1) ローレンツ変換。
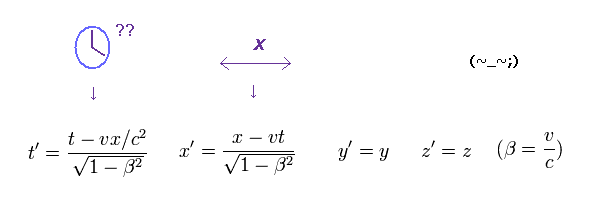
Fig.20 でも 棒の静止長を l0 とする。
この棒は K' 慣性系と伴に 速度 "v" で K 慣性系に対して動いている。
つまり、K' では この棒は静止しており、その両端の座標は 常にx'2 と x'1 になる。
(Fig.20) 棒が K 対して 速度 "v" で K' 慣性系と伴に動いている。
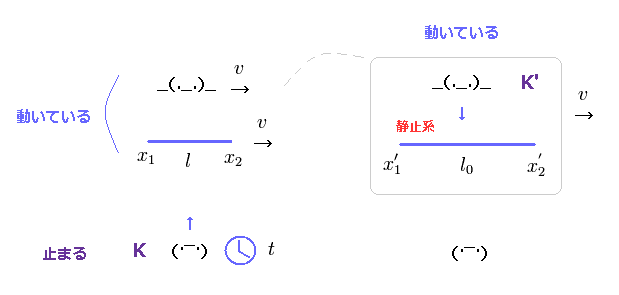
時刻 "t" に、この棒の両端は K 系で x2 と x1 にある。
つまり K 系での この棒の長さは l = x2 - x1 になる。
物体の長さというのは ある同時刻 "t" で測定したという意味である。
Eq.1 のローレンツ変換を使用すると、K' 系における両端の x' 座標 は、
(Eq.2)
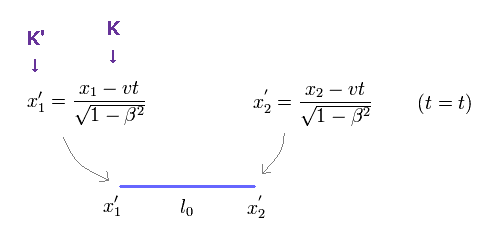
この棒の静止長が l0 = x'2 - x'1 であることを考慮すると、
(Eq.3)
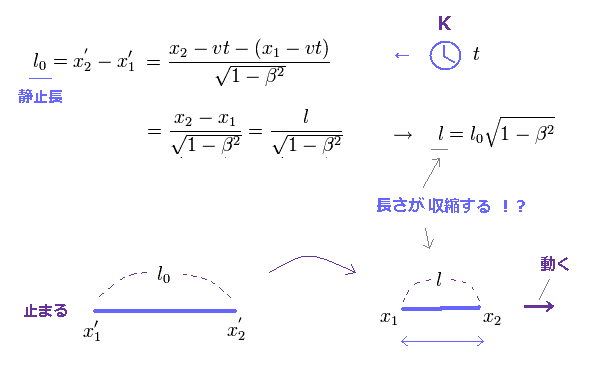
Eq.3 にあるように、動く物体は 進行方向に 収縮して見えることになる。
( K 系の観測者から見た棒の長さは 元の長さ l0 よりも短く見える。 )
これを "ローレンツ収縮" という。
(Fig.21) ローレンツ収縮は "リアル" なのか?
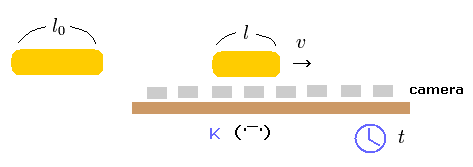
特殊相対論によれば、物体のローレンツ収縮した長さは "リアリティー" として扱われる。
Fig.21 では 静止長 l0 の物体が 速度 "v" で K 方向へ運動している。
そして たくさんのカメラが K 系の壁に沿って並べてあり、それらは 同時刻 "t" に一斉に 眼前の物体を撮影するとする。
( 物体と壁の距離は 非常に近いとする。)
特殊相対論によれば、撮影されたものには 物体の長さが "l0" でなく "l" ということになる。
ただし、このサイトにあるように、ローレンツ収縮の直接的な観測実験は 今のところ存在しない。
(Fig.22) どっちが本当に円周?
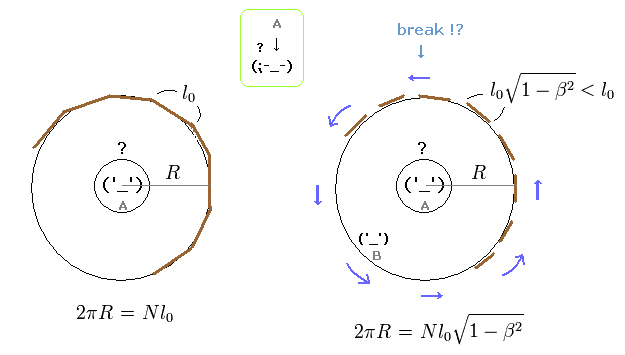
Fig.22 では、丸い円盤の円周が 2πR ( R は 半径 ) である。
また Fig.22 左の 静止した円盤では この 2πR は ちょうど N l0 に等しいとする。 ( 2πR = Nl0. )
ディスクが回転し始めると、その 円周は ローレンツ収縮することになる。なぜなら 回転とは 接線方向の運動だからである。
しかし 半径 "R" は ローレンツ収縮しない。なぜなら 動径方向の運動はゼロだからである。( R → R )
回転円盤の 各長さ l0 が 収縮することを考慮すると、 その円周は 2πR に等しくなくなる。 ( 2πR < Nl0 ? )
これは 特殊相対論における 致命的なパラドックスの一つである (= エーレンフェストのパラドックス。 )
例え 回転する "固い"円盤が壊れたとしても、その各亀裂も 収縮することになる。これは奇妙である。
残念ながら これらの "本当"のパラドックスは 通常の相対論の教科書には皆無である。なぜなのだろうか?
( 注意:観測者 A は この円盤の中心の静止した穴の中にいるので、遠心力ポテンシャル = 一般相対論 とは 何の関係もない。)
(Fig.23) "ローレンツ収縮する" ベルトコンベヤー。 ← パラドックス !
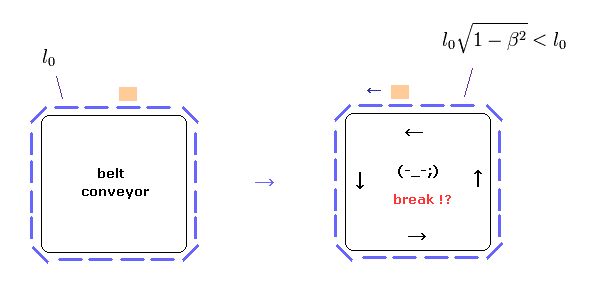
上記の エーレンフェストのパラドックスは ベルトコンベヤーを用いると簡単に理解できる。
Fig.23 左では、ベルトコンベヤーは 動いていない。
もし このベルトコンベヤーを 回転させると 特殊相対論によれば これはローレンツ収縮する ( Fig.23 右 )。
このベルトのあらゆる部分が ローレンツ収縮する必要があるため、このベルト全体の長さが縮むことになる。
これは明らかなパラドクスである。なぜなら内側の四角のフレームは動いていないので 同じ長さのままだからである。
(Fig.24) 観測者の運動に応じて、ベルトは 収縮もしくはしない。
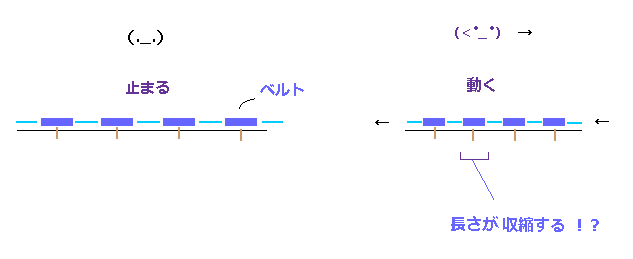
上で述べたように、 動く物体は 静止した観測者から見たら 短く収縮している。
観測者のほうがベルトに対して動きだしても 状況は同じである。
(Fig.25) 観測者の動きとベルトの長さの関係。
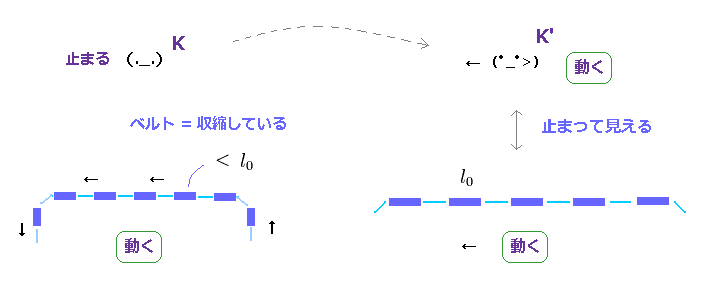
Fig.25 左では、ベルトコンベヤーは K 系の観測者に対して 動いている。
つまり この場合では、動くベルトは ローレンツ収縮していることになる。
観測者がベルトと同じ速度で動きだしたとしたら、彼の視点 (= K', Fig.25 右 ) からは ベルトは静止して見える。
K' 系では、 静止したベルトは元の長さに戻っているため、K 系のときよりも 長くなっている。
(Fig.26) K' では、内側のフレームが縮む。
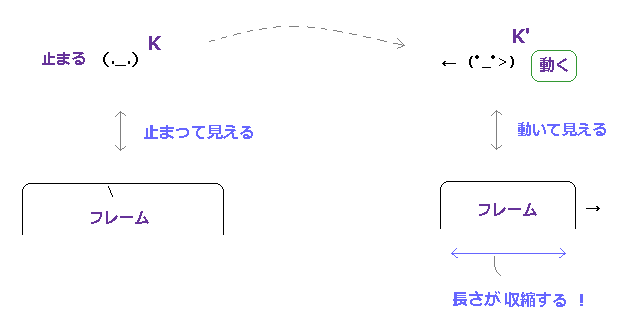
一方、内側のフレームは K 系では静止している。
そのため、観測者が動くと (= K' )、このフレームは 収縮する。
なぜなら K' 系の視点では、静止していたフレームが 逆方向へ 動いているからである。
(Fig.27) ベルトが 観測者の動きで 内側のフレームから "分離" ??
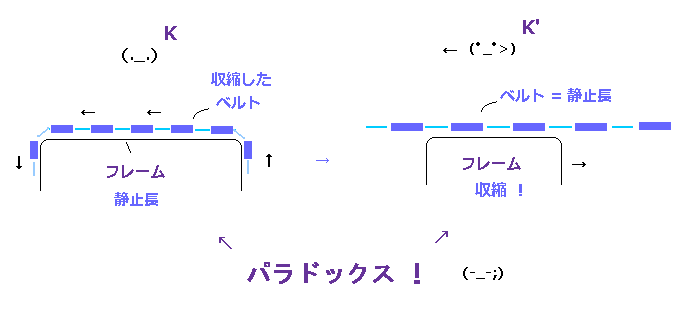
Fig.25 と Fig.26 から、これらのベルトコンベヤーと フレームは 長さが異なるため、分離してしまうことになる。 これは非常に奇妙である。
(Fig.28) 観測者の運動で、針金の数が 5 から 3 に減る!?
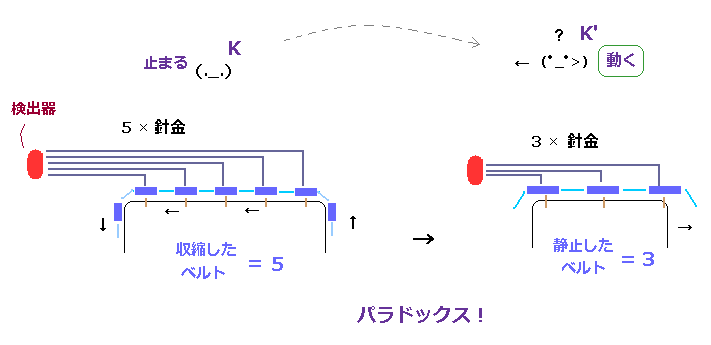
Fig.28 左では、 内側のフレームは静止しており、ベルトが動いて 収縮している。
ベルトの 5つの部分が フレームの1辺に含まれており、上辺にある 各ベルトから 細い針金が 水平方向に突き出ているとする。
すると、Fig.28 左のケースでは、水平方向に位置する検出器では 5つの針金を常に検出していることになる。
Fig.28 右では、動いているベルトの視点からは、ベルトは静止長に戻っており、内側のフレームが動いており 収縮している。
つまり 3つのベルトのみしか このフレームの 上部1辺内に入れないことになる。
この場合では 水平方向にある検出器では 常に 3つの針金しか検出できていないことになる。
観測者の単純運動のみで、検出器の針金の数が変わるため、明らかに致命的なパラドックスである。
このように、相対論の弱点は クーロン力や、長い針金のような 連続した作用物を数えるときに発生する。
(Fig.28') 長い針金のついたベルト と 点状の検出器。
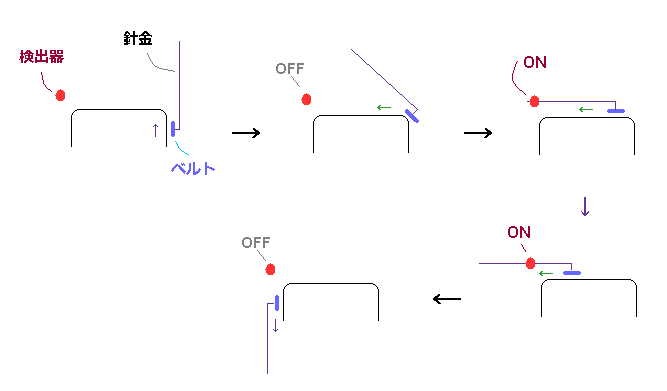
Fig.28 のベルトコンベヤーに Fig.28'の説明を補足する。
各ベルトは それに平行な 長い針金を つけていることとする。
Fig.28'に示したように、このベルトが フレームの上部の部分にあるときのみ、 点状の検出器が この針金を検出することができる。
結果的に 上部に位置するベルトの数において、致命的なパラドックスが発生することになる。 ( 5 → 3 ).
この検出器は ベルトが上部サイドにあるとき、 継続して このベルトを検出し続ける。
そのため、よくある同時性の解決策として、異なった慣性系では 時間が異なる といったものが ここでは通用しなくなる。
連続した作用こそが 異なった慣性系における 異なった長さのような 真のパラドックスを 露呈させることになる。 相対論は 本当に終わり も参照のこと。
(Fig.29) 動いている棒と納屋。

ここでは K 系に対して 1つの棒が動いており、 ローレンツ収縮している。
K 系では、納屋が静止しており、納屋の長さが ローレンツ収縮した棒と同じになっている。
そのため 時間 "t" に シャッターを下ろすと、この棒は 納屋の中に完全に入ることができる。
(Fig.30) 異なった視点。

しかし 動いている棒の視点 (= K' 系 ) からは、納屋が 逆方向に動いている。
つまり K' 系では 納屋のほうが 棒の代わりに ローレンツ収縮している。
結果的に 棒は納屋の中に入れないのだろうか?
(= 棒と納屋の パラドックス。 )
(Fig.31) 時間は K と K' 系で異なっている。

これは所謂 特殊相対論における 同時性の問題である。
K 系 における時間が t のとき、x=a と x=0 の地点の K' 系における時間は 異なるのである。
つまり K' 系では、x = a における時間 t' は x = 0 のときよりも 早いのである。
(Fig.32) 前面の壁が壊れる → 棒が入る → シャッターが下りる。

結果的に K' 系では 最初に 棒が 納屋の前面の壁にぶつかり、その壁が壊れる。
次に 棒が納屋に入っていき、シャッターが下りる。
よって K' 系においても 棒は 納屋の中に入っていけるのである。
物理学者達は こういう理由により パラドックスは存在しないとした。
しかし、この説明では 相対論の根本的なパラドックスの問題を 解決してはいない。
結果として、回転するベルトコンベヤーや エーレンフェストという
致命的なパラドックスが 起きてしまうわけである。
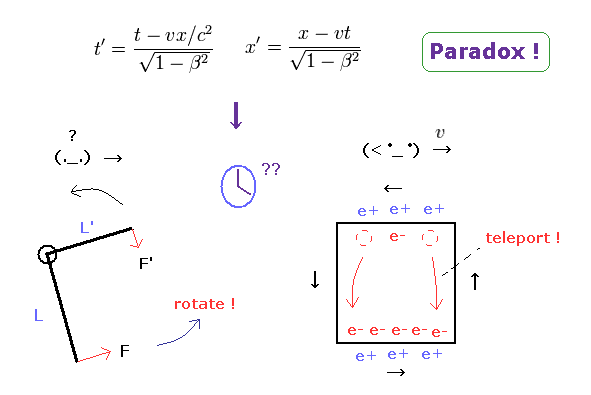
(Fig.33) 直角レバーは回転するしない?
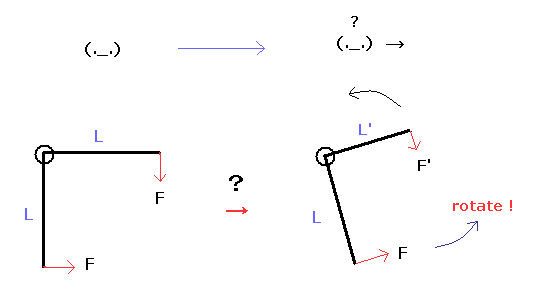
Fig.33 左では、レバーに作用する2つの力は 釣り合っており、静止系の観測者からは トルクはゼロである。
しかし Fig.33 右では、1つの腕の ローレンツ収縮と 力の変化 ( ここ (p.232), ここ (p.675) 参照のこと ) のために このレバーは 観測者の単純移動のみで回転してしまう ( このページを参照のこと。 )
この直角レバーのパラドックスは まだ解決されておらず、特殊相対論が 間違いであることを示している。
様々なウェブサイトやテキストをチェックすると、決まって 架空の 4元ベクトル力の変換に関してばかり扱っており、肝心の 通常の力のローレンツ変換に関しては ほとんど触れていない。なぜなのだろうか?
(Fig.34) 観測者の見る力が 荷電粒子を動かした?

これは 明らかに パラドックス であり、もちろんまだ解決されていない。
観測者の単純移動のみで、外にある荷電粒子が S' 系で 電線に引きつけられてしまう。静止系の観測者 (S) からは それらは 中性の電線には引きつけられないにも関わらずだ。
( 電荷と電流は 4元電流であり、ローレンツ変換のもとで 時空間と同じように変換する。)
この方向が 特殊相対論における弱点である。
なぜなら 特殊相対論によれば、観測者の単純移動のみで 新たな奇妙な電荷が発生してしまうからである。
このサイト (p.65) や このサイト (p.3) 参照のこと。
(Fig.35) 電子が下部の電線にテレポート → 反発力?
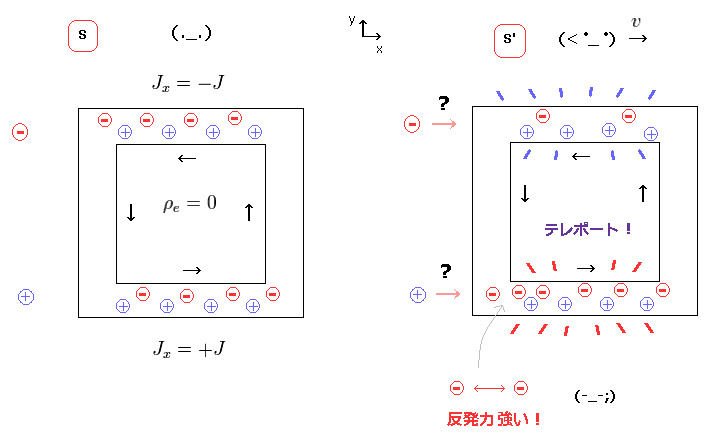
特殊相対論の 4元電流密度によれば、観測者の単純移動のみで 負の電荷が 下部の電線内にテレポートしてしまうことになる。
この場合は Fig.34 に示したように 致命的なパラドックスが出現する。
またお気づきのとおり、Fig.35 の状態は 非常に不自然である。
なぜなら 下部の電線内の電子間の 反発力が強くなるため このテレポーテーションは 力学的に起こり得ない。
つまり 特殊相対論は 自然の法則に反していることになる。
(Fig.36) 特殊相対論の弱点は 2方向の矛盾。
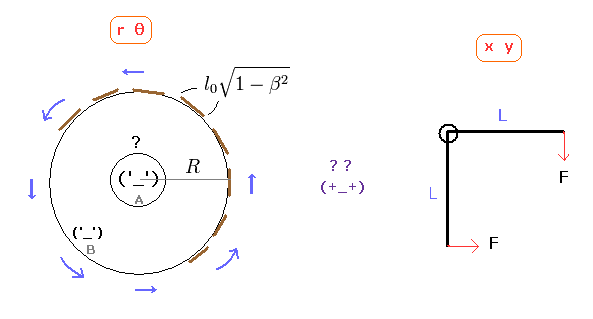
結果的に、特殊相対論の致命的なパラドックスが 2方向を扱おうとすると 出現してしまう。
2方向 ( r と θ、 x と y、 円形の電線 ) が特殊相対論の弱点である。
(Fig.37) K と K' 系は 逆方向に移動している。
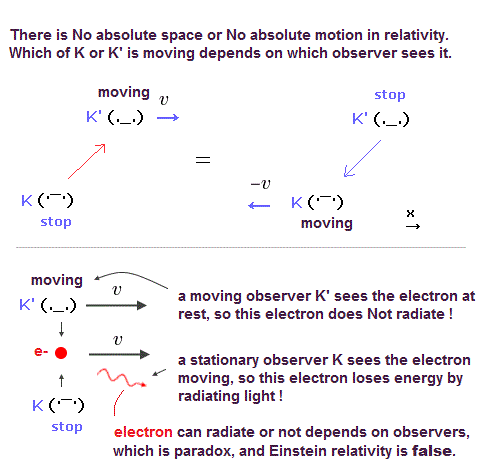
Fig.37 左では、K' が 速度vで x 方向へ K 系に対して動いている。
しかし K' 系からの視点では K 系が マイナス x 方向へ動いている (= Fig.37 右 )。
つまり Eq.2 のそれらの座標を交換して v を -v に変更する。
(Eq.4)
K' の座標は ( t', x', y', z' ) で、 K 系の座標は ( t, x, y, z ) である。
Eq.4 の逆変換は、
(Eq.5)
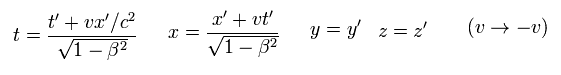
Eq.5 を Eq.4 を代入すれば、Eq.5 が正しいことが確認できる。
(Eq.6) 移動する時計 K' の時間の遅れ。
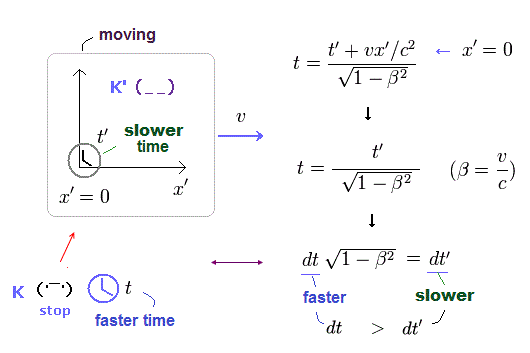
再び、K' 系が 速度vで x 方向に K 系に対して動いているとする。
驚くことに K' の x' = 0 に固定した時計は K 系に静止した観測者の時計よりも ゆっくりと進む ( dt > dt' )
このサイト参照のこと。
"x' = 0" を Eq.5 の最初の式に代入して Eq.6 を得ることができる。
(Eq.7) 動く K 系の時計の時間の遅れ。
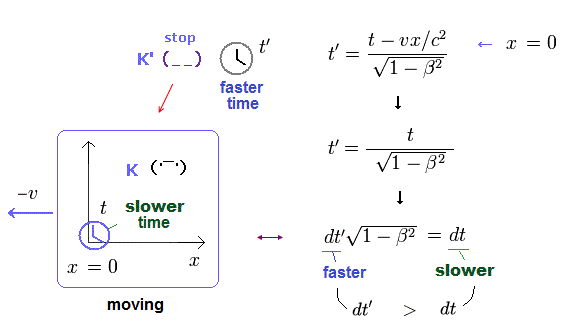
K' 系からの視点では、K 系が逆方向へ動いている。
すると、今度は逆に K 系の x = 0 に固定した時計は K' 系の時計よりも ゆっくりと進む。 ( dt < dt' )
つまり K か K' の系に関係なく、 運動している時計の時間が 静止したいるのより ゆっくり進むことになる。
(Fig.38) どっちの時計が ゆっくり進む??
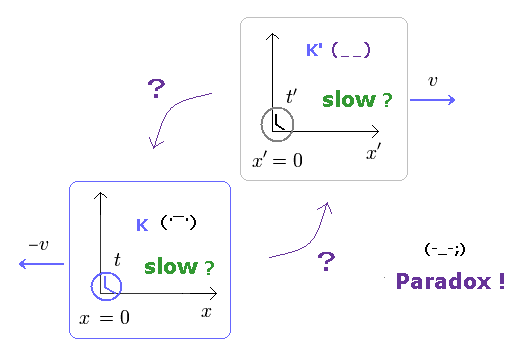
つまり 特殊相対論によれば、移動している系の時計は 必ずゆっくり進むのである。
K 系の観測者からは K' が動いている ( K' < K )。しかし K' の観測者からは K が動いている ( K < K' )。
結果的に 私達は どっちの時計がゆっくり進んでいるのか 理解できないことになる。
これは明らかなパラドックス (= ふたごのパラドックス ) であり、相対論の奇妙な世界の一面を表している。
通常の教科書は このふたごのパラドックスは 本当のパラドックスでなく 私達の誤解からくるものだと しばしば書かれている。
そして このパラドックスの解決には 加速系の一般相対論が必要とも書かれている。
しかし あの有名な GPS の時間の補正にも ふたごのパラドックスは当然含まれていることになり、すなわち GPS は相対論に関係ないことになる。
また 横ドップラー効果 も ふたごのパラドックスを含んでいる。
(Fig.39) 誰がミューオンを注文したのか?
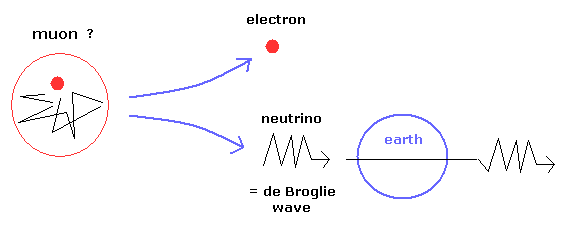
ミュー粒子の寿命は 奇妙な時間の遅れによって伸びるとよく書かれているが 自然に ミュー粒子の高エネルギーそのものによるものと考えたほうがしっくりくる。
不要で不安定な素粒子ミュー粒子は 電子と高エネルギーのドブロイ波 (= ニュートリノ ) の組み合わさったものと考えられる。
なぜなら ニュートリノは 地球を簡単に通り抜けられるからである。
(Fig.40) 2つの人工衛星における ふたごのパラドックス。

問題は 動く物体の この時間の遅れを GPS の人工衛星の時計に使用していることである。
相対論学者によれば、GPS の人工衛星は 私たちよりも 速い速度で動いているため、GPS の時計は 1日に 私たちの時計より 7 μs 遅くなる。
また 弱い重力のために、GPS の時計は 1日 45 μs 速く進むことになる。結果的に 45 - 7 = 38 μs 速く進むことになる。
お気づきかもしれないが、この GPS の時間の計算には 上で述べた ふたごのパラドックスを含んでいる。
なぜなら 動く人工衛星の視点からは 私たち観測者が速く動いているからである。
このページに示したように、2つの同一の人工衛星が 地球の周囲の同一軌道を反対方向に進んでいるとき、それらの時計は明らかにパラドックスを示す。
( これは 遠心力ポテンシャルを含めた一般相対論を用いて示すことができる。)
つまり 特殊相対論を用いた GPS 人工衛星の相対論的補正は ふたごのパラドックスを含んでおり、間違いということになる。
人工衛星の原子時計は 電磁波の振動数を用いている。
( 決して 私たちが それらの時計の針を直に見ているわけではない。)
つまり 空中の何らかの媒質によって それらの振動数に少しの違いが生じたと考えるほうが、架空の粒子、グラビトンなどより 真実味がある。
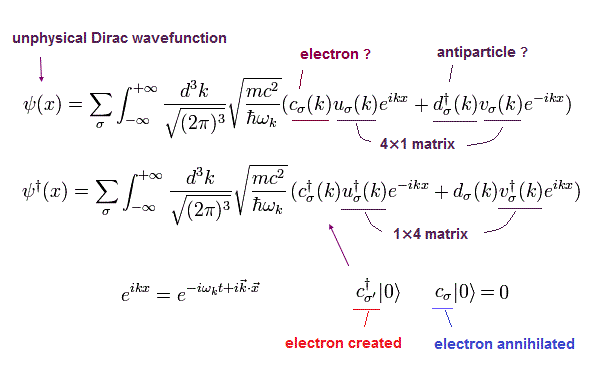
(Fig.41) 特殊相対論 ( ディラック方程式 ) は 最も影響力のある理論の1つである。
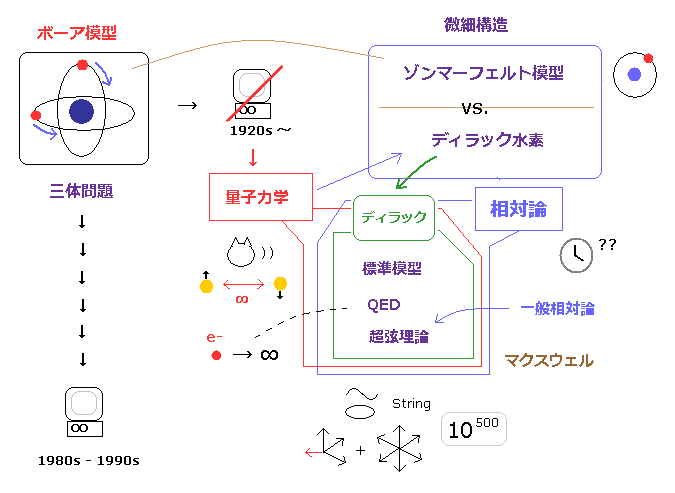
これら致命的なパラドックスに関わらず 相対論は 100 年以上もの間 生き残った。
そのため 決定的なパラドックスを抱えた相対論が どうしてこれほども生き延びたのか という理由を説明しなければならない。
( また どうしてこれら重要なパラドックスが 通常の教科書に皆無なのかも 考えなければならない。)
1980 年から 1990 年代にコンピューターが一般的になるまで、ボーア・ゾンマーフェルト模型は 難解な3体問題である ヘリウムを扱うことができなかった。
この状況の中で デイラック方程式は たくみに スピンと相対論効果を結びつけることに成功した。
もちろん、ディラック方程式は クライン・ゴルドン方程式と同じ意味であり、この中で 相対論は生き残ったのである。
また 非現実的な量子力学は リアルなドブロイ波 (= エーテル ) を好まず、奇妙なパラレルワールドを より愛していることも理由である。
(Fig.42) フィゾーの実験と 光行差現象は エーテル引き摺り仮説を否定したのか?
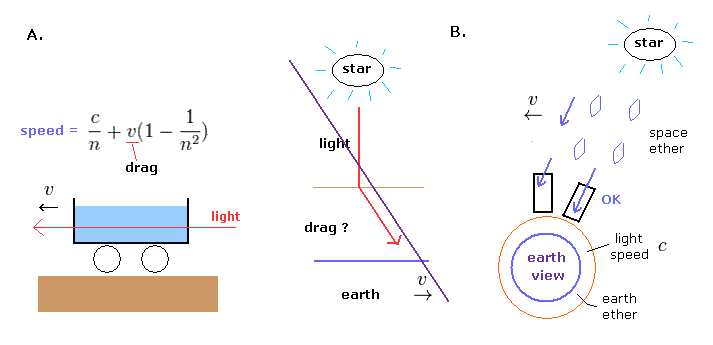
フレネルの エーテル部分引きずり仮説は 1851 年の フィゾーの実験で確かめられた。
この実験では Fig.42A に示すように 動く水 (媒質) が 部分的に 光速度 (エーテル) を引き摺ることを示した。
相対論学者達は たびたび この実験は "完全"エーテル引きずり仮説 を否定したと主張している。
しかし お気づきのとおり、彼らの主張は 非常に小さな水と 非常に大きな地球の 影響力の違い や 媒質の運動とその屈折率の変化 などについては 完全に無視している。
(Fig.43) 光子は 水中で遅くなれない。

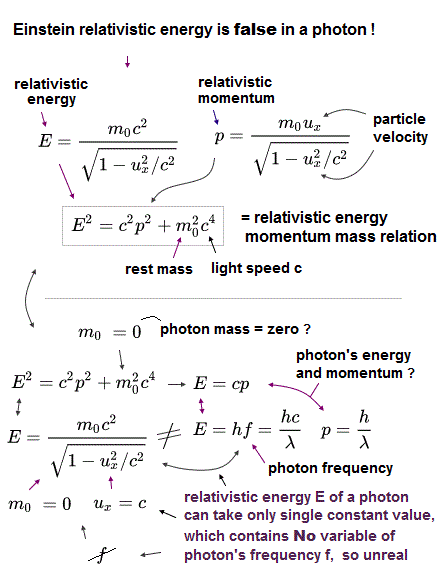
相対論によれば、質量のある粒子が 光速 c で動くと そのエネルギー E は 無限大に発散してしまう (Fig.43 上)。
つまり 光子の質量は ゼロでなければならない。
もし 水中で 光子のスピードが c/n に減速すると、光子の質量がゼロのため そのエネルギー E は ゼロになってしまう (Fig.43 下) 。
もちろん このことは 光子のエネルギー E=hν の関係式と矛盾する。
結果的に 相対論は 光子が "c" より遅くなることを許していないのである。
相対論学者達は フィゾーの実験は ローレンツ変換を示していると よく主張しているが、そもそも 水中で "c/n" に減速するのを認めること自体 光速が媒質に完全に依存していることを認めていることと同じである。
( "n" は 水の屈折率 1.33 である。)
(Fig.44) 屈折なし → 望遠鏡は傾ける必要がある。
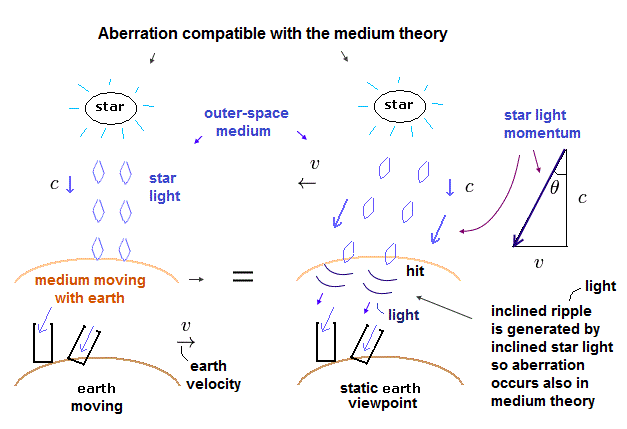
Fig.42B や Fig.44 に示したように、エーテル引きずりによる 光行差現象 の説明には誤解がある。
動く地球からの視点では、星から放射された光は 雨のしずくのように その向きが少し変わる。
もし 動く地球の視点から 光の向きがまっすぐだとしたら、光の元の方向が そもそも まったく逆の方向になる。
つまり 望遠鏡を少し傾けなければ、それらは 望遠鏡の底に届かない。
Fig.44 では、宇宙空中の 光の見かけの速度は 少し早くなる。そして "地球周囲のエーテル" に入ったあと、その速度は "c" になる。
この場合 屈折について考える考える必要がある。
私たちが 光行差の角度を計算する際、通常 sinθ が tanθ に等しいと見なす。
これはつまり v/c の 2次の効果を無視できることを意味する。( "v" は "c" に比べて非常に小さい。)
つまり 屈折は起こらず、光が望遠鏡の底に届くには それを少し傾かせる必要がある。
(Fig.45) もし エーテルが光を引き摺ると → 光行差現象見られない?
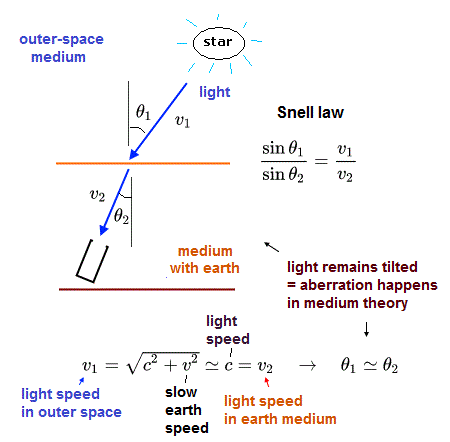
ある日 Fig.45 のような エーテル引き摺り仮説に対する 間違った解釈を見つけた。
彼らが言うには、ある星からの光は 地球のエーテルに入るやいなや 横方向へ 速度 "v" で引き摺られる。
結果的に 地球と伴に動く観測者からの視点では、Fig.45 真ん中の図に示すように 光行差現象は観測できないので、エーテル引き摺り仮説は間違いであると。
もちろん、この説明は間違いである。あなたがたは どこが間違いかお気づきになられるだろうか?
スネルの法則によれば、屈折率 (= n ) は 2つの媒質中における 光の速度の比 ( = v1/v2 ) で表される。
これは 光の角度の比にちょうど等しい。 ( v1/ v2 = sin θ1/ sin θ2 ).
彼らの主張が正しいとすると、この比は 無限大に発散する。これは はっきり言って あり得ない現象である。
正しい答えは 星からの光は ほとんど曲げられず (= Fig.44 )、エーテル引きずり仮説でも 自然に 光行差現象を説明できることになる、
(Fig.46) 横ドップラー効果。
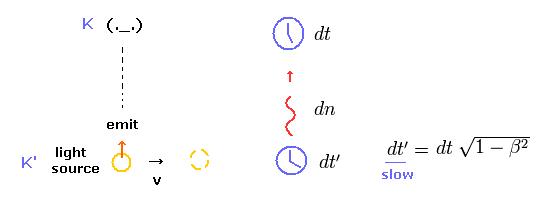
”横ドップラー効果”は 非相対論効果では説明できないと言われている。
しかし 本当にそうだろうか?
光源が 動いているために 時間が遅れ、結果として 元の光の振動数が 静止した観測者のところでは 小さくなるという理屈である。
(Fig.47) 横ドップラー効果 = 時間の遅れ !?
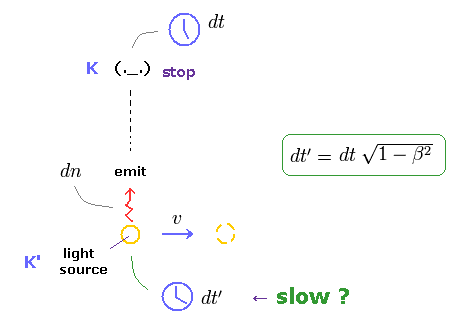
Fig.46,47 では 光源が 速度 v で 右方向に進んでおり、ちょうど観測者の横を通り過ぎた瞬間に光を放つとする。
上で述べたように、動く物体 (= K' の光源 ) は K 系の時計よりもゆっくりと進む。
(Eq.8) 元の光の振動数 (= ν0 )。
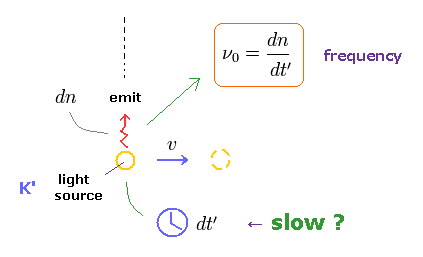
時間 dt' の間に、dn の数の光が 光源から放射されるとする。
l
つまり K' 系における光の振動数は ν0 = dn/dt' となる。
(Eq.9) 観測される振動数 (= ν' ) は ν0 よりも低くなる。
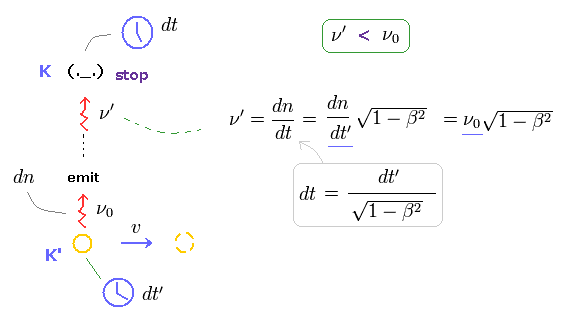
K' 系で 時間 dt' が 経過する間に、K 系では 時間 dt が経過する。 ( dt > dt' )
結果的に K 系の観測者で観測される 光の振動数は 小さくなる。なぜなら、dn が同じなのに dt が dt' より大きくなるからである。
そのため 彼らは この横ドップラー効果は 時間の遅れによるものと主張しているのである。
しかし 光源の視点からは K 系の観測者が動いている ( dt < dt' )、つまり この結果は 逆になる (= ふたごのパラドックス )。これは奇妙である。
結果的に、横ドップラー効果は 時間の遅れや 相対論とは 何の関係もないのである。
(Fig.48) 古典力学による 横ドップラー効果。
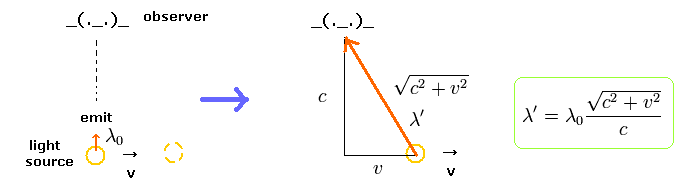
この奇妙な時間の遅れを使うかわりに、単純に 古典的な手法で この効果を表せる。
Fig.48 に示したように、光源の動きによって、放射された電磁波 ( の長さ ) は 引き伸ばされる。
結果的に、観測される波長 λ は 次のように引き伸ばされることになる。
(Eq.10)
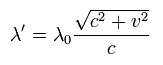
振動数は 波長の逆数であるため、観測される振動数 (= ν' ) は
(Eq.11) 観測される振動数 (= ν' ) は 古典力学でも ν0 よりも低くなる

Eq.11 は Eq.9 に等しい。
よって 横ドップラー効果を 通常の古典力学で説明することができた。
お気づきの通り、Eq.9 と Eq.11 の結果は 観測者に向かってくる光の振動数と 観測者から遠ざかる光の振動数の 中間地点あたりを示しているだけの話である。
なぜなら ”横”方向だからである。
もし 純粋に相対論的に 横ドップラー効果を説明しようとするならば、 通常の電磁波のかわりに 光子という粒子を使う必要がある。なぜなら 相対論は クーロン力に "仮想光子" を使用しているからである。
しかし、根本的に "光子という粒子が振動している" と考えることは奇妙なことである。
つまり、このケースでは 通常の古典的な電磁波を使用するのが自然なのである。
(Fig.49) 相対論的不変性 = 数学化と無限大。
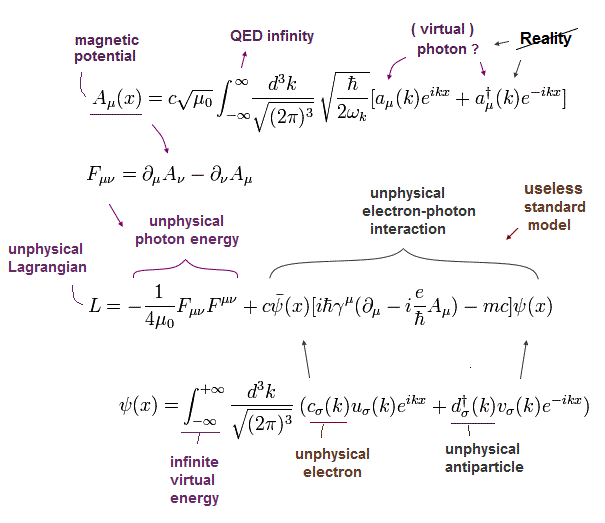
あなた方は 相対論と量子力学は 互いに合わないと聞いたことがあるかもしれない。
しかし 実際は、特殊相対論は ディラック方程式を介して QED, 標準模型、超対称性 などの 重要な相対論的な理論すべての基礎になっているのである。
相対論的な制限は 非常に強いため、私たちは 非常に抽象的な数式しか使用できず、その中には 具体的な物が存在しない。
さらに、ローレンツ対称性を守るために、相対論的な波動関数は 無限種類の運動量とエネルギーを含まなければならず、それは 無限大に発散する。
ディラックとパウリは 無限大を故意に取り除く QED が嫌いだった。
パウリは 相対論的な場の量子論が 必ず無限大に発散することに失望し、物理学者を辞めて小説家にでもなろうかと考えていると ディラックに手紙を書いている。
(Fig.50) 陽電子は実在するのか ?
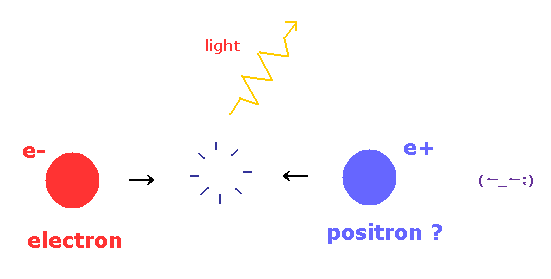
陽電子は 電子の反粒子である。
陽電子は 電子と 同じ質量で、かつ 反対の電荷 +e を持つ。
現在の量子論によれば、陽電子は 容易に 電子と 対消滅し、 γ 線 を形成する。
重要な点は、これから説明するが、この反粒子の存在は 物理の基本的な原理と 矛盾するということである。
これはつまり、反粒子には 最初から 実在性が ないのである。
(Fig.51) 陽電子は 光子から生成される。 なのに なぜ "原子核" が必要?
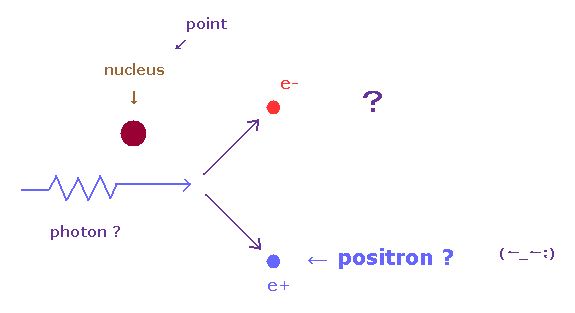
このサイトによれば、 高エネルギーの電子が 原子核の近くを 通るとき、光子を 放射し、 この光子が 電子・陽電子対に 変化する としている。
しかし、この説明が正しいとすると、原子核 (= 標的 ) は まったく 必要ない ことになってしまう。
なぜなら、強力な電磁場の条件さえあれば、各電子は 高エネルギーの光を放射できるからである。
では なぜ 陽電子を生成するのに 電子を 他の原子核に 衝突させる必要があるのだろうか?
実は この理由は 非常に 理不尽で 許されざるものである。
(Fig.52) 入射した光の運動量が 突然 ゼロになる ( p = 0 ) !?
このウェブサイト には 次のような説明がある。
----------------------------
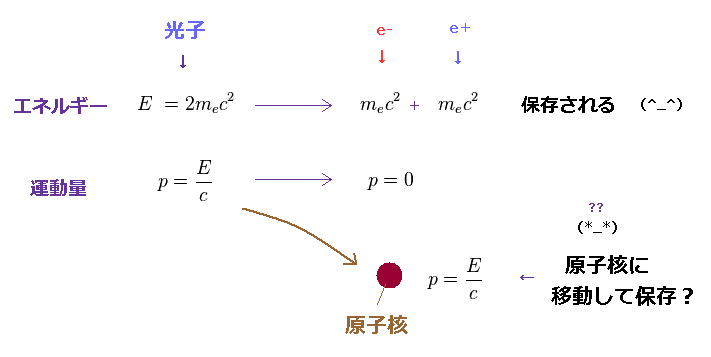
もし、光子が ちょうど 電子・陽電子対の質量エネルギーを生成するだけの エネルギー (= 2mc2 ) を持っているとき、生成された 電子と陽電子は 静止することになる。
このとき、 運動量の保存則 を 破ってしまう。
なぜなら 入射した光子には 運動量 ( p = E/c ) があるが、生成された 電子・陽電子は 静止しているため、運動量を 持たない からである ( p = 0 )。
これはつまり、この対生成は 原子核の近くで 起きなければならない。
なぜなら、この原子核に 光子の運動量を 吸収してもらう必要があるからである。
-----------------------------
実は、この説明は 自己矛盾を含んでいるのである。 このサイトも参照のこと。
なぜなら、原子核が (運動)エネルギーを吸収せずに、 運動量のみを 吸収することは 不可能だからである。
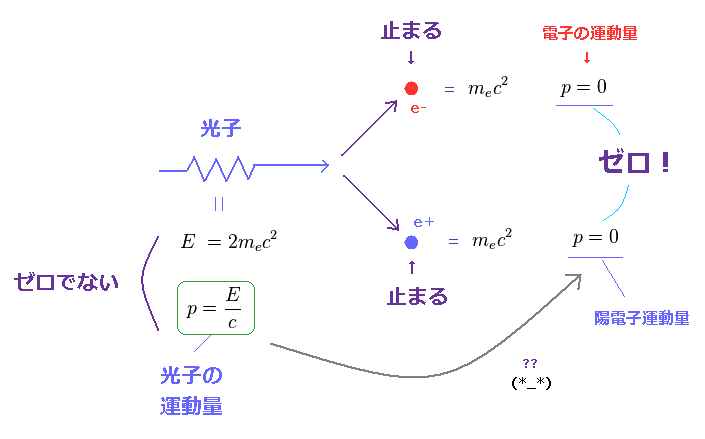
(Fig.53) 運動量のみが 保存されない !?
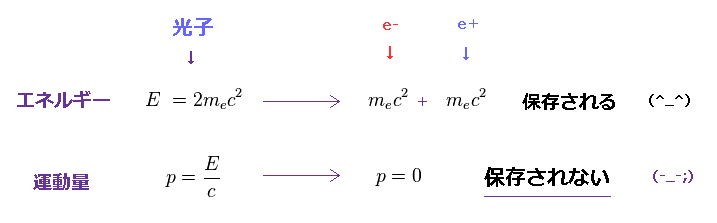
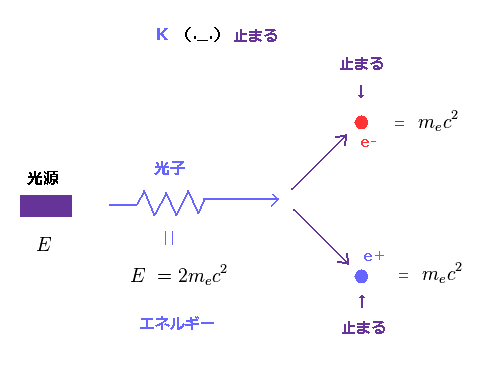
Fig.53 に示したように、入射した光子が ちょうど 2mc2 のエネルギーを持つとき、アインシュタインの質量公式によれば、1対の電子と陽電子が生成される。
しかしこのケースでは、生成された電子・陽電子は 静止しているため 運動エネルギーを 持っていない ことになる。
なぜなら、入射光のすべてのエネルギーが 質量エネルギーに 使われてしまうからである。
もちろん、入射光は 運動量 ( p = E/c ) を持つ。
しかし、生成された電子・陽電子は 運動量を 持っていないのである ( p = 0 )。
これは明らかに 致命的な矛盾である。
(Fig.54) 便利な原子核が "余分な" 運動量を吸収してくれる ?
もちろん、全運動量 ( と エネルギー ) は 保存されなければならない。
この 物理の基本的なルールを満たすために、彼らは 光子の近くにある原子核が この余分な運動量を 吸収する と考えたわけである。
お気づきのとおり、この説明は 非常に理不尽である。
(Fig.55) この原子核は "運動量" があるが、運動エネルギーを持たない !?

奇妙なことに、この原子核は 運動量を持つのに、運動エネルギーを 持たない のである。
もちろん、この現実の世界では こんなことは 不可能である。
よって この事実は 電子・陽電子対の生成自体が あり得ない現象であることを示している。
つまり、陽電子は 単に 正電荷のイオン、陽子、もしくは 散乱された電子群 が混ざったものということになる。
事実、彼らは 陽電子発生のために、必ず 原子核との衝突 に頼っている。
このサイトや このサイト (p.17-18) にあるように、光子・光子衝突実験では 電子などの粒子の衝突に付随する ”仮想の”光子を利用しているだけで、リアルな光子・光子実験をしているわけではないので注意。
(Fig.56) ちょうど1ペアが生成され得る 光子 ( = 光 ) のエネルギー.
このセクションでは、どうして 陽電子生成が 非現実的な現象であるか 説明する。
Fig.56 では、光子のエネルギーは ちょうど 2mc2 である。
そのため 電子と陽電子の1ペアが生成されて、それらは 静止していることになる。
K の観測者も 静止している。
(Fig.57) もし 光子が それより低いエネルギーを持つとき、 このペア生成は 抑制される。
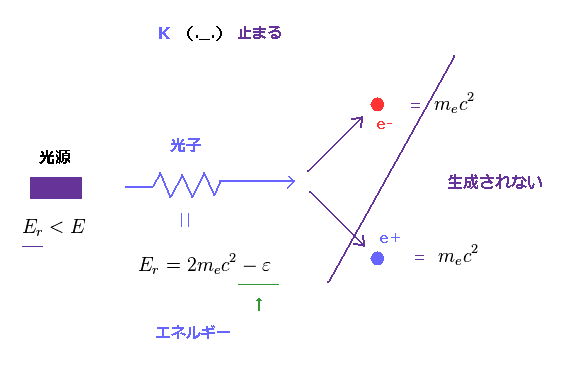
結果的に、このときの光源が Fig.56 のときよりも わずかに小さいエネルギー (= E - ε ) を放出したとき、このペア生成は 起きないことになる。
なぜなら 光子のエネルギーが 2mc2 にわずかに到達してないからである。
(Fig.58) 観測者が動くと、 新たな "運動エネルギー" が 陽電子と電子に発生する?
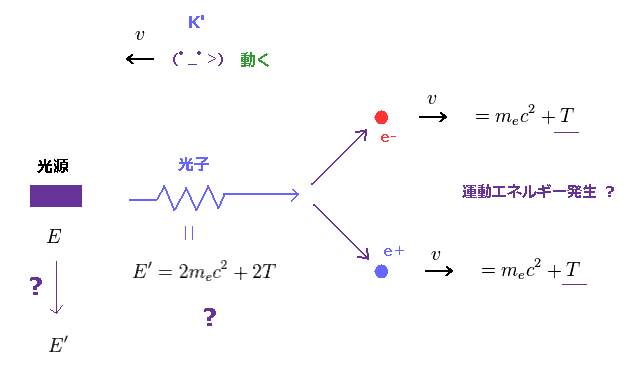
もし Fig.56 の観測者が 動き出すとする (= K' 系 ) と、陽電子と電子の両者も K' の観測者から見て 動き出すことになる。
つまり、 K' 系では、生じた陽電子と電子は さらに運動エネルギーを 元の静止質量エネルギーに加えて持っていることになる。
光源は まったく同じ光子を放出しているにも関わらずである。
(Fig.59) では ここで 低エネルギーの光子を 放出したら ... ?
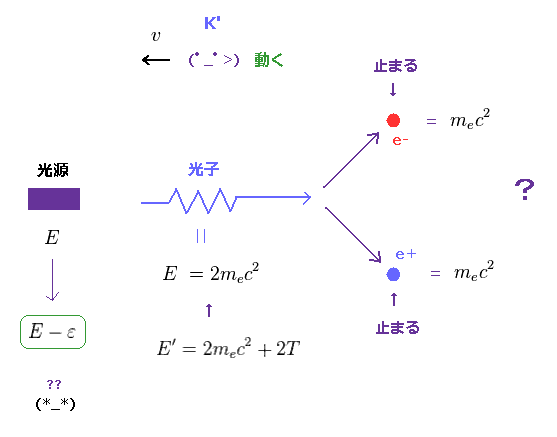
Fig.58 にあるように、生じた 陽電子と電子が 余分の運動エネルギーを持つとしたら、光源が 今よりも 低いエネルギーの光子を放出させたとしても 静止した陽電子、電子対を生成することが可能ということになる。
しかし それだと Fig.57 の結果と矛盾してしまう。
これはつまり 反粒子のペア生成は 特殊相対論自体と 矛盾することになる。
(Fig.60)

ドップラー効果によれば、光子 (= 光 ) のエネルギーは K' のほうが K よりも増加することになる。
なぜなら 光子の振動数が 大きくなるからである。
これはつまり、ペア生成のための光子のエネルギーの量は 観測者の運動に依存していることになる。
これはおかしいと言わざるを得ない。
(Fig.61) 運動エネルギーは 観測者の運動に依存して変化 !?

もしエネルギーが 反粒子の静止質量エネルギーに変化するとしたら、観測者の運動が 反粒子の生成をコントロールできることになる。
なぜなら 物体の速度 (= 運動エネルギー ) は 観測者の運動に応じて変化するからである。
つまり K 系で 陽電子が生成されなくとも、K' 系で生成できてしまうことになる。
このパラドックスは 明らかに 反粒子の実在性が 非常に疑わしい証拠である。 このページも参照のこと。
(Fig.62) 生成された陽電子と電子間の距離がゼロ ... V = -∞ ?
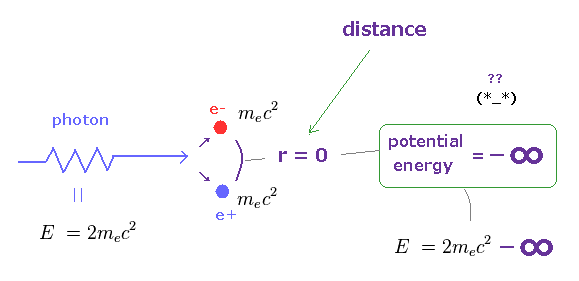
光子が ちょうど 2mc2 のエネルギーを持つとき、生成された陽電子と電子は 静止していることになる。
しかし この場合、それらの間の距離は ほぼゼロになるため、ポテンシャルエネルギーが −無限大 になってしまう。
つまり エネルギーが保存されないことになる ( 2mc2 → 2mc2 - ∞ )。
これもまた パラドックスである。
(Fig.63) ある質量の物体を いくら粉々にしても トータルの質量は 同じまま。
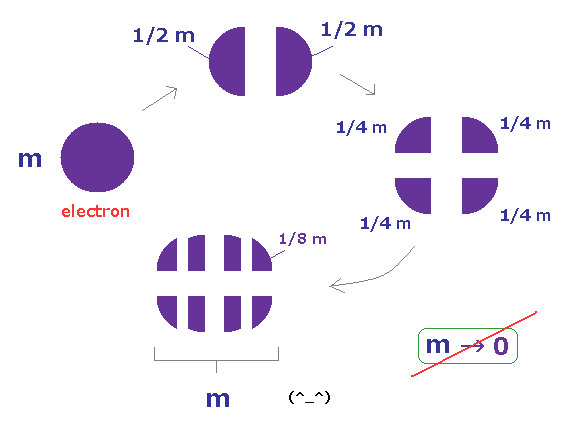
重要な点は 質量エネルギーという考え自体が 非現実的だということである。
例え ある質量 (= m ) の物体を 無限小レベルにまで 粉々に分解しても、トータルの質量は m のまま変わらない。
つまり ある質量が 質量ゼロの光子に変化するという考え自体があり得ないことが分かる。
ディラック方程式は QED、標準模型、ひも理論にとって、必要不可欠な存在である。
ここでは ディラック方程式が 相対論的な運動量とエネルギー (= 4元運動量 ) を使用していることを示す。
また これらの4元運動量は 直角レバーのパラドックスという致命的なパラドックスを引き起こし、このことが 上記すべての相対論的な場の量子論が間違いであることを意味している。
相対論的な理論では、時計は 慣性系によって 異なった進み方をする。
そのため ローレンツ変換の下で不変な 新たな時間の概念を導入する。
これを 固有時 ( τ ) という。
(Eq.12)
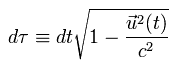
Eq.12 では、"u(t)" は K 系における 物体の速度であり、"t" は K 系における時間である。
( 相対論では、異なった慣性系で 速度も異なって見える。)
固有時は 動く物体に伴った時計で測った時間のことを言う。
つまり この固有時は ローレンツ変換で 変化しない。(= ローレンツ変換不変。 )
Eq.12 より、固有時は、
(Eq.13)
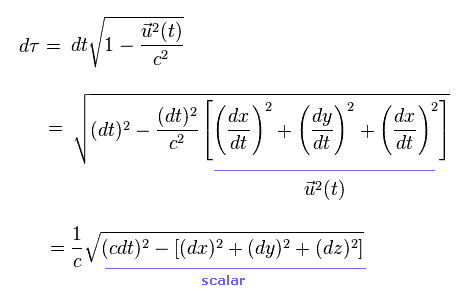
Eq.13 は ローレンツ変換不変なスカラー値である ( Fig.64 も参照のこと )。
(Fig.64)
そのため この固有時を ローレンツ変換の下で "定数" のように扱える。
(Eq.14)
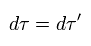
Fig.64 と ローレンツ変換を考慮して、特殊相対論は 次の4元ベクトルを定義している。
(Eq.14')
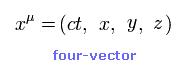
後で説明するが、動いている物体の 相対論的な質量は 相対論によれば 重くなる。
つまり 相対論的な運動量 (= p ) は 次のように表せる。
(Eq.15)
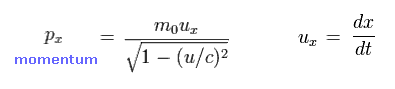
Eq.15 は 次のように表せる。
(Eq.16)
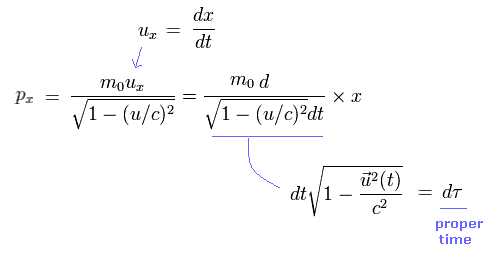
Eq.12-Eq.14 (= 固有時 ) より、Eq.16 の分母は定数のように扱える。
つまり Eq.16 は ローレンツ変換のもとで 4元ベクトルの x 成分 として変化する。
x を ct (= 4元ベクトルの ゼロ成分 ) に置き換えると、Eq.16 は、
(Eq.17)
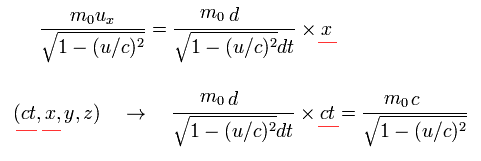
Eq.17 より、4元ベクトルの ゼロ成分を次のように定義できる。
(Eq.18)
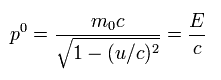
ここで E は 次の相対論的エネルギーである。
(Eq.19)
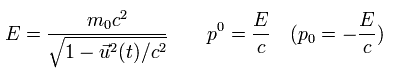
ここでは p0 = - p0 の表記法を用いている。
Eq.17 に見られるように、これらの相対論的な運動量は ローレンツ変換のもとで 時空間座標 ( ct, x, y, z ) のように変換する。
そのため これらは "4元運動量" と呼ばれる。
Fig.64 に見られるように、Eq.15 や Eq.18 から 相対論的な運動量やエネルギーは 次の重要な関係式を満足する。
(Eq.21)
重要な点は Eq.21 は 異なった速度の観測者から見ても 変化しないということである (= ローレンツ変換不変 )。
量子力学では、相対論的エネルギー (E) と 運動量 (p) は 次のような演算子に置き換わる。
(Eq.22)
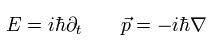
Eq.22 を用いると Eq.21 は 次のように表せる。
(Eq.23)

ここで φ(x) は スカラー場 (= クライン・ゴルドン場 ) と呼ばれるものである。
つまり クライン・ゴルドン (K-G) 方程式は 特殊相対論にちょうど等しいと言える。
φ(x) が スカラーになるには、この φ は 無限種類の運動量を含む必要があり、これが 紫外発散につながる。
このページに示したように、ディラック方程式は クライン・ゴルドン方程式から得られる。
つまり ディラック方程式は 特殊相対論と等価なものである。
ディラック (もしくは K-G ) 方程式は 時間と空間 (= kx ) を 4元ベクトルとして扱っている。
(Eq.24)
もし 超光速のニュートリノが正しいとすると、これはつまり QED、標準模型、ひも理論は ディラック方程式を用いているため これら相対論的な理論はすべて 間違いということになる。
この計算も参照のこと。
このセクションでは ローレンツ変換の下で 光速が定数 "c" になることを計算する。
K' 系が x 軸に沿って右方向へ 速度 "v" で動いている。
(Ap.1) K' 系が K に対して 右方向へ動いている。
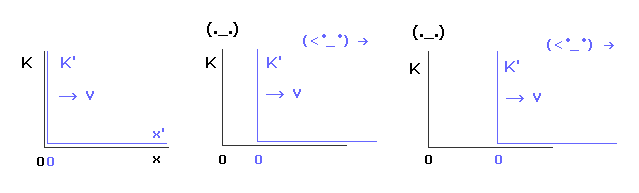
t = 0 のとき、原点にある光源から 光が 放射されるとする。
( 時刻 t = 0 のとき、 K と K' 系の両方の原点は 同地点にあるとする。 )
(Ap.2) 光速度は K と K' の量慣性系で 同じ "c" になる。

ある時間経過後 ( K では t、 K' では t' )、量慣性系の観測者は 光の進行地点を計測する。
K' 系のみが動き、 K 系が静止しているにも関わらず、 相対論では両観測者の視点からでも 光速は 同じ "c" になる必要がある。
(Ap.3) 光速は 観測者の運動に関わらず 光速の "c" 。

結果的に 特殊相対論は Ap.3 の両式が 同時に満たされることを要求する。
そうするには 時間と空間の変数が 次のように変換する必要がある。
(Ap.4) ローレンツ変換。
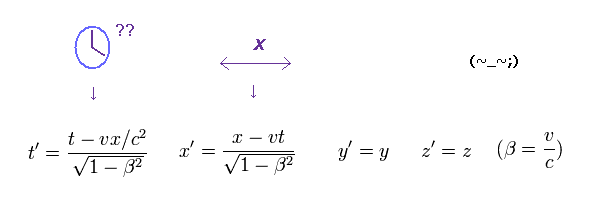
Ap.4 のローレンツ変換によれば、 運動している系の時計の時間は 遅く進むことになってしまう。
また、運動している物体の長さは 収縮して見えることになる。 このサイト参照のこと。
この 超自然的な変換が 深刻な パラドックスを引き起こすことになる。
(Ap.5) 古典的 vs. ローレンツ変換。
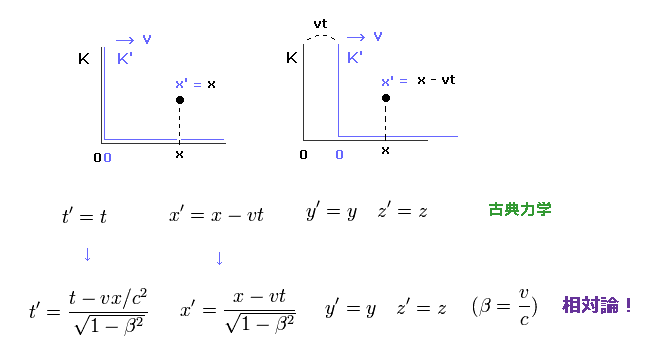
Ap.5 上の式にあるように、通常の古典力学では、K' が x 軸正の方向へ動いているとき、x 座標のみが x' = x - vt のように変換する。
このケースでは、Ap.3 の2つの等式は 成り立たない。
(Ap.6) 古典的な変換。

しかしもちろん、この古典力学では、致命的なパラドックスは 出現しない。
(Ap.7) ローレンツ変換は 非現実的。
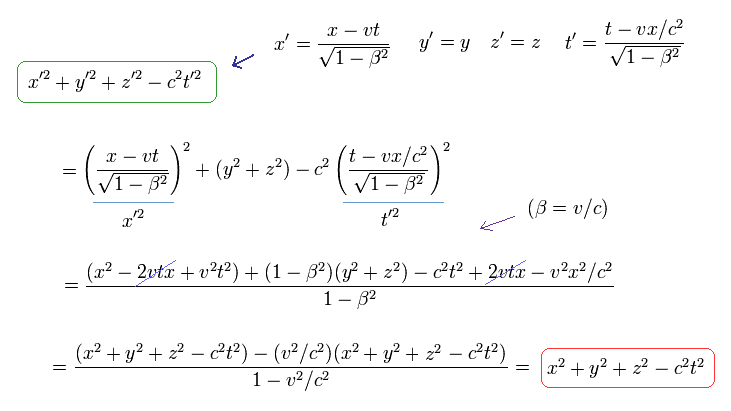
Ap.4 を Ap.3 の最初の式に代入すると、 Ap.3 の2番目の式が成り立つことが分かる。
これを "ローレンツ変換" という。
お気づきのとおり、単なる物体の運動で 時計の時間が遅く進むという考え自体が
非現実的である。
"時間" という概念は 物体の速度に関わらず 共通のものであるのは当たり前の話である。
(Ap.8) マイケルソン・モーリーの実験 = 地球と伴に動く "エーテル" ?

私達の周囲を見渡せば、空気も含めたすべてのものが 地球と伴に動いている。
これらのすべてのものは 電子や原子核で構成されて、電場によって 引き合っている。
つまり、地球と伴に動くエーテルを認めれば、奇妙なローレンツ変換に頼らずとも、一定の光速度 "c" を自然に説明することができる。
(Ap.9) 異なった慣性系における速度の変化。

K' 系が K 系に対して 速度 "v" で 動いている。
K と K' の慣性系の観察者からすると、同じ1つの粒子の速度は次のように表される。
(Ap.10)
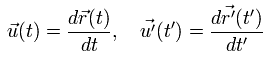
ここでは u(t) は K からみた速度、u'(t') は K' から見た速度である。
Ap.10 に示したように、同じ1つの粒子の速度は 異なった慣性系からは、違ったふうに見える。
なぜなら、時間と空間は 異なった系では 異なったように変化するからである。
この速度 u(t) は ローレンツ変換 (Eq.2) の β の v とは 違うものである。
(Ap.11)
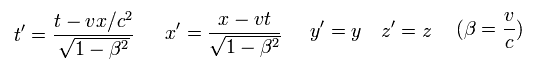
β の "v" は K' 系そのもの ( 粒子でなく ) の速度であり、これは相対論では定数である。
粒子の座標 ( x, y, z ) は 時間 t (もしくは t' ) の関数である。なぜなら その位置は 時間 t と伴に変化するからである。
つまり 粒子の位置 ( x, y, z ) は 時間 t から 独立した値ではない。
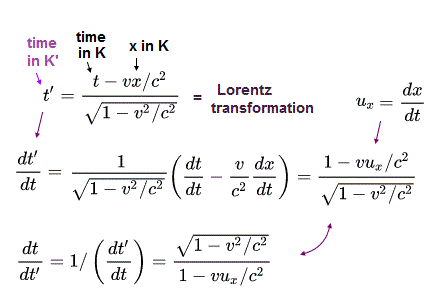
例えば、Ap.11 の時間の変換は 次のように表せる。
(Ap.12)

Ap.11 ( Ap.12 ) によれば、K' 系からみた x 方向の速度 u'x(t') は 次のように表される。
(Ap.13)
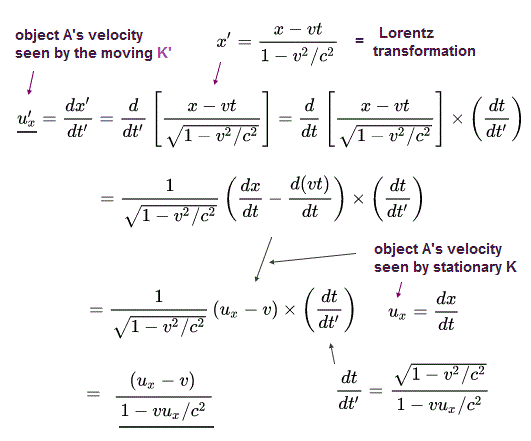
上で述べたように、ローレンツ逆変換は、
(Ap.14)
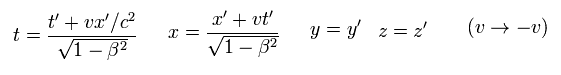
Ap.14 から 次を得る。
(Ap.15)

Ap.15 を Ap.13 に代入して、
(Ap.16)

Ap.16 を解くと、次を得る。
(Ap.17)

Ap.11 と Ap.15 を用いて 速度の y 成分は、
(Ap.18)

Ap.17 を Ap.18 に代入して それを解くと
(Ap.19)
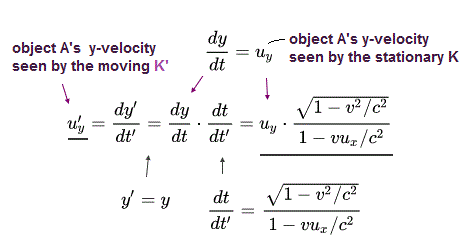
同じように z 方向の速度の解は、
(Ap.20)
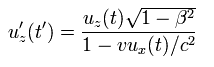
次に Ap.17 を t に関して微分する。
(Ap.21)

Ap.11 より、 次を得る。
(Ap.22)
Ap.21 を Ap.22 で割って、
(Ap.23)
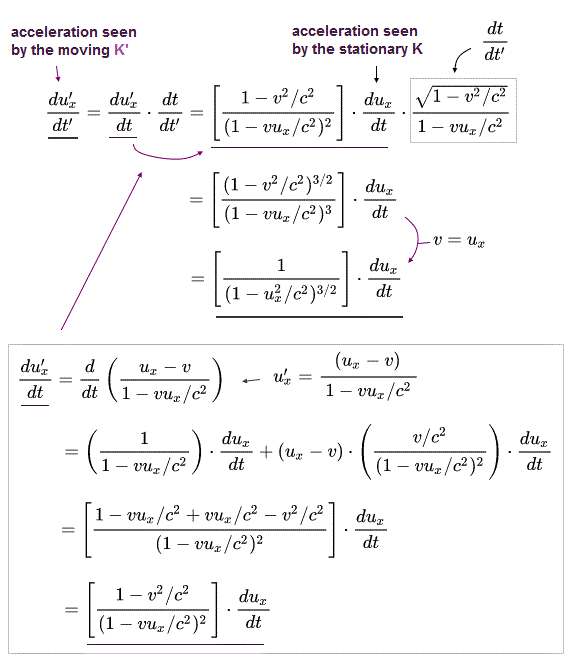
Ap.23 は K' の系から見た加速度 を意味している。
ここで 粒子の速度 ux が K'系の速度 "v" と等しくなる瞬間をチョイスする。
つまり K 系で動いている粒子は K' 系に対しては静止していることになる。
(Ap.24)
K' 系からは、粒子は 静止しており、それは ニュートン力学の力 F' を用いて ニュートン力学を満足しなければならない。
(Ap.25)
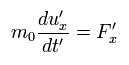
Ap.25 のニューロン力学は 相対論的な運動量を得るための基となる。
Ap.24 を Ap.23 に代入すると、
(Ap.26)

ここで 次の関係式を使う。
(Ap.27)

Ap.25 - Ap.27 より、次の相対論的運動量 (= px ) を得る。
(Ap.28)

相対論的な運動量を得るためには、次のような定義をする必要がある。
(Ap.29)
Ap.29 の定義 (= ニューロン力学の力の変換 ) は 非常に重要である。
しかし この定義は 相対論的な運動量を得るための "人為的な" ものである。
Ap.28 では ローレンツ変換で ニュートン力学の力 Fx が変化しないと仮定した。
しかし 他の方向では 適切な相対論的質量を得るために その力を変化させる必要がある。
( つまり 相対論的運動量は もともと 特殊相対論から "自然に" 得られるものではないのである。 )
K' 慣性系では、y方向の加速度は、
(Ap.30)

Ap.19 を t に関して微分すると、
(AP.31)

Ap.31 と Ap.22 を Ap.30 に代入して、
(AP.32)
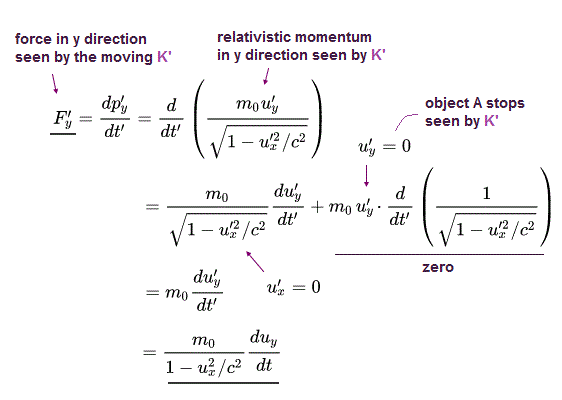
Ap.32 では、 Fy のみ存在するとする。
また ここでは uy は ゼロである。
粒子は K 系では x 方向に動いており、力 Fy は その粒子を y 方向へ加速しようとしている。
K' は ux の速度で x 方向に運動している。Ap.24 を Ap.32 に代入して、
(Ap.33)

Ap.28 と Ap.33 の相対論的な運動量の定義を用いて、
(Ap.34)

粒子は K'系では静止しているため、K' 系では 通常の古典力学の関係式 ( F' = m0a' ) を使用できる。
Ap.34 を Ap.28 (= 相対論的な運動量 ) に合わせるには、力 Fy を 次のように変化させる必要がある。
(Ap.35)
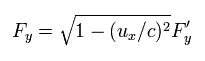
この定義は Ap.29 と異なるものである。
(Ap.36) ニュートン力学の力と 相対論的運動量のまとめ。
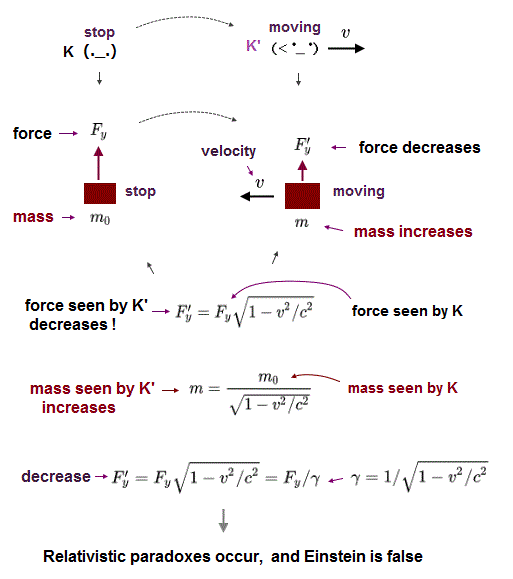
重要な点は これら人為的に定義した力が 直角レバーのパラドックスという致命的なパラドックスを引き起こすということである。
(Ap.37) 直角レバーのパラドックス。

1-2-3 の直角の形をしたレバーがあるとする。固定した回転ポイントが1つある。
K 系に関して このレバー (= K' に対して静止 ) は 速度 ux で x 方向に動いているとする。
このレバーの静止系 (= K' ) では、2つの力と 2つの腕の長さが同じで、トルクはゼロとする。
(Ap.38) K 系でのみ 回転するのか ?

しかし K 系では、レバーは x 方向に動いているため、レバーの腕の1つは ローレンツ収縮しており、また Fy のみ弱くなっている。
つまり トルクは K 系でのみゼロにならず、観測者の単純移動のみで レバーが K 系でのみ回転してしまう。
(Ap.39) どっちが本当?

このページに示したように、この致命的なパラドックスは解決されておらず、QED、標準模型、ひも理論などの相対論的な理論がすべて間違いであることを示している。
なぜなら これらの理論はすべて ディラック方程式を介して 相対論的な運動量とエネルギーに依存しているからである。
次に 相対論的な運動量とエネルギーを得るための別の方法にトライする。
" 4元速度 " (= ω ) を 次のように定義する。
(Eq.51)
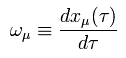
ここでは、固有時 (= τ ) は ローレンツ不変であるため、 Eq.51 は ローレンツ変換において、(t, x, y, z) のように 4元ベクトル として 変化する。
ここで、次の表記を使う。
(Eq.52)
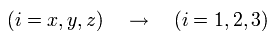
4元ベクトルの i = 1, 2, 3 成分 は、
(Eq.53)
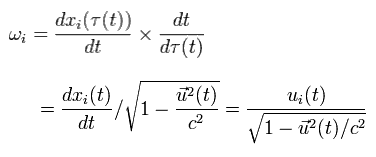
ここでは、Eq.12 を用いている。
また、ω0 は、
(Eq.54)
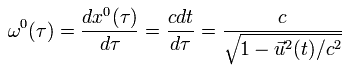
ここで、このページに示すように、 x0 = ct である。
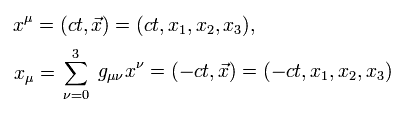
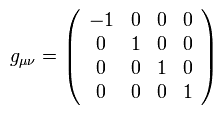
μ = 0、 1、 2、 3 を使うと、 Eq.2 のローレンツ変換は次のように表せる。
(Eq.56)
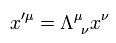
ここで、ローレンツ変換の行列は、
(Eq.57)
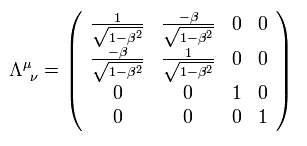
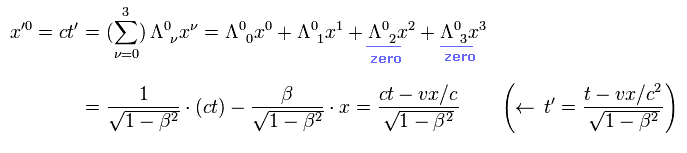
つまり、 Eq.1 は、
(Eq.59)
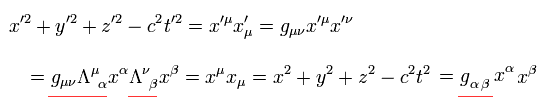
すると、次の関係式が得られる。
(Eq.60)
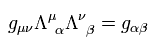
ここで、次の新しい方程式を定義する。
(Eq.61)
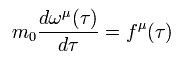
Eq.53 と Eq.54 を使うと、
(Eq.62)
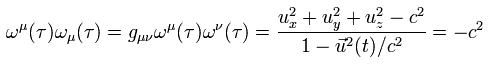
このように 同じ変数を 2回 ( μ μ のように ) 使うときは、 0 から 3 までの成分を足し合わせることを意味する。
Eq.62 を 固有時 ( τ ) で微分して、さらに 2 で割ると、
(Eq.63)
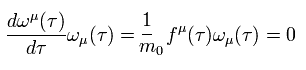
ここで Eq.61 を使っている。
もともと、 ωμ(τ) と fμ(τ) は、特に慣性系の指定なく導入したので、次の関係式が自然に満たされる。
(Eq.64)
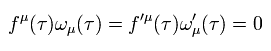
Eq.51 に示したように、 ωμ(τ) は 4元ベクトルとして変化する。 そのため、もし fμ(τ) も 4元ベクトルとして変化すると、
(Eq.65)
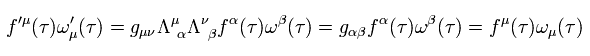
Eq.64 を得ることができる。
つまり、Eq.61 の fμ(τ) も ωμ(τ) のように 4元ベクトルとして変化する。
この fμ(τ) を " 4元力 " と呼ぶことにする。
ここで、 f i (τ) (i = 1, 2, 3 ) を 次のように定義する。
(Eq.66)
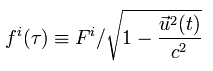
ここで F は ニュートン力学の力である。
Eq.66 の定義は 相対論的運動量を得るための 人為的な定義と言える。
Eq.53、 Eq.54、 Eq.66 を Eq.64 に代入すると、
(Eq.67)
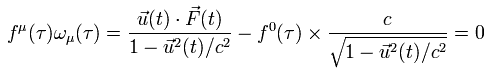
Eq.67 より、 0 成分の解 ( = f 0 (τ) ) は、
(Eq.68)
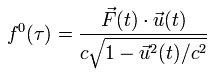
Eq.12 を使うと、 Eq.61 は 次のように表せる。
(Eq.69)
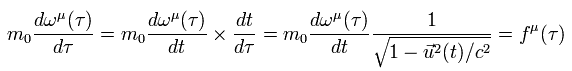
Eq.53 と Eq.66 を Eq.69 に代入すると、 次の運動方程式が得られる。
(Eq.70)
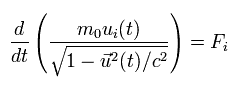
よって、次の 相対論的な運動量 ( = p ) を得ることができた。
(Eq.71)
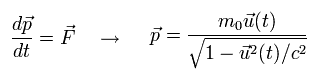
また、 Eq.54 と Eq.68 を Eq.61 に代入すると、
(Eq.72)
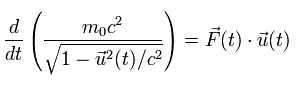
よって、 次の 相対論的なエネルギー ( = E ) も得ることができた。
(Eq.73)
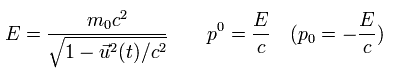
これらの結果は 上のセクションと同じものである。
すでに述べたように、Eq.66 の定義は ニュートン力学の力 F と 4元力の関係を表すものであり、相対論的な運動量を得るための人為的なものである。
また これは 直角レバーのパラドックスを引き起こし、このレバーの回転は 相対論における弱点を示している。
マクスウェル方程式によれば、 電流密度 (= J ) と 電荷密度 (= ρe ) は 次の関係式を満たす。
(Eq.74)
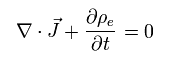
もちろん、全電荷は 慣性系に関係なく 保存される。
そのため、Eq.74 は ローレンツ変換不変でなければならない。
( このページも参照のこと。)
しかし このページに示したように、Eq.74 の定義は結局 電線内の全電荷の保存則を破ってしまう。
これはすなわち 特殊相対論とローレンツ変換そのものが破綻していることを意味している。
もし ”地球とともに動いているエーテル” を認めたとしたら、ローレンツ変換そのものがなくなるため、保存則の破れは当然起こらない。
Eq.74 は 4元ベクトル ( xμ ) を使って次のように表せる。
(Eq.75)
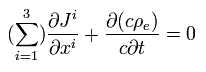
ct は x0 の意味と同じである。
また、ここで 新しい4元ベクトル (= 4元電流密度 ) を次のように定義すると、
(Eq.76)
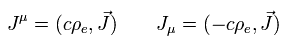
Eq.75 は次のように表せる。
(Eq.77)
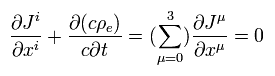
Eq.56 の ローレンツ変換を使うと、 xμ による微分は、
(Eq.78)
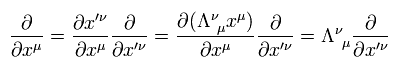
Eq.78 を Eq.77 に代入すると、次の式が得られる。
(Eq.79)
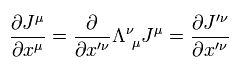
結果として、 Eq.77 (= Eq.74 ) は ローレンツ変換不変であることを証明できた。

2014/5/17 updated This site is link free.