トップページ (ヘリウムを含む正確な新ボーア模型)
( H2 )、( C-C、C=C )、
(CH4、H2O)。
原子半径。
2原子分子。
多原子分子計算。
分子結合の電子。
生体金属錯体。
PDB グルカゴン
2量体 PDB タンパク質間相互作用。
何が タンパク質の構造を決めているのか? (13/10/19)
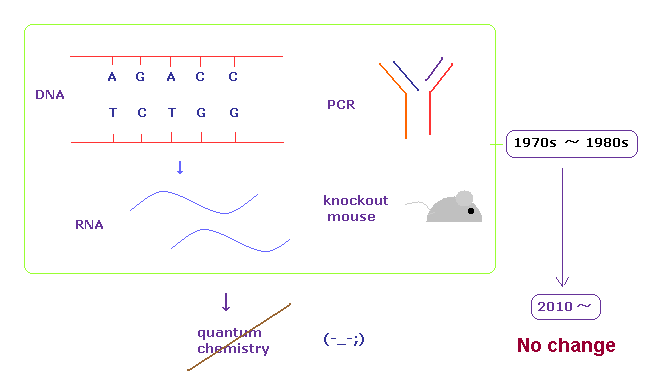
(Fig.A-1) バイオ技術の根幹技術は 1970 年代から進歩していない。

あなたがたは 「 分子生物学の進展は 日に日に速くなっている。」などという見出しのニュースを見聞きすることが よくあると思われる。
しかし例えば 癌や 様々な 脳神経 運動機能障害などの深刻な病気などには まったく 私達は 無力である。
現在の遺伝子工学の根幹をしめる DNA、RNA、PCR, 培養細胞、ノックアウト技術 などは 1970 年代から 1980 年代に確立されたものである。
実は 21 世紀になった今でも 最先端の分野においてさえ これら古い技術が 今だに主導的な役割を果たしているのである。
この状況は奇妙としかいいようがない。
この深刻な状況は 非実在的で 曖昧な 量子力学 (化学) が 実質的に その上の 遺伝子工学などの応用分野で まったく使い物になっていないことに起因する。
(Fig.A-2) すべての生物は 個々の原子 から生成された。
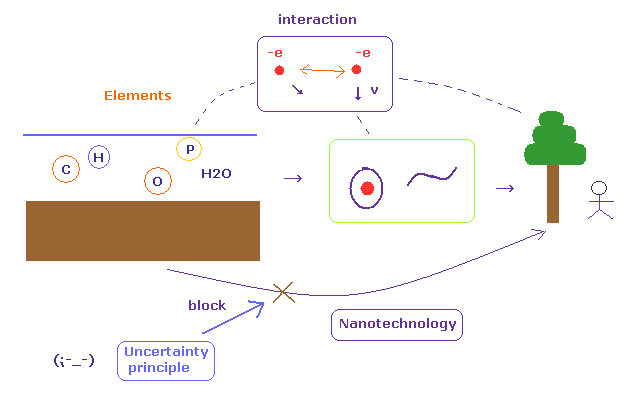
考えてみよう、地球上のすべての生物は 元は 何の生命もない 個々の原子だったことは周知のことである。
非常に長い時をかけて 地球上の自然界 が徐々に 様々な原子を組み合わせて すべての生物を形作ってきた。
この事実は 私達に ある十分な知識があれば すべての生物を 地球上で 個々の原子を反応させて形づくれる可能性を示唆している。
これは極端な話だが、自然が地球上で リアルにしてきたことなので 地球上で再現コントロールすることが 実質的に可能であることに変わりはない。
しかし 現在の科学の状況は 原子、分子レベルで すべての進展が阻まれ ( 不確定性原理やら多世界やらのせいで )、哺乳類どころか 原生動物でさえ コントロール、生成できない。
人間の体などは 非常に複雑だが、原子構造は 非常にシンプルであり、単に 電子と原子核から成り立っているだけである。
このことは 人間の体の 様々な複雑な機能を決定、統括しているのは 個々の電子の 様々な運動パターンであることを示唆している。
つまり できるだけ早く 何の電子の運動状態も許さず それらの具体的な状態も問うことを許さない 不確定性原理は 捨てるべきと思われる。
(Fig.A-3) 現在の科学は 非実在かつ 幻想の世界にのみ 向かっている。

よくサイエンスニュースで 膨張宇宙、ブラックホール、量子コンピューター、余剰次元、 スピンエレクトロニクス に関するニュースを見聞きする。
これらの概念を うさんくさいと思われた方々も多いと思われるが、 これら擬似科学は 単なる幻想にすぎないものばかりである。
実際に これらの非実在かつ 役に立たないことを研究しても 私たちの生活や技術に何の進展も もたらしてこなかったし、 これからもそうだろう。
また 特殊相対論が間違っていることの証明は、標準模型、ひも理論、一般相対論などが どう転んでも 本当の理論には なれないことを示している。
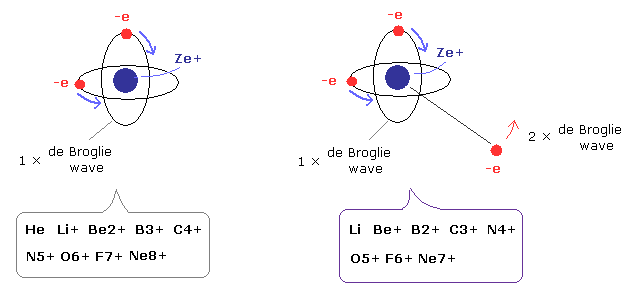
(Fig.1) 2電子・3原子原子模型。
新しいボーア模型によって、ヘリウム原子の基底状態エネルギーの計算で、量子力学的な変分法よりも正確な結果をだすのに成功した。(トップページ参照のこと)。
この成功した新ボーア模型では、ヘリウム原子 (He) の2つの電子は、ちょうど1ド・ブロイ波長の互いに垂直な軌道上を運動している。
なぜなら 2つの電子が同一の円軌道上にあると それらの 1ドブロイ波長の互いに逆位相の波が キャンセルしあうからである。
また、この新しい原子模型は、パウリの排他原理の現象も正確に説明できる。
なぜなら、この新しいボーアの2電子原子には、3つめの電子 ( 1ドブロイ波長の ) が入りこむスペースがないからである。
驚くべきことに、この新しいボーアのヘリウム構造は、他のすべての 2電子 もしくは 3電子原子(イオン)にも正確にあてはめることができる。
| 原子 | r1 (MM) | WN x 4 | 同一円軌道 | 計算値 (eV) | 実験値 (eV) | 誤差 (eV) |
|---|---|---|---|---|---|---|
| He | 3074.0 | 1.000000 | -83.335 | -79.0037 | -79.0051 | 0.001 |
| Li+ | 1944.5 | 1.000000 | -205.78 | -198.984 | -198.093 | -0.89 |
| Be2+ | 1422.0 | 1.000000 | -382.66 | -373.470 | -371.615 | -1.85 |
| B3+ | 1121.0 | 1.000000 | -613.96 | -602.32 | -599.60 | -2.72 |
| C4+ | 925.0 | 1.000000 | -899.67 | -885.6 | -882.1 | -3.50 |
| N5+ | 788.0 | 1.000000 | -1239.8 | -1223.3 | -1219.1 | -4.20 |
| O6+ | 685.3 | 1.000000 | -1634.38 | -1615.44 | -1610.70 | -4.74 |
| F7+ | 607.3 | 1.000000 | -2083.3 | -2062.0 | -2057.0 | -5.00 |
| Ne8+ | 544.5 | 1.000000 | -2586.7 | -2563.0 | -2558.0 | -5.00 |
(Fig.2) 2電子原子模型 ( He, Li+, Be2+, B3+, C4+ ... )
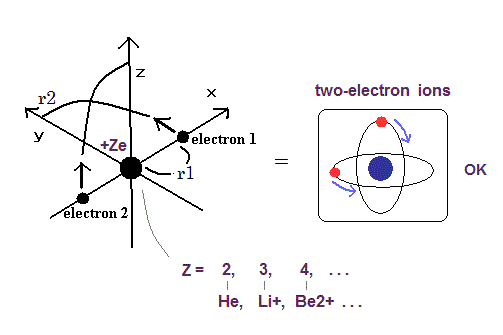
Table 1 の計算結果は 明らかに Fig.2 の原子模型が正しいことを示している。
( 2つの 1 × ドブロイ波長の軌道が互いに垂直な模型。)
(Fig.3) 同一円軌道の 2電子原子模型。
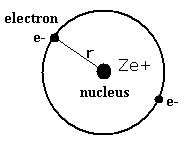
Table 1 の 同一円軌道は 2つの電子が Fig.3 に示すように 同一軌道上の 互いに逆の位置を運動している模型のことを意味している。
もちろん、Fig,3 の模型は 間違いである。
なぜなら それら 1 × ドブロイ波長の互いに逆位相の波が お互いを打ち消しあって不安定になってしまうからである。
| 原子 | r1 (MM) | WN x 4 | 計算値 (eV) | 実験値 (eV) | 誤差 (eV) |
|---|---|---|---|---|---|
| Li | 1949.0 | 1.000000 | -203.033 | -203.480 | 0.47 |
| Be+ | 1427.0 | 1.000000 | -388.785 | -389.826 | 1.04 |
| B2+ | 1125.0 | 1.000000 | -635.965 | -637.531 | 1.56 |
| C3+ | 928.0 | 1.000000 | -944.46 | -946.57 | 2.11 |
| N4+ | 790.5 | 1.000000 | -1314.25 | -1317.01 | 2.76 |
| O5+ | 688.0 | 1.000000 | -1745.70 | -1748.82 | 3.12 |
| F6+ | 609.4 | 1.000000 | -2237.60 | -2242.21 | 4.61 |
| Ne7+ | 546.0 | 1.000000 | -2791.15 | -2797.12 | 5.97 |
(Fig. 4) 3電子原子模型。
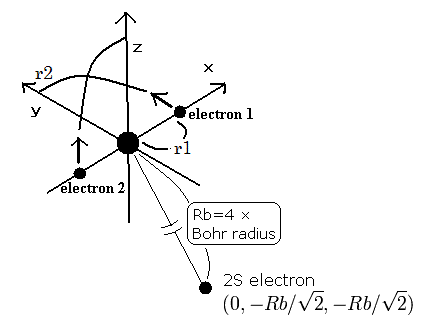
3電子原子模型では、外殻の 2S 電子の半径は リチウムで 4 × ボーア半径になる。
(Eq.1)
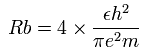
他のイオンでは Z を原子番号として (Z-2) で上記の値を割ればいい。
なぜなら 内殻の2つの 1S 電子が Z 原子核に非常に近いため、外の 2S 電子が +(Z-2) の原子核の周囲を 水素様原子のように 回っていると見なすことが可能だからである。
大きい原子になるほど、この近似は Table 2 に示すように 誤差が大きくなる。
( しかし これらの非常に実験値に近い計算結果から Fig.4 や Fig.2 の原子構造が 実際に正しいと言える。)
ここで 様々な原子のイオン化エネルギー( 実験値 )を示す。
| 原子名 | 1st | 2nd | 3rd | 4th | 5th | 6th |
|---|---|---|---|---|---|---|
| ヘリウム (He) | 24.58741 | 54.41778 | - | - | - | - |
| リチウム (Li) | 5.39172 | 75.64018 | 122.45429 | - | - | - |
| ベリリウム (Be) | 9.32270 | 18.21116 | 153.89661 | 217.71865 | - | - |
| ホウ素 (B) | 8.29803 | 25.15484 | 37.93064 | 259.37521 | 340.22580 | - |
| 炭素 (C) | 11.26030 | 24.38332 | 47.88780 | 64.49390 | 392.08700 | 489.99334 |
Table 3 の最後の2つの大きな値が Table 1 における 2電子原子(イオン)の全エネルギーを表している。
そして 最後の3つの値が Table 2 における 3電子原子(イオン)の全エネルギーを表している。
見てのとおり、1S 電子のイオン化エネルギー ( Table 3 の赤い数値 ) は 他と比べて非常に大きい。
これは 様々な原子において、2つの 1S 電子のみ 原子核に非常に近づいていることを示している。
もちろん、これは ドブロイ波の整数倍に関係しているからである。
次に Fig.3 と Table 1 の 同一円軌道のエネルギー値について説明する。
(Fig.3)

遠心力とクーロン力が釣り合っていることから、
(Eq.2)
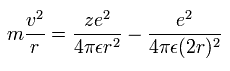
ここで r は 円形軌道の半径 (meter)、 m は 電子質量である。
また "z" は原子番号である。
円形軌道が ドブロイ波長の整数倍 (n) と仮定すると、
(Eq.3)
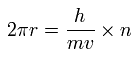
ここで h/mv は ドブロイ波長である。
全エネルギー E は 2つの電子の運動エネルギーとクーロンポテンシャルエネルギーの和であるから、
(Eq.4)
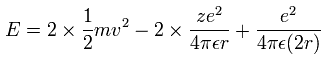
上の3つの式を解くと、全エネルギー E は、
(Eq.5)
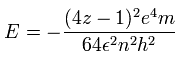
z に原子番号と n=1 を代入すると、Table 1 の同一円軌道の値を得ることができる。
この模型は 実験値よりも大きなイオン化エネルギーを与える。
なぜなら 1つの 1 × ドブロイ波長の軌道が 2つの電子を含んでいるため 互いの波の状態を乱してしまい、実際と異なるからである。
(Fig.2) 2電子原子模型 ( He, Li+, Be2+, B3+, C4+ ... )

このセクションでは 新しいボーアのヘリウムと同じ方法で Li+、Be2+、B3+ の基底状態のエネルギーを計算してみることにする。
詳細な計算方法に関しては、トップページ (He) も参照のこと。
ここでは 次のサンプル JAVA プログラム ( または C 言語 )を使用する。
2電子原子軌道の JAVA プログラム。
2電子原子軌道の C 言語 プログラム。
このプログラムでは 次の単位を使用する。
(Eq.6)
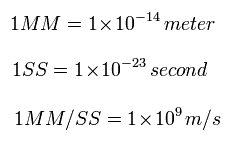
Eq.6 から、 加速度は、
(Eq.7)
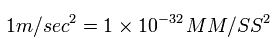
このプログラムでは 最初に 原子番号 Z (= 2, 3, 4, 5, ... 10 ) を入力する。
そして 1 SS ごとに 2電子と原子核間のクーロン力を計算し、それぞれの速度を変化させていく。
電子1が (x, y, 0) にあるとき、電子2は (-x, 0, y) にあることになる。
つまり 電子1の加速度 (MM/SS2) の x と y 成分は、
(Eq.8) 加速度の x と y 成分。
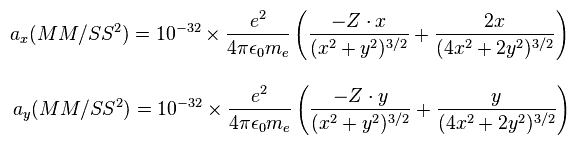
ここでは 最初の項が 電子1と原子核間のクーロン力、2番目の項が 2電子間のクーロン反発力を示している。
ヘリウムとリチウムなどの軽い原子では 質量中心が原子核の位置にある場合を除いて 換算質量を使用する。
rm =1/2 × (2me × nucleus)/(2me + nucleus)
( 3体問題の換算質量のページも参照のこと。 )
さらに 1 SS ごとに 速度から ドブロイ波長 ( λ = h/mv ) を 計算する。
その微小移動時間に含まれる ドブロイ波 ( 長さが λ ) の数 ( その合計が WN ) は、
(Eq.9) 1SS の間に進む微小距離内に含まれる ドブロイ波の数。
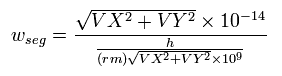
ここで ( VX, VY ) は 電子1の速度 ( MM/SS )、Eq.9 の分子は 1 SS の間の移動距離 ( meter )、分母はドブロイ波長 ( meter ) である。
ここでは 推定される電子軌道は 100 万以上の微小区間に分割して計算していくことになる。
電子1が その軌道の 1/4 を進んで その x 座標がゼロになったとき、このプログラムは 電子1の速度の y 成分 ( last VY ) をチェックする。
この last VY がゼロのとき、2つの電子は 決まった軌道上を周期的に運動することになる。
よって -0.0001 < last VY < 0.0001 ( MM/SS ) を満たすとき、このプログラムは 次の数値を画面に表示する。
r1, VY, preVY ( 1SS 前の VY )、 (mid)WN ( 1/4 軌道に含まれるドブロイ波の合計 )。
( "Wrong Ene" は Eq.5 で与えられる間違ったエネルギー値である。 )
| E (eV) | r1 (MM) | WN | WN x 4 |
|---|---|---|---|
| -194.0 | 1995.0 | 0.253191 | 1.012764 |
| -196.0 | 1974.0 | 0.251895 | 1.007580 |
| -198.0 | 1954.0 | 0.250620 | 1.002480 |
| -198.984 | 1944.5 | 0.250000 | 1.000000 |
| -200.0 | 1935.0 | 0.249364 | 0.997456 |
| -202.0 | 1916.0 | 0.248126 | 0.992504 |
| -204.0 | 1897.5 | 0.246907 | 0.987628 |
Table 4 は Li+ の様々なエネルギー準位における last VY がゼロのときの r1 と WN の結果を示している。
つまり Li+ の全エネルギーが -198.984 eV のとき、1軌道に含まれるドブロイ波の合計は ちょうど 1.000000 になる。
Li+ のエネルギーの実験値は -198.093 eV である。
誤差は たった -0.89 eV ( 0.4 %) である。
つまり、リチウムイオン ( Li+ ) においても、2つの電子の軌道面が互いにほぼ垂直であると言える。
| E (eV) | r1 (MM) | WN | WN x 4 |
|---|---|---|---|
| -367.0 | 1447.0 | 0.252194 | 1.008776 |
| -369.0 | 1439.0 | 0.251510 | 1.006040 |
| -371.0 | 1431.0 | 0.250831 | 1.003324 |
| -373.47 | 1422.0 | 0.250000 | 1.000000 |
| -375.0 | 1416.0 | 0.249490 | 0.997960 |
| -377.0 | 1409.0 | 0.248827 | 0.995308 |
| -379.0 | 1401.0 | 0.248169 | 0.992676 |
Table 5 は Be2+ の様々なエネルギー準位における last VY がゼロのときの r1 と WN の結果を示している。
つまり Be2+ の全エネルギーが -373.47 eV のとき、1軌道に含まれるドブロイ波の合計は ちょうど 1.000000 になる。
Be2+ のエネルギーの実験値は -371.62 eV である。
誤差は たった -1.85 eV ( 0.4 %) である。
つまり、ベリリウムイオン ( Be++ ) においても、2つの電子の軌道面が互いにほぼ垂直であると言える。
| E (eV) | r1 (MM) | WN | WN x 4 |
|---|---|---|---|
| -596.0 | 1133.0 | 0.251322 | 1.005288 |
| -598.0 | 1129.0 | 0.250902 | 1.003608 |
| -600.0 | 1125.0 | 0.250482 | 1.001928 |
| -602.32 | 1121.0 | 0.250000 | 1.000000 |
| -604.0 | 1118.0 | 0.249652 | 0.998608 |
| -606.0 | 1114.0 | 0.249240 | 0.996960 |
| -608.0 | 1110.0 | 0.248830 | 0.995320 |
Table 6 は B3+ の様々なエネルギー準位における last VY がゼロのときの r1 と WN の結果を示している。
つまり B3+ の全エネルギーが -602.32 eV のとき、1軌道に含まれるドブロイ波の合計は ちょうど 1.000000 になる。
B3+ のエネルギーの実験値は -599.601 eV である。
誤差は たった -2.72 eV ( 0.4 %) である。
つまり、ホウ素イオン ( B+++ ) においても、2つの電子の軌道面が互いにほぼ垂直であると言える。
(Fig.4) 3電子原子模型。

次に 3電子原子(イオン)にトライする。
例えば、リチウム原子は 1S 軌道に2つの電子と、2S 軌道に1つの電子をもっている。
1S の2つの電子は、3e+ の原子核に強くひきつけられているため、2S の電子に比べてかなり原子核に距離的に近いところにある。
つまり、近似的に、2S 電子が、 +e 原子核 ( +3e - 2e = +e ) の周りの 2ド・ブロイ波長 の円軌道を回っているとみなすことができる。
(これは、2S 電子において、近似的に水素原子の式を使えることを意味する。)
原子番号が Z のイオンの 2S 電子は +(Z-2) 原子核の周囲を 水素様原子のように周回しているとみなせる。
ボーア模型によれば、2ド・ブロイ波長の軌道の半径 (Rb) は、次のように ( 4 × ボーア半径 ) となる。(リチウムで)
(Eq.10)
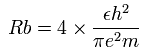
計算すると、この Rb は 2.1167 × 10-10 meter ( = 21167 MM ) となる。
次に n = 2 のエネルギー準位 は、 (水素原子のエネルギー準位の式を使って)
(Eq.11)
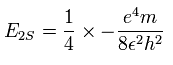
1S の2つの電子はなるべく 2S 電子を避けるように運動する。そこで、2S 電子を Fig.4 に示すように ( 0, - Rb / √2, - Rb / √2 ) に固定する。
( Fig.4 は3つの電子の相対的な位置関係を示している。実際は、この 2S の電子は 1S の電子よりもゆっくりと核の周りを周回している。)
2電子原子のように、電子1が、( x, y, 0 ) にあるとき、電子2は、 ( -x, 0, y ) にある。
つまり、各粒子間の距離は、
(Eq.12)
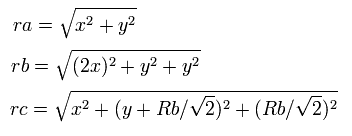
となる、ここで、ra は電子1と核の距離、
rb は2つの 1S 電子間の距離、rc は電子1と 2S の電子の距離である。
電子1の加速度 (m/sec2) の x成分は、( リチウムの場合 )
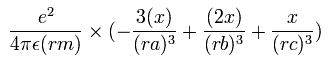
同様に、電子1の加速度 (m/sec2) の y成分は、
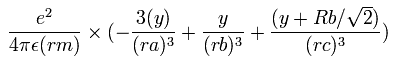
となる。
それから 2電子イオンのときのように 1S 軌道の 1/4 周に含まれる ドブロイ波の数を計算する。
JAVA プログラム ( 3電子原子 )
C 言語 プログラム ( 3電子原子 )
このプログラムでは 最初に原子番号 Z = 3, 4, 5, 6, 7, 8, 9, or 10. ( Li Z=3, Ne7+ Z=10 ) を入力する。
次に 電子1の最初の x 座標 r1 (MM) と、3電子原子(イオン)の 全エネルギー E (eV) の絶対値を入力する。
これらの入力値から このプログラムは 1/4 周後の 電子1の速度の y 成分、WN ( 軌道 1/4 周に含まれる ドブロイ波の数 ) を表示する。
"Rbb" は 2S 電子の半径 (MM) を意味している。
| E (eV) | r1 (MM) | WN | WN x 4 |
|---|---|---|---|
| -197.0 | 2010.0 | 0.253889 | 1.015556 |
| -199.0 | 1990.0 | 0.252579 | 1.010316 |
| -201.0 | 1969.0 | 0.251290 | 1.005160 |
| -203.033 | 1949.0 | 0.250000 | 1.000000 |
| -205.0 | 1930.0 | 0.248770 | 0.995080 |
| -207.0 | 1911.0 | 0.247538 | 0.990152 |
| -209.0 | 1892.0 | 0.246324 | 0.985296 |
Table 7 は Li の様々なエネルギー準位における last VY がゼロのときの r1 と WN の結果を示している。
つまり Li の全エネルギーが -203.033 eV のとき、1軌道に含まれるドブロイ波の合計は ちょうど 1.000000 になる。
Li のエネルギーの実験値は -203.48 eV である。
誤差は たった 0.447 eV ( 0.2 %) である。
つまり、リチウム原子 ( Li ) においても、2つの電子の軌道面が互いにほぼ垂直であると言える。
| E (eV) | r1 (MM) | WN | WN x 4 |
|---|---|---|---|
| -383.0 | 1450.0 | 0.251968 | 1.007872 |
| -385.0 | 1442.0 | 0.251282 | 1.005128 |
| -387.0 | 1434.0 | 0.250602 | 1.002408 |
| -388.785 | 1427.0 | 0.250000 | 1.000000 |
| -390.0 | 1422.0 | 0.249593 | 0.998372 |
| -392.0 | 1415.0 | 0.248926 | 0.995704 |
| -394.0 | 1407.0 | 0.248265 | 0.993060 |
Table 8 は Be+ の様々なエネルギー準位における last VY がゼロのときの r1 と WN の結果を示している。
つまり Be+ の全エネルギーが -388.785 eV のとき、1軌道に含まれるドブロイ波の合計は ちょうど 1.000000 になる。
Be+ のエネルギーの実験値は -389.826 eV である。
誤差は たった 1.041 eV ( 0.2 %) である。
つまり、ベリリウムイオン ( Be+ ) においても、2つの電子の軌道面が互いにほぼ垂直であると言える。
このセクションでは 新しいボーア模型を使った様々な原子、分子模型を紹介する。
ただ 現時点では これらのモデルは単なる近似の段階である。
そのため 専門家を含めた様々な人たちが もっと正確で リアリティーのある 原子、分子模型を発見してくれると非常に喜ばしい。
重要な点は 本当の科学の発展のために 半ば盲目的に 曖昧な波動関数をただ信じて進むことをやめようということである。
実際 シュレディンガーの波動関数は ヘリウムや 他の原子について クリアなイメージを示すことができない。
このことが 波動関数が ただ確率密度のみを与えることで、奇妙な多世界解釈の概念が 支配的になっている要因である。
つまり最初から クリアなイメージを示せない量子力学のヘリウムは ボーア模型と同じ舞台に立っていないのである。
(原子)
新ボーア模型のリチウム 新ボーア模型のベリリウム
新ボーア模型の炭素 - (イメージ化) 新ボーア模型の酸素 - (イメージ化)
ボーアのフッ素と窒素 新ボーア模型のネオン - (イメージ化)
(分子) - ビリアル定理の証明 -
新ボーア模型の水素分子イオン 新ボーア模型の水素分子
分子結合 (CH4、H2O) の本質 ( new ! )
分子結合 ( C-C、C=C ) の本質 ( new !)
本当の原子半径と 電気陰性度。
2原子分子模型の相互作用計算機。
様々な多原子分子の相互作用計算。
ボーア模型の共有結合 (CH4,H2O,NH3)、 ボーアの2重結合 ( C=C, O=O, ビリアル)。
ボーア水分子のイメージ化

2010/7/30 updated This site is link free.