トップページ (2電子原子も含む正確な新ボーア模型)
電子スピンは存在しない。単なる数学上の産物。
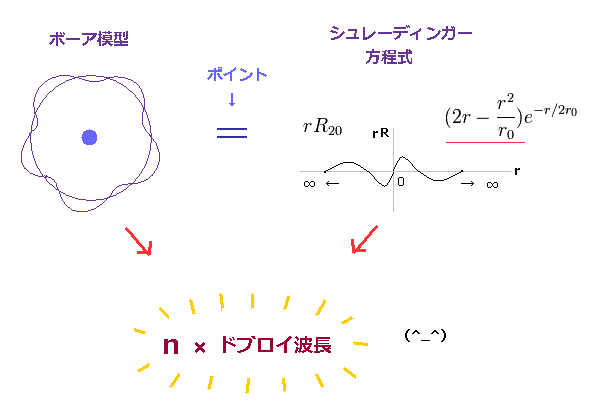
(Fig.1) n × ドブロイ波長。

ボーア模型は 水素原子において シュレーディンガー方程式や 実験値に完全に 一致することが知られている。
ボーア模型では、軌道の円周が ドブロイ波長の整数倍になる。
驚くことに、シュレーディンガー方程式においても、動径、角の両方の波動関数において、ドブロイ波長の整数倍の条件を満たすのである。
これは 波動関数の節の数として現れる。 ( このサイト や このサイト (p.3) 参照のこと。 )
(Fig.2) "円形の" ボーア模型から "楕円形の" ゾンマーフェルト模型へ。
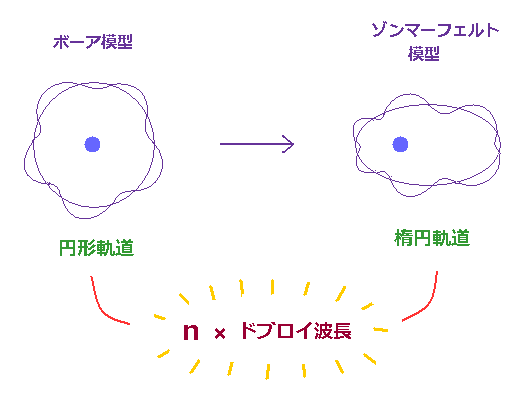
1916 年、ゾンマーフェルトは ボーアの円形軌道を "楕円軌道" に拡張した。
もちろん、このゾンマーフェルトの楕円軌道も ドブロイ波の整数倍を満足している。
この状態は 動径方向と 接線 (= 角度 ) 方向 の両方向において ゾンマーフェルトの 量子化条件を満たすことで実現される。 このサイト や このサイト (p.119) を参照のこと。
(Fig.3) n × ドブロイ波長。
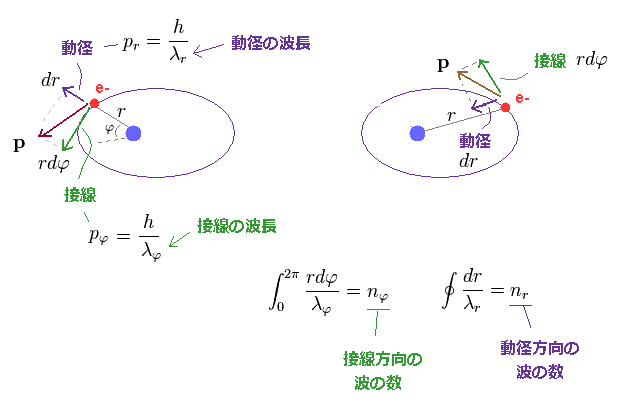
ここで "r" は 半径で φ は 回転角度 である。
単純な ボーアの円形軌道と異なり、楕円軌道は"動径" 方向の運動も含んでいる。
軌道上の各地点における運動量を 互いに垂直な 角度方向 (= 接線方向 ) と 動径方向 に分離することができる。
"垂直" ということは これら2つの成分 (= ドブロイ波 ) が 互いに 独立しており、各方向で 量子化条件を設定する必要があることを示している。
各方向のドブロイ波長の数 (= n ) は その方向の1軌道分の長さを ドブロイ波長 (= λ ) で割ることによって得られる。
(Fig.4) n × ドブロイ波長は 接線、動径方向に分離できる。
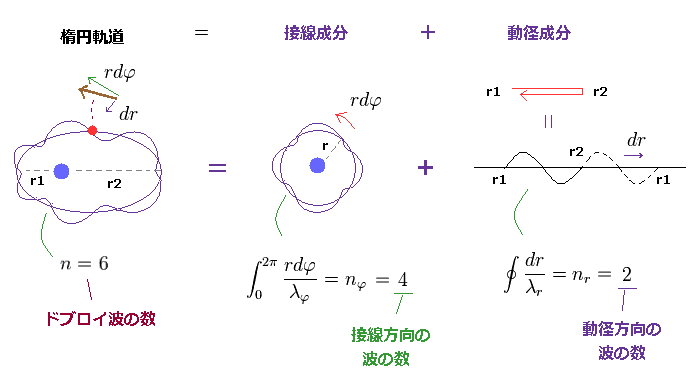
楕円軌道の 円周の長さが n × ドブロイ波長のとき、この整数 "n" は 接線 (= 角度 ) 方向と 動径方向の波の数の 合計 で与えることができる。 このセクション参照のこと。
Fig.4 では、 n は "6" に等しく、これは 主量子数の値とも一致する。
接線 (= 角度 ) 方向に特化した 軌道の長さは nφ (= 4 ) × λφ (= 接線方向のドブロイ波長 ) である。
また 動径方向の軌道の長さは nr (= 2 ) × λr (= 動径方向のドブロイ波長 ) である。
これが 動径、接線方向の ゾンマーフェルトの量子化条件である。
(Fig.5) 単純な円形軌道 = 角度 (= 接線 ) 方向の運動のみ。
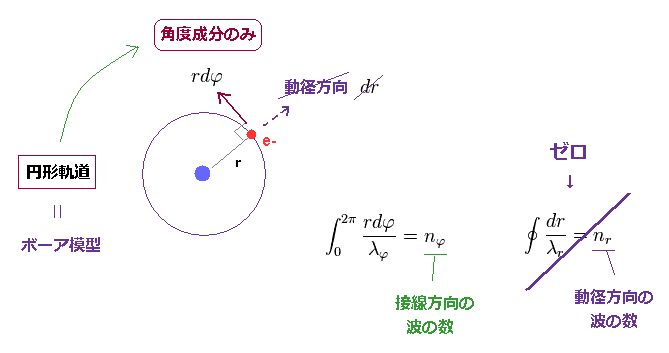
Fig.5 に示したように、電子が 円形軌道を動いているとき、 それは 接線 (= 角度 ) 方向のみ しか 動かない。
つまり、円形軌道においては、動径方向の運動量やドブロイ波長という概念が 存在しない。
つまり、全軌道の長さは n (= nφ ) × 接線方向のドブロイ波長で表わされる。
楕円軌道の時と異なり、動径方向の波の量子化を 考える必要は まったくない。
(Fig.6) n (= nφ ) × 接線方向のドブロイ波長。

Fig.6 では、この円軌道の円周は 5 × ドブロイ波長である。
( つまり、エネルギーを表す 主量子数も "5" になる。 計算に関しては このセクションを参照のこと。 )
このケースは 円軌道のため、これら "5つ"すべてのドブロイ波は 接線 (= 角度 ) 方向 ということになる。
"動径方向" の運動量とドブロイ波は 円形軌道には まったく含まれていないのである。
(Fig.7) シュレーディンガーの水素も 動径、角度部分から成る。
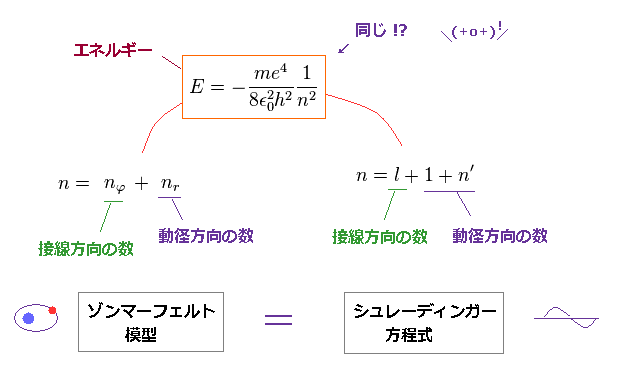
シュレディンガー方程式も 動径、接線方向で ドブロイ波長の整数倍条件に依存しているのである。
このサイト (p.2-4)、 このサイト、 このサイトなどにあるように、波動関数の "節" が 動径の波長の数と関係している。
ボーア模型 と シュレーディンガー方程式のエネルギー解を比較すると、両者は 完全に一致することが分かる。
また 主量子数 "n" は 両模型においても 動径、角度量子数の 和 で表わされる。
(Fig.8) 1s 波動関数 = 1 × ドブロイ波長 2s = 2 × ドブロイ波長。
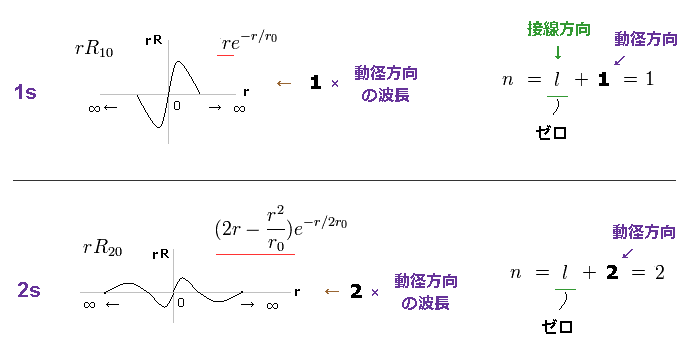
このサイトにあるように、シュレーディンガーの 1s と 2s の波動関数は Fig.8 のようになる。
動径波動関数 χ = "rR" が Eq.1 や このセクションにあるように ドブロイの条件を満たす。
1軌道とは ある地点から同一地点までの円周のことである。
Fig.8 では、 r = ∞ (= スタート ) から r = ∞ (= 最後 ) の 1s 軌道に 1 × ドブロイ波長が含まれている。
また 2s の波動関数は 2 × ドブロイ波長を含む。
1s、2s の両方において 角度方向の波動関数を含まず、よって 角量子数 l の値は ゼロになる。
(Eq.1) シュレーディンガーの水素原子の ( 動径の ) 式。

このサイトの後半部分に、動径方向の振幅 χ = rR の例が 載っている。
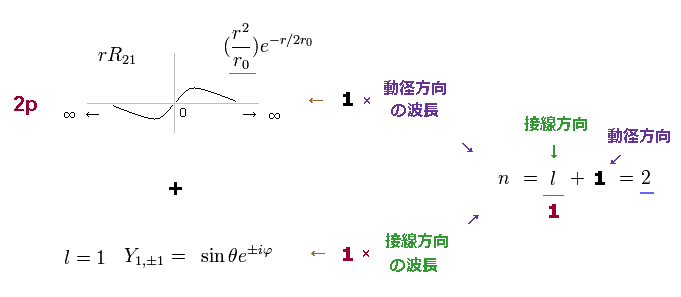
2p 軌道の動径の波動関数は 1s 軌道のように 1 × ドブロイ波長になる。
しかし 2p は 角度量子数 l = 1 の 角度方向の波動関数も併せ持つ。
主量子数 n は 動径と角度方向の波の数の合計で表わされる。
つまり 2p は 2s 軌道のように、n = 1 ( 角度 ) + 1 ( 動径 ) = 2 の エネルギー準位を持つ。
(Fig.9) 2p の波動関数: n = 1 ( 接線方向 ) + 1 ( 動径方向 ) = 2.
何らかのウェブサイトか教科書で確認してもらうと分かるが 1s の動径方向の波動関数は Fig.10 のようになる。
rR12 は 1/2 ドブロイ波長 (= Fig.10 右 ) であるため、軌道1周 ( ∞ → 0 → ∞ ) は 動径方向に 1 × ドブロイ波長含まれていることになる。
(Fig.10) 1s の水素の波動関数 = 1 × ドブロイ波長。

このサイト や このサイト にあるように ゾンマーフェルトの量子化条件は
(Eq.2) ゾンマーフェルトの量子化条件。

L は 角運動量 で、定数である。
φ は 軌道平面における 方位角 である。
pr は 電子の 動径方向の運動量である。
h、 nφ、 nr は それぞれ プランク定数、角、動径量子数 である。
(Eq.3) ゾンマーフェルトの量子化 = ドブロイ波長の整数倍。
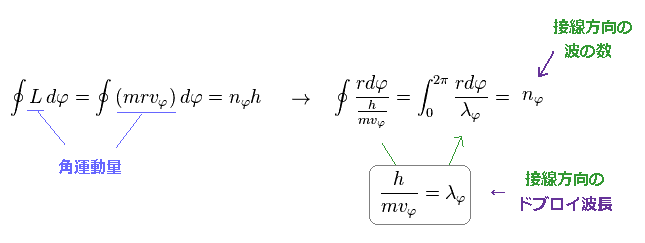
Eq.2 と ドブロイの関係式 ( λ = h/mv ) を用いて、 Eq.2 の条件は 接線方向の軌道に 整数倍のドブロイ波長 (= nφ × λφ ) が 含まれていることと等価であることが分かる。
(Fig.11) 接線方向のドブロイ波長の数。
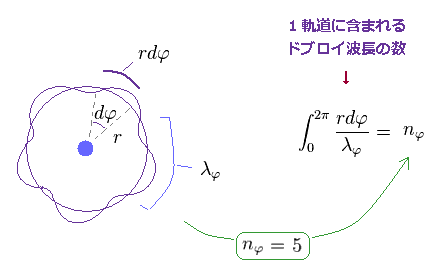
例えば、Fig.11 では、接線方向の1軌道分に 5 × ドブロイ波長が含まれている。
もちろん、この波長 (= λφ ) は 接線方向の運動量 ( λφ = h / pφ ) のみ に依存している。
(Fig.12) ゾンマーフェルトの動径成分の量子化 → nr × ドブロイ波長。

Eq.2 の 動径成分の量子化条件も 動径方向の軌道1周分に 整数倍のドブロイ波長が含まれることを意味している。
つまり Eq.2 のゾンマーフェルトの量子化条件は 動径、接線の両方向の 量子化を要求している。
(Fig.13) "動径"、 "角度" 方向への 電子の運動。

楕円軌道では、電子は Fig.13 にあるように 角度、動径の両方向に動いている。
三平方の定理を用いて、全運動量 "p" を 各地点で
動径 (= pr ) と 接線 (= pφ ) 成分に分離できる。
これらの2方向は 各地点において 互いに垂直である。
つまり、動径方向 (= λr ) と 接線方向 (= λφ ) のドブロイ波は 互いに 独立している。
(Fig.14)

このセクションに示したように、ドブロイ波の 全数 (= n ) は 角度方向 (= nφ ) と 動径方向 (= nr ) のドブロイ波の和で 表わされる。
Fig.14 軌道では、 主量子数 は n = 6 であり、これは ドブロイ波長の全数とも等しい。
角度、動径方向の量子数 (= 各方向の 波の数 ) は それぞれ"4" と "2" である。
つまり n = 6 = 4 + 2 の関係が成り立っている。
(Fig.15) ドブロイ波長の整数倍である シュレーディンガーの動径方向の関数。
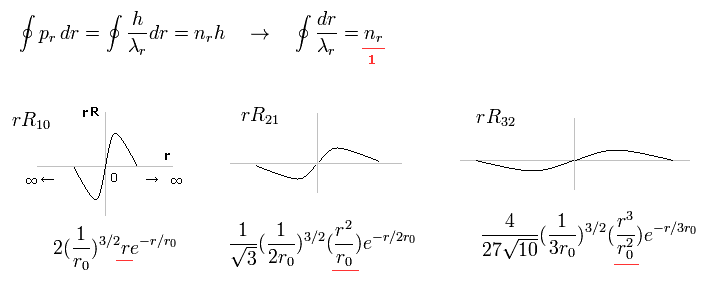
Fig.15 は 1軌道に含まれる 動径方向の波の数が 1つである シュレディンガーの波動関数の例を示している。
( 1軌道とは ある地点から 同一地点まで戻ってくる距離をいう。 ∞ → 0 → ∞ )
例えば、R32 の波動関数は 主量子数 n = 3 で、角運動量 (= 接線方向の運動 ) が l = 2 である。
つまり 動径方向の波の数は 3-2 = 1 となる。
これらの波の数は ドブロイ波の整数倍を特徴とする ボーア・ゾンマーフェルト模型と 同じ意味を持つ。
(Fig.16) シュレーディンガーの動径関数で 波が2つ、3つのケース。
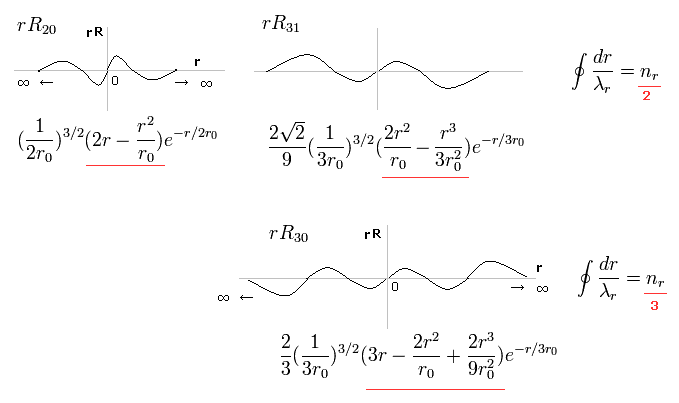
Fig.16 の上の行は、動径方向1周が 2ドブロイ波長の波動関数である。
例えば、R31 は 主量子数が "3" で 角運動量 (= 接線方向の運動 ) が "1" である。
結果、動径方向の波の数は 3-1 = 2 となる。
また 下の行は n = 3 で l = 0 であるため、動径方向の波は 3-0 = 3 となる。
(Fig.17) シュレーディンガーの接線方向の波動関数=ボーア・ゾンマーフェルト模型。

Fig.17 において、シュレディンガーの水素の球面調和関数が 1軌道に含まれる接線方向の ドブロイ波の数を示している。
例えば、e2iφ = cos2φ + isin2φ の関数は 2ドブロイ波長を含んでいる。このセクションを参照のこと。
なぜなら π の回転で その位相が元に戻るからである。
結果的に 動径方向と接線方向のドブロイ波の合計 が 主量子数 ( n = エネルギー準位 ) を表す。
これは ボーア・ゾンマーフェルト模型と シュレーディンガー方程式の両方に共通した規則である。
(Fig.18) 負の運動エネルギーは あり得ない。
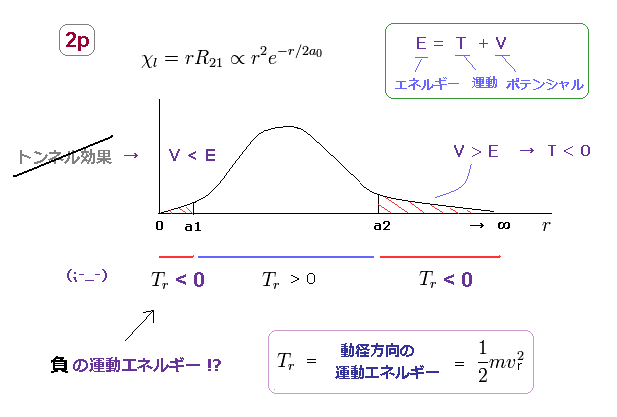
非現実的なことに、シュレディンガーの水素のすべての軌道の動径方向の範囲は 0 から ∞ になる必要がある。
Fig.18 は 水素の 2p 軌道である。
2p 軌道では、動径方向の運動エネルギーは 両端の2つの領域で 負 の値になってしまう。 ( r < a1, a2 < r )
もちろん、この現実の世界では、運動エネルギー (= 1/2mv2 ) は 負の値を とることはできないので、シュレーディンガー方程式の水素は 実在しないことになる。
r < a1 の領域では、ポテンシャルエネルギー V は 全エネルギー E よりも 低いため、トンネル効果などとは 何の関係もないことが分かる。
そもそも 原子核に 束縛された状態の電子が r が無限のかなたに 飛び去って かつ 戻ってくるという現象が 安定な原子、分子などで 起きているはずがないのである。
(Fig.19) "楕円軌道" ( 角運動量 = 1).
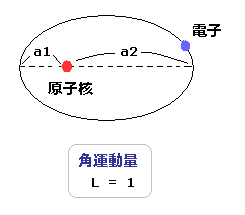
ここでは 2p 軌道のように 角運動量 = 1 を持つ 古典的な楕円軌道について考える。
近日点 ( 遠日点 ) と 原子核間の距離を a1 ( a2 ) とする。
古典的な軌道では、電子が角運動量を持つとき、近日点 (= a1 ) よりも 原子核に近づくことが できない。
(Eq.4)
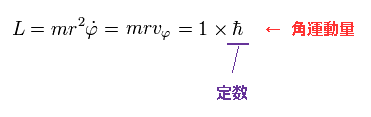
この軌道の角運動量 (= L ) を ħ とする。これは 定数である。
Eq.4 を用いて、 接線方向の運動エネルギー (= Tφ )は、
(Fig.20) 接線方向の運動エネルギーは r → 0 につれて発散する。
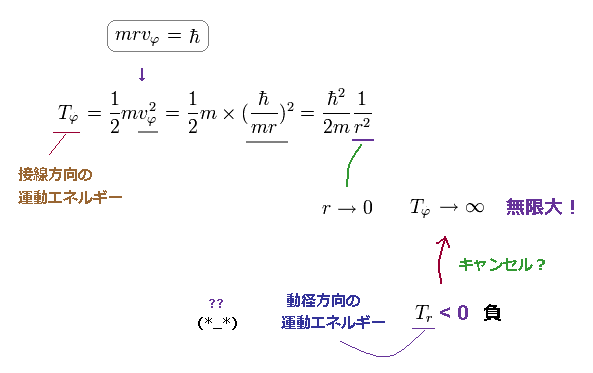
Fig.20 に示したように、この接線方向の運動エネルギーは r が ゼロに近づくにつれて 無限大 に発散する。
この Tφ は r2 の逆数のため クーロンエネルギー (= -1/r ) によってキャンセルすることができない。
そのため この接線方向の運動エネルギーの発散を キャンセルするために、動径方向の運動エネルギーは 負 にならなければならないのである。
残念ながら、自然界が このような 都合のいい理屈に従っているはずがないことは 火を見るよりも明らかである。
(Fig.21) 動径方向で a1 から a2 の範囲のみ選ぶと、 "不連続" になってしまう。
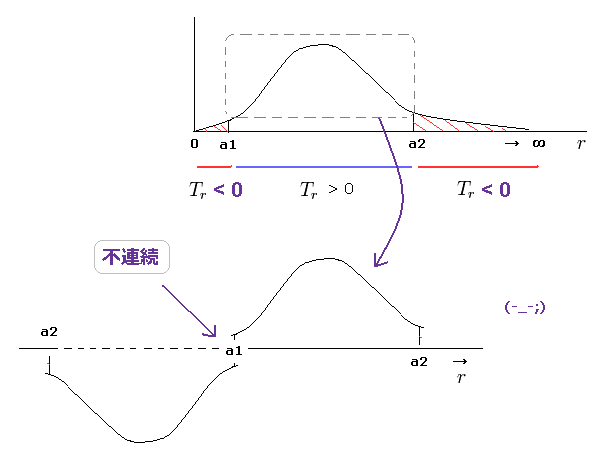
なら a1 < r < a2 の 現実的な範囲 (= 運動エネルギーが 正 ) のみピックアップすればいいではないか と思われる人がいるかもしれない。
しかし このケースでは a1 と a2 において 波動関数が不連続になってしまうため あり得ないことが分かる。
1軌道とは 電子が a1 と a2 において U-ターン して元の地点へ戻ることである。
(Fig.22) 不連続 → シュレーディンガー方程式が成り立たない。
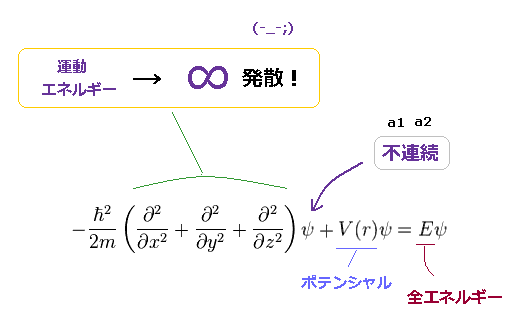
結果的に Fig.21 の 不連続な波動関数は 水素原子のシュレーディンガー方程式で 成り立たないことがわかる。
なぜなら "不連続" とは この波動関数の傾き (= 微分 ) が 無限大に発散することを意味しているからである。
a1 と a2 の地点においては、 ポテンシャルエネルギー V と 全エネルギー E は 有限にならなければならない。
つまり 突然の U-ターンは この動径波動関数を 元の式を満たさないものに変えてしまう。
(Fig.23) シュレーディンガーの 2p の動径波動関数は 非実在的な "負" のエネルギーを含む。
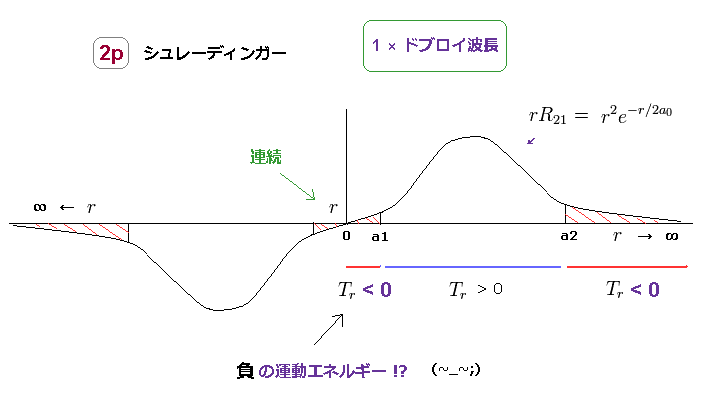
Fig.23 に示したように、元の 2p の動径波動関数は r = 0、 ∞ の両地点で 連続になる。
なぜなら 波動関数の 傾き と 振幅が これらの地点でゼロになるからである。
代わりに、この波動関数は 負の運動エネルギーという非現実的な領域を含まなければならない。
Fig.18 に述べたように、この領域は トンネル効果とは 何の関係もない。
(Eq.5) シュレーディンガーの水素の動径方向の波動関数。
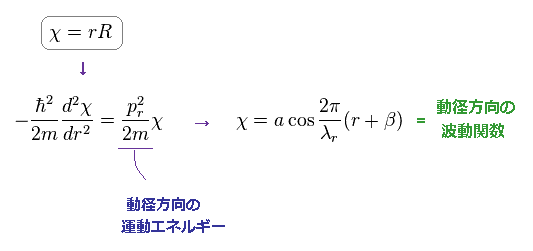
このサイト や このサイトに示したように、動径部分の変数を ドブロイの関係式を満たすために χ = rR と置き換えて計算している。
Eq.5 にあるように、この波動関数は ある波長 λr を持つ コサイン、サイン の関数で表わすことができる。
(Eq.6) ドブロイの関係式が 動径方向でも成り立つ。

結果的に、シュレーディンガー方程式は ドブロイの関係式 ( 動径方向の運動量 pr = h/λr ) を与える。
ここで λr は 動径方向のドブロイ波長である。
(Eq.7) ゾンマーフェルト + ドブロイの関係式 = シュレーディンガー方程式。

Eq.6 を用いて、Eq.2 のゾンマーフェルトの量子化条件は Eq.7 のようになる。
Eq.7 は 動径方向の軌道に含まれる ドブロイ波長の数が "nr" であることを示している。
これはつまり シュレーディンガーの水素も ボーア模型のように ドブロイ波長の整数倍を満たすことを意味している。
(Fig.24) 2p の動径方向の波動関数は 異なった波長の集まりである。
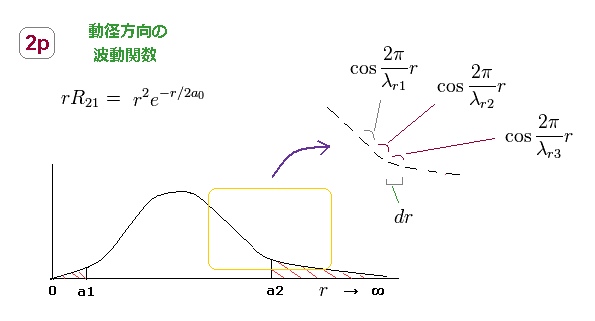
楕円軌道のように、動径方向の運動量 (= 波長 ) は 異なった地点のおいて
常に 変化している。
つまり、 2p の動径の波動関数は Fig.24 に示したように 無限種類のドブロイ波長から成り立っていることになる。
各微小区間 (= dr ) 内では、ドブロイ波長は 定数 であると見なせる。
(Fig.25) 動径方向の波長の量子化。
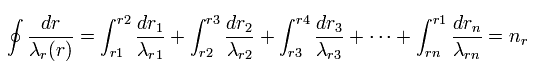
結果的に 異なった地点における 異なった波長 (= λr ) を用いて、1軌道内の ゾンマーフェルトの量子化条件は Fig.25 のように表せる。
(Eq.8) 方位角のシュレーディンガー方程式。
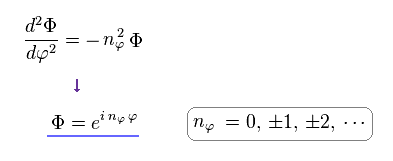
Eq.8 は 方位角のシュレーディンガー方程式と 波動関数 (= Φ ) である。
このセクションでは、この 量子化された方位角波動関数が 接線方向のドブロイ波長の整数倍を 表わしていることを示す。
(Eq.9) シュレディンガーの方位角関数 = nφ × ドブロイ波長。
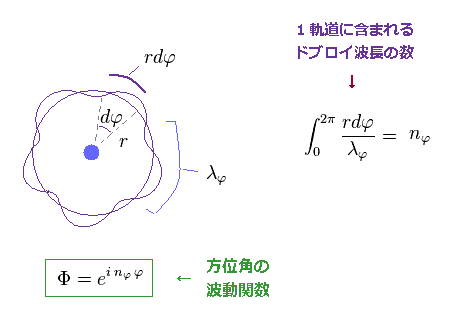
通常の運動量演算子 ( 接線方向 ) を この方位角波動関数 (= Φ ) に作用させると 次のような 接線方向の運動量 (= pφ ) を得ることができる。
(Eq.10)
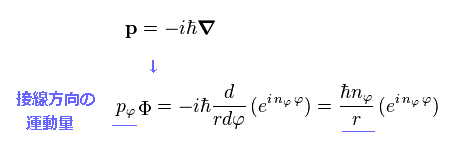
ドブロイの関係式を用いて、接線方向のドブロイ波長 (= λφ ) は、
(Eq.11)

ここでは ħ = h/2π ( h は プランク定数。 ) を用いた。
Eq.11 を用いて、ドブロイ波長の (接線方向の) 1軌道に含まれる数は
(Eq.12)
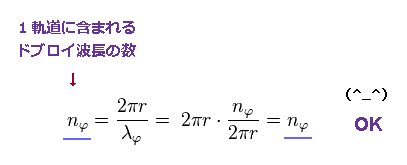
この等式が成り立っていることが証明できた。
結果的に Eq.8 の方位角波動関数も ゾンマーフェルト模型のように ドブロイ波長の整数倍を意味している。
(Fig.25) ボーア・ソンマーフェルト模型。
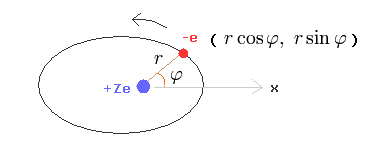
ここで、1つの電子が +Ze の原子核の周囲を運動している (= 回転もしくは振動) と仮定する。
( もちろん、水素原子のシュレーディンガー方程式においても、電子は クーロン力 によって、+Ze の原子核の周囲を運動していることはいうまでもない。)
このセクションは 1916 年の ゾンマーフェルトの論文 ( Annalen der Physik [4] 51, 1-167, A. Sommerfeld. ) を基にしたものである。
次のように直交座標を極座標に変換させる。
(Eq.13)
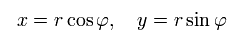
原子核が原点にあるとき、電子の運動方程式は、クーロン力を考慮して 次のようになる。
(Eq.14)
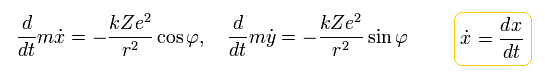
ここで、次のように定義する。
(Eq.15) p = 定常な角運動量。

このセクションのみ、角運動量として L の代わりに "p" の記号を用いているので注意。
もし、1つの電子が1つの中心の正電荷の周りを運動しているとき、この角運動量 ( p ) は、定数になる。(= 面積速度一定の法則)。
変数 r は、φ の関数であるため、Eq.15 を用いて t (=時間)による微分を次のように表せる。
(Eq.16)
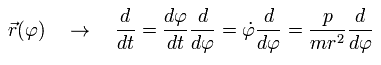
また、ここで次のように定義する。
(Eq.17)
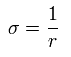
Eq.13 と Eq.16 を使って、各運動量はそれぞれは次のようになる。
(Eq.18)
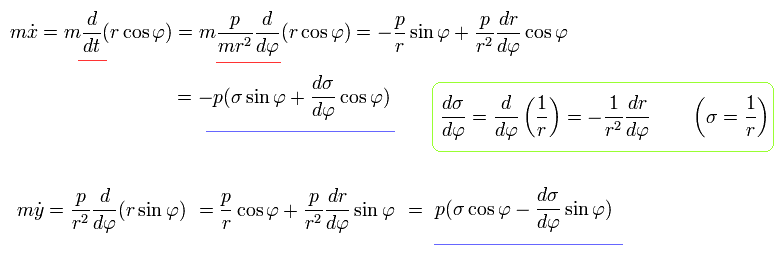
Eq.14、Eq.16、Eq.18 を使って、 運動方程式は次のようになる。
(Eq.19)
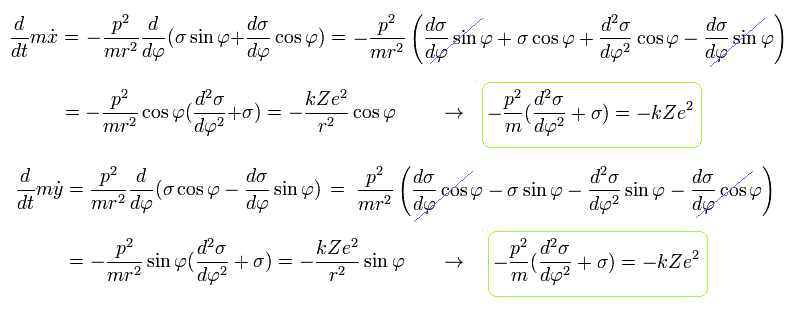
Eq.19 から 次のような共通の関係式が得られる。
(Eq.20)
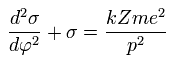
Eq.20 の σ の解は次のようになる。
(Eq.21)
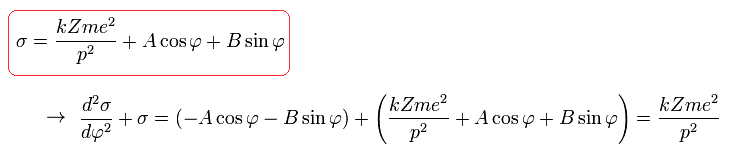
ここで、φ がゼロのとき、電子が近日点 にあると仮定すると、B=0 となる。
(Eq.22)
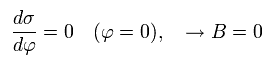
(Fig.26) 水素様原子の "楕円"軌道。
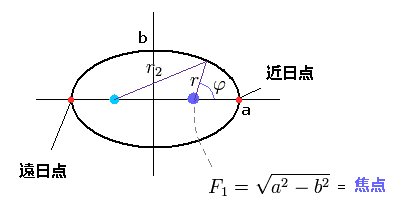
ここで、原子核の焦点(F1)と離心率 (ε) はつぎのようになる。
(Eq.23)
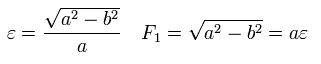
ここで Eq.21 ( B=0 ) の式 が 焦点に原子核がある楕円形であることを示す。
Fig.26 で 余弦定理と 楕円の定義式より、
(Eq.24)
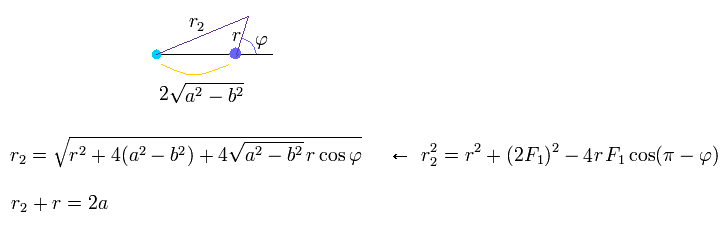
Eq.24 から 次を得る。
(Eq.25)
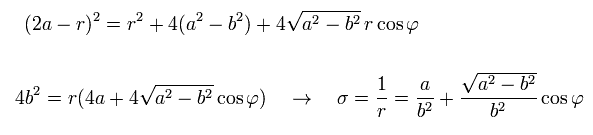
Eq.21、 Eq.22、 Eq.25 から 次を得る。
(Eq.26)
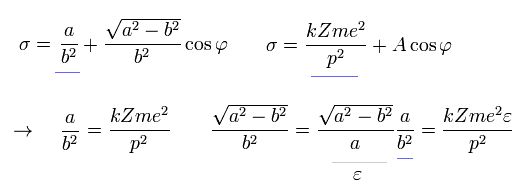
結果的に σ は 次のようになる。
(Eq.27)
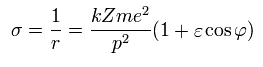
Eq.16 と Eq.27 を使うと、
(Eq.28)
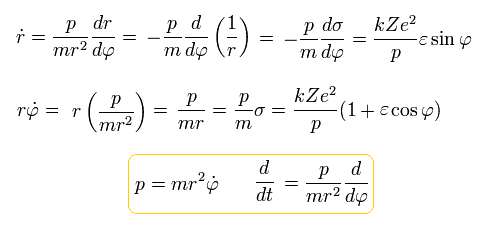
となり、運動エネルギー (T) は次のようになる。
(Eq.29)
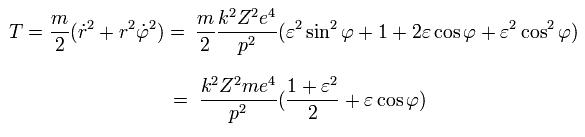
Eq.27 から位置エネルギー (V) は次のようになる。
(Eq.30)
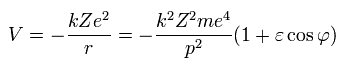
結果、全エネルギー (W) が求められる。
(Eq.31)
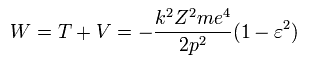
ボーア・ゾンマーフェルトの量子化条件では、次の関係式を使う。
(Eq.32)
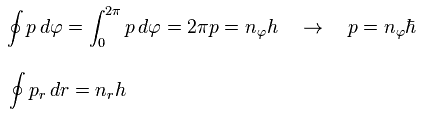
ここで 角運動量 p は 定数である。
その p は ħ の整数倍となる。
ところで、Eq.32 の式の意味は何なのだろう?
ドブロイの関係式を 接線と動径方向に使用する。、
(Eq.33)
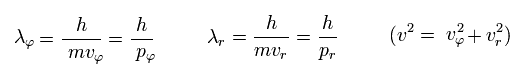
Eq.32 は
(Eq.34)
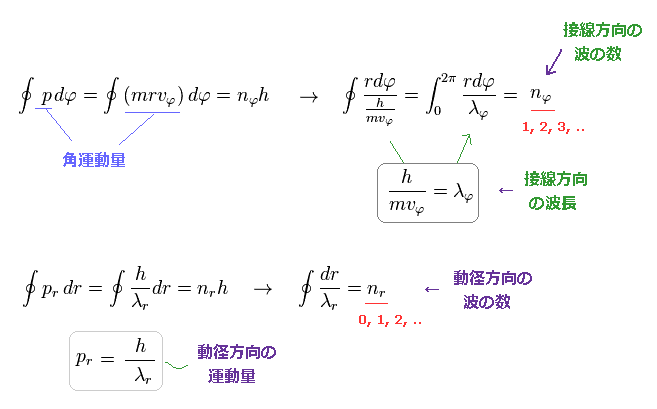
つまり これらは 各方向に関して ドブロイ波長の量子化を意味している。
( シュレーディンガー方程式では 角運動量が ゼロ の状態が存在する。)
動径方向の量子化条件を次のように書きかえる。
(Eq.35)
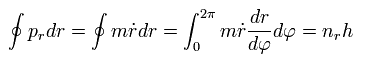
Eq.27 を使うと、,
(Eq.36)
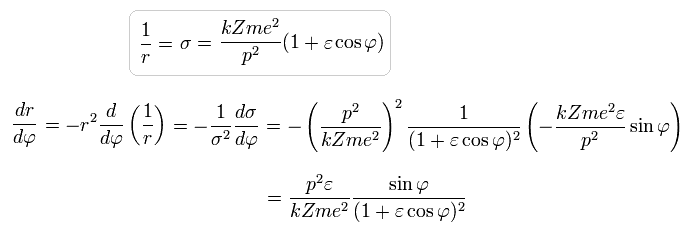
また Eq.28 より、
(Eq.37)
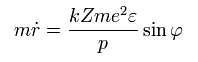
となる。 Eq. 35-37 から、 次の関係式が得られる。
(Eq.38)
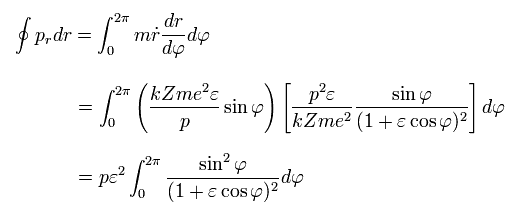
Eq.38 の 部分積分を 次のようにやる。
(Eq.39)
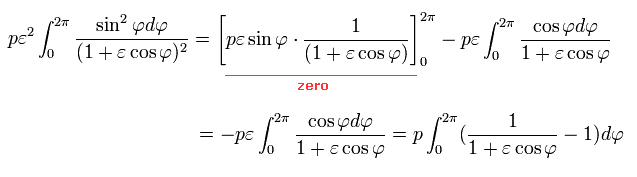
ここで、次の知られた公式を使う。 ( 複素積分, このサイト参照。 )
(Eq.40)
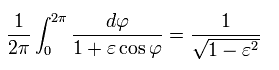
------------------------------------------------------------------
オイラーの公式により、cos は 複素数 z を用いて表せる。
(Eq.41)
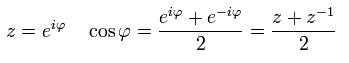
つまり、
(Eq.42)
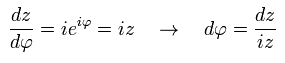
Eq.41 と Eq.42 を用いて、Eq.40 の左辺は、
(Eq.43)
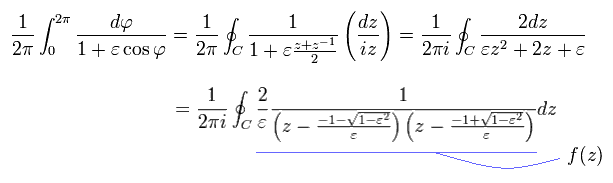
ここでは
(Eq.44)
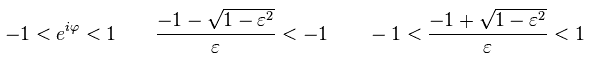
つまり Eq.44 の 後の数のみ 留数定理の "極" として働く。
留数定理では 1/(z-a) の係数のみ残る。
(Eq.45)
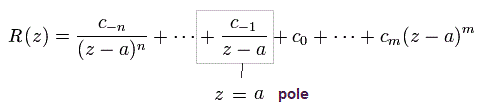 と
と
(Eq.46)
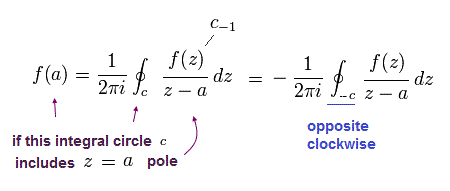
Eq.43 から Eq.46 までより、結果は、
(Eq.47)
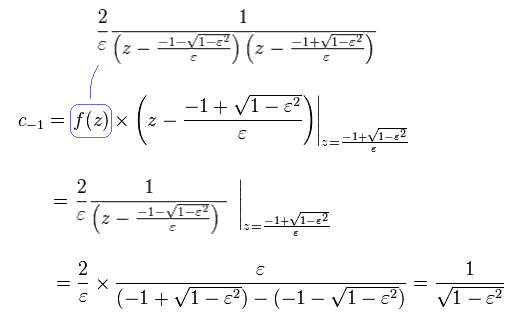
Eq.40 を証明することができた。
---------------------------------------------------------------
Eq.40 の公式を用いると、Eq.38 (Eq.39) は
(Eq.48)
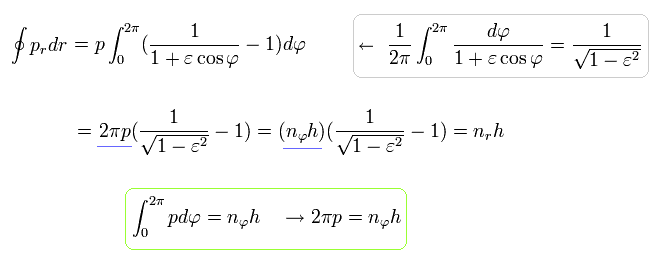
ここでは Eq.32 の量子化を使用した。
Eq.48 より、次を得る。
(Eq.48')
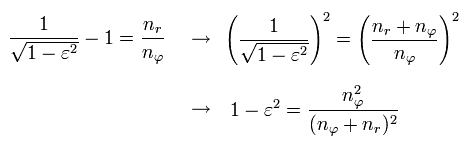
Eq.48' を Eq.31 に代入して、Eq.32 を用いると、全エネルギー W は、
(Eq.49)
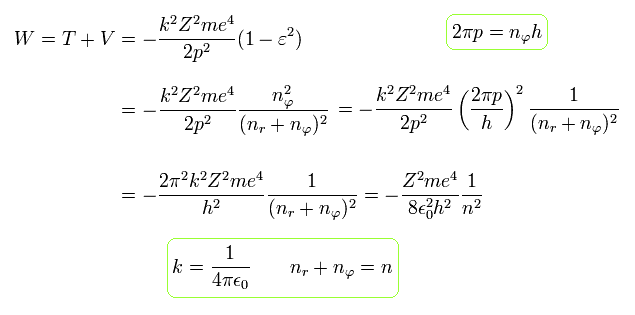
この結果は 完全に シュレディンガーの水素原子と同じものである。
ここで Eq.49 の ボーア・ゾンマーフェルトの解が シュレーディンガーの水素原子にも適用されることを確かめる。
このページに示したように、動径方向の量子数 (= nr ) は 動径方向の軌道に含まれる ドブロイ波の数を表している。
また nφ は 量子化された角運動量 (= 接線方向の軌道のドブロイ波の数 ) を意味している。
(Eq.50)
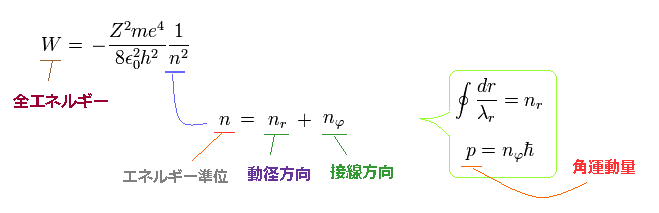
シュレディンガーの波動関数の例として、
(Fig.27) シュレーディンガーの水素 = ボーア・ゾンマーフェルト模型。
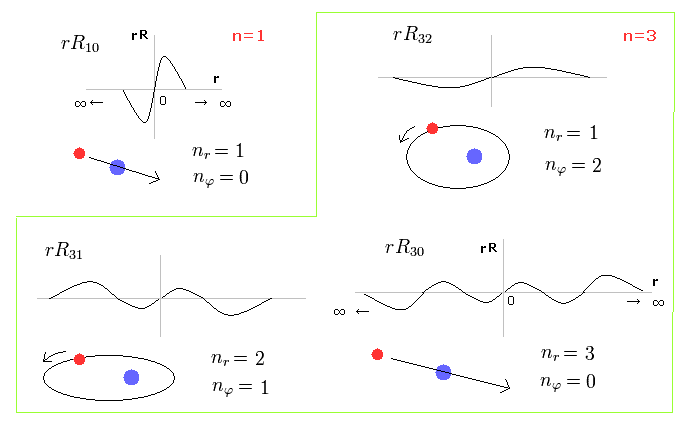
Fig.27 は シュレーディンガーの波動関数のエネルギー準位が ボーア・ゾンマーフェルトの量子化のルールに従っていることを示している。
重要な違いは シュレーディンガーの解は 必ず ゼロから無限大の範囲のため 非実在の状態も含んでいることである。
(Fig.28) どうして シュレディンガーの水素原子は 円軌道になれないのか?
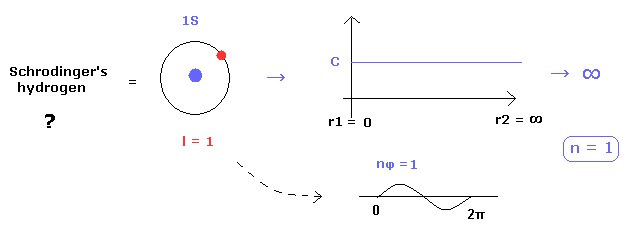
シュレーディンガーの水素原子の固有関数は "動径方向" と 角運動量 (= "接線" ) 方向の 2つの部分を含んでいる。
ご存じのとおり、シュレーディンガーの動径の波動関数は 必ず "動径方向" の運動量を含んでいるため シュレーディンガーの水素原子には 純粋な円軌道が存在しないことになる。
なぜなら もし円軌道が このシュレーディンガーの水素原子に含まれているとしたら、動径方向の関数は Fig.28 に示すように 定数 (= C ) にならなければならないからである。
すると、この定数 C が ゼロでないと、それを規格化しようとしたとき、ゼロから無限大の範囲のため 発散してしまう。
これが シュレーディンガーの水素原子に 非実在の 角運動量ゼロの "S" 状態が 存在してしまう理由である。
(Fig.29) S の波動関数の 角運動量 L = 0 → ドブロイ波の干渉で打ち消し合う。

当たり前だが、ボーア・ゾンマーフェルト模型では、軌道は 楕円、もしくは 円形になり 線形にはなれない。
つまり 角運動量は ゼロにならず、電子は 核に衝突することなく 運動している。
" 整数倍 " ということは ドブロイ波の位相が 波端同士で 互いに フィットして キャンセルし合わないことを意味する。
しかし "s" の軌道を含むシュレーディンガーの波動関数では、角運動量 L は ゼロに なれる。
これらのケースでは 軌道形が 1次元の線上になるため 電子のドブロイ波の 正反対の位相同士が 互いに キャンセルし合って 打ち消し合ってしまう。
つまり 安定な波動関数というものが 不可能であることが分かる。
(Fig.30)
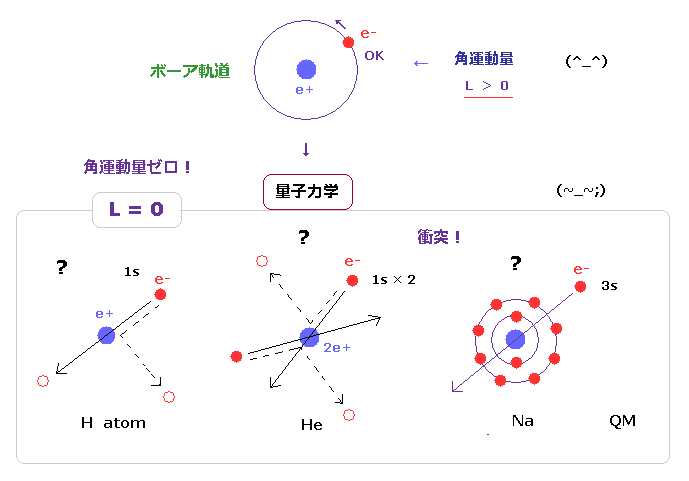
量子力学では、 "s" 軌道は 角運動量が ゼロ の状態である。 ( L = 0 ).
この 量子力学による ヘリウム原子は Fig.30 真ん中に示したように、不規則な跳ね返りにより 非常に不安定な状態 になってしまう。
また ナトリウム (= 3s ) や カリウム (= 4s ) の最外殻電子も
ゼロ の 角運動量を持つことになる。
これはつまり これら最外殻電子が 継続的に 内殻 n = 1, 2 の電子群 と 原子核を
貫通 もしくは 跳ね返りし続けていることになるのだろうか?
これも あり得ない状況である。
また このページでは、より厳密に シュレーディンガーと ボーア・ゾンマーフェルト模型が同じエネルギー準位を与える理由を示した。
(Ap.1) ボーア模型の水素 -- 円形軌道。
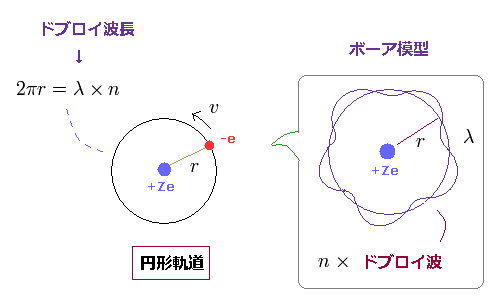
このセクションでは、通常のボーア模型について 振り返る。
( このサイトも参照のこと。 )
まず、 このページに示したように、ボーア模型の単一電子は 加速度運動によって 原子核に落ちていくことはない。
単一の電子の周囲の 真空のエネルギーは エネルギーではないからである。
(Ap.2) ボーア模型の条件。

Ap.2 では、最初の式は 遠心力が クーロン力に等しいことを意味している。
2番目の式は クーロンポテンシャルエネルギーと運動エネルギーの和である。
3番目の式は 円形軌道の円周が ドブロイ波長の整数倍 (= n ) であるという条件である。
条件 "1" は 条件 "2" に含まれているため、 "2" と "3" の条件が 基本的なボーア模型に必要である。
式 "1" を 式 "2" に代入して、
(Ap.3)
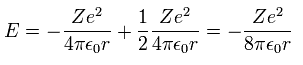
式 "3" の v を 式 "1" に代入して 次を得る。
(Ap.4)
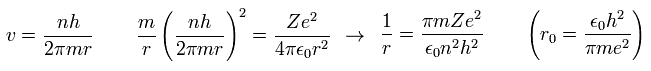
ここでは、 "r0" ( n = Z = 1 ) は "ボーア半径" である。
"ボーア半径" や "ボーア磁子" は 量子力学においても 必要不可欠な概念であるため、ボーア模型が 今なお 学校で教えられている理由となっている。
Ap.4 を Ap.3 に代入して、ボーア模型の全エネルギーは
(Ap.5) ボーア模型 = シュレディンガー方程式。

このエネルギー E は シュレーディンガーの水素と まったく同じ値になる。
Ap.4 から、粒子の速度 v ( n=Z=1 ) と 光速 c の比は、
(Ap.6) 微細構造定数 α
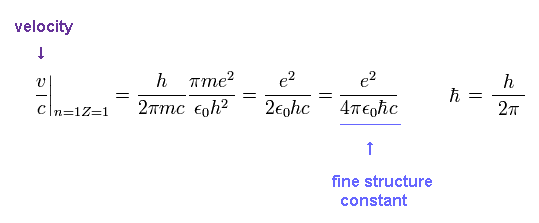
これが 有名な微細構造定数 α である。
つまり 微細構造定数と ボーア軌道には 強い結びつきがある。
(Ap.7) 動径方向 (= pr )、 接線方向 (= pφ )
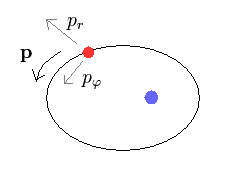
楕円軌道では、運動量 (= p ) を 動径方向 (= pr )
と 接線方向 (= pφ ) の成分に分離できる。
3平方の定理により、
(Ap.8)
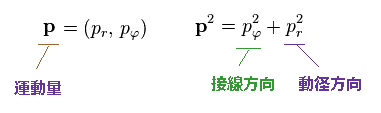
運動量 (= p ) を 質量 (= m ) で割って、 速度 "v" を得る。
電子が 微少時間 "dt" の間に 距離 "dq" を進むとする。
(Ap.9)

3平方の定理を用いて、移動距離 "dq" は 動径、接線 (= 角度 ) 方向へ 分離できる。
(Ap.10)

Ap.10 では、 "r" は 半径で、 φ は 角度である。
Ap.9 のように、次を得る。
(Ap.11)
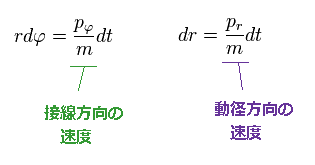
ドブロイの関係式 (= λ = h/p ) を用いると、微小区間 "dq" に含まれるドブロイ波の数は Ap.9 を用いて、
(Ap.12)
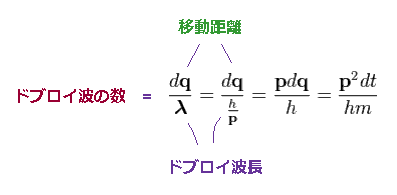
同様に、動径 (= λr )、接線 (= λφ ) 方向のドブロイ波長と Ap.11 を用いて、各区間に含まれる波の数は、
(Ap.13)
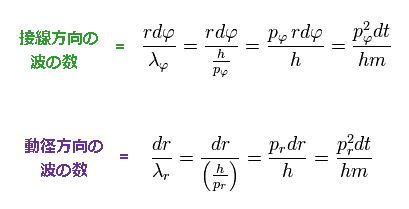
Ap.12 と Ap.13 から、次の関係式を得る。
(Ap.14)
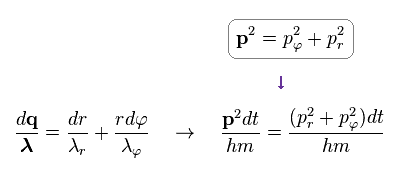
結果、次を得る。
(Ap.15) ドブロイ波の全数。 n = nr + nφ
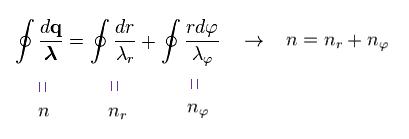
Ap.14 の両辺を 軌道1周の線積分をすることによって、Ap.15 の結果を得た。
"n" は ドブロイ波長の全数であり、これは 主量子数と同じである。
"nr" は 動径方向の軌道の ドブロイ波長の数。
"nφ" は 接線方向の ドブロイ波長の数である。
n = nr + nφ の関係式が成り立っていることが分かる。
(Ap.16) 接線、動径方向の波長の 実際の波における関係。
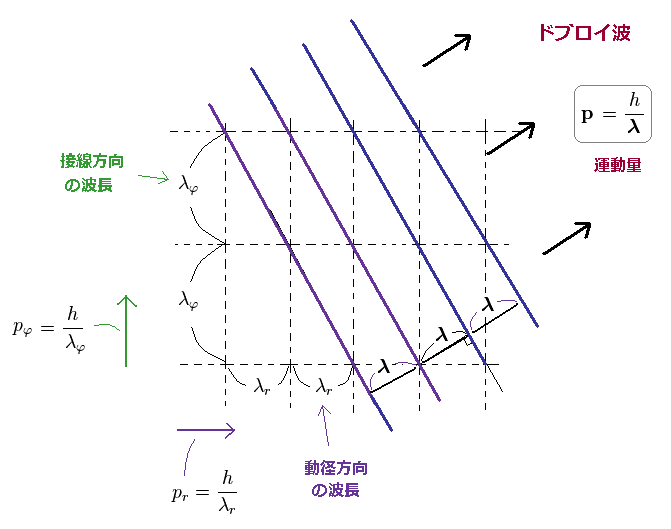
ドブロイ波が 接線、動径方向に分離できる理由を説明することができた。
Ap.16 の物質波は λ のドブロイ波長をもつため、全運動量は p = h/λ になる。
Ap.16 を見て分かるように、角度、動径方向のドブロイ波長は トータルの波長よりも 長くなる。
( λφ, λr > λ ).
(Ap.17) 運動量 "p" の 角度方向と動径方向の成分。
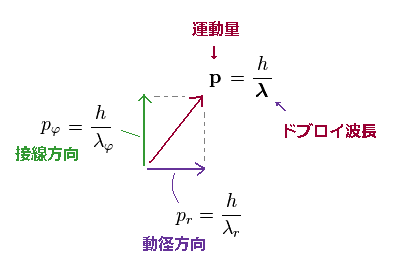
全運動量 "p" の 接線方向 (= pφ ) と 動径 方向(= pr ) の成分は Ap.17 に示したように 三平方の定理を満たす。
Ap.16 から、λ は 次のように表せる。
(Ap.18)
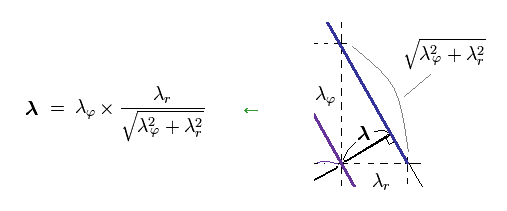
Ap.18 を Ap.17 の全運動量 p に代入して、次のように ドブロイの関係式が三平方の定理を満足することが分かる。
(Ap.19)
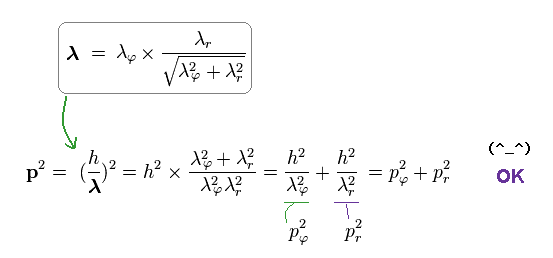
結果的に p = h/λ のドブロイの関係式も 古典力学に一致することが示せた。
(Ap.20) 全、角度、動径方向ともに ドブロイ波長の整数倍。
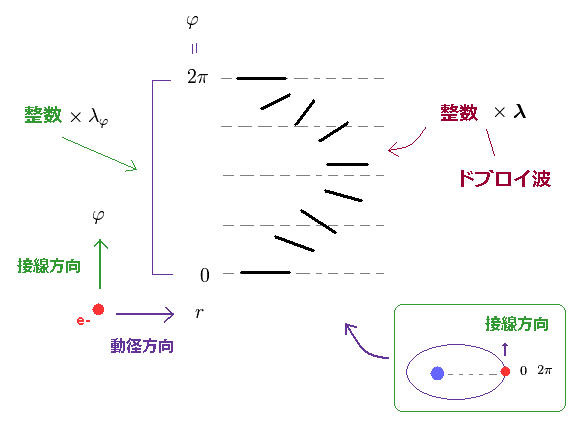
水素様原子では、軌道は 楕円もしくは円形になる。
つまり、2つの地点 ( 近日点と遠日点 ) において、電子は 接線方向のみに動いていることになる。
もちろん、同一の地点 ( φ = 0 and 2π ) では、波の位相は 互いに一致しなければならない。
Ap.20 に示したように、 楕円の全軌道が ドブロイ波長の整数倍に等しい時、 角度方向も ドブロイ波長の 整数倍を満たすことになる。
Ap.15 に述べたように、 "動径方向" の波の数は nr = n - nφ で表わされる。
つまりこのケースでは、 "動径"方向も 整数 (= nr ) × ドブロイ波長を満足する必要がある。
(Ap.21) 水素のシュレーディンガー方程式。

このセクションでは、 このサイト や このサイトのように、シュレーディンガー方程式の水素原子を解くことにする。
ψ は 水素の 全波動関数である。
シュレーディンガー方程式と ボーア模型の両方において、全エネルギー E は 運動エネルギー と クーロンポテンシャル (= V ) の和で表わされる。
(Ap.22)
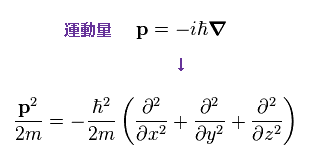
シュレーディンガー方程式も ドブロイの関係式 ( λ = h/p ) を用いているため、運動量 p は Ap.22 に示したように 演算子 に置き換える。
極座標系を用いて、
(Ap.23)
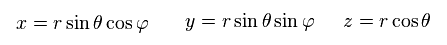
Ap.22 は、
(Ap.24)
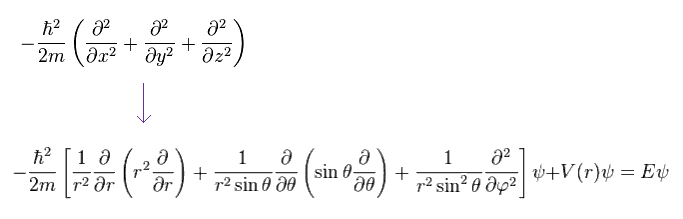
波動関数を 動径 (= R )、 角度 (= Y ) 部分に 変数分離できると仮定する。
(Ap.25)
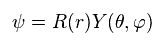
Ap.24 の両辺を 次の式で割ると、
(Ap.26)
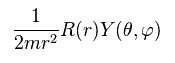
次を得る。
(Ap.27)
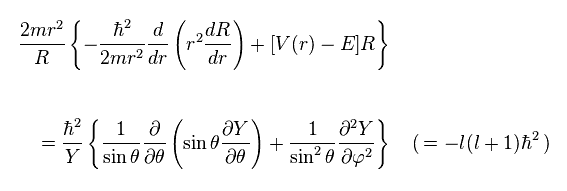
Ap.27 の左辺は 動径方向の変数 "r" のみに依存している。
また 右辺は 角度の変数 (= θ and φ ) のみを含む式である。
そのため 両辺を 定数 (= -l(l+1)ħ2 ) と見なすことができる。
結果的に Ap.27 の左辺は 次のようになる。
(Ap.28)
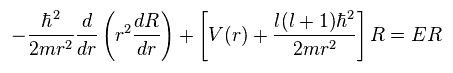
また、Ap.27 の右辺は
(Ap.29)
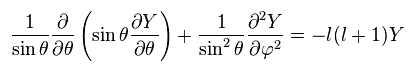
Y を さらに2つの角度変数に分離する ( Y → θ and φ )。
(Ap.30)
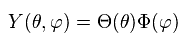
Ap.30 を Ap.29 に代入して、それを Φ で割ると、
(Ap.31)
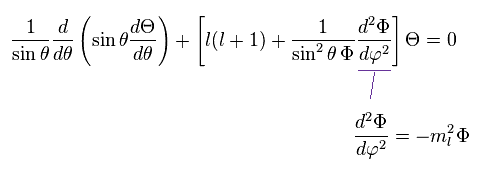
結果的に 方位角の波動関数 Φ は 次のように表せる。
(Ap.32)

ml は 整数になる必要がある。でないと Ap.33 に示したように 波動関数の値が φ = 0 と φ = 2π で 異なった値になってしまうからである。
そのため このケースでは、Ap.24 の式が 壊れてしまう。
(Ap.33)

このセクションでは、 Ap.32 は シュレーディンガーの水素も ドブロイ波長の整数倍の条件を 満足することを示した。 ← ゾンマーフェルトの量子化。
(Ap.34)
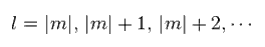
Ap.31 の角度の式が 有限の解を持つには、角度定数 l が Ap.34 を満たす必要がある。
(Ap.28) 水素の動径方向の式。
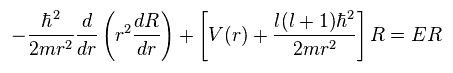
(Ap.35)
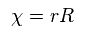
計算式を簡単にするために、Ap.35 に示したように 動径方向の式で rR を χ に置き換えた。
このサイト や このサイト を参照のこと。
この χ を Ap.28 に使用して 次を得る。
(Ap.36)
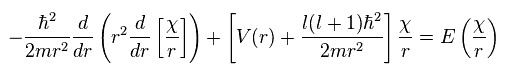
ここでは
(Ap.37)
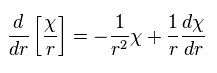
結果的に Ap.28 の動径部分は 次のようになる。
(Ap.38)

Ap.38 は 動径方向のドブロイの関係式を表す運動量演算子 を使用している。
つまり この波動関数 χ は 動径方向のドブロイ波を表わしていることになる。
βr を ρ という変数に置き換えて、
(Ap.39)
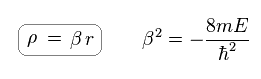
χ を 次のように定義した。
(Ap.40)
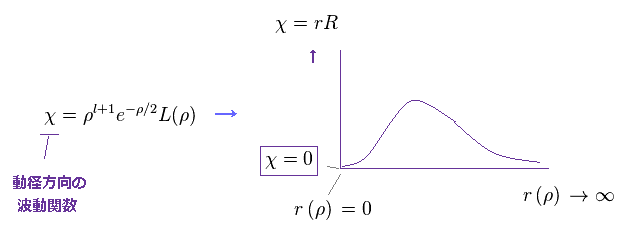
Ap.40 の χ の形を見て分かるように、 動径方向の波動関数は 必ず 両端 ( χ = 0, r =0 と ∞ ) において ゼロになる。
つまり この時点で χ が ドブロイ波長の整数倍になることが 決定したことになる。
L(ρ) は ρ の多項式である。
(Ap.41)
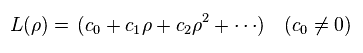
この多項式が 有限の項を持つには、 エネルギー E は 次のように 量子化される必要がある。
(Ap.42)
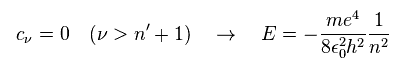
主量子数 n は 角度、動径の量子数の和で表わされる。
(Ap.43)

このエネルギー解は ボーア・ゾンマーフェルト模型の解と 一致する。
シュレディンガーとボーア模型の両方の水素において、動径と接線方向の波の数の和が エネルギー準位 (= n ) を 表わすことになる。
(Ap.44) シュレーディンガーとゾンマーフェルト模型で 共通の機構が使われている。


2014/6/14 updated This site is link free.