トップページ (2電子原子も含む正確な新ボーア模型)
特殊相対論は間違い?
超対称性変換とモジュラー変換不変性
共形場理論とセントラルチャージは本当か?
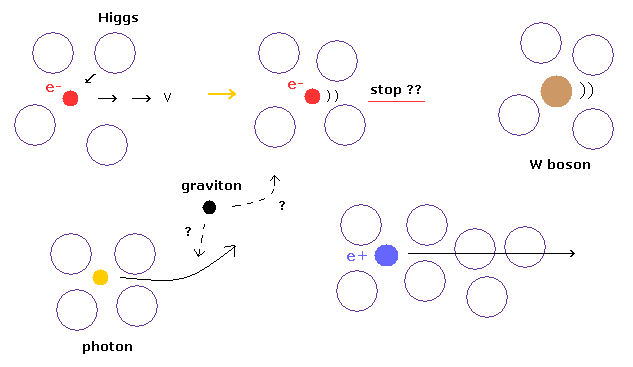
(Fig.1) 動いている電子が ヒッグスによって止まる??

ご存じのとおり、報道によれば ヒッグス粒子が 加速器内で見つかったとされている。
ヒッグス粒子 (場) は すべての空間を埋め尽くしており、電子、W ボソン、クォーク などの "抵抗" (= 質量 ) として作用すると言われている。
しかし 加速器内では 数兆回もの衝突で ようやく ヒッグス粒子が1つできるかできないかの低確率なのである。
( この非常に低確率な粒子が 本当に空間を埋め尽くしているのだろうか??)
ヒッグス粒子が 電子などの抵抗 として作用するとしたら、他の力がまったくない状態でも 定常速度で動いている電子は 無限のヒッグス場によって すぐにストップしてしまう。 これは変である。
また 無限のヒッグス場は 陽子の質量や 光子などには まったく作用しないことになっている。
ご存じのとおり、光子の進行方向は 重力によって曲げられる。
残念ながら 現在の標準模型には これらの一貫性のない現象に まったく回答できない。
(Fig.2) ひも理論に リアリティーはない。
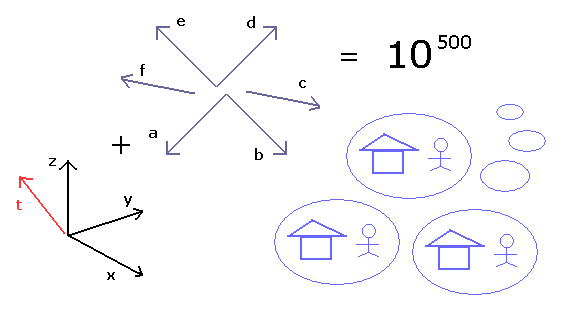
もし これらの理由を ひも理論 ( 超弦理論 )に求めたとしても、ひも理論は あなたがたが期待しているような回答を与えてくれない。
標準模型 のような 相対論的な場の量子論は 非常に抽象的な "数学的言語" であり、具体的なイメージを持たない。
こういう数学的な世界だからこそ Fig.1 のような一貫性のない問題が浮上してしまう。
( こういう問題がでてきても 数学の世界だから許されるという具合である。)
それに加えて 一般相対論の 非常に厳しい制限が加わった超ひも理論は 標準模型よりも より抽象的かつ 非実在的な理論なのである。
標準模型は 20 の根本的なパラメーターをまったく予想できない。
さらに 超ひも理論は 10500 もの異なった理論 を含んでいる。( それらのほとんどは 非実在の理論である。)
また ひも理論は 26 次元、超ひも理論は 10 次元もの次元を必要とする。( はっきり言って あり得ない世界である。)
つまり 現在の物理学の最終形態である 超ひも理論は 非常に非実在的で 何も予測する力がないということである。
(Fig.3) ひも理論の失敗は 何を意味するのか?
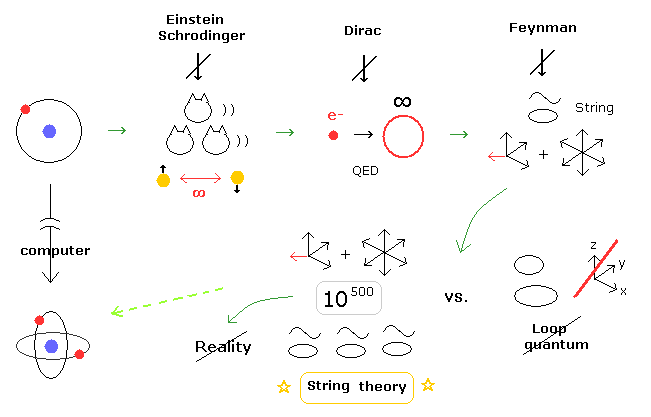
奇妙な ひも理論の他にも 現在の量子論は 物理界の偉人達の承認を得られていないのである。
アインシュタイン や シュレディンガー 達は 非実在的な 量子力学に断固として反対した。
また ディラックは 無限大を人為的に除去する 量子電磁力学 (QED) に 非常に不満だった。
また ファインマンは 10 次元の超ひも理論を 嫌っていた。
しかし ループ量子重力理論 などの 他の量子重力理論が 量子力学と一般相対論を統合することができないため ひも理論は生き残った。
( ひも理論が誕生してから すでに 30年もの歳月が流れている。つまり 他の量子重力理論が 完全に排除されたという 十分な時間は経過したといっていい。)
10次元なんて 現実的には あり得ないのに 超ひも理論のみが唯一の最終理論として残ってしまった。
この非常に矛盾した状態を打開するには 1つしか選択肢は残っていない。
私達は 初期の量子論に立ち返って それを修正するしかないのである。
( なぜなら ひも理論は 完全に 量子力学と相対論が正しいという前提条件に依存しているからである。)
このページに示したように、これら悲惨な状況は 1920 年代における 非常に難解な3体問題によって生じたといっていい。
(Fig.4) ひも理論だめ → 何が残る??
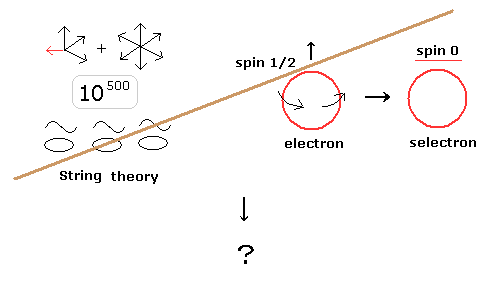
超ひも理論や 超対称性理論 (SUSY) を批判している方々がいるが、もし ひも理論を批判するならば それに 取って変われる 新しい理論を提示すべきである。
( もし 超対称性粒子が存在しなければ ひも理論は 26 次元になり "タキオン" が出現してしまう。)
なぜなら 重力を始め 自然界のすべての力は 見るからに 統一されて かつ互いに規則正しく調和しているからである。
(Fig.4') 一般相対論を捨て去ることはできるのか?
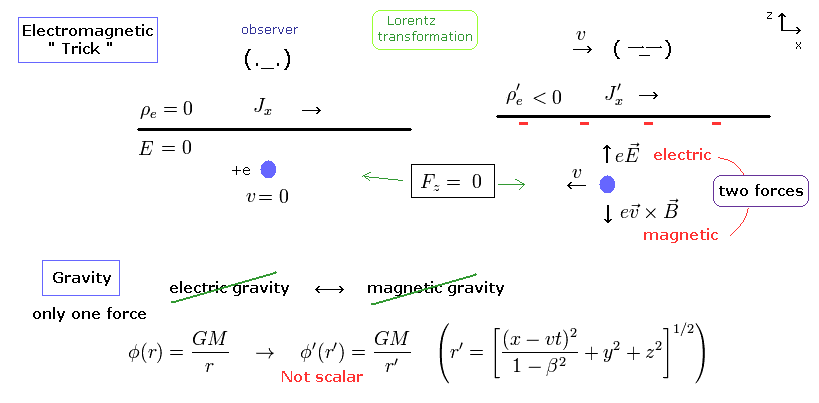
特殊相対論は マクスウェル方程式を 共変形式として表現するのに成功したと言われている。
もし 自然界の法則が 特殊相対論に従っているとしたら 重力も 相対論的に共変な形式で表す必要がある。
( ただし このページに示したように 相対論的なマクスウェル方程式には 致命的なパラドックスが出現する。)
たとえ 宇宙空間が わずかな荷電粒子を含んでいるとしても それだけでは 非常に巨大な星を操れるほどの 力はない ( エーテルなしとした場合 )。
つまり 重力という新たな概念も必要になってくる。
また もし一般相対論が間違いだとしたら 重力による時間の遅れや 光の曲がりを どう説明することができるのだろうか?
もし これらの現象を 星々の周囲の エーテルの密度の違いなどで 説明しようとするならば それはすなわち 特殊相対論自体が間違いということになる。
結果的に ディラック方程式、QED、標準模型のすべてが間違いということになる。
( ただし QED や素粒子理論は 相対論に反する 仮想粒子なるものに完全に依存しているが・・。)
ひも理論では 重要なエネルギーなどを計算するのに ゼータ関数の 誤った数式を用いている。
(Fig.5-1) ゼータ関数。
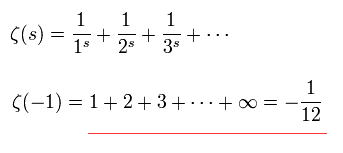
一目で Eq.5-1 の等式は 間違いであると分かる。
しかし ひも理論は この等式を 様々な重要な値を計算するのに用いている。
(Eq.5-2) グラスマン数 "c".
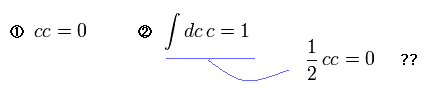
このページに示したように、ひも理論の共形場理論は 私達の世界の 非常に重要な次元の数を決定する際に 人為的な グラスマン数を使用している。
Fig.5-2 の "1" の定義は Fig.5-2 の "2" の定義と矛盾している。
( "1" を満たすなら、 "2" はゼロになるべきだが ゼロでない。)
これらの定義は 私達人間による人為的なものであり、自然界の法則そのものを意味していない。
(Fig.6) スピンとは 何なのか ??
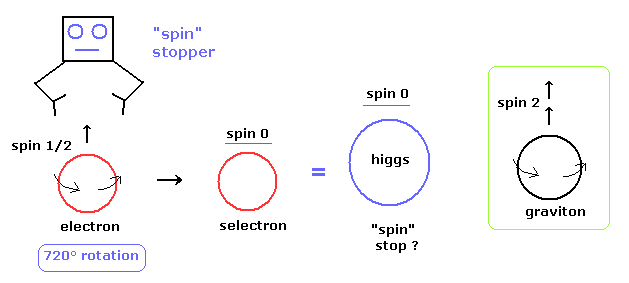
このページに示したように、スピンとは 非常に奇妙なものである。
あなた方が スピンの 本質的な意味を 超ひも理論に求めたとしても この回答は得られない。
スピノル、720o 回転、フェルミ粒子の反交換関係などは 通常の量子論と同じ数式のままである。
つまり たとえ ひも理論を学んだとしても パウリの排他原理を引き起こす ミステリアスな力 の原因を知ることはできない。
重力子の スピン "2" は ひもの 左回りと右回りによって生じるとされているが、それ以上のことは 何も語ってくれない。
つまり スピンというのは 根本的に数式であり リアリティーがないということである。
(Fig.7) どうして 電子と陽電子は 融合して光子になるの?
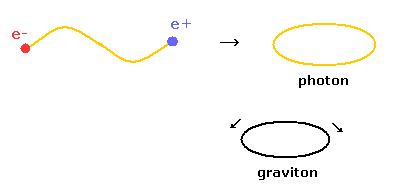
ひも理論には いろいろなバージョンがあるが、すべてのバージョンは 閉じたリング状の ひも を含んでいる必要がある。
その中には 開いたひもが出現するバージョンもあり、例えば 電子と陽電子が光子のひもの両端にあり、それが融合して光子のリングができたりする。
しかし ひも理論は どのように電子が 陽電子と他の正電荷の粒子を区別しているのかというメカニズムに関して具体的な説明を与えてくれない。
また このページに示したように、電子と陽電子が融合して生成される光子は すべての慣性系で 特殊相対論を破っている。
標準的な ヒッグス粒子が見つかれば 素粒子物理学に関して 何もすることはなくなるという人達がいる。
しかし 上で述べたように、現在の理論は スピン、仮想粒子、反粒子の性質などの様々なものに関して 何の明確な回答を与えてくれてない。
彼らは これら基本的なものに関して もっと具体的なものを示すべきである。
通常の場の量子論のように、計量テンソル gμν は 量子化できる。 これが "重力子" を表している。
(Eq.1)
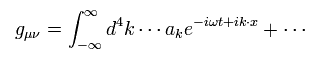
しかし 一般相対論では、微分は 次のように非常に込み入っている。
(Eq.2)
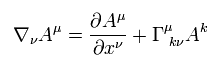
Eq.2 では、クリストッフェル記号 Γ は、
(Eq.3)
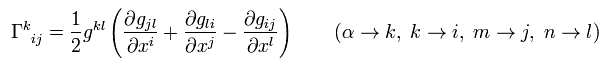
これは非常に複雑である。
複雑な クリストッフェル記号や 共変微分は 場の量子論において 様々な発散を引き起こす。
( 場の量子論では 微分は 指数関数との組み合わせで 無限大から無限大の 運動量を表す。)
もし これらやっかいな発散をすべて取り除こうとすると、Fig.8 右に示すような 新たな相互作用が出現する。
これはつまり これらを繰り込もうとすると 巨視的な重力の関係式が壊れてしまうことを意味する。
そのため 一般相対論においては繰り込み手法が使えない。
(Fig.8) 場の量子論における一般相対論は マクロの重力関係を壊してしまう。
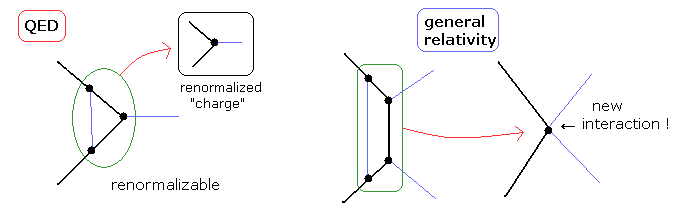
基本的に これらの発散は 非常に厳しい 相対論的な対称性の制限に起因している。
ローレンツ不変性 (= ローレンツ対称性 ) を維持するためには、運動方程式のもととなる ラグランジアンが 様々な 無限大から無限大までの範囲の 経路積分 を含まなければならない。
つまり、この時点ですでに 相対論的な場の量子論は リアリティーを失っているのである。
( 相対論は間違い? のページも参照のこと。)
(Fig.9) 現実の世界では ローレンツ対称性は不可能である。
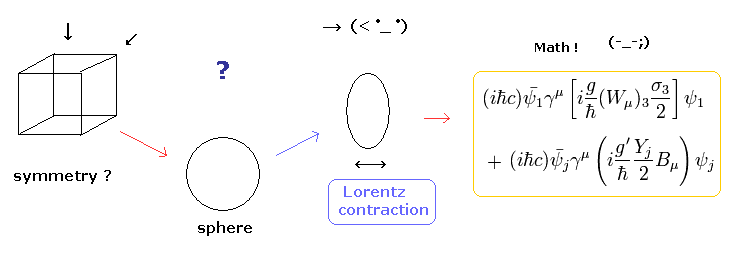
もちろん、自然解において "対称性"の概念は非常に重要であることはいうまでもない。
例えば、Fig.3 の正六面体は 対称的な形をしている。
しかし Fig.3 の2つの矢印に示したように 方角によって、この立方体は違って見える。つまり これは 相対論による対称性を満足していないのである。
なら ”球”はどうであろうか? 確かに球だと より対称的な形となる。しかし 違った速度で運動する観測者からの視点では この球はある一方向で ローレンツ収縮する。つまり これも 対称的ではないということになる。
相対論では 時間と空間の概念を等しく対称的に扱わなければならない。このことが 相対論的な場の量子論から リアリティーがなくなった原因である。
( この現実の世界の物を 完全対称な理論で表現することは不可能なのである。)
(Fig.10) 超ひも理論は ”数学上”の対称性のみ (現実性から遊離した) を追及している。
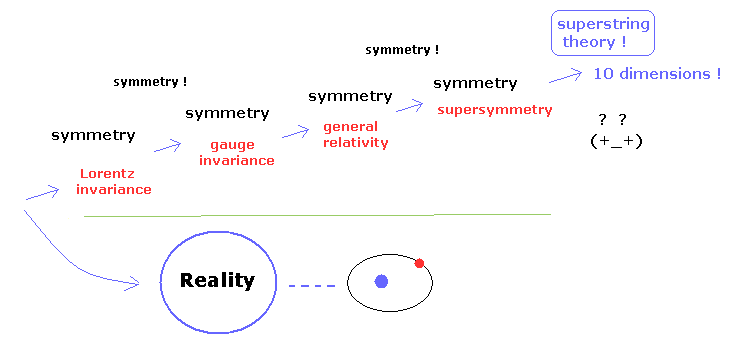
相対論の非常に厳しい条件のもとで、彼らは 標準模型を説明するために "ゲージ" 対称性の理論を作りだした。
なぜなら この非常に厳しい "数学上"の牢の中では "対称性" に注目する以外 他に道がないからである。
つまり 現在の超ひも理論は 様々な数学上のみの対称性を追及しているだけなのである。もちろん ここには 何のリアリティーもクリアなイメージもない。
(Fig.11) 超ひも理論は 発散を除去できるのか?
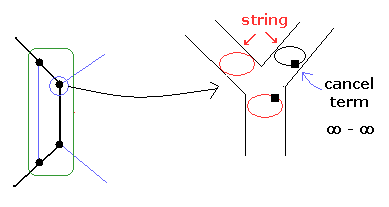
Fig.11 に示すように、超ひも理論は 点状粒子のかわりに 1次元のひも (時間とあわせて 2次元) を使用している。
このひもの中では、 無限大を除去するために さまざまな 数学上の項、変数、係数を 操作することができる。
( 点状粒子の中では、これらの様々な操作が行えない。)
(Fig.12) 超ひもは 実在のひもとは違う。
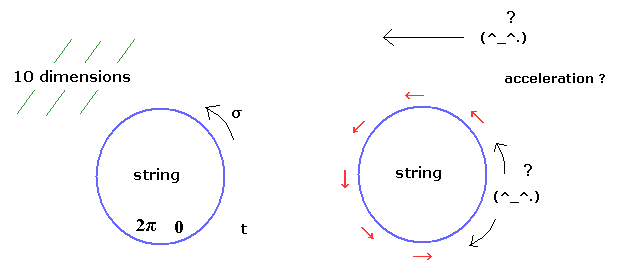
超ひも理論では、1次元の空間の変数 σ と 1次元の時間の変数 τ の 2次元 (1+1) の世界面 (= worldsheet) というものが 10次元 (= 10D ) の ミンコフスキーの背景時空間の中を動き回っている。
基本的に この空間変数 σ は 0 から 2π をとり、これは 閉じた環を意味している。
( 開いた環では、このひもは 0 から π の範囲となり、他のひもや膜と結合することができる。)
彼らが この単純かつ奇妙な 1+1 次元のひもを使用した理由は 相対論的な非常に厳しい対称性が原因である。
お気づきかもしれないが、この 1+1 次元のひもは 実在のものでは表現できない。
Fig.12 に示すように、閉じた環は 少なくとも ( x , y ) や ( r と θ ) のように 2次元の空間が必要である。
そのため、 ある物が σ の線に沿って 等速直線運動していると、これは 世界面上では 遠心力を生じないことになる。
しかし 背景のミンコフスキー時空間からの視点では、この円運動は 遠心力を引き起こしてしまい、何かしらの引きとめる外力がないと 別の次元に飛んで行ってしまうことになる。
つまり、このひも理論は 最初から 自己矛盾を含んでいることになる。これは後でも説明する。
(Eq.4) 数学上のトリック。
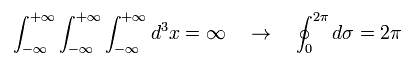
Eq.4 に示すように、もし 1次元の人為的なリングを定義すると、Eq.4 左の無限大の 空間積分が Eq.4 右の 単純な 2π で表すことができる。
また 共形場理論 ( このページ ) では、1次元のリングは 閉じた円の複素積分と見なすことができる。
つまり 単に数学上の理由のみのために この 1+1 次元のひもが選ばれたと言っていい。
(Eq.5)
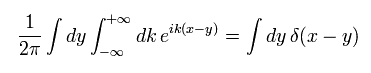
(Eq.6)
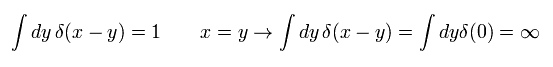
場の量子論では ローレンツ対称性を満たすために ある変数に関して マイナス無限大からプラス無限大の範囲で 指数関数を積分する。
Eq.5 と Eq.6 に示すように、x が y にちょうど等しいとき これは発散する。
x が y と異なるとき、指数関数の振動によって それはゼロになる。
(Fig.13) 格子ゲージ理論。
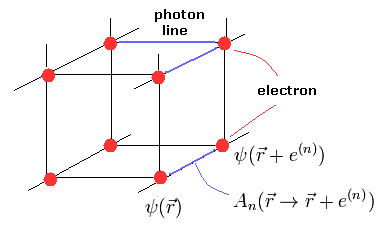
発散を回避するために、"格子ゲージ理論" が生まれた。
このページ (Eq.5-46) に示したように、ディラックのラグランジアンは 電子 (= ψ ) と 光子 (= A ) の相互作用を含んでいる。
Fig.13 では 格子点が電子、光子 (= ベクトルポテンシャル A ) が それらを繋ぐ結合線 を表している。
もちろん、 Fig.13 の模型は Fig.9 に示すように すべての方向で対称的ではない。
つまり 間隔を後で無限小にする必要がある。
格子理論では、ディラックの運動量 (= 微分 ) の項は 次のように表せる。
(Eq.8)
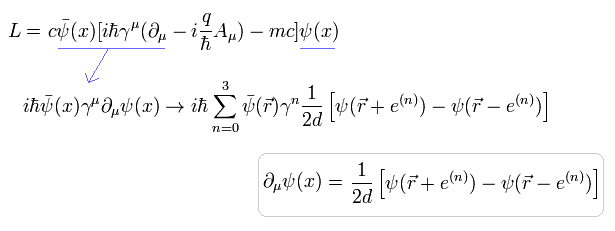
ここで "d" は 格子点間の単位長を意味している。
Eq.8 は "n" 方向において対称的な形をしている。
4次元世界では、各格子点は 次のように表せる。
(Eq.9)
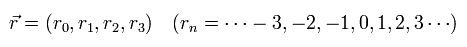
2つの電子間をつなぐ 光子 (= A ) は、
(Eq.10)
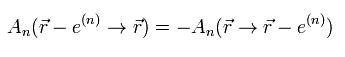
逆方向は マイナスになる。
つまり 光子と電子の相互作用項は
(Eq.11)
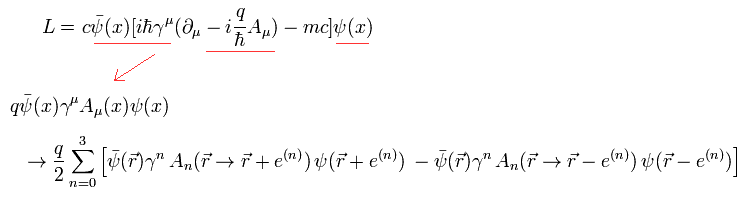
Eq.8 と Eq.11 の合計は 次を含んでいる。
(Eq.12)
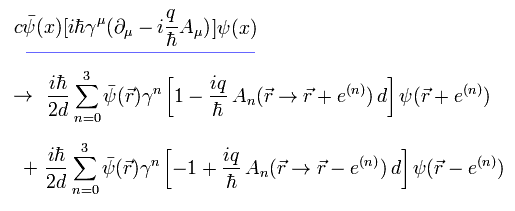
次のゲージ変換のもとで、
(Eq.13)
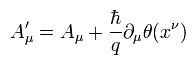
式は不変である。
Eq.13 の 格子バージョンは、
(Eq.14)
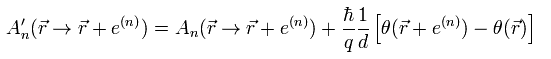
Eq.10 の関係式を用いて、反対方向は、
(Eq.15)
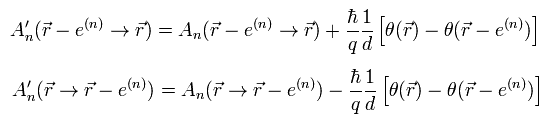
間隔 "d" が小さいとき、
(Eq.16)
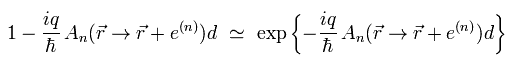
Eq.14、Eq.15 を Eq.12 に代入して、Eq.16 の関係式を用いると、"r" 地点における ゲージ θ(r) は ちょうど相殺される。
(Eq.17)
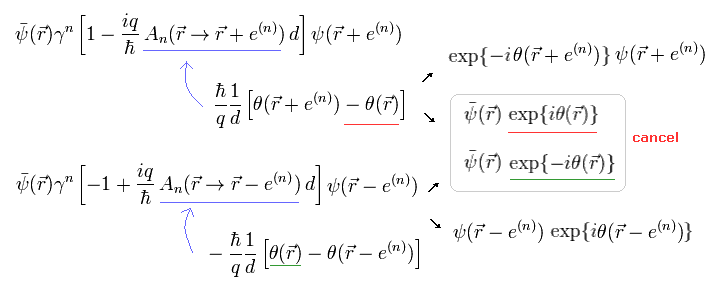
しかし Eq.14 と Eq.15 の両端 ( r+e と r-e ) のゲージは残る。
これらのゲージをすべて 消去するには、あるループを考えて 両端をつなげる必要がある。
(Eq.18)
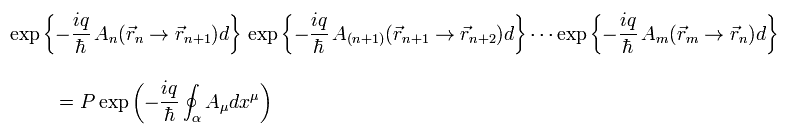
Eq.18 のループ状態では、すべてのゲージ θ は ちょうど相殺され、すなわち ゲージ変換不変 となる。
(Fig.14) ループ量子。
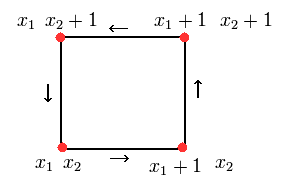
ここで Fig.14 のような 最小のループを考える。
( もちろん このループは ゲージ不変性である。)
上下の線のベクトルポテンシャルは
(Eq.19)
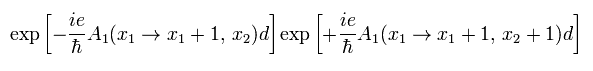
ここで 上 ( Eq.19 右 ) と 下 ( Eq.19 左 ) は逆方向である。
Eq.19 の 指数関数を展開して
(Eq.20)
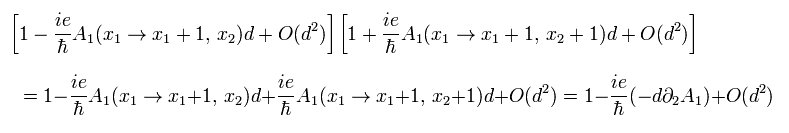
Fig.14 の左と右の線を 同じように計算して それらを結合すると 次を得る。
(Eq.21)
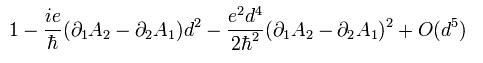
Eq.21 の " d2 " の項は 全微分のため作用の積分で消失する。
" d4 " の項は 4次元時空間の積分で残る。
この項は 光子のラグランジアンである。 ( このページも参照のこと。 )
(Fig.15) ループ量子重力理論。
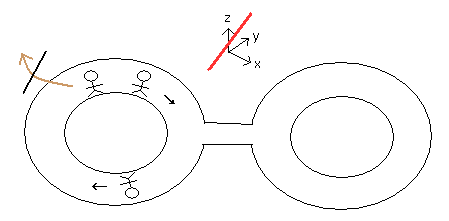
ループ量子重力理論では、物は 1次元上のループ内のみ行き来できる。
( この現実世界が 3次元空間で構成されているのは明らかなのだが。)
つまり ループの存在していない 空間には x, y, z のような 空間座標などの概念が存在しないことになる。
一般相対論の一般座標変換は ゲージ変換に似ている。
次の無限小座標変換のもとで
(Eq.22)
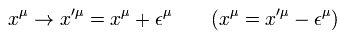
ベクトルは次のように変化する。
(Eq.23)
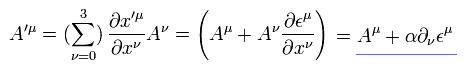
Eq.23 は ゲージ変換 (Eq.13) に似ている。
(Eq.13)
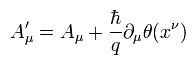
これはつまり ループは Eq.18 と Eq.23 に示すように ゲージ変換と 一般相対論の 座標変換に対して不変ということを意味している。
ループ量子重力理論では 次の変数が使用される。
(Eq.24)
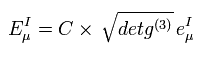
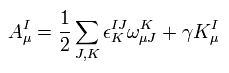
しかし ループ量子重力理論では、計量テンソルは 3 × 3 (= 空間のみ )である。
これは少し奇妙である。
また ループは次のように表せる ( Eq.18 のように )。
(Eq.25)
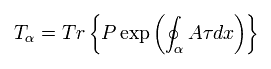
(Fig.16) ループ量子重力理論にリアリティーはあるのか?
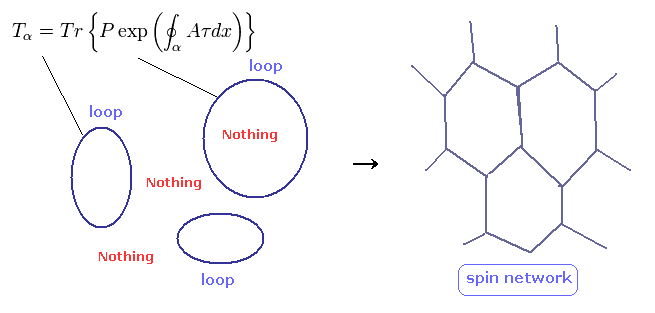
ループ量子重力理論では、背景の時空間には何も含まれていない。
何も含まれていないということは、要するに、背景世界には 時間や空間の概念も存在しないということである。
( 超ひも理論では、背景時空間は 10 次元のミンコフスキー時空間として存在する。これがループ量子重力理論との違いである。)
この非常に制限された空間では、座標変換の不変性が ゲージ変換の不変性として扱われる。
これらのループを結合させていくと いわゆる "スピンネットワーク" となる。
問題は、これらの奇妙かつ特殊なループは 通常の QED や ゲージ理論に使えないということである。
一般相対論的な条件は 最も強いものである。そのため 一般相対論を考慮すると、この理論は通常の量子論を満足しなくなる。
また、この世界が 時間も空間も含めて これらのループのみでできていると考えるのは 非常に受け入れ難いことである。
背景のミンコフスキー時空間 ( 次元 D = 10 ) は 次のように表せる。
(Eq.26)
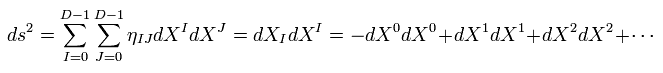
XI は 背景時空の座標である。
背景時空間は "標的空間" とも呼ばれる。
ここでは (-1, 1, 1 ..) バージョンの D 次元の計量テンソルを使用している。
(Eq.27)
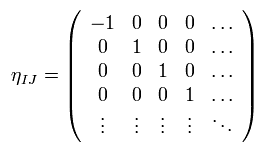
ひもの状態は 2次元 ( 2 = 空間1次元+時間1次元 ) の変数で表される。
(Eq.28)
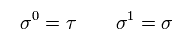
ここで τ は "時間"の変数、σ は 1次元 の空間の変数である。
もちろん この状態は 非常に想像するのが難しい。
このページに示すように、一般相対論の計量テンソルは ある座標変換のもとで通常のミンコフスキーの計量テンソル (= η ) に変換できる。
(Eq.29)
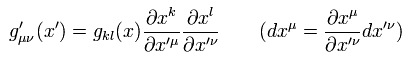
(Eq.30)
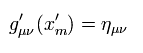
Eq.29 と Eq.30 から、各行列式 (= 行列式 × 行列式 × ... ) を考慮すると、
(Eq.31)
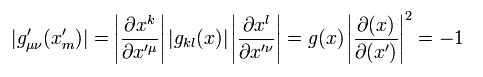
ここで ミンコフスキーの計量テンソル = -1 を使った。
つまり 一般の計量テンソルの行列式 g(x) は
(Eq.32)
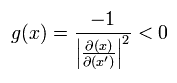
Eq.32 から 次を得る。
(Eq.33)
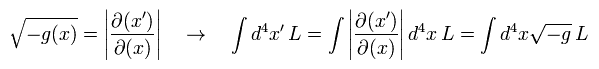
Eq.33 は 一般相対論における スカラーの作用積分である。
ひも理論における 作用 S (= スカラーラグランジアンの積分 ) は、
(Eq.34)
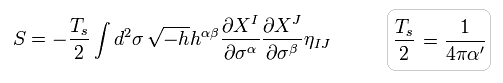
ここで hαβ は 2次元の計量テンソルである。
Eq.34 は 各世界 ( 2次元と 背景時空 ) における 計量テンソルと テンソルの組み合わせになっている。
つまり この作用は 一般相対論の座標変換のもとで 変化しない スカラーの形となっている。
計量テンソル h の変分は
(Eq.35)
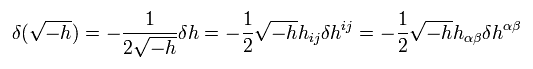
ここでは 次の関係式を用いている。
(Eq.35')
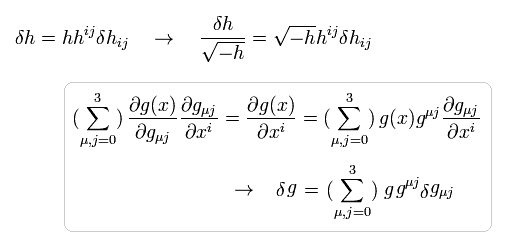
このページ (Eq.74-Eq.77) も参照のこと。
Eq.35 を用いると、計量テンソル h に対する Eq.34 の作用の変分は
(Eq.36)
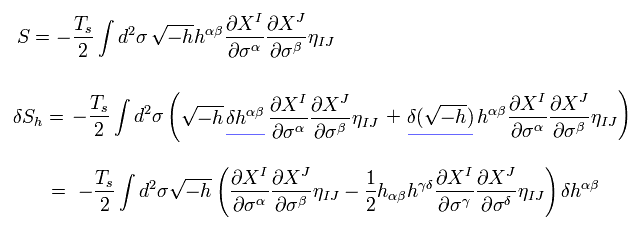
作用の変分 (Eq.36) が ゼロのとき ( δS = 0 )、これは 運動方程式を意味している。
つまり 運動方程式は
(Eq.37)
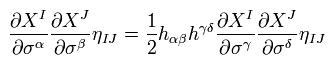
次のように テンソル G ( αβ に対する ) を定義する。
(Eq.38)
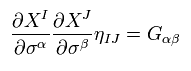
Eq.37 における 両サイドの行列式は
(Eq.39)
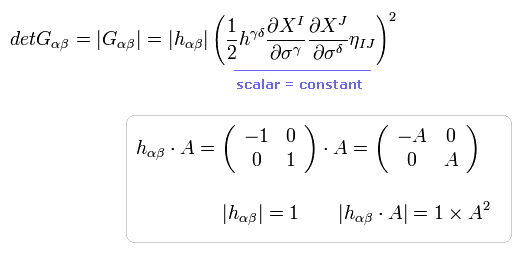
Eq.39 の最後の項の 二乗の部分は スカラー値である。
そのため 行列式では この定数は 二乗になる。
Eq.39 から、次を得る。
(Eq.40)
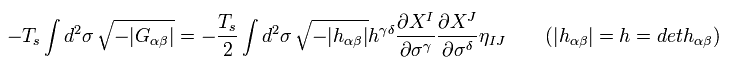
結果、Eq.34 の作用は Eq.40 の左辺と等しくなる。
ある座標変換のもとで、計量テンソル h は 2次元のミンコフスキーの計量となり得る。
(Eq.41)
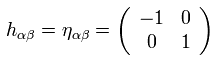
基本的に Eq.28 の空間座標 (= σ ) は 0 から 2π である。
( もし この範囲が -∞ から ∞ だとしたら、この非常に長いひもが実際に見えてしまう。 )
つまり 1周で元に戻る。
ここで "実在の" 閉じたリングについて考える。
背景時空からの視点では 角振動数 ω で回転する この閉じたリングは、
(Eq.42)
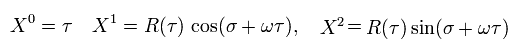
Fig.12 も参照のこと。 他の XI は ( τ σ ) の関数でないとする。
計量テンソルが Eq.41 のとき、Eq.40 ( 右辺 ) の作用 S は、
(Eq.43)
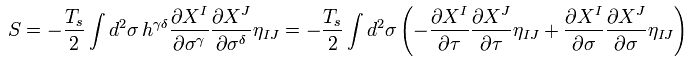
Eq.43 を オイラー・ラグランジュ方程式に代入すると、
(Eq.44)
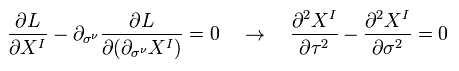
I = 1 のとき、 Eq.42 を 運動方程式 (= Eq.44 ) に代入して、
(Eq.45)
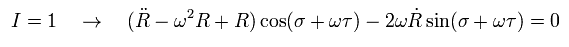
ここでは "点" は τ に対する微分を意味している。
円の半径 R が定数のとき、次の解を得る。
(Eq.46)
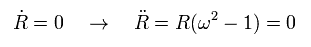
Eq.46 は 奇妙である。 ω が 1 でないとき、加速度 R は ゼロでない。これは 定常な半径 R と矛盾する。
これはつまり この超ひもには リアリティーがないことを意味する。
この矛盾は 1+1 次元の円形リングという設定に起因している。
Eq.40 (右辺) の作用は 次の変換のもとで不変 (= ワイル対称性 ) である。
(Eq.47)
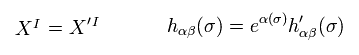
ここでは
(Eq.48)
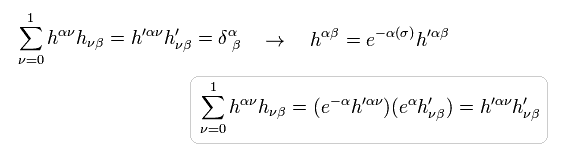
つまり
(Eq.49)
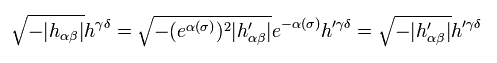
Eq.39 も参照のこと。
Eq.47 は Eq.40 の非常に抽象的なひもには "スケール" の概念がないことを意味している。
つまり 数学上のものと言える。
Eq.43 に示すように、計量テンソル h が 通常のミンコフスキー計量テンソルのとき、作用は
(Eq.50)
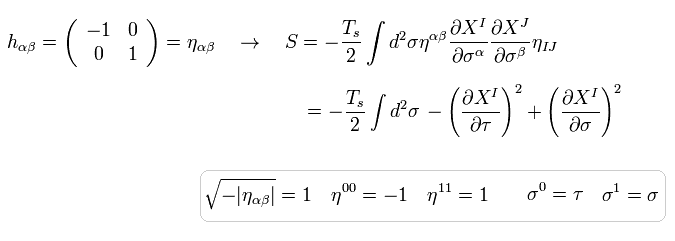
ここでは 時間と空間の変数を 次の変換で より対称的なものにする。
(Eq.51)
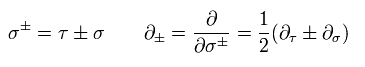
Eq.44 の運動方程式は Eq.51 の新しい変数を用いて 次のように表せる。
(Eq.52)
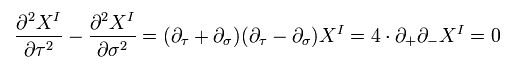
Eq.52 の解は、
(Eq.53)
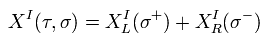
ここで σ+ は 左回り (= L ) を意味する。
また σ- は 右回り (= R ) を意味する。
ひも理論では、定数 Ts は 単位エネルギー (= H ) あたりの質量を意味する。
(Eq.54)
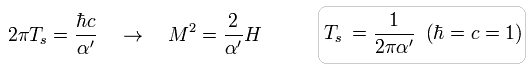
Eq.53 から、 次のように解を定義する。
(Eq.55)
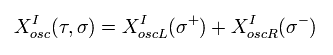
Eq.51 の新しい変数を使って、ハミルトニアンは 次のように分離できる。
(Eq.56)
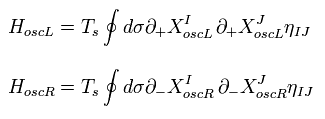
ここで Eq.56 を証明する。
Eq.50 から、 次のハミルトニアン H を得る。
(Eq.57)
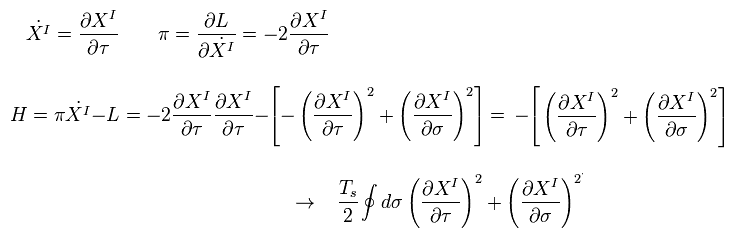
Eq.51 と Eq.55 から、
(Eq.58)
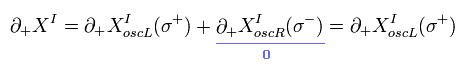
つまり Eq.56 ( "I" の項 ) は、
(Eq.59)
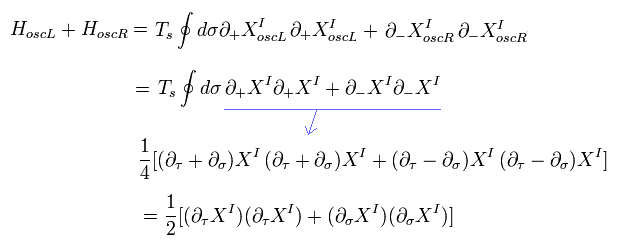
これは Eq.57 に等しい。
ひもが 次の境界条件を満たすとき
(Eq.60)
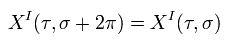
解は、
(Eq.61)
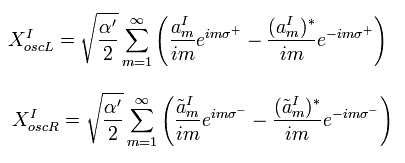
演算子が 次の交換関係を満たすとき、
(Eq.62)
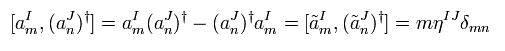
Eq.62 に示すように、ドブロイ様の関係式は ひも理論においても有効である。
つまり ひも理論は 量子力学内の より根本的なメカニズムに答えることができない。
単純に 同じ数学を真似しているだけである。
Eq.62 の a+ は 生成演算子である。 次の数演算子を用いて、
(Eq.63)
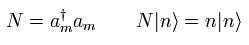
(Eq.64)
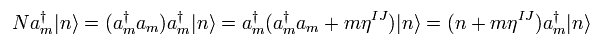
つまり "mηIJ" が 生成演算子によって追加された。
これはつまり I,J = 0,0 のとき、 この生成演算子は "マイナス" のエネルギー (= マイナスの数 ) を生成し、リアリティーがない。.
この非実在の ゼロ成分は 相対論的な共変形式に由来している。
Eq.61 から、次を得る。
(Eq.65)
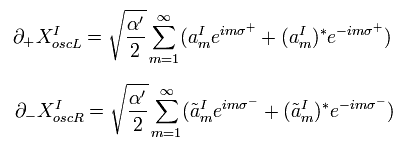
(Eq.56) ハミルトニアン。
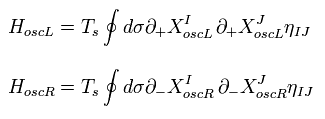
Eq.65 を Eq.56 に代入すると、 左回りのハミルトニアンは、
(Eq.66)
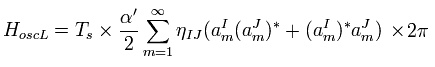
ここで 2π は、
(Eq.67)
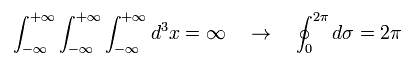
Eq.66 において、 m が n に等しくないとき、境界条件 2π より、それはゼロになる。
(Eq.68)
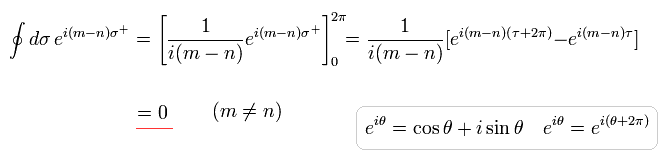
Eq.54 から、
(Eq.69)
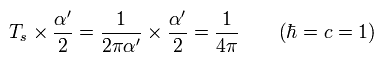
Eq.69 と Eq.62 の交換関係を用いて、 Eq.66 のハミルトニアンは ( I=J のケースのみ残る )
(Eq.70)
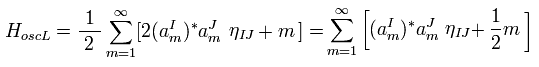
ここで 次を使う。
(Eq.71)
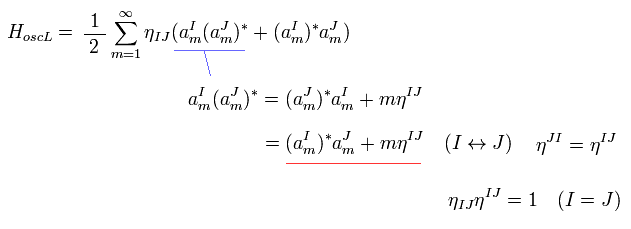
同様に
(Eq.72)
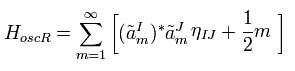
Eq.64 に示したように、 I,J = 0,0 のとき、生成されたエネルギー (= 数 ) は "マイナス" になる。
(Eq.73)
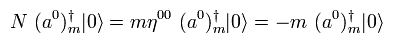
この深刻な状況を回避するために、この非実在のゼロ成分を 別の1成分でキャンセルする。
つまり 残ったハミルトニアン ( D 次元の ) は、
(Eq.74)
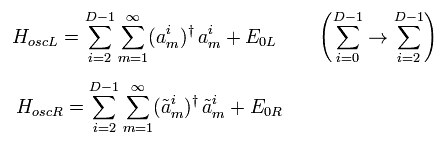
結果 (D-2) 成分のみ残った。
よって ハミルトニアン (Eq.70) の η は 次のように "1" となる。
(Eq.75)
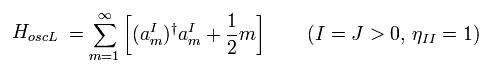
Eq.75 から、D-2 成分のすべて真空のエネルギーは 発散する。
(Eq.76)
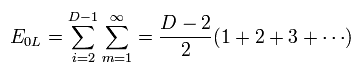
フェルミ粒子の真空のエネルギーは マイナスになる。
つまり この発散は "R" セクターのフェルミ粒子で除去される。
"NS" セクターのフェルミ粒子は 反整数であり 真空のエネルギーをキャンセルできない。
( これらのルールは 人為的なものである。 )
この無限大を "人為的に" キャンセルしようとすると、この理論は 相対論的な対称性を満足しなくなる。
対称性を満足するためには、次の ゼータ関数という ”数学上”のトリックを使用する。
(Eq.77)
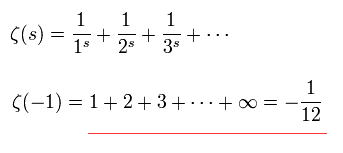
もちろん、 Eq.77 は 間違いである。しかし ひも理論は この間違った数学を 対称性を保つために 使用しているのである。
次に Eq.77 を証明する。
G(β) を 次のように定義する。
(Eq.78)
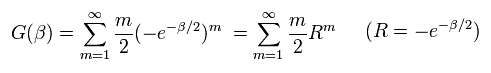
つまり
(Eq.79)
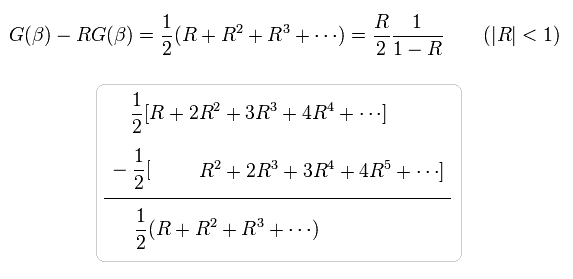
Eq.79 と Eq.78 から、
(Eq.80)
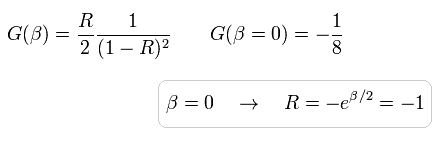
もちろん、 β がゼロのとき、 R = -1 となり、それは収束しない。
Eq.77 から、
(Eq.81)
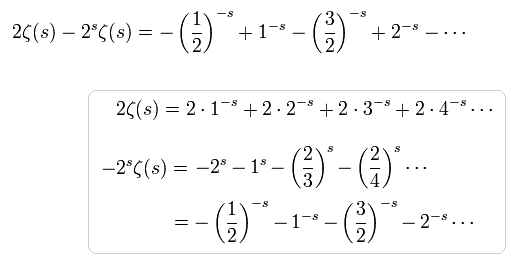
s=-1 のとき、 Eq.81 は ちょうど Eq.78 に等しい。
(Eq.82)
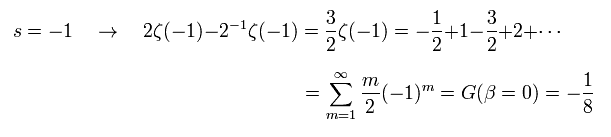
結果的に 次を得る。
(Eq.83)
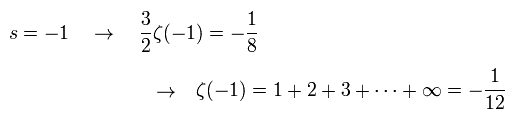
Eq.77 と Eq.83 から、Eq.76 の真空のエネルギーは、
(Eq.84)
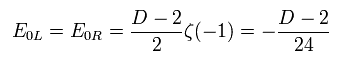
Eq.54 から、ひもの質量は
(Eq.85)
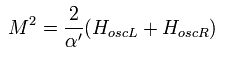
(Eq.86)
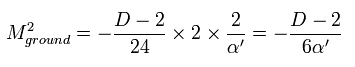
D 次元数が 2 より大きいとき、このひもは タキオン (= 質量の2乗がマイナス ) を含む。
各左回りと右回りに 粒子が1つづつ生成されたとき、質量は、
(Eq.87)
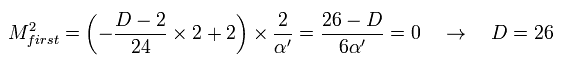
ゼロ質量のボソンを説明するには 次元は 26 になる必要がある。
つまり ひもが "超対称性" (= ボゾン = フェルミ粒子 ) を満たさないとき、ひも理論は タキオンを含む 26 次元 になってしまう。
残念ながら ここには何のリアリティーもない。
セントラルチャージと臨界次元も参照のこと。
(Fig.17) 重力のテンソル場。
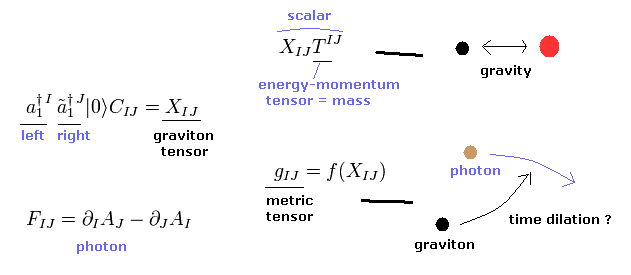
対称性を保つため、励起されたエネルギーは 左回り、右回りで 等しくなる。
Eq.87 において 最初に励起された質量ゼロのペアは テンソル場 (= 重力子 ) を意味する。
彼らの解釈によれば、左回り+右回り = スピン "2" ということになる。
それらの1つだけだと スピン "1" になる。しかし これらは単なる数学上の定義にすぎない。
背景世界の時空の 計量テンソル (= g ) が 2 次元のひもの変数の関数のとき、これは 重力子が 時空を歪ませていることを意味している。
つまり、この場合は 光子が 重力の時間の遅れによって 進行方向を曲げられるような状態にあたる。
背景場の関数が 反対称テンソルを形成するとき、これが光子の場を意味している。
残念ながら これらは単なる数式の世界であり、まったくリアリティーがない。彼らは 重力子や他の粒子について まったく具体的なイメージを示すことができない。
これら数学上のみの世界が Fig.1 のような矛盾を生じさせてしまった要因である。
もうそろそろ 実在的 かつ 物理的 な世界に 人類は戻るべき頃だと思われる。
”タキオン”を除去し 次元数を減らすためには、ひも理論は 対称的な フェルミ粒子を含む必要がある。
ボゾンとフェルミ粒子を区別するには、周期境界条件 (= R セクター ) と 反周期条件 (= NS セクター ) を定義する必要がある。
NS+R と R+NS は フェルミ粒子様の性質。NS+NS と R+R は ボソン用の性質を示す。
( つまり 超ひもは 様々な非実在の力の粒子を含んでいる。)
ボソン+フェルミ粒子の作用 は、 ( すでに述べたように、D-2 次元のみ残っている。 )
(Eq.88)
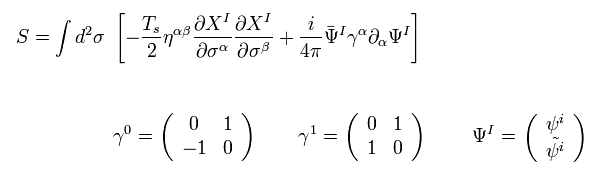
これらの質量は 互いに等しい。
もし 何かしらの超対称性変換を選ぶと、Eq.88 が 超対称性であることを示せる。( このページも参照のこと。)
つまり、超対称性粒子は ボソンとフェルミ粒子のラグランジアンが 1つの作用 S に詰め込まれている状況によって生じる。
( これらに具体的なイメージはない。)
NS セクターの フェルミ粒子の展開式は
(Eq.89)
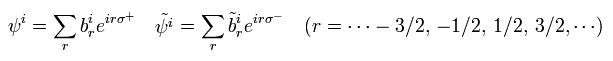
これは 半整数の角運動量に関係している。
つまり 最終形態である 超ひも理論でさえも 半整数のスピンが何なのか 根本的なことを答えてくれない。
なぜなら、すでに述べたように、スピンそのものに実在性がないからである。
フェルミ粒子は 次の 反交換関係を満たす。
(Eq.90)
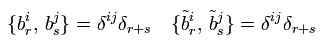
Eq.90 は 超ひも理論でさえも 反交換関係 (= パウリの排他原理 ) の起源が 謎のままだということである。
超ひも理論は 実数 ( † でなく ) を使用しているため、r が マイナス s のとき、Eq.90 の右側はゼロでないとする。
Eq.88 より、作用 S のフェルミ粒子部分は
(Eq.91)
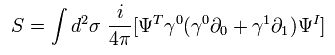
ここでは
(Eq.92)
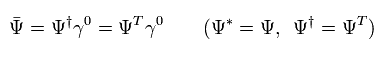
これらのフェルミ粒子は "実" グラスマン数と仮定する。
Eq.88 の 2次元γ行列を用いると、Eq.91 の作用は
(Eq.93)
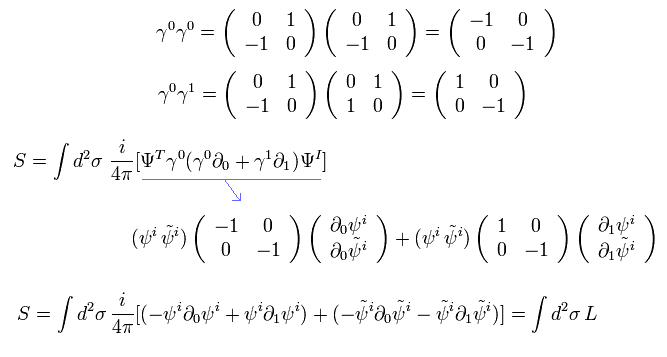
正準運動量は
(Eq.94)
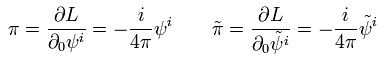
定義によれば、ハミルトニアンは
(Eq.95)
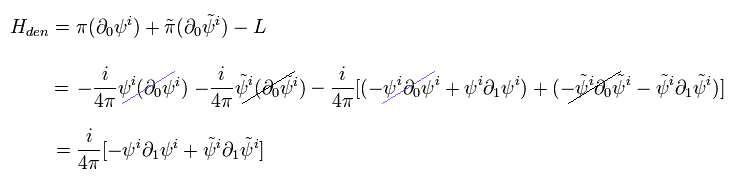
Eq.89 から、
(Eq.96)
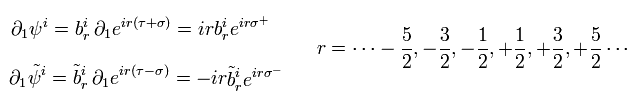
Eq.89、 Eq.90 (= 反交換 )、 Eq.95、 Eq.96 を用いて、 ハミルトニアン密度を積分すると、次のハミルトニアンを得る。
(Eq.97)
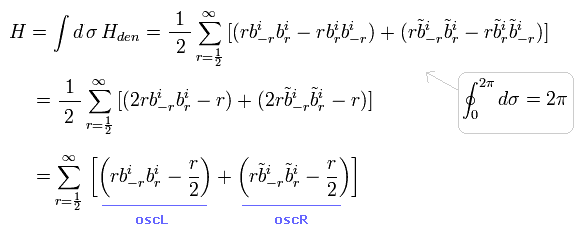
Eq.97 の真空は E.75 のボソンのケースの逆である。
Eq.75 と Eq.97 の真空のエネルギーの和は
(Eq.98)
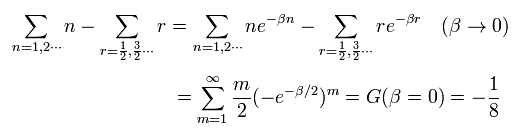
ここで Eq.78- Eq.80 を用いた。
左回りの真空のエネルギーは
(Eq.99)
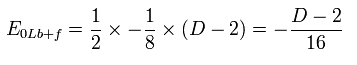
Eq.99 は タキオンを含んでいる。
タキオンを除去するためには、超対称性と 人為的な操作が必要になる。
最初の励起状態の質量 ( 左回りの ) は、
(Eq.100)
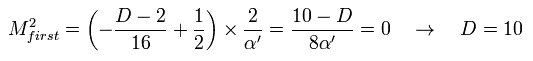
Eq.100 は ゼロ質量の 粒子の存在には 10 次元 が必要であることを意味している。
しかし 残念ながら これらは 単なる "数式" であり、あなた方は これらの数学上のトリックが この現実の世界を表していると思われるだろうか?
"タキオン" を除去するには、超ひも理論は 超対称性を必要とする。
( 超対称性とモジュラー変換不変性を参照のこと。 )
超ひも理論は 対称性を保つために 厳密に様々な異常項(アノマリー)を除去しているようである。
しかし 何といっても この理論には 数学的な仮定が多すぎる。
「迷走する物理学」(リー・スモーリン著) の本によれば、超ひも理論の余剰次元の幾何学的構造は無数に存在するそうである。
つまり 現在のひも理論(と 11 次元の M 理論)は 実験結果をまったく予測することができないことを意味している。
( 人為的に 操作することによって 結果に近づけさせることはできる。)
さらに、実際には存在しない多くの奇妙な力を含んでいるようである。
そのため、今までに 多くの研究者達が ひも理論をあきらめた。
しかし ひも理論に 取って変われる 新しい理論が出現してこないかぎり、彼らは 統一理論として ひも理論を選ぶしか他に道がなかったのである。
これが これら奇妙で非現実的な ひも理論が現在にいたるまで生き残ってきた最大の理由である。
しかし この現在の物理 (+ 量子化学 + 分子生物学などナノテクノロジー ) の状況を修正するには、私達は トップページに示したように ボーア模型まで戻らなければならない。
現在のところ、超対称性粒子はまったく見つかっていない。
私が現在 心配していることは、研究者達の意志が 実験結果を変えてしまうことである。超光速のニュートリノのケースのように。
そのため、いつの日か "非実在"の 超対称性粒子が見つかったというニュースを聞く可能性があるかもしれない。
( なぜなら 量子力学と相対論が正しいという前提条件では、超対称性粒子がないと 統一理論が不可能だからである。)

2012/7/21 updated This site is link free.