
トップページ (2電子原子も含む正確な新ボーア模型)
ディラック方程式 (+繰り込み) によるスピンg因子導出は単なるトリックである。
ディラック方程式による水素原子解の真実。(13/1/14)
量子電磁力学 (QED) は本当に正確なのか? (13/1/25)
何が 実在する素粒子なのか? (12/ 10/12)
超ひも理論とループ量子重力は本当なのか? (12/11/23)
(Fig.1) "数式" ?

場の量子論は 非常に難しく学ぶのに多大な時間を要する。
( このページは なるべく詳細でかつ分かりやすくなることを目指して作った。)
もし あなたがたが この場の量子論が正しく 私たちの自然界について 基本的な答えを与えてくれると信じて 長きにわたって 場の量子論を 一生懸命 勉強したとしても、場の量子論は単なる数式しか示さず リアルな物理でないことに愕然とするだろう。
このページでは この事実について なるべくはっきりと説明していくことにする。
(Fig.2) アインシュタインのエネルギー・運動量の関係式。
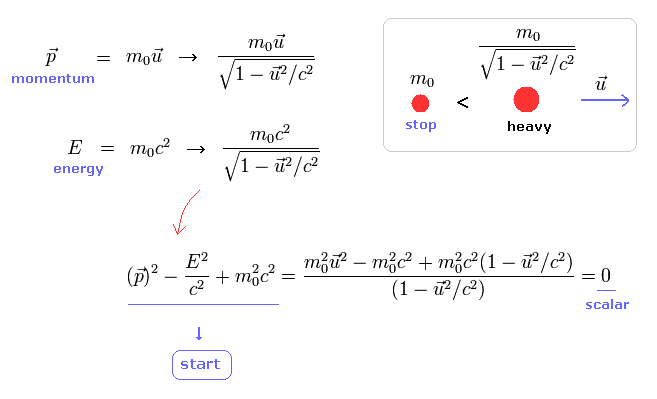
特殊相対論によれば、物体が 速度 "u" で動いているとき、その質量は重くなる。
この相対論的な質量を考慮して、彼らは 4元運動量を定義した。
このページに示したように、 4元運動量 (= 運動量 p と エネルギー E ) は ローレンツ変換で 時空間変数のように変換する。
これはあたりまえの話である。なぜなら 4元運動量は 時空間変数 (= ct, x, y, z ) を元に作られたものだからである。
(Eq.0-1)
これらの4元運動量は Fig.2 のエネルギー・運動量の関係式を満たし、ここが すべての場の量子論の出発点となる。
また Fig.2 の式は すべての速度 "u" で成り立つため、これを "ローレンツ変換不変な スカラー" と呼ぶ。
( "スカラー" とは ローレンツ変換の下で 変化しないことを意味する。)
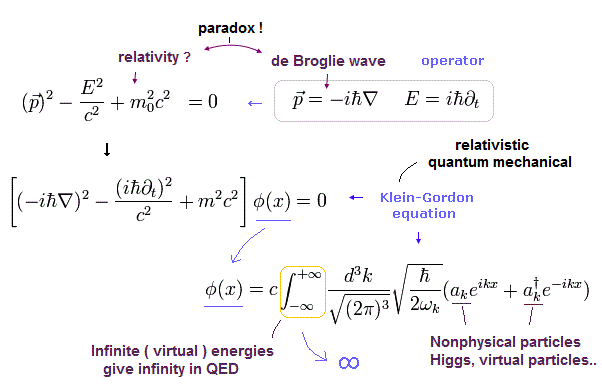
相対論的な場の量子論では、まず最初に クライン・ゴルドン ( K-G ) 方程式について学ぶ。
なぜなら クライン・ゴルドン方程式の意味は Fig.2 の 特殊相対論にちょうど等しいからである。
クライン・ゴルドン方程式は Fig.2 の 運動量とエネルギーを 量子力学の演算子で置き換えて得られる。
(Eq.0-2) クライン・ゴルドン方程式。
上で述べたように、Fig.2 は ローレンツ変換のもとで 不変である。そのため Eq.0-2 もローレンツ変換不変でなければならない。
結果的に クライン・ゴルドン方程式の波動関数 φ は 積分区間に 無限大の運動量を含まねばならず これが無限大に発散する。
もし 有限の運動量しか含まないと、ローレンツ変換で積分区間が変化してしまい、Eq.0-2 は ローレンツ変換不変ではなくなる。
Eq.0-2 に見られたように、クライン・ゴルドン方程式は 時間微分が 2次なため、非常に使うのが不便である。
そのため 彼らは クライン・ゴルドン方程式をベースに 1次のディラック方程式を導いた。
(Eq.0-3) ディラック方程式。
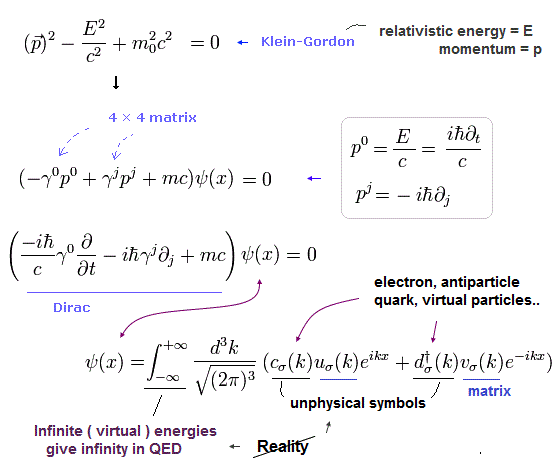
Eq.0-3 では、 γ は 4 × 4 γ 行列 で p0 は E/c の意味である。
Eq.0-3 に見られるように、1次の式を得るためには、”数学上”の行列に頼らなければならない。
つまり 現在の場の量子論は 単なる "数学上" の産物であり、まったく 物理的なイメージがない。
次に Eq.0-3 の デイラック方程式が クライン・ゴルドン方程式にちょうど等しいことを示す。
(Eq.0-4) ディラック方程式 = クライン・ゴルドン。

Eq.0-4 に示すように、ディラック方程式の左側から そのペア演算子をかけると ディラック方程式がちょうどクライン・ゴルドン方程式 (= 特殊相対論 ) に等しいことが分かる。
Eq.0-4 の関係式を得るために、 4 × 4 γ 行列は 次の関係式を満たす必要がある。
(Eq.0-5)
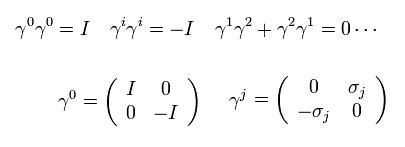
ここで σ は 2 × 2 パウリ行列である。
そのため 彼らは 相対論的なディラック方程式は 量子力学的な スピン を含んでいると主張している。
ディラック方程式は 電子。陽電子、ニュートリノ、クォークなどのすべてのフェルミ粒子を表すため、場の量子論の中で 最も影響力のあるものである。
量子電磁力学 ( QED )、標準模型、ひも理論などは もちろん このディラック方程式に依存している。
Eq.0-3 の ディラックの波動関数 (= φ ) は 次のように表せる。
(Eq.0-6)

クライン・ゴルドンのように、Eq.0-6 の積分範囲は 無限大であり 発散する。
また 演算子 "c" と "d" は それぞれ 粒子と反粒子を意味する。
後で説明するが、正の演算子を得るために、"c" や "d" の演算子は 反交換の関係式を満たさなければならない。
そのため 彼らは ディラック方程式は パウリの排他原理のミステリアスな力を表していると主張しているのである。
反交換の性質のため、2つの同じ演算子は Fig.3 に示すようにゼロになる。
( しかし残念ながら、ここには まったく物理的なイメージがない。)
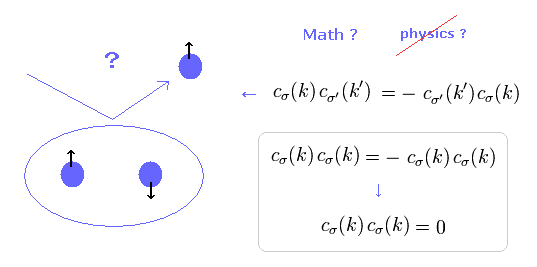
反交換関係は ひも理論にも使用されている。
Eq.0-6 に見られるように、この抽象的な単なる数式記号のみから パウリの排他原理の 本当の姿形を知ることはできない。
つまり 例え ひも理論を学んでも、ミステリアスなパウリの排他原理が何なのか 知ることはできない。
スピンエレクトロニクスや 物性物理学の分野では ほぼ無限の 学術論文がある。
しかし その中に "スピンそのもの"はいったい何か を説明した論文は 1つもない。これだけ世界の科学技術が発達した今でさえ分からないとは 奇妙としか言いようがない。
このパウリの排他原理とシュレディンガーの波動関数が 何なのか 謎のままなために、
現在の 量子化学 は 実際に役にたたず、単なる数学上の産物と化している。
(Eq.0-7) ディラックのラグランジアン + 光子 → QED。
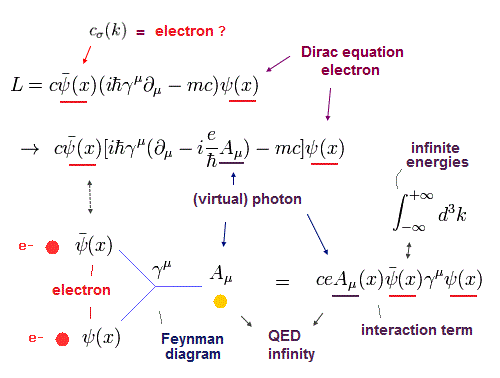
後で説明するが、古典的なローレンツ力を考慮すると、ディラックのラグランジアンの運動量演算子を変換する必要がある ( Eq.0-7 )。
Eq.0-7 のベクトルポテンシャル "A" が "光子" を意味している。
ここから 光子とフェルミ粒子間の 相互作用項を得て、それが 量子電磁力学 (QED) や ゲージ理論に使用されている。
また 相対論的な制限は 厳しすぎるために、この非常に抽象的な単なる数式が 唯一の相互作用となる。
( あなたがたは この単なる数学上の記号から "光子の真の姿" などを思い浮かべることができるだろうか? )
(Eq.0-8) 弱い力の相互作用。

量子電子力学では、無限大の値を 人為的に 粒子の電荷や質量の中に組み込んでしまう。
( つまり 裸の電荷や質量は 無限大ということになる。)
Eq.0-8 は W ボソンとフェルミ粒子の相互作用を表している ( このページも参照のこと。 )
この W ボソンに質量がないと、それは Eq.0-7 の光子の相互作用に似た形となる。
結果的に 弱い力も繰り込み可能となる。
しかし、あなたがたは 本当に 無限大の裸の電荷や質量が実在すると思われるだろうか?
もっとも重要な点は QED, 標準模型、ひも理論などの現在の場の量子論には 私たちが期待しているような 具体的でクリアなイメージがまったくないということである。
静止した 1つの電子 (= p ) が 1つの光子 (= q ) を吸収して p' の電子になったとする。
(Fig.4)
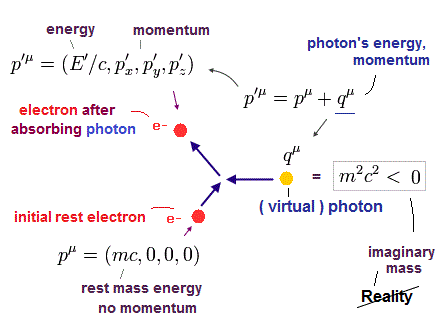
静止した電子 (= p ) のエネルギーは 単に 静止エネルギー ( E/c = mc ) だけである。
( 静止した この電子の運動量はゼロである。)
光子を吸収した後の電子 (= p' ) には運動量がある。
Eq.0-1 に示したように 光子との相互作用の前と後の電子は エネルギーと運動量の関係式を満たす必要がある。
(Eq.0-9)
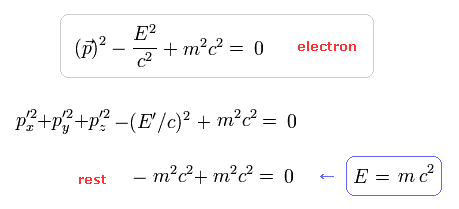
Fig.4 と エネルギー、運動量の保存より、光子のエネルギーと運動量は
(Eq.0-10)
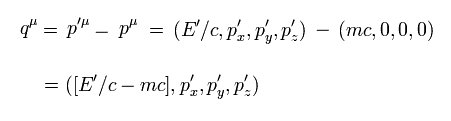
ご存じのとおり、光子の質量は ゼロである。しかし Eq.0-10 と Eq.0-9 より、
(Eq.0-11)

Eq.0-11 は この光子の質量が 虚数であることを意味している。
なぜなら Eq.0-11 のエネルギー、運動量の式は ゼロ以下 になる必要があるからである。
(Eq.0-12)
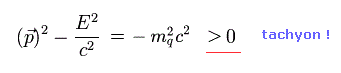
Eq.0-11 は この光子が 相対論に反する タキオンであることを示している。
この事実にも関わらず、彼らは このタキオン様の粒子を加速器や QED で頻繁に使用している。
結果的に 相対論的な場の量子論は 自己矛盾を含んでいることになる。
エネルギーと時間の不確定性原理により、短い時間ならこのタキオンが許されることになっているが、本当にこの矛盾した粒子が実在すると思われるだろうか?
最近の実験によれば 陽子のサイズが QEDの計算値より 4 % ほど小さいことがわかった。
(Pohl, R. et. al. Nature 466, 213-216 (2010).)
もしこの結果が本当なら QED 自体が間違いということになる。
(Fig.5) ローレンツ変換不変なスカラー。
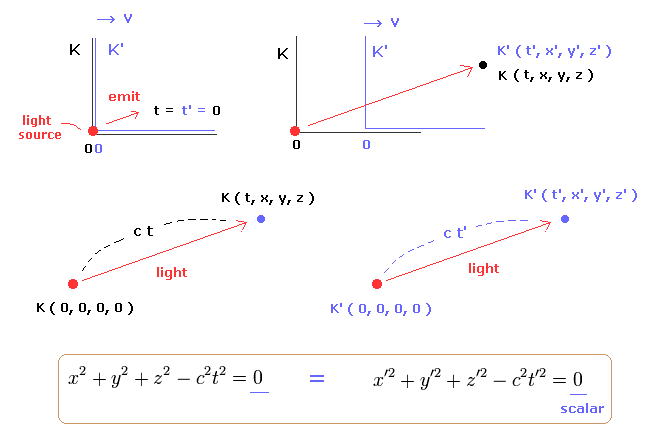
Fig.5 では、光が 原点 ( x=x'=0、t=t'=0 ) から 放射されて、しばらくした後 K 系 と 動いている K' 系 の各慣性系で t と t' に同時に検出した。
特殊相対論によれば、すべての慣性系で そのスピードは必ず "c" にならなければならない。
つまり、Fig.5 の最後の行の式は すべての慣性系で変化しない。
この式を "ローレンツ変換不変なスカラー" と呼ぶ。
相対論的な場の量子論では、作用 S ( もしくはラグランジアン ) の不変性からスタートして 運動方程式を得る。
つまり ローレンツ変換不変な 作用 ( もしくは ラグランジアン ) は 相対論にとって 最も重要な概念である。
(Eq.1-1) 4元ベクトル。
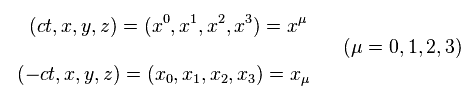
Fig.5 の式のような スカラー値を表すには Eq.1-1 のような 4元ベクトルを定義すると便利である。
Eq.1-1 では、添え字 μ が 下の位置にあるとき (= xμ )、ゼロ成分の "ct" のみ 負になる ( x0 = - ct ).
他の成分 ( μ = 1, 2, 3 ) は 添え字の位置によって その符号を変えない。
(Eq.1-1')
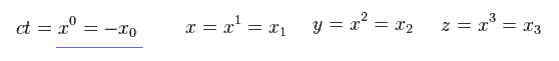
この表記法は ( -1, 1, 1, 1 ) バージョンの計量テンソルと呼ばれる。
(+1, -1, -1, -1) バージョンに変更したいときは、 付録を参照のこと。)
Eq.1-1 を用いて、Fig.5 の式は 次のように表される。
(Eq.1-2)
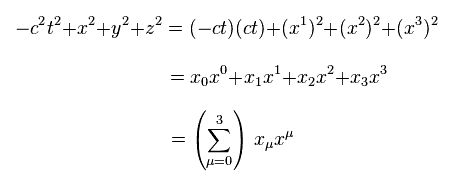
Eq.1-2 の表記法は 相対論的な理論で頻繁に使用される。
このスカラーは 添え字が下と上にある変数の組み合わせで表現される。
同じ項に 同一の変数 (= 例えば μ ) が使用されるとき、μ = 0, 1, 2, 3 の項をすべて足し合わせることを意味する。
( Σ の記号が省かれても 同じ意味である。)
次のような ミンコフスキー計量テンソルを定義する。
(Eq.1-3)
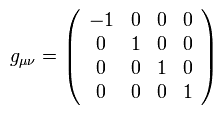
Eq.1-1 の4元ベクトルにおいて この計量テンソルを使うと、添え字の位置を次のように変更できる ( xμ → xμ )。
(Eq.1-4)
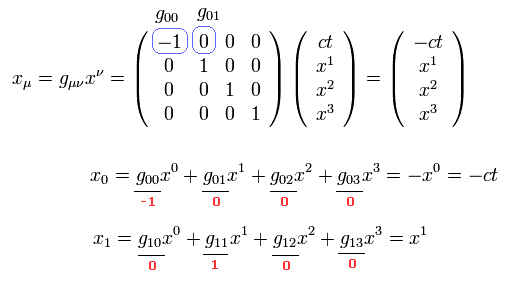
Eq.1-4 では、 "ν" が 1つの項で2回使われているので、これに関して ν = 0, 1, 2, 3 の項を足し合わせることを意味する。
Eq.1-4 の関係を用いて、Eq.1-2 のスカラーの式を次のように表せる。
(Eq.1-5)
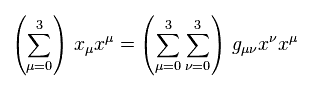
特殊相対論によれば、相対論的な運動量は 4元運動量として変化する。
(Eq.1-6)
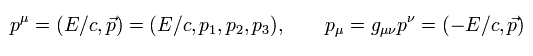
Eq.1-6 を用いて、Fig.2 の ローレンツ変換不変な エネルギー・運動量の関係式は 次のように表せる。
(Eq.1-7)
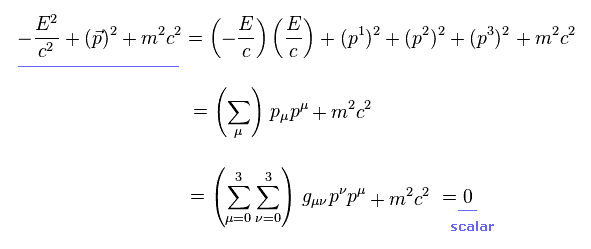
次に 微分について説明する。
空間座標 ( i = 1, 2, 3 ) の 偏微分 は、
(Eq.1-8)
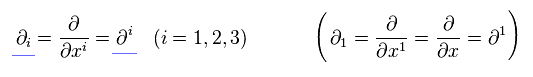
空間微分の符号は 添え字の位置で変化しない。
ゼロ成分 (= 時間 ) の偏微分は、
(Eq.1-9)
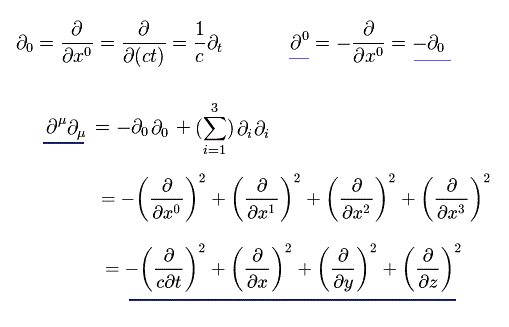
ここで x0 = "ct" である。
Eq.1-1 と異なり、添え字 " 0 " が 上部の位置にあるとき、
時間微分は 負になる。
なぜなら 通常の微分は このページに示したように 共変ベクトルだからである。
( このページでは 単にルールとして覚えておくだけでいい。 )
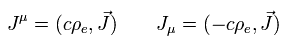
ここで ρe は "電荷密度"、 J は 電流密度である。
Eq.1-10 は ρe と J が ローレンツ変換のもとで 時空間変数 ( t, x, y, z ) のように変化することを示している。
(Eq.1-10')
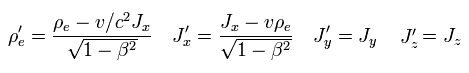
Eq.1-10 の定義は 相対論的なローレンツ力と 電流、電荷密度の関係の維持にとって 必要不可欠なものである。
しかし このページに示したように Eq.1-10 は 観測者の超能力を生じさせてしまう。
Eq.1-10 の4元電流は 4元ベクトルポテンシャル ( A ) と調和して変化する必要がある。
もちろん、これらの定義は 相対論とマクスウェル方程式の融合のために "人為的"に導入されたものである。
相対論的な場の量子論では、ラグランジアンが最も重要な概念である。
ラグランジアンから クライン・ゴルドン や ディラック方程式などの重要な式が得られる。
( ラグランジアンがすべてと言っていい。)
(Fig.6) 古典力学と場の量子論のラグランジアン。
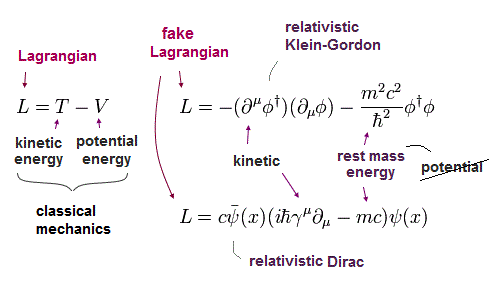
Fig.6 の左が 古典力学のラグランジアン ( L = 運動エネルギー T - 位置エネルギー V )。
Fig.6 右は クライン・ゴルドンのラグランジアンで 古典力学よりも 物理的な意味が少ないといっていい。
このラグランジアンの形式は クライン・ゴルドン方程式を得る目的のみのために 決められたと言っていい。
クライン・ゴルドン方程式のように、このラグランジアンもローレンツ変換不変なスカラーになる必要がある。
(Fig.7) オイラー・ラグランジュ → 運動方程式。

古典力学では、作用 S が ある座標変換のもとで 不変のとき、ラグランジアンは オイラー・ラグランジュ方程式を通して 運動方程式を与える。
場の量子論でも 同じロジックが使用されている。
違いは 場の量子論では 場の演算子 ( φ ) などで ラグランジアンを微分するため、μ = 0, 1, 2, 3 の成分による導関数を含んでいる点である。
(Fig.8) 正準運動量 → ハミルトニアン。

ハミルトニアンは 古典力学における 全エネルギーであり、ルシャンドル変換と正準運動量から得られる (Fig.8)。
同じ方法論が 場の量子論でも使用される (= Fig.8 下部 )。
古典力学では、ラグランジアンは 運動エネルギー T と 位置エネルギー V を使って 次のように表す。
(Eq.1-11)
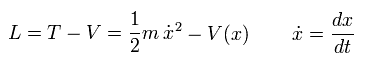
ここで ”点”は時間微分を意味している。
ラグランジアンは 運動方程式と そのハミルトニアン (= エネルギー ) を得るための 道具である。
相対論的な場の量子論も このラグランジアン形式に完全に依存しているが こちらの場合は 正準運動量などのそれぞれの実態がよく分かっていないのに信じきっている感がある。
彼らは ラグランジアンと その関連する数式を この現実世界の物体と いちいち関連させることなく 淡々と数学のみ進めようとしているようである。
Eq.1-11 の ラグランジアン (L) を 次の オイラー - ラグランジュ方程式 に代入する。
(Eq.1-12)
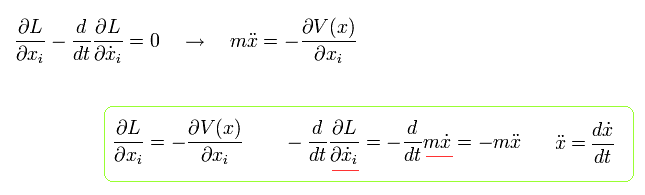
すると、 運動方程式を得ることができる。
ところで、どうやって、上の オイラー - ラグランジュ方程式を得ることができるのだろうか?
ラグランジアンの時間積分は 作用 と呼ばれ、 S と表す。
(Eq.1-13)
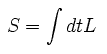
場の量子論では ラグランジアン密度が主要なツールのため、この作用は 時空間すべて (= d4x ) で積分する必要がある。
作用 S が 定常状態 のとき、 その 一次の変化
(Eq.1-14)
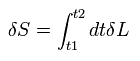
は ゼロにならなければならない。
相対論的な場の量子論では 作用の不変性に ローレンツ変換不変性が含まれている必要がある。
q と q の時間微分 による変分を考慮して、Eq.1-14 は 次のように表せる。
(Eq.1-15)
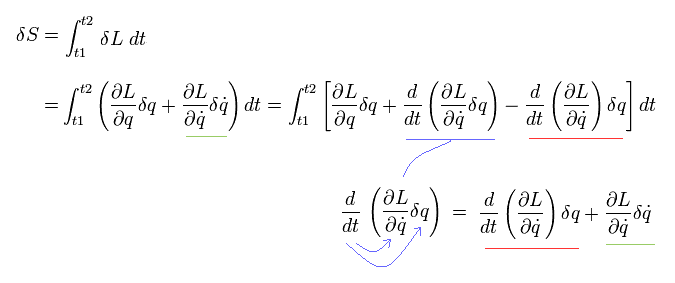
ここで
(Eq.1-16)
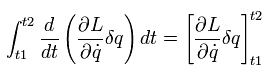
q は 一般化座標である。
作用の末端 ( t1 と t2 ) は 固定されているとする。 すると Eq.1-16 は 次のように ゼロになる。
(Eq.1-17)
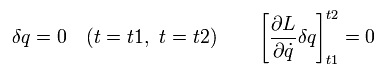
結果として、作用の変化 (= Eq.1-14 ) がゼロのとき、次の条件が満たされる。
(Eq.1-18)
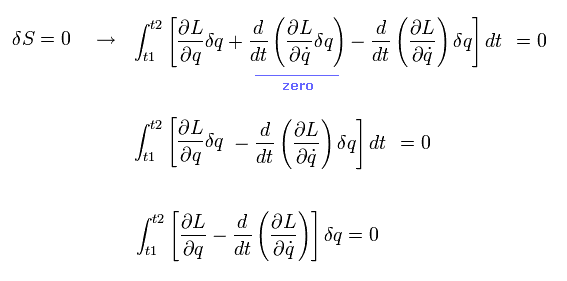
最終的に、次の オイラー・ラグランジュ方程式が得られる。
(Eq.1-19)
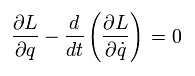
場の量子論では ある場の演算子 ( 例えば φ ) に関して 次のように変分を行う。
(Eq.1-20)
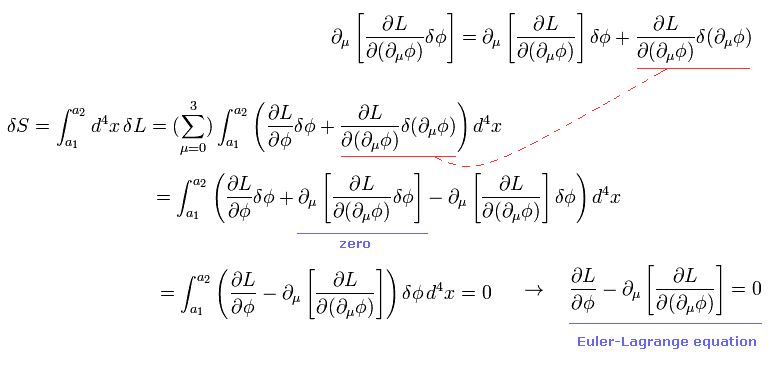
場の量子論の演算子 φ は xμ = ( ct, x, y, z ) すべての関数であるため、これらに関する導関数の変分も考慮している。
Eq.1-16、Eq.1-17 のように 端点 ( a1 と a2 ) において δφ = 0 と仮定しているため 2行目の全微分の項はゼロになる。
ラグランジアンから ルシャンドル変換を通して ハミルトニアン (= 全エネルギー ) の式を得る手法は 相対論的な場の量子論の 最も重要な方法の一つである。
古典力学と場の量子論の 最も大きな違いは 場の量子論の方には 物理的な実態が乏しいことである。
そのため 単なるルールとして 受け入れるしかない。
ラグランジアンでは、 正準運動量 (= p ) は 次のように定義される。
(Eq.1-21)
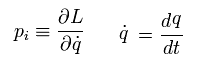
ハミルトニアン (= 全エネルギー ) は ラグランジアンの ルジャンドル変換によって求まる。
(Eq.1-22)
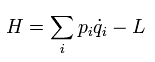
ラグランジアンが Eq.1-11 (= 古典力学 ) とき、 ハミルトニアンは、
(Eq.1-23)

よって、次の古典的なハミルトニアン (= 運動エネルギー + 位置エネルギー ) を得ることができる。
(Eq.1-24)
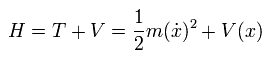
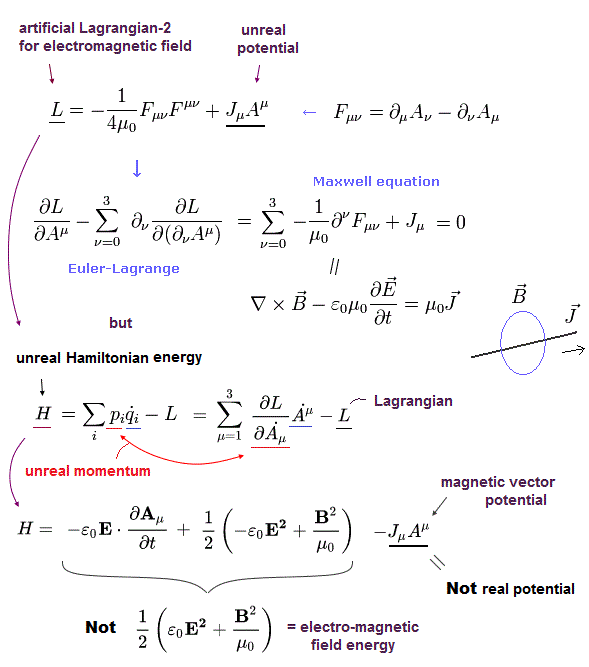
(Fig.9) ローレンツ力 → QED の相互作用項?
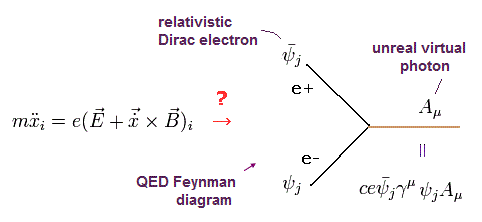
量子電磁力学 (QED) や 標準模型では、粒子+(反)粒子+光子 間の 相互作用項 は ファインマンダイアグラムなどで 最も重要な概念である。
この相互作用項は 古典的なローレンツ力 (ラグランジアン) が基になっている。
しかし 上で述べた通り、この相互作用項は 特殊相対論に反する "仮想"光子を生じさせてしまう。
(Fig.10) 概要。

最初に オイラー・ラグランジュ方程式を介して ローレンツ力を得るラグランジアンを見つける。
2番目に 通常の正準運動量の定義を用いて、ラグランジアンから ハミルトニアンを得る。
3番目に 外電磁場によって 各運動量とエネルギーの演算子が変化することから ハミルトニアンにおける 置き換えを見つける。
この置き換えは ディラック方程式にも使用され QED における光子との相互作用を生じる。
電荷 ( e > 0 ) が 外電場 (E) と 外磁場 (B) の中を運動しているとき、 運動方程式 は、
(Eq.2-1)
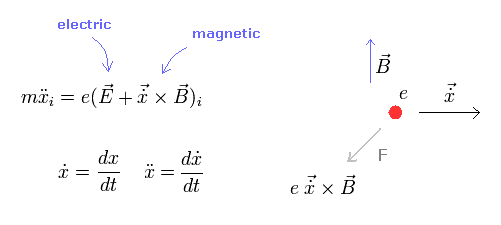
この力は "ローレンツ力" と呼ばれている。
4元電流密度のように "4元ベクトルポテンシャル" を用いる。
(Eq.2-2)
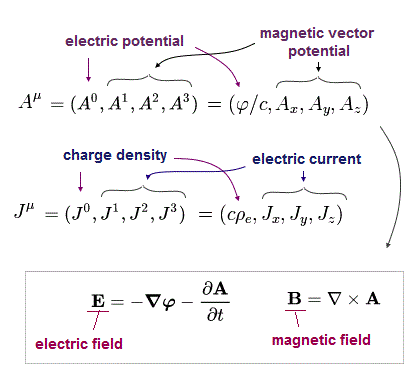
Eq.2-2 では、 "A" は、 " ベクトルポテンシャル " で、 φ は " スカラーポテンシャル " である。
"4元ベクトル" は ローレンツ変換のもとで 時空間 ( ct, x, y, z ) のように変換することを意味する。
(Eq.2-2') ローレンツ変換。

歴史的観点からみると、これらの 人為的な定義は 特殊相対論とマクスウェル方程式の融合のために 導入されたと言っていい。
なぜなら ご存じのとおり、電磁波の速度 "c" は マクスウェルの方程式で示せるが、それは すべての慣性系で 必ず "c" でなければならないからである。
つまり マクスウェル方程式と 相対論の間の矛盾は 相対論そのものの破綻を意味する。( このページも参照のこと。)
Eq.2-3 の φ と A は それぞれ スカラー (クーロン) ポテンシャル、ベクトル (磁気) ポテンシャルである。
これらのベクトルポテンシャルとスカラーポテンシャルを用いて、電場 (E) と 磁場 (B) は次のように表せる。
(Eq.2-3)
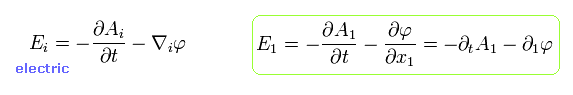
(Eq.2-4)
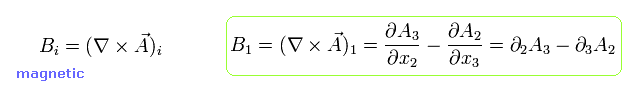
これらの人為的な定義は 相対論とマクスウェル方程式の融合のために導入された。
( 率直に言えば、相対論のために ベクトルポテンシャル "A" が導入されたと言っていい。)
Eq.2-1 のローレンツ力を得るためのラグランジアンは 次のようになることが知られている。
(Eq.2-5)
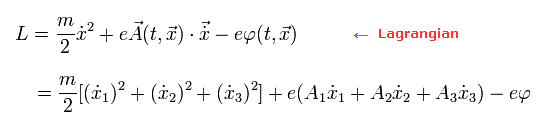
最初に、運動の x (= 1 ) 成分のみを考えることにする。
Eq.2-5 の L を Eq.1-19 の オイラー・ラグランジュ 方程式に代入する。
(Eq.1-19)
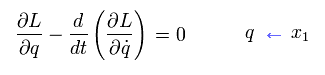
その最初の項は、
(Eq.2-6)
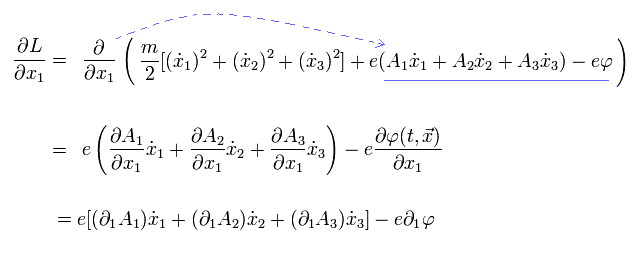
ここで、 A や φ は、時間と空間座標の関数であることに注意。
Eq.1-19 の 2番目の項は、
(Eq.2-7)
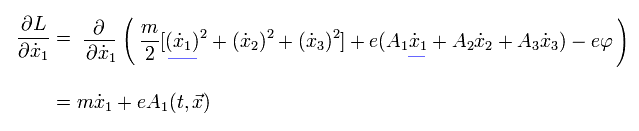
さらに、
(Eq.2-8)
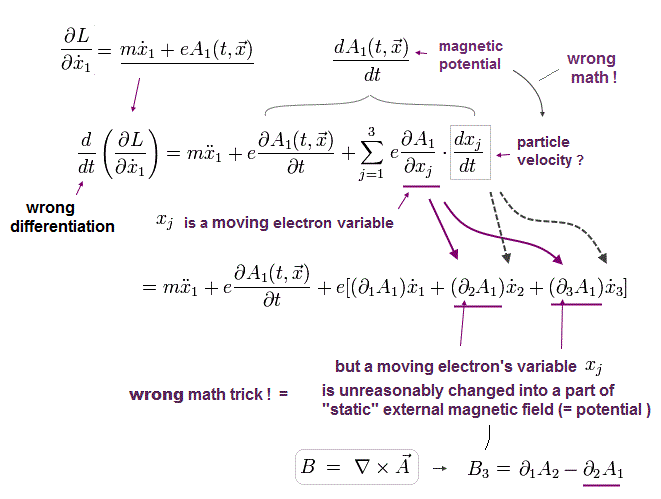
Eq.2-8 は t に関しては 偏微分ではないことに注意 (全微分である)。
そのため、A の中の 空間座標 ( xj ) にも 時間 t が含まれる ことも考慮しなければならない。
なぜなら 動いている粒子の存在地点の ベクトルポテンシャル が 関係しているからである。
Eq.2-6 と Eq.2-8 から、 ローレンツ力 の オイラー・ラグランジュ方程式は、
(Eq.2-9)

次に、 Eq.2-9 が ローレンツ力の関係式 (= Eq.2-1 ) を意味していることを示すことにする。
Eq.2-3 と Eq.2-4 を Eq.2-1 に代入して、
(Eq.2-10)

Eq.2-10 は Eq.2-9 と ちょうど同じである。
よって、Eq.2-5 が ローレンツ力の ラグランジアンであることを証明することができた。
Eq.1-21 を使って、 正準運動量 (= p ) は、
(Eq.2-11)

これは Eq.2-7 に等しい。
Eq.1-22 から、ローレンツ力の ハミルトニアンは、
(Eq.2-12)
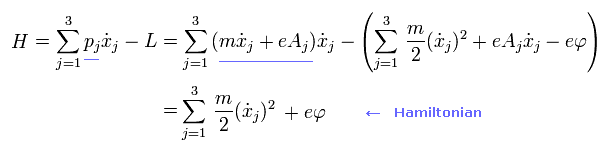
つまり、磁気力 (= ベクトルポテンシャル) は 全エネルギーに寄与していないことがわかる。
また Eq.2-12 の 運動量は、Eq.2-11 の正準運動量を使って、次のように表せる。
(Eq.2-13)
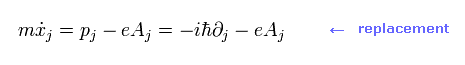
つまり、正準運動量 (= p ) は 荷電粒子の ド・ブロイ波 を意味している。
(これに関しては、もう少し議論が必要かもしれない・・。)
つまり ローレンツ力を考慮した場の量子論では 次の重要な置き換えを用いる。
(Eq.2-16)

運動量とハミルトニアン内の Eq.2-16 の置き換えは 量子電磁力学 (QED) と ゲージ理論にとって 最も重要な概念である。
ベクトルポテンシャル A が ローレンツ変換のもとで 4元ベクトルのように変換すると、この置き換えが クライン・ゴルドン方程式でも使用できる。
( Eq.2-16 は 古典的極限と言える。)
このベクトルポテンシャルの変換は 4元電流密度の変換にリンクしている。
そのため もし 4元電流が間違いだと、QED における この置き換えも間違いということになる。
Eq.5-46 に示したように、ディラックのラグランジアンは この置き換えを QED のために使用している。
しかし ディラックのラグランジアンは 1次であり、通常の電流と一致しない。これは後で説明する。
(Fig.11) 概要。
マクスウェル方程式においても、最初に オイラーラグランジュ方程式を通じて マクスウェル方程式を与える ラグランジアンをみつける。
Eq.2-2、Eq.2-3、Eq.2-4 に示したように、彼らは 人為的に 4元ベクトルポテンシャルのような 特殊相対論に一致する新しい概念を導入した。
そのため 通常のマクスウェル方程式を ベクトルポテンシャル "A" を用いて表す必要がある。
最初に 次のような 反対称テンソル ( F
(Eq.3-1)
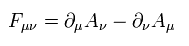
ここで、 A は ベクトル ( スカラー ) ポテンシャルを意味する。
マクスウェル方程式を与える ラグランジアン は 次のように定義される。
(Eq.3-2)
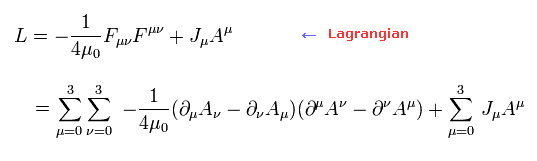
μ0 は 真空の透磁率である。
上で述べたように、ここでは μ と ν の両方ともにおいて 0, 1, 2, 3 成分の合計 をしなければならない。
なぜなら、両方とも 1項に2つの文字が使われているからである。
また Eq.3-2 は μ と ν において 上下の添え字の組み合わせのため スカラー形式になっている。
Eq.3-2 のラグランジアンを 次の オイラー・ラグランジュ方程式に代入すると 通常のマクスウェル方程式を ベクトルポテンシャル形式で得ることができる ( Eq.1-20 も参照のこと。)
(Eq.3-3)
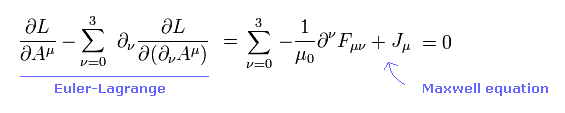
すると 通常のマクスウェル方程式が得られる。
( E と B 場を A と φ に置き換えれば これが 通常のマクスウェル方程式であることを 示すことができる。)
ここで Eq.3-3 の詳細な計算方法について説明することにする。
μ = 1 のケースでは、Eq.3-2 のラグランジアンを用いて、Eq.3-3 のオイラー・ラグランジュ方程式の最初の項は、
(Eq.3-4)
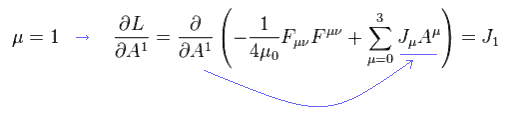
A1 の微分は 2番目の項にのみ作用する。
ここで Eq.3-3 で ν =2 ( μ = 1 ) のケースについて考える。
このケースでは F12 と F21 の2つの F が関係している。
つまり Eq.3-3 のオイラー・ラグランジュ方程式の2番目の項は
(Eq.3-5)
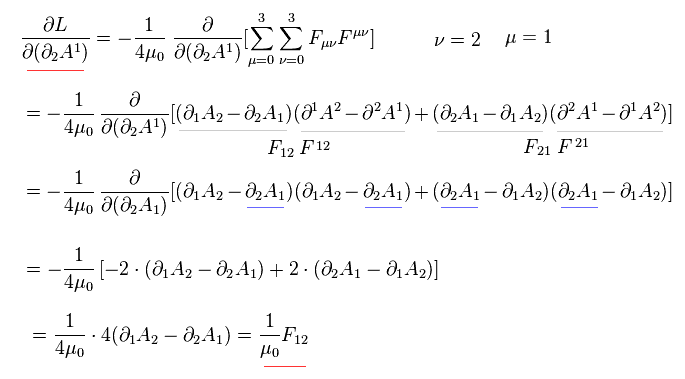
ここでは次を使っている。
(Eq.3-6)
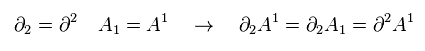
Eq.1-1 と Eq.1-8 に示したように、1、2、3 の成分は 添え字の上下の位置によって 符号を変えない。
添え字の位置に関しては ゼロ成分のみ注意すればいい。
例えば、μ = 1、 ν = 0 のとき、 F10 と F01 が関係しているので Eq.3-3 の2番目の項は
(Eq.3-7)
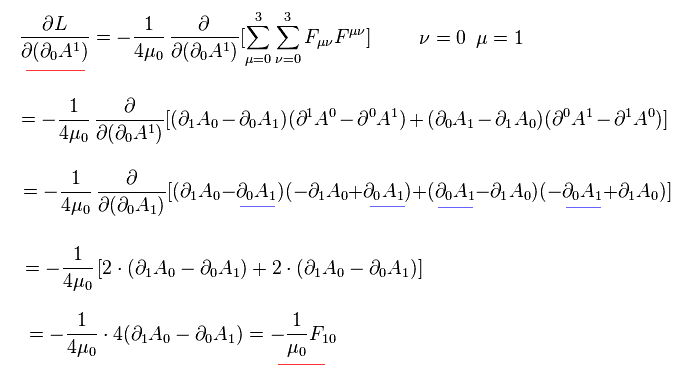
ここで次を使っている。
(Eq.3-8)
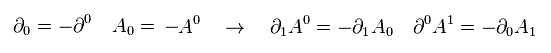
Eq.3-8 の符号は Eq.3-5 の結果の反対である。
しかし Eq.3-8 より、最終の微分形式は Eq.3-3 と同じになる。
(Eq.3-9)
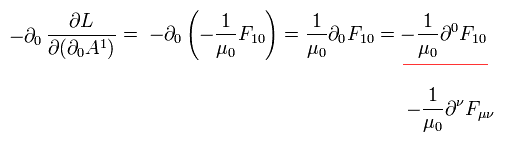
結果的に すべてのケースで 同じ形のマクスウェル方程式を得ることができた。
Eq.2-4 によれば、磁場 B は 次のように表せる ( F を用いて )
(Eq.3-10)
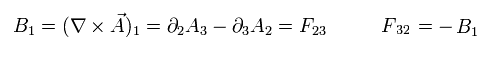
Eq.2-3 によれば、電場 E は
(Eq.3-11)
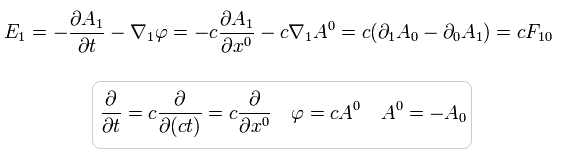
ここで A0 = - A0 = φ/c である ( Eq.2-2 )。
( 上で述べたように、これらの人為的な定義は 相対論とマクスウェル方程式の融合のためである。)
Fμ ν を Eq.3-10 と Eq.3-11 のように 電磁場で置き換えると、Eq.3-3 が 通常のマクスウェル方程式であることを示せる。
例えば、 Eq.3-3 で μ = 1 のとき、
(Eq.3-12)
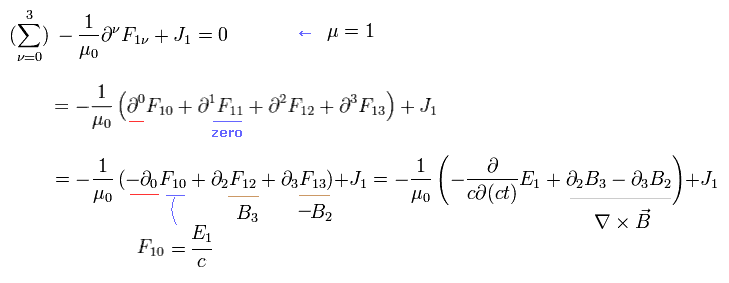
F11 は Eq.3-1 より ゼロである。
Eq.3-12 は 次のマクスウェル方程式に等しい。
(Eq.3-13)
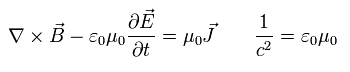
同じように μ = 0 のとき、
(Eq.3-14)

ここで J0 = -J0 = cρe. ( Eq.1-10 を参照のこと )。
このページ示したように、4元ベクトルの定義は 触れずして電荷をテレポートする 超能力を生じさせる。
次に Eq.3-3 の計算について 少し説明する。
上で述べたように Eq.3-2 の 2つの F は、
(Eq.3-15)
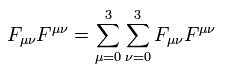
次のケースのとき、
(Eq.3-16)
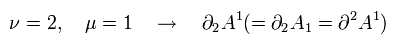
Eq.3-2 (Eq.3-15) を Eq.3-16 で微分すると、
(Eq.3-17)
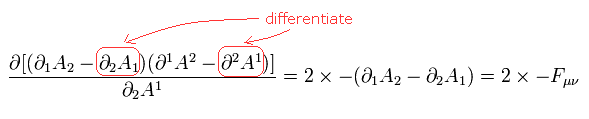
Eq.3-15 を考慮すると、 次も計算する必要がある。
(Eq.3-18)
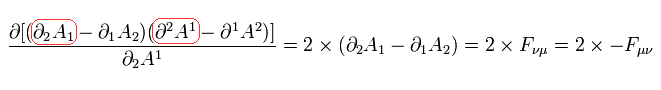
Eq.3-17 と Eq.3-18 を合計すると、Eq.3-2 の 1/4 の係数が Eq.3-3 では 消えることになる。
ゼロ成分を扱うときは 符号と添え字の位置に留意する必要がある。
このページに示したように、 相対性理論は 次の式を満足する。
(Eq.4-1)
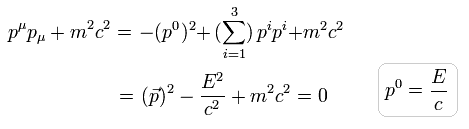
ここでは ( -1, 1, 1, 1 ) バージョンの計量テンソルを使用している。
量子力学では、エネルギー (E) と 運動量 (p) は 次の演算子で置き換えられる。
(Eq.4-2)
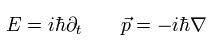
Eq.4-2 の運動量は ドブロイの関係式である。
Eq.4-2 を用いると、 Eq.4-1 は 次のように表せる。
(Eq.4-3)

ここでは ∂0 = - ∂0 と ∂i = ∂i ( i = 1, 2, 3 ) である。
Eq.4-3 は クライン・ゴルドン方程式と呼ばれる。
ここでは φ(x) は ローレンツスカラー場 (= クライン - ゴルドン 場 ) と呼ばれる。
クライン・ゴルドン場は ヒッグス粒子を表す。 ( 他の粒子は 光子を除けば すべてディラック場である。)
(Fig.12) クライン・ゴルドン場の概観。
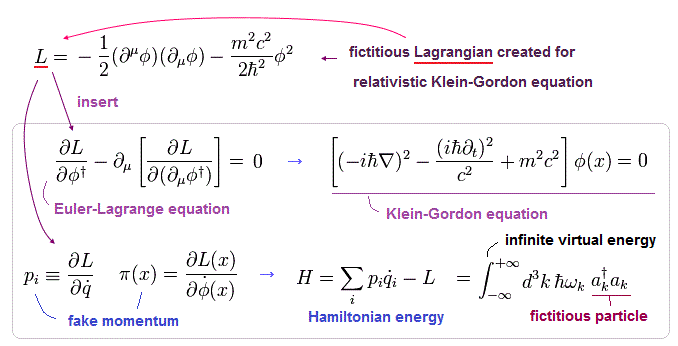
Fig.12 は クライン・ゴルドン場の 全体の流れを示したものである。
相対論的な場の量子論では、基本的なツールは ラグランジアン、オイラーラグランジュ方程式、正準運動量、ハミルトニアンである。
場 φ(x) は Eq.4-3 を満たす。 そのため 次のように表せる。
(Eq.4-4)
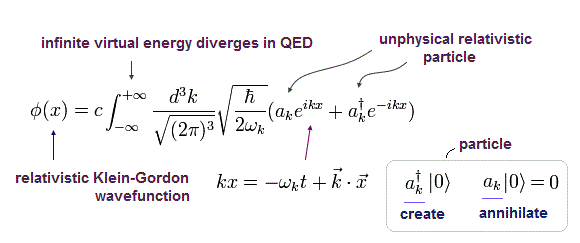
ここでは、
(Eq.4-5)
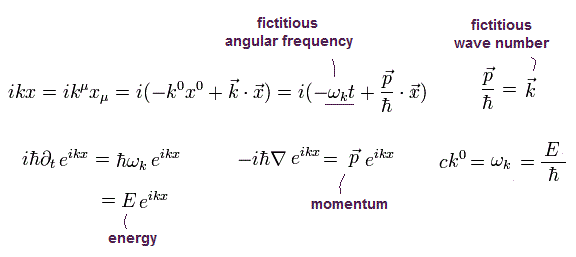
かつ
(Eq.4-6)
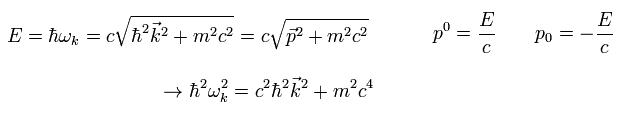
これは Eq.4-1 に等しい。
Eq.4-4 では、ローレンツ不変性を保つために 1つの粒子は全空間に 同時に 生成(もしくは消滅)する。
また Eq.4-4 には あらゆる 運動量とエネルギー ( -∞ から + ∞ ) を持つ 無限の 粒子が存在する。
つまり、場の量子論は はっきりいって 現実の世界を表していない。
また Eq.4-4 の 係数 ω は ローレンツ変換不変のためと、エネルギー値の導出にとって 重要である。
ご存じのとおり、波の速度は 振動数 f ×;波長 λ ( v = fλ ) で与えられる。
そのため この波動関数の速度は
( Fig.T-1 )
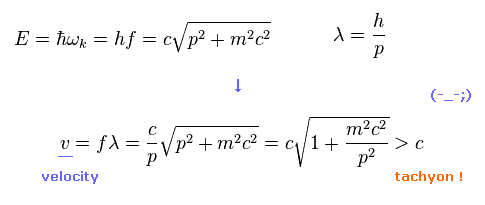
このスピードは 超光速である。
この理不尽な波動関数は 式のローレンツ変換不変性の要請から生じたものである。
皮肉にも 相対論的な制限が 想像上の粒子 "タキオン" を生じさせてしまったのである。
ディラック方程式で 正と負のエネルギー解を融合させれば、タキオンは消えると 彼らは主張しているが、電子と陽電子のそれぞれは 超光速であることに変わりはない。
Eq.4-7 から Eq.4-11 の式は このページに移動しました。
(Eq.4-11)
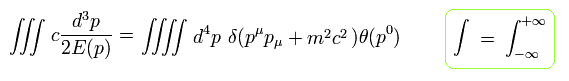
ここで θ は "階段関数" を意味する。
Eq.4-11 は 伝播関数の係数が d4p 積分を含み、積分範囲が マイナス無限大から無限大なため、ローレンツ変換不変である。
しかし このことが深刻な発散問題を引き起こす。
ハミルトニアンを得るためのラグランジアンは 次のように定義できる。
(Eq.4-12)

ここで "点" は 時間微分を意味する。
Eq.4-12 を Eq.1-20 のオイラー・ラグランジュ方程式に代入すると、クライン・ゴルドン方程式を得ることができる。
(Eq.4-13)

Eq.4-12 と Eq.1-21 の定義より、正準運動量は、
(Eq.4-14)

Eq.1-22 より、 クライン・ゴルドン場の ハミルトニアン (密度) は、
(Eq.4-15)
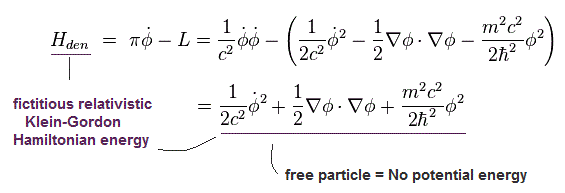
Eq.4-4 を Eq.4-15 に代入して 全空間で積分すると、ハミルトニアンを得ることができる。
(Eq.4-16)

場の量子論は Eq.4-16 に示すように 単なる 抽象的な 数式記号であることに留意しておく必要がある。
Eq.4-16 では a†a は 数演算子 (= N ) を意味する。
数演算子の 生成消滅演算子の順序が 非常に重要であり、ディラック方程式では これがパウリの排他原理に関係している。
最初に Eq.4-4 のスカラーの波動関数を Eq.4-15 の φ2 に代入する。
k と k' ( -∞ から +∞ の範囲 ) の各運動量は 2つの φ2 において 互いに独立していることに注意する。
そのため次を用いる。
(Eq.4-17)
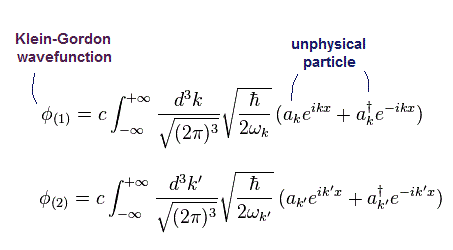
Eq.4-17 を用いて、 φ2 は、
(Eq.4-18)

ここで次を使う。
(Eq.4-19)
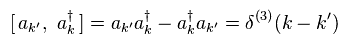
Eq.4-19 は スカラー場の 交換関係を表している。
後で説明するが、この交換関係は 正準運動量と場の演算子の間の ドブロイの関係式にとって 必要である。
Eq.4-18 の最後の行で、k と k' を交換して もう1つの項と融合させている。
Eq.4-18 の最初の項を 空間積分すると、
(Eq.4-20)
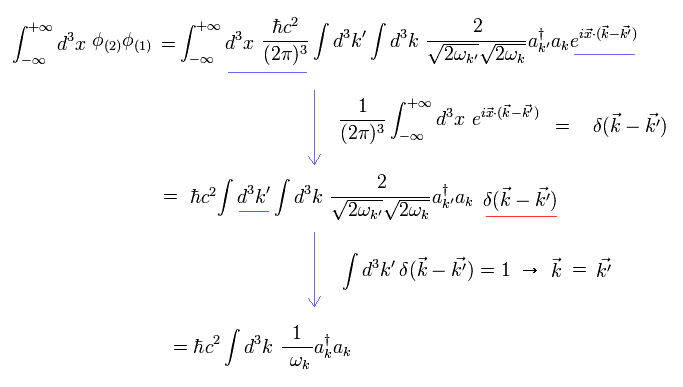
ここでは デルタ関数の公式を用いている。
Eq.4-5 の定義から
(Eq.4-21)
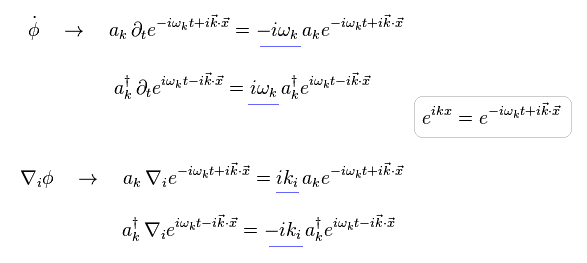
Eq.4-15、 Eq.4-20、 Eq.4-21 から、 ハミルトニアンは、
(Eq.4-22)
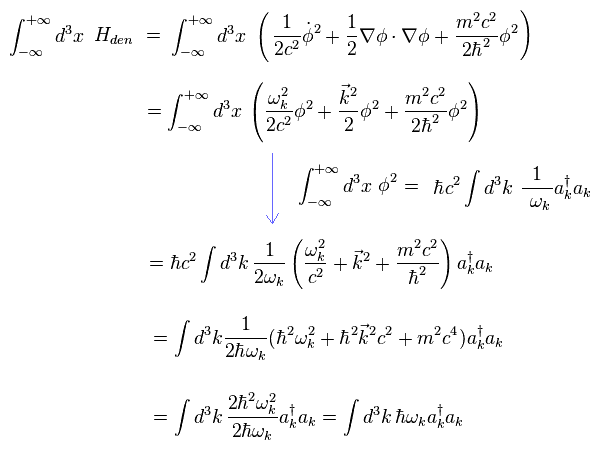
Eq.4-22 の最後から2番目の行で、次の関係式を用いる。
(Eq.4-6)
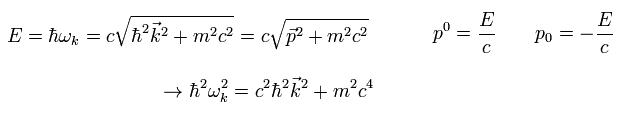
結果的に Eq.4-18 のデルタ関数を付加すると、次のクライン・ゴルドンのハミルトニアンを得ることができる。
(Eq.4-23)

Eq.4-23 の最後の項は 発散項である。
しかし 場の量子論はこの項を無視 ( もしくは 超対称性で除去 ) している。
これらの発散項は 相対論的な場の量子論が ローレンツ対称性をキープするために あらゆる種類の運動量を含むことに起因している。
Eq.4-19 が満たされるとき、 Eq.4-4 と その 正準運動量 (Eq.4-14) は 次の 交換関係を満たす。
(Eq.4-24)
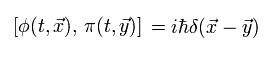
Eq.4-24 は 少し長い計算によって確かめられる。
ご存じのとおり、有名な Eq.4-24 の交換関係は、 次の ド・ブロイの関係式 からきている。
(Eq.4-25)

もちろん、電子を含む いろんな粒子は ド・ブロイの関係式を満たすことが知られている。
しかし、ディラック方程式の "反交換関係" は この基本的なルール (= ド・ブロイの関係式 ) を 電子においても破っている。
( これは 後で、説明することにする。)
ここでは 手短に 因果律の破れについて述べる。
基本的に 伝播関数は 粒子と反粒子の2つのプロセス を含んでいる。
もし、そのうちの 粒子のみの伝播を考慮すると、
(Eq.4-26)
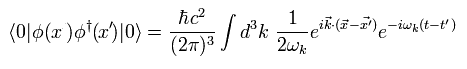
ここで 同時刻 ( t = t' ) のときを考える。
Eq.4-26 が ωk を 係数として含まないとすると、 Eq.4-26 は 次のように デルタ関数になる。
(Eq.4-27)
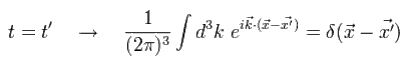
Eq.4-27 は、x が x' と異なるとき、 Eq.4-27 がゼロになることを意味する。
つまり、 Eq.4-27 は 相対論的因果律を満足する。
しかし、Eq.4-26 は ωk を 係数として含む。
そのため、Eq.4-26 の計算結果は、
(Eq.4-28)
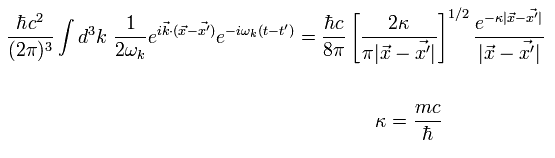
Eq.4-28 は 次のような空間的な領域においても ゼロにならない。
(Eq.4-29)

つまり、相対論的な場の量子論 (QFT) によれば、 粒子は 光速度を超えているのである。 それが相対性理論を使っているのにも関わらずだ。
これは 明らかに 自己矛盾である。
しかし、もし 粒子と反粒子の 両方向 の伝播を考慮すると、 これは因果律を満足する。
そのことにより、量子力学の物理学者達は満足しているのである。
( あなたたちは どう思われるだろうか ? )
クライン・ゴルドン場は π 中間子 や ヒッグス 粒子を表す。
お気づきのとおり、これらの粒子には 何の具体的なイメージも 存在しない。
ディラック場は最も重要である。なぜなら それは 電子やミュー粒子などの レプトンや、クォークなど多くの粒子を表すからだ。
( しかし もし相対性理論が間違っているとしたら、ディラック方程式をベースとした これらの理論はすべて間違いということになる。 )
しかし、このセクションで説明するとおり、残念ながら これらの粒子に関する具体的なイメージはまったくない。
単なる ”数学的な産物”となっている。これを説明していこう。
(もちろん、例えば 電子は実在する。しかし、量子力学は それらを 具体的に表現する力がない。)
(Fig.13) ディラック場の概要。
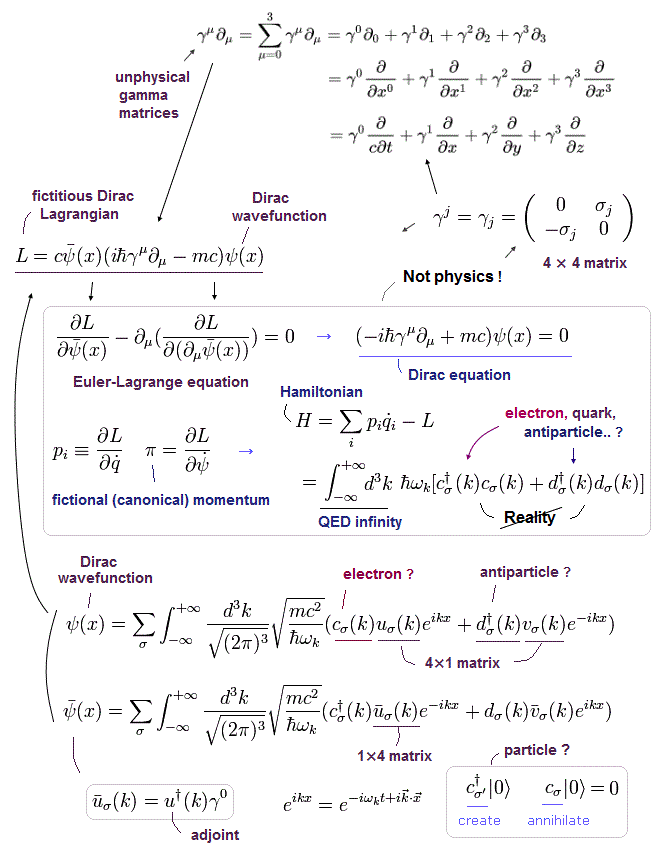
クライン・ゴルドン (K-G) 方程式を "強制的" に 時間に関して 1次 の式に変換しようとすると、 4 × 4 行列 の力に頼らなければならない。
行列に頼るということは、 ディラック方程式は 物理的な性質よりも "数学的"な性質を持つ ことを意味する。
最終理論である超ひも理論においてさえ、フェルミ粒子は スピノル+γ行列で表現しなければならない。
つまり 量子力学(+スピノル)に頼る限り 電子などを リアルな物で表現することは不可能である。
ディラック方程式は、
(Eq.5-1) ディラック方程式。

ここで ψ(x) は 4-成分の波動関数 ( 4 × 1 行列 ) で、 γμ は 4 × 4 の行列である。
Eq.5-1 は 次に等しい。
(Eq.5-2)
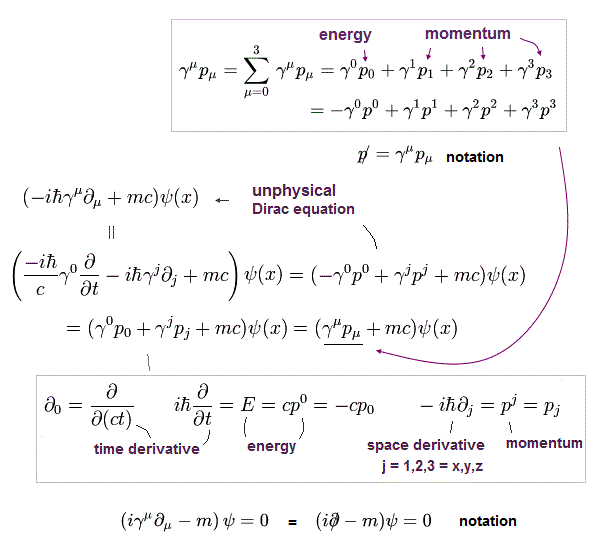
ここで Eq.1-6 と Eq.4-2 を使っている。
ディラック方程式の Eq.5-2 は 相対性理論に等しくなるために クライン・ゴルドン方程式 を満たさなければならない。
Eq.5-2 の左側から、次の式を付け加えると、
(Eq.5-3)

クライン・ゴルドン方程式に一致するには、γ 行列は 4×4 行列 になる必要がある。
( この頃あたりから 場の量子論は "物理"というよりは "数学"の産物になってしまったと思われる。)
γ 行列は次の関係を満たす。
(Eq.5-4)
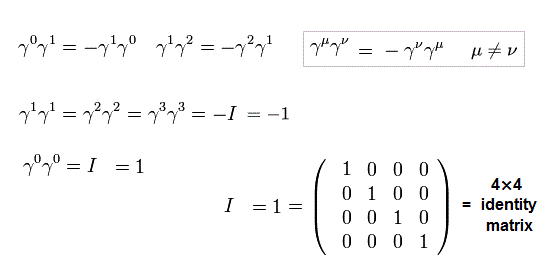
Eq.5-4 は 異なった γ 行列は 互いに反交換し、2つの同じ γ は 4×4 I もしくは -I になることを意味している。
Eq.5-4 を しばしば 計量テンソル "g" を用いて次のように表す。
(Eq.5-4')
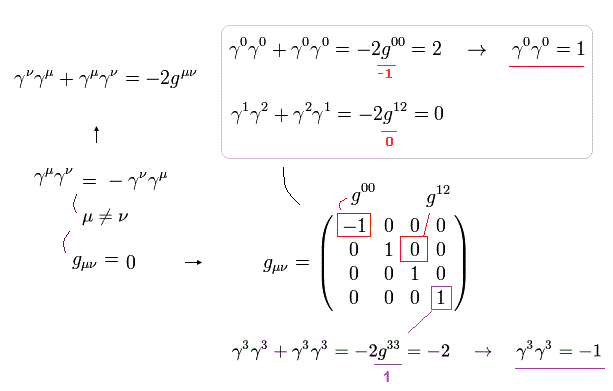
( 計量テンソル )
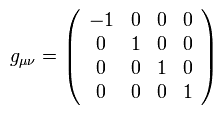
Eq.5-4 を満たす γ行列は
(Eq.5-5)
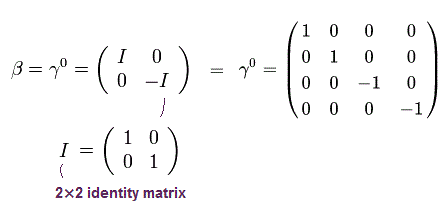
ここで I は 2 × 2 の 単位行列である。
また、
(Eq.5-6)
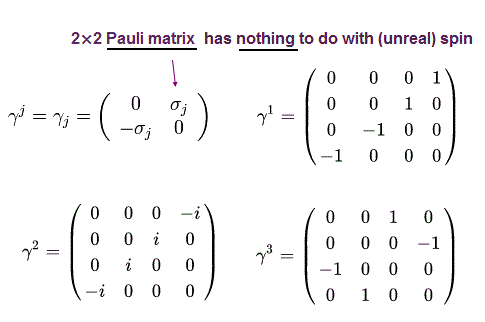
ここで σj は 2 × 2 の パウリ行列である。
(Eq.5-6')
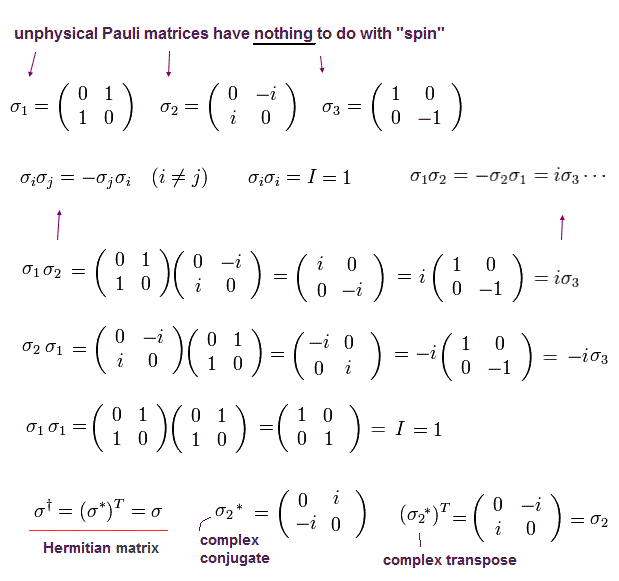
Eq.5-6' のパウリ行列の関係式は 場の量子論では頻繁に登場するので 覚えておく必要がある。
問題は 私たちは パウリ行列の "実在的"な意味を知らないまま ただ用いていることにある。
例えば、 γ0γ0 = I ( = 4× 4, 単位行列 )、
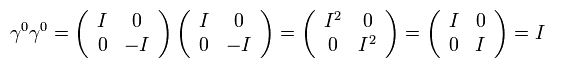
また γ 行列は 次のような 反交換関係を満たす。
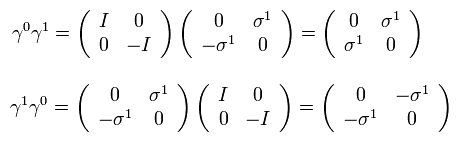
上記の γ行列の性質を用いると、Eq.5-3 は 次の クライン・ゴルドン方程式に等しくなる。
(Eq.4-1)
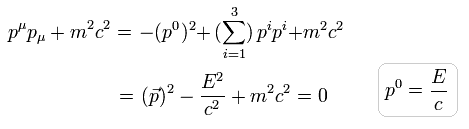
他の項は γ行列の反交換の性質で消えた。
また、ディラック方程式 Eq.5-1 の左側から cγ0 をかけて、γ0γ0 = 1 と x0 = ct を用いると、
(Eq.5-7)

Eq.5-7 は ディラック場のハミルトニアンを得るときに 再びでてくる。
ディラック方程式の 平面解波 は 次のように表せる。
(Eq.5-10)
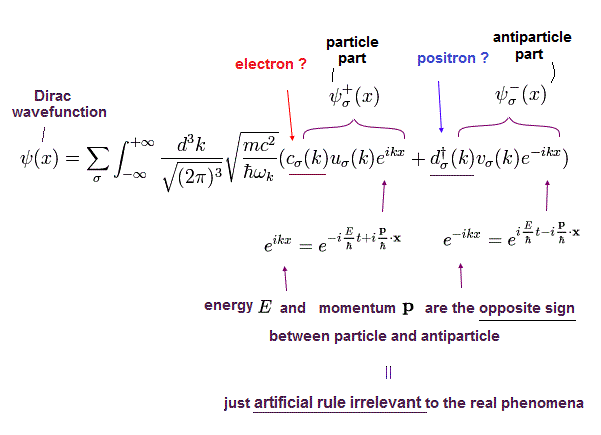
ここで ψ+ は プラス のエネルギー解、 ψ- は マイナス のエネルギー解である。
また u(p) と v(p) は 4 × 1 の行列である。
Eq.5-10 の 指数関数 ( kx ) は 次のクライン・ゴルドンの関係式と等しい。
(Eq.4-5)

と
(Eq.4-6)
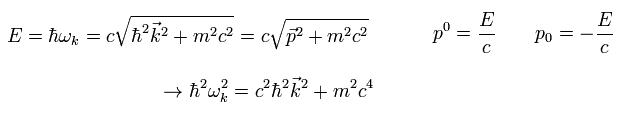
Eq.5-10 の解を ディラック方程式である Eq.5-1 に代入して、プラスのエネルギー解は、
(Eq.5-11)

ここで p0 = - p0.
また マイナスのエネルギー解は、
(Eq.5-11')

Eq.5-11 と Eq.5-11' から、 行列 u(p) と v(p) は 次の式を満たす。
(Eq.5-12)

と
(Eq.5-13)
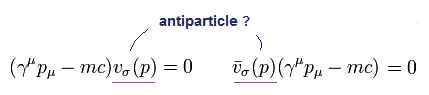
Eq.5-15 を用いると、Eq.5-12 の左側の方程式の 共役な転置行列 は次のようになる。
(Eq.5-14)
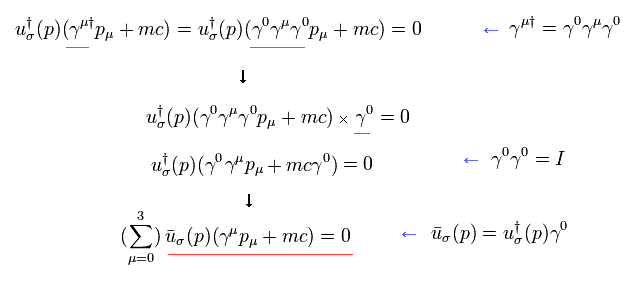
ここで u†(p) (1 × 4 matrix) は u(p) の 共役な転置行列 である。
u†(p) = (u(p)*)T
Eq.5-14 の右側から γ0 行列を付け加え、また 次の関係を使っている。
(Eq.5-15)
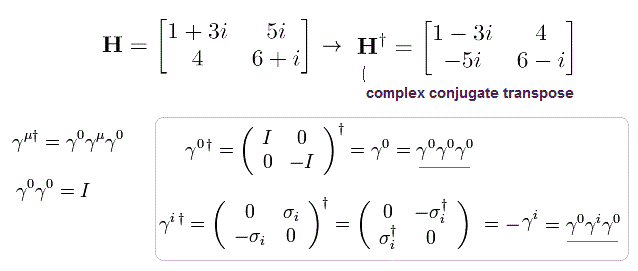
Eq.5-15 の関係式は Eq.5-5, Eq.5-6 や Eq.5-6' の パウリ行列 σ† = σ を用いると証明できる。
( 反交換 γ0γi = - γiγ0、 と γ0γ0 = 1. )
よって μ= 0, 1, 2, 3 のすべてのケースで Eq.5-15 の 関係式が成り立つ。
また
(Eq.5-16)
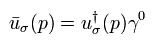
すると、 Eq.5-12 の 右側の式が得られる。
重要な点は ディラック方程式では、単純な平面波においてさえ、 具体的な 解が得られないことである。
なぜなら、その解は 行列 を含まなければならないからである。
つまり、ディラック方程式は "数学的な" 産物といえる。
ここで 解 u(p) を次のように定義する。
(Eq.5-17)
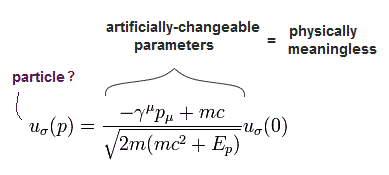
( この解 u(p) は γμ 行列を 含まなければならない。 )
Eq.5-17 を Eq.5-12 の左側の式に代入すると、
(Eq.5-18)
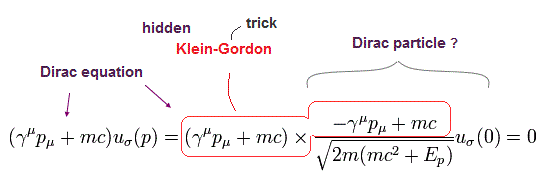
Eq.5-18 は Eq.5-17 が クライン・ゴルドン 方程式を満足することを意味する。
つまり Eq.5-17 は ディラック方程式の解として ふさわしいことになる。
同じように 解 v(p) は 次のように定義できる。
(Eq.5-19)
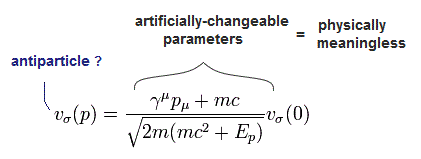
Eq.5-19 を Eq.5-13 に代入すると、 Eq.5-19 が クライン・ゴルドン方程式を満足することが分かる。
Eq.5-17 の γμ 行列を Eq.5-5 と Eq.5-6 に変換すると、 Eq.5-17 の 分子 は次のように表せる。
(Eq.5-20)
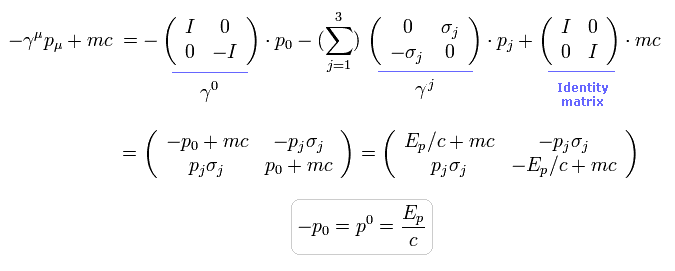
ここで Eq.1-6 を使った。
Eq.5-17 と Eq.5-19 の u(0) と v(0) を 次のように定義できる。
(Eq.5-21)
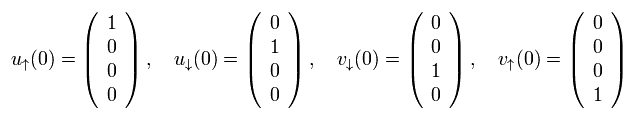
つまり u(0) は 上 2成分のみ、 また v(0) は 下 2成分のみである。
5-20 を使うと、 Eq.5-17 は次に等しくなる。
(Eq.5-22)
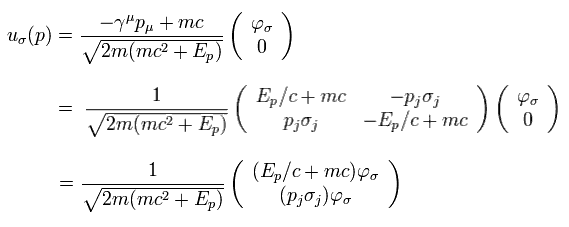
ここでは、
(Eq.5-23)
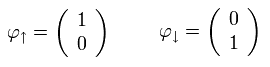
つまり、u(p) の バー付きの 共役な転置行列は (= Eq.5-16) 次のように表せる。
(Eq.5-24)

ここで パウリ行列は σ† = σ である。
Eq.5-22, Eq.5-24 を使って、
(Eq.5-25)
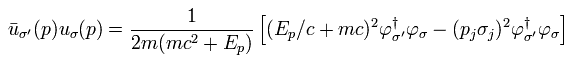
ここで、
(Eq.5-26)
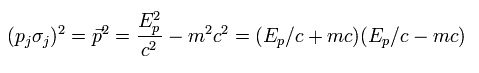
ここでは、クライン・ゴルドン方程式と パウリ行列における σj σj = 1 と 反交換の関係を使っている (Eq.5-6')。
Eq.5-26 を Eq.5-25 に 代入すると、次の式が得られる。
(Eq.5-27)
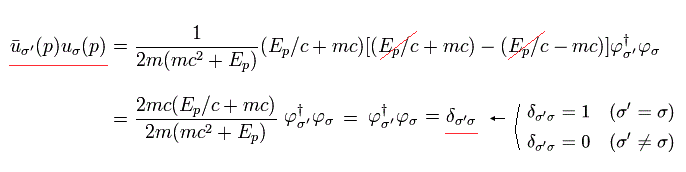
ここで、次の関係を使う。
(Eq.5-28)
この 添え字 σ は Eq.5-23 の "スピン" を表す。
また u(p) と同じように計算すると、 次の式が得られる。
(Eq.5-29)
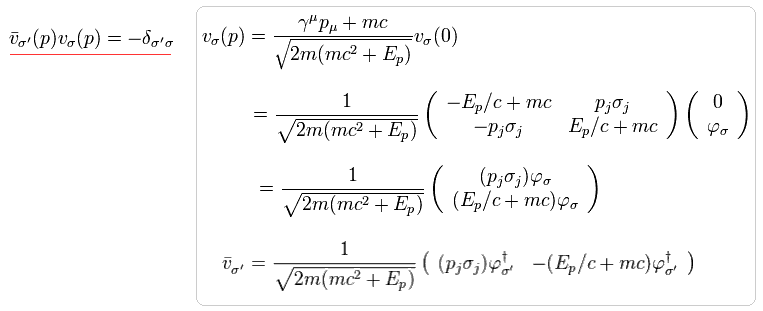
このマイナスの符号は v(p) の指数関数の マイナスエネルギー に由来する。
また Eq.5-24 において、γ0 を 消去 すると、
(Eq.5-30)
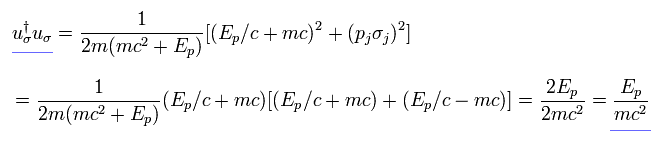
同じように、
(Eq.5-31)
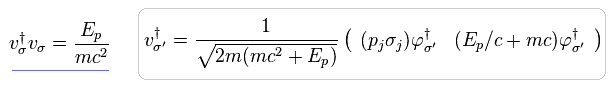
γ0 がないときは、 Eq.5-30 は Eq.5-31 に等しくなる。
ディラック方程式につながる ラグランジアンは 次のように定義できる。
(Eq.5-32)
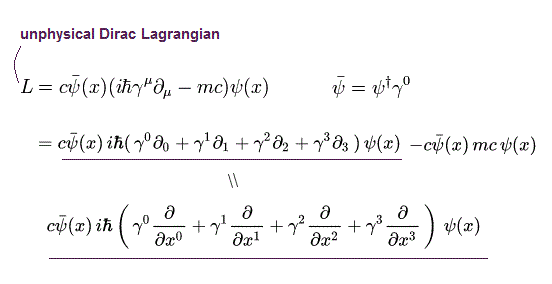
もちろん このラグランジアンは ローレンツ不変なスカラーである。
最初に ψ の バー付き 共役転置行列 を使うと、オイラー・ラグランジュ方程式は、
(Eq.5-33)
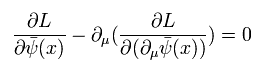
Eq.5-33 の 2項目は ゼロになる。 ( Eq.5-32 を参照。)
すると、Eq.5-33 の最初の項は、
(Eq.5-34)
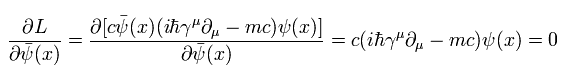
Eq.5-34 は ディラック方程式 Eq.5-1 に等しくなる。
次に ディラック方程式 (Eq.5-1) の共役な転置行列を考えると、
(Eq.5-35)
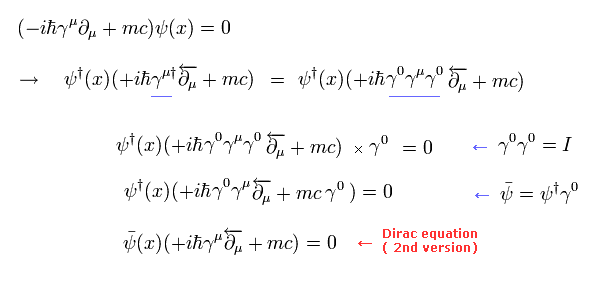
ここでは Eq.5-15 を用い、右側から γ0 をかけた。
また 微分の方向は Eq.5-1 と 逆 であることに注意。
しかし Eq.5-35 の意味は Eq.5-1 と同じである。
そのため、 ψ(x) を オイラーラグランジュ方程式に使用すると、
(Eq.5-36)

Eq.5-36 は Eq.5-35 に等しい。
結果として、 Eq.5-32 の ラグランジアンから、ディラック方程式を得ることができた。
ディラック方程式の正準運動量は、 ( Eq.1-21 も参照 )
(Eq.5-37)

また、ハミルトニアンは、
(Eq.5-38)

ここで 最初の行は "j" に関して 1 から 3 成分で和をとることを意味する。
Eq.5-7 から、 Eq.5-38 は、
(Eq.5-39)
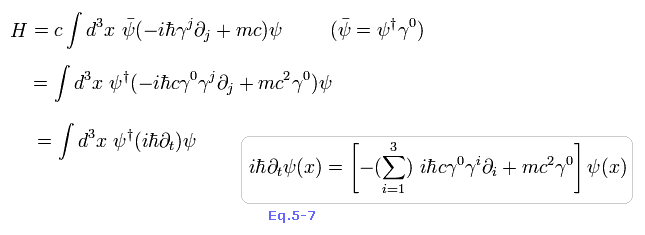
つまり、これは ディラック方程式 のハミルトニアンを意味する。
(もちろん Eq.5-39 を得るために Eq.5-32 のラグランジアンが 用意されたのである。)
また Eq.5-39 のハミルトニアンに通じる 解は 次のように表せる。
(Eq.5-40)
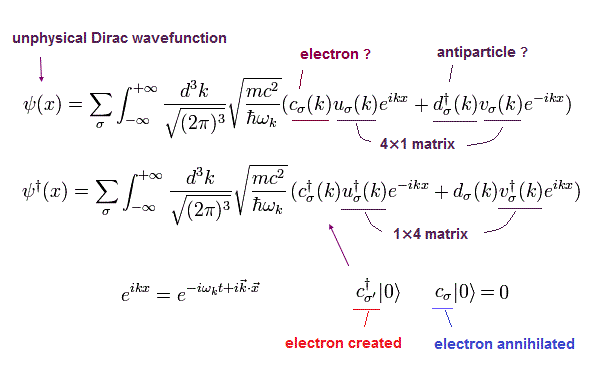
また、その バー付きの共役な転置行列 は、
(Eq.5-41)
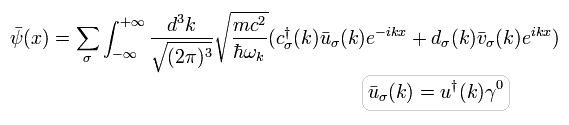
これらの u(p) と v(p) は、それぞれ Eq.5-17 と Eq.5-19 である。
また c(k) と d(k) は それぞれ 粒子と反粒子の 消滅演算子を意味する。
つまり c†(k) と d† (k) は 生成演算子を意味する。
Eq.5-40 を Eq.5-39 に代入して、Eq.4-5、Eq.5-30、Eq.5-31 を使うと 次を得る。
(Eq.5-42)
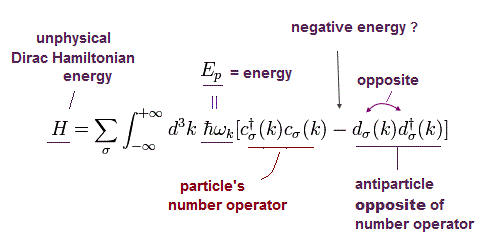
例えば、Eq.5-39 の c† c 部分は、
(Eq.5-42')
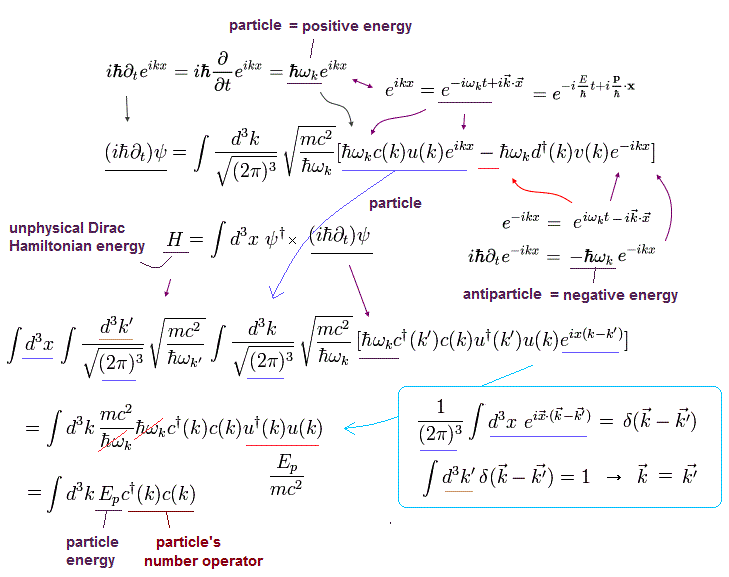
Eq.5-42' の最初の行の マイナス符号のために、Eq.5-42 の d d† 部分は マイナスになる。
( なぜなら ディラック方程式は クライン・ゴルドン方程式と違い 一次式のため 負号を隠せなかったからである。)
(Eq.5-42'')

Eq.5-42 の 反粒子において、d†(k) d(k) のような プラスの 数演算子を得るには、次の 反交換関係を満たす必要がある。
(Eq.5-43)

Eq.5-43 を使うと、 Eq.5-42 は、
(Eq.5-44)
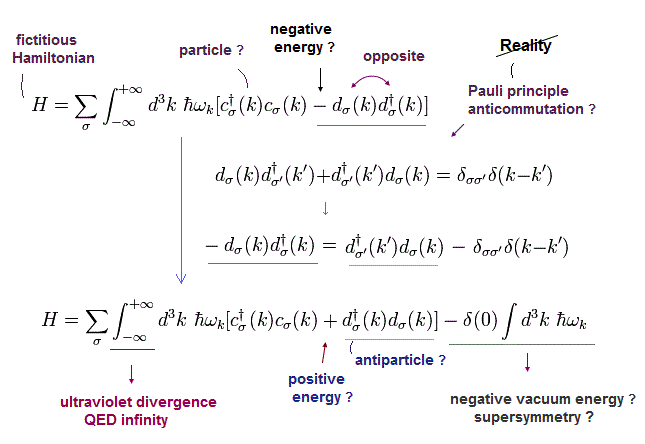
すると、d†(k) d(k) (= 反粒子における 正のエネルギー ) という プラスの 数演算子を得ることができた。
そのため 彼らは Eq.5-43 は パウリの排他原理のミステリアスな力を表していると主張しているのである。
しかし残念ながら この非常に抽象的な 数式記号から このパウリの排他原理の真の実像を知ることがまったくできない。
また 超ひも理論においても 特に進展なく 同じ反交換の記号を用いているにすぎない。
つまり 例え 超ひも理論を知ったとしても、この本当の意味を知ることはできない。これは奇妙である。
Eq.5-44 の真空のエネルギーの符号は Eq.4-16 のと反対であり、これは 超ひも理論の超対称性で使用される。
そのため、量子力学の物理学者達は ディラック方程式が フェルミ粒子の 反対称の性質を証明できたと主張しているのである。
(= パウリの排他原理 )
ディラック方程式は 導関数において、 1次であり、これは クライン・ゴルドン方程式と違う。
このことにより、ディラック方程式は マイナスのエネルギー解を 隠すことができなかった。
そもそも Eq.5-10 のスタート地点において、 マイナスのエネルギー解を定義し、これが Eq.5-42 のマイナスのエネルギーにつながったのである。
それに もし Eq.5-43 が満たされるとすると、 ψ と その 正準運動量 π (= Eq.5-37) は、
(Eq.5-45)

この ディラック方程式の反交換関係は、 クライン・ゴルドン方程式の Eq.4-24 の交換関係と異なる。
しかし、重要な点は Eq.5-45 は 次のド・ブロイの関係式と矛盾しているということである。
(Eq.4-24)

もし、Eq.5-45 の新しい関係を導入するとなると、ド・ブロイの関係式にかわる 新しい理論 を発見しなければならない。
しかし、ド・ブロイ理論は 量子力学において 基本中の理論であり、決して取り除くことはできない。
それだったら、Eq.5-37 の π を ハミルトニアンを得るための正準運動量 として使うことができるのだろうか?
これは非常に変である。ある意味 交換から反交換への変更は しりとりみたいな 浅はかな変更なのである。
Eq.2-16 の ローレンツ力 と、、 Eq.3-2 の マクスウェル方程式のラグランジアンを使うと、
(Eq.5-46)
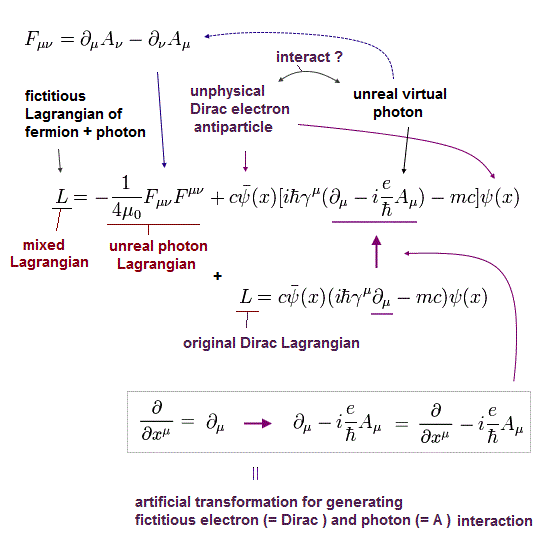
Eq.5-46 は ディラック方程式とマクスウェル方程式をミックスしたものである。
(また ここでは 電荷を +e としている。 )
Eq.5-46 の次の部分は、
(Eq.5-46')

つまり Eq.5-46 において、Eq.2-16 の置き換えが使用されている。
ここで スカラーポテンシャル φ = cA0 = - cA0.
Eq.5-46 の 相互作用項 ( 粒子 と ベクトルポテンシャルAの ) は、
(Eq.5-47) 相互作用項。
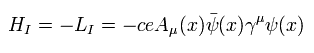
Eq.5-47 の相互作用項は QEDにおいて 非常に重要である。
なぜなら 素粒子物理学や 量子電磁力学において 電子、クォーク、陽電子などのフェルミ粒子と 光子 の相互作用を意味する式は Eq.5-47 が 唯一のものだからである。
残念ながら、非常に抽象的な 相対論的な場の量子論では 様々なパターンの相互作用項を使用することができない。
また Eq.5-47 は 相対論に反する仮想光子を生じさせてしまう。
Eq.5-46 を 次の Eq.3-2、Eq.3-3 と比較する。
(Eq.3-2)
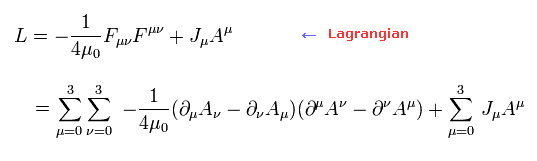
と
(Eq.3-3)
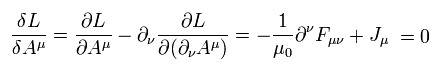
結果として、ディラックの電流密度 (J) は、
(Eq.5-48)
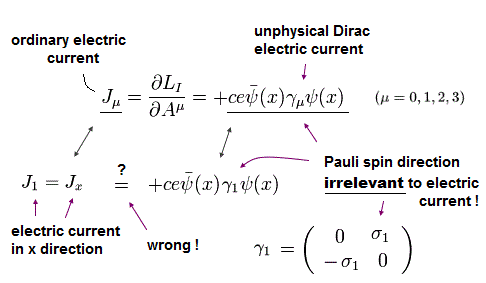
このことより、物理学者達は Eq.5-48 で ディラック方程式が 電流密度を表すのに成功したと主張しているのである。
しかし Eq.5-6 に示すように、 γ 行列は パウリ行列から成り立っている。
これはつまり、 γ 行列は スピンの成分を表しており、 電流の方向とは 何の関係もない ことを意味する。
しかし Eq.5-48 では、 スピンの成分が なんと 電流の方向を表しているのである。
要するに Eq.5-48 と Eq.5-47 は とても奇妙な解釈がもとになっているのである。
しかし、どうして ディラック方程式で Eq.5-48 の結果を得たのだろうか?
実は、 γ 行列 (= σ 行列) は ディラック方程式に特異的なものではないのである。
シュレディンガー方程式 (もしくは 古典力学 ) においてでさえ、 次のように σ 行列が含まれている。
(Eq.5-49)
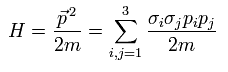
ここでは 次の パウリ行列 (= σ ) の関係を使っている。
(Eq.5-50)
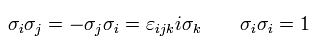
粒子が Eq.2-13 のローレンツ力のもとでは、量子力学は次のような数学上のトリックを用いる。
(Eq.5-51)
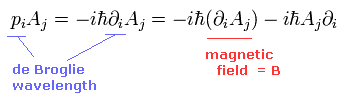
ここでは p は 微分演算子を含んでおり、 Aj の前と後に作用している。
つまり 粒子のドブロイ波長が いつのまにか 外磁場を得るために ベクトルポテンシャルの微分に転化されているのである。
これは奇妙である。
また 次のトリックも使用する。
(Eq.5-52)
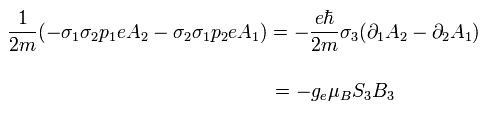
Eq.5-52 では ボーア磁子 に合わせるために スピンのg因子 ge が "2" にならなければならないとしている。
できすぎた話だと思わないだろうか?
Eq.5-50、 Eq.5-51、Eq.5-52 を考慮すると、Eq.2-13 の置き換えのもとで、Eq.5-49 は 次のようになる。
(Eq.5-53)

Eq.5-53 は スピンと磁場 (= ベクトルポテンシャル) の相互作用は シュレディンガー方程式においても存在することを意味する。
Eq.5-53 の ラグランジアン ( LI = - HI ) の ベクトルポテンシャル (A) による 偏微分は、
(Eq.5-54)
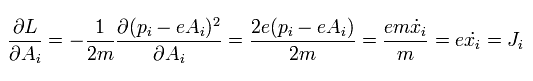
シュレディンガー方程式における電流 (J) は Eq.5-54 に示すように 電荷と その速度から成り立っている。
そして、 σ 行列は Eq.5-53 に示すように σσ = 1 として 隠れており、J の一部としては もちろん使用されていない。
一方で、 Eq.5-46 に示すように、ディラック方程式は 運動量に関して 一次式である。
(つまり、ベクトルポテンシャルにおいても ディラック方程式は一次式になる。)
結果として、ディラック方程式においては、 ベクトルポテンシャル (A) による 微分により 粒子の運動量が消えてしまう のである !
(要するに この時点で ディラック方程式には 電荷の流れは存在しない のである。 )
このことは 1次式であるディラック 方程式は ローレンツ力による置き換え (Eq.2-13) を利用することが できない ことを意味する。
(ローレンツ力による相互作用は "もともとは" 古典力学における 2次の式 において考え出されたものである。 )
Eq.5-47 の 相互作用項は 量子電磁力学においても利用される。
つまりこの理論は 深刻な欠陥を含んでいることになる。
光子という粒子は存在していると言われている。しかし実は、波という概念だけで光電効果やコンプトン効果などすべての現象を説明することができる。
また、もし光子を粒子ではなく電磁波として扱ったなら、光速を越える奇妙な伝達(エンタングルメント)を考えなくてよくなるのである。 (このページ を見てほしい)
量子電磁力学 (quantum electrodynamics) は、この光子という粒子を表現するために作られたものだ。
電磁場 (B と E) は、Eq.3-4 と Eq.3-5 に見られるように、ベクトルポテンシャル (Ai) とスカラーポテンシャル(φ = cA0 = -cA0) で表すことができる。
しかし、この Aμ を次のように変換すると、(ゲージ変換)
(Eq.6-1)
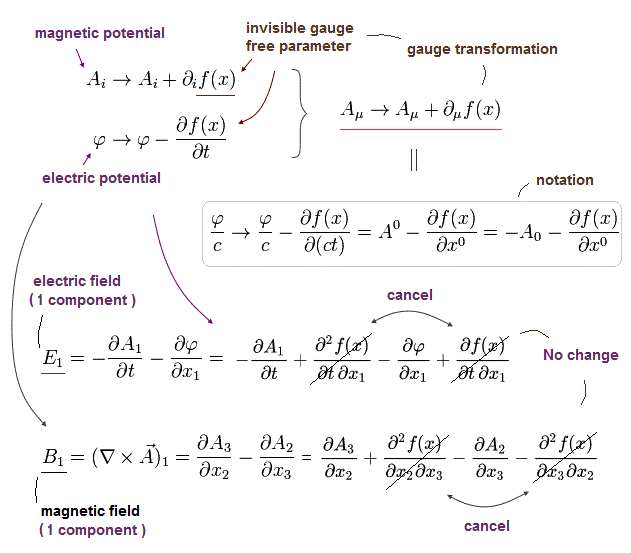
任意の関数 f(x) において、電磁場 B と E は変化しない。
Eq.6-1 を Eq.3-10 や Eq.3-11 に代入してみるといい。
そのため、次のような関係(ローレンツゲージ)を満たすように f(x) を選ぶことが可能である。
(Eq.6-2)

このローレンツゲージという条件を選ぶ理由は、マクスウェル方程式をローレンツ変換不変な形に保つためである。
実際 Eq.6-2は 反変ベクトルと共変ベクトルのペアでスカラー形式になっている。
ローレンツ変換のもとでは、Eq.6-2 は次のようになる。
(Eq.6-3)

よって Eq.6-2 が ローレンツ変換不変であることを証明できた。
Eq.3-1 を用いて、Eq.3-3 のマクスウェルの方程式は次のように表せる。
(Eq.6-4)
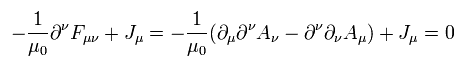
Eq.6-2 のローレンツ条件を使うと、 Eq.6-4 のマクスウェル方程式は 次のようになる。
(Eq.6-5)
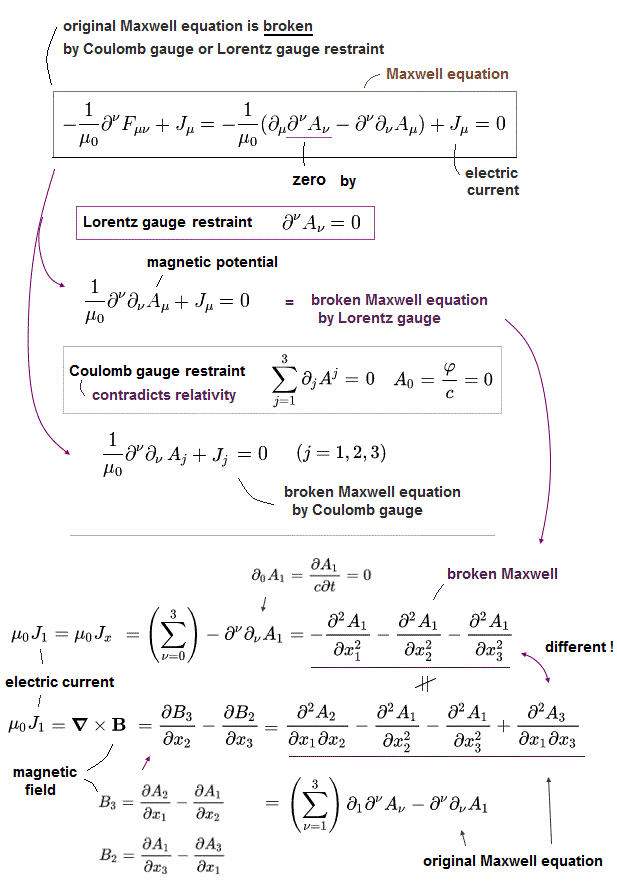
Eq.6-5 は ローレンツ変換のもとで 共変なベクトルとして変化する。。
結果として、ローレンツ変換のもとで、Eq.6-5 の式の形は 変化しない。
ここで 真空 ( J=0 ) における 光子という粒子について考えることにする。
この場合は、
(Eq.6-6)
となる。実際この方程式は、電磁場 B と E を Aμ で置きかえれば分かるが、マクスウェル方程式と同じであることがわかる。(後、ローレンツゲージの条件も使って。)
Eq.6-6 の解は、
(Eq.6-7)
ここでもし、場の演算子と運動量演算子の間に一般的な正準交換関係を満たすとすると、この式の生成・消滅演算子は次のような交換関係を満たす必要がある。
(Eq.6-8)

ここで、この式 Eq.6-8 の右辺で g00 の時だけ、符号がマイナスになる。しかし、もしまた Eq.6-2 のローレンツゲージの条件をまた使えば、この問題は解決できる。
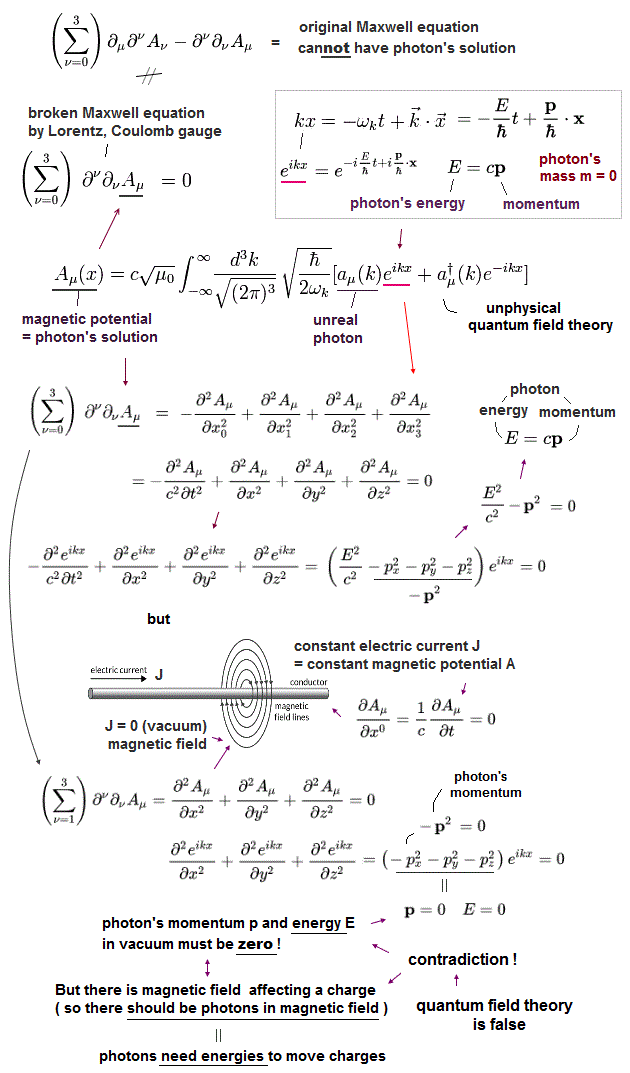
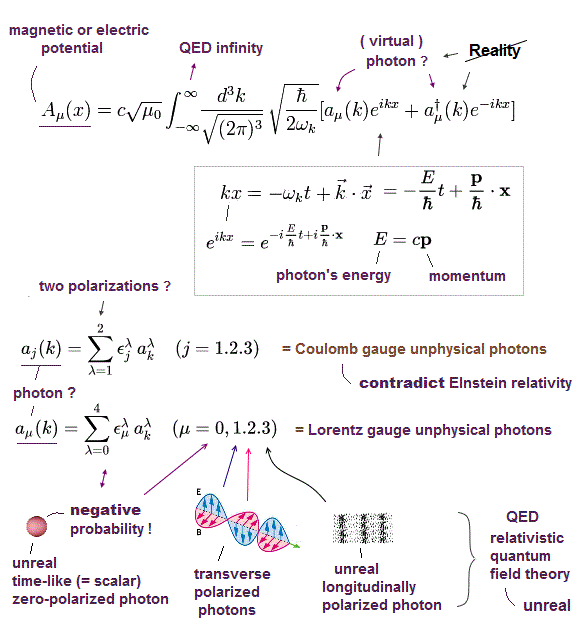
この 光子のゼロ成分の負の数演算子は 相対論の共変形式に由来するもので、奇妙なことに g因子を得るときの量子電磁力学などにこの非実在の光子が使用されている。
これが ”光子”の正体である。
すなわち、光子という粒子は生成演算子で生成される、単なる”数学上の”産物だということだ。
量子電磁力学には、光子という粒子を具体的に表現できる力はない。残念ながら、それは単なる”数式”のみを示すだけである。
クーロン力などは "仮想光子" によって生じると言われている。
しかし、QEDには 生成演算子以上に具体的な状態を示す力はない。
よって、量子力学や QED のもとでは、新しい具体的なメカニズムの解明にこれ以上進めないことになる。
量子力学や場の量子論では、状態は、時間とともに ei Ht のように変化する。
そして、式を”ローレンツ変換不変”の状態に保つためには、この(相互作用)ハミルトニアン (H) に無限大の運動量とエネルギーを持ち得る無限大の粒子が含まれていなければならない。 しかしこれが相対論的な場の量子力学というものだ。
もし、方程式に、有限な運動量の粒子いくらかしか含まれていないとしたら、この式の形は、ローレンツ変換によって各慣性系ごとに変化してしまう。なぜなら、この運動量もローレンツ変換のもとで4元ベクトルとして変化するからである。
もしそうだとしたら、ディラック方程式そのものの形がローレンツ変換によって壊れてしまうということになってしまう。
これを避けるためには、ハミルトニアンにはあらゆる運動量を持つ無限の粒子が存在しなければならない。しかし、このことは、伝播関数で粒子間の相互作用を考えるとき、発散という問題が発生する原因となる。
この発散問題を解決するために、組り込み理論 (renormalization theory) というものを使う。これは、伝播関数に生じた無限大を新しく人工的に作った無限大で除去するという考えだ。
例えば、電子の周囲にある”無限大の刺激”をキャンセルするために、その電子の”裸の”電荷と質量が無限大でなければならないというわけだ。
要するに、相対論的な場の量子論というのはこういう非常に奇妙なものなのである。
(このページ や g因子は操作できる も参照のこと。)
また、素粒子物理学の 標準模型は 約 20 の重要なパラメーターを含んでおり、これは 意図的に操作可能である。
(つまり、これらの重要なパラメーターは 標準模型から得られたものではなく、純粋に実験からの経験から得たものである。)
これは、標準模型は いずれは 別の新しい理論に入れ替わる可能性を意味している。
(このページも参照のこと。)
もし 素粒子学の専門家の誰かが、(ボーア模型のような) 現実的な視点から この新しい理論を発見したなら、非常に喜ばしい。
ご存じのとおり、超ひも理論は あまりにも現実離れしすぎていて、もちろん 永遠にその信憑性を 確かめることはできない。
10次元以上もの次元が必要なんて あまりにも非現実的すぎる。
まさに "間違ってさえいない (Not even wrong)" 理論である。
なぜなら、ひも理論なんて 永遠に間違っているかどうかさえ確かめることができないからである。
また 超ひも理論には 無数の非実在の理論が含まれていて 理論が定まることがない。

2012/9/24 updated This site is link free.