トップページ (正確な新ボーア模型)
量子力学の波動関数の 終わり。(14/6/14)
ゾンマーフェルトによる微細構造定数 の導出。
プランク定数 の真の意味と 磁束の量子化。
役に立たない量子化学の本当の原理とは ? (13/11/23)
量子力学のシュレーディンガー方程式は 様々な原子において 非常に正確な値をだせると言われている。
しかし 単純な水素様原子以外の式を実際に解くことができない。
そのため 何らかの近似を使用する必要がある。
これらの近似の中で 変分法が 原子のエネルギー値に関して 最も正確な値を与えることができる。
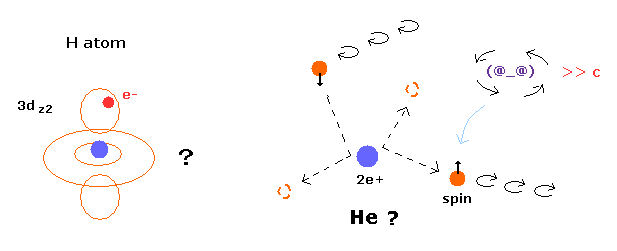
(Fig.1) 量子力学のヘリウムは 不安定なカオス状態になる。

しかし ご存じのとおり、量子力学の原子は 決して 電子運動の本当の状態を教えてくれない。
単一の電子は 実験によれば 確かに 決まった質量と電荷を持つ量子化された粒子である。
つまり 1つの電子が 雲として 全空間に広がっていると主張することは 実験結果と矛盾している。
さらに 安定なヘリウム原子の2つの電子が 角運動量ゼロ (= 1s ) だとしたら、このヘリウム原子模型は 非常に不安定になる。
これはつまり 量子力学的な 摂動法や変分法は 原子のリアルな状態を表すことができないことを意味している。
(Eq.1) ヘリウム原子のハミルトニアン。
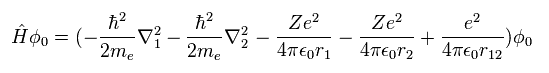
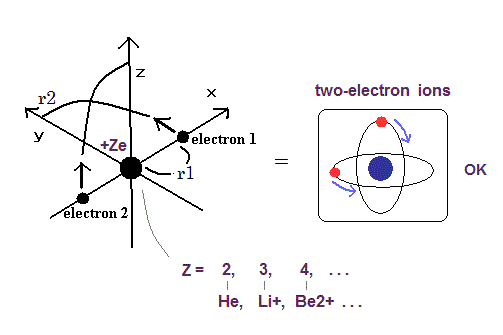
ヘリウム様の原子は 2つの負の電子 ( 1、 2 ) と 1つの正の原子核 (= +Ze ) を持つ。
( 中性のヘリウム原子では この Z は "2" である。)
Eq.1 の最初の2つの項は 電子1と電子2の運動エネルギーを表している。
また Eq.1 の最後の項は 2つの電子間のクーロン反発力を表している。
( r12 2つの電子間の距離の意味である。 )
(Eq. 2) 水素様原子の "1s" の波動関数。
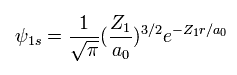
ヘリウムのシュレーディンガー方程式を解こうとすると、水素様原子の 1s の波動関数を使用する。
( Z1 = 1 は 水素原子で、 Z1 = 2 ヘリウムイオンである。 )
Eq.2 の 2つの波動関数を用いて、中性のヘリウムの波動関数を次のように表せる。
(Eq. 3)
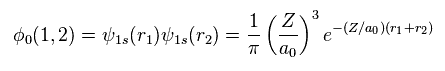
Eq.1 と Eq.3 を 次のエネルギー (= W ) の式に代入すると、
(Eq. 4)
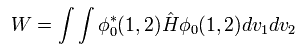
次を得る。
(Eq. 5)
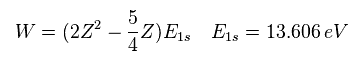
Z = 2 のとき、ヘリウムの全エネルギー W は -74.833 eV となり、これは 実験値 -79.0051 eV と異なる。
原子番号 Z を変えると、次の ヘリウム様の原子 (イオン) の基底状態のエネルギーを得る。
| 原子 | 実験値 (eV) | 新ボーア (eV) | 摂動法 (eV) | ボーア 誤差 | 摂動法 誤差 |
|---|---|---|---|---|---|
| He | -79.0051 | -79.0037 | -74.8330 | +0.001 | +4.172 |
| Li+ | -198.093 | -198.984 | -193.885 | -0.89 | +4.21 |
| Be2+ | -371.615 | -373.470 | -367.362 | -1.85 | +4.25 |
| B3+ | -599.60 | -602.320 | -595.262 | -2.72 | +4.34 |
Table 1 の "摂動法" は 量子力学の近似計算を意味し、 "新しいボーア"は トップページ もしくは Fig.2 に示した 互いに垂直な軌道をもつ模型のエネルギーである。
(Fig.2) 新しいボーア模型のヘリウム。
新しいボーア模型のヘリウムは わずかな相対論的効果を除いて ちょうどピッタリの基底状態のエネルギーを与える。
またもちろん、ボーア軌道は 具体的な電子の運動を示せて かつ ドブロイ波の性質とヘリウムの安定性も説明することが可能である。
つまり 私達は この模型を 他の様々な原子の 1s の内殻電子状態に 応用可能である。
お気づきのとおり、量子力学の摂動計算は 原子番号が大きくなっても ほぼ同じ誤差を出す (= 約 +4 eV )。
これは 不自然である。
(Eq. 6) 変分関数。
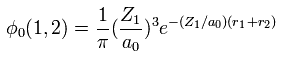
次に ヘリウム様原子の 量子力学的変分法を行う。
ここでは Z1 を 変分パラメーターとして扱い 変化させる。
Eq.6 を Eq.4 に代入して、
(Eq. 4)
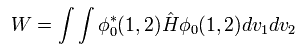
次を得る。
(Eq. 7)
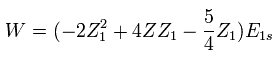
Eq.7 では、 "Z" は Eq.1 に含まれるハミルトニアンの原子番号である。
つまり この Z は 固定値であり、変分パラメーター Z1 とは異なるものである。
Z1 の偏微分を行い エネルギーの最小値を得るとき、
(Eq. 8)
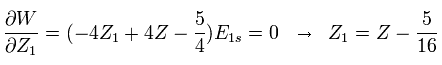
例えば、中性のヘリウム ( Z = 2 ) では、 Z1 = Z -5/16 = 2-5/16 = +1.6875 のとき、全エネルギーは 最も低い値になる。
この Z1 = Z - 5/16 を Eq.7 に代入すると、全エネルギー W は、
(Eq.9)
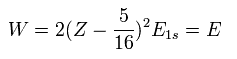
例えば Z = 2 と E1s = -13.606 を Eq.9 に代入すると、全エネルギー (E) は -77.49 eV となり、これは Table 1 の摂動法よりも 実験値 (-79.005 eV) に近い。
しかし 2電子原子に関しては これが この方法の限界である。
| 原子 | 実験値 (eV) | 新ボーア (eV) | 変分法 (eV) | ボーア 誤差 | 変分法 誤差 |
|---|---|---|---|---|---|
| He | -79.0051 | -79.0037 | -77.4904 | +0.001 | +1.515 |
| Li+ | -198.093 | -198.984 | -196.552 | -0.89 | +1.55 |
| Be2+ | -371.615 | -373.470 | -370.019 | -1.85 | +1.60 |
| B3+ | -599.60 | -602.320 | -597.919 | -2.72 | +1.68 |
Table 2 に示すように、 新しいボーア模型も 変分法も ともに良い結果をだす。
しかし お気づきのとおり、変分法は とりわけ 中性ヘリウムとリチウムイオンにおいて 正確な値をだすことができない。
また 原子番号が大きくなっても 誤差 ( 約 +1.5 eV ) があまり変化しないのも 非常に不自然である。
これらの結果は 量子力学の変分法が ヘリウムの真の状態を表していないことを示している。
( もちろん、もともと量子力学にはリアリティーがないが。)
原子番号が大きくなるにつれて ( 2電子間の 反発力による ) 本当の誤差が 大きな正の原子核の影響下に隠れてしまうことを意味しているからである。
(Eq.10) 量子力学のヘリウム。
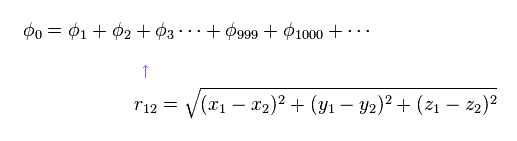
実験値に近づけるには Eq.10 に示すような 千以上もの 変分関数の項を使用しなければならない。
電子間の反発力を表すために これらの項は 電子間距離の変数 ( r12 ) を含む必要がある。
r12 の存在は 電子1を ある場所で見つける 確率密度が 電子2の位置に応じて変化していることを意味している。
つまり Eq.10 は 定常な確率密度波ではないのである。
(Eq.10') 電子雲 = 単一電子は分離している?
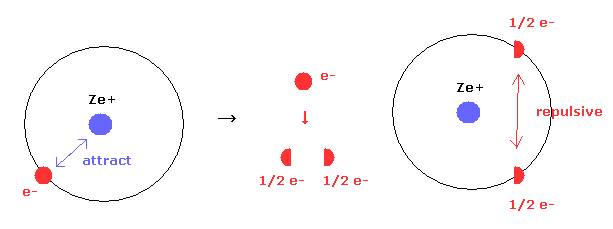
量子力学は 水素原子 ( もしくは 他の原子 ) の単一電子が 電子雲として 全空間に広がっていると主張している。
しかし 単一電子が 実際に分離しているとすると、分離した電子間に発生した 新たな反発力のために これらのエネルギー値が 著しく高くなってしまう。
Eq.10' 左では、原子核と単一電子間のクーロン引力のみが存在する。
しかし もし単一電子が 2つの分数電荷に 電子雲として 分離すると ( e- = -1/2 e -1/2 e )、 新たな 反発力が その間に発生する。クーロン引力はそのままなのにである。
この事実は 明らかに 単一電子は 原子や分子内で 分離していないことを意味している。
このセクションでは、上記の非現実的な変分法が どうして 実験値に近い値をだすのか説明する。
( 役に立たない量子化学の本当の原理 も参照のこと。)
(Eq. 11) 水素様原子の "1s" の波動関数。
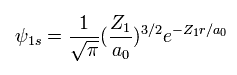
上のセクションでは、ヘリウムの基底状態のエネルギーを得るために 1s の水素様の波動関数を使用した。
ご存じのとおり、 ボーア模型は 水素様原子のエネルギー準位において 量子力学のものと完全に一致する。
(Fig.3) ボーア模型 = "1s" 波動関数。
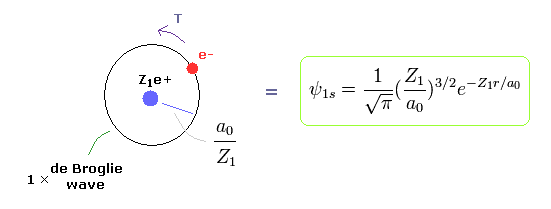
量子力学の水素原子も ビリアル定理, E = 1/2V = -T を満たす。
( シュレディンガーの水素のビリアル定理も参照のこと。 )
つまり 同じエネルギー E では 同じ平均の運動エネルギー T と 電子分布 (= ボーア半径 / Z1 ) を意味する。
よって ここからは 1s の波動関数のかわりに、ボーア軌道を用いて変分法の原理を説明する。
電子が +Z の原子核周囲の 半径 r の軌道上を運動しているとき、その位置エネルギー (V) は
(Eq. 12)
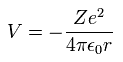
ボーア軌道が 1 × ドブロイ波長のとき、平均の半径 r は
(Eq. 13)
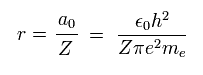
ここで a0 は ボーア半径である。
すでに述べたように、シュレーディンガーの波動関数も Ze+ の原子核周囲を 1 × ドブロイ波長の軌道を表している。
このページも参照のこと。そのため 平均の位置エネルギー (= 電子分布半径 ) は ボーア模型と同じである。
ビリアル定理によれば、平均の半径 r における 全エネルギー (E) と 運動エネルギー (T) は、
(Eq. 14)
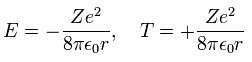
ここで E = 1/2 V と T = -E である。
Fig.3 の変分パラメーター Z1 が 変化するとき ( 原子核の電荷 Z は変化しない )、
電子の 分布 (= 軌道半径 ) は 次のように変化する。
(Eq. 15)
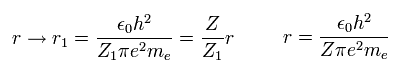
運動量演算子が 波動関数に作用するとき、それは運動エネルギーを与える。
そのため 波動関数そのものは 運動エネルギー (= 運動量 ) の情報を含んでいる。
結果的に、波動関数の変化は 次のように 運動エネルギー (T) の変化を生じさせる。
(Eq. 16)
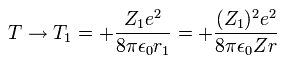
ここで Eq.14 と Eq.15 を用いた。
波動関数の電荷 Z1 のみが変化し、原子核の電荷 (Z) は 変化しないままである。
そのため r1 における 平均の位置エネルギーは、
(Eq. 17)
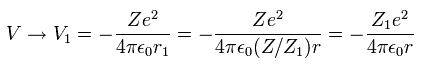
結果的に Eq.16 と Eq.17 から 全エネルギー ( E = T + V ) は
(Eq. 18)
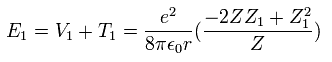
Eq.18 の Z1 による偏微分は
(Eq. 19)
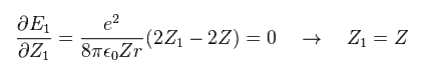
この結果は Z1 = Z のとき、 全エネルギー (E1) は 最も低くなる。
(Eq. 19') 変分法のメカニズム。
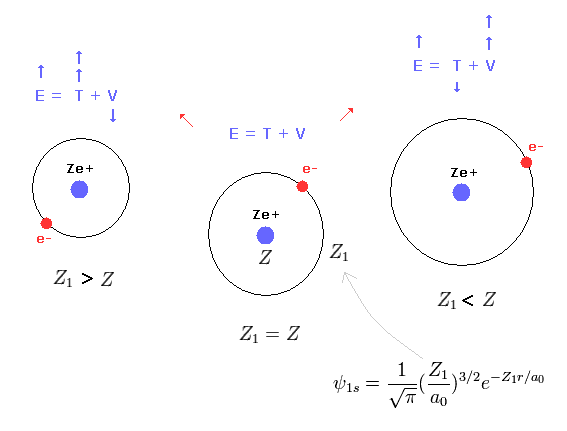
Z1 が Z (= Eq.19' 左 ) より大きくなると、運動エネルギー T の増加 が 位置エネルギー (= V ) の減少よりも大きくなる。 ( T は Z1 の 2乗である。 Eq.16 と Eq.17 を比較するように。 )
Z1 が Z (= Eq.19' 右 ) より小さいとき、運動エネルギーの減少は 位置エネルギーの増加よりも小さい。 ( そのため Z1 =Z のとき、 全エネルギー E は もっとも低くなる。 )
これが 変分法の真のメカニズムである。
ここで 原子番号 Z を用いた。
しかし 系が 複数の原子核と電子を含んでいるとき、全粒子を含む平均の正電荷が この Z になる。
(Eq. 20) 2s (もしくは 2p) の波動関数を用いると?
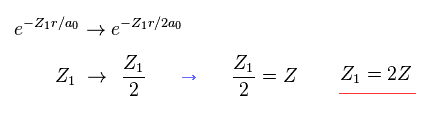
例え 2s (もしくは 2p ) タイプの波動関数を用いても、この結果は 1s の関数と同じである。
違いは Z1 が 本当の原子番号 Z の 2倍になるところである。
( この場合、2s と 2p の波動関数も 1 × ドブロイ波長を意味している。)
(Eq.21) 水素分子イオン (H2+).
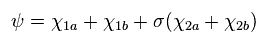
ここでは
(Eq.22)
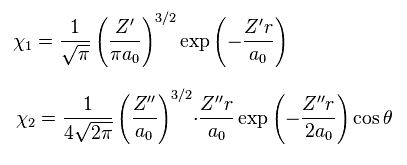
このページに示したように、水素分子イオン (H2+) の変分関数は 非実在の Z の値を与える。
Eq.21 では、χ1 は 水素の 1s 波動関数、 χ2 は 水素の 2p 波動関数である。
σ、 Z'、 Z'' は 変分パラメーターである。
変分法の計算結果は
(Eq.23)
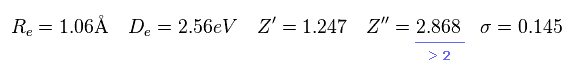
Eq.23 に見られるように、2p の波動関数の正電荷は
2.868 になる。
もちろん、 H2+ 分子イオンは 2 つしか 原子核を持たない。 そのため Z'' = 2.868 は あり得ない数値である。
彼らは 1 × ドブロイ波長を 2p の波動関数を用いて表そうとしたので、変分電荷 Z'' が 実在の値の 2倍 になってしまったのである。 ( Eq.20 も参照のこと。 )
(Fig.4) 2 × 1s 波動関数 = ヘリウム。
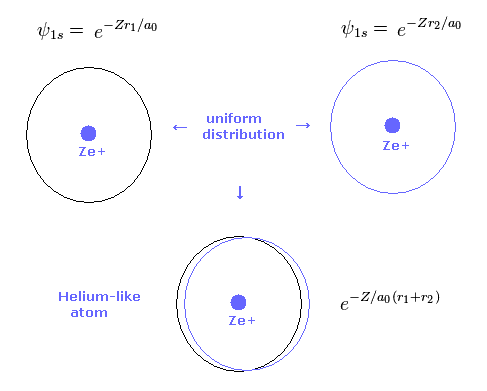
Table 2 に示したように、変分法は 新しいボーア模型と似た結果を与える。
基本的に 1s の水素原子の波動関数は 原子核周囲に 均等に分布している。
そのため 変分法のヘリウム原子模型においても、2つの電子が 原子核周囲に均等に分布している。
(Fig.5) 新しいボーア模型 = 2つの電子が均等に分布している。
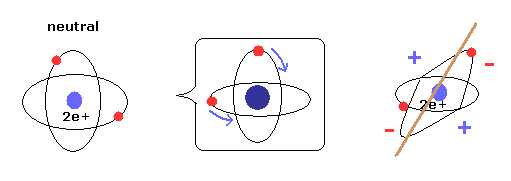
トップページに示したように、2つの電子軌道が 互いに垂直のとき、それはつまり 2つの電子が 原子核周囲に 均等に分布している。
結果的に ヘリウムは 電気的に分極しておらず、他の原子やそれ自身と化合物を形成しない。
均等分布 + 変分電荷 Z (= 平均電荷、 Eq.19 参照のこと ) のため、Table 2 の変分法は 新しいボーア模型と似た結果を与える。
(Fig.6) 変分法の弱点 = 明確な運動を示せない。
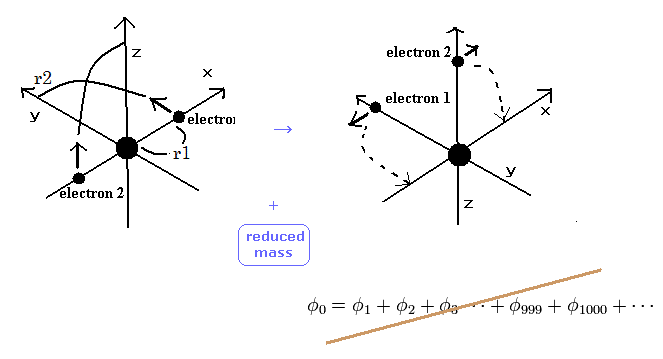
Table 2 に示したように、 2 × 1s の波動関数を用いた 変分法は -77.4904 eV の結果を与え、これは実験値 -79.0051 eV と少し異なる。
一方で 新しいボーア模型は わずかな相対論効果を除けば -79.0037 eV と 実験値にきっかりの値を与えることができた。
-77.4904 eV と -79.0051 eV の違いは 非常に重要である。
なぜなら この違いは 明らかに 2つの電子間の 反発相互作用 ( 運動 ) によって生じたものだからである。
シュレディンガーの波動関数は 明確な電子の運動や 2つの電子間の 相対的な位置関係、換算質量の影響などを 具体的に示せない。
これが 変分法の限界である。
上のセクションでは、ヘリウムの変分法が新しいボーア模型ヘリウムに性質が似ている理由を示した。
リチウム原子に関してはどうであろうか?
リチウム原子の基底状態エネルギーは -203.48 eV である。
リチウムのハミルトニアン演算子は、次に示したものだ。
(Eq. 24)
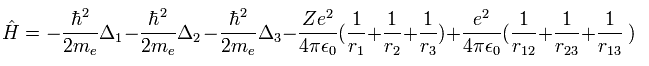
ここで Δ = ∇2 である。
もし、リチウムのエネルギーを Eq.4 や Eq.6 のように計算してみると、結果は -214.3 eV となり、これは実験値よりも低く なってしまう。
これは変である。
この変な結果は、リチウムの3番目の電子が 1S 軌道に実際には入れないことから生じる。
そのため、正しい結果をだすには、変分波動関数を制限する必要がある。
リチウムの変分法では、変分波動関数として、次のような3次の行列式を使用する。
(Eq. 25)
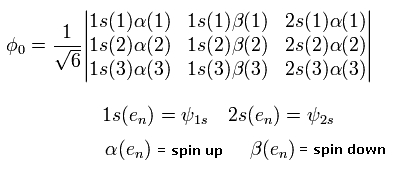
ここでは、1S() と 2S() は 水素原子の波動関数である。
また、1, 2, 3 の数字は電子の番号を示している。
ところで、どうして この行列式を使うのだろうか?
行列式においては、それらの2つの電子が 同じ状態のとき、波動関数全体は ゼロになってしまう。
波動関数がゼロになると、全エネルギーは ゼロになり、これはもちろん基底状態のエネルギー ( -203.48 eV ) よりも 高い。
そのため、リチウムの3番目の電子として、1S の波動関数を使うことはできなくなる。
Eq.25 を使って、変分パラメーター Z1 と Z2 を変化させると、リチウムの最低値は -201.2 eV となり、これは実験値 (-203.48 eV) に近い。
この場合は、Z1 と Z2 はそれぞれ +2.686 と +1.776 になる。
なぜなら 1S 電子は 2S の電子よりも核に近いからである。
驚くべきことに、実験値に近いこれらの近似値は 変分法を使った手計算で 1933 年 に得られた。
(E.B. Wilson, Jr., J. Chem. Phys., 1, 210, 1933)
しかし もちろん "実在の"ボーア模型は コンピューターがない時代なので このようなすばらしい結果を 1933 年に得ることはできなかった。
| 原子 | r1 (MM) | WN x 4 | 計算結果 (eV) | 実験結果 (eV) | 誤差 (eV) |
|---|---|---|---|---|---|
| Li | 1949.0 | 1.000000 | -203.033 | -203.480 | 0.47 |
| Be+ | 1427.0 | 1.000000 | -388.785 | -389.826 | 1.04 |
| B2+ | 1125.0 | 1.000000 | -635.965 | -637.531 | 1.56 |
| C3+ | 928.0 | 1.000000 | -944.46 | -946.57 | 2.11 |
| N4+ | 790.5 | 1.000000 | -1314.25 | -1317.01 | 2.76 |
| O5+ | 688.0 | 1.000000 | -1745.70 | -1748.82 | 3.12 |
| F6+ | 609.4 | 1.000000 | -2237.60 | -2242.21 | 4.61 |
| Ne7+ | 546.0 | 1.000000 | -2791.15 | -2797.12 | 5.97 |
(Fig.7) 3電子原子模型。
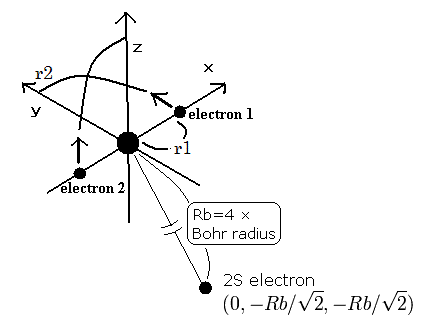
Table 3 もしくは このページに示したように、
新しいボーア模型のリチウムは -203.033 eV という より正確な値をだすことに成功した。)
また 他の3電子原子 (イオン) も 新しいボーア模型を用いて正確に表わせた。
Z1 が大きく、 Z2 が小さくなると、1S と 2S の電子の 分布はお互いにより離れる (Fig.8)。
(Fig.8) 1S と 2S の電子の確率密度の変化。
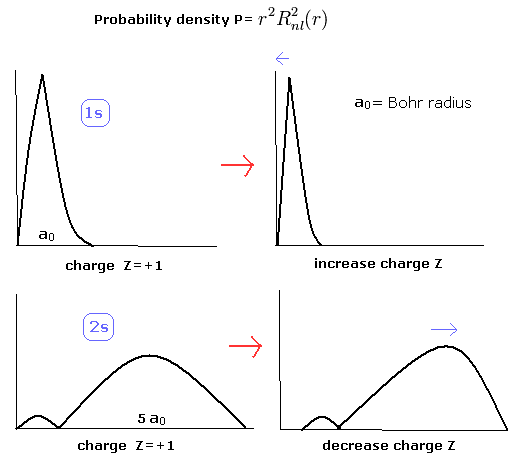
そのため、リチウムでは 1S と 2S の波動関数の重なった部分は 小さくなり、行列式の反対称な性質による消失も小さくなる。
もちろん、1S (Eq.2) と 2S の電子の分布 (水素様原子の)は、ボーア模型と 同じである。 ( ボーア模型と量子力学では位置エネルギーが同じであるから。)
よって、リチウムにおいてもボーア模型は量子力学と酷似している。
しかし このページに示したように、波動関数や行列式のような 数学上の ( 物理でなく ) 概念は 明らかに科学の発展を妨げている。
(Fig.9) 重ね合わせ = 非現実的な多世界 !
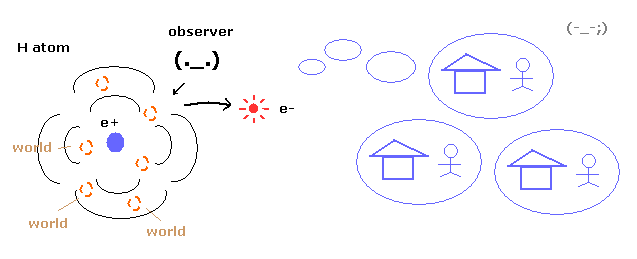
ご存じのとおり 量子力学は 電子の具体的な運動をまったく示すことができない。
それは 水素原子における 電子の確率密度のみを示すだけである。
そのため 波動関数の 収縮 (収束) を説明するためには、非現実的な多世界を必要とする。
(Fig.10) 1 × ドブロイ波長 = 水素の基底状態。

このページに示したように、シュレーディンガーの水素原子も ドブロイ波長の整数倍の条件を満足する。
これが シュレーディンガーの水素原子が ボーア模型と完全に同じ結果を与える理由である。
Fig.10 に示すように、水素原子の基底状態では ボーア模型は 接線方向のドブロイ波で シュレディンガーの水素 ( rR ) は 動径方向のドブロイ波で構成されている。
( 確率密度 |rR|2 のグラフを見ても このことを容易に理解できる。)
実際に、水素原子の基底状態の確率密度は ボーア半径周囲で もっとも高い。
問題は シュレディンガーの動径方向の波動関数は 必ず ゼロから無限大に広がっていなければならない。
また 1s のドブロイ波は 線状なため、それらの逆位相どうしが 重なり合って互いに打ち消しあってしまう。
(Fig.11) シュレーディンガーの波動関数は 必ず無限大まで広がっている。
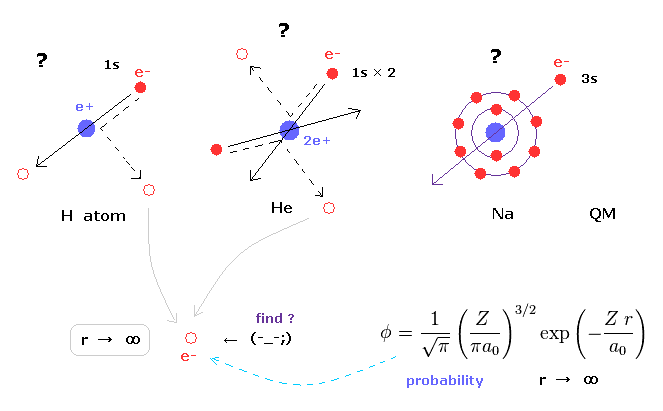
ヘリウムや水素分子なども含めた 様々な原子、分子における シュレーディンガーの波動関数は 必ず 無限大まで広がっている。
これはつまり 非常に安定なヘリウムの 基底状態の電子でさえ、無限遠の近くで見つけることができるという意味である。
もちろん こんなことはあり得ないので 量子力学(化学)は 様々な原子や分子のリアルな状態を説明できる能力がないことになる。
ヘリウム原子のシュレーディンガー方程式は解くことができないが、その変分関数は 必ず無限大まで広がっている。
(Fig.12) シュレーディンガーの 2P の "動径方向" の波動関数 ( 角運動量 = 1 )。
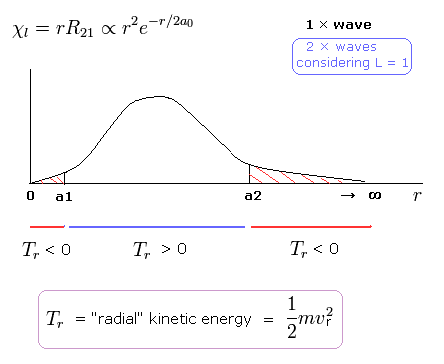
例えば、シュレーディンガーの 2P の状態では、Fig.12 に示すように 動径方向の運動エネルギー (= 1/2mv2 ) が 両サイドで マイナスになる。
( 2P 状態では、 エネルギー準位は n = 2 で 角運動量は L = 1 である。 )
この奇妙な状態は いわゆるトンネル効果とは何の関係もない。
なぜなら Fig.12 の 0 から a1 の領域では、位置エネルギーは 全エネルギーよりも低いからである。
接線方向の運動エネルギーの増加をキャンセルするために、動径方向のエネルギーが マイナスにならなければならないのである。
これらの不合理な状態が シュレディンガーの水素原子が 間違いであることを示している。
(Fig.13) 量子力学のヘリウムは カオスになり不安定である。

量子化学では もし 水素原子の 1s の波動関数を使用すると、ヘリウムの近似的な基底状態のエネルギーを得ることができる。
お気づきのとおり、1s の状態は 角運動量がゼロである。
この状態では ヘリウムの2つの状態は カオス状態になり、それらの間のクーロン反発力のため 非常に不安定になる。
つまり 量子力学のヘリウムは リアルなヘリウム原子とは まったく異なるものである。
(Fig.14) 量子力学のヘリウム。
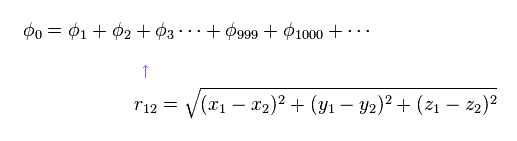
シュレーデインガー方程式を用いて ヘリウム ( もしくは 水素分子 ) などの 正確な基底状態を得るためには Fig.14 に示すように 千以上の変分関数を使用しなければならない。
(Fig.15) ヘリウム もしくは H2 の確率密度 ?
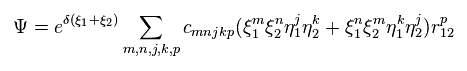
これらの変分関数は 2電子間の距離を表す変数 (= r12 ) を含まなければならない。
そのため 定常な水素原子と異なり、ヘリウム (もしくは H2 ) の電子 1 を発見する確率密度は 電子 2 の位置に応じて絶えず変化していることになる。
つまり このヘリウムの変分関数は 曖昧な確率密度波の点からも 2つの電子が実際に動いていることを示している。
(Fig.16) 換算質量 = 電子と原子核は実際に動いている。
ご存じのとおり、電子の換算質量を用いると、水素原子においても より正確な エネルギー準位の値を得ることができる。
この事実は 明確に電子と原子核が互いに相互作用しながら実際に動いていることを示している。
もちろん、電子の分数電荷は 実際に見つかっていないため、ヘリウムの2つの電子のリアルな動きを直に示す必要がある。
このページに示したように、量子力学では ガイド波 (ボーム) 理論でさえ 2電子のヘリウムを説明できない。
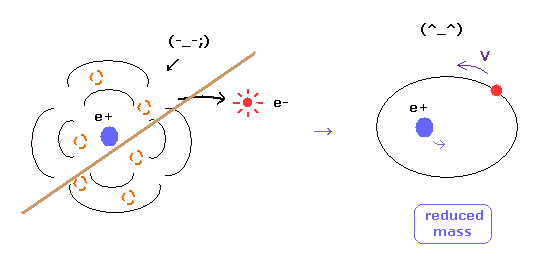
(Fig.17) 換算質量を用いた計算結果は より正確になる。
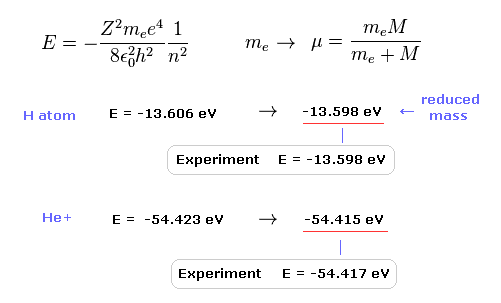
水素原子の基底状態エネルギーの実験値は -13.598 eV である。
この基底状態のエネルギーをシュレーディンガー方程式 ( もしくは ボーア模型 ) を用いて計算すると、
それは -13.606 eV になる。
原子核の運動を考慮して 通常の電子質量を 換算質量に置き換えると、この計算結果は より正確になる (= 13.598 eV )。
この結果は 明らかに 原子内の電子と原子核が 実際に動いていることを示している。
He+ イオンにおいても、換算質量を用いると、より正確な値 (= -54.415 eV ) を得ることができる。通常の電子質量だと -54.423 eV となる。
He+ の実験値は -54.417 eV である。
(Fig.18) 2電子原子モデル ( He, Li+, Be2+, B3+, C4+ ... )

トップページに示したように、もし 2つのドブロイ波 (= 1 × 波長 ) が 互いに重なりあっているとすると、それらの逆同士の位相は干渉で打ち消し合う。
( この電子のドブロイ波の打ち消し合いは ダビッソン・ガーマーの実験で確認されている。)
そのため 2つの電子軌道は 打ち消し干渉を避けるために 互いに垂直にならなければならない。
| 原子 | r1 (MM) | WN x 4 | 同一円軌道 | 計算結果 (eV) | 実験結果 (eV) | 誤差 (eV) |
|---|---|---|---|---|---|---|
| He | 3074.0 | 1.000000 | -83.335 | -79.0037 | -79.0051 | 0.001 |
| Li+ | 1944.5 | 1.000000 | -205.78 | -198.984 | -198.093 | -0.89 |
| Be2+ | 1422.0 | 1.000000 | -382.66 | -373.470 | -371.615 | -1.85 |
| B3+ | 1121.0 | 1.000000 | -613.96 | -602.32 | -599.60 | -2.72 |
| C4+ | 925.0 | 1.000000 | -899.67 | -885.6 | -882.1 | -3.50 |
| N5+ | 788.0 | 1.000000 | -1239.8 | -1223.3 | -1219.1 | -4.20 |
| O6+ | 685.3 | 1.000000 | -1634.38 | -1615.44 | -1610.70 | -4.74 |
| F7+ | 607.3 | 1.000000 | -2083.3 | -2062.0 | -2057.0 | -5.00 |
| Ne8+ | 544.5 | 1.000000 | -2586.7 | -2563.0 | -2558.0 | -5.00 |
Table 4 に示すように、これらの2電子原子模型は 様々な原子における 実際のエネルギー状態を完全に再現することが可能である。
このヘリウムの基底状態エネルギー ( -79.0037 eV ) は 量子力学的な変分法 ( -79.015 eV ) よりも より正確な値を出すことができた。
なぜなら 量子力学のヘリウムは 原子核の動き (換算質量) を正確に扱えないからである。
具体的な計算プログラムに関しては このページを参照のこと。
(Fig.19) 新しいボーア模型のヘリウム (= A.) は 電気的に分極していない。
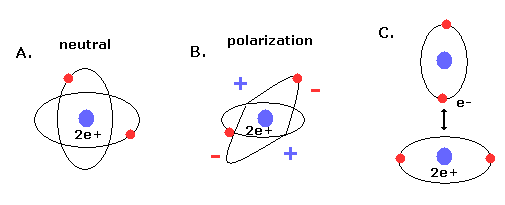
さらに このヘリウム模型は ヘリウムが最も安定な原子で かつ 他の原子 もしくは 自分自身と化合物を形成しない という事実と ちょうど一致する。
なぜなら 2つの軌道が 互いに垂直だと、2e+ 原子核の周囲の空間は 電子の均等分布のため ちょうど中性になるからである。
また ドブロイ波の安定性を考慮すると、Fig.18 のヘリウムには 3番目の電子が入っていく空間は残っていない。(= パウリの排他原理 )。
もし 3番目の電子が そこに入っていくと ドブロイ波どうしで 打ち消し合うものがでてきて 不安定になってしまうからである。
(Fig.20) "数学上の" シュレーディンガー方程式 vs. "リアルな" ボーア模型。
私達は シュレーディンガーの波動関数が何なのかを知ることができず、それが何かを問うことを諦めている。
さらに、このページに示したように、たとえ 相対論的な場の量子論を勉強したとしても ミステリアスなパウリの排他原理が何なのか知ることができない。
彼らは 数学上の演算子の反交換性が パウリの排他原理を意味しているという主張しかできない。
このページに示したように、私たちは この非常に制限された 曖昧な条件のもとでは より簡単で有用な方法を試して発展させることができない。
この役になっていない現在の量子化学を 分子生物学や ナノテクノロジーなどの他分野に 応用することができないため、それらの発展は 分子レベルにおいて 現在 すべてストップしている。
(Fig.21) 密度汎関数法 = 近似。
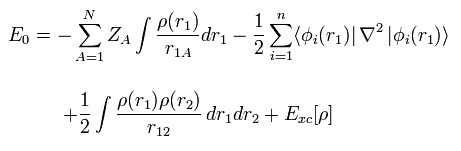
最初に、現在頻繁に使用されている 密度汎関数法 (= DFT ) は 単なる近似 であり、第一原理 ( ab-initio 方法 ) ではないということである。
DFT は 半経験的な手法の1つである。
実験結果に合わせるため LDA などの様々な近似方法を 人為的に選択しているだけにすぎない。
つまり 現在人気がある DFT そのものは 真の理論ではない。

2013/2/12 updated This site is link free.