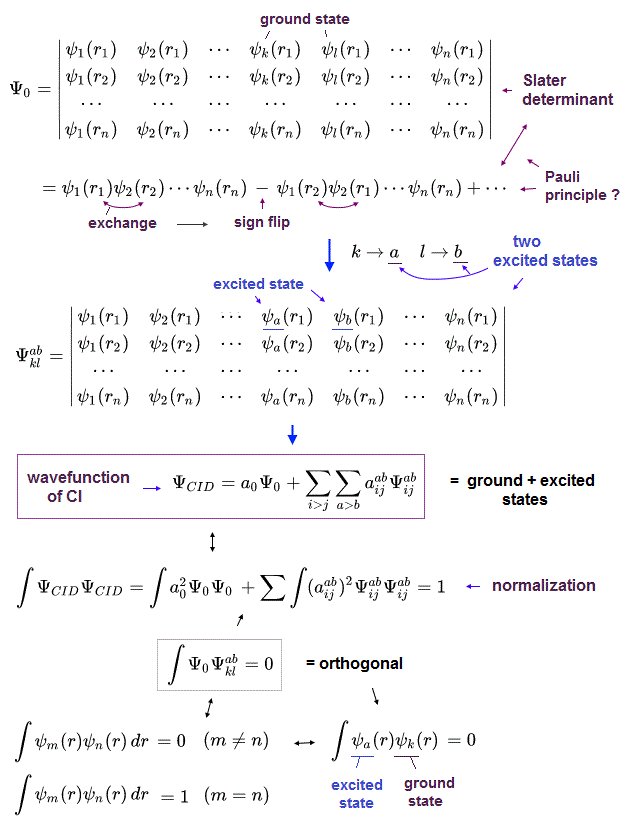
トップページ (2電子原子も含む正確な新ボーア模型)
シュレディンガー方程式は ボーア・ゾンマーフェルト模型の一部。
加速膨張宇宙は間違っている。
(Fig.1) ↓ これは本当に役に立つの ?
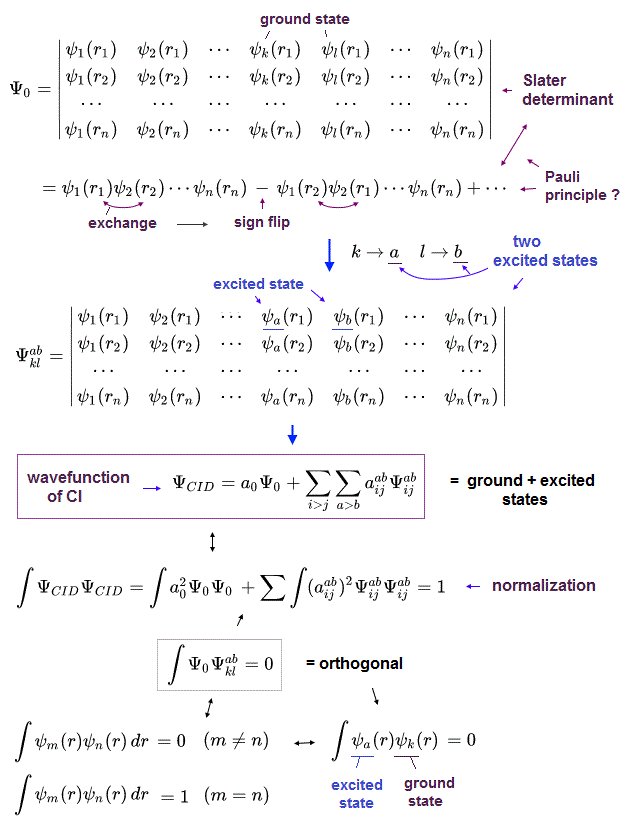
このページに示したように、現在の量子化学は パウリの排他原理と波動関数の 真のメカニズムに関して 決して問おうとはしない。
そのため 私達は シュレディンガー方程式と 非常にやっかいな数学上の 行列式を 盲目的に信じて進むしか他に方法がないのが現状である。
( Fig.1 のような行列式では、 2つの軌道 (= 行や列 ) が 同じとき、この行列式は ゼロになってしまうため、これがパウリの排他原理だと 彼らは主張している。)
小さな複数電子原子でさえ、シュレディンガー方程式を 正確に解くことはできない。
ましてや シュレディンガー方程式を使って タンパク質などの大きな分子を扱うことは
不可能である。
現在の量子化学の計算手法は すでに限界に足しているのにも関わらず、彼らは 決して 波動関数やパウリの排他原理の 真の意味を問おうとはしない。
これらの姿勢は 明らかに自己矛盾である。
このページや このページに示したように、パウリの排他原理を 未知なままに放置 (= 単なる 生成消滅演算子の 反交換子として諦める ) しているからこそ、 スピン、光子、フォノン、仮想粒子などの 架空の粒子を 作らざるを得なくなった。
(Fig.2) どうして 量子化学は 正確な値を与えられるのか ?

Fig.1 の複雑な波動関数と変分法を用いて、量子化学は 様々な原子や分子で ほぼ正確な値を出せる。
重要な点は ほとんどの教科書は シュレディンガー方程式による エネルギー計算値が 実験値に近くなる本当の理由について 決して 書こうとしないことである。
ただ 盲目的に シュレディンガー方程式を信じ、その波動関数の真の意味を 問うこと自体は 意味がないと主張しているだけである。
しかし 科学は 宗教の様に ただ信じればいいってもんじゃない。
実は この答えは これらの量子化学的手法は クーロンエネルギーと 様々なエネルギー準位の水素様原子の波動関数 ( 1s, 2s, 2p ... ) を介して 整数倍のドブロイ波長 という概念 に基づいているため 正確な値をだせるのである。
これが 現在の量子化学の 本当のメカニズムである。
(Fig.3) ドブロイ波長 + 変分法 = 量子化学の核心。

量子化学における ハートリー・フォック ( Hartree-Fock ) 法と 配置間相互作用法は 1s, 2s, 2p, 3s, 3p などの水素原子の原子軌道に基づく変分原理を用いている。
また 各係数と 電荷 Z は 変分パラメーターとして扱われる。
それらの変分パラメーターを変えることによって 最も低いエネルギー値を探していく。
重要な点は ドブロイ波長の整数倍という概念は 必須事項であり、これらの変分法には 必ず 密かに使用されている。ほとんどの教科書は 決してこの重要な事実を 表に出そうとはしないが・・。
後で説明するが、水素様の変分関数は 適切な電荷 Z を探していく過程で
必ず それに特異的なドブロイ波長を維持している。
(Eq.1) シュレディンガーの波動関数。

ここで Eq.1 の 1s と 2p の水素様原子の波動関数を 変分法のメカニズムの説明に使用する。
このシュレディンガーの水素様原子 (= 原子核の電荷 Z ) は 次のエネルギー準位を与える。
(Eq.2)
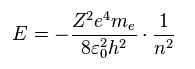
これらのエネルギー準位はすべて ボーア模型と 完全に 等しい。
ボーア模型では、主量子数 n=1 は この軌道が ドブロイ波長の 1 倍 であることを示している。
シュレディンガーの波動関数も まったく同じエネルギー準位を与えることを考慮すれば、この波動関数も ドブロイ波長の整数倍の条件を満たすのだろうか?
実は、 このセクションに示したように、シュレディンガーの波動関数も 必ず ボーア・ゾンマーフェルト模型と同じ 整数倍のドブロイ波長の概念を 採用しているのである。
ほとんどの教科書は この非常に重要な真実に 決して 触れようとはしないが。
(Eq.3) ビリアル定理。
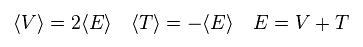
このページに示したように、シュレディンガーの水素原子も ボーア模型のように ビリアル定理を 満足する。
Eq.3 では、平均のポテンシャル (位置) エネルギー V は 全エネルギー E の 2倍になる。
全エネルギー E は ポテンシャルエネルギー V と 運動エネルギー T の和である。
Eq.2 と Eq.3 から、ポテンシャルエネルギー V は エネルギー E の2倍になる。
(Eq.4)
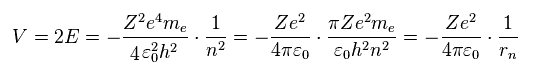
ここでは
(Eq.5)
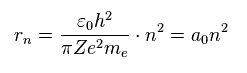
rn は シュレディンガーの水素原子とボーア模型の両方において 平均的な軌道半径となる。
Eq.5 の "n" は 主量子数で、これは エネルギー準位を表す。
つまり n = 1 と n = 2 のとき、各平均の軌道半径は、
(Fig.4) 各エネルギー準位における 軌道半径。

原子核の電荷 Z = 1 で、 n = 1 のとき、軌道半径 a0 を "ボーア半径" と呼び、シュレディンガーとボーア模型の両方の水素で 重要な値である。
(Eq.6) 変分関数 1s, 2p.
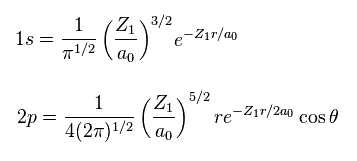
量子化学では、変分パラメーター Z1 を含む水素様波動関数が使用される。
これらは スレーター ( Slater ) 型の軌道と呼ばれる。
Eq.6 は 1s と 2p のスレーター型の軌道である。
Eq.6 を用いて、 波動関数の パラメーター Z を Z1 に変える。
(Eq.7)
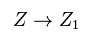
ここでは 電子の波動関数内に含まれる 変分パラメーター Z のみ 変更した ( → Z1 )。
原子核の電荷 Z は 変更していない。
(Fig.5) 波動関数内の パラメーターを Z1 に変更。

Fig.5 の状況を考慮し、 Z1 を Eq.4 と Eq.5 に代入して、 軌道半径 rn と ポテンシャルエネルギー V は
(Eq.8)
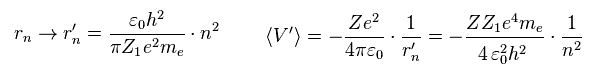
波動関数に含まれる Z が変わると ( → Z1 )、平均の運動エネルギー (= T ) は
( ビリアル定理 T = -E を用いて )
(Eq.9) 平均の運動エネルギー T。
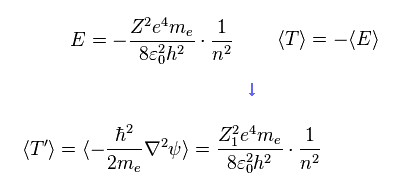
Eq.7、 Eq.8、Eq.9 では、波動関数そのものに含まれる 電荷のパラメーター Z のみ Z1 に変えた。
そして 原子核の電荷 Z は 変えていない。 ( Fig.6 参照のこと。 )
なぜなら 波動関数内の この Z1 は 量子化学において 変分パラメーターとして使用されているからである。
結果的に 運動エネルギー T 内の すべての Z が Z1 に変わる。なぜなら 運動エネルギー T の情報は 波動関数の中に含まれているからである (Eq.9)。
そして ポテンシャルエネルギー V 中の Z は 1つだけ Z1 に変わった。なぜなら もう1つの Z は 原子核の電荷 Z に由来しているからである ( Eq.8 参照。 )
(Fig.6) 波動関数内の変分パラメーターを Z1 に変更。

新たな全エネルギー E' は ポテンシャルエネルギー V' (= Eq.8 ) と 運動エネルギー T' (= Eq.9 ) の和である。
(Eq.10)
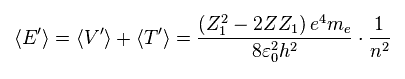
Eq.10 の パラメーター Z1 を変更して、全エネルギー E は このパラメーター Z1 が 原子核の電荷 Z に ちょうど等しいとき、最も低くなることが分かる。
(Eq.11) Z1 = Z のとき → 全エネルギー E は 最も低くなる。
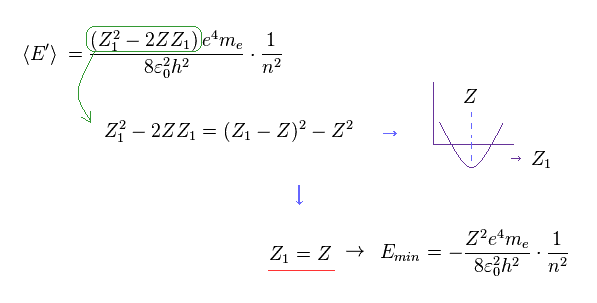
これが ハートリー・フォックや 配置間相互作用法 (= CI ) などの 量子化学の すべての 第一原理計算における 真のメカニズムである。 .
Eq.11 の結果は 波動関数内に含まれる変分パラメーター Z1 は 電子が感じる 本当の電荷 Z に 最も近づく必要があることを示している。
さらに重要な点は このメカニズムは すべてのエネルギー準位 "n" の波動関数で成り立っているということである。( Eq.11 参照 )。
(Fig.7) 変分パラメーター Z1 = Z のとき、エネルギー E は 最も低くなる。

Fig.7 は 変分法で使用されているメカニズムの概要である。
例えば、1s の水素様波動関数を使うと、この波動関数は必ず 1 × ドブロイ波長になる。
そして 変分パラメーター Z1 が 電子が感じる原子核の電荷 Z に等しいとき、全エネルギー E が最も低くなり 安定となる。
波動関数内の この Z1 が Z よりも 大きいときは ( Fig.7 左 )、運動エネルギー T が 大きくなりすぎて、これが ポテンシャルエネルギー V の減少を上回る。よって 全エネルギー E は 高くなる。
この Z1 が Z よりも 小さいとき、原子半径が 大きくなり ポテンシャルエネルギー V が 高くなる。
結果的に Z1 = Z のとき、全エネルギー E は 最も低くなる。
(Fig.8) Z1 = Z のとき → n = 2 でも エネルギー E が 最も低くなる。

2p の波動関数 ( n = 2 ) を用いても、Fig.7 の変分メカニズムは 有効である。
Eq.11 に示したように、主量子数 "n" に関係なく、 波動関数内のZ1 が 原子核の電荷 Z に等しいとき、 全エネルギー E は 最も低くなる。
1s と 2p の波動関数の主要な違いは 2p の関数は 2 × ドブロイ波長を表しているということである。
2p の波動関数を 試行関数として用いると、その原子半径は 1s の波動関数よりも大きくなる。
( Z1 を ある値よりも 大きくして 原子半径を小さくしようとすると、全エネルギーは 高くなって不安定になる。 )
(Fig.9) S 軌道 の波動関数の角運動量 L = 0 → ドブロイ波が 打ち消し合ってしまう。

もちろん、シュレディンガー方程式も 様々なエネルギーを計算する際に 完全に ドブロイ理論 ( p = h/λ ) に依存していることは言うまでもない。
この事実にも関わらず、量子力学は リアルなドブロイ波を認めることを 非常に嫌っている。なぜなのだろうか?
このセクションや このページに示したように、シュレディンガーの水素も 整数倍のドブロイ波長に依存していることを証明できる。
ボーア・ゾンマーフェルト模型では、軌道は 楕円形もしくは 円形になり、線状 ( L = 0 ) にはなることはできない。
なぜなら S 軌道 の波動関数のように 角運動量 L がゼロのとき、逆位相を持つドブロイ波が 互いに打ち消しあってしまうからである。
" 整数倍 " ということは これらのドブロイ波の位相が 軌道1周した末端どうしでフィットし、波同士の打ち消しを 回避できることを意味する。
( また L = 0 のとき、電子は 原子核に 必ず衝突してしまう。これはあり得ない状況である。 )
しかし、シュレディンガーの水素では S の波動関数を含んでいるため、角運動量 L は ゼロになることができてしまう。
これらの状況では、電子のドブロイ波の逆位相同士が 重なって 互いにキャンセルし合ってしまう。ダビッソン・ガーマーの電子干渉実験によれば、この状況では 電子が軌道から 追い出されてしまう。
この現在の不合理なモデルが 彼らが 量子力学において 実在のドブロイ波を 認めず、奇妙な 多世界様の重ね合わせという概念が 支配的になっている要因の1つである。
(Eq.12) ヘリウム原子 ( He ) のシュレディンガー方程式。

量子力学は ヘリウム原子の ほぼ正確なエネルギー値を与えられると言われている。
もちろん、3体問題は 正確に解くことができないため、何らかの近似に頼らざるを得ない。
Eq.12 は ヘリウム原子のハミルトニアン (= 全エネルギー ) である。
ヘリウム (= He ) は 2つの電子 (= 1, 2 ) と Z = 2 の正電荷の原子核を含んでいる。
Eq.12 の 最初の2つの項は 2つの電子の運動エネルギーである。
そして 残りの項が Z = 2 の原子核と 2つの電子間の ポテンシャルエネルギー である。
r12 は 2つの電子間の距離である。
(Eq.13) ヘリウムの 1s × 1s 波動関数。

2つの電子において 1s 型の変分関数 ( Eq.6 参照 ) を使用する。
"Z1" は 電荷の変分パラメーター、
"a0" は ボーア半径である。
Eq.13 の波動関数と Eq.12 のハミルトニアンから、全エネルギー W は
(Eq. 14)
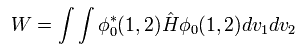
Eq.14 を解いて、次を得る。
(Eq. 15)
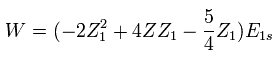
Eq.15 では、 E1s は -13.606 eV である。
変分パラメーター Z1 を変更して 最も低いエネルギー W を探す。
W を Z1 に関して微分して
(Eq.16)

Eq.16 に示したように、変分パラメーター Z1 が 1.687 のとき、 ヘリウムの全エネルギーは 最も低くなる。
(Eq.17)
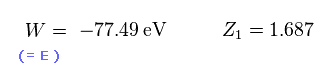
ヘリウムの基底状態のエネルギーは 実験値で -79.005 eV である。
Eq.17 は 実験値に近いが 少し違う。
なぜなら 量子力学の 定常な波動関数は 互いに避け合う2つの電子を 正確に 扱えないからである。
量子力学は 粒子の具体的な動きを 非常に嫌っており、ただ 漠然とした確率密度を示すだけである。
2つの負電荷の電子が 互いに避け合うには、静的な波動関数を 動的な波に変更する必要がある。
しかし この 動的な波動関数は明らかに 確率密度を示すという量子力学の基本的な波動関数の性質と
矛盾していると言わざるを得ない。
あなたがたも思われたとおり、2つの電子が 互いに避け合うのを 素直に表そうとすれば リアルな 動く複数の粒子を使用するしかないのである。
(Fig.10) 水素とヘリウム原子。
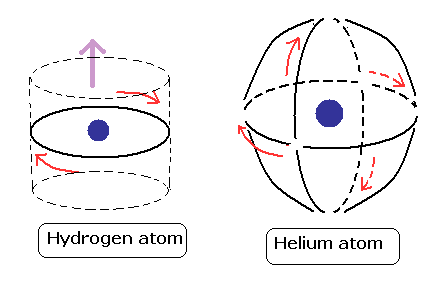
トップページに示したように、ヘリウムの2つの軌道が 互いに 垂直であるとすると、自然に 正確な基底状態エネルギーを得ることができる。 ( 計算値 -79.0037 eV は -0.0013 eV だけわずかに異なるが これは いわゆる相対論的効果である。 )
2つの軌道を互いに垂直にする理由は 2つのドブロイ波の 干渉による打ち消しを回避するためである。
このドブロイ波の打ち消しを考慮すれば、パウリの排他原理 (= Li の三番目の電子が 1s 軌道に入れない ) を 新しいボーア模型によって自然に 説明することができる。
スピン・スピン相互作用は クーロン引力に打ち勝って 強力な パウリの排他原理を引き起こすには 余りにも弱すぎる。 (= 微細構造レベル、 0.00005 eV。 )
例えば、Li の 3番目の電子を 1s から追い出すには 少なくとも10 eV 以上の反発力が必要である。
| 原子 | r1 (MM) | WN x 4 | 円軌道 (eV) | 計算結果 (eV) | 実験結果 (eV) | 誤差 (eV) |
|---|---|---|---|---|---|---|
| He | 3074.0 | 1.000000 | -83.335 | -79.0037 | -79.0051 | 0.001 |
| Li+ | 1944.5 | 1.000000 | -205.78 | -198.984 | -198.093 | -0.89 |
| Be2+ | 1422.0 | 1.000000 | -382.66 | -373.470 | -371.615 | -1.85 |
| B3+ | 1121.0 | 1.000000 | -613.96 | -602.32 | -599.60 | -2.72 |
| C4+ | 925.0 | 1.000000 | -899.67 | -885.6 | -882.1 | -3.50 |
| N5+ | 788.0 | 1.000000 | -1239.8 | -1223.3 | -1219.1 | -4.20 |
| O6+ | 685.3 | 1.000000 | -1634.38 | -1615.44 | -1610.70 | -4.74 |
| F7+ | 607.3 | 1.000000 | -2083.3 | -2062.0 | -2057.0 | -5.00 |
| Ne8+ | 544.5 | 1.000000 | -2586.7 | -2563.0 | -2558.0 | -5.00 |
驚くことに、この新しいボーア模型のヘリウムの手法は 他の 2電子、3電子の原子 (イオン) にも正確にあてはまる。
計算手法に関しては このページを参照のこと。
(Fig.11) 変分パラメーター Z1 は 本当の電荷と等しくなる必要がある。

Eq.17 で述べたように、変分パラメーター Z1 が 1.687 のとき、この基底状態のエネルギーは 最も低くなる (= -77.49 eV )。
この電荷の値 1.687 は適切な値である。なぜなら 他の電子の存在のために 各電子が実際に感じる有効電荷が Z = 2 よりも小さくなるからである。
この 1.687 の代わりに Z1 = 2 を代入すると、エネルギーは -77.49 eV よりも 高くなる (= -74.83 eV ) ことがわかる。( このページも参照のこと。 )
これは Fig.7 と同じパターンである。
本当の 中心電荷は 他の電子の存在のために 必ず "2" 未満になる。
波動関数内で 間違った電荷のパラメーターを採用すると、このエネルギーは 増加した運動エネルギーのために 高くなってしまう。
(Fig.12) 各電子の確率密度は r12 に応じて変化している?

Eq.17 に示したように、通常の変分法では ヘリウムの正確な基底状態を得ることができない。
なぜなら シュレディンガーの波動関数は 互いに避けあって動き回る 2つの電子を表現できないからである。
そこで 1928-1930 年に、ヒレラス ( Hylleraas ) は Fig.12 のような 2つの電子間距離 r12 を含む 特殊な波動関数を採用した。
この波動関数は この電子間距離 r12 が長くなるにつれて、絶対値が
大きくなる。
つまり、お気づきのとおり、このヒレラスの波動関数は 定常ではないのである。
この 非定常な波動関数は 明らかに 確率密度を表すという波動関数の原理原則に 違反していると言える。
(Eq.18)
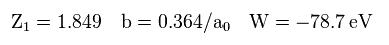
Fig.12 の計算結果は -78.7 eV になり、これは Eq.17 の -77.49 eV よりも低い。しかし 依然として 真の実験値 (= -79.005 eV ) よりも高い。
そもそも 電子間距離に応じて 各地点における確率密度が変化してしまうことは 不合理である。
(Eq.19)

実験値にさらに近づけるには、Eq.19 のような 1000 以上もの変分関数 (= 非常に 非現実的な手法である ) を使用しなければならない。
つまり これらの量子化学的手法は 単純なヘリウムにおいて すでに限界に達しているのである。
さらに 量子化学による最新の計算結果 -79.015 eV は 実験値 (= -79.005 eV ) と少し異なる。
なぜなら ヘリウム原子の波動関数は 原子核の動き (= 換算質量 ) を正確に読めないからである。
(Eq.20) 各電子 = 様々な波動関数の "重ねあわせ" ?

電子間距離を含むヒレラス関数は 大きな原子に適用するには 不可能である。
そのため もっと大きな原子では しばしば 配置間相互作用 (= CI ) 法が使用される。
CI では、原子軌道は 様々な主量子数の波動関数の重ね合わせ状態として扱う。
例えば、Eq.20 では、各電子の波動関数は 5つの異なった変分関数から成り立っている。
驚くことに、これらの変分関数は 非現実的な電荷 (= 2.377, 4.396, 6.527 .. ) を含んでいるのである。
ヘリウムは Z = 2 の正電荷の原子核のため、この Z > 2 の電荷は はっきり言って あり得ない。
これが 変分法における 致命的な欠陥である。
(Eq.21) ヘリウム ( Z = 2 ) における 異なった原子半径の関数の組み合わせ。

結果的に、このヘリウムの波動関数は異なった 原子半径を持つ関数の 組み合わせになる。
例えば、 Eq.21 では、 Z1 = 1.417 における原子半径は Z1 = 7.942 のよりもはるかに大きい。
( すでに述べたように、現実的に Z=2 のヘリウムが Z1=7.942 の電荷の軌道を含むことは 不可能であるが・・。)
Eq.20 の計算結果は -77.9 eV となり、これは Eq.17 (= 重ね合わせなし ) の -77.49 eV よりも 少し低い。
(Fig.13) 2つの電子が 互いに避け合う。

結果的に Eq.20 の重ね合わせ状態では、2つの電子間の 反発相互作用は 異なったタイプの波動関数を含む項で 弱くなる。
Z5 = 7.942 ( ← 非実在 ) の変分パラメーターは 現実のヘリウム電荷 Z=2 よりも大きいため、Fig.7 で述べたように この関数のみを含む項では エネルギーは高くなる。
しかし 異なった大きさの軌道が混ざった項の存在のために 2つの電子間の反発エネルギーが 弱くなるため 結果、全エネルギーが少し低くなる。
この電子相関の原理が 現在の量子化学の第一原理全体に使用されている基本的概念である。
あなたがたも奇妙に思われたとおり、2つの電子が避け合っているのに、決して 量子力学は 個々の電子の粒子像を認めないため、こんなにも厄介な計算手法に頼るしか他に道がないのである。
(Eq.22) リチウム Li ( Z = 3 ) の ハミルトニアン。

リチウム原子 (= Li ) は Z = +3e の正電荷の原子核、2つの 1s 電子と 1つの 2s 電子から成る。
よって ハミルトニアン (= 全エネルギー E ) は Eq.22 に示したようになる。
(Eq.23) スレーター (= 水素 ) 型軌道。

1s、 2s の波動関数は 水素原子に由来する。
Z1 と Z2 は 電荷の変分パラメーターであるため、この Li のケースも Fig.7 や Fig.8 と 同じである。
(Eq.24) もし Li の3つすべての電子が 1s 軌道にあるとしたら ....

重要な点は Li の3つの電子軌道すべてが 1s の波動関数だとしたら、Li の基底状態エネルギーは -214.3 eV 以下となり、これは 実験値 (= -203.5 eV ) よりも低くなってしまう。
つまり この結果は 完全に 変分原理に違反している。なぜなら 変分法を試行する前に 計算結果が 実験値よりも すでに低くなっているからである。
結果的に Li の3つの電子すべてが 1s 状態にあるという考えは 間違いということになる。
Eq.24 の結果を見て分かる通り、 Li 原子は パウリの排他原理の 強力な反発力に完全に依存している。
このパウリの排他原理による 反発力は 10 eV 以上にもなり、これは スピン・スピン相互作用 (= 微細構造レベル, 0.00005 eV ) によるエネルギーよりも はるかに強力なものである。
つまり パウリの排他原理が スピン・スピン相互作用によって生じることは 絶対に あり得ないのである。
(Eq.25) パウリの排他原理 = 行列式 ??

そのため 彼らは 数学上の行列式こそが パウリの排他原理の原因だと主張し始めた。
行列式では、2つの行、もしくは 列が同じとき ( 例えば、 1s = 2s )、この波動関数全体は ゼロになってしまう。
つまり Eq.25 の 2s の関数は 1s にはなり得ない、と彼らは主張している。
しかし 見て分かるとおり、この行列式は 単に "数学的に" 2s が 1s と同じになるのを防いでいるだけで 物理的な意味は まったくないと言っていい。
実際、彼らは パウリの排他原理の具体的な機構に関して、何も語ろうとしない。
このページに示したように、相対論的な場の量子論においても、単に 抽象的な 反交換子 を示したにすぎず、それ以上の具体的なものは 何もない。
この 曖昧で よく分かってないパウリの排他原理 (= 反交換子 ) こそが 現在の場の量子論 ( 物性物理学、素粒子物理も含めて ) が 完全に 役に立たない数学の産物と化している主要な要因である。
(Eq.26)

Eq.25 を Eq.22 に用いると、計算結果は -201.2 eV になる。
このページに示したように、新しいボーア模型は -203.033 eV の基底状態エネルギーを出すことができ、これは 実験値-203.5 eV にほぼ等しい。
Eq.25 で述べたように、スピン・スピン相互作用は クーロン引力に打ち勝って パウリの排他原理を引き起こすには どう転んでも 弱すぎる。
つまり この強い反発力を引き起こす原動力は 1つしか残っていないのである。
このページに示したように、 ドブロイ波の干渉 こそが パウリの排他原理を引き起こす主要な要因である。
(Eq.27) 水素分子イオン (H2+) のハミルトニアン。

水素分子イオン (H2+) は 2つの原子核 +e と 1つの電子から成る。
Eq.27 は この H2+ のハミルトニアンである。
1s の水素の波動関数を用いて、 H2+ の波動関数は
(Eq.28) H2+ の波動関数?

Z1 は変分パラメーターであり、対称性を考慮して、波動関数 ψ が 原子核1と2の波動関数の和と仮定する。
Eq.28 を Eq.27 に用いて、次を得る。
(Eq.29) 核間距離 (= Re ) と 解離エネルギー (= De ).

変分パラメーター Z1 が 1.24 のとき、n1 と n2 の核間距離 (= Re) は 1.06 Å となる。
また 解離エネルギー (= De ) は 2.25 eV となる。
Eq.29 の結果は 次の実験値と異なる。
(Eq.30) H2+ の実験値。
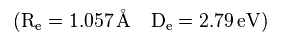
Fig.7 で述べたように、 1s の波動関数は 必ず 1 × ドブロイ波長となる。
変分パラメーター Z1 が 電子が感じる 真の電荷に ちょうど等しいとき、計算結果のエネルギーは 最も低くなる。
( Z1 = 1.24 は 1 より少し大きく、 2 未満であり、この結果は適切である。 )
(Fig.7) 変分パラメーター Z1 = Z のとき、エネルギー E は 最も低くなり安定。

つまり 量子化学による H2+ イオンも ボーア・ゾンマーフェルト模型と同じ ドブロイ波の整数倍という概念を用いている。
Eq.29 の結果は まだ Eq.30 と違う。そこで 彼らは 1s と 2s 水素原子のの波動関数を 次のように 結合させた。
(Eq.31) H2+ イオンの波動関数 ?

ここでは
(Eq.32)

Eq.31 と Eq.32 を Eq.27 に用いて、計算結果は
(Eq.33) H2+ は 2つの陽子から成る。 → この電荷 Z2 は 正しいのか?

有効電荷のパラメーターが Eq.33 のとき、エネルギーは最低になり ( 解離エネルギー = 2.73 eV )、より実験値に近くなった。
しかし 重要な点は 2p の変分関数に含まれる 電荷のパラメーター Z2 は 実際には あり得ない値 (= +2.965 e ) になっているという点である。
H2+ 分子イオンは 2つの 陽子の原子核からなり (= 2 × +e )、 この有効電荷 +2.965 e という値は 存在し得ず、量子化学に 現実性がないことの 動かぬ証拠である。
もちろん、 Fig.8 に示したように、2p の波動関数は 必ず 2 × ドブロイ波長をキープしており、 Z2 が 本当の電荷 ( < 2 ) に等しいときエネルギーは最も低くなる傾向にある。
しかし この H2+ のケースでは この 2p の波動関数は 両方の原子核とも なるべく近づく必要がある。
Z2 が 実際の値 "2" より小さいとき、この波動関数は 他の原子核から 遠く離れすぎてしまう。
( しかしもちろん、現実的に Z2 > 2 という有効電荷は あり得ない。 )
(Fig.14) H2+ の波動関数は 対称、反対称 になれるのか?

何らかの教科書を見ると分かるが、H2+ イオン の波動関数は 対称 (= Fig.14 上 ) と反対称 (= Fig.14 下 ) の波動関数から成るとされる。
しかし現実的な視点からすれば、反対称の波動関数は 単なる数学的なツールで、リアリティーが ないと言える。
(Fig.15) 対称的な関数。

H2+ の波動関数が 対称的だと、2つの原子核が 互いに近づくにつれて 変分パラメーター Z1 は 2 に近づく。
(Fig.16) 反対称の波動関数は 非実在的。

一方で、反対称の波動関数の場合、2つの原子核が 互いにくっつくと、この有効電荷の変分パラメーター Z1 は 0.4 になる。
これは 明らかに あり得ない値である。
この反対称の波動関数は 電子間の 仮想の反発力を表すため、配置間相互作用などに しばしば使用される。
つまり 現在の量子化学というのは 単なる数学上のものにすぎない。
実際、これらの波動関数が 実在のものか問おうとしても、彼らはただ 「問うこと自体に意味がない。」と繰り返すだけで、 物理的な意味での進展は 皆無である。
(Eq.34) 水素分子 (H2) のハミルトニアン。

水素分子は 2つの +e の原子核と 2つの電子から成る。
原子価結合 ( VB = Heitler-London ) 法は MO 法よりも より正確な値を出すことができるため 多くの教科書で紹介されている。
しかし この ハイトラー・ロンドン法は ビリアル定理に従わないことが知られている。
H2 の波動関数は、
(Eq.35) ハイトラー・ロンドン法による H2 の波動関数。

Eq.35 を Eq.34 に用いて、次を得る。
(Eq.36)
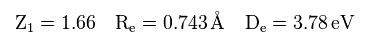
Eq.36 の解離エネルギーは 次の実験値と異なる。
(Eq.37) H2 の実験値。
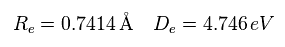
なぜなら H2 分子は 2つの電子間の反発力を含んでいるからである。
ヘリウムのセクションで述べたように、2つの電子が避け合うためには これらの定常な波動関数が動的になる必要がある。
この動的な確率密度という概念は 元の確率密度の概念に反している。
(Eq.38) 本当の水素分子 ? = 100 項以上。
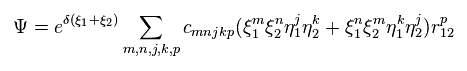
正確な値を得るためには、 r12 を含む 非常に複雑な波動関数を使用しなければならない。
" r12 " は 2つの電子間の距離であるため、ある地点での 電子1の確率密度が 電子2の位置関係に応じて 変化していることになる。
つまり 波動関数が確率密度を表すという 本来の意味は 1電子の水素原子にしか 当てはまらないのである。
(Eq.39) 複数の励起した波動関数の組み合わせ ← 実在の科学として役に立つ?

ハートリー・フォックの波動関数の欠点 ( ex. 電子相関 ) を克服するために、配置間相互作用 ( CI ) 法が 導入された。
量子化学の すべての第一原理計算は この CI 法に基づいている。
各電子配置状態関数 (= CSF ) は スレーター行列式の線形結合で表される。
(Eq.40) 2電子励起の行列式。

CI は 1電子励起配置 (= Eq.39 )、2電子励起配置 (= Eq.40 )、3電子励起配置などの 仮想の関数を用いている。
一見して分かるとおり、これらの関数は うんざりするほど 複雑すぎである。
(Eq.41) 電子は 互いに避け合うのか ?

それなら どうして CI は 実験値に近い計算結果を出せるのだろうか?
主要な要因は、Fig.7 や Fig.8 で述べたように、CI も スレーター型 (= 水素原子 ) 軌道を通して
整数倍のドブロイ波長と 変分法 に完全に依存しているからである。
様々な励起関数を組み合わせると、異なった軌道の2つの電子は 互いに避け合うことができる。
様々な項を増やすことで、CI は 実験値に近い値を出せる 適切な波動関数を見つけることができる。
しかし、 Eq.21 (= He の CI ) や Eq.33 (= H2+ の CI ) で述べたように、励起された仮想軌道の 電荷の変分パラメーター (= Z2 ) は 非現実的である。
( H2+ の場合、 Z2 = 2.965 は 2つの +e の原子核の和よりも 大きい。 )
(Eq.42) CI 法の波動関数。

Eq.39、 Eq.40、 Eq.42 に示したように、この CI の行列式は 大きな分子に適用するには 余りにも複雑すぎである。
そのため 反発しあう電子を表すのに もっとシンプルで現実的な方法を探さなければならない。
波動関数とパウリの排他原理の 具体的なメカニズムを放置したままで それができるわけがない。
(Eq.43) STO と GTO 型の関数。

スレーター型 (= STO ) の軌道は 水素原子に由来しており、これは ガウス型の軌道 (= GTO ) よりも正確な値を出せる。
しかし GTO の基底関数系は STO よりも簡単に計算できるため こちらがよく使用される。
(Eq.44)

GTO の基底関数形を使用するには STO の関数を 複数の GTO 関数の線形結合で表す。
(Eq.45)
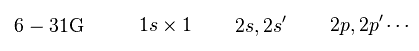
6-31 G 法は 内殻に 6 × GTO、原子価殻に 3 × GTO の関数を用いている。
この原子価殻には 各軌道に 2種類の関数を使用している。
これらの関数の 変分パラメーターや 係数などは 実験値に近い値を出せるよう あらかじめ決めておく。
つまり、 6-31G も CI と同じ整数倍のドブロイ波長と 変分法に依存している。
(Eq.46)

CI 法は 非常に時間がかかるため、もっとシンプルな MP 法が考案された。
例えば、 MP2 ( もしくは MBPT2 ) は Eq.46 に示したような 2次摂動までのエネルギーを用いて計算している。
仮想のエネルギー (= a, b ) は、元のエネルギー (= i, j ) よりも常に高いため、この2次の摂動エネルギーは 必ず負の値になる。
結果的に MP2 は 必ず ハートリー・フォック法よりも 低い基底状態エネルギーを与えうる。
そのため MP2 は 実際の実験値よりも 低い 間違った基底状態エネルギーを 与えてしまうことがある。
( もちろん、実際の値より 低い計算結果をだしてしまう理論は 間違いである。)
(Fig.17) 1s の水素の波動関数 = 1 × ドブロイ波長。

何らかのウェブサイトか教科書で確認してもらうと分かるが 1s の動径方向の波動関数は Fig.17 のようになる。
rR12 は 1/2 ドブロイ波長 (= Fig.17 右 ) であるため、軌道1周 ( ∞ → 0 → ∞ ) は 動径方向に 1 × ドブロイ波長含まれていることになる。
(Fig.18) 2s の水素の波動関数 = 2 × ドブロイ波長。

2s の波動関数の場合は、 1 × ドブロイ波長 (= 1つの山 と 1つの谷 ) が 0 から ∞ の部分に含まれている。
そのため 1周の軌道 ( ∞ → 0 → ∞ ) には 2 × ドブロイ波長が含まれていることになる。
このページに示したように、 ボーア模型における 水素の n=1 と n=2 の軌道は それぞれ 1 × と 2 × ドブロイ波長である。
つまり シュレディンガーとボーア模型の両方の水素で ドブロイ波長の整数倍を満足していることになる。
(Fig.18') 水素原子のシュレディンガー方程式。

χ = rR が ドブロイ波長の整数倍を満たす理由は Fig.18' に示すように 動径関数 R を rR に置き換えると それが 基本的なドブロイの運動量を示す式になるからである。
(Fig.19) 6-s の水素の波動関数の確率密度。

Fig.19 は 6s の水素の波動関数の確率密度 (= 確率振幅の2乗 ) である。
確率密度の関数の 節 の数は
( n - l ) のなることが知られている。
( "n" は 主量子数で、 "l" は 角運動量である。 )
つまり 6s の確率密度の波動関数 ( n = 6, l = 0 ) では、節 の数は 6 - 0 = 6 になる。
結果、波の確率振幅 (= rR6s ) は 3 × 山 と、 3 × 谷 で構成されることになり、これは 0 から ∞ の範囲に 3 × ドブロイ波長が含まれていることになる。
これはつまり 1軌道 ( ∞ → 0 → ∞ ) は 6 × ドブロイ波長 を含んでいることになり、この数は ボーア模型と等しい。
(Eq.45) ゾンマーフェルトの量子化条件 (A) + ドブロイの関係式 (B).
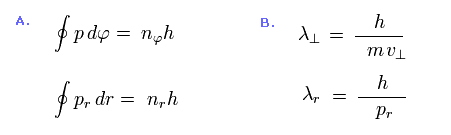
Eq.45 は ボーア・ゾンマーフェルトの量子化条件を表している。
Eq.45A では、 "p" は 角運動量、 "pr" は 動径方向の運動量を表している。
Eq.45B は 接線方向 (= 上 ) と 動径方向 (= 下 ) のドブロイ波長 (= λ ) の式である。
(Eq.46) ゾンマーフェルトの量子化条件 = ドブロイ波長の整数倍。

Eq.45B のドブロイの関係式を Eq.45A のゾンマーフェルトの条件に代入して、接線方向と 動径方向の 両方の軌道で ドブロイ波長の整数倍になることが分かる。
(Fig.20) 2p の動径の波動関数 = 1 × ドブロイ波長 角運動量 = 1.

Fig.20 に示したように、 2p の水素の波動関数は 1つの山のみを含んでおり、1軌道は1 × ドブロイ波長になる。
2p は n=2 のエネルギー準位なのに、どうして 2p の動径方向の軌道は 1 × ドブロイ波長だけなのだろうか?
( Fig.20 右 と Fig.18 右を比較すると分かる。 )
なぜなら 2p は 角運動量 ( l = 1 ) を持つため、 接線方向の 軌道1周にも 1 × ドブロイ波長が含まれているからである。 ( 位相は φ = 0 → 2π で元に戻る。)
結果的に 動径と接線方向の波の和が "2" となり、これは n = 2 のエネルギー準位に一致する。
(Eq.47) ゾンマーフェルトの量子化条件 = ドブロイ波長の整数倍。

基本的に シュレディンガー方程式の角運動量も ボーア模型と同じくħ の整数倍に量子化されている。
つまり シュレディンガーの水素の接線方向が ドブロイ波の整数倍を満たすことは 容易に理解できる。
重要な点は シュレディンガー方程式の 動径方向 ( 1s, 2s, 2p .. ) においても、ドブロイ波長の整数倍を満たすということである。
動径方向の波長 (= λr ) は 動径方向の運動量 (= pr ) を用いて Eq.47 のように表せる。
(Eq.48) ゾンマーフェルト模型と 2p のシュレディンガーの動径方向の関数。

Eq.48 に示すように、1軌道とは A (= 遠日点 ) → B (= 近日点 ) → A (= 遠日点 ) の意味である。
楕円軌道の A と B 地点で、動径方向の運動量は ゼロ になる ( pr = 0 )。
つまり Eq.47 のドブロイの関係式によれば、動径方向の波長は これらの地点で無限大になる ( λr → ∞ )。
2p の動径関数では、両端 ( r = 0 と r = ∞ ) で、波の位相は ストップするため、ドブロイ波長は無限大になる。
( = 波動関数の傾きは 両端でゼロになる。 )
(Eq.49) ボーア模型と シュレディンガーの水素。

Eq.49 の上は ボーア模型の式、 Eq.49 の下は シュレディンガーのハミルトニアンである。
運動量 p は シュレディンガー方程式では 空間微分に置き換えられる。
両方の水素原子とも 完全に同じ関係式 ( E = T + V ) を用いている。
(Eq.50) 楕円軌道の1周。

Eq.50 に示したように、1軌道とは A (= 遠日点 ) → B (= 近日点 ) → A (= 遠日点 ) と動いた範囲である。
水素原子では 軌道形は 対称的なため、1軌道は 2 × ( A → B ) と表される。
Eq.50 では、近日点での半径は r1、遠日点での半径は r2 である。
つまり 動径方向の r の範囲は r1 から r2 の間となる。
( もちろん、 円形軌道では 動径方向の運動は 完全に ゼロになるため 考える必要はない。 )
(Eq.51) 1軌道 (= 左 ) と 半周軌道 (= 右 )。

1軌道が 1 × ドブロイ波長を含むとき、半軌道 ( A → B ) は 0.5 × ドブロイ波長を含む。
(Eq.52) 運動量 p = 1次の微分 ∇

Eq.49 で述べたように、シュレディンガー方程式では、運動量 p は 1次の 導関数 (= ∇ ) に置きかえられる。
(Eq.53) ドブロイの関係式。

近日点と遠日点では、動径方向の運動量は ゼロになる。
シュレディンガーの水素では、ゼロの運動量は 波長 λ が 無限大ということになる。
つまり ドブロイ波長が無限大になる端を見つければ、それが シュレディンガーの水素での 近日点、遠日点ということになる。
(Eq.54) 2p の動径方向の波動関数。

2p の動径方向の波動関数では、ドブロイ波長は r=0 と r=∞ で無限大になる。
なぜなら これらの地点で、一次の導関数 (= 運動量 ) は ゼロになるからである (= 傾きがゼロ )。
(Eq.55)

Eq.55 に示したように、波長 λ が無限大に近づくと、位相の変化はゼロになっていく (= Eq.55 右 )。
(Eq.56) 1次の導関数 = 運動量 p.

Eq.56 は r に関して 1次の導関数であり、これは 動径方向の運動量 pr を意味する。
Eq.56 と Eq.57 に示したように、この導関数は r = 0 と r = ∞ の両端で ゼロになる。
(Eq.57)

Eq.57 は シュレディンガーの水素における半軌道 ( 近日点から遠日点 ) は r=0 から r=∞ であることを示している。
Eq.54 に示したように、このエリアには 0.5 × ドブロイ波長が含まれている。
つまり 軌道1周で 動径方向に 1 × ドブロイ波長含まれていることになる。
(Eq.58)

重要な点は シュレディンガー方程式では 運動量 p = 0 の地点で、運動エネルギー (= p2 ) は ゼロにならないということである。
これは奇妙である。
Eq.58 に示したように、 p2 (= 2階微分 ) がゼロの地点は r =0 や r = ∞ のところと異なる。
(Eq.59)

もちろん、Eq.47 のボーア・ゾンマーフェルトの量子化条件は 1次の運動量 p を用いている。
つまり 波動関数の 1次の導関数を この状況では考慮する必要がある。
結果、この条件での動径方向の両端は r = 0 と r= ∞ になる。
(Fig.21) シュレディンガーの 2Pの "動径" 波動関数。
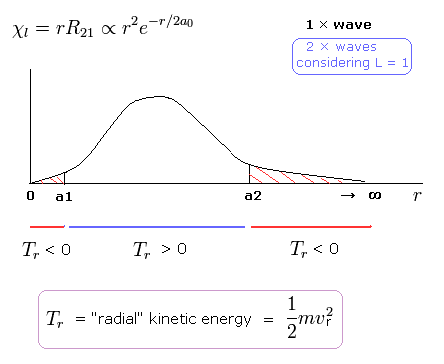
Fig.21 に示すように 2P の動径波動関数 ( χ = rR21 ) は 非現実的な マイナスの運動エネルギー領域を含んでいるのである ( r < a1, a2 < r )。
半径 r が a2 よりも大きいとき、クーロン位置エネルギーは ある上限値よりも 高くなる。
この領域では、全エネルギー (E < 0) を一定に保つためには、動径方向の運動エネルギーがマイナスにならなければならない ( T < 0 ) 。
a1 以下の領域でも 動径方向の運動エネルギーは マイナスになる。接線方向の運動エネルギー (= 角運動量 ) は 正のままなのにである。
これは 明らかに 自己矛盾である。
この不可解な事実は 明らかに シュレディンガーの水素原子は間違いで、ボーア・ゾンマーフェルト模型が
正しいということを示している。

2013/11/23 updated This site is link free.