トップページ (正確な新ボーア模型)
シュレディンガー方程式とボーア・ゾンマーフェルト模型。
ドブロイ波 と 電磁場 の具体的な "姿" とは?
1923 年、ルイ・ド・ブロイが "ド・ブロイ波"を提唱し、これは 1927 年に ダビッソン・ジャーマーによって実験的に証明された。
ド・ブロイの関係式は 電子、中性子、原子などの様々な粒子で確かめられた。
(もちろん、電磁波においても満たされる。)
また、ド・ブロイ波長 (λ) は 運動量 ( p = mv ) のみに影響を受ける。
これは、ド・ブロイ波を生じさせる場は 粒子の速度でなく運動量を感知することを意味する。
なぜなら、異なった質量をもつ様々な粒子は、運動量が同じでも その速度が異なるからだ。
λ = h / p = h / mv
このページでは、シュレディンガー方程式も ド・ブロイ波長の整数倍という考えを使っており、ボーア・ゾンマーフェルト模型の 特殊な1亜系であることを数学的に証明した。
さらに どうして シュレデインガー方程式が間違っているかも示した。
ところで、
我々は、古典力学的な波によって、ド・ブロイ波を表すことが可能であろうか?
このページでは、このことに挑戦することにする。

このページでは、我々は 電子の運動量を 2つの方向に分けた。(接線方向と動径方向に。)
ド・ブロイ波長は 運動量に逆比例している。
では、ド・ブロイ波を ド・ブロイの関係式を満足した形で 2つの方向に正確に分離することは可能だろうか?
(Fig.1) ド・ブロイ波の2つの方向への分離。
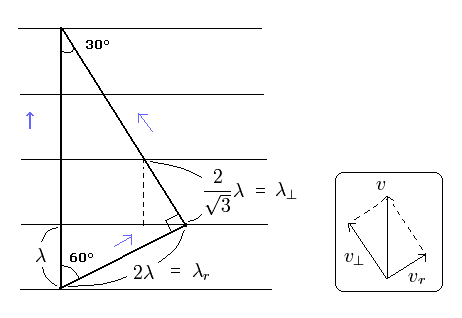
最初に、Fig.1 のケースを考えることにする。
Fig.1 では、移動方向への波長は λ である。
また、接線方向と動径方向の 各波長は Fig.1 に示すようになる。
ところで、これらの波長は 運動量に変換して 三平方の定理を満たすのだろうか?
(Eq.1) 三平方の定理+ド・ブロイの関係式。
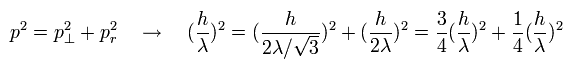
Eq.1 に示すように、ド・ブロイ波長は 何と 三平方の定理を正確に満たしていた。
このことは、ド・ブロイ波が "古典的な"波に等しいことを示している。
また 波の位相 は 次のように表すことができる。
(Eq.1-2)
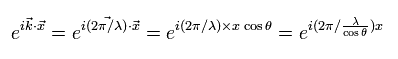
ここで θ は ベクトル x と、移動方向 (k) の間の角度を示している。
Eq.1-2 は 角度 θ が ゼロから θ に変化したとき、 波長 λ は 次のように変化することを意味する。
(Eq.1-3)
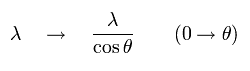
つまり、ベクトル x が 波の移動方向 (k) を向いていないとき、x 方向の波長は λ よりも 長くなる。
このモデルを 任意の角度 θ を使って 一般化する。(Fig.2)
(Fig.2) 任意の角度 θ.
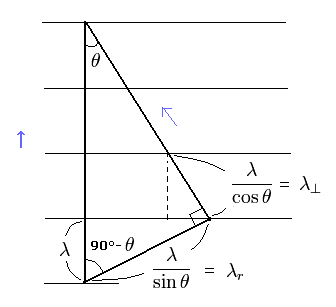
Fig.2 は 運動量において、次の三平方の定理を満足している。
(Eq.2)
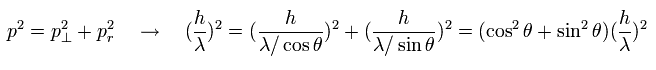
このことは、ド・ブロイ波が古典的な波の性質を持っていることを示している。
Fig.3 では 別の方法でこのことを証明した。
(Fig.3) 2つの直交する波の干渉。
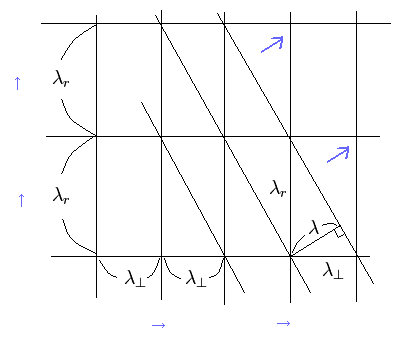
Fig.3 では、接線方向と動径方向の2つの波が互いに 直交している。
斜めの線は 波の位相が強めあう (山+山、谷+谷) 地点を結んだものである。
この斜めの線の間の距離を 新しい波の波長 λ と見なしたとき、これは次の関係式を満たす。
(Eq.3)
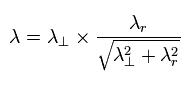
また、これらの波長が、ド・ブロイの関係式を使うことによって、運動量の三平方の定理を満たすことを 次のように示せる。
(Eq.4)
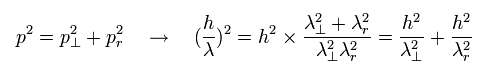
このページに示したように、ボーア・ゾンマーフェルトの量子化条件では、1軌道 (= 2π 回転) に含まれる 接線方向と動径方向の両方のド・ブロイ波が整数倍になる条件を使用している。
ここでは このゾンマーフェルトの量子化条件を 具体的に視覚化してみることとする。
ボーア模型の水素原子の基底状態や、干渉実験の結果を考察すると、1つのド・ブロイ波長には 電子が存在できるスペースは 1つだけあると考えられる。
(Fig.4)
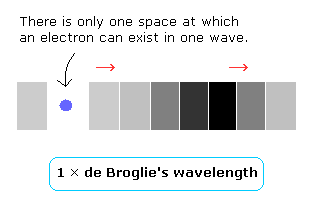
また、この電子の存在するスペース (= 波の位相) は 電子の速度に応じて 移動していると考えられる。
なぜなら、電子は 1つの波の1つの場所(位相)にしか存在できないからだ。
(Fig.5)
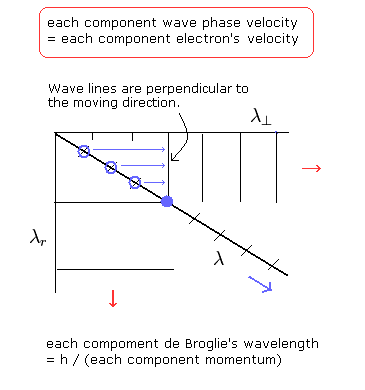
Fig.5 に示すように、波の位相速度の 接線方向と動径方向の各成分は 電子の速度の各成分に等しいと考えられる。
そのため、接線方向の波の位相線は 図に示すように 接線方向に対して 垂直になる。
水素原子では、角運動量 (L) は 次のように表せる。
(Eq.5)
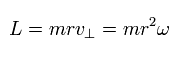
この L は 水素原子の楕円軌道では 定数になる。
上で言ったように、ド・ブロイ波長は 運動量のみに関係している。
そのため、接線方向の ド・ブロイ波長は 次のようになる。
(Eq.6)
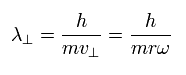
ここで、中心の角度 θ1 の 扇形を考える。
この扇形の外周の長さは r × θ1 となる。 ( r は 半径である。 )
(この θ が とても小さいとき、半径 r は 楕円軌道において、定数とみなせる。)
この小さな扇形の外周に含まれる ド・ブロイ波の数 (n) は 次のようになる。
(Eq.7)
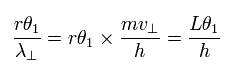
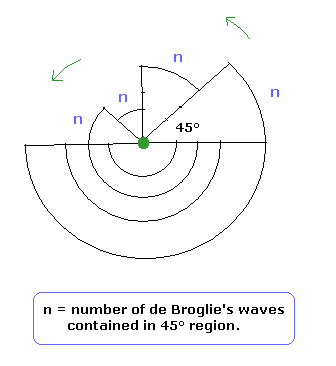
このことは、半径 r の長さに関係なく、もし 中心角が同じときは、同じ数の ド・ブロイ波 (= n) が含まれることを意味する。
例えば、Fig.6 は 45°のときの場合である。
( L が ħ のとき、1軌道 (θ = 2π) には 1 × ド・ブロイ波が含まれている。これを Eq.7 に代入して試してみるといい。)
"接線方向"の波の位相が 元の状態に戻るときには、Eq.7 の 角運動量 (L) は ħ の整数倍にならなければならない。
(Fig.6) 半径 r に関係なく 各扇形には 同じド・ブロイ波 (=n) が含まれる。
ところで、接線方向 (= θ) の波を さらに2つ以上の方向に分離することは可能であろうか? (例えば Fig.7B の a1 と a2 の方向のように)。
そして、この a1 と a2 の方向の 各軌道にも 接線方向のように 整数倍のド・ブロイ波の概念を考えることは必要であろうか?
(Fig.7)
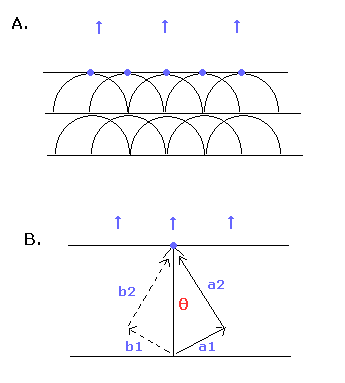
ホイヘンス・フレネルの原理によれば、波の通過した媒質の各地点が あらたな波源となる。(Fig.7A)
つまり、a1 と a2 方向の波は それに対称的な波 b1 と b2 と干渉する。(Fig.7B)
結果として、接線方向 (θ) のみ 残ることになる。
そのため、接線方向の波をさらに多くの方向へ分離して考える必要はない。
基本的に ホイヘンスの原理によれば、Fig.7B に示すように、θ 方向に対して 最も短い波のみが残る。
水素原子では、軌道は閉じている。
そのため、2π 回転後の 波の位相を考えるとき、最短距離の軌道 (= 接線方向) のみを考慮すればいいことになる。
(もちろん、回転にまったく寄与しない、動径方向のド・ブロイ波も別に考慮する必要はある。)
このページに示したように、ド・ブロイ波と 電磁波の概念を使えば、光電効果と とびとびのエネルギー準位を "自然に"説明することができる。
ここで, 光源が 宇宙空間に 電磁波もしくは光子を放出する場合を考える (Fig.8)。
(Fig.8)
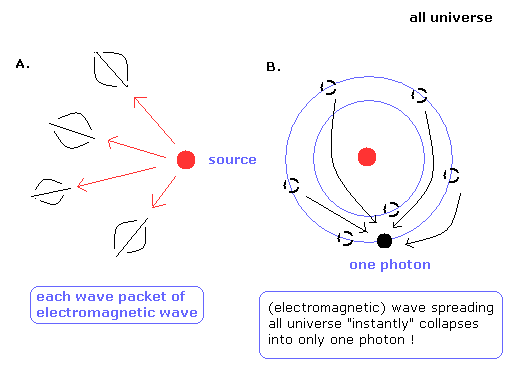
電磁波が 宇宙空間に どこまでも均等に広がり続けるという概念は 非常に不自然である。
光源から放出された電磁波は、多少は偏っていて、このことは より広い空間に広がったときに顕著になると考えるのが自然である。
それは、宇宙空間を 波束 (wave packet) として 進行することになる。(Fig.8A)
結果として、我々は 宇宙から届いた 電磁波の 各波束を検出することができる。
光子が粒子 である場合はどうなるだろう?
量子力学によれば、単一光子の 確率波 (= 電磁波)は 全宇宙空間に 無限に均等に拡大し続ける。
そして、ある地点で、この光子を検出したとき、全宇宙空間の電磁波が ”一瞬にして”たった1つの光子のもとに収縮してしまうのだ! (Fig.8B)
結論からして、この 光子のモデルはとうてい受け入れ難いものと言わざるを得ない。
一方、Fig.8A の電磁波モデルは 非常に自然なモデルである。
ボーア模型の水素原子では、基底状態の軌道は 次のように 1ド・ブロイ波長である。
(Eq.8)
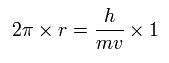
また、この軌道における 電子の 振動数 は 次のように 速度 / 軌道長 で表せる。 (Eq.8 を用いて。)
(Eq.9)
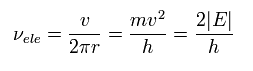
ここでは 次の関係式を使用している。
(Eq.10)
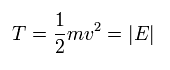
水素原子の円形軌道では、運動エネルギー (T) は 全エネルギー (E) の絶対値に等しい。
光電効果では, 次のエネルギーの光を水素原子に照射したとき、
(Eq.11)
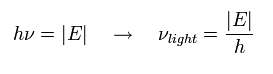
電子が水素原子から放出される。
電子の振動数 (Eq.9) は 光の振動数 (Eq.11) の ちょうど 2倍である。
電子の持つ運動エネルギーも光電効果に寄与することを考慮すれば、この結果は妥当と考えられる。
もし、電子の元の速度を保ったまま、放出させようとすると、必要な 光の振動数は次のようになる。
(Eq.12)
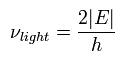
何と、Eq.12 は Eq.9 にちょうど等しくなるのである!
つまり、電磁波が 電子の運動を 振動させていることになる。(Eq.12 では それらの周期が同じである。)
Eq.9, Eq.11 (Eq.12) の結果は 光電効果の プランク定数 (h) は ド・ブロイ波に関係していることを意味している。
そのため、光電効果が 電磁波と ド・ブロイ波の相互作用によって生じると考えることは 非常に自然なことなのである。
電磁波による 光電効果に関しては、このページも参照のこと。
--------------------------------------
普通のマクスウェルの方程式を解くと、次の関係式が得られる。
(Eq. M-1)
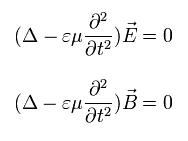
ここでは、次の関係式が満たされる。
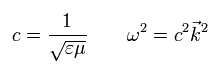
上の式から ”自然に”電磁波の解を得ることができる。(Eq.13)
例えば z 方向へ進む 電磁波は 次の変動する電場と磁場より構成される。
(Eq.13)
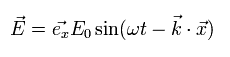
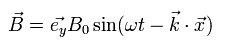
Eq.13 は 上の Eq.M-1 の式の 解 である。
Eq.13 に示すように、本来の 電磁波における E と B の振幅は 減衰しないで進行する。
しかし、加速度運動する電荷に対する 古い式によれば、電磁波の振幅が次のように減衰してしまう。
(Eq. M-2)

ここでは、p は 電気双極子を意味している。
Eq M-2 では、加速度運動する 電気双極子が 電磁波を放出することを示している。
また、この双極子と 観測地点の距離 (= r) が長くなるほど、E と B の振幅は Eq.M-2 に示すように 弱くなる。
どうして、Eq.M-2 の結果は Eq.13 と異なるのだろうか?
重要な点は、Eq.M-2 は ド・ブロイ波の概念をまったく使用していないことである。
すべての運動する粒子は ド・ブロイ波を生じるにも関わらず、どうして Eq.M-2 は このことを無視しているのだろうか?
これが、我々が 電磁波について誤解している原因である。
特に、原子などにおいては、我々は 量子化されたド・ブロイ波を考慮しなければならない。
もしそうすると、電磁波(束)の発生方向に偏りが存在し、Eq.13 に示すように減衰されないことになる。
古いマクスウェル方程式のみの概念によれば、電磁波の エネルギー密度 (u) は次のように表される。
(Eq.14)
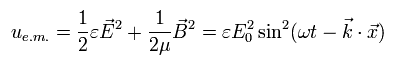
しかし、Eq.14 のエネルギー密度の式はある欠陥を含んでいる。
Eq.14 によれば、角振動数 (ω) が まったく エネルギーに貢献していないのである。(原子レベルにおいて。)
Eq.14 の角振動数を次のように変化させても、全エネルギーはまったく変化しないのである。
(Eq.15)
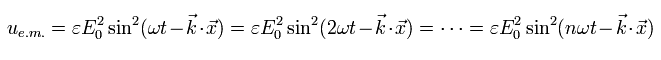
[ これらの電磁波のエネルギーは本当に同じなのか? ]
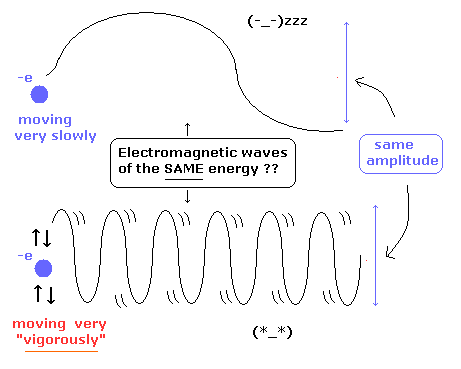
ここでは、上の電子は ゆっくりと上下に揺れている。一方 下の電子は 非常に激しく振動している。
また、これらの 振幅は同じ である。
Eq.15 の解釈によれば、これらの電磁波のエネルギーが 何とまったく同じになるとしている。
これは 非常に不合理 と言わざるを得ない。
つまり、Eq.15 のエネルギー密度の式は 不完全なものなのである。
そのため、我々は 光電効果に対する 古い概念を改めなければならない。
基本的に 振動数なるものは、波の性質によるものである。(粒子のよるものでない。)
このことは しごくあたりまえの話である。
もし 電磁波に 振動数 を組み合わせれば、 我々は 光子という概念をまったく使用する必要がないのである。
ご存じのとおり、電子のド・ブロイ波は それ自身と干渉し、また電子の運動方向に影響を与える。
そのため、1つのド・ブロイ波の中に 電子が存在できる場所とできない場所の2つの 位相の場所を考えるのが自然である。
ここでは 電子が存在できるところの位相を Ψ+ と定義する。(逆の場所の位相を Ψ- と定義する。)
(Fig.9) 短い (= A. ) もしくは 長い (= B. ) ド・ブロイ波長。
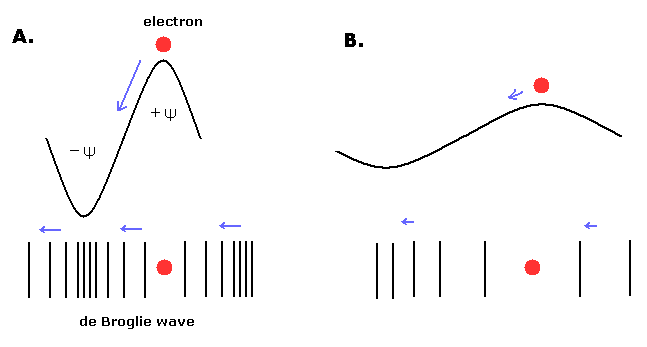
電子の運動方向は ド・ブロイ波の位相変化の方向と一致する。
そのため、我々はド・ブロイ波を 縦波と考えるのが自然である。
Fig.9A は "短い" ド・ブロイ波長を意味しており、つまり 電子の運動量 (= 速度) は 大きい場合である。( λ = h/mv. )
Fig.9A では、山 (= +Ψ ) と 谷 (= -Ψ ) のペアが 短い区間に押し込まれている。
つまり、”坂が急”な状態と言える。(= 媒質の密度の偏りが急。)
よって 電子は Fig.9B の 長いド・ブロイ波長の場合よりも 速い速度で進むことになる。
媒質の偏りが小さくなるにつれ (= Fig.9B )、電子を押す力が弱くなり 電子の速度が遅くなる。
(Fig.10) 水素原子の "円軌道" における 1 × ド・ブロイ波。
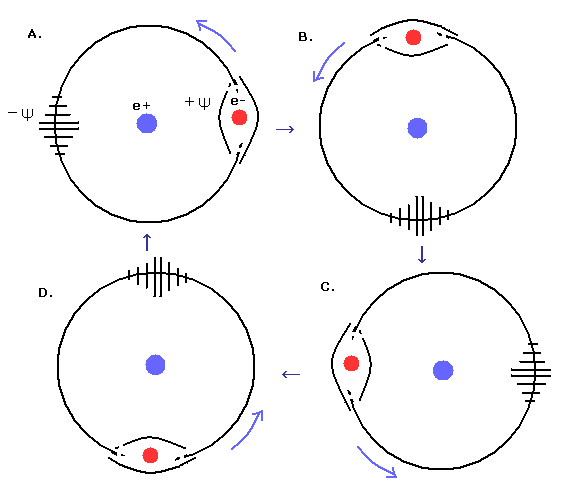
Fig.10 は 軌道長が ド・ブロイ波長の 1倍である水素原子の 1S の円軌道を表している。
円軌道では、電子の運動量 (= 速度 ) は 軌道の全地点で 等しくなる。
そのため、ド・ブロイ波の 位相速度は Fig.10 に示すように 一定になる。( A. → B. → C. → D. → A. )
(Fig.11) ”楕円軌道”における ド・ブロイ波。
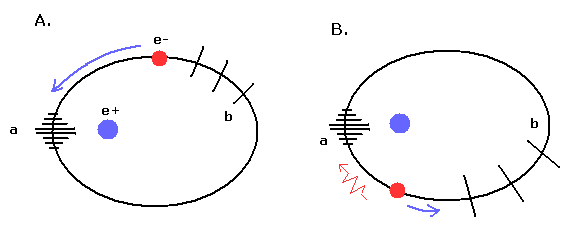
Fig.11 のような楕円軌道は少し 複雑である。
Fig.11 では 地点 "a" は 近日点 である。
つまり、Fig.11A の状態は 電子が近日点に近づきつつあり、速度が加速されていく状態である。
よって、近日点あたりの ”場”に 皺がよって 場が凝集することになる。
Fig.11B では、電子は 近日点から離れていく状態で 電子速度は 減速傾向にある。
そのため Fig. 11B においても、 近日点 (= "a" ) 周囲の ”場” が 電子のブレーキのために しわが寄って凝集する傾向になる。
結果として、近位点 (= "a" ) 周囲では、”場”が凝集してしわがよりやすく、結果 ド・ブロイ波長が”短く”なる。
一方で、遠位点 (= "b" ) 周囲では 場が 引き伸ばされるため ド・ブロイ波長が "長く" なる傾向にある。
電子が近位点周囲を通過するとき、その場の位相の急なスロープのために 電子速度が速くなる。
(電子が存在し得るスペース Ψ+ は 基本的に "空の"空間である。なぜなら、電子が その場の 媒質を Ψ- の方へ 押しのけるからである。)
(Eq.16) 位相速度 (= v ).
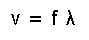
Eq.16 は 位相速度を意味している。ここで f は 振動数で λ は 波長を表している。
ド・ブロイ波長が短い領域では, 凝集して しわのよった 場のために f が大きくなる。
(振動数 f が バネ定数 "k" に関係していることを思い出してみるといい。 )
しかし、もちろん 全地点における 軌道1周の間の振動数は等しくなる必要がある。
ポイントは 電子が通過しているときのみ、”一時的な”振動数が 異なる波長の領域で変化するということである。
電子が 遠位点 (= "b" ) を通過しているとき、そのスピードは "緩い" 場のために 遅くなる。
そして、その遅い電子の運動は もちろん 反対地点 "a" にも影響を与える。
つまり、この 電子が "b" を通過している状態では、"a" 地点周囲の位相速度も ゆっくりになる。
( "a" 地点周囲では、場が凝集傾向になるというわけである。)
一方で、電子が 近位点 "a" を通過中、そのスピードは "急な" 位相 のために 速くなる。
この状態では "b" 周囲の 位相速度も早くなる。
(つまり、”b”周囲は 薄まる傾向を好むということである。)
結果として、楕円軌道においても 全地点における 軌道1周の振動数は等しくなる。
(Fig.12) 楕円軌道における位相の変化。
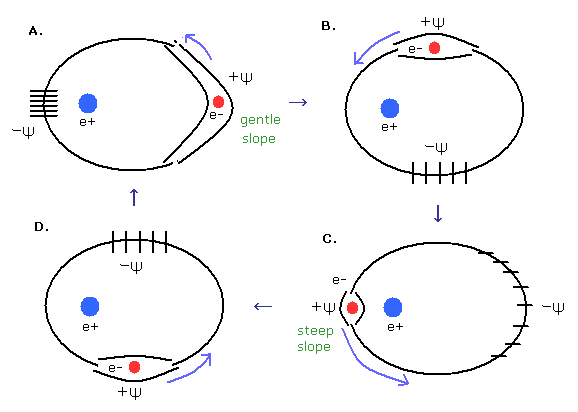
ド・ブロイ理論によれば、ド・ブロイ波長 λ は 粒子の運動量 (p) に依存している。
( λ = h / p )
ここでは 電場のもとで 運動量 p に達するまで 電子を加速させる場合について考えることにする。
(Fig.13) 電子の加速。
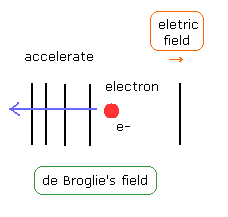
電子が 電場のもとで 加速されていくにつれて、ド・ブロイ波長は Fig.13 に示すように 短くなっていく。
もちろん、この過程においては 電子周囲のド・ブロイ場は不安定であり、これは 電場という外力のもとで 加速される電子によって”押し曲げられて”いく。
電子が ある一定の運動量 p に到達した後、それは 自由電子 になって 外力なしでも 安定になる。(Fig.14)
(Fig.14) 一定速度で進む自由電子。
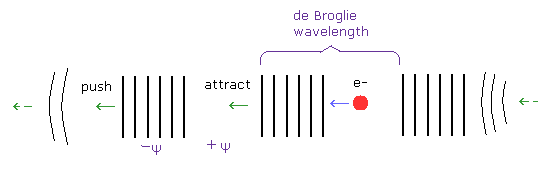
自由電子では そのド・ブロイ波長は一定でかつ安定である。
場のゆがみ (= 波長) は 粒子の運動量の動源力となる。
位相 -Ψ (= "凝集した"場 ) は その前方の場を 押して そこを新たな -Ψ の位相とする。
一方で、+Ψ の位相 (= "うすい"場 ) は 後方の -Ψ の位相を引きつける。(両者の力は同じである。)
このようにして、自由電子のド・ブロイ波は 一定のド・ブロイ波長を保ったまま 前方に進んでいくことができると考えられる。
( 電子の運動量と その周囲のド・ブロイ場が 互いに 調和しているため、その両者とも安定的に運動できる。)
(Fig.15) 同じ運動量だが、違う速度。
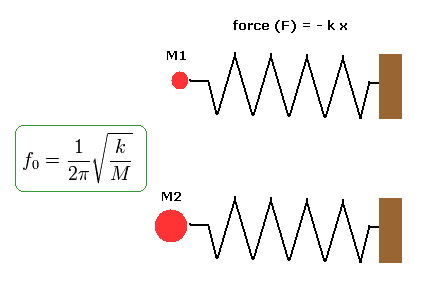
例えば、電子と中性子は違う質量を持つ。( 例えば、 m = M1 もしくは M2 )
そのため それらが 同じ運動量 ( p = mv ) を持つとき、それらの速度 (= v ) は異なる。
ここでは Fig.15 に示すように バネの例を使って このメカニズムを説明してみる。
Fig.15 では 上と下のバネは 同じバネ定数 k と 振幅を持つ。
つまり、粒子をプッシュする 力 ( F = -kx ) と バネのエネルギー (= 1/2 kx2 ) は それらで 同じである。
しかし バネにくっついている粒子の質量は それらで異なっている。( 上の粒子 = M1, 下の粒子= M2 ).
このケースでは、 同じバネエネルギーを持つにも関わらず、振動数 ( f0 ) と 位相速度は異なる。
( 質量が重くなるにつれて、その速度は遅くなる。)
もちろん、バネのゆがみ (= バネエネルギー) は 保存される。
つまり、我々は このバネのゆがみを ド・ブロイ場のゆがみ (= 波長) のようなものと考えることができる。
(Fig.15') 円軌道と楕円軌道。
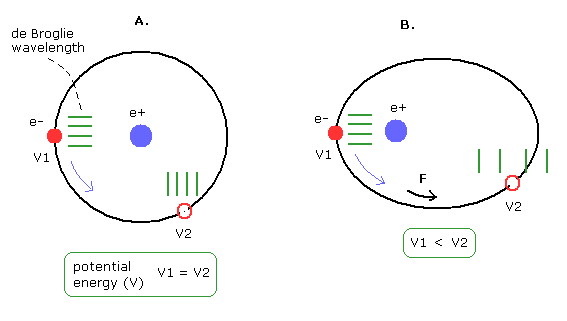
Fig.15' A の円軌道では、位置エネルギー (V) は 全地点において同じである。
そのため、電子の運動にさいし "余計な"力は必要ない。
結果として、電子の "有効"質量は 保存されて、かつ位相速度も一定になる。
しかし Fig.15'B のような 楕円軌道においては 電子の位置に応じて 位置エネルギーが変化する。
つまり、電子が動くには "余計な"力が必要になってくる。
このケースを 電子の "有効"質量の変化のように扱うことができる。( V1 → V2, M1 → M2 ).
(例えば、位置エネルギーが高くなるにつれて、”有効”質量は重くなっていく。)
このとき、位相速度は連続的に変化していく。(Fig.15 も参照のこと。)
(Fig.16) 各地点における ド・ブロイ場 (= "ゆがみ" ) は 保存される。
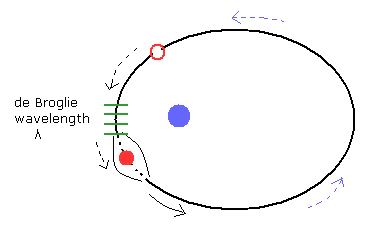
楕円軌道の ある地点における波長が λ のとき、我々は その地点における その波長が保存されると考えるのが自然である。
運動量 p を持つ電子が この地点 ( λ = h/p ) を通り過ぎた後、薄い場の位相部分 +Ψ は、同じ波長の -Ψ の位相を そこにひきつける。なぜなら その地点における "バネエネルギー"は保存されているからである。
もし 電子が その地点を通過後 ド・ブロイ波長が保存されないとすると、それは 深刻な問題を引き起こす。
(Fig.17) ド・ブロイ波を放出して 電子運動が不安定になる。
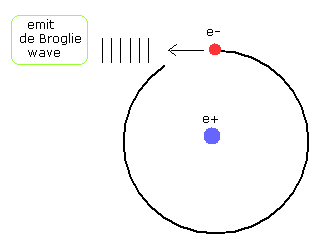
Fig.17 では 軌道の各地点における ド・ブロイ波長は 保存されない場合である。
運動量 p を持つ電子が この地点に入ってきたとき、この地点に ド・ブロイ波長 λ (= h/p ) を生じさせる必要がある。
( 動く電子が 前方の場を プッシュして しわを寄せさせる。)
しかし、ド・ブロイ波の進行方向は "接線方向" であるため、そのド・ブロイ波は 接線方向に 放出されてしまうことになる。
結果として、ド・ブロイ波 (場のエネルギー)が保存されず、電子の運動が不安定になることになる。
(そのため、このケースは 普通の原子では起こらない。)
(Fig.18) 各地点における ド・ブロイ場のゆがみは保存される。
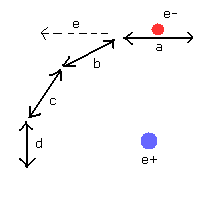
Fig.18 に示されるように、軌道の各地点における ド・ブロイ波長は 波長と方向において 保存される。
この状態においては、変化し得る運動量(その方向とスピードにおいて)を持つ電子は ド・ブロイ場と調和しながら 次の場に スムーズに進行することができる。
もし、Fig.18 の "b" の場が 存在しないとすると、”a” の場の電子が "b" に入ってくるとき、"a" にあった ド・ブロイ波が "e" の方向に逃げてしまう。
そのため、ド・ブロイ波を安定させるには、”b” 場のド・ブロイ場が "a" 場のド・ブロイ波を "b" の方向に誘導する必要がでてくる。
それに、仮に "e" 方向に ド・ブロイ波が 一部放出されると、"e" と "b" にある ド・ブロイ波が 互いに干渉しあう。
(もちろん、それらは 異なった運動量の方向を持つため、この干渉によって "b"場の波長が不安定になってしまう。)
結果として、ド・ブロイ場が安定するためには、"b" 場に 適切な波長と方向を持つド・ブロイ場が 保存されており あらかじめ用意されている必要がある。
(Fig.19) ド・ブロイ波長の整数倍は 保存される必要がある。
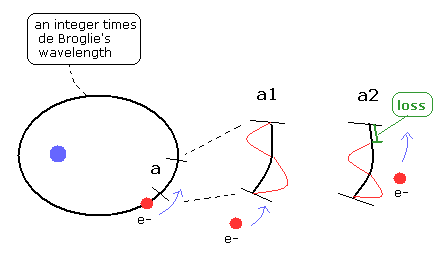
ご存じのとおり、電子の ド・ブロイ波は互いに干渉しあう。
そのため、互いに打ち消し合うのを防ぐには、それらの位相の端が 互いに一致している必要がある。
これは 1軌道が ド・ブロイ波長の整数倍になる必要がある。
もし、各地点における ド・ブロイ波長が 保存されないとすると、これは深刻な問題を引き起こす。
例えば、ある時点で 軌道上の "a" 領域に あるド・ブロイ波長の場が存在するとする。
ここで このド・ブロイ波長が 電子がここを通過するときの運動量と 異なっていると仮定する。
この時点で 波自体が打ち消されず存在するには 軌道1周には ド・ブロイ波長の整数倍の波が含まれている必要がある。
電子が "a" 領域に入ったとき、この領域の ド・ブロイ波長は 電子の運動量と同じになる必要がある。( Fig.19 の a2 )
しかし、ここでは 電子が領域 "a" に存在しないときの "a" 領域の波長が 通過するときの電子の運動量と異なると仮定している。
すると、この "a" 領域に含まれる 波の数が Fig.19 の a2 に示すように 変化することになる。
結果として、軌道1周が ド・ブロイ波長の整数倍でなくなってしまい、波と電子の運動は不安定になる。
(この時点で軌道全体の波長が一瞬に変化してまた整数倍になるようにうまく調節されるというのは不自然極まりない。)
結果として、各地点における ド・ブロイ波長は 電子が通過後でさえも 各地点で保存される必要がある。

2011/3/6 updated This site is link free.