トップページ (2電子原子も含む正確な新ボーア模型)
電子スピンは現実には存在しない。 単なる数学上の産物
特殊相対性理論は間違っている。
QED のラムシフトは間違い。 (13/11/3)
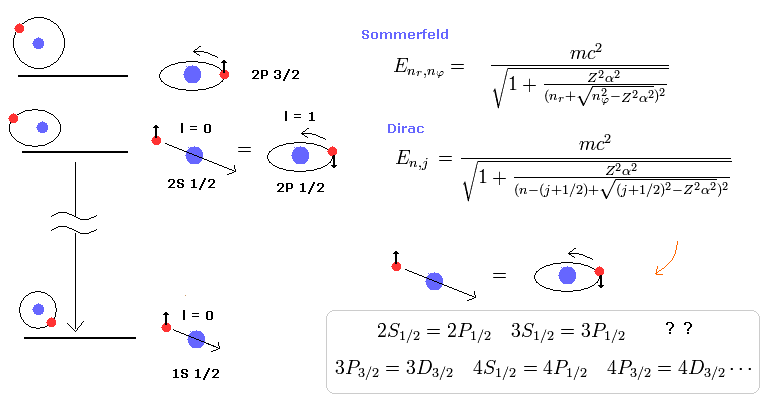
(Fig.1) ディラックの水素原子 = ボーア・ゾンマーフェルト模型。

このページに示したように、微細構造は 1916 年に ボーア・ゾンマーフェルト模型によって 最初に説明された。
後に ディラックの水素原子は 偶然にも ボーア・ゾンマーフェルト模型と同じ解を得ることができた。
ディラックの水素原子は スピンを持っているにも関わらず、観測される水素原子のスペクトル線は ディラックの水素原子が予測するものよりも はるかに少なかった。
そのため、彼らは 多くの偶然の一致 ( 2s1/2 = 2p1/2, ... ) が 起きているため 観測されるスペクトル線は 少なく見えるのだと主張し始めた。
(Fig.2) ディラックの水素原子は 多くの架空の状態を含んでいる。
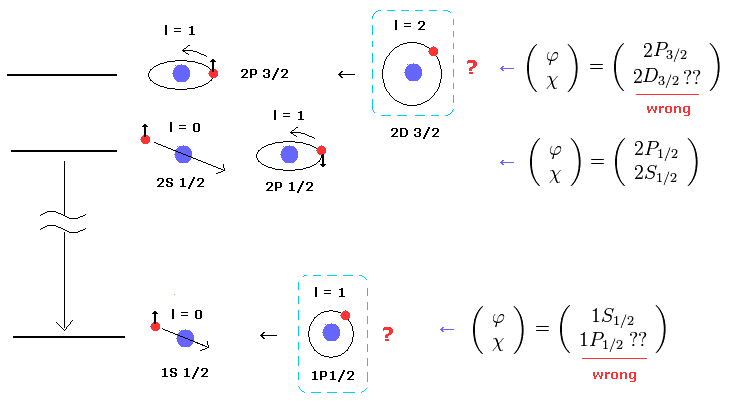
問題は ディラックの水素原子は 1p1/2 や 2d3/2 などの多くの間違った状態を含んでいることである。( このページ参照のこと。 )
もし これらの間違った状態が 存在しなければ、ディラックの水素原子は 解を得ることができない。
例えば、1p1/2 の状態は エネルギー準位が n = 1 で、軌道角運動量は l = 1 であるため、量子力学の水素原子には存在しない状態である。
このことは明らかに ディラックの水素原子が間違いで ボーア・ゾンマーフェルト模型が正しいことを示している。
(Fig.3) 直角レバーは 回転する、しない?
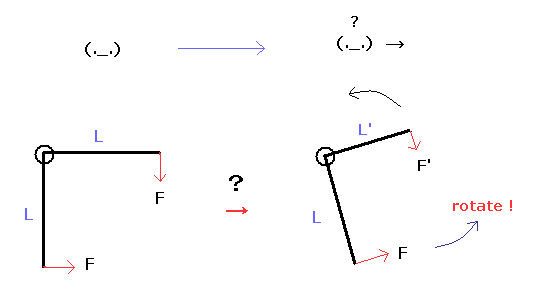
さらに 様々な致命的なパラドックスが 特殊相対論が間違いであることを明らかに示している。
ディラック方程式は エネルギーと運動量が 1次で 4×4 γ 行列を含んでいる。
ディラック方程式のこれらの形式は クライン・ゴルドン方程式 (= 特殊相対論 ) にちょうど等しい。
一方で、ボーア・ゾンマーフェルト模型は 相対論に特徴的な E2/c2 = p2 + (mc)2 という式を用いておらず、通常の 1次のエネルギー = T + V という関係式を使用している。
もちろん、もし特殊相対論が間違っているとしたら、γ 行列に頼るディラック方程式も間違いということになる。
そのため ラムシフトの解釈を見直す必要がでてくる。
なぜなら 非常に小さなラムシフトの現在の解釈は ディラックの水素原子が正しいという前提条件に完全に依存しているからである。
(Fig.3) ラムシフトは本当なの?

ディラックの水素原子は 2s1/2 と 2p1/2 のエネルギー準位において同じ値をだす。
そして 故意に無限大を除去する 量子電磁力学によって これらの準位間のわずかなエネルギー差を説明できるとされている。
これをラムシフトといい、これは 微細構造の10分の1であり、核の超微細構造と同じぐらいの大きさである。
もちろん、この非常に小さな値 (= 0.0000043 eV ) は 通常のスペクトル線で 直接 確認できるものではない。
彼らは ディラックの水素原子が正しいという前提条件のもとで この存在を推定しているだけである。
重要な点は 私達は ラムシフトが本当に 2s1/2 と 2p1/2 の間のエネルギー準位を意味しているのか 確認する方法がないということである。
(Fig.4) 電子を衝突させる方法。
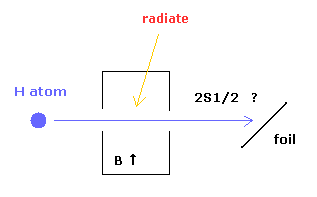
ラムシフトのオリジナルの実験は 異常ゼーマン効果、共鳴、衝突などの方法を使用している [1]。
Fig.4 に示したように、励起した水素原子に 磁場のもとで ある振動数の電磁波を照射する。
非常に弱い磁場のもとでは、水素原子は 異常ゼーマン効果を示すと言われている。
しかしこれは推測にすぎない。なぜなら 水素原子が ナトリウムなどと比較して 非常に少ないスペクトル線しか見せないということは有名なことで、また正常ゼーマン効果を通常示す。
( バルマー線の一部で 偶数に分離したラインが見られることがあるが、これもナトリウムと比較して少なく、ボーア・ゾンマーフェルト模型の微細構造から予測できる範囲のものである。)
(Fig.5) 微細構造 = "光子" のスピン 1 ??
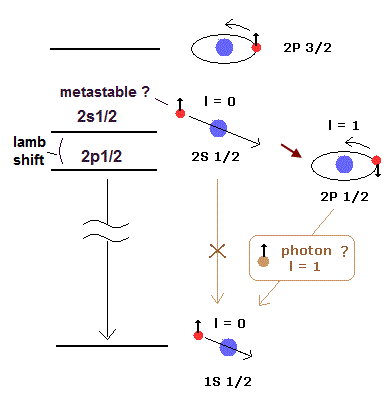
2s1/2 は 2p1/2 よりも 選択規則のために 安定であるとされている。
この選択規則は 光子のスピン1 によって生じるとされている。
そのため この準安定の 2s1/2 状態の水素原子は Fig.4 のタングステンフォイルに届くことができ、そこで電子を励起して 電流が検出されると 彼らは主張している。
電磁波放射で 2s1/2 から 2p1/2 の遷移を引き起こすと、それは 基底状態にすぐに落ちていくため フォイルを励起できないことになる。
つまり この遷移に必要な光の振動数を測定することで、ラムシフトを知ることができるのか?
重要な点は 私達は "準安定"状態が 本当に 2s1/2 なのか 知ることができないということである。
さらに 後に ラム自身 "光子などという粒子は存在しない" と言いだしている。このことは 準安定の 2s1/2 が間違いであることを意味している。
(Fig.6) 遅延選択実験 = 多世界 = 光子。
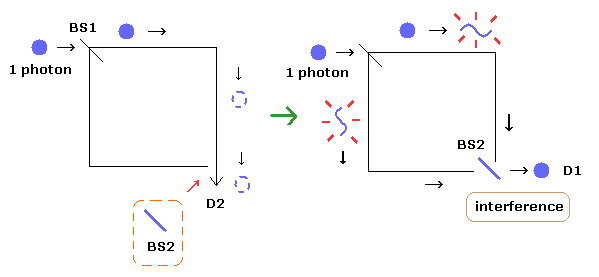
このページに示したように、奇妙な光子の存在は 非実在の多世界と 超光速の不気味なリンクを引き起こしてしまう。
ラムのオリジナルペーパー [1] によると、準安定な 2S1/2 の状態に関する様々な意見が存在したことがわかる。
例えば、Franck と Jordan は、 2S1/2 が準安定であることに疑問を呈する 理由を挙げている [1]。
また、Snoek と von Keussler は、H のスペクトルの強度を調べて 2S1/2 が それほど準安定ではないと結論づけている [1]。
(もちろん 2S1/2 の準安定を支持する人たちもいた。)
この状況の中で ラムは 2S1/2 は準安定と仮定して ラムシフトを調べようとした。
(ちなみに 1電子原子であるヘリウムイオン (He+) においては 準安定が得られなかった。)
(Fig.7) 異常ゼーマン効果。
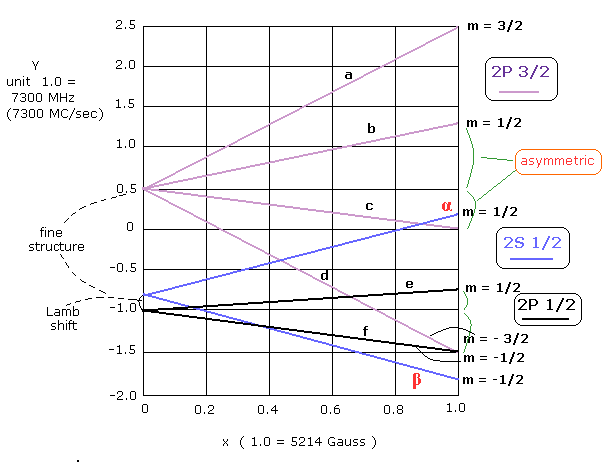
異常ゼーマン効果が正しいと仮定すると、2P3/2 の電子のエネルギー準位は ランデのg因子によれば 次の4つのレベルに分裂する。
μBH × 4/3 × 3/2 = 2μBH ( m=3/2 )
μBH × 4/3 × 1/2 = 2/3 μBH ( m=1/2 )
μBH × 4/3 × -1/2 = -2/3 μBH ( m= -1/2 )
μBH × 4/3 × -3/2 = -2μBH ( m= -3/2 )
しかし Fig.7 に示したように、m = 1/2 と m = -1/2 の状態は実は ランデのg因子を満たしていない。
もし それらが ランデのg因子を厳密に満たしているとすると、エネルギー準位は 上下に "対称的に" (= ± 2/3 μBH ) 分裂する必要がある。
しかし、Fig.7 によれば これらは "非対称 (= asymmetric)" になっている。
このことは ランデのg因子が m = ± 1/2 の状態において 有効ではない ことを示している。
彼らは m = ± 1/2 の状態は 次の非常に込み入った式を満たす必要があるとしている。
(Eq.1)
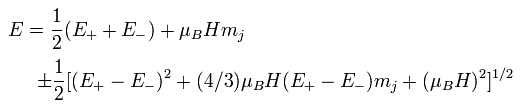
ここで E+ と E- は 2P3/2 と 2P1/2 の ゼロ磁場におけるエネルギーを意味している。
しかし もちろん 私達は この込み入った式が 本当に 水素原子の非常に弱い磁場のもとで成り立っているかどうかは知ることができない。
(もし この式が成り立っていなければ ラムシフトの解釈自体が完全に変わることになる。)
2P1/2 の状態 ( j=1/2, l=1, s=1/2, m=±1/2 ) においても、 次の ランデのg因子が成り立っていない (Fig.7)。
( これらの定義は推測にすぎない。なぜなら 通常のスペクトル線で これらのラインは観測できないからである。)
μBH × 2/3 × 1/2 = 1/3 μBH ( m=1/2 )
μBH × 2/3 × -1/2 = -1/3 μBH ( m= -1/2 )
(Fig.8) 観察された遷移 ? (小円)
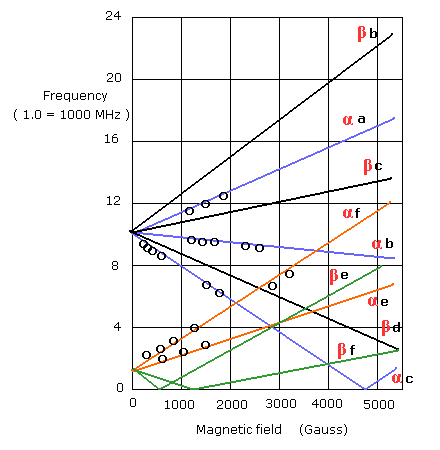
上で述べたように、2s1/2 と 2p1/2 の遷移がおきると、Fgi.4 の フォイル電流が分かる可能性がある。
Fig.7 から 各遷移に必要な 共鳴するマイクロ波の振動数を Fig.8 のように推定することができる。
(例えば、”α a ” の線は 2S1/2 "α" から 2P3/2 "a" の状態への遷移に必要な マイクロ波の振動数を意味している。)
彼らは 小さな円が 観察された振動数としており、約 1000 MHz のラムシフトが得られたとしている。
しかし 実際には この方法で 正確な結果を得ることはとても難しい。
最初に、原子核スピンによる hyperfine structure の影響を無視することができない。なぜなら ラムシフトはとても微小だからである。
そのため、彼らは 観察される 広く広がった スペクトルから 理論的にこれらの影響を取り除く必要がある。
彼らは 2S から 2P1/2 や 2P3/2 への遷移が起きたとき、電子は不安定になり 1S 状態へ 落ちると主張している。
その後 水素原子が 検出プレートにぶつかる。
1S 状態の水素は 電子を励起することはできず、2S は電子を励起して その結果 電流を生じさせると仮定している。
そのプレートからの電流の量を調べることで (2S → 2P → 1S) の遷移が置きたかどうか判断している。
広く広がったスペクトル幅や 熱雑音の影響で、実際には 共鳴ポイントを正確に決定することはできない。
(つまり Fig.8 の 小さな円の位置を精密に決定することはできない。)
また Fig.8 に示したように、Fig.7 の 2S1/2 の β 状態はどういうわけか観察されない (= 丸がない)。 これも準安定状態にも関わらずだ。
これも 非常に奇妙である。
また Fig.8 の 小さな円の分布は ”不規則である”。
そのため Fig.8 において 各線の他のポイントのところがどうして 観察されなかったのか不思議に思う。
(Fig.9) 飽和分光法。
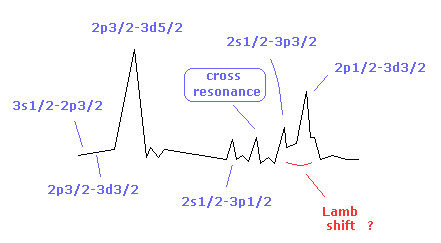
水素原子を衝突させる方法は 荒く、非常に小さなラムシフトを確認するには適当な方法ではない。
ドップラー・フリーの飽和分光法は 非常に小さな線幅の光を 水素原子に通してその吸収を測定するものである。
しかし 上で述べたように、ラムシフトは 核のスピンの 超微細構造ぐらいに小さいため、この共鳴が 本当にラムシフトを意味しているのか 知ることができない。
原子核や電子の わずかな振動か何かが これらの結果に影響を与えている可能性もあるわけである。
また 3s1/2-2p3/2 などの共鳴は 観測しにくく、偽の共鳴 (= cross resonance ) も混ざっている。
ボーア・ゾンマーフェルト模型では、右の波 ( 2s1/2, 2p1/2 が関係 ) は 楕円軌道を意味しており 原子核に近い。
そのため 右側のギザギザは 核の動きと関係している可能性がある。
重要な点は これらの非常に小さな値が 本当にラムシフトを意味しているのか確認する方法がないということである。
これらの解釈は ディラックの水素原子が正しいという仮定のもとに完全に依存している。
(Fig.10) ディラックの水素原子 = 非相対論的。

このページに示したように、ディラックの水素原子のハミルトニアンは 相対論的に共変形式でない。
なぜなら クーロン位置エネルギーは Fig.10 のように ローレンツ変換のもとで 複雑に変換するからである。
これはつまり 本当の相対論的なディラックの水素原子は ( もし存在するならば ) 違うエネルギー解を与えることを意味している。
ラムシフトは 非常に小さいため、陽子や電子のかすかな動きのもとで クーロン位置エネルギーの この形が変化すれば、その値にも影響がでてしまう。
つまり ラムシフトの解釈を変更する必要があるのである。
[1] W.E. Lamb, Jr. and R.C. Retherford, Phys. Rev., 79 No.4 549-572 (1950).

2010/6/30 updated This site is link free.