トップページ (正確な新ボーア模型)
電子スピンは存在しない。
どこで 科学が止まっているのか?
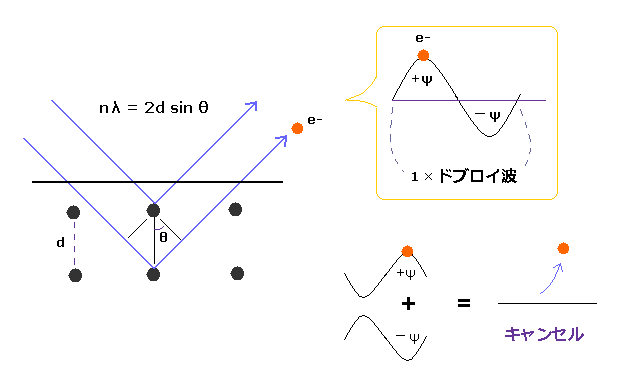
(Fig.1) ダビッソン・ガーマーの実験は 電子が ドブロイ波であることを示した。

ダビッソン・ガーマー の実験では、電子を 電場によって加速し、それを ニッケル結晶で反射させた。
電子のドブロイ波長 は 単一電子の干渉パターンから得られるが、これと 電場の強さから計算したものと一致した。
この実験は 単一電子が ドブロイ波という 波動的性質 をもち、そこでは 互いに逆位相の電子波 ( ±ψ ) が キャンセルしあって 電子を追い出している (Fig.1)。
(Fig.2) ドブロイ波の両端が合う。
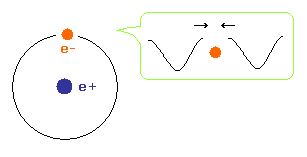
ドブロイ波が打ち消しあわないために、水素原子の電子波の両端の位相は ちょうどぴったりあう必要がある。
(Fig.3) 古いボーア模型の失敗。互いに逆位相のドブロイ波が打ち消し合う。
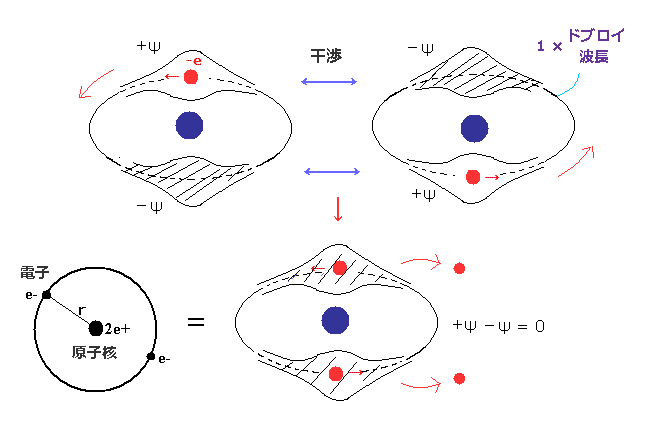
古いボーアのヘリウム (Fig.3) では、2つの電子は 同一円軌道上 (= 1ドブロイ波長 ) を 原子核を挟んで互いに正反対に位置しながら運動している。
Fig.1 と Fig.2 を考慮すると、古いボーア模型のヘリウムの2つの電子は 互いに逆位相のドブロイ波がキャンセルしあって、不安定になる。
実際に Fig.3 の 古いボーアのヘリウム模型は 間違ったヘリウムの基底状態のエネルギーを与える。
( Fig.3 は -83.33 eV の基底状態エネルギーを与え、これは 実験値 -79.005 eV と異なる。 )
(Fig.4) 安定で 互いに独立した ドブロイ波 (= 互いに垂直 )。
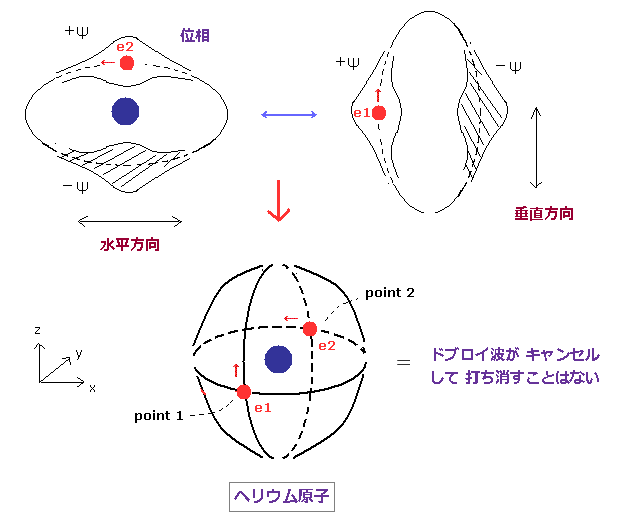
ドブロイ波の位相を安定に保つには 互いに逆位相間の波同士の 消滅的な干渉を 防ぐ必要がある。
もし 2つの電子軌道が互いに垂直だと、それらの波の位相は 互いに 独立で 安定な形を保つことができる。
なぜなら、互いに独立な方向のため、波同士がキャンセルして打ち消し合うのを防げるからである。
実際に この新しいボーア模型のヘリウムは このページに示すように 正確な基底状態のエネルギーを与える。
(Fig.5) 電子の運動量 ( p = mv ) と ドブロイ波長 (= λ ).
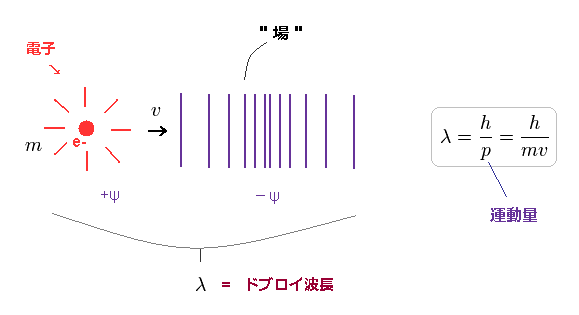
ドブロイの関係式によれば、電子の波長は h/mv で与えられる。 h は プランク定数 (= h )、 mv は 電子の運動量である。 ( "m" は 電子質量、 "v" は その速度 )
このサイトにあるように、運動量は 力積 (= 力 × 時間 ) と同じ意味である。
つまり 運動量を持つ動いている電子は 周囲の場に
力 (= 圧力 ) を与えて、ドブロイ波 を生じさせる。
もちろん、周囲の場を "リアル"な 物質 (= エーテル ) をして考えるには 特殊相対論の否定 は 必須条件である。 ( 致命的なパラドックスも参照のこと。 )
(Fig.6) 速度 (= v )、運動量 (= mv )、波長 (= λ ) の関係。
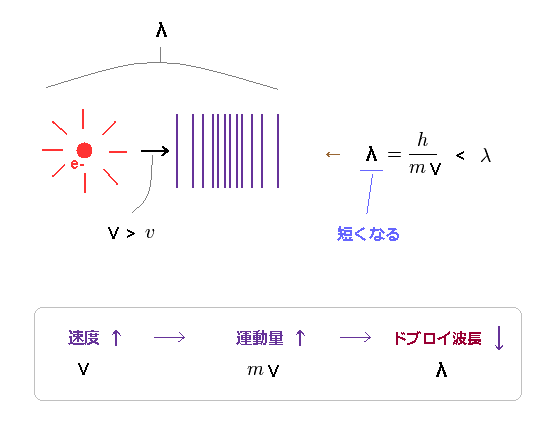
電子の速度が 速くなるにつれて、その運動量は 大きくなり、ドブロイ波長は 短くなる。
なぜなら 大きくなった運動量によって 周囲の "場" に加えられる 圧力 が強くなるからである。
つまり、このドブロイの関係式は このような古典力学的な機構が 働いていると考えると 自然に理解することができる。
各電子は その周囲に電場を 伴っているため、 広い範囲に ドブロイ波 を生じさせることができる。
そもそも 電場 ( 磁場 ) のみで構成される 電磁波自体 ドブロイ波の1つであることを 忘れてはならない。
(Fig.7) 1 × ドブロイ波長は 互いに逆位相 (= ±ψ ) のペア から成り立つ。
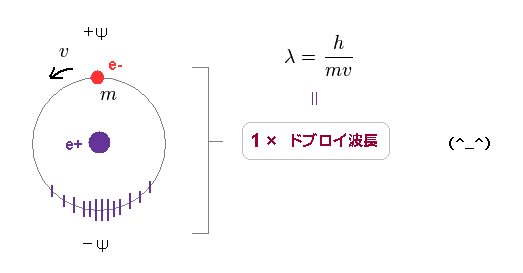
このページで、ボーア模型とシュレディンガーの水素原子の両方において ドブロイ波長の 整数倍 の条件を満たしていることを示した。
1 × ドブロイ波長は 互いに逆位相のペアで構成されている。
( ここでは +ψ は 電子側、 -ψ は その 逆サイド である。 )
ドブロイの関係式によれば、周囲の "場" は、電子の運動量 "mv" を 圧力として感じ取り、その力の大きさに応じて 収縮すると 考えられる。
(Fig.8) もう1つの電子が 同一軌道に入ると、全運動量は "2mv" に変化する。
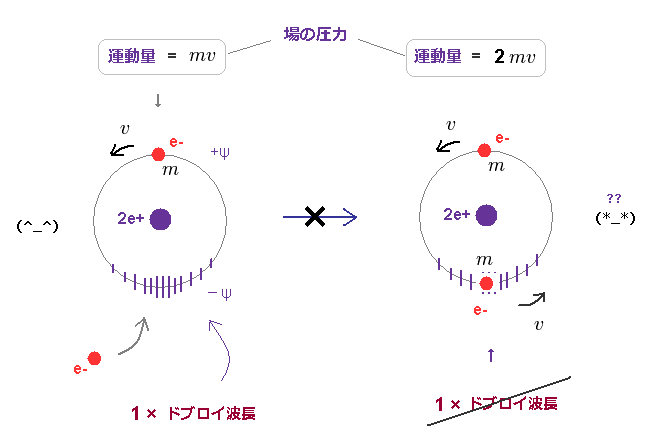
最初に、2つの電子が 同一軌道状の原子核の逆サイドで運動している 古いボーア模型のヘリウム について考える。
Fig.8 左図は ヘリウムイオン (= He+ ) で 電子の運動量 (= mv ) の圧力の下で 場が収縮 (= -ψ ) している。
その軌道長は ちょうど 1 × λ (= h/mv ) のときに 安定になる。
もう1つの電子が この同一軌道に入ると、周囲の場に与える圧力は 2倍 ( mv → 2mv ) になる。
なぜなら 軌道半径が変わらないとすると、この軌道上には トータルで "2mv" の運動量が含まれることになるからである。
場に加えれらる圧力が 2倍になると、その場は より収縮し、 ドブロイ波長を変化させる。
結果的に 元の関係式 ( 軌道長 = 1 × ドブロイ波長 ) が Fig.8 右 にあるように 保たれなくなってしまう。
(Fig.9) 全運動量が2倍 → 波長が "半分" になる。
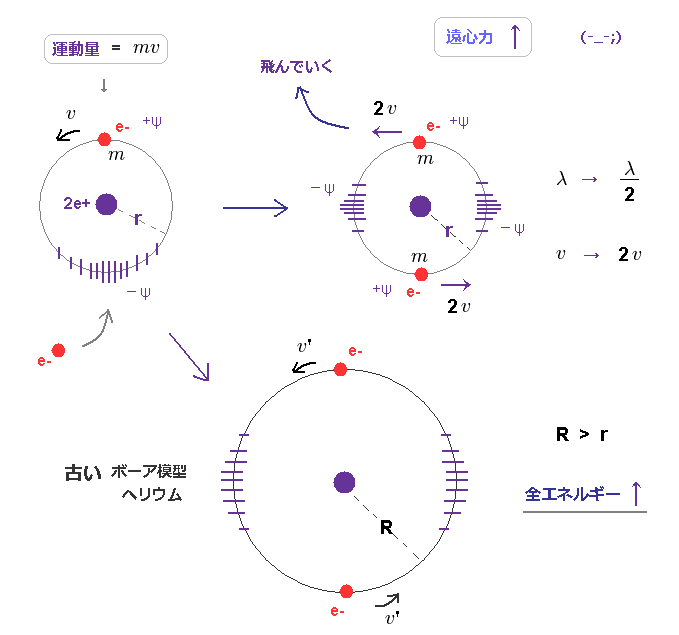
全運動量が 2倍 ( mv → 2mv ) になると、より 場 が収縮する。
軌道半径が "r" のままとすると、各電子の速度 ( 運動量 ) は その場の収縮を保つには 2倍 に増加する必要がでてくる。
クーロン引力は 変化しないため、この状態だと 遠心力がクーロン力に打ち勝って、電子が どこかへ 飛び去ってしまう。
遠心力がクーロン力と等しくなる状態では 軌道半径が 元の長さより はるかに大きくなってしまう (= Fig.9 下図 )。
なぜなら 次に許される軌道長というのが
2 × ドブロイ波長だからである。 ( 半径は "n" の2乗に比例する。 )
つまり、各軌道が (= 1 × ドブロイ波長 ) が 1つの電子のみ を含んでいるとき、全エネルギーが 最も低くなる。
(Fig.10) 古いボーア模型のヘリウムでは 電子が 弾かれてしまう。
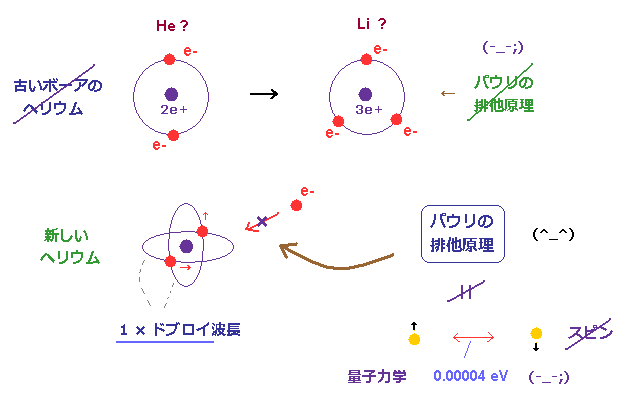
Fig.10 下図に示したように、2つの電子軌道が 互いに垂直のとき、それらの運動量は 互いに独立状態になる。
そのため、各場は 1つの電子の運動量 (= 圧力 ) のみを受けるため、
1 × ドブロイ波を 安定に 生じさせることができる。
これが "実在的"なドブロイ波に基づいた 正確なヘリウム模型の メカニズムである。
一方で、古いボーア模型のヘリウム (= Fig.10 上図 ) では、周囲の場に与えられる力は 2倍になるため、 元の 1 × ドブロイ波長 の状態を保てなくなり、結果として 電子が 基底状態の軌道から 追い出されてしまうことになる。
(Fig.11) 光子が電子から放出 → その時の加速度が "無限大" !
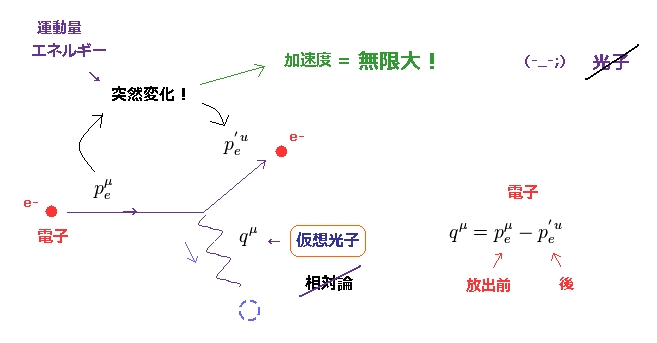
基本的に 場の量子論によれば、光子の現象は ファインマンダイアグラム によって記述されることになる。
驚くことに、放射 ( もしくは吸収 ) された光子と 電子が エネルギー・運動量保存という基本的な法則を満足するとき、この光子は 必ず仮想光子 というものになる。
このページ や このサイト にあるように、この仮想光子は "タキオン" のように 特殊相対論に 従わない。これが "仮想" と呼ばれる所以である。
さらに 光子が 電子から放出 ( もしくは 吸収 ) されるとき、この電子の運動量とエネルギーは 突然変化する。
これはつまり、この時点での電子の加速度は 無限大 ということになり、あり得ない現象であることが分かる。
私達は この変化の様子を その場、ドブロイ波全体も含めた ダイナミックで具体的かつ現実的なモデルで置き換える必要がある。
(Fig.12) エネルギー量子数が "2" から "1" へと遷移するとき・・・。
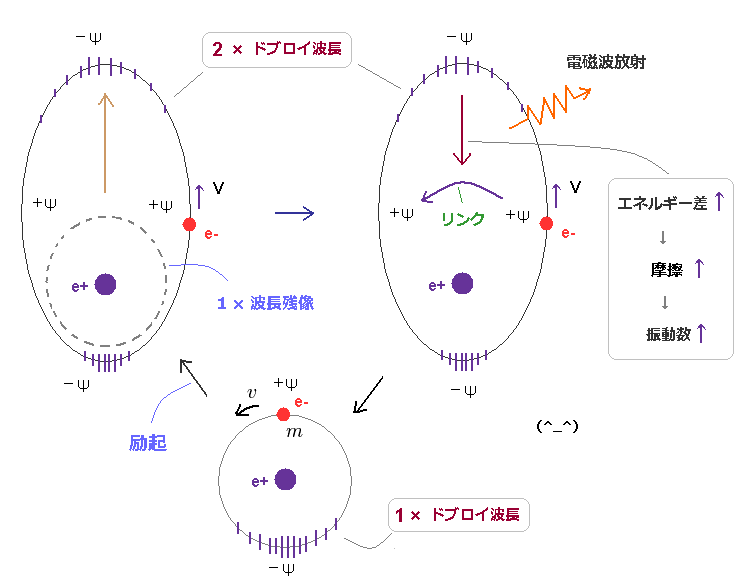
Fig.12 では、1×ドブロイ波長の軌道 ( n = 1 ) が基底状態である。
この電子が 電磁波を吸収して 2×ドブロイ波長の軌道 ( n = 2 ) に励起している。
励起状態は 一時的なものであるため、元のドブロイ波 (= 1 × 波長 ) の振動が この間 場に残っていて 放射を開始するかどうかの 水先案内役になると考えられる。
軌道長が ドブロイ波長の整数倍でないとき、軌道内で 電子のドブロイ波同士の位相の衝突が起きて、電磁波放射を開始し始める。
軌道内の位相同士の調和、不調和かを察知するシグナルは 瞬時に (= c ) 軌道全体に伝わり、電磁波放射を続行 もしくはストップ (= 軌道が整数倍の波長になるまで ) を判断することになる。
電子が加速した後を考慮すれば、ポテンシャルエネルギーは すべて運動エネルギー (= ドブロイ波長 ) に繰り込むことができる。
両準位間のエネルギー差 (= 振動数 ) に応じて、放射される電磁波の振動数 (= エネルギー ) が決まることになる。
そのエネルギー差が大きければ大きいほど、電子が下位準位に強い力で落ち込み、周囲の場から 電子が 大きな抵抗を受け ( もしくは与えて )、放射される電磁波も より シャープになり 短波長になると考えられる。
(Fig.13) 電磁波は 両方向に放射される。
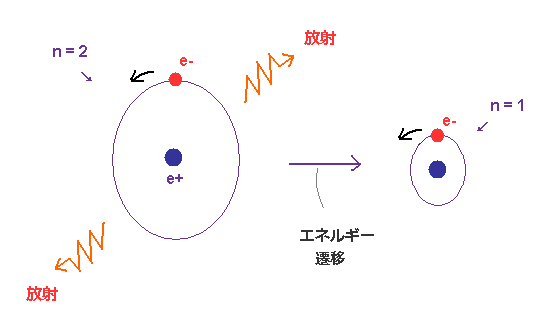
この現実的な遷移モデルでは 電子は 徐々に加速しながら 電磁波を放射していくため、Fig.11 の量子力学のような 加速度が 無限大になるようなことは ない。
またもちろんのこと、仮想光子 (= タキオン ) も このモデルには 出てこない。
Fig.13 に示したように、電子は 円形の軌道上を回っているため、そのトータルの運動量の方向は ゼロ になる。
そのため 作用反作用の法則により、運動量保存則を満たすには、全原子が 逆方向に押されるか、両側に電磁波が放射される必要がある。
電子の運動方向と 放射される電磁波の向きは コンプトン散乱のときとは異なっている。
(Fig.14) 電子波と "場" の摩擦が 電磁波を 水平方向へ押しだす。
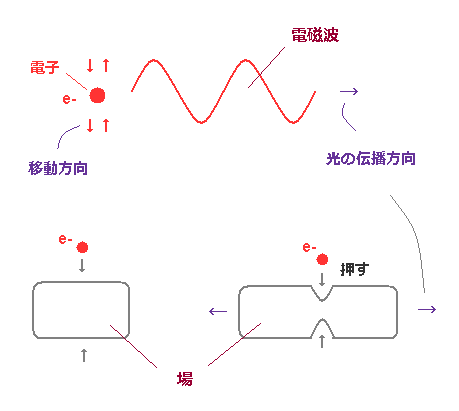
コンプトン散乱に見られるように、電磁波にも ドブロイ波 ( p = h/λ ) の性質がある。
もちろん、電磁波とは "場" の 振動であり、粒子ではない。その伝播速度が一定の "c" であることからも分かる。
原子軌道では、各電子は 正電荷の原子核周囲を回っており、閉じた系である。
この閉じた系では 電子の平均の運動量の方向は 左右上下対称のため ゼロになる。
全運動量保存を考慮すれば、電磁波は 電子の運動方向に 垂直な向きに 両方向へ放射されると考えられる (→ 横波の電磁波 )。
また ドブロイ波は 主に電子の電場によって生じる。
各場 (= ドブロイ波 ) には 周期的に振動する電場の残像があり、電子と周囲の場の摩擦の大きさに応じて 放射される電磁波のエネルギーや電場の位相が決まると考えられる。
このような 電場とドブロイ波を用いた 具体的なモデルを用いない限り、 場の量子論に見られる 非実在的な仮想光子 (= タキオン ) から 逃れることができない。
(Fig.15) 電子の波と "場" との摩擦が 電磁波を "押し出す"。
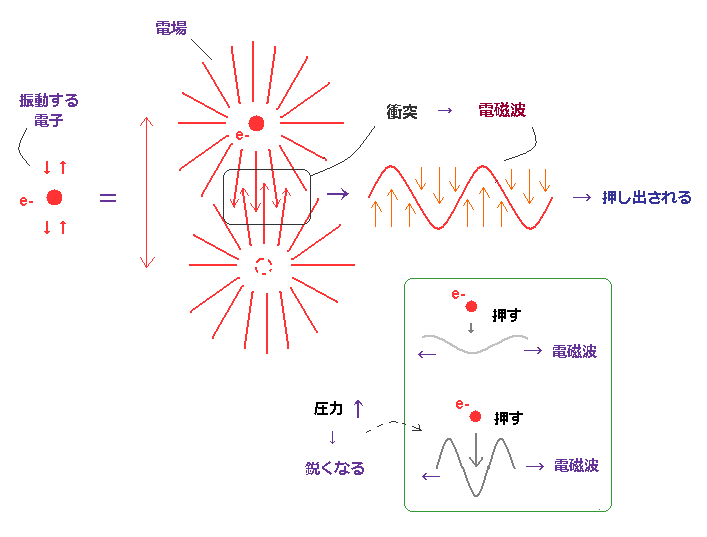
基本的に、円形 もしくは 楕円形の軌道では、電子は ある閉じた系内を 周期的に動いて (= 振動して ) いる。
その軌道長が ちょうど ドブロイ波長の整数倍 のとき、 それらの波の位相は 互いにぴったり フィットし、 安定になる。
それ以外のケースでは、2つの異なる位相を持つドブロイ波同士が 衝突し合い、横方向に その衝突時のエネルギーが 電磁波という形で 放出される と考えられる。
この衝突 (= 摩擦 ) 時の 衝撃が強いほど、生じた衝撃波 (= 電磁波 ) は より鋭く (= 短波長に ) なり、多くのエネルギー波を放出する。
Fig.15 にあるように、2つの波間の衝突の波面には ほぼ垂直方向の電場の線がある。
そのため、この衝突したドブロイ波 (= 垂直な電場線で構成された ) が押し出されたとき、この放射された電磁波は "横波" になると考えられる。
電磁波自体は 中性であり、 "正"の場 (= ↑ ) と 負の場 (= ↓ ) 同士が引き合うことを考慮すれば、電磁波を構成する電場の順番は (= ↑↓↑↓... ) のようになる。
もちろん、円形軌道などで 原子核周囲を回っている電子が 2つの波間の衝突によって 自身の角運動量を減じるときは、円偏光様の電磁波が生じると考えると しっくりくる。
(Fig.16) 直線状と曲がった電場によるドブロイ波
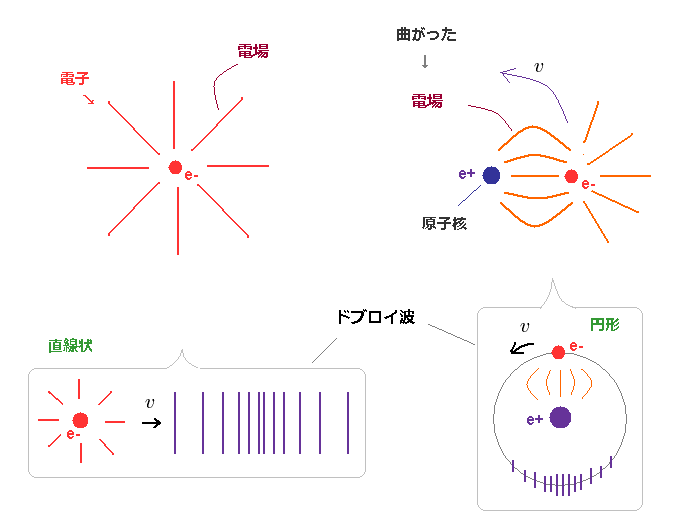
"直線状の" 電場は Fig.16 左図にあるように 自由電子の周囲に等方向に広がっている。
この自由電子が動くとき、電子とその周囲の電場が ”直線状”のドブロイ波を生じることになる。
一方で、原子核と結合した電子 (= Fig,16 右図 ) の周囲の電場は ねじ曲がっており、正電荷の原子核側に 凝集している。
この電子が 原子核周囲を回るとき、ドブロイ波も その経路にそって 円形 ( もしくは 楕円形 ) に曲がることが 理解できる。
(Fig.17) 同じ方向の電流が流れる 2つの電線。
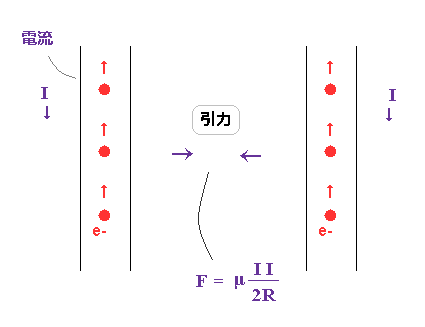
アンペール ( ビオ・サバール ) の法則によれば、2つの同じ方向に流れる電流は 互いに 引き付け合う。
古典的電磁気学は この現象を 磁気力と 右ねじの法則で説明している。
しかし ご存じのとおり、いわゆる 磁荷 (= モノポール ) というのは存在せず、電荷しか実在しない。
つまり 磁気力 ( 磁場 ) というのは 何か別の 実在的なもので
置き換える必要がある。
(Fig.18) "磁気力"の本当の姿とは?
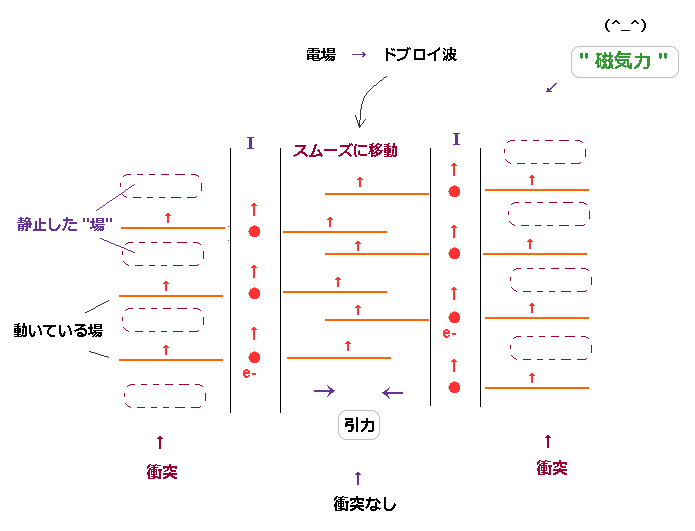
Fig.18 では、2つの電流 (= 電子 ) は 同じ方向に流れている。
つまり これら2つの電子のドブロイ波も 同方向に動いていることになる。
これら2つの電線の外側では ドブロイ波が 周囲の静止した場と 衝突して 所謂 圧力を生じる。
一方で、2つの電線の間では、ドブロイ波が 同じ方向に動いており、互いに 進行を妨げることはない。
そのため このエリアでは圧力が 低くなる。
結果的に 2つの同じ方向の電流は 互いに引き合うことになる
これが 磁場 ( 磁気力 ) の本当のメカニズムと考えられる。これは マグヌス効果の原理に似ている。
(Fig.19) 電子の運動量 ( p = mv ) と ドブロイ波長 (= λ ).

ドブロイ波長 (= λ ) は 粒子の運動量 ( λ = h/mv ) で決まる。
粒子の運動量が大きくなるにつれて、それが 周囲の場に与える圧力も 強くなる。
つまり、ドブロイ波とは 周囲の場が感じる 一種の圧力と考えられる。
(Fig.20) 異なった密度の 場の物質。
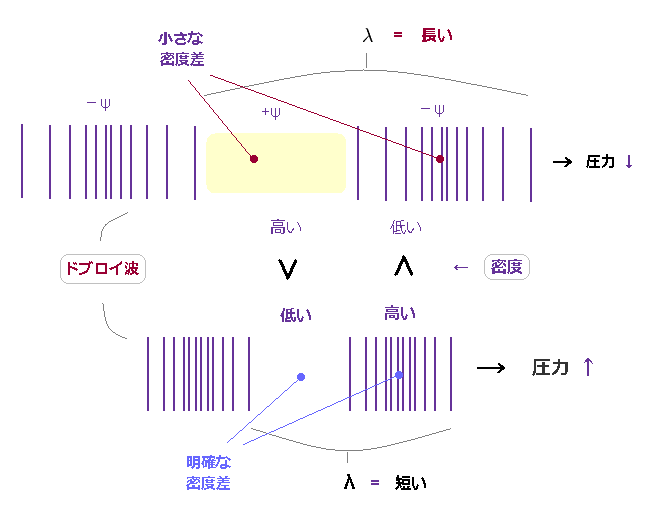
もし、ドブロイ波長が 粒子による圧力の強さを表しているとしたら、その時の 場の物質の密度が 圧力の原因と考えられる。
古典的な "バネ" のように、 加える圧力が強くなるほど、場 は 収縮して 短くなる。
大きな運動量を持つ粒子ほど 周囲の場に強い圧力を与え、その場 (= バネ ) を より収縮させる。
ドブロイ波長が 短くなるにつれて、より多くの "場の物質" が押し出されるため、 その密度 ( -ψ における ) は 高くなる。
( 逆に +ψ の位相側では、 短波長のドブロイ波の密度は 低くなる。 )
つまり 短波長のドブロイ波の ±ψ 位相間には
明確な密度差が存在する。
この ±ψ 間の顕著な密度差が 後続の場を 強く引き付けて、同じく短波長を生じる原動力になる。
(Fig.21) 運動量が同じでも 違う質量の粒子の速度は異なる。
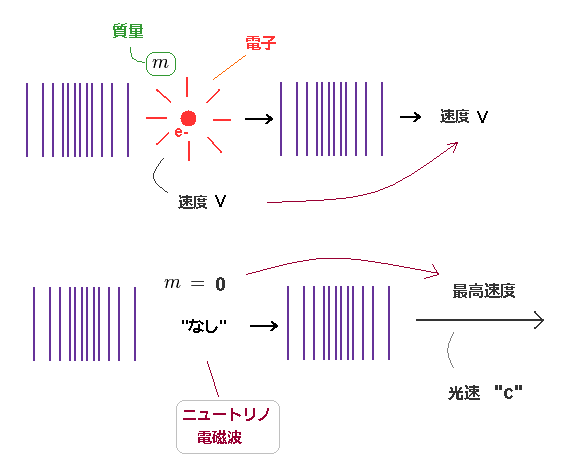
ドブロイ波長は 粒子の運動量 ( λ = h/mv ) で決まる。
つまり、運動量 ( p = mv ) が同じとき、異なった "質量" (= m ) を持つ粒子の速度 (= v ) は 違ったものになる。
ドブロイ波の収縮は 粒子の圧力によって生じる。
そのため、波の収縮は 場に継続的に影響を与える粒子と共に動く。
より多くの場の物質が前方方向に押し出されると、元の場所に より多くの他の物質が流れ込むため、同じ波長の波が続くことになる。
( このメカニズムは 古典的な波と同じものである。)
ニュートリノと電磁波には 質量がない。
そのため、それらのドブロイ波は 光速度 "c" で 伝播する。( もしくは 媒質によって変化。 )
つまり "質量" というのは 周囲の場の中を進行するときに "抵抗" を生じさせる 何らかの "物質の密度差" によって生じると考えられる。
(Fig.22) "静電荷"の陽子は "負電荷"の電子よりも はるかに重い。
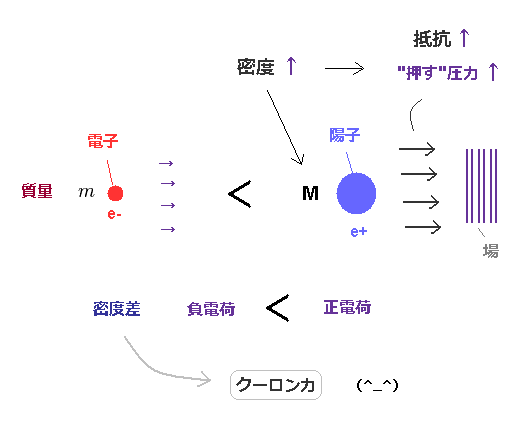
粒子の質量が大きくなるにつれて、その密度も高くなり、すなわち 一度に より多くの場の物質を 押し出すことになる。
つまり 速度が同じでも、 重い粒子は より大きな収縮と抵抗を 生じさせる。
これが 異なった質量の粒子が 違う速度で動いているにも関わらず、同じ波長のドブロイ波を生じる原因と考えられる。 ( それらの運動量 p = mv は 同じである。 )
"正電荷" の陽子が "負電荷" の電子よりも はるかに 重い (= 高密度である ) 事実を考えると、正と負の電荷の違いは ±電荷を形成する何らかの物質の"密度差" によって生じると考えると しっくりくる。
基本的に 力の平衡状態のため、すべての場の圧力は 一様になる傾向にある。
要するに、高密度、高圧力の場の物質 (= 正電荷 ) は、低密度、低圧力 (= 負電荷 ) の場の方に 流れ込もうとし、このことが 異なった電荷間が引き合う原因となると考えられる。
(Fig.23) ドブロイの関係式。
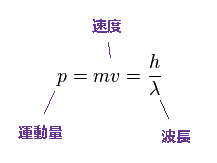
ドブロイの関係式によれば、 運動量 ( p = mv ) は ( p = h/λ ) の式で表わされる。
ここでは、 p = 運動量、 m = 質量、 v = 速度、 h = プランク定数、 λ = 波長。
このサイトにあるように、電磁波の全エネルギー (= E ) は E = hf の関係式を通じて エネルギーと 線形な 比例関係にあり、これは 光電効果で確認されている。
驚くことに、電磁波以外の 電子、陽子など 他のすべての粒子においても、もしドブロイの関係式が成り立つなら、振動数が それらの全エネルギーと 比例関係にあることが分かる。
(Fig.24) 電子の速度が半分 ( v → 1/2 v ) になると、 その波長は 2倍になる ( λ → 2λ )。
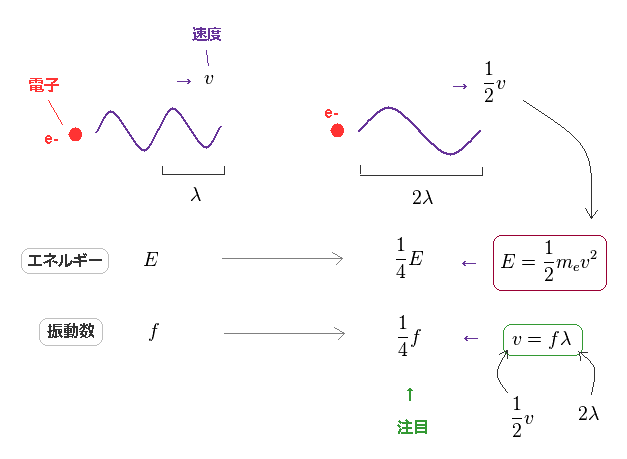
電子の速度 (= v ) が 半分 (= 1/2 ) になると、 その全 ( 運動 ) エネルギー (= E ) は 元の 1/4 になる。 なぜなら E は 速度の2乗 に比例するからである ( E = 1/2 mv2 )。
ドブロイの関係式 ( mv = h/λ ) によれば、電子の波長は 速度が 半分 になると 2倍に伸びる ( λ → 2λ )。
波の関係式 ( v = fλ ) により、電子の振動数 (= f ) は このケースでは 元の値の 1/4 になる。.
見てのとおり、電子のドブロイ波においても、エネルギーは 振動数に 比例していることが分かる ( E/f = 定数 )。
(Fig.25) 運動量 ( p = h/λ ) が一定のとき。
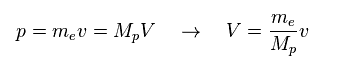
ここでは、運動量 (= p ) が "軽い"電子 と "重い"陽子で 共通の値の時を考える。
つまり、ドブロイの関係式 ( λ = h/p ) を通じて、 それらの波長 (= λ ) も 同じになる。
陽子の重い質量 ( Mp ) のために、陽子の速度 (= V ) は 電子の速度 (= v ) よりも はるかに遅くなる。
結果、陽子の全運動エネルギー ( E = 1/2 MpV2 ) は 電子のエネルギー (= 1/2 mv2 ) よりも かなり小さくなる。
(Fig.26) 電子、陽子とも、エネルギー (= E ) が 振動数 (= f ) に比例。
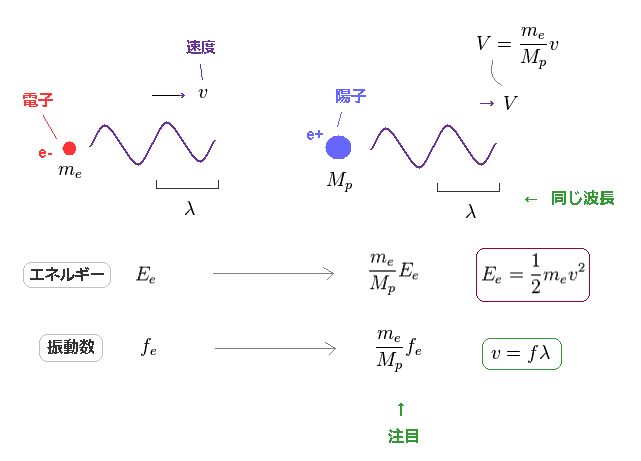
また、波の関係式 v = fλ を通じて、陽子の振動数を 知ることができる。
Fig.26 に示したように、陽子の電子の間においても、エネルギー (= E ) が 振動数 (= f ) に比例するという関係式が 成り立つ。
つまり 電磁波だけでなく 電子や陽子においても 振動数が 全エネルギーを決めるのに 重要な役割を果たしていることが分かる。
(Fig.27) 電子と陽子の全エネルギー。
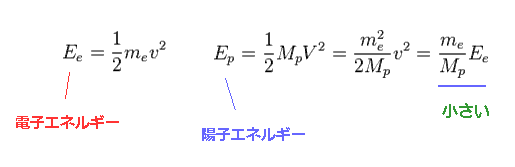
Fig.25 を用いると、運動量が同じでも、陽子の運動エネルギーが その重い質量のために 電子に比して かなり小さくなることが分かる。
(Fig.28) 電子と陽子の質量比。
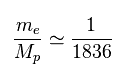
陽子 (= Mp ) は 電子 (= me ) よりも 1836 倍も重い。
(Fig.29) 振動数 = 速度 / 波長。
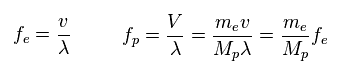
波の関係式を用いて、陽子の振動数が 電子よりも はるかに小さくなることが分かる。
( ここでは 電子と陽子の波長 ( 運動量 ) は 同じである。 )
(Fig.30) 光のエネルギーも 振動数に比例する。
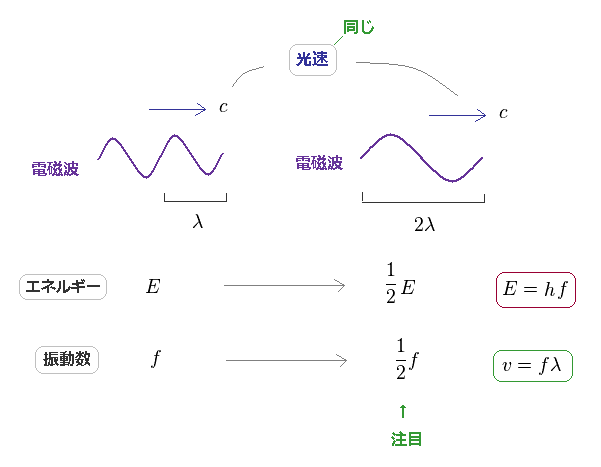
電磁波のエネルギーも E = hf の関係式を通して 振動数と比例することが分かっている。
重要な点は 他の粒子と違い、電磁波の速度は 必ず 定数である "c" になるという点である。
これはつまり、電磁波 ( や ニュートリノ ) などには "加速" という概念が
ない ことになる。
電子や陽子の波長が変わるときは、その速度と運動量の両方が 変化することになる。
つまり 電子の振動数は Fig.24 に示すように、波長の2乗に反比例する。
一方で、光は速度変化の分を考える必要がないため、その振動数は 単に波長に反比例することになる。
このように ドブロイ波長 ( λ = h/p ) は 粒子の速度に関係なく 運動量による 場の平衡状態からの "収縮" ( 拡張 ) などを表していることが分かる。
(Fig.31) クーロン力のメカニズム。
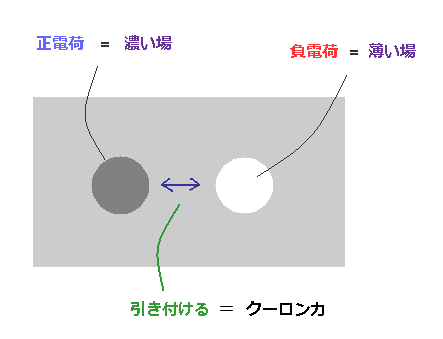
Fig.22 で述べたように、陽子と電子の質量間の大きな差が クーロン力の正負電荷を特徴づける基になっていると考えるとしっくりくる。
基本的に、 平衡状態を保とうとするために、高濃度 (= 正電荷 ) の場の物質は 低濃度 (= 負電荷 ) の場へと 流れ込もうとする傾向にあり、この原動力こそが クーロン力の源と考えれば、 非現実的な仮想光子に頼る必要がなくなる。
逆に 高濃度-高濃度、低濃度-低濃度の場同士が近づくときは、 さらなる "アンバランス" の状態を引き起こすため 反発力 を生じさせる。
(Fig.32) 電子が陽子に近づくと 運動エネルギーが増加する。
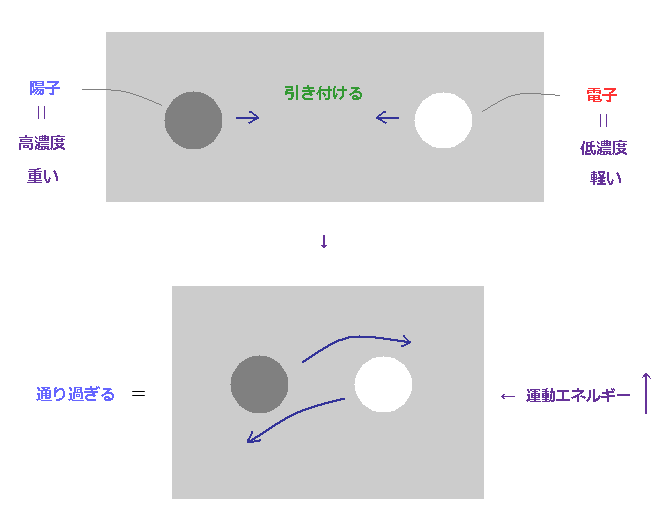
当然、全エネルギーは 常に 保存されなくてはならない。
場の変位や アンバランスな状態 ( ±電荷間の ) は その場に 位置エネルギーを生じさせる。
正電荷の陽子が電子を引き付けるとき、それら ( 主に軽い電子 ) は 加速されて 自身の運動エネルギーを増加させ、元の位置エネルギーに取って代わる。
結果的に 非常に大きな運動エネルギー状態で近づくため、正電荷の陽子と 負電荷の電子は 融合して納まることはできない。
( 非常に不安定な反粒子である陽電子は 物理の基本的な法則と 矛盾しているため、 非現実的である。 )
(Fig.33) バネの伸び縮みのように、場の変位 (= 電荷 ) は 保存される。
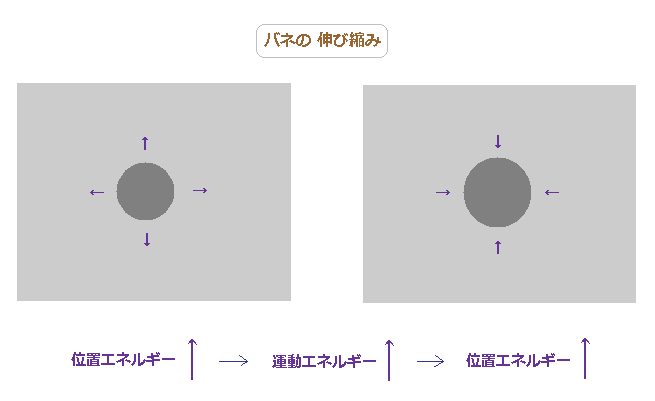
例えば、正電荷の陽子では、その場は 周囲よりも濃い濃度の状態と考えられる。
この状態は そのアンバランスの密度のため 大きな位置 ( ポテンシャル ) エネルギーを有する。
ひとたび 位置エネルギーを得たなら、このエネルギーは保存されなければならない。
この濃い部分の物質が 周囲との濃度差によって 拡散しようとするとき それらは
加速されることになる。
この過程では、この陽子周囲の場が 拡散する物質の圧力で収縮し、バネのように
新たな抵抗によって押し返すことになる。
一方、陽子内部の密度は 元のよりも低くなるため 逆に 拡散していく物質を
引き戻そうとする。
結果的に、これらの物質は 全エネルギーの保存側のために、元の高濃度の状態に戻ることになり、 ±の電荷の状態は維持されることになる。
(Fig.34) 電磁波の本当の正体は?
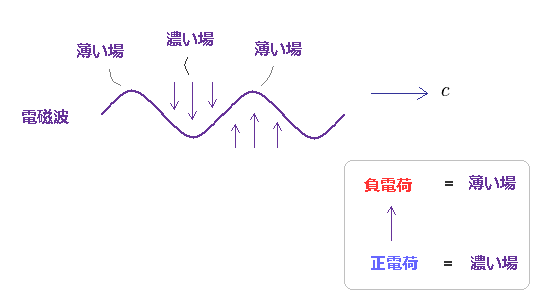
Fig.15 で述べたように、電磁波は 2つのドブロイ波 (= エネルギー、電場 ) が 衝突したとき、横方向に押し出されてできると考えられる。
電磁波が中性であることと、正電場 (= ↑ ) と 負電場 (= ↓ ) が聞かれ合うことを考慮すると、 この "押し出された" 電磁場は↑ と ↓ の繰り返しになると考えられる。
すでに述べたように 正電場は 負電場よりも 濃い密度分布を有すると考えられる。
そのため 電磁場は 通常のドブロイ波のように 低、高濃度の繰り返しになる。
この状態が コンプトン効果で見られるように 電磁波が 横波にも関わらず ドブロイの関係式を満足する理由だと思われる。
つまり 電磁波は "複合ドブロイ波の特殊系" ということになる。
(Fig.35)
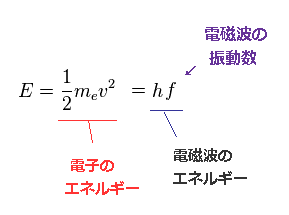
ここで 電子の振動数 (= fe ) と 放射された電磁波の振動数 (= f ) の関係について調べる。
Fig.35 では、電子の全運動エネルギー (= 1/2mv2 ) が そこから放射された電磁波のエネルギー (= hf ) に等しいとしている。
(Fig.36)
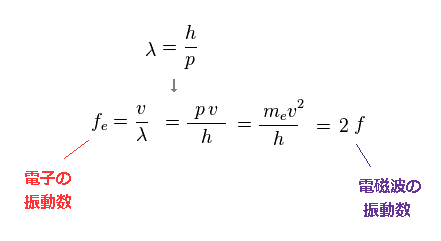
波の関係式 ( v = fλ ) と ドブロイの関係式 ( λ=h/p ) を用いて、 電子の ( ドブロイ波の ) 振動数 (= fe ) は 放射された電磁波の振動数 (= f )の 2倍になることが分かる。
(Fig.37) 振動する電子は 電磁波を放射して 徐々にエネルギーを失っていく。
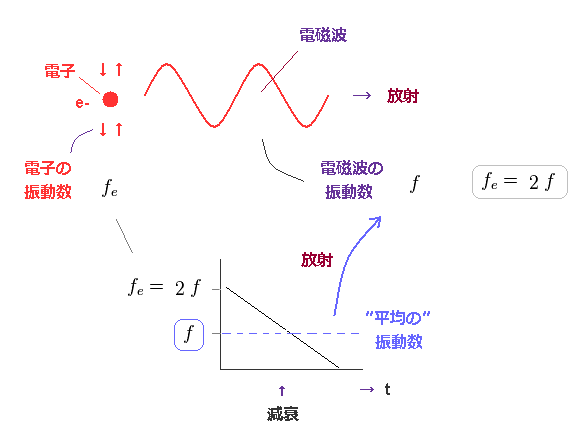
Fig.37 では、振動している電子が 徐々に電磁波を 放射して 自身の運動エネルギーを減らしていっている。
電子の最初の振動数は Fig.36 に示したように 2 × f (= 放射された光の振動数 ) に相当する。
電子が さらに電磁波を放射して エネルギーを失っていくと、その振動は減衰していく ( 最後は止まる )。
つまり このケースでの 平均の電子の振動数は 元の値 (= 1/2 × fe = f ) の半分 ということになる。
結果的に 電子と 放射された電磁波の振動数の間には 重要な関係式があることが証明できた。
(Fig.38) 励起状態 ( n = 2, f=4 ) から 基底状態 ( n =1, f = 2 ) への遷移。
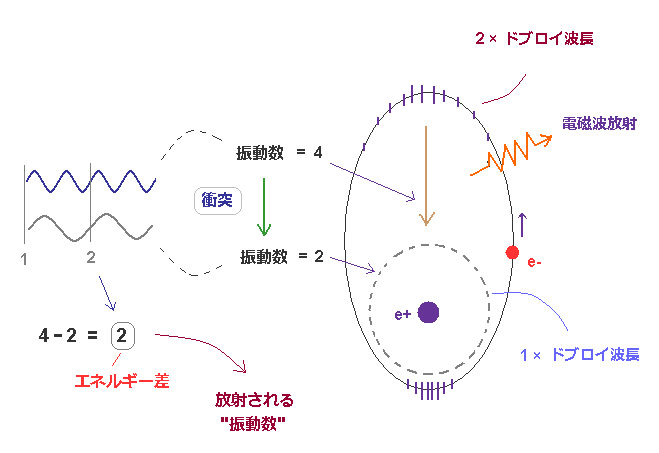
Fig.38 は、 2 × ドブロイ波長の励起軌道から 1 × ドブロイ波長の基底状態に 電磁波放射して戻る様子である。
クーロン力によって 加速され、励起状態の電子のドブロイ波の最終の振動数 は f = 4 になったとする。
場に残っている基底状態の時のドブロイ波 (= 1 × 波長 ) を f = 2 とする。
これら 遷移前後の2つのドブロイ波の振動数は異なるため、 それらは互いにフィットしない。
そのため このドブロイ波間の衝突によって 振動数が 状態間の差である 2 ( 4-2 = 2 ) の うねり が生じる。
励起されたドブロイ波は 電磁波放射の際に 減衰していく。
つまり 放射された電磁波の平均の振動数は Fig.37 で説明したように、半分の 2 (= 1 ) になる。
(Fig.39) バネで 上下に振動している 質量 (= m ) の物体。
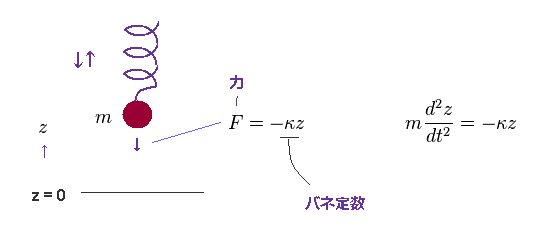
フックの法則によれば、 質量 (= m ) の物体に及ぼすのバネの力 (= F ) は F = -κz で与えられる。 κ は バネ定数で、 "z" は 平衡状態からの 変位である。
(Fig.40) バネの振動数 (= f )。
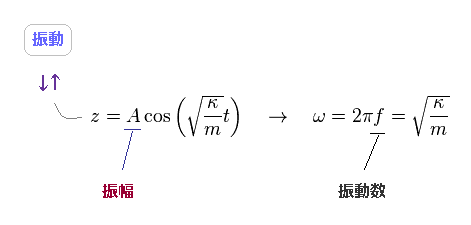
Fig.39 を解いて、 Fig.40 を得る。
見てのとおり、角振動数 (= ω ) は バネ定数 (= 硬さ κ ) と 物体の質量 で決まり、振幅 (= A ) からの影響はない。
(Fig.41) 全エネルギー E.

全エネルギー (= E ) は 運動エネルギー (= T ) と 位置エネルギー (= V ) の和で与えられる。
Fig.41 に示したように、この全エネルギーは 角振動数 (= ω ) と 振幅 (= A ) によって決まる。
(Fig.42) 進行する横波 = 小さなバネの集合。
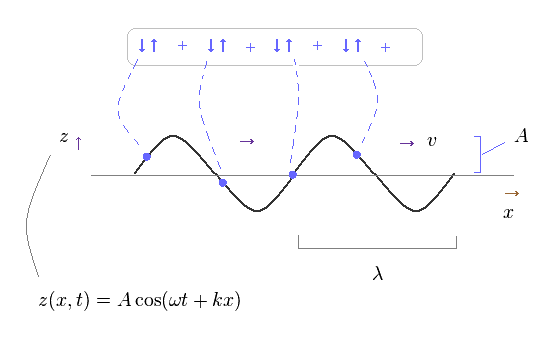
基本的に 進行している波は 場における無数の単純な調和振動子の集合体とみなせる。
このサイト参照のこと。
つまり 波全体が 1方向へ進んでいても、各場は その方向に進んでおらず その位置で 上下 ( もしくは 左右 ) に振動しているだけである。
(Fig.43)
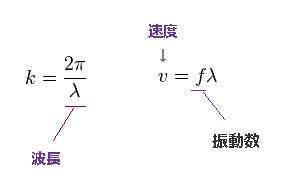
波数 "k" は 2π/波長 (= λ ) で与えられる。
波の速度 "v" は fλ と等しく、 ここで "f" は 振動数である。
注意すべきは この波の速度というのは 単なる位相速度であり、各場の振動速度とは 違った概念だということである。
例え、各場の振動速度がゆっくりだとしても、波長が長くなれば 位相速度は 速くなれる。
(Fig.44) 各場は 波の進行方向に平行に振動している。
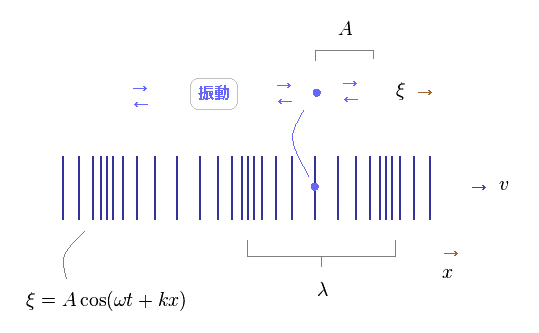
横波と異なり、 縦波 の 各場は 波の進行方向に対して 平行に振動している。
基本的な調和振動子の関係式は 両方の波で 同じである。
(Fig.45) 体積 1 × Δx の場の密度変化。
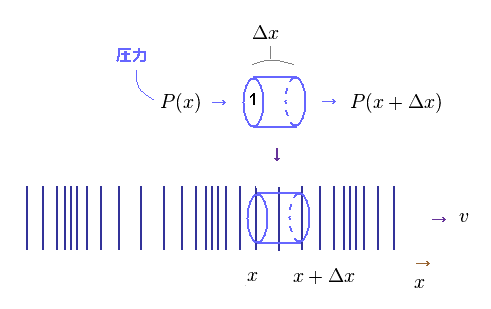
ここで 縦波においても 基本的な調和振動子の関係式が成り立つことを示す。
Fig.45 では、 ある圧力 (= P ) が 体積 1 × Δx の円柱状の場にかかっている。
この場の両端の x 座標は "x" と x+Δx である。
(Eq.1) 圧力と 場の密度。
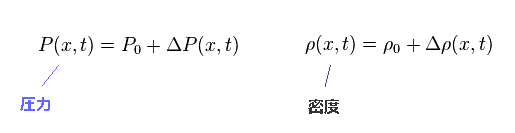
各場の 圧力 (= P ) と 密度 (= ρ ) は Eq.1 で与えられる。
P0 と ρ0 は それぞれ "平均の" 圧力と密度を表している。
(Eq.2)
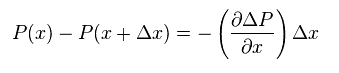
上記の場にかかるトータルの力は "x" と "x+Δx" 地点にかかる圧力の差で与えられる。
(Eq.3)
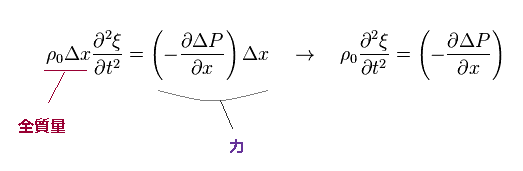
上記の場に含まれる全質量は ρ0Δx ( 底面積は "1" ) である。
つまり 運動方程式は Eq.3 になる。
(Eq.4)
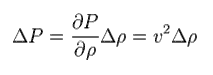
圧力は 密度に比例する。
それらの比を "v2" とすると、
(Eq.5)
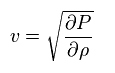
体積 (= V ) の変化は 次のようになる。
(Eq.6)
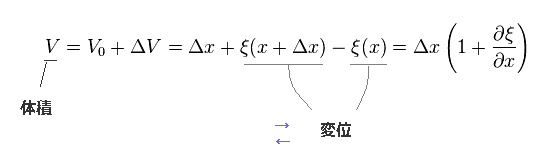
場全体の物質量は一定のため、
(Eq.7)
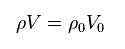
Eq.6 と Eq.7 から 次を得る。
(Eq.8)
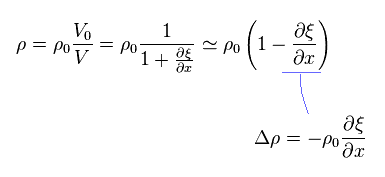
Eq.3、 Eq.4、 Eq.8 から、通常の波の式を得る。
(Eq.9)
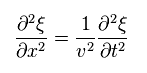
ここでは
(Eq.10)
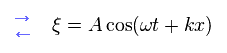
と
(Eq.11)
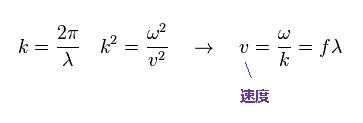
このように、音波などの縦波も 場の振動機構に関して 横波 ( 電磁波など ) と同じであることが分かる。
(Fig.46) N 個の動く粒子を含む箱。
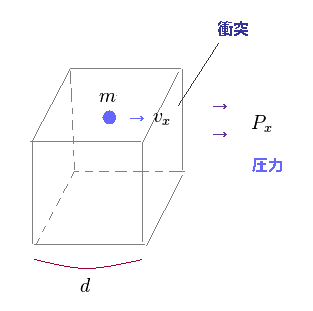
このセクションでは、同じ量のエネルギーが与えられたとき、 同じ大きさの圧力が、 粒子の密度 (= 負、正電荷 ) に関わらず 生じることを示す。
この機構のために、原子核周囲の ドブロイ波長の整数倍という条件が いろんな条件でも 正確に満たされることになる。
(Eq.12)
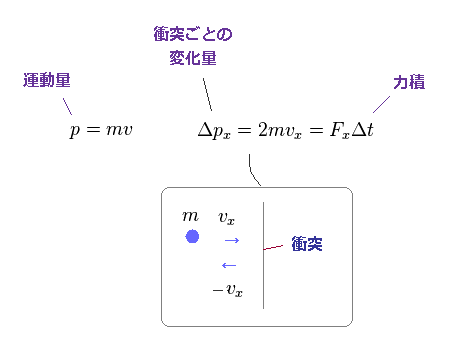
このサイトにあるように、 各粒子 (= 場の物質 ) が 速度 "v" で動いているとする。
x 方向の運動量は mvx である。
各粒子が この箱の1つの面に衝突するとき、跳ね返って 運動量は -mvx になる。
この方向での運動量の変化量は "2mvx" であり、この量の "力積" (= FΔt ) が 与えられたことになる。
(Eq.13)

衝突ごとに、粒子は 往復して 距離 "2d" を進む必要がある。
そのため 衝突に必要な時間は Eq.13 で与えられる。
(Eq.14)
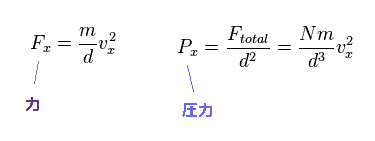
Eq.12 と Eq.13 から、 1つの面に働く力 (= Fx ) はEq.14 のようになる。
圧量は F/面積 (= d2 ) で与えられる。
ここで "N" 個の粒子が この箱の内部に含まれているとする。
"n" が 数密度で、 "v" が 各粒子の速度である。
(Eq.15)
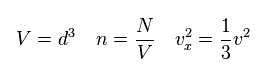
Eq.14 と Eq.15 から、次を得る。
(Eq.16)
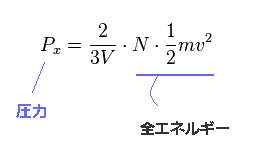
Eq.16 に示したように 圧力 (= P ) は 粒子の数 (= N ) に関係なく、全エネルギー量に 比例することが分かる。

2014/10/24 updated This site is link free.