
トップページ (2電子原子も含む正確な新ボーア模型)
光子は本当に粒子なの? ベルの不等式の破れとの関係
ボーア模型のパウリの排他原理は役に立つ。
ボーア模型は水素原子のすべてのエネルギー準位において、量子力学と同じ結果をだす。
また、このページ や このページに示したように、ボーア・ゾンマーフェルト模型は 微細構造を含むすべてのエネルギー準位で ディラック方程式と等しい。
たいていの本には、これらは単なる偶然の一致だと書いてある。
実は 水素原子のシュレディンガー方程式は 数学的にボーア・ゾンマーフェルト模型の 一部にすぎないのである。 ( 詳細は、このページ を参照のこと。)
さらに シュレディンガーの水素原子は 非実在の状態も含んでおり、このことは シュレディンガー方程式が間違いであることを示している。
(Eq.1) ボーア・ゾンマーフェルトの量子化条件。

ドブロイの関係式 ( 波長 λ = h/mv , mv = 運動量 ) を使うと ボーア・ゾンマーフェルトの楕円軌道が ちょうど 各方向で ドブロイ波長の整数倍になっていることがすぐに理解できる。
( Eq.1 では pr が 動径方向の運動量で "p" が 定常な角運動量 ( p = r × mv ) を意味している。)
1周して 波の位相が同じになるには 接線方向と動径方向の両方において 波の位相の端がそろう必要がある。
( Eq.1 では 上が接線方向、下が動径方向である。)
このセクションで示したように、1軌道の 全ドブロイ波の数は 動径方向と接線方向の波の合計で表される。
(Fig.1) ドブロイ波長の整数倍である シュレディンガーの動径方向の関数。
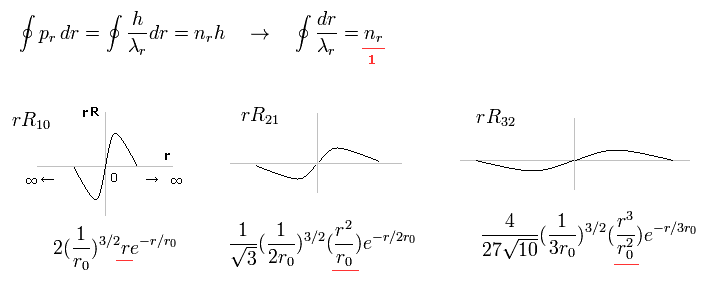
Fig.1 は 1軌道に含まれる 動径方向の波の数が 1つである シュレディンガーの波動関数の例を示している。
( 1軌道とは ある地点から 同一地点まで戻ってくる距離をいう。 ∞ → 0 → ∞ )
例えば、R32 の波動関数は 主量子数 n = 3 で、角運動量 (= 接線方向の運動 ) が l = 2 である。
つまり 動径方向の波の数は 3-2 = 1 となる。
これらの波の数は ドブロイ波の整数倍を特徴とする ボーア・ゾンマーフェルト模型と 同じ意味を持つ。
( この理由は 後で説明する。)
(Eq.2) シュレディンガーの水素原子のドブロイ波形式。
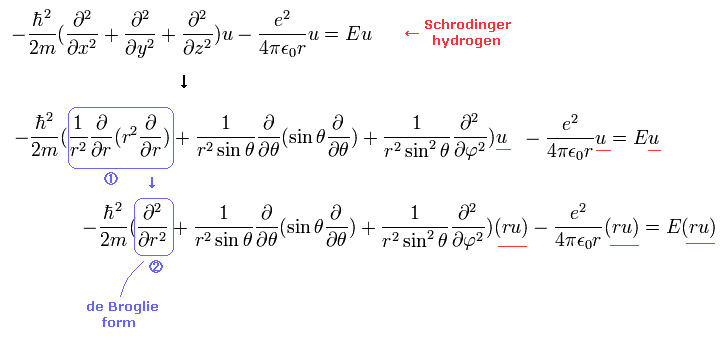
重要な点は シュレディンガー方程式を 動径、接線方向ともに ドブロイ波形式で表すことである。
(Eq.3)
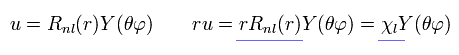
Eq.2 と Eq.3 に示すように、Rnl のかわりに χ = rRnl を用いると、Fig.1 に示すように この動径方向の波動関数が ドブロイ波を表すようになる。
(Eq.4)
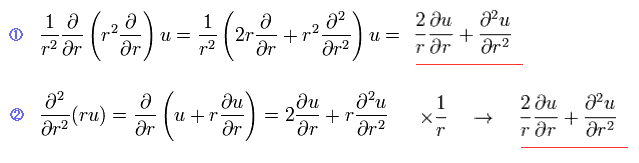
Eq.4 を見れば Eq.2 の変換が正しいことがわかる。
(Fig.2) シュレディンガーの動径関数で 波が2つ、3つのケース。
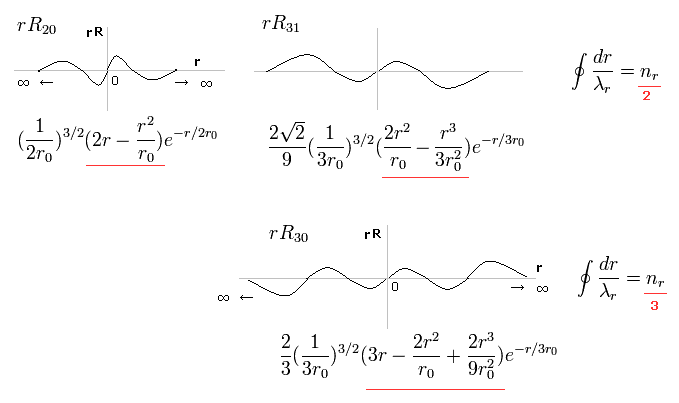
Fig.2 の上の行は、動径方向1周が 2ドブロイ波長の波動関数である。
例えば、R31 は 主量子数が "3" で 角運動量 (= 接線方向の運動 ) が "1" である。
結果、動径方向の波の数は 3-1 = 2 となる。(意味は後で説明する。)
また 下の行は n = 3 で l = 0 であるため、動径方向の波は 3-0 = 3 となる。
(Fig.3) シュレディンガーの接線方向の波動関数=ボーア・ゾンマーフェルト模型。

Fig.3 において、シュレディンガーの水素の球面調和関数が 1軌道に含まれる接線方向の ドブロイ波の数を示している。
結果的に 動径方向と接線方向のドブロイ波の合計 が 主量子数 ( n = エネルギー準位 ) を表す。
( 詳細は、このページ を参照のこと。 )
(Fig.4)
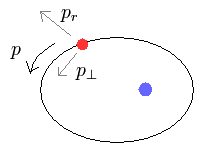
楕円軌道の各地点において、粒子の運動を 動径方向と接線方向に分離できる。
(Eq.4)
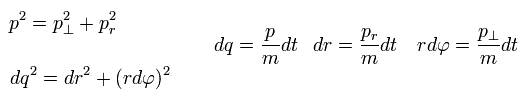
ここでは p は "運動量"、 "m" は粒子の質量を表す。
( このセクションのみ "p" は 全運動量を意味し、この p と Eq.1 の角運動量とは別物であることに注意。)
"dq"、 "dr"、"rdφ"は 各方向に 微小時間 dtの間に進んだ距離とする。
もちろん 動径方向と接線方向のベクトルは 3平方の定理を満たす。
Eq.4 と ドブロイの関係式 ( λ = h/p = h/mv ) を用いると、各方向の微小区間に含まれるドブロイ波の数は、
(Eq.5)
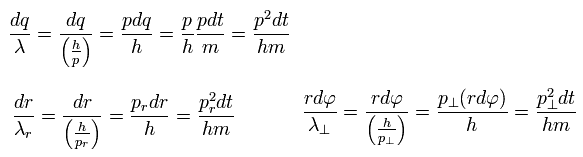
結果、
(Eq.6)
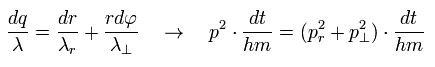
つまり 1軌道に含まれる全ドブロイ波の数は 動径方向と接線方向の波の合計となる ( Eq.1 も参照のこと )。
(Eq.7)
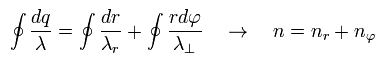
このセクションでは 通常のボーア模型について簡単に説明する。
最初に このページで説明したとおり、ボーア模型の単一電子は 加速しただけでは 核に落ちていくことはない。
(Eq.8)
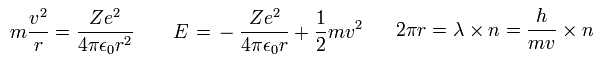
Eq.8 の最初の式は 遠心力がクーロン力に等しいことを意味している。
2番目の式は クーロンポテンシャルエネルギーと運動エネルギーの合計を意味する。
3番目の式は 円軌道1周 が ドブロイ波長の整数倍 (= n )であることを表している。
1番目の式を2番目の式に代入して、
(Eq.9)
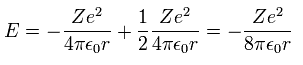
3番目の式の v を Eq.8 の 最初の式に代入すると、
(Eq.10)
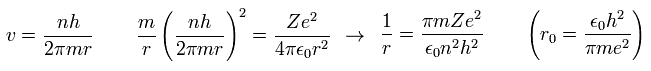
ここで r0 ( n = Z = 1 ) は "ボーア半径" である。
Eq.10 を Eq.9 に代入すると、ボーア模型の 全エネルギー E は、
(Eq.11)
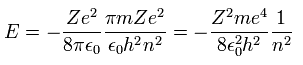
これは シュレディンガーの水素原子とまったく同じ解である。
Eq.10 より、粒子の速度 v ( n = Z = 1 ) と 光速 c の比は、
(Eq.12)
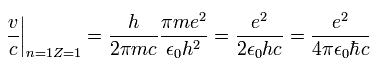
これが 有名な微細構造定数 α である。
このページに示したように、動径方向の量子数 (= nr ) は 動径方向の軌道に含まれる ドブロイ波の数を表している。
また nφ は 量子化された角運動量 (= 接線方向の軌道のドブロイ波の数 ) を意味している。
(Eq.13)
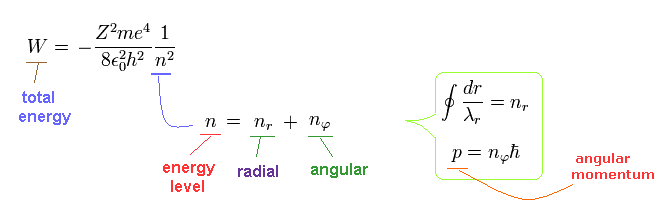
Fig.1 と Fig.2 のシュレディンガーの波動関数を振り返ってみる。
(Fig.5) シュレディンガーの水素 = ボーア・ゾンマーフェルト模型。
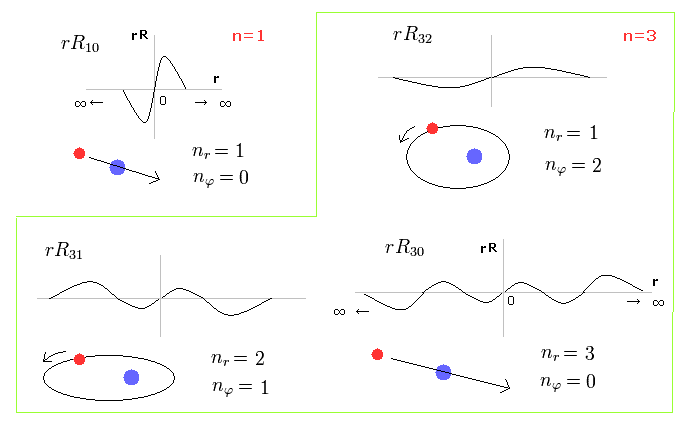
Fig.5 は シュレディンガーの波動関数のエネルギー準位が ボーア・ゾンマーフェルトの量子化のルールに従っていることを示している。
重要な違いは シュレディンガーの解は 必ず ゼロから無限大の範囲のため 非実在の状態も含んでいることである。
もし シュレディンガーの水素が ボーア軌道の 1s 軌道のような 円軌道を含んでいるとすると、その動径の波動関数は 定数になる。
この場合、規格化しようとすると この定数がゼロでないかぎり 波動関数が 発散してしまう。
そのため シュレディンガーの波動関数は 円軌道を含むことができず、そのかわりに "非実在"の ゼロの角運動量が出現する。
これらの性質が シュレデインガーの水素が間違いであることを示している。
(Fig.6) 思いがけない偶然の一致?
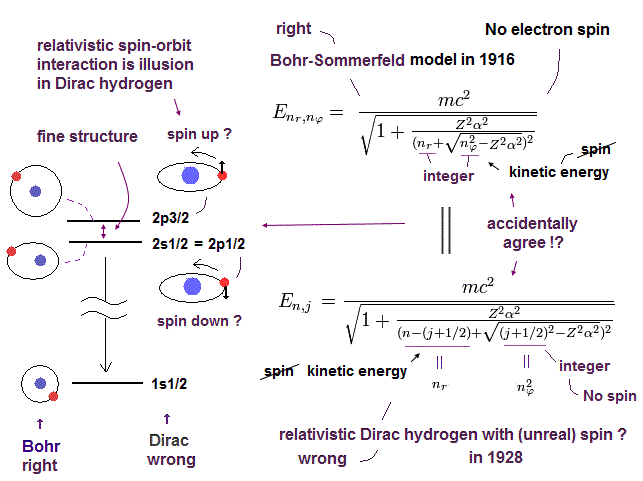
このページに示したように、微細構造は ボーア・ゾンマーフェルト模型によって最初に説明された。
後に偶然にもディラック方程式の水素原子解が ボーア・ゾンマーフェルト模型と完全に一致した。
( このページも参照のこと。)
もちろん この両者の解の意味やメカニズムはまったく異なるものである。
なのにどうして偶然にも一致してしまったのだろうか?
なぜなら 彼らは ディラック方程式の水素を考慮していたとき 実験値によく一致する ボーア・ゾンマーフェルトの解と同じものを得ることを目標にしていたからである。
また 奇妙なことに ディラックの水素原子は 2S1/2 = 2P1/2, 3S1/2 = 3P1/2, 3P3/2 = 3D3/2 .... などのような 多くの偶然の準位の一致を含んでいるのである。
( ディラックの水素原子は 多くの架空の状態を必要とする。 )
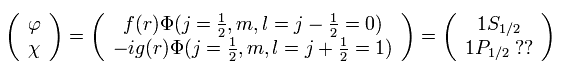
このページでは ディラックの水素原子模型が 解を得るために 多くの架空の状態を必要としていることを示した (= 1p1/2, 2d3/2, 3f5/2 .... )。
このことは 明らかに 標準的な量子力学と矛盾しており、ディラックの水素原子が間違いであることを示している。
もし ディラックの水素原子が間違いだとすると、ラムシフトなどの解釈も当然変わる。
なぜなら QED におけるラムシフトの計算は ディラックの水素原子が正しいという前提条件に 完全に頼っているからである。
Fig.6 の2つの のエネルギー解を注意深く見比べると、これらの解は実はまったく同じものだということに気づくだろう。
例えば、水素様原子の n =2 のエネルギー準位においては、ボーア・ゾンマーフェルト模型では次のような2種類の軌道が存在する。
2S orbital = nφ=1, nr=1 ----- 楕円形軌道 (角運動量=1)
2P orbital = nφ=2, nr=0 ----- 円形軌道 (角運動量 =2)
一方で、ディラックの水素模型でも、n = 2 のエネルギー準位では次のように2パターン存在する。
2S1/2 , 2P1/2 orbitals----- j = 1/2, n = 2
2P3/2 orbital---- j = 3/2, n = 2
つまり、ボーア・ゾンマーフェルト模型の 2S 軌道は ディラックの水素模型の 2S1/2 と 2P1/2 に同じになることがわかる。
また、ボーア・ゾンマーフェルト模型の 2P 軌道は ディラックの水素模型の 2P3/2 と同じである。
これは、両方の模型において、微細構造のエネルギー差は完全に一致することを意味する。(解釈だけが違うということ。)
[1] A. Sommerfeld., Annalen der Physik 1916 [4] 51 p1-94
[2] P.A.M. Dirac., The Principle of Quantum Mechanics (Fourth edition)

2010/4/24 updated This site is link free.