
トップページ (正確な新ボーア模型)
電子スピンは存在しない。
特殊相対論は間違っている。
(Fig.1) 4元運動量。

特殊相対論は 4元運動量 (= E/c, p ) が ローレンツ変換の下で、時間と空間の座標 ( ct, x, y, z ) のように変換することを要求している。
"E" と "p" は それぞれ 相対論的なエネルギーと運動量である。
ニュートン力学上の 通常の力 F は 運動量 p の時間変化で定義される。
また エネルギー E の時間変化は 力 F × 速度 (= u ) で与えられる。
(Fig.2) 通常の力 Fy は 動くと 弱くなる。
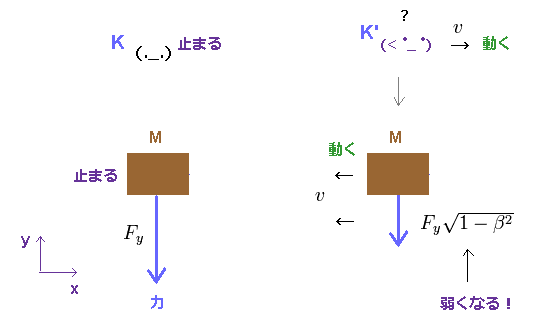
相対論的な運動量とエネルギーが Fig.1 の関係式を満足するには 力 Fy が 動いた時 減少する必要がある。
次のサイトなど参照のこと。 ( ここ (v=0), ここ (p.3), ここ (p.4,5), ここ (p.15) )。
Fig.2 左では、観測者 (= K ) と 物体 (= M ) が静止しており、力 Fy が この物体に y 方向に作用している。
観測者が x 方向へ 速度 "v" で動きだすと、この物体は 彼の視点から 逆方向へ動いて見える
(= K', Fig.2 右 )。
K' 系での y 方向の力は、 特殊相対論によれば 減少する必要がある。
(Fig.3) 2つの等しい力 Fy が 釣り合っている。
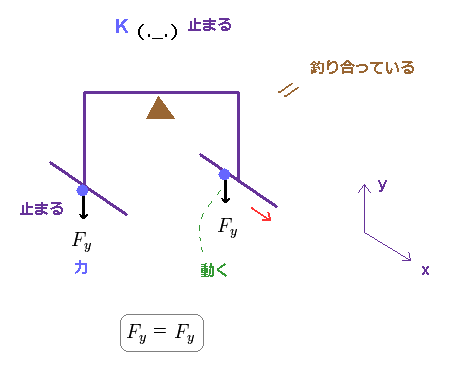
Fig.3 では、2つの等しい力 Fy が K 系 (= 観測者は静止 ) において 静止したレバーに加えられている。
このレバーは 支点の両側に等しい長さの腕を持ち、K 系においては ちょうど釣り合って動かない。
これらの力の1つ (= Fig.3 左 ) は 静止しており、もう1つの力は x 方向へ 速度 "v" で 動いている。
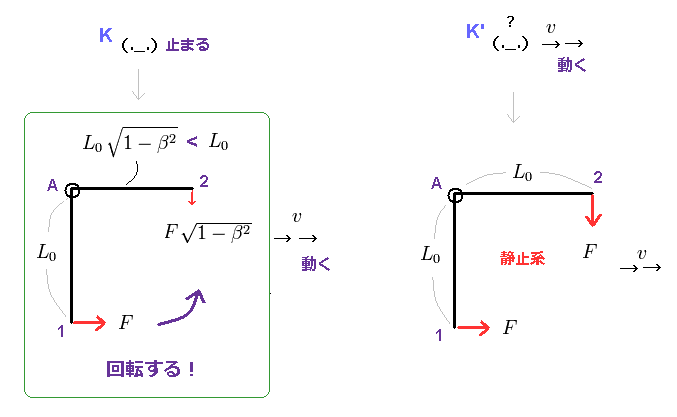
(Fig.4) レバーは 動く観測者の視点 (= K' ) でのみ 回転する?
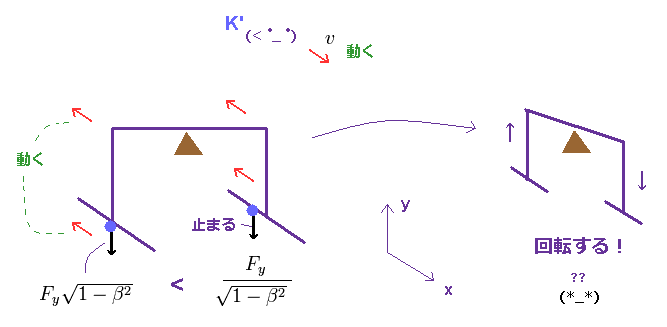
観測者が x 方向へ 速度 "v" で動きだすと、このレバーと左側の力は 逆方向へ
動きだすことになる。
結果、この力 (= Fig.4 左 ) は Fig.2 に示したように 減少することになる。
一方で、右の力は K' 系においては 逆に 静止しているため、観測者の動きによって 増加してしまう。
結果、このレバーは K' 系でのみ 時計方向に 回転してしまうことになる。
この理不尽な 力 Fy の変換は 下記の直角レバーのパラドックスの原因の1つである。
もちろん、このパラドックスには 解決策は 何もなく、よって 相対論的なエネルギー、運動量の概念が 間違いであることを示している。
(Fig.5) 特殊相対論は 観測者に "超能力" を与えた?
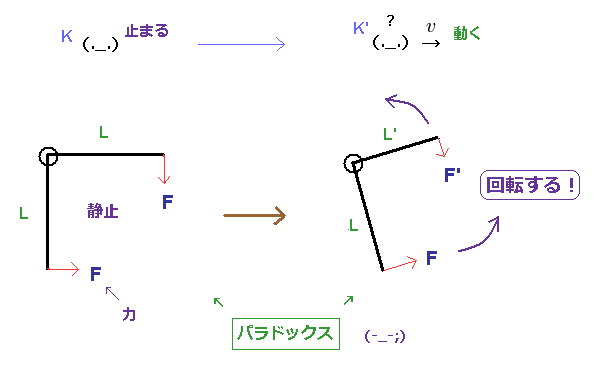
1つの回転軸のある直角型のレバーがある。
Fig.5 左図では、レバーの2つの腕の長さは 等しい。
また それに作用する互いに垂直な2つの力 F の大きさも等しい。
Fig.5 左では、このレバーは 力が釣り合っているため 回転せず 静止している。 ( トルク: F×L = F×L. )
しかし 観測者が動きだした途端に、触れずして このレバーは 回転し始めることになる (= Fig.5 右 )。
これは明らかに致命的なパラドックスであり、特殊相対論が 間違いであることを示している。
(Fig.6) どうして 観測者の移動で レバーが "回転"するのか?
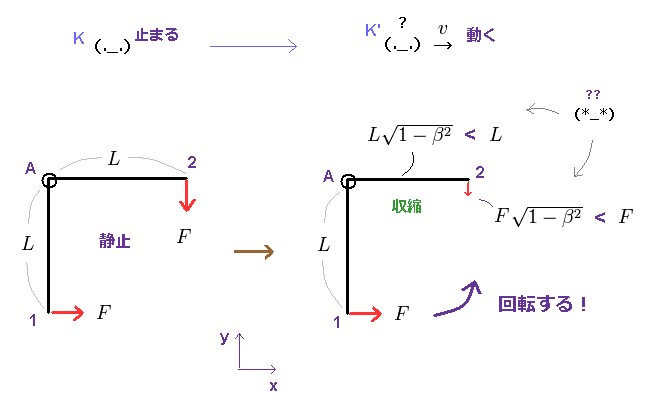
ここでは レバーが回転する理由を説明する。
(A-2) の水平な腕のみ 移動方向 (= x 方向 )のため ローレンツ-収縮する。
さらに 相対論によれば、運動方向に垂直方向の 力は (1-β2)1/2 の因子の分だけ、元の力よりも 弱くなる。
結果的に、移動する観測者の視点のみで、レバーの回転トルクは ゼロに ならないことになる。
静止した観測者からは レバーのトルクは ゼロなのにである。これは明らかなパラドックスである。
(Fig.7) x、 y 方向のニュートン力学の力のローレンツ変換。
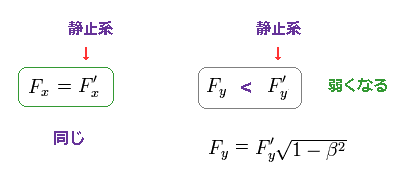
ローレンツ変換によって、x 方向の力は 同じまま ( F'x = Fx ) で、y 方向の力のみ 小さくなってしまう ( F'y < Fy )。 ( ここ (v=0), ここ (p.3), ここ (p.4,5), ここ (p.15) ) など参照のこと。
Fig.7 では、ローレンツ変換は x 方向である。
また "静止系" とは 静止した物体に対して加えられた力の意味である。
(Fig.8) 観測者の運動に平行な力成分は 不変である。 ( Fx = F'x )
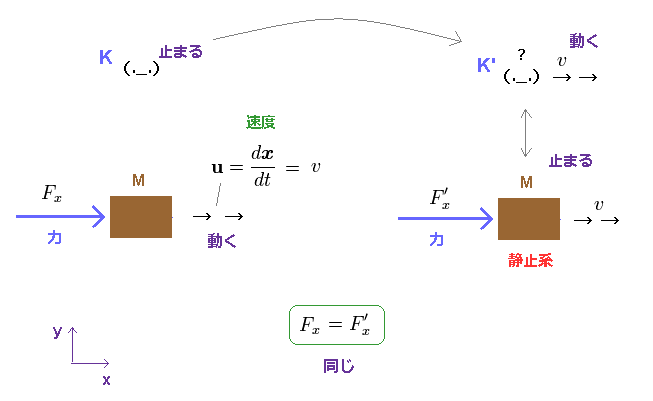
Fig.8 では、K 系で静止している観測者に対して、物体 (= M ) が 速度 u = v で x 方向へ 動いている。
K 系では、力 Fx (= 4元力でなく 通常の力 ) が この物体にくわえられている。
x 方向に 速度 "v" で 動いている観測者 (= K' 系 ) からは、この物体は 静止して見える。
つまり K' 系は この物体の静止系ということになる。
力 Fx は K' 系では F'x に変換する。
特殊相対論によれば、これら運動方向の力は いかなる慣性系においても変化しない
( Fx = F'x )。
(Fig.9) 観測者の運動に垂直な力は 減少する。 ( Fy < F'y )
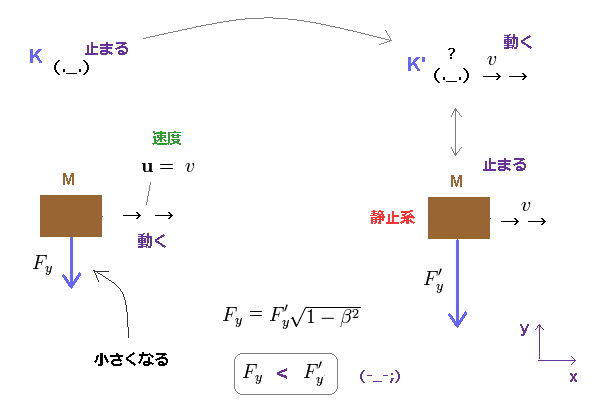
一方で、観測者の運動に垂直な力 (= Fy ) は K 系において 弱くなる。
物体の静止系での力 (= F'y ) のほうが強いということである。
K' 系での 動いている観測者の視点では、物体は静止しており、そこに 力 F'y が加えられている (= Fig.9 右 )。
一方、K 系からの視点では 物体は
動いており、その力は 減少するらしい ( Fy < F'y )。
(Eq.1) 時空間座標のローレンツ変換。

相対論によれば、時間と空間の座標 (= t, x, y, z ) は、 ローレンツ変換に従って変換する。
(Eq.2)
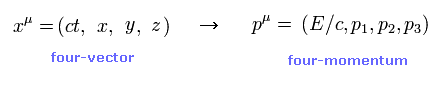
特殊相対論によれば 四元運動量は ローレンツ変換のもとで 時空間座標 ( ct, x, y, z ) と同じように変換する。 このサイト 参照のこと。
これら 相対論的なエネルギー (= E ) と 運動量 (= p ) の変換は このページにあるように ディラック方程式にも使用されている。
上記の ニュートン力学の力の変換は この4元ベクトルにとって
必要不可欠なものである。
(Eq.3)

つまり K' 系での運動量 (= p'x ) は、 Eq.3 で与えられる。
K 系での x 方向の運動量 (= px ) と エネルギー (= E ) は 混合することになる。
(Eq.4) "静止した" 観測者からの視点 (= K )。
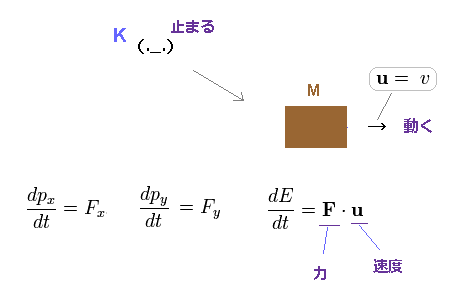
静止した観測者からの視点 (= K ) では、物体は 速度 u (= v ) で 右方向へ動いている。
力 (= F ) は 運動量 (= p ) の時間変化に等しい。
エネルギー (= E ) の時間変化率は、力 × 速度 "u" に等しい。
なぜなら 力 × 移動距離は エネルギー E になるからである。
(Eq.5) 運動する観測者からの視点 (= K' )。
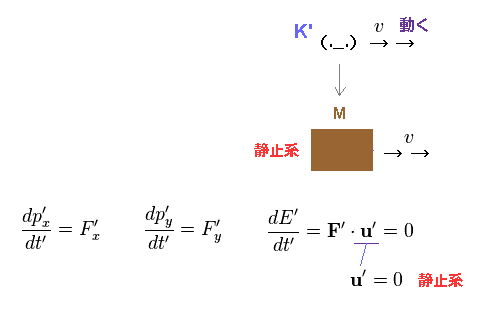
K' 系では、観測者は 右方向へ 速度 "v" で動いている。
物体も 同方向へ動いているため、K' では観測者から見て 物体は静止している。
つまり K' での物体の速度はゼロ ( u' = 0 ) ということになる。
運動量 (= p' ) と エネルギー (= E' ) は Eq.3 の関係式で与えられる。
各方向の力のローレンツ変換の計算については、 このセクションを参照のこと。
(Eq.6) レバーは K' 系では 静止しているが、 K 系では回転する。
直角型のレバーが 速度 u = v で x 方向へ動いている。
K' 系での観測者も 同速度 v で x 方向へ動いている。
(Eq.7) レバーは K' 系 (= 動く観測者の視点 ) では静止している。
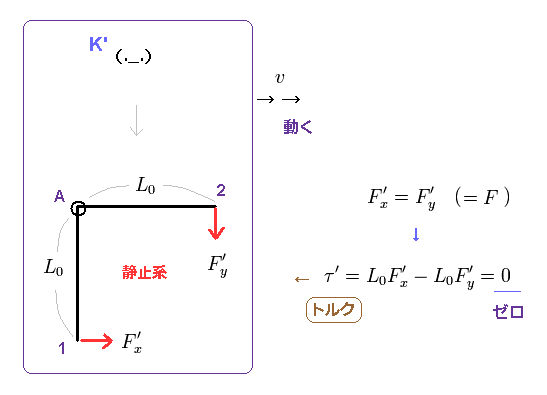
つまり このレバーは K' 系 (= レバーの静止系 ) では 静止している。
この K' においては レバーの長さと 加えられた力は 等しく釣り合っているとする。
結果的に、レバーは K' では 回転トルクは ゼロになるため、回転しないことになる。
(Eq.8) K 系でのみ レバーは回転する。 K 系でのトルクはゼロではない。
K 系での静止している観測者の視点では、このレバーは 右方向へ動いている。
移動方向に平行なレバーの腕は ローレンツ収縮している。
また ニュートン力学上の y 方向の力 Fy は 静止系での力F'y よりも 弱くなってしまう。
結果的に トルク τ は Eq.8 に示したように ゼロではない。
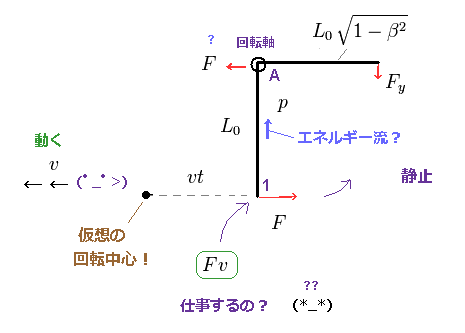
(Fig.10) レバー内の奇妙なエネルギーの流れ? 仮想の回転中心 !?
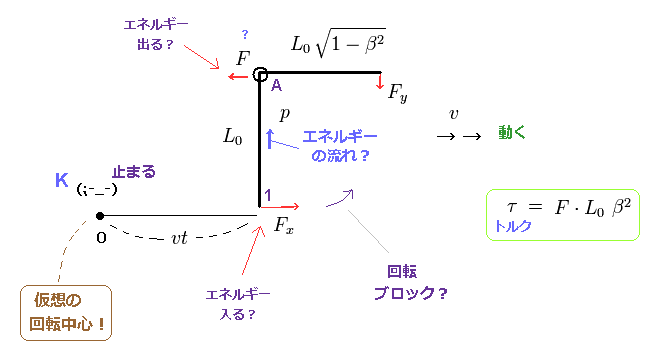
この直角レバーのパラドックスを解決するために、彼らは 仮想の回転中心と 非実在的なエネルギーの流れというものを導入した。 このサイト や このサイト参照のこと。
"p" も レバー内を流れる "仮想の"運動量である。
この仮想の回転中心が 観測者の地点にあると 仮定した。
(Fig.11) "仮想の"トルクは リアルな物でない。
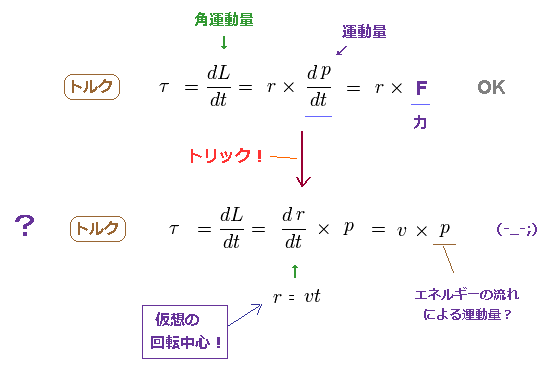
トルクは 力 × 半径 で与えられる。
しかし この解決策では Fig.11 下や このページに示したように トルクの中身をを まったく別の物に変更してしまった。
彼らは 観測者の地点に 仮想の回転中心を設定した。 .
つまり この ( 仮想の ) 半径 "r" は、 r = vt ( "v" は速度 ) のように増加していくことになる。
トルクは この半径 "r" の時間微分 × 偽の運動量 p で与えられる。
Fig.10 では、レバーが K 系に対して 速度 "v" で x 方向へ 動いている。
そのため 彼らは 外力 Fx が レバーの "1" の地点に 単位時間 "Fv" の仕事をすると 主張している。
(Eq.9) ↓ 仮想のエネルギーの流れ。

そして この奇妙なエネルギーが 速度 U で レバー内を A地点のほうへ流れていくと 強引に仮定した。
Eq.9 では、 T は このエネルギーが "A" 地点に到達するのに必要な時間を表している。
また E は この時間 T の間に 腕 "1-A" 内に 蓄積するエネルギーということになる。
(Eq.10) ↓ レバー内に溜まった "仮想の" エネルギー。

相対論的なエネルギー "E" と 運動量 "p" を用いると、 Eq.10 は レバーの腕 "1-A" 内に蓄積する 運動量を表す。
( 相対論的な運動量 p = エネルギー E × U/c2. U は 奇妙なエネルギーの速度である。 )
また、このエネルギーが 作用反作用を考慮すると、支点 A から レバーの外に流れだしていくと仮定した。
(Eq.11) ↓ "偽の" トルク。

さらに K 系の観測者の地点に 偽の 回転中心を設定した。
この仮想中心は レバーとは 何の繋がりもないため まったく無意味なのにである。
トルクは 角運動量の時間微分で与えられる。
しかし 彼らは Fig.11 に示したように トルクの意味を人為的に
他の 非実在的な概念に すり替えてしまった。
(Fig.12) "仮想中心" によるトルクが "リアルな" トルクと偶然に一致する !?
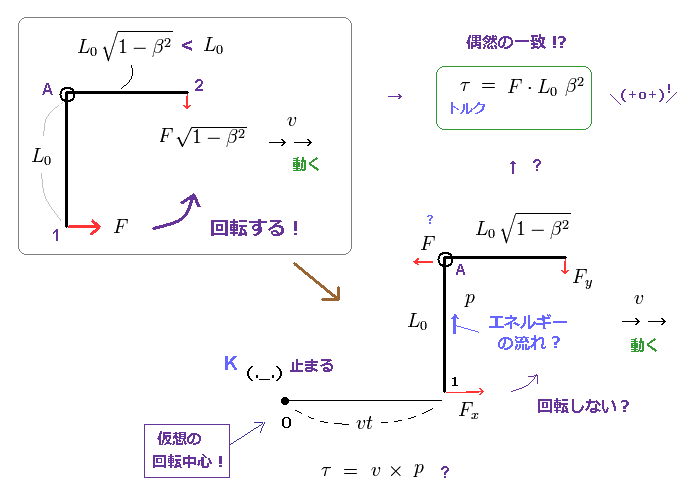
レバーと観測者間の距離は "vt" のため、新たな角運動量は L = "vtp" になる。
そのため この L の時間微分は "vp" になると 彼らは主張している。
結果、トルク τ = "vp" (= Eq.11 ) は Eq.8 と偶然にも一致し、奇妙なエネルギー流に基づいて 回転が防止できたというわけである。
(Fig.13) 力 F は 地点 1 に仕事をしない。
しかし この方法は 理不尽な前提条件に依存している。
まず最初に、レバーのトルクがゼロ ( もしくは弱まっている ) とき、
力 Fx は 地点 "1" に対して 仕事をしない。
( レバーは剛体のため、この力 Fx は Fy によって 遠隔的にキャンセルされるからである。 )
例えば、力 (= F ) が釣り合った静止した直角レバーがあるとする。
このとき この力 F は レバーが静止しているため 仕事をしていない。
しかし 上記の 不合理な定義が正しいとすると、観測者が 左方向へ動き始めると レバーは 右方向へ動いて見えるため、この力が 仕事をし始めることになる。
もちろん こんなことはあり得ない。
(Fig.14) レバーは 同時に 回転 "+" 回転しない? ← パラドックス !

またお気づきのとおり、レバー内の エネルギーの流れをいうのも まったく真実味がない。
結果的に 直角レバーのパラドックスに 解決策はなく、QED や 標準模型などの相対論的な理論は 間違いということになる。
(Eq.12) 相対論的な運動量 p.
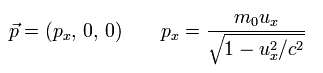
この論文では、このパラドックスを x、y 方向の 異なった相対論的質量を用いて 解決しようとしている。
静止質量が m0 の物体が 速度 ux で x 方向へ動いている。
そのため 相対論的な運動量は Eq.12 で与えられる。
(Eq.13) x 方向への相対論的な質量。
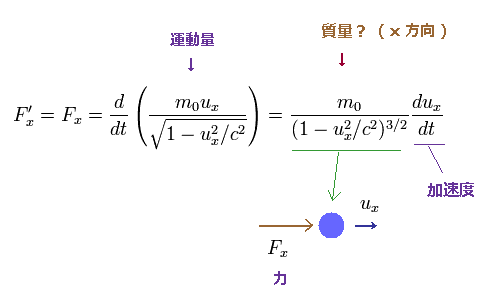
運動量 Eq.12 を用いて、Eq.13 に示したように x 方向の相対論的な質量を得た。
ここでは 次を用いた。
(Eq.14)

同様に y 方向の相対論的な質量は、
(Eq.15) y 方向の相対論的な質量。
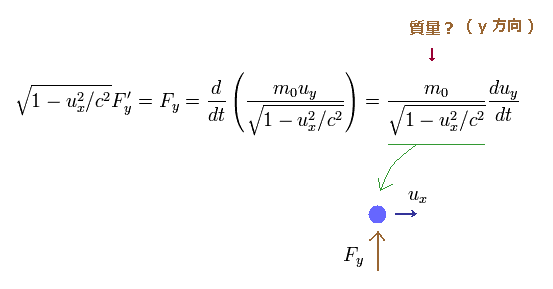
Eq.13 と Eq.15 から、x 方向の相対論的な質量は y 方向の質量よりも 重くなることが分かる。
(Eq.16) x 方向の質量は y 方向のよりも重い。
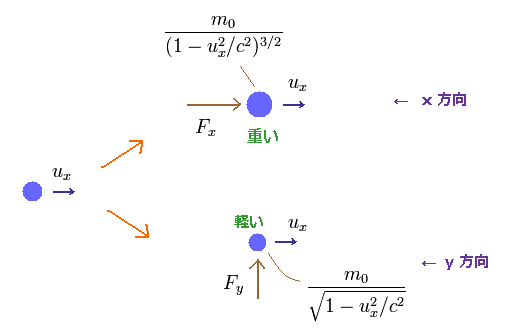
Eq.13 から、x 方向の加速度 (= ax ) は、
(Eq.17)

Eq.15 から、y 方向の 加速度 (= ay ) は、
(Eq.18)

つまり x、y 方向の相対論的な質量が異なるため、加速度が y 方向のほうが大きくなるというわけである。
(Eq.19) トルク = 加速度 ( 力の代わりに ) × 長さ ?

彼らは トルクの計算の際に "力" の代わりに "加速度" を用いた。
Eq.17、 Eq.18、 Eq.19 から、 K 系 (= レバーが動いている系 ) でのトルクは
(Eq.20)

結果的に K 系においても トルクがゼロになり、パラドックスは解決されたと 主張しているわけである。
この方法は x と y 方向の相対論的な質量の違いが トルクの違いをキャンセルさせる機構を利用している。
しかし実際は 相対論的な質量の違いは発生せず、 よってトルクはキャンセルされずに パラドックスは残ることになる。
(Fig.15) 相対論的な質量は 両方向で " 同じ "。
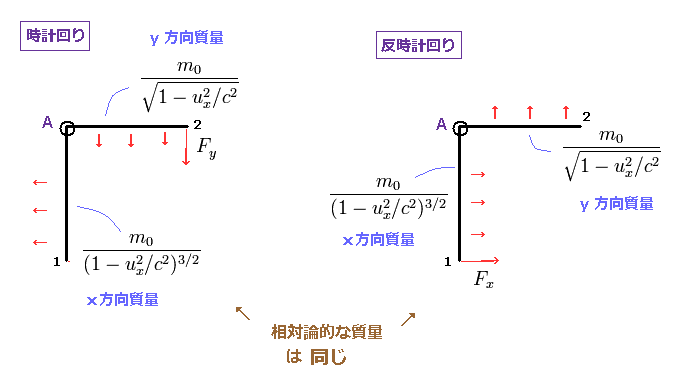
Fig.15 左では、力 F
このケースでは 1-A の腕が x 方向へ加速しており、 A-2 の腕が y 方向に加速している。
つまり この回転は 異なった相対論的な質量を 含んでいることになる。
Fig.9 右では、力 Fx が レバー全体を 反時計方向に回転させようとしている。
このケースにおいても 1-A の腕は x 方向へ加速しており、 A-2 の腕は y 方向へ加速している。
結果的に ( Fx と Fy による ) 両回転とも 同じ相対論的な質量を加速させようとしていることになる。
つまり トルク = "力 × 長さ" は "加速度 × 長さ" に等しいままで、状況は何も変わっていないことになる。
よって 力を加速度に代替させる方法も解決策になり得ず、直角レバーのパラドックスが 特殊相対論の致命的な欠陥であることに 何の変更もない。
(Ap.1) K' と 物体が x 方向に 速度 v (= u ) で動いている。
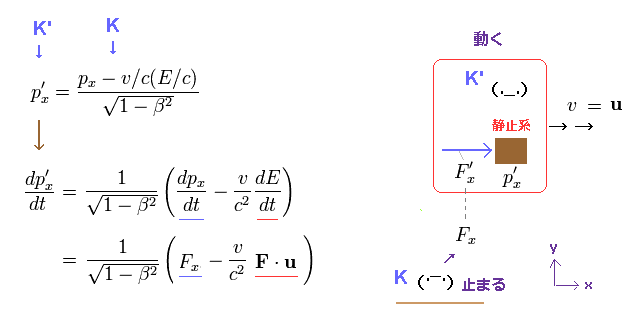
K' 系と 物体が K 系に対して 速度 u = v で x 方向へ動いているとする。
K と K' 系の観測者から見た 物体の運動量とエネルギーは それぞれ
( p, E ) と ( p', E' ) とする。
p'x (= K' 系での運動量 ) を 時間 t (= K ) で微分すると、 Ap.1 を得る。
ここでは Ap.2 の変換と Ap.3 の定義を用いる。
(Ap.2) 4元運動量のローレンツ変換。

(Ap.3) 異なった観測者からの視点 ( K と K'系 )。

時間のローレンツ変換を用いて、t' を t に関して微分すると、次を得る。
(Ap.4)

"ux" は K 系の視点から見た 物体の x 方向の速度である。
Ap.4 を用いて、その結果を Ap.1 と比較すると 次を得る。
(Ap.5)

ここでは K 系において 物体は x 方向に 速度 u = v で動いている。
(Ap.6) x 方向の力は 変化しない ( Fx = F'x )。
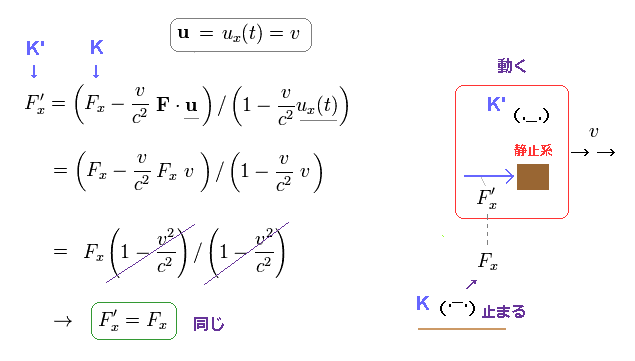
F'x は K' 系 (= 物体の静止系 ) での 物体に作用する力である。
特殊相対論によれば、x 方向の力は いかなる慣性系においても 変化しない ( F'x = Fx )。
(Ap.7) y 方向の力の変換。

(Ap.8) y 方向の力は 減少する。 ( F'y > Fy )

Ap.8 にあるように、y 方向の力 (= Fy ) は 物体の静止系での力 (= F'y ) に比べて 減少することが分かる。
(Ap.9) K 系での静止した観測者から見た 通常の速度 (= u )。
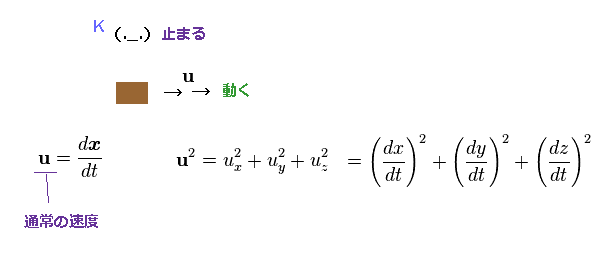
このセクションでは、相対論的な4元力に関する 力の変換を説明する。
Ap.9 では、物体が 静止した観測者 (= K 系 ) に対して 速度 "u" で動いているとする。
(Ap.10) ローレンツ変換不変な 固有時間 (= τ )。
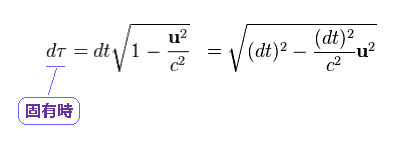
相対論的な運動方程式では 固有時 という ローレンツ変換で不変な 時間の概念を 便利なため 頻繁に使用する。
この固有時は 各慣性系における リアルな時間ではない。
彼らは この固有時を 式をローレンツ変換で共変系にするためだけに 利用しているわけである。
(Ap.11)

Ap.11 より、この固有時 τ が ローレンツ変換不変な形であることが分かる。
このページ参照のこと。
Ap.11 より、次を得る。
(Ap.12)

相対論的な世界では、 通常の速度 (= u ) は 非常に複雑な変換をする。
なぜなら 時間 (= dt ) と 空間 (= dx ) の両座標が 混ざり合って変化するからである。
そのため 4元速度 (= ω ) という便利な速度を使用する。 ここ (p.6) 参照のこと。
(Ap.13) 通常の速度 (= u ) と 4元速度 (= ω )。
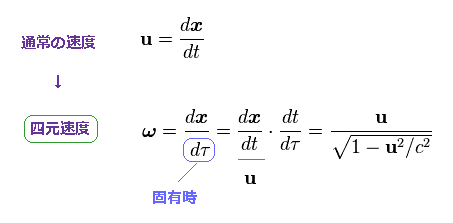
4元速度 ω の分母は ローレンツ変換不変な 固有時である。
そのため、その分子 (= dx, dy, dz, cdt ) のみが ローレンツ変換で変換する。
(Ap.14) この4元速度の 0-成分。

(Ap.15) 相対論的な運動方程式。
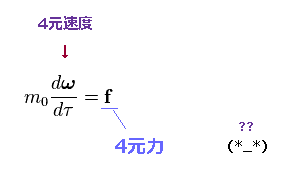
彼らは 相対論的な運動方程式を Ap.15 のように定義した。
左辺は 固有時間による 4元速度の微分である。
つまり この式も 4元ベクトルのように変換する。 このサイト参照のこと。
Ap.15 の右辺 (= f ) を "4元力" といい、非常に人為的な概念である。
(Ap.16) 4元力 f、 通常の力 F.
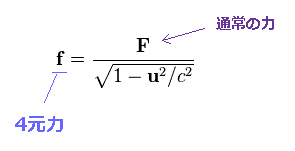
このページでは "F" が 通常のニュートン力学的な 力 を意味し、 "f" が 4元力を表わすとする。
この4元力もまた 本当の力ではない。
Ap.10 の固有時を用いると、次を得る。
(Ap.17)

Ap.13、 Ap.16、 Ap.17 を 相対論的な運動方程式 (= Ap.15 ) に代入すると、Ap.18 の関係式を得る。
(Ap.18)

相対論的な運動量 p を 次のように定義すると、
(Ap.19)

Ap.18 は、
(Ap.20)

Ap.20 は 通常の運動方程式である。
"p" のみが Ao.19 にあるように 相対論的な運動量ということになる。
(Ap.21)

これらの4元力が 4元ベクトルとして変換するために、その 0 成分は Ap.21 の形になる必要がある。
Ap.14 と Ap.21 を Ap.15 に代入して、次を得る。
(Ap.22)

ここで 相対論的なエネルギーを定義する。
(Ap.23)

ある物体が K 系において 速度 u = v で x 方向へ 動いているとする。
(Ap.24)

Ap.24 を Ap.16 と Ap.21 に代入して、次を得る。
(Ap.25)

4元力は ローレンツ変換の下で 4元ベクトル ( ct, x, y, z ) として変換する。
Ap.25 の 0 と x 成分を用いて、次を得る。
(Ap.26)
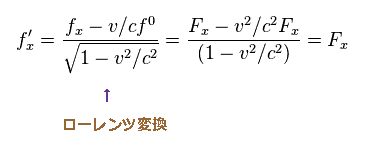
K' 系では、物体は 静止しているため、K' 系での物体の速度 (= u' ) はゼロになる。
つまり K' 系での 4元力は 通常の力と 等しい。
(Ap.27)

Ap.26 と Ap.27 から、x 方向のニュートン力学上の力は ローレンツ変換で 不変になる。
一方で、4元力 fy は ローレンツ変換で 変化しないため、
(Ap.28)

Ap.8 と同じ結果を得ることができた。

2012/6/2 updated This site is link free.