＜＜テクニックのチェーンによる説明（３）＞＞
・ ある１つのマスに ”配置可能な数字が ２つ に限られる” こと と，
・ ある数字が１つの領域（行，列，大マス）で ”配置可能なマスが ２つ に限られる” こと
をつなげていくことで情報を得るテクニックを チェーン(Chain)系のテクニック と呼びます。
５）グループ化，命題の一般化，ＡＬＳ，ＡＨＳ から この考え方を拡張します。
チェーン について考察することは，論理的思考能力を向上させる ために有効です。
（チェーン系のテクニックを積極的に使用することをお勧めする訳では決してありません。ナンプレを楽しみながら論理的思考能力を高めるには，むしろ，名前のついた基本的な中上級のテクニックを理解し，利用することの方が有効です）
１）代表的なチェーン系テクニック
１－１）X-Chain
１－２）XY-Chain
１－３）その他（色分け法 （Simple Colors, Multi Colors）, Remote Pair）
２）テクニックのチェーンによる解釈（その１）
２－１）筋違見張塔排除 （Skyscraper, 2-String Kite, Turbot Fish）
２－２）賢い見張兵排除（X-Wing）
２－３）末っ子の甘え排除（XY-Wing）
２－４）二都物語排除（Naked Pair）
３）チェーン系テクニックの原理
３－１）強いリンク，弱いリンク
３－２）ＡＩＣ(Alternate Inference Chain)，チェーン系テクニックの原理
４）テクニックのチェーンによる解釈（その２）
４－１）ネコとネズミ排除(W-Wing)
４－２）姉妹排除（Hidden Pair）
４－３）浜田ロジック
５）グループ化，命題の一般化，ＡＬＳ，ＡＨＳ
５－１）グループ化
５－２）命題の一般化
５－３）ＡＬＳ(Almost Locked Sets)
５－４）ＡＨＳ(Almost Hidden Sets)
６）テクニックのチェーンによる解釈（その３）
６－１）信長の野望排除（XYZ-Wing）
６－２）二守備線見張塔過多排除（Finned・Sashimi X-Wing）
６－３）三・四都物語排除(Naked Triple・Quadruple)
６－４）三・四姉妹排除(Hidden Triple・Quadruple)
６－５）カーブミラー排除（Empty Rectangle）
６－６）三・四人の賢い見張兵排除(Swordfish・Jellyfish)
６－７）Ｓｕｅ ｄｅ Ｃｏｑ
このページでは，６）テクニックのチェーンによる解釈（その３） を説明します。
・ ある１つのマスに ”配置可能な数字が ２つ に限られる” こと と，
・ ある数字が１つの領域（行，列，大マス）で ”配置可能なマスが ２つ に限られる” こと
をつなげていくことで情報を得るテクニックを チェーン(Chain)系のテクニック と呼びます。
５）グループ化，命題の一般化，ＡＬＳ，ＡＨＳ から この考え方を拡張します。
チェーン について考察することは，論理的思考能力を向上させる ために有効です。
（チェーン系のテクニックを積極的に使用することをお勧めする訳では決してありません。ナンプレを楽しみながら論理的思考能力を高めるには，むしろ，名前のついた基本的な中上級のテクニックを理解し，利用することの方が有効です）
１）代表的なチェーン系テクニック
１－１）X-Chain
１－２）XY-Chain
１－３）その他（色分け法 （Simple Colors, Multi Colors）, Remote Pair）
２）テクニックのチェーンによる解釈（その１）
２－１）筋違見張塔排除 （Skyscraper, 2-String Kite, Turbot Fish）
２－２）賢い見張兵排除（X-Wing）
２－３）末っ子の甘え排除（XY-Wing）
２－４）二都物語排除（Naked Pair）
３）チェーン系テクニックの原理
３－１）強いリンク，弱いリンク
３－２）ＡＩＣ(Alternate Inference Chain)，チェーン系テクニックの原理
４）テクニックのチェーンによる解釈（その２）
４－１）ネコとネズミ排除(W-Wing)
４－２）姉妹排除（Hidden Pair）
４－３）浜田ロジック
５）グループ化，命題の一般化，ＡＬＳ，ＡＨＳ
５－１）グループ化
５－２）命題の一般化
５－３）ＡＬＳ(Almost Locked Sets)
５－４）ＡＨＳ(Almost Hidden Sets)
６）テクニックのチェーンによる解釈（その３）
６－１）信長の野望排除（XYZ-Wing）
６－２）二守備線見張塔過多排除（Finned・Sashimi X-Wing）
６－３）三・四都物語排除(Naked Triple・Quadruple)
６－４）三・四姉妹排除(Hidden Triple・Quadruple)
６－５）カーブミラー排除（Empty Rectangle）
６－６）三・四人の賢い見張兵排除(Swordfish・Jellyfish)
６－７）Ｓｕｅ ｄｅ Ｃｏｑ
このページでは，６）テクニックのチェーンによる解釈（その３） を説明します。
６）テクニックのチェーンによる解釈（その３）
このページでも 既存のテクニックを チェーンとして解釈します。 ＡＩＣ:Alternate Inference Chain に加え ５）で説明した グループ化，命題の一般化も利用します。 実際の問題を解くのにはあまり役立たない知識です。 ナンプレのテクニックを 論理学的に解釈して楽しむための説明と考えてください。 説明も 数学の問題の解答のように 簡潔に記載します。 場合によっては，細かい説明は省略して論理の飛躍があるように感じるところがあるかも知れません。 論理学的考え方をある程度理解していることを前提とします。
このページでの記載方法，前提となる論理学の知見を最初に説明しておきます。
［行ｎ列ｍ：数字Ｘ］：行ｎ列ｍ に 数字Ｘ を配置する。
［行ｎ１列ｍ１，行ｎ２列ｍ２：数字Ｘ：数字Ｙ］：
２つのマス 行ｎ１列ｍ１，行ｎ２列ｍ２ に ２つの数字 数字Ｘ：数字Ｙ を配置する。
（［行ｎ１列ｍ１：数字Ｘ］かつ［行ｎ２列ｍ２：数字Ｙ］） または （［行ｎ１列ｍ１：数字Ｙ］かつ［行ｎ２列ｍ２：数字Ｘ］） と同意。
３つ以上のマス，数字を記載した場合も同様とします。
強いリンク：
命題Ｐ ⇒ 命題Ｑ
命題Ｐ と 命題Ｑ は必ずどちらかが成り立ちます。同時に成り立つことはありません。
弱いリンク：
命題Ｐ → 命題Ｑ
命題Ｐ と 命題Ｑ は同時に成り立つことはありません。どちらも成り立たないかもしれません。
重要なお断り 矢印の向きは 命題をつなげていく説明のための 便宜的な方向です。
命題Ｐ ならば 命題Ｑ という意味ではありません。
ならば（含意） は 黒矢印 で 命題Ｐ ⇒ 命題Ｑ と表現します。
ＡＩＣ（Alternate Inference Chain）：
強いリンク と 弱いリンク が交互につながったチェーン
命題Ｐ0⇒命題Ｐ1（強いリンク）
命題Ｐ1→命題Ｐ2（弱いリンク）
命題Ｐ2⇒命題Ｐ3（強いリンク）
・・・
命題Ｐｎ-2→命題Ｐｎ-1（弱いリンク）
命題Ｐｎ-1⇒命題Ｐｎ（強いリンク）
上記のように 最初 と 最後 が 強いリンク になった ＡＩＣ では， 『最初の命題Ｐ0 と 最後の命題Ｐｎ のどちらかが必ず成立します』。
命題Ｐ0 または 命題Ｐｎ は 真 になります。
論理記号：
￢：否定
∨：論理和
∧：論理積
優先順位は ￢，∧，∨ です。この優先順位で明らかな場合でも，より理解しやすいように（）を記載することがあります。
⇒：含意
⇔：同値
分配律：
命題Ｐ∧（命題Ｑ∨命題Ｒ） ⇔ （命題Ｐ∧命題Ｑ）∨（命題Ｐ∧命題Ｒ）
命題Ｐ∨（命題Ｑ∧命題Ｒ） ⇔ （命題Ｐ∨命題Ｑ）∧（命題Ｐ∨命題Ｒ）
ド・モルガン律：
￢（命題Ｐ∨命題Ｑ） ⇔ ￢命題Ｐ∧￢命題Ｑ
￢（命題Ｐ∧命題Ｑ） ⇔ ￢命題Ｐ∨￢命題Ｑ
命題Ｐ と ￢命題Ｐ とには 強いリンク があります。
このページでも 既存のテクニックを チェーンとして解釈します。 ＡＩＣ:Alternate Inference Chain に加え ５）で説明した グループ化，命題の一般化も利用します。 実際の問題を解くのにはあまり役立たない知識です。 ナンプレのテクニックを 論理学的に解釈して楽しむための説明と考えてください。 説明も 数学の問題の解答のように 簡潔に記載します。 場合によっては，細かい説明は省略して論理の飛躍があるように感じるところがあるかも知れません。 論理学的考え方をある程度理解していることを前提とします。
このページでの記載方法，前提となる論理学の知見を最初に説明しておきます。
［行ｎ列ｍ：数字Ｘ］：行ｎ列ｍ に 数字Ｘ を配置する。
［行ｎ１列ｍ１，行ｎ２列ｍ２：数字Ｘ：数字Ｙ］：
２つのマス 行ｎ１列ｍ１，行ｎ２列ｍ２ に ２つの数字 数字Ｘ：数字Ｙ を配置する。
（［行ｎ１列ｍ１：数字Ｘ］かつ［行ｎ２列ｍ２：数字Ｙ］） または （［行ｎ１列ｍ１：数字Ｙ］かつ［行ｎ２列ｍ２：数字Ｘ］） と同意。
３つ以上のマス，数字を記載した場合も同様とします。
強いリンク：
命題Ｐ ⇒ 命題Ｑ
命題Ｐ と 命題Ｑ は必ずどちらかが成り立ちます。同時に成り立つことはありません。
弱いリンク：
命題Ｐ → 命題Ｑ
命題Ｐ と 命題Ｑ は同時に成り立つことはありません。どちらも成り立たないかもしれません。
重要なお断り 矢印の向きは 命題をつなげていく説明のための 便宜的な方向です。
命題Ｐ ならば 命題Ｑ という意味ではありません。
ならば（含意） は 黒矢印 で 命題Ｐ ⇒ 命題Ｑ と表現します。
ＡＩＣ（Alternate Inference Chain）：
強いリンク と 弱いリンク が交互につながったチェーン
命題Ｐ0⇒命題Ｐ1（強いリンク）
命題Ｐ1→命題Ｐ2（弱いリンク）
命題Ｐ2⇒命題Ｐ3（強いリンク）
・・・
命題Ｐｎ-2→命題Ｐｎ-1（弱いリンク）
命題Ｐｎ-1⇒命題Ｐｎ（強いリンク）
上記のように 最初 と 最後 が 強いリンク になった ＡＩＣ では， 『最初の命題Ｐ0 と 最後の命題Ｐｎ のどちらかが必ず成立します』。
命題Ｐ0 または 命題Ｐｎ は 真 になります。
論理記号：
￢：否定
∨：論理和
∧：論理積
優先順位は ￢，∧，∨ です。この優先順位で明らかな場合でも，より理解しやすいように（）を記載することがあります。
⇒：含意
⇔：同値
分配律：
命題Ｐ∧（命題Ｑ∨命題Ｒ） ⇔ （命題Ｐ∧命題Ｑ）∨（命題Ｐ∧命題Ｒ）
命題Ｐ∨（命題Ｑ∧命題Ｒ） ⇔ （命題Ｐ∨命題Ｑ）∧（命題Ｐ∨命題Ｒ）
ド・モルガン律：
￢（命題Ｐ∨命題Ｑ） ⇔ ￢命題Ｐ∧￢命題Ｑ
￢（命題Ｐ∧命題Ｑ） ⇔ ￢命題Ｐ∨￢命題Ｑ
命題Ｐ と ￢命題Ｐ とには 強いリンク があります。
６－１） 信長の野望排除（XYZ-Wing）
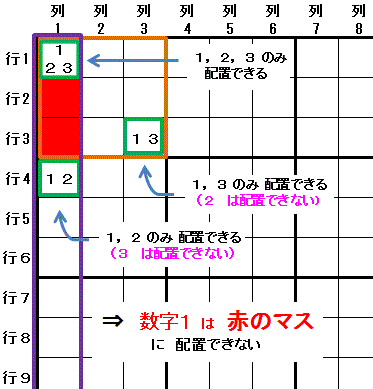行１列１ に 数字１ を配置すると
行１列１ に 数字２ を配置する
または 行１列１ に 数字３ を配置する
と の間に 強いリンク があることから始めます。
後者の場合
行１列４ に 数字１ が配置される
または 行３列３ に 数字１ が配置される
ことを示します。
［行１列１：数字１］
⇒
［行１列１：数字２］∨［行１列１：数字３］
→
［行１列４：数字２］∧［行３列３：数字３］
⇒
￢（［行１列４：数字２］∧［行３列３：数字３］）
⇔
￢［行１列４：数字２］∨￢［行３列３：数字３］
⇔
［行１列４：数字１］∨［行３列３：数字１］
数字１を行１列１に配置する と （数字１を行１列４に配置する または 数字１を行３列３に配置する）
のどちらか一方が必ず成り立ちます。
数字１を行１列１に配置する または 数字１を行１列４に配置する または 数字１を行３列３に配置する
が 真 になります。
行１列１，行１列４，行３列３ 全てと同じ領域にある 行２列１，行３列１ に 数字１ は配置できません。
６－２） 二守備線見張塔過多排除（Finned・Sashimi X-Wing））
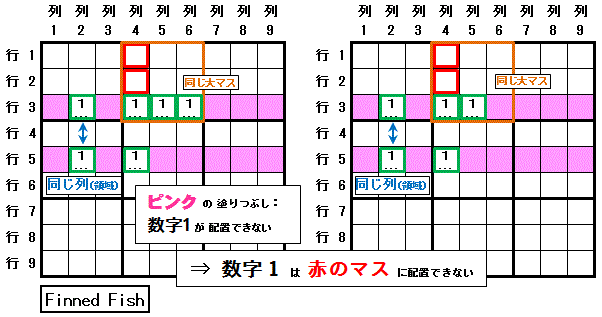
Finned Fish(X-Wing) の 左の図で説明します。
行５列４ に 数字１ を配置する
と
行５列２ に 数字１ を配置する
と の間に 強いリンク があることから始めます。
後者の場合
行３列４ に 数字１ が配置される または 行３列５ に 数字１ が配置される
または 行３列６ に 数字１ が配置される
ことを示します。
［行５列４：数字１］
⇒
［行５列２：数字１］
→
［行３列２：数字１］
⇒
［行３列４：数字１］∨［行３列５：数字１］∨［行３列６：数字１］
数字１を行５列４に配置する
と （数字１を行３列４に配置する または 数字１を行３列５に配置する または 数字１を行３列６に配置する）
のどちらか一方が必ず成り立ちます。
数字１を行５列４に配置する または 数字１を行３列４に配置する または 数字１を行３列５に配置する
または 数字１を行３列６に配置する
が 真 になります。
行５列４，行３列４，行３列５，行３列６ 全てと同じ領域にある 行１列４，行２列４ に 数字１ は配置できません。
６－３） 三・四都物語排除(Naked Triple・Quadruple)
三都物語排除を説明します。
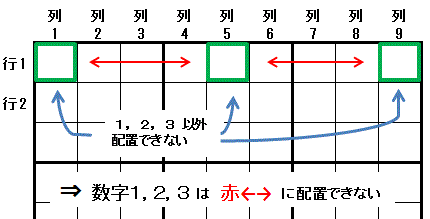行１列１ に 数字１ を配置すると
行１列１ に 数字２ を配置する
または 行１列１ に 数字３ を配置する
と の間に 強いリンク があることから始めます。
後者の場合
行１列５ に 数字１ が配置される
または 行１列９ に 数字１ が配置される
ことを示します。
（論理式は 実際には 後ろから展開しています）
［行１列１：数字１］
⇒
［行１列１：数字３］∨［行１列１：数字２］
→
［行１列５，行１列９：数字３，数字２］
⇔
（［行１列５：数字３］∧［行１列９：数字２］）∨（［行１列５：数字２］∧［行１列９：数字３］）
⇔
（［行１列５：数字２］∧［行１列９：数字２］）∨（［行１列５：数字３］∧［行１列９：数字２］）
∨（［行１列５：数字２］∧［行１列９：数字３］）∨（［行１列５：数字３］）∧［行１列９：数字３］）
⇔
（（［行１列５：数字２］∨［行１列５：数字３］）∧［行１列９：数字２］）
∨（（［行１列５：数字２］∨［行１列５：数字３］）∧［行１列９：数字３］））
⇔
（［行１列５：数字２］∨［行１列５：数字３］）∧（［行１列９：数字２］∨［行１列９：数字３］）
⇔
￢（￢［行１列５：数字２］∧￢［行１列５：数字３］）∧￢（￢［行１列９：数字２］∧￢［行１列９：数字３］）
⇔
￢（（￢［行１列５：数字２］∧￢［行１列５：数字３］）∨（￢［行１列９：数字２］∧￢［行１列９：数字３］））
⇔
￢（［行１列５：数字１］∨［行１列９：数字１］）
⇒
［行１列５：数字１］∨［行１列９：数字１］
数字１を行１列１に配置する と （数字１を行１列５に配置する または 数字１を行１列９に配置する）
のどちらか一方が必ず成り立ちます。
数字１を行１列１に配置する または 数字１を行１列５に配置する または 数字１を行１列９に配置する
が 真 になります。
行１ のそれ以外のマス 行１列２，行１列３，行１列４，行１列６，行１列７，行１列８ に 数字１ は配置できません。
数字２，数字３ も同様に それらのマスには配置できません。
四都物語排除 では 最初の 強いリンク として
［行１列１：数字１］
⇒
［行１列１：数字２］∨［行１列１：数字３］∨［行１列１：数字Ｘ］
として 同様の論理を進めます。
６－４） 三・四姉妹排除(Hidden Triple・Quadruple)
三姉妹排除を説明します。
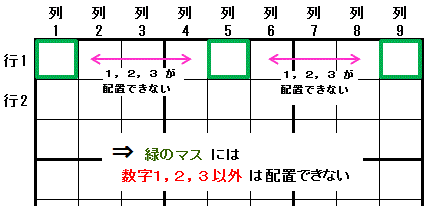行１列１ に 数字１ を配置すると
行１列５ に 数字１ を配置する
または 行１列９ に 数字１ を配置する
と の間に 強いリンク があることから始めます。
後者の場合
行１列１ に 数字２ が配置される
または 行１列１ に 数字３ が配置される
ことを示します。
（論理式は 実際には 後ろから展開しています）
［行１列１：数字１］
⇒
［行１列５：数字１］∨［行１列９：数字１］
⇒
（［行１列９：数字２］）∧［行１列５：数字３］）∨（［行１列５：数字２］∧［行１列９：数字３］）
⇔
（［行１列５：数字２］∧［行１列５：数字３］）∨（［行１列９：数字２］∧［行１列５：数字３］）
∨（［行１列５：数字２］∧［行１列９：数字３］）∨（［行１列９：数字２］∧［行１列９：数字３］）
⇔
（（［行１列５：数字２］∨［行１列９：数字２］）∧［行１列５：数字３］）
∨（（［行１列５：数字２］∨［行１列９：数字２］）∧［行１列９：数字３］）
⇔
（［行１列５：数字２］∨［行１列９：数字２］）∧（［行１列５：数字３］∨［行１列９：数字３］）
⇔
￢（￢［行１列５：数字２］∧￢［行１列９：数字２］）∧￢（￢［行１列５：数字３］∧￢［行１列９：数字３］）
⇔
￢（（￢［行１列５：数字２］∧￢［行１列９：数字２］）∨（￢［行１列５：数字３］∧￢［行１列９：数字３］））
⇔
￢（［行１列１：数字２］∨［行１列１：数字３］）
⇒
［行１列１：数字２］∨［行１列１：数字３］
数字１を行１列１に配置する と （数字２を行１列１に配置する または 数字３を行１列１に配置する）
のどちらか一方が必ず成り立ちます。
数字１を行１列１に配置する または 数字２を行１列１に配置する または 数字３を行１列１に配置する
が 真 になります。
行１列１ には 数字１，数字２数字３ 以外の数字 は配置できません。
行１列５，行１列９ も同様に 数字１，数字２，数字３ 以外の数字 は配置できません。
四姉妹排除 では 最初の 強いリンク として
［行１列１：数字１］
⇒
［行１列５：数字１］∨［行１列９：数字１］∨［行１列ｍ：数字１］
として 同様の論理を進めます。
６－５） カーブミラー排除（Empty Rectangle）
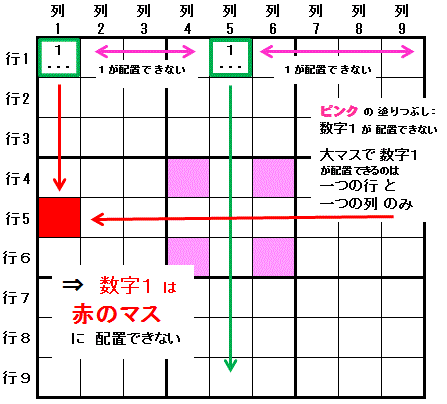行１列１ に 数字１ を配置すると
行１列５ に 数字１ を配置する
と の間に 強いリンク があることから始めます。
後者の場合
行５列４ に 数字１ が配置される
または 行５列５ に 数字１ が配置される
または 行５列６ に 数字１ が配置される
ことを示します。
［行１列１：数字１］
⇒
［行１列５：数字１］
→
［行４列５：数字１］∨［行６列５：数字１］
⇒
［行５列４：数字１］∨［行５列５：数字１］∨［行５列６：数字１］
数字１を行１列１に配置する と
（数字１を行５列４に配置する または 数字１を行５列５に配置する または 数字１を行５列６に配置する）
のどちらか一方が必ず成り立ちます。
数字１を行１列１に配置する
または 数字１を行５列４に配置するまたは 数字１を行５列５に配置する または 数字１を行５列６に配置する
が 真 になります。
行１列１，行５列４，行５列５，行５列６ 全てと同じ領域にある 行５列１ に 数字１ は配置できません。
６－６） 三・四人の賢い見張兵排除(Swordfish・Jellyfish)
三人の賢い見張兵排除 を説明します。
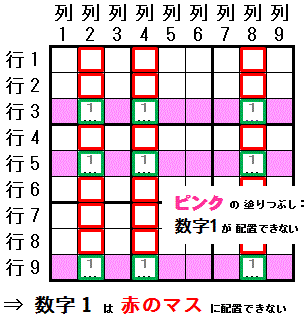行３列２ に 数字１ を配置すると
行３列４ に 数字１ を配置する
または 行３列８ に 数字１ を配置する
と の間に 強いリンク があることから始めます。
後者の場合
行５列２ に 数字１ が配置される
または 行９列２ に 数字１ が配置される
ことを示します。
（論理式は 実際には 後ろから展開しています）
［行３列２：数字１］
⇒
［行３列４：数字１］∨［行３列８：数字１］
→
（［行５列８：数字１］）∧［行９列４：数字１）∨（［行５列４：数字１］∧［行９列８：数字１］）
⇔
（［行５列４：数字１］∧［行９列４：数字１）∨（［行５列８：数字１］）∧［行９列４：数字１）
∨（［行５列４：数字１］∧［行９列８：数字１］）∨（［行５列８：数字１］∧［行９列８：数字１］）
⇔
（（［行５列４：数字１］∨［行５列８：数字１］）∧［行９列４：数字１］）
∨（（［行５列４：数字１］∨［行５列８：数字１］）∧［行９列８：数字１］）
⇔
（［行５列４：数字１］∨［行５列８：数字１］）∧（［行９列４：数字１］∨［行９列８：数字１］）
⇔
￢（￢［行５列４：数字１］∧￢［行５列８：数字１］）∧￢（￢［行９列４：数字１］∧￢［行９列８：数字１］）
⇔
￢（（￢［行５列４：数字１］∧￢［行５列８：数字１］）∨（￢［行９列４：数字１］∧￢［行９列８：数字１］））
⇔
￢（［行５列２：数字１］∨［行９列２：数字１］）
⇒
［行５列２：数字１］∨［行９列２：数字１］
数字１を行３列２に配置する と （数字１を行５列２に配置する または 数字１を行９列２に配置する）
のどちらか一方が必ず成り立ちます。
数字１を行３列２に配置する または 数字１を行５列２に配置する または 数字１を行９列２に配置する
が 真 になります。
列２では 行３列２，行５列２，行９列２，以外のマス 行１列２，行２列２，行４列２，行６列２，行７列２，行８列２ に 数字１ は配置できません。
列４。列８ についても同様です。
四人の賢い見張兵排除 では 最初の 強いリンク として
［行３列２：数字１］
⇒
［行３列４：数字１］∨［行３列８：数字１］∨［行３列ｍ：数字１］
として 同様の論理を進めます。
６－７） Ｓｕｅ ｄｅ Ｃｏｑ
（最後に Sue de Coq の 例題 を示します）
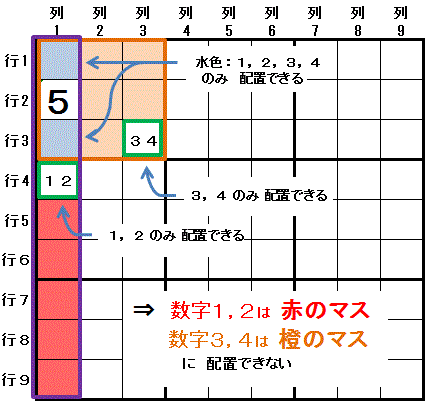Sue de Coq は行（または 列）と 大マス が共通部分を持つ場合に
共通部分の ２マス に配置可能な数字が ４個 で，
そのうちの２つの数字 が 行（または 列）の共通部分の外に その２つのみが配置可能なマスがあり，
残りの２つの数字 が 大マスの共通部分の外に その２つのみが配置可能なマスがあると，
行（または 列）で制約された数字は その行（または 列）の 共通部分と２つのみが配置可能なマス 以外のマスには配置できない，
大マスで制約された数字は その大マスの 共通部分と２つのみが配置可能なマス 以外のマスには配置できない，
と いうものです。
共通部分の ３マス に配置可能な数字が ５個 の場合は 残りの２つの数字 が 大マスの．．． が 残りの３つの数字のうちの２つの数字 が 大マスの．．．
と いう条件で 同様の結論が得られます。
共通部分の ２マス に配置可能な数字が ４個 の場合を説明します。
行４列１ に 数字１ を配置する
と
行４列１ に 数字２ を配置する
と の間に 強いリンク があることから始めます。
後者の場合
大マス１ の 行３列３ に 配置可能な数字が 数字３ と 数字４ の２つのみであることを利用して
行１列１ に 数字１ が配置される
または 行３列１ に 数字１ が配置される
ことを示します。
［行４列１：数字１］
⇒
［行４列１：数字２］
→
［行１列１：数字２］∨［行３列１：数字２］
⇒
￢（［行１列１：数字２］∨［行３列１：数字２］）
⇔
￢［行１列１：数字２］∧￢［行３列１：数字２］
⇔
（［行１列１：数字１］∨［行１列１：数字３］∨［行１列１：数字４］）
∧（［行３列１：数字１］∨［行３列１：数字３］∨［行３列１：数字４］）
⇔
［行１列１：数字１］∧［行３列１：数字１］
∨［行１列１：数字１］∧［行３列１：数字３］
∨［行１列１：数字１］∧［行３列１：数字４］
∨［行１列１：数字３］∧［行３列１：数字１］
∨［行１列１：数字３］∧［行３列１：数字３］
∨［行１列１：数字３］∧［行３列１：数字４］
∨［行１列１：数字４］∧［行３列１：数字１］
∨［行１列１：数字４］∧［行３列１：数字３］
∨［行１列１：数字４］∧［行３列１：数字４］
⇔
［行１列１：数字１］∧［行３列１：数字３］
∨［行１列１：数字１］∧［行３列１：数字４］
∨［行１列１：数字３］∧［行３列１：数字１］
∨［行１列１：数字３］∧［行３列１：数字４］ ①
∨［行１列１：数字４］∧［行３列１：数字１］
∨［行１列１：数字４］∧［行３列１：数字３］ ②
⇔ ①，② は 偽 です。 ∵ もし 真なら 行３列３ に配置できる数字がなくなる。
［行１列１：数字１］∧［行３列１：数字３］
∨［行１列１：数字１］∧［行３列１：数字４］
∨［行１列１：数字３］∧［行３列１：数字１］
∨［行１列１：数字４］∧［行３列１：数字１］
→
［行１列１：数字２］∧［行３列１：数字３］
∨［行１列１：数字２］∧［行３列１：数字４］
∨［行１列１：数字３］∧［行３列１：数字２］
∨［行１列１：数字４］∧［行３列１：数字２］
⇔
［行１列１：数字２］∧［行３列１：数字３］
∨［行１列１：数字２］∧［行３列１：数字４］
∨［行１列１：数字３］∧［行３列１：数字２］
∨［行１列１：数字３］∧［行３列１：数字４］
∨［行１列１：数字４］∧［行３列１：数字２］
∨［行１列１：数字４］∧［行３列１：数字３］
⇔
［行１列１：数字２］∧［行３列１：数字２］
∨［行１列１：数字２］∧［行３列１：数字３］
∨［行１列１：数字２］∧［行３列１：数字４］
∨［行１列１：数字３］∧［行３列１：数字２］
∨［行１列１：数字３］∧［行３列１：数字３］
∨［行１列１：数字３］∧［行３列１：数字４］
∨［行１列１：数字４］∧［行３列１：数字２］
∨［行１列１：数字４］∧［行３列１：数字３］
∨［行１列１：数字４］∧［行３列１：数字４］
⇔
（［行１列１：数字２］∨［行１列１：数字３］∨［行１列１：数字４］）
∧（［行３列１：数字２］∨［行３列１：数字３］∨［行３列１：数字４］）
⇔
￢［行１列１：数字１］∧￢［行３列１：数字１］
⇔
￢（［行１列１：数字２］∨［行３列１：数字２］）
⇒
［行１列１：数字２］∨［行３列１：数字２］
数字１を行４列１に配置する と （数字１を行１列１に配置する または 数字１を行３列１に配置する）
のどちらか一方が必ず成り立ちます。
数字１を行４列１に配置する または 数字１を行１列１に配置する または 数字１を行３列１に配置する
が 真 になります。
行４列１，行１列１，行３列１ 全てと同じ領域にある 行５列１，行６列１，行７列１，行８列１，行９列１ に 数字１ は配置できません。
数字２，数字３，数字４ についても同様です。
興味がおありなら 共通部分の ３マス に配置可能な数字が ５個 の場合も証明してみてください。命題の長さはかなり長くなります。
Ｓｕｅ ｄｅ Ｃｏｑ の例題
数字３ は 行６ では 行６列１，行６列２ にしか配置できません。行４列１ に配置できないことがわかります（そこのけ排除［Locked Candidate］）。
数字１ は 列５ では 行７列５，行８列５ にしか配置できません。行８列６，行９列６ に配置できないことがわかります（そこのけ排除［Locked Candidate］）。
数字１ は 行４ では 行４列１，行４列９ にしか配置できず，大マス３ では 列９ と 行１ にしか配置できません。行１列１ に配置できないことがわかります（カーブミラー排除［W-Wing］）。
数字１ は 列１，列６，列９ では 行２，行３，行４ にしか配置できません。行３列３ に配置できないことがわかります（三人の賢い見張兵排除［Swordfish］）。
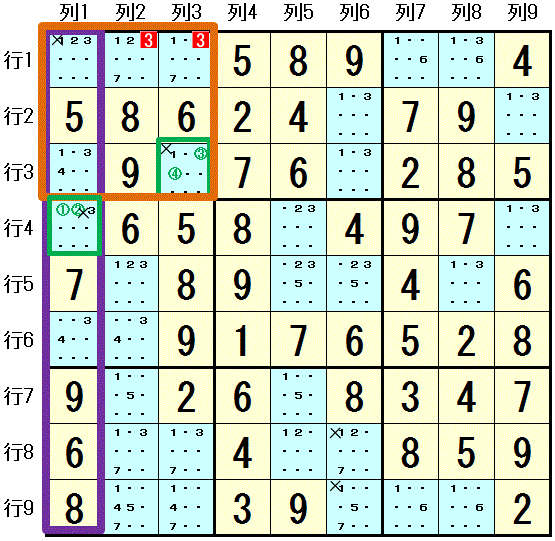
列１ と 大マス１ の共通部分の ２つのマス（行１列１，行３列１） には ４つの数字 数字１，数字２，数字３，数字４ しか配置できません。
列１の共通部分ではないマス 行４列１ には そのうちの２つの数字 数字１，数字２ しか配置できません。
大マス１の共通部分ではないマス 行３列３ には 残りの２つの数字 数字３，数字４ しか配置できません。
Sue de Coq が成立して，
数字３ を 行１列２，行１列３ に配置できないことがわかります。