<<チェーン(Chain)系テクニックの原理>>
・ ある1つのマスに ”配置可能な数字が 2つ に限られる” こと と,
・ ある数字が1つの領域(行,列,大マス)で ”配置可能なマスが 2つ に限られる” こと
をつなげていくことで情報を得るテクニックを チェーン(Chain)系のテクニック と呼びます。
5)グループ化,命題の一般化,ALS,AHS から この考え方を拡張します。
チェーン について考察することは,論理的思考能力を向上させる ために有効です。
(チェーン系のテクニックを積極的に使用することをお勧めする訳では決してありません。ナンプレを楽しみながら論理的思考能力を高めるには,むしろ,名前のついた基本的な中上級のテクニックを理解し,利用することの方が有効です)
1)代表的なチェーン系テクニック
1−1)X-Chain
1−2)XY-Chain
1−3)その他(色分け法 (Simple Colors, Multi Colors), Remote Pair)
2)テクニックのチェーンによる解釈(その1)
2−1)筋違見張塔排除 (Skyscraper, 2-String Kite, Turbot Fish)
2−2)賢い見張兵排除(X-Wing)
2−3)末っ子の甘え排除(XY-Wing)
2−4)二都物語排除(Naked Pair)
3)チェーン系テクニックの原理
3−1)強いリンク,弱いリンク
3−2)AIC(Alternate Inference Chain),チェーン系テクニックの原理
4)テクニックのチェーンによる解釈(その2)
4−1)ネコとネズミ排除(W-Wing)
4−2)姉妹排除(Hidden Pair)
4−3)浜田ロジック
5)グループ化,命題の一般化,ALS,AHS
5−1)グループ化
5−2)命題の一般化
5−3)ALS(Almost Locked Sets)
5−4)AHS(Almost Hidden Sets)
6)テクニックのチェーンによる解釈(その3)
6−1)信長の野望排除(XYZ-Wing)
6−2)二守備線見張塔過多排除(Finned・Sashimi X-Wing)
6−3)三・四都物語排除(Naked Triple・Quadruple)
6−4)三・四姉妹排除(Hidden Triple・Quadruple)
6−5)カーブミラー排除(Empty Rectangle)
6−6)三・四人の賢い見張兵排除(Swordfish・Jellyfish)
6−7)Sue de Coq
このページでは,3)チェーン系テクニックの原理 を説明します。
・ ある1つのマスに ”配置可能な数字が 2つ に限られる” こと と,
・ ある数字が1つの領域(行,列,大マス)で ”配置可能なマスが 2つ に限られる” こと
をつなげていくことで情報を得るテクニックを チェーン(Chain)系のテクニック と呼びます。
5)グループ化,命題の一般化,ALS,AHS から この考え方を拡張します。
チェーン について考察することは,論理的思考能力を向上させる ために有効です。
(チェーン系のテクニックを積極的に使用することをお勧めする訳では決してありません。ナンプレを楽しみながら論理的思考能力を高めるには,むしろ,名前のついた基本的な中上級のテクニックを理解し,利用することの方が有効です)
1)代表的なチェーン系テクニック
1−1)X-Chain
1−2)XY-Chain
1−3)その他(色分け法 (Simple Colors, Multi Colors), Remote Pair)
2)テクニックのチェーンによる解釈(その1)
2−1)筋違見張塔排除 (Skyscraper, 2-String Kite, Turbot Fish)
2−2)賢い見張兵排除(X-Wing)
2−3)末っ子の甘え排除(XY-Wing)
2−4)二都物語排除(Naked Pair)
3)チェーン系テクニックの原理
3−1)強いリンク,弱いリンク
3−2)AIC(Alternate Inference Chain),チェーン系テクニックの原理
4)テクニックのチェーンによる解釈(その2)
4−1)ネコとネズミ排除(W-Wing)
4−2)姉妹排除(Hidden Pair)
4−3)浜田ロジック
5)グループ化,命題の一般化,ALS,AHS
5−1)グループ化
5−2)命題の一般化
5−3)ALS(Almost Locked Sets)
5−4)AHS(Almost Hidden Sets)
6)テクニックのチェーンによる解釈(その3)
6−1)信長の野望排除(XYZ-Wing)
6−2)二守備線見張塔過多排除(Finned・Sashimi X-Wing)
6−3)三・四都物語排除(Naked Triple・Quadruple)
6−4)三・四姉妹排除(Hidden Triple・Quadruple)
6−5)カーブミラー排除(Empty Rectangle)
6−6)三・四人の賢い見張兵排除(Swordfish・Jellyfish)
6−7)Sue de Coq
このページでは,3)チェーン系テクニックの原理 を説明します。
3)チェーン系テクニックの原理
3−1) 強いリンク,弱いリンク
(最初は,この項の最後に表示している 図 と その説明 で 強いリンク,弱いリンク を理解していただければ十分です)
チェーン系テクニックでは 関連がある2つの命題の組み合わせ をつなげて,それを論理的に解析して 数字が配置できないマス を見つけます。 組み合わされる2つの命題の関連 には,強いリンク と 弱いリンク があります。
命題P と 命題Q の間の 強いリンク,弱いリンク は次のように定義されます。
強いリンク : 命題P と 命題Q は同時に成り立つことはない。どちらか一方が必ず成り立つ。
弱いリンク : 命題P と 命題Q は同時に成り立つことはない(両方とも成り立たない場合もある)。
2つの命題の間に 強いリンク があるとき,その2つの命題の間には 弱いリンク もあります。その逆は成り立ちません。
このサイトでは,2つの命題の間に 強いリンク があるとき,その2つの命題を ピンクの線 で結んで表示します。 命題をつなげていくときは,つなげる方向を矢印で明示します。
例)命題P と命題Q の間に強いリンクがある : 命題P ⇒ 命題Q
2つの命題の間に 弱いリンク があるとき,その2つの命題を 青の線 で結んで表示します。 命題をつなげていくときは,つなげる方向を矢印で明示します。
例)命題P と命題Q の間に弱いリンクがある : 命題P → 命題Q
実際のナンプレ局面に 強いリンク を方向を考慮して表示するときには,
ピンクの実線 ------→,
弱いリンク を方向を考慮して表示するときには,
青の点線 ---→
で表示します。
強いリンク を 弱いリンク と考えて利用するときには,
青の実線 ------→
で表示します。
ナンプレ で使用する命題は,”ある数字をあるマスに配置する”というものです(後述する グループ化 で使用する命題の範囲を拡張します)。
命題を,”ある数字をあるマスに配置する” としたときには,
1)ある数字が ある領域(行,列 または 大マス)で配置可能なマスが2つに限られる 場合に,
その数字をそれぞれのマスに配置すること の間に 強いリンク があります。
2)あるマスに 配置可能な数字が2つに限られる 場合に,
それぞれの数字をそのマスに配置すること の間に 強いリンク があります。
そして,
3)ある数字を配置可能な2つのマスが同じ領域(行,列 または 大マス)にある 場合に,
その数字をそれぞれのマスに配置すること の間に 弱いリンク があります。
4)2つの数字が同じマスに配置可能な 場合,
それぞれの数字をそのマスに配置すること の間に 弱いリンク があります。
それぞれの リンク を下図で説明します。下図には,行1 の 各マス に配置可能な数字が すべて記載されているものとします。

1)数字1 は 行1 で 配置可能なマスが2つ(行1列1,行1列3) に限られています。
数字1を行1列1に配置する ことと 数字1を行1列3に配置する ことの間には 強いリンク があります。
2)行1列8 に 配置可能な数字が2つ(数字2,数字3) に限られています。
数字2を行1列8に配置する ことと 数字3を行1列8に配置する ことの間には 強いリンク があります。
3)数字7を配置可能な2つのマス(行1列2,行1列4)が同じ領域(行1)にあります。
数字7を行1列2に配置する ことと 数字7を行1列4に配置する ことの間には 弱いリンク があります。
4)2つの数字(数字4,数字5)が同じマス(行1列9)に配置可能です。
数字4を行1列9に配置する ことと 数字5を行1列9に配置する ことの間には 弱いリンク があります。
それぞれのリンクは,以下のように記載します。
1) 行1列1⇒行1列3:数字1,行1(強いリンク)
2) 数字2⇒数字3:行1列8(強いリンク)
3) 行1列2→行1列4:数字7,行1(弱いリンク)
4) 数字4→数字5:行1列9(弱いリンク)
リンクの記載では 自明な情報は適宜省略します。 また,一つのマスの中のリンク(の矢印)は通常図示しません。

3−2) AIC(Alternate Inference Chain),チェーン系テクニックの原理
◎ AIC(Alternate Inference Chain) (Alternate :交互の)
2つのリンクに 同じ命題 があるとき リンクとリンクがつながり,一連の命題で チェーン が形成されます。すなわち,
命題P0−命題P1(リンクがある)
命題P1−命題P2(リンクがある)
命題P2−命題P3(リンクがある)
・・・
命題Pn-2−命題Pn-1(リンクがある)
命題Pn-1−命題Pn(リンクがある)
という形の 命題のつながり(鎖:チェーン)が形成されます。
ナンプレで利用するチェーンは,強いリンク と 弱いリンク が交互につながったチェーンです(AIC:Alternate Inference Chain)。 さらに,何らかの排除の情報(ある数字をあるマスに配置できない)を得るためのチェーンは,最初 と 最後 が 強いリンク になったチェーンです。 次の形になります。
命題P0⇒命題P1(強いリンク)
命題P1→命題P2(弱いリンク)
命題P2⇒命題P3(強いリンク)
・・・
命題Pn-2→命題Pn-1(弱いリンク)
命題Pn-1⇒命題Pn(強いリンク)
このチェーンに含まれる 命題の数 を チェーンの長さ と定義します。
このチェーンは n個のリンク で形成され nは奇数 なので, 両端が 強いリンク となる AIC(Alternate Inference Chain) の長さ(命題の数)は 偶数 となります。
ナンプレでは,この 強いリンク と 弱いリンク が交互で 両端が強いリンク になっている(あるいはこの形に解釈できる)チェーン を利用して情報を得るため, 両端が強いリンク になっていることも条件にいれて,この形のチェーンを AIC(Alternate Inference Chain) と呼ぶこともあります。
また,この形のチェーンを見つけて排除の情報を得るテクニック自体を AIC と呼ぶこともあります。
命題と命題は 矢印(⇒,→) で結ばれていますが,これは,左の命題が成り立つと右の命題が成り立つという 論理学上の表現 ではありません。 単に,命題のつながりの流れの方向を示しているものに過ぎません。
チェーンの端が 強いリンク ではないチェーンで説明されるテクニックもありますが,端の 弱いリンク の一つ手前の 強いリンクまでのチェーン と解釈すると,そのようなテクニックは必ず理解することができます。
ナンプレで利用するチェーンには AIC(Alternate Inference Chain) のほかに,ある数字が ”同じ領域(行,列 または 大マス)で配置可能なマスが2つに限られる” という 強いリンク だけで形成されたチェーンもあります。 これを利用するテクニックは 色分け法(Coloring) で説明しています。
◎ チェーン系テクニックの原理
強いリンク と 弱いリンク が交互で,両端が 強いリンク になっているチェーンでは,
チェーンをつなげていくのに使われていない
両端の命題 はどちらか一方が必ず成り立ちます。
この 原理 を前述の AIC で説明した 命題のチェーン で説明します。
命題P0 が成立するときは,この 原理 が成り立っているのは自明です。
もし,命題P0 が成立しないと 命題P1 が成り立ちます(1行目:強いリンク)。
すると,命題P2 が成り立たなくなります(2行目:弱いリンク)。
命題P2 が成立しないと 命題P3 が成り立ちます(3行目:強いリンク)。
以後,同様に,
強いリンクの右側の命題は成り立ち,
弱いリンクの右側の命題は成り立ちません。
一番最後のリンクは 強いリンク なので,右側の 命題Pn が成り立ちます。
よって,チェーンをつなげていくのに使われなかった 両端の命題 のどちらか一方が必ず成り立つことがわかります。
ナンプレで,この 原理 が 直感的に理解しやすく,一番多く使われるのは,両端の命題が ”同じ一つの数字をあるマスに配置する” 形になっているチェーンです。
この条件を満たすチェーンでは 両端のマスの ”両方と同じ領域にあるマス” にはその数字を配置できません。
チェーン系の代表である X-Chain はこの排除の考え方を使います。X-Chain の例題を再掲します。数字1 に関して,行4列8 をスタートのマスとしてチェーンを形成します。
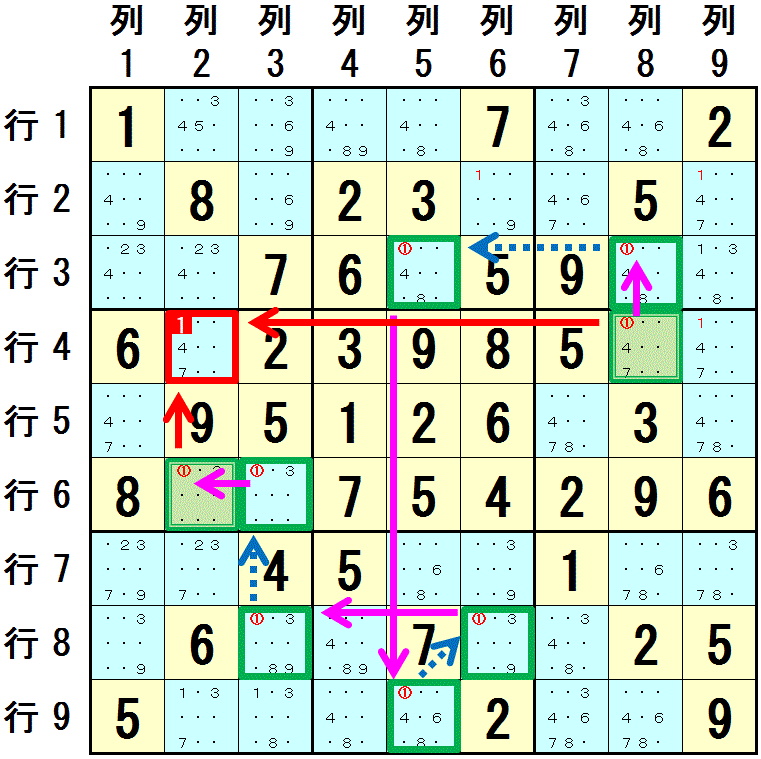
行4列8⇒行3列8:列8(強いリンク)
行3列8→行3列5:行3(弱いリンク)
行3列5⇒行9列5:列5(強いリンク)
行9列5→行8列6:大マス8(弱いリンク)
行8列6⇒行8列3:行8(強いリンク)
行8列3→行6列3:列3(弱いリンク)
行6列3⇒行6列2:行6(強いリンク)
強いリンク と 弱いリンク が交互で,両端は 強いリンク になっています。チェーンの両端で チェーンをつなげていくのに利用されていないのは,
数字1 を 行4列8 に配置すること と,数字1 を 行6列2 に配置すること です。
この時 数字1は,行4列8 と 行6列2 の両方と同じ領域にある 行4列2 には配置できません。
XY-Chain も,”1つのマスに配置可能な数字が2つに限られる” ことを,”それぞれの数字をそのマスに配置することの間に 強いリンクがある” と解釈して,この排除の考え方を利用します。 例題の 最後 で説明しています。
その他,X-Chain,XY-Chain で解釈可能な Coloring, Remote Pair, テクニックのチェーンによる解釈(その1)で説明したテクニック もこの排除の考え方を利用しています。
両端の命題 の形を,両端の命題を記述するのに使われている 数字の異同,マスの位置関係 を元に 分類し,網羅します。
・両端の命題が ”同じ一つの数字を異なるマスに配置する” 形
両端のマスの 両方と同じ領域のマス にはその数字を配置することができません。
X-Chain など上で説明したパターンです。
(両端のマスが同じ領域にあるときは その数字はその領域では両端のマス以外のマスには配置できません)
・両端の命題が ”同じ一つの数字を同じマスに配置する” 形
そのマスにその数字を配置することが確定します。前項の特殊形と考えられます。
別のページで説明する 浜田ロジックの チェーン3 による解釈 で利用する形です。
・両端の命題が ”異なる2つの数字を同じマスに配置する” 形
そのマスにはその2つの数字以外の数字を配置できません。
別のページで説明する 姉妹排除(Hidden Pairs)のチェーンによる解釈 で利用する形です。
・両端の命題が ”異なる2つの数字を同じ領域にある2つののマスに配置する” 形
一方の端のマスには もう一方の端のマスに配置される数字 を配置できません。
別のページで説明する 浜田ロジックの チェーン4 による解釈 で利用する形です。
AIC(Alternate Inference Chain) type2 と呼ばれることがあります。
このリストの最初に挙げた形が AIC type1 になります。
・両端の命題が ”異なる2つの数字を異なる領域の2つののマスに配置する” 形
他の条件がないと排除に関する情報を得ることはできません。
両端の命題に利用されている 数字,マスの位置関係 を網羅し,分析することは チェーン系のテクニックを網羅していくときに利用されます。 別のページで 命題と命題のつながり方 をいろいろ組み合わせて検討します。
AIC の両端の命題の間に 弱いリンクがあると,強いリンク と 弱いリンク が交互につながる ループ(AIC Loops) になります。 このループは,どこの 弱いリンク で切っても AIC(強いリンク と 弱いリンク が交互で,最初と最後が 強いリンク のチェーン)になります。 一気にたくさんの排除の情報が見つかることがあります。
このループは Continuous Nice Loops と呼ばれることもあります。





