＜＜テクニックのチェーンによる説明（２）＞＞
・ ある１つのマスに ”配置可能な数字が ２つ に限られる” こと と，
・ ある数字が１つの領域（行，列，大マス）で ”配置可能なマスが ２つ に限られる” こと
をつなげていくことで情報を得るテクニックを チェーン(Chain)系のテクニック と呼びます。
５）グループ化，命題の一般化，ＡＬＳ，ＡＨＳ から この考え方を拡張します。
チェーン について考察することは，論理的思考能力を向上させる ために有効です。
（チェーン系のテクニックを積極的に使用することをお勧めする訳では決してありません。ナンプレを楽しみながら論理的思考能力を高めるには，むしろ，名前のついた基本的な中上級のテクニックを理解し，利用することの方が有効です）
１）代表的なチェーン系テクニック
１−１）X-Chain
１−２）XY-Chain
１−３）その他（色分け法 （Simple Colors, Multi Colors）, Remote Pair[リニア]）
２）テクニックのチェーンによる解釈（その１）
２−１）筋違見張塔排除 （Skyscraper, 2-String Kite, Turbot Fish）
２−２）賢い見張兵排除（X-Wing）
２−３）末っ子の甘え排除（XY-Wing）
２−４）二都物語排除（Naked Pair）
３）チェーン系テクニックの原理
３−１）強いリンク，弱いリンク
３−２）ＡＩＣ(Alternate Inference Chain)，チェーン系テクニックの原理
４）テクニックのチェーンによる解釈（その２）
４−１）ネコとネズミ排除(W-Wing)
４−２）姉妹排除（Hidden Pair）
４−３）浜田ロジック
５）グループ化，命題の一般化，ＡＬＳ，ＡＨＳ
５−１）グループ化
５−２）命題の一般化
５−３）ＡＬＳ(Almost Locked Sets)
５−４）ＡＨＳ(Almost Hidden Sets)
６）テクニックのチェーンによる解釈（その３）
６−１）信長の野望排除（XYZ-Wing）
６−２）二守備線見張塔過多排除（Finned・Sashimi X-Wing）
６−３）三・四都物語排除(Naked Triple・Quadruple)
６−４）三・四姉妹排除(Hidden Triple・Quadruple)
６−５）カーブミラー排除（Empty Rectangle）
６−６）三・四人の賢い見張兵排除(Swordfish・Jellyfish)
６−７）Ｓｕｅ ｄｅ Ｃｏｑ
このページでは，４）テクニックのチェーンによる解釈（その２） を説明します。
４）テクニックのチェーンによる解釈（その２）
”ある領域（行，列，または，大マス）で配置可能なマスが２つに限られる”や ”１つのマスに配置可能な数字が２つに限られる” という条件をつなげて，数字が排除されるマスを見つけるテクニックは，チェーン系の考え方で解釈することができます。 ここでは，その条件が複雑に絡んだテクニック（ AIC:Alternate Inference Chain）について説明します。
４−１） ネコとネズミ排除(W-Wing)
下に ネコとネズミ排除(W-Wing) の説明 に利用した図を示し，テクニックの説明をします。
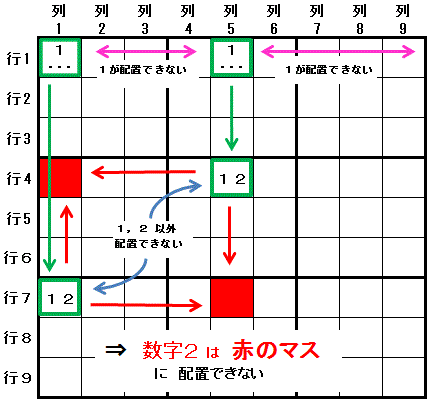最初に，配置可能なマスが２つ（行１列１，行１列５）に限られる数字（数字１：第一の数字）が存在する領域（行１）を見つけます。
それら２つのマス（行１列１，行１列５）それぞれと 同じ領域（列１ および 列５）にあって， 配置可能な数字が 第一の数字（数字１）と第二の数字（数字２）の ２つの数字に限定されるマス（行７列１ および 行４列５）が存在すると，
それら２つのマス（行７列１ と 行４列５）の両方のマスと同じ領域にあるマス（行４列１ および 行７列５）には 第二の数字（数字２）は配置できません。
この図に 数字２ を 行７列１ に配置すること をスタートとして，強いリンク と 弱いリンク を記載し，チェーンを作成します。
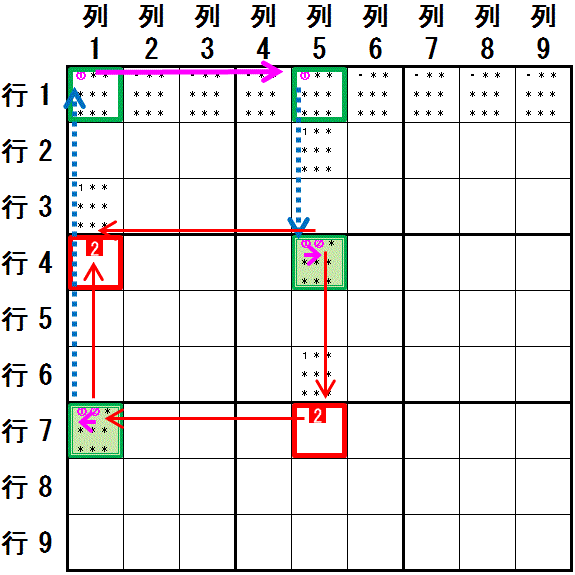数字２⇒数字１：行７列１（強いリンク）
行７列１→行１列１：数字１，列１（弱いリンク）
行１列１⇒行１列５：数字１，行１（強いリンク）
行１列５→行４列５：数字１，列５（弱いリンク）
数字１⇒数字２：行４列５（強いリンク）
強いリンク と 弱いリンク が交互で，両端が強いリンク である チェーンが形成されました。チェーンの両端は 同じ数字２ を 行７列１，行４列５ に配置する ことになっています。
このチェーンの内容を，”ある数字をあるマスに配置すること” をつなげることでより詳細に表現します。
数字２ を 行７列１ に配置する ⇒ 数字１ を 行７列１ に配置する：行７列１（強いリンク）
数字１ を 行７列１ に配置する → 数字１ を 行１列１ に配置する：数字１，列１（弱いリンク）
数字１ を 行１列１ に配置する ⇒ 数字１ を 行１列５ に配置する：数字１，行１（強いリンク）
数字１ を 行１列５ に配置する → 数字１ を 行４列５ に配置する：数字１，列５（弱いリンク）
数字１ を 行４列５ に配置する ⇒ 数字２ を 行４列５ に配置する：行４列５（強いリンク）
チェーンの両端は，数字２ を 行７列１に配置する ことと 同じ 数字２ を 行４列５ に配置する ことになっています。 数字２ は 行７列１，行４列５ の 両方と同じ領域にあるマス 行４列１，行７列５ には配置できません。
ネコとネズミ排除（W-Wing） がチェーンの考え方で解釈できました。チェーンの長さは ６ となります。
４−２） 姉妹排除(Hidden Pairs)
下に 姉妹排除(Hidden Pairs) の説明 に利用した図を示し，テクニックの説明をします。
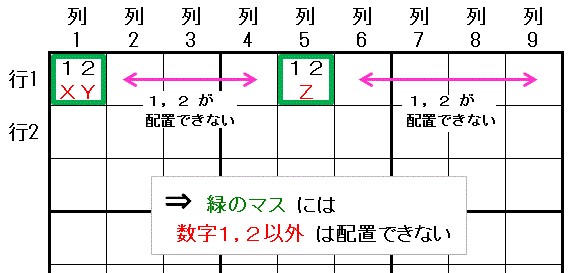［テクニック］
同じ領域（行１）で，２種類の数字（数字１，数字２）が配置できるマス が 同じ２つのマス（行１列１，行１列５） に限られると， その２つのマスには，それら２つの数字以外の数字（数字Ｘ，数字Ｙ，数字Ｚ） は配置できません。
この図に 数字１ を 行１列１ に配置すること をスタートとして，強いリンク と 弱いリンク を記載し，チェーンを作成します。
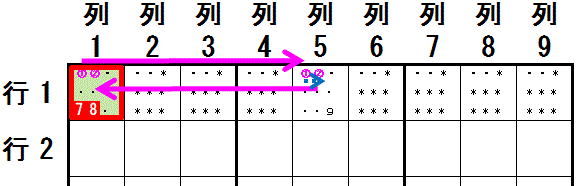行１列１⇒行１列５：数字１，行１（強いリンク）
数字１→数字２：行１列５（弱いリンク）
行１列５⇒行１列１：数字２，行１（強いリンク）
強いリンク と 弱いリンク が交互で，両端が強いリンク である チェーンが形成されました。 チェーンの両端である 数字１を行１列１ と 数字２を行１列１ に配置する ことは どちらか一方が必ず成り立ちます。 行１列１ には 数字１，数字２ 以外の数字（左図の例では 数字７，数字８）は配置できません。
このチェーンの内容を，”ある数字をあるマスに配置すること” をつなげることでより詳細に表現します。
数字１ を 行１列１ に配置する ⇒ 数字１ を 行１列５ に配置する：数字１，行１（強いリンク）
数字１ を 行１列５ に配置する → 数字２ を 行１列５ に配置する：行１列５（弱いリンク）
数字２ を 行１列５ に配置する ⇒ 数字２ を 行１列１ に配置する：数字２，行１（強いリンク）
チェーンの両端は，数字１ を 行１列１に配置する ことと 数字２ を 同じ行１列１ に配置する ことになっています。 この配置のどちらか一方は必ず成立します。 行１列１ には 数字１，数字２以外の数字（この図の例では 数字７，数字８） は配置できません。
同様に 数字１ を 行１列５ に配置すること をスタートとして，強いリンク と 弱いリンク が交互になっているチェーンを作成すれば， 行１列５ には 数字１，数字２ 以外の数字（この例では 数字９）が配置できないことがわかります。
姉妹排除(Hidden Pairs) がチェーンの考え方で解釈できました。チェーンの長さは ４ となります。
４−３） 浜田ロジック
※ お断り
浜田ロジックに関しては，本サイトも含めて，多くは 同じ２つの数字しか配置できない３マスが，同じ領域（行，列，大マス）にあることでつながっている状態で適応を考えられるテクニックとして説明されています。
しかし，本来”浜田ロジック”は，世界文化社のナンプレ本の関係者が称しているテクニック名です。同社のナンプレ本の浜田ロジックに関する解説からは，ある数字が，一つの領域で２マスにしか配置できないパターンがたくさんあるとき， 複合的にその組み合わせを考えてみるテクニックと解釈できそうです。この項の 最後 に説明します。
最初に 浜田ロジック について説明をします。
［テクニック］
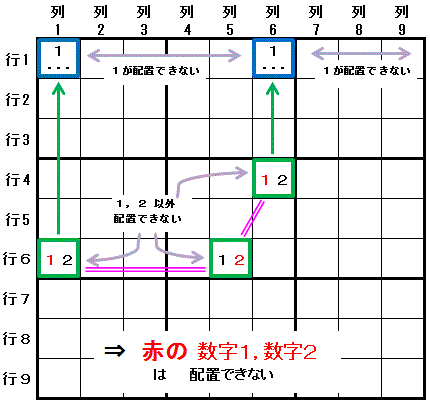
最初に，配置可能な数字が同じ２種類の数字（数字１，数字２）に限られる３つのマスで， １つのマス（行６列５：中央のマス）が他の２つのマス（行６列１，行４列６：両端のマス）と同じ領域（行６，大マス５）にある状況を見つけます。 この時，両端のマス（行６列１，行４列６）それぞれと同じ領域（列１，列６）にある２つのマスで，２種類の数字の片方の数字（数字１）が配置可能なマスがその２マス（行１列１，行１列６）に限られる領域（行１）があると， 両端のマス（行６列１，行４列６）にはその数字（数字１）が，中央のマス（行６列５）にはもう一つの数字（数字２）が配置できません （各３マスでは配置できないとされた数字とは異なる数字の配置が確定します）。
説明） ３つのマス（行６列１，行６列５，行４列６）のつながり と その３つのマスに配置可能な数字が 数字１，数字２ に限られることから， 数字１ は，両端のマスに配置される（中央のマスには配置されない） か 中央のマスに配置される（両端のマスには配置されない） かのどちらかです。 数字１ は，行１ では配置可能なマスが 行１列１，行１列６ の２つのマスに限られるので その２つのマスのどちらか一方に必ず配置されます。 その２マスのうちで 数字１ が配置されるマス（行１列１，行１列６ のどちらか） と同じ領域にある ３マスのつながりの端のマス（行６列１，行４列６ のどちらか）には 数字１ が配置されません。 すると，もう一つの端のマス（行４列６，行６列１ のどちらか）にも 数字１ が配置されない（数字２ が配置される）ことがわかり，中央のマス（行６列５）に 数字１ が配置される（数字２ が配置されない）こともわかります。
［テクニック”浜田ロジック”の例］
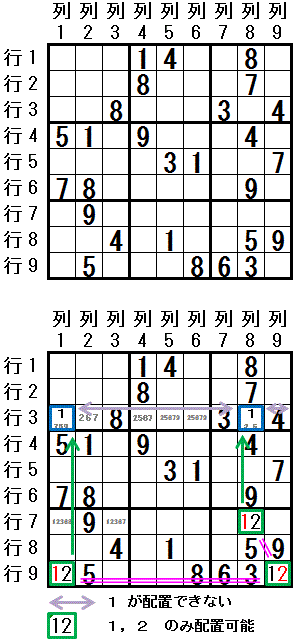左図で 行９列１，行９列９，行７列８ では 配置可能な数字が 数字１，数字２ の２種類の数字に限られています。
その３マスは 記載した順に２つずつのマスが 同じ行９，同じ大マス９ に属しています。
その順につながる３マスの両端のマス 行９列１，行７列８ のそれぞれと 行３列１，行３列８ は同じ領域（列１，列８）にあります。
行３では 数字１ が配置可能なマスは，その２つのマス 行３列１，行３列８ だけに限られています。
浜田ロジック の成立条件を満たしています。 数字１ は 行３列１，行３列８ に配置できません（数字２ が配置されることが確定します）。 数字２ は 行９列９ に配置できません（数字１ が配置されることが確定します）。
［浜田ロジック のチェーンとしての解釈］
浜田ロジック をチェーン（AIC:Alternate Inference Chain）として解釈します。 後半では それを元に 浜田ロジック と 他のテクニック の関係にも言及します。
上記の例題でのチェーンを考えます。
いろいろなチェーン（AIC）が存在します。
最初は，浜田ロジック と ネコとネズミ排除（W-Wing） の関係を検討できるチェーンを説明します。
（チェーン１）
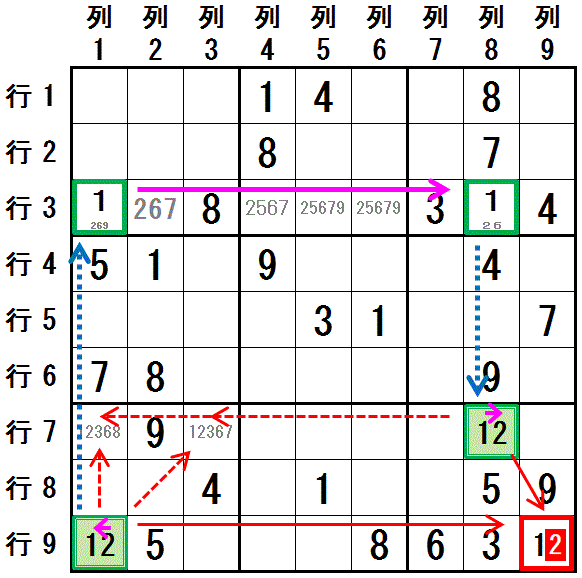
上記の例題で スタートを 数字２ を 行９列１ に配置する こととして左図に 強いリンク と 弱いリンク を記載します。
（赤い点線の矢印はあとで補足説明するときに使用します。最初は無視してください）
以下に，チェーンの内容を ”ある数字をあるマスに配置すること” のつながりとして詳細に記載します。
数字２ を 行９列１ に配置する ⇒ 数字１ を 行９列１ に配置する：行９列１（強いリンク）
数字１ を 行９列１ に配置する → 数字１ を 行３列１ に配置する：数字１，列１（弱いリンク）
数字１ を 行３列１ に配置する ⇒ 数字１ を 行３列８ に配置する：数字１，行３（強いリンク）
数字１ を 行３列８ に配置する → 数字１ を 行７列８ に配置する：数字１，列８（弱いリンク）
数字１ を 行７列８ に配置する ⇒ 数字２ を 行７列８ に配置する：行７列８（強いリンク）
チェーンの両端は，数字２ を 行９列１に配置する ことと 同じ 数字２ を 行７列８ に配置する ことになっています。 浜田ロジック で 数字２ が配置されないことがわかった 行９列９ は， この２つのマス（行９列１，行７列８） の 両方と同じ領域（行９，大マス９）にあり， チェーンとしての解釈でも 数字２ を 行９列９ に配置できないことがわかります。
浜田ロジック がチェーンの考え方で解釈できました。このチェーンの長さは ６ となります。
浜田ロジック を解釈したこのチェーンは ネコとネズミ排除（W-Wing） を解釈したチェーン と同一です（ネコとネズミ排除 を解釈したチェーンの数字やマス を単に置き換えたものです）。 浜田ロジック が ネコとネズミ排除（W-Wing） の特殊形（浜田ロジックを成立させるため条件 は ネコとネズミ排除を成立させる条件 にいつくかの条件を加えたもの）であることがわかります。
※ テクニックの条件・結論の記載内容の違い と あるテクニックが別のテクニックの特殊形（あるテクニックの成立条件が別のテクニックの成立条件にさらにいくつかの条件が加わっている）であること について記述します。読み飛ばして構いません。
テクニックの（条件・）結論の記載内容の違いにより 浜田ロジックを適応したとき よりも ネコとネズミ排除（W-Wing）を適応したとき のほうがたくさんの排除の情報が得られます。 この例のチェーンでは，数字２ は 行９列９ だけでなく，赤の点線矢印で示した 行９列１と同じ領域（大マス７） かつ 行７列８と同じ領域（行７） にある 行７列１，行７列３ にも配置できないことがわかります。 これは ネコとネズミ排除（W-Wing）の結論と一致します。
浜田ロジック としての結論は，このチェーンとしての結論の一つ 数字２ が 行９列９ に配置できないこと および そのことからすぐに導き出される 数字２ が 行７列８，行９列１ に配置されること，数字１ が 行９列９ に配置されること（および 各マスで配置が確定する数字の反対の数字がそのマスに配置されないこと）です。 浜田ロジック の結論は ネコとネズミ排除 の結論を網羅していませんが，ネコとネズミ排除 の結論にある 数字２ が 行７列１，行７列３ に配置できないことは，浜田ロジック でも 数字２ が 行７列８（または 行９列１）に配置されることが確定することからわかります。
次に あるテクニックが別のテクニックの特殊形（あるテクニックの成立条件が別のテクニックの成立条件にさらにいくつかの条件が加わっている）であること について記述します。
一般的には よりたくさんの条件が付けられている 特殊形 のほうが 元のテクニックよりたくさんの情報をもたらします。
この例でも 前述のように配置が確定する情報まで考慮に入れれば，よりたくさんの条件で成り立つ 浜田ロジック の方が ネコとネズミ排除 よりもたくさんの情報をもたらします。 例えば，浜田ロジックの条件が成立していれば 数字２ が 行７列８ に配置されることが確定しますが，ネコとネズミ排除では 行７列８ の 数字２ は確定しません。 浜田ロジック では 数字２ は 行７ では 行７列８以外のマス には配置できないことがわかりますが， ネコとネズミ排除 では 数字２ が 行７で 行９列１ と同じ領域（大マス７）でないマス（大マス８のマス（行７列４〜６）大マス８（行７列７，９））に配置できないこと はわかりません。
浜田ロジック をチェーンで解釈することに話を戻して，前述の チェーン１ とは別の形のいくつかのチェーンを作成して 数字１ が 行７列８ に配置できないことを示してみます。
二都物語排除（Naked Pairs，２国同盟） や 強いリンク が 弱いリンク として利用できることも使います （二都物語排除：例えば 行９ で ２つのマス（行９列１，行９列９）で配置可能な数字が 数字１，数字２ の２種類に限られているので， 数字１，数字２ は 行９では 配置可能なマスが その２マスに限られます）。
（チェーン２）
数字１ を 行９列９ に配置する ⇒ 数字１ を 行９列１ に配置する：数字１，行９（強いリンク）
数字１ を 行９列１ に配置する → 数字１ を 行３列１ に配置する：数字１，列１（弱いリンク）
数字１ を 行３列１ に配置する ⇒ 数字１ を 行３列８ に配置する：数字１，行３（強いリンク）
チェーンの両端は，数字１ を 行９列９ に配置する ことと 同じ 数字１ を 行３列８ に配置する ことになっています。 数字１ はこの両方のマス（行９列９，行３列８） と同じ領域にあるマス 行７列８ には配置できません。
このチェーンは 筋違見張塔排除（Skyscraper）を解釈したチェーン と同一です。 浜田ロジック は 筋違見張塔排除（Skyscraper） の特殊形と見ることができます。 筋違見張塔排除（Skyscraper） で見つかる 数字１ が 行１列９，行２列９ に配置できないことは，浜田ロジックでも 数字１ が 行９列９ に配置されることからわかります。。
浜田ロジック は リンクする領域の種類（行，列，大マス）によって 筋違見張塔排除（Skyscraper, 2-String Kite, Turbot Fish）の特殊形と解釈することができます。
（チェーン３）
（このチェーンは チェーンの両端が 同じ数字を同じマスに配置すること の例として提示します）
数字２ を 行７列８ に配置する ⇒ 数字２ を 行９列９ に配置する：数字２，大マス９（強いリンク）
数字２ を 行９列９ に配置する → 数字２ を 行９列１ に配置する：数字１，数字２，行９（弱いリンク）
数字２ を 行９列１ に配置する ⇒ 数字１ を 行９列１ に配置する：行９列１（強いリンク）
数字１ を 行９列１ に配置する → 数字１ を 行３列１ に配置する：数字１，列１（弱いリンク）
数字１ を 行３列１ に配置する ⇒ 数字１ を 行３列８ に配置する：数字１，行３（強いリンク）
数字１ を 行３列８ に配置する → 数字１ を 行７列８ に配置する：数字１，列８（弱いリンク）
数字１ を 行７列８ に配置する ⇒ 数字２ を 行７列８ に配置する：行７列８（強いリンク）
チェーンの両端は，同じ 数字２ を 同じマス 行７列８ に配置する ことになっています。 数字２ が 行７列８ に配置されることが確定します。 数字１ 行７列８ に配置できません。
（チェーン４）
（このチェーンは チェーンの両端が 異なる２つの数字を同じ領域のマスに配置すること の例として提示します）
数字１ を 行９列９ に配置する ⇒ 数字１ を 行９列１ に配置する：数字１，行９（強いリンク）
数字１ を 行９列１ に配置する → 数字１ を 行３列１ に配置する：数字１，列１（弱いリンク）
数字１ を 行３列１ に配置する ⇒ 数字１ を 行３列８ に配置する：数字１，行３（強いリンク）
数字１ を 行３列８ に配置する → 数字１ を 行７列８ に配置する：数字１，列８（弱いリンク）
数字１ を 行７列８ に配置する ⇒ 数字２ を 行７列８ に配置する：行７列８（強いリンク）
チェーンの両端は，数字１，数字２ を 同じ領域（大マス９）にあるマス（行９列９，行７列８） に配置する 形になっています。 数字１ が チェーンのスタートの端で 数字１が配置される行９列９ と同じ領域にある チェーンの終点の端で 数字２が配置される 行７列８ に配置できないことがわかります。
［浜田ロジック の色分け法（Coloring）としての解釈：Multi Colors］
浜田ロジック を 色分け法（Coloring）で解釈します。先の例題を利用します。数字１ に注目します。
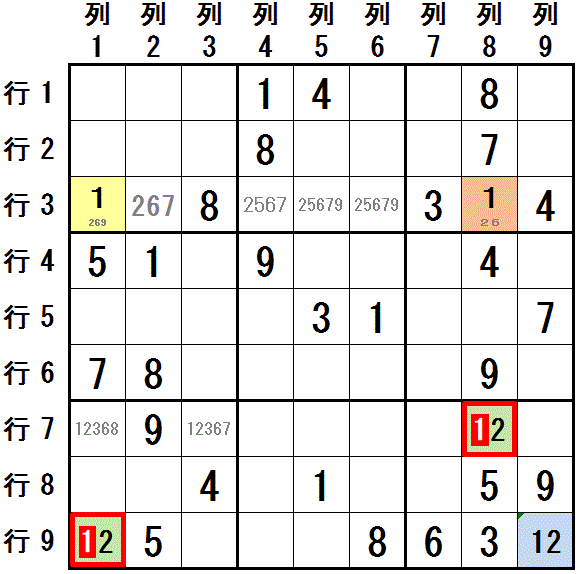行９ で ２つのマス（行９列１，行９列９）で配置可能な数字が 数字１，数字２ の２種類に限られているので，
数字１（，数字２） は 行９ では 配置可能なマスが その２マスに限られます（二都物語排除（Naked Pairs，２国同盟）。
同様に 数字１ は 大マス９ で 配置可能なマスが 行９列９，行７列８ に限られます。
色分け法で 行９列１ を薄緑色，行９列９ を水色，行７列８ を薄緑色に塗り分けることができます（第１の系列）。
一方 行３ では 数字１ は 配置可能なマスが 行３列１，行３列８ に限られます。
色分け法で 行３列１ をクリーム色，行３列８ をだいだい色に塗り分けることができます（第２の系列）。
第１の系列で 薄緑色に塗られた 行９列１は第２の系列のクリーム色に塗られた行３列１ と同じ領域（列１）に，行９列１と同じ薄緑色に塗られた 行７列８は第２の系列のだいだい色に塗られた行３列８ と同じ領域（列８）にあります。
一つの系列で ある同じ色に塗られたマスが もう一つの系列の異なる色で塗られたマスと同じ領域にあるとき，最初の系列で その同じ色に塗られたすべてのマス に 検討している数字 は配置できません （Multi Colors:Type 2）。
数字１ が 行９列１，行７列８ に配置できないことがわかります。
※ 浜田ロジック を利用して解ける問題が，他のテクニック（ネコとネズミ排除（W-Wing），筋違見張塔排除（Skyscraper, 2-String Kite, Turbot Fish），色分け法（Coloring）） を使えば解けることを説明してきましたが，浜田ロジック を利用することの有用性を否定するものでは決してありません。 むしろ，浜田ロジックは きちんと理解して 積極的に使うべきと考えます。 多くのナンプレ解答者は ネコとネズミ排除（W-Wing）などのテクニックが適応可能かどうかは かなり進んだ段階で検討します。 一方 浜田ロジックが適応可能かどうかの検討は，基本のテクニックだけでは手が進まない状況になったときに， 比較的早い段階で 二都物語排除（Naked Pairs） を検討する際に，もし面白く感じられるあるパターンが見つかれば 考察を少し演繹することで行うことができます。
面白く感じられるあるパターン とは，二都物語排除 を成立させる 数字・マス・領域（ある領域の２つのマスで配置可能な数字が同じ２種類の数字に限られる）が見つかったときに，そのうちの１つのマスと同じ領域に 配置可能な数字が同じ２種類の数字に限られるマスがあった場合です。
考察の演繹 とは，上記のパターンが見つかったとき 浜田ロジックを成り立たせるためのもう一つの領域（上記二都物語排除に関係する数字のうちの１つが配置可能なマスが２つに限られる領域で，その配置可能な２つのマスそれぞれが 上記のパターンの両端のマスと同じ領域にある）があるかどうかを検討することです。
・ ある１つのマスに ”配置可能な数字が ２つ に限られる” こと と，
・ ある数字が１つの領域（行，列，大マス）で ”配置可能なマスが ２つ に限られる” こと
をつなげていくことで情報を得るテクニックを チェーン(Chain)系のテクニック と呼びます。
５）グループ化，命題の一般化，ＡＬＳ，ＡＨＳ から この考え方を拡張します。
チェーン について考察することは，論理的思考能力を向上させる ために有効です。
（チェーン系のテクニックを積極的に使用することをお勧めする訳では決してありません。ナンプレを楽しみながら論理的思考能力を高めるには，むしろ，名前のついた基本的な中上級のテクニックを理解し，利用することの方が有効です）
１）代表的なチェーン系テクニック
１−１）X-Chain
１−２）XY-Chain
１−３）その他（色分け法 （Simple Colors, Multi Colors）, Remote Pair[リニア]）
２）テクニックのチェーンによる解釈（その１）
２−１）筋違見張塔排除 （Skyscraper, 2-String Kite, Turbot Fish）
２−２）賢い見張兵排除（X-Wing）
２−３）末っ子の甘え排除（XY-Wing）
２−４）二都物語排除（Naked Pair）
３）チェーン系テクニックの原理
３−１）強いリンク，弱いリンク
３−２）ＡＩＣ(Alternate Inference Chain)，チェーン系テクニックの原理
４）テクニックのチェーンによる解釈（その２）
４−１）ネコとネズミ排除(W-Wing)
４−２）姉妹排除（Hidden Pair）
４−３）浜田ロジック
５）グループ化，命題の一般化，ＡＬＳ，ＡＨＳ
５−１）グループ化
５−２）命題の一般化
５−３）ＡＬＳ(Almost Locked Sets)
５−４）ＡＨＳ(Almost Hidden Sets)
６）テクニックのチェーンによる解釈（その３）
６−１）信長の野望排除（XYZ-Wing）
６−２）二守備線見張塔過多排除（Finned・Sashimi X-Wing）
６−３）三・四都物語排除(Naked Triple・Quadruple)
６−４）三・四姉妹排除(Hidden Triple・Quadruple)
６−５）カーブミラー排除（Empty Rectangle）
６−６）三・四人の賢い見張兵排除(Swordfish・Jellyfish)
６−７）Ｓｕｅ ｄｅ Ｃｏｑ
このページでは，４）テクニックのチェーンによる解釈（その２） を説明します。
４）テクニックのチェーンによる解釈（その２）
”ある領域（行，列，または，大マス）で配置可能なマスが２つに限られる”や ”１つのマスに配置可能な数字が２つに限られる” という条件をつなげて，数字が排除されるマスを見つけるテクニックは，チェーン系の考え方で解釈することができます。 ここでは，その条件が複雑に絡んだテクニック（ AIC:Alternate Inference Chain）について説明します。
４−１） ネコとネズミ排除(W-Wing)
下に ネコとネズミ排除(W-Wing) の説明 に利用した図を示し，テクニックの説明をします。
最初に，配置可能なマスが２つ（行１列１，行１列５）に限られる数字（数字１：第一の数字）が存在する領域（行１）を見つけます。それら２つのマス（行１列１，行１列５）それぞれと 同じ領域（列１ および 列５）にあって， 配置可能な数字が 第一の数字（数字１）と第二の数字（数字２）の ２つの数字に限定されるマス（行７列１ および 行４列５）が存在すると，
それら２つのマス（行７列１ と 行４列５）の両方のマスと同じ領域にあるマス（行４列１ および 行７列５）には 第二の数字（数字２）は配置できません。
この図に 数字２ を 行７列１ に配置すること をスタートとして，強いリンク と 弱いリンク を記載し，チェーンを作成します。
数字２⇒数字１：行７列１（強いリンク）行７列１→行１列１：数字１，列１（弱いリンク）
行１列１⇒行１列５：数字１，行１（強いリンク）
行１列５→行４列５：数字１，列５（弱いリンク）
数字１⇒数字２：行４列５（強いリンク）
強いリンク と 弱いリンク が交互で，両端が強いリンク である チェーンが形成されました。チェーンの両端は 同じ数字２ を 行７列１，行４列５ に配置する ことになっています。
このチェーンの内容を，”ある数字をあるマスに配置すること” をつなげることでより詳細に表現します。
数字２ を 行７列１ に配置する ⇒ 数字１ を 行７列１ に配置する：行７列１（強いリンク）
数字１ を 行７列１ に配置する → 数字１ を 行１列１ に配置する：数字１，列１（弱いリンク）
数字１ を 行１列１ に配置する ⇒ 数字１ を 行１列５ に配置する：数字１，行１（強いリンク）
数字１ を 行１列５ に配置する → 数字１ を 行４列５ に配置する：数字１，列５（弱いリンク）
数字１ を 行４列５ に配置する ⇒ 数字２ を 行４列５ に配置する：行４列５（強いリンク）
チェーンの両端は，数字２ を 行７列１に配置する ことと 同じ 数字２ を 行４列５ に配置する ことになっています。 数字２ は 行７列１，行４列５ の 両方と同じ領域にあるマス 行４列１，行７列５ には配置できません。
ネコとネズミ排除（W-Wing） がチェーンの考え方で解釈できました。チェーンの長さは ６ となります。
４−２） 姉妹排除(Hidden Pairs)
下に 姉妹排除(Hidden Pairs) の説明 に利用した図を示し，テクニックの説明をします。
［テクニック］同じ領域（行１）で，２種類の数字（数字１，数字２）が配置できるマス が 同じ２つのマス（行１列１，行１列５） に限られると， その２つのマスには，それら２つの数字以外の数字（数字Ｘ，数字Ｙ，数字Ｚ） は配置できません。
この図に 数字１ を 行１列１ に配置すること をスタートとして，強いリンク と 弱いリンク を記載し，チェーンを作成します。
行１列１⇒行１列５：数字１，行１（強いリンク）数字１→数字２：行１列５（弱いリンク）
行１列５⇒行１列１：数字２，行１（強いリンク）
強いリンク と 弱いリンク が交互で，両端が強いリンク である チェーンが形成されました。 チェーンの両端である 数字１を行１列１ と 数字２を行１列１ に配置する ことは どちらか一方が必ず成り立ちます。 行１列１ には 数字１，数字２ 以外の数字（左図の例では 数字７，数字８）は配置できません。
このチェーンの内容を，”ある数字をあるマスに配置すること” をつなげることでより詳細に表現します。
数字１ を 行１列１ に配置する ⇒ 数字１ を 行１列５ に配置する：数字１，行１（強いリンク）
数字１ を 行１列５ に配置する → 数字２ を 行１列５ に配置する：行１列５（弱いリンク）
数字２ を 行１列５ に配置する ⇒ 数字２ を 行１列１ に配置する：数字２，行１（強いリンク）
チェーンの両端は，数字１ を 行１列１に配置する ことと 数字２ を 同じ行１列１ に配置する ことになっています。 この配置のどちらか一方は必ず成立します。 行１列１ には 数字１，数字２以外の数字（この図の例では 数字７，数字８） は配置できません。
同様に 数字１ を 行１列５ に配置すること をスタートとして，強いリンク と 弱いリンク が交互になっているチェーンを作成すれば， 行１列５ には 数字１，数字２ 以外の数字（この例では 数字９）が配置できないことがわかります。
姉妹排除(Hidden Pairs) がチェーンの考え方で解釈できました。チェーンの長さは ４ となります。
４−３） 浜田ロジック
※ お断り
浜田ロジックに関しては，本サイトも含めて，多くは 同じ２つの数字しか配置できない３マスが，同じ領域（行，列，大マス）にあることでつながっている状態で適応を考えられるテクニックとして説明されています。
しかし，本来”浜田ロジック”は，世界文化社のナンプレ本の関係者が称しているテクニック名です。同社のナンプレ本の浜田ロジックに関する解説からは，ある数字が，一つの領域で２マスにしか配置できないパターンがたくさんあるとき， 複合的にその組み合わせを考えてみるテクニックと解釈できそうです。この項の 最後 に説明します。
最初に 浜田ロジック について説明をします。
［テクニック］最初に，配置可能な数字が同じ２種類の数字（数字１，数字２）に限られる３つのマスで， １つのマス（行６列５：中央のマス）が他の２つのマス（行６列１，行４列６：両端のマス）と同じ領域（行６，大マス５）にある状況を見つけます。 この時，両端のマス（行６列１，行４列６）それぞれと同じ領域（列１，列６）にある２つのマスで，２種類の数字の片方の数字（数字１）が配置可能なマスがその２マス（行１列１，行１列６）に限られる領域（行１）があると， 両端のマス（行６列１，行４列６）にはその数字（数字１）が，中央のマス（行６列５）にはもう一つの数字（数字２）が配置できません （各３マスでは配置できないとされた数字とは異なる数字の配置が確定します）。
説明） ３つのマス（行６列１，行６列５，行４列６）のつながり と その３つのマスに配置可能な数字が 数字１，数字２ に限られることから， 数字１ は，両端のマスに配置される（中央のマスには配置されない） か 中央のマスに配置される（両端のマスには配置されない） かのどちらかです。 数字１ は，行１ では配置可能なマスが 行１列１，行１列６ の２つのマスに限られるので その２つのマスのどちらか一方に必ず配置されます。 その２マスのうちで 数字１ が配置されるマス（行１列１，行１列６ のどちらか） と同じ領域にある ３マスのつながりの端のマス（行６列１，行４列６ のどちらか）には 数字１ が配置されません。 すると，もう一つの端のマス（行４列６，行６列１ のどちらか）にも 数字１ が配置されない（数字２ が配置される）ことがわかり，中央のマス（行６列５）に 数字１ が配置される（数字２ が配置されない）こともわかります。
［テクニック”浜田ロジック”の例］
左図で 行９列１，行９列９，行７列８ では 配置可能な数字が 数字１，数字２ の２種類の数字に限られています。
その３マスは 記載した順に２つずつのマスが 同じ行９，同じ大マス９ に属しています。
その順につながる３マスの両端のマス 行９列１，行７列８ のそれぞれと 行３列１，行３列８ は同じ領域（列１，列８）にあります。
行３では 数字１ が配置可能なマスは，その２つのマス 行３列１，行３列８ だけに限られています。浜田ロジック の成立条件を満たしています。 数字１ は 行３列１，行３列８ に配置できません（数字２ が配置されることが確定します）。 数字２ は 行９列９ に配置できません（数字１ が配置されることが確定します）。
［浜田ロジック のチェーンとしての解釈］
浜田ロジック をチェーン（AIC:Alternate Inference Chain）として解釈します。 後半では それを元に 浜田ロジック と 他のテクニック の関係にも言及します。
上記の例題でのチェーンを考えます。
いろいろなチェーン（AIC）が存在します。最初は，浜田ロジック と ネコとネズミ排除（W-Wing） の関係を検討できるチェーンを説明します。
（チェーン１）
上記の例題で スタートを 数字２ を 行９列１ に配置する こととして左図に 強いリンク と 弱いリンク を記載します。
（赤い点線の矢印はあとで補足説明するときに使用します。最初は無視してください）
以下に，チェーンの内容を ”ある数字をあるマスに配置すること” のつながりとして詳細に記載します。
数字２ を 行９列１ に配置する ⇒ 数字１ を 行９列１ に配置する：行９列１（強いリンク）
数字１ を 行９列１ に配置する → 数字１ を 行３列１ に配置する：数字１，列１（弱いリンク）
数字１ を 行３列１ に配置する ⇒ 数字１ を 行３列８ に配置する：数字１，行３（強いリンク）
数字１ を 行３列８ に配置する → 数字１ を 行７列８ に配置する：数字１，列８（弱いリンク）
数字１ を 行７列８ に配置する ⇒ 数字２ を 行７列８ に配置する：行７列８（強いリンク）
チェーンの両端は，数字２ を 行９列１に配置する ことと 同じ 数字２ を 行７列８ に配置する ことになっています。 浜田ロジック で 数字２ が配置されないことがわかった 行９列９ は， この２つのマス（行９列１，行７列８） の 両方と同じ領域（行９，大マス９）にあり， チェーンとしての解釈でも 数字２ を 行９列９ に配置できないことがわかります。
浜田ロジック がチェーンの考え方で解釈できました。このチェーンの長さは ６ となります。
浜田ロジック を解釈したこのチェーンは ネコとネズミ排除（W-Wing） を解釈したチェーン と同一です（ネコとネズミ排除 を解釈したチェーンの数字やマス を単に置き換えたものです）。 浜田ロジック が ネコとネズミ排除（W-Wing） の特殊形（浜田ロジックを成立させるため条件 は ネコとネズミ排除を成立させる条件 にいつくかの条件を加えたもの）であることがわかります。
※ テクニックの条件・結論の記載内容の違い と あるテクニックが別のテクニックの特殊形（あるテクニックの成立条件が別のテクニックの成立条件にさらにいくつかの条件が加わっている）であること について記述します。読み飛ばして構いません。
テクニックの（条件・）結論の記載内容の違いにより 浜田ロジックを適応したとき よりも ネコとネズミ排除（W-Wing）を適応したとき のほうがたくさんの排除の情報が得られます。 この例のチェーンでは，数字２ は 行９列９ だけでなく，赤の点線矢印で示した 行９列１と同じ領域（大マス７） かつ 行７列８と同じ領域（行７） にある 行７列１，行７列３ にも配置できないことがわかります。 これは ネコとネズミ排除（W-Wing）の結論と一致します。
浜田ロジック としての結論は，このチェーンとしての結論の一つ 数字２ が 行９列９ に配置できないこと および そのことからすぐに導き出される 数字２ が 行７列８，行９列１ に配置されること，数字１ が 行９列９ に配置されること（および 各マスで配置が確定する数字の反対の数字がそのマスに配置されないこと）です。 浜田ロジック の結論は ネコとネズミ排除 の結論を網羅していませんが，ネコとネズミ排除 の結論にある 数字２ が 行７列１，行７列３ に配置できないことは，浜田ロジック でも 数字２ が 行７列８（または 行９列１）に配置されることが確定することからわかります。
次に あるテクニックが別のテクニックの特殊形（あるテクニックの成立条件が別のテクニックの成立条件にさらにいくつかの条件が加わっている）であること について記述します。
一般的には よりたくさんの条件が付けられている 特殊形 のほうが 元のテクニックよりたくさんの情報をもたらします。
この例でも 前述のように配置が確定する情報まで考慮に入れれば，よりたくさんの条件で成り立つ 浜田ロジック の方が ネコとネズミ排除 よりもたくさんの情報をもたらします。 例えば，浜田ロジックの条件が成立していれば 数字２ が 行７列８ に配置されることが確定しますが，ネコとネズミ排除では 行７列８ の 数字２ は確定しません。 浜田ロジック では 数字２ は 行７ では 行７列８以外のマス には配置できないことがわかりますが， ネコとネズミ排除 では 数字２ が 行７で 行９列１ と同じ領域（大マス７）でないマス（大マス８のマス（行７列４〜６）大マス８（行７列７，９））に配置できないこと はわかりません。
浜田ロジック をチェーンで解釈することに話を戻して，前述の チェーン１ とは別の形のいくつかのチェーンを作成して 数字１ が 行７列８ に配置できないことを示してみます。
二都物語排除（Naked Pairs，２国同盟） や 強いリンク が 弱いリンク として利用できることも使います （二都物語排除：例えば 行９ で ２つのマス（行９列１，行９列９）で配置可能な数字が 数字１，数字２ の２種類に限られているので， 数字１，数字２ は 行９では 配置可能なマスが その２マスに限られます）。
（チェーン２）
数字１ を 行９列９ に配置する ⇒ 数字１ を 行９列１ に配置する：数字１，行９（強いリンク）
数字１ を 行９列１ に配置する → 数字１ を 行３列１ に配置する：数字１，列１（弱いリンク）
数字１ を 行３列１ に配置する ⇒ 数字１ を 行３列８ に配置する：数字１，行３（強いリンク）
チェーンの両端は，数字１ を 行９列９ に配置する ことと 同じ 数字１ を 行３列８ に配置する ことになっています。 数字１ はこの両方のマス（行９列９，行３列８） と同じ領域にあるマス 行７列８ には配置できません。
このチェーンは 筋違見張塔排除（Skyscraper）を解釈したチェーン と同一です。 浜田ロジック は 筋違見張塔排除（Skyscraper） の特殊形と見ることができます。 筋違見張塔排除（Skyscraper） で見つかる 数字１ が 行１列９，行２列９ に配置できないことは，浜田ロジックでも 数字１ が 行９列９ に配置されることからわかります。。
浜田ロジック は リンクする領域の種類（行，列，大マス）によって 筋違見張塔排除（Skyscraper, 2-String Kite, Turbot Fish）の特殊形と解釈することができます。
（チェーン３）
（このチェーンは チェーンの両端が 同じ数字を同じマスに配置すること の例として提示します）
数字２ を 行７列８ に配置する ⇒ 数字２ を 行９列９ に配置する：数字２，大マス９（強いリンク）
数字２ を 行９列９ に配置する → 数字２ を 行９列１ に配置する：数字１，数字２，行９（弱いリンク）
数字２ を 行９列１ に配置する ⇒ 数字１ を 行９列１ に配置する：行９列１（強いリンク）
数字１ を 行９列１ に配置する → 数字１ を 行３列１ に配置する：数字１，列１（弱いリンク）
数字１ を 行３列１ に配置する ⇒ 数字１ を 行３列８ に配置する：数字１，行３（強いリンク）
数字１ を 行３列８ に配置する → 数字１ を 行７列８ に配置する：数字１，列８（弱いリンク）
数字１ を 行７列８ に配置する ⇒ 数字２ を 行７列８ に配置する：行７列８（強いリンク）
チェーンの両端は，同じ 数字２ を 同じマス 行７列８ に配置する ことになっています。 数字２ が 行７列８ に配置されることが確定します。 数字１ 行７列８ に配置できません。
（チェーン４）
（このチェーンは チェーンの両端が 異なる２つの数字を同じ領域のマスに配置すること の例として提示します）
数字１ を 行９列９ に配置する ⇒ 数字１ を 行９列１ に配置する：数字１，行９（強いリンク）
数字１ を 行９列１ に配置する → 数字１ を 行３列１ に配置する：数字１，列１（弱いリンク）
数字１ を 行３列１ に配置する ⇒ 数字１ を 行３列８ に配置する：数字１，行３（強いリンク）
数字１ を 行３列８ に配置する → 数字１ を 行７列８ に配置する：数字１，列８（弱いリンク）
数字１ を 行７列８ に配置する ⇒ 数字２ を 行７列８ に配置する：行７列８（強いリンク）
チェーンの両端は，数字１，数字２ を 同じ領域（大マス９）にあるマス（行９列９，行７列８） に配置する 形になっています。 数字１ が チェーンのスタートの端で 数字１が配置される行９列９ と同じ領域にある チェーンの終点の端で 数字２が配置される 行７列８ に配置できないことがわかります。
［浜田ロジック の色分け法（Coloring）としての解釈：Multi Colors］
浜田ロジック を 色分け法（Coloring）で解釈します。先の例題を利用します。数字１ に注目します。
行９ で ２つのマス（行９列１，行９列９）で配置可能な数字が 数字１，数字２ の２種類に限られているので，
数字１（，数字２） は 行９ では 配置可能なマスが その２マスに限られます（二都物語排除（Naked Pairs，２国同盟）。同様に 数字１ は 大マス９ で 配置可能なマスが 行９列９，行７列８ に限られます。
色分け法で 行９列１ を薄緑色，行９列９ を水色，行７列８ を薄緑色に塗り分けることができます（第１の系列）。
一方 行３ では 数字１ は 配置可能なマスが 行３列１，行３列８ に限られます。
色分け法で 行３列１ をクリーム色，行３列８ をだいだい色に塗り分けることができます（第２の系列）。
第１の系列で 薄緑色に塗られた 行９列１は第２の系列のクリーム色に塗られた行３列１ と同じ領域（列１）に，行９列１と同じ薄緑色に塗られた 行７列８は第２の系列のだいだい色に塗られた行３列８ と同じ領域（列８）にあります。
一つの系列で ある同じ色に塗られたマスが もう一つの系列の異なる色で塗られたマスと同じ領域にあるとき，最初の系列で その同じ色に塗られたすべてのマス に 検討している数字 は配置できません （Multi Colors:Type 2）。
数字１ が 行９列１，行７列８ に配置できないことがわかります。
※ 浜田ロジック を利用して解ける問題が，他のテクニック（ネコとネズミ排除（W-Wing），筋違見張塔排除（Skyscraper, 2-String Kite, Turbot Fish），色分け法（Coloring）） を使えば解けることを説明してきましたが，浜田ロジック を利用することの有用性を否定するものでは決してありません。 むしろ，浜田ロジックは きちんと理解して 積極的に使うべきと考えます。 多くのナンプレ解答者は ネコとネズミ排除（W-Wing）などのテクニックが適応可能かどうかは かなり進んだ段階で検討します。 一方 浜田ロジックが適応可能かどうかの検討は，基本のテクニックだけでは手が進まない状況になったときに， 比較的早い段階で 二都物語排除（Naked Pairs） を検討する際に，もし面白く感じられるあるパターンが見つかれば 考察を少し演繹することで行うことができます。
面白く感じられるあるパターン とは，二都物語排除 を成立させる 数字・マス・領域（ある領域の２つのマスで配置可能な数字が同じ２種類の数字に限られる）が見つかったときに，そのうちの１つのマスと同じ領域に 配置可能な数字が同じ２種類の数字に限られるマスがあった場合です。
考察の演繹 とは，上記のパターンが見つかったとき 浜田ロジックを成り立たせるためのもう一つの領域（上記二都物語排除に関係する数字のうちの１つが配置可能なマスが２つに限られる領域で，その配置可能な２つのマスそれぞれが 上記のパターンの両端のマスと同じ領域にある）があるかどうかを検討することです。
［世界文化社のナンプレ本の 浜田ロジック に関しての解釈］
世界文化社のナンプレ本では 浜田ロジックに関しては ナンプレ超上級編（第２７巻には説明がありますが第３１巻では説明がなくなっています），超難問ナンプレＡＡＡ，世界で一番美しくて難しいナンプレ，難問ナンプレに挑戦（ナンプレ超上級編と同じ説明） の４つのシリーズで説明しています。
このうち ナンプレ超上級編，世界で一番美しくて難しいナンプレ，難問ナンプレに挑戦 の３シリーズでは，３ないし４つのマスで配置可能な数字が 同じ２つの数字 に限られることから説明が始まります。 本サイトを含め 浜田ロジックに関する説明の多くは，これを元にしていると思われます。 これらの３ないし４マスのうちの１つのマスは他の２つのマスと同じ領域（行，列または大マス）にあるという位置関係にあります。
別の見方として，これらのマスのうちの２マスを持つ領域では どちらの数字に関しても，その領域で配置可能なマスが２マスに限られるとも解釈できます（定員確定の法 もしくは すでに７マスが埋まっている）。 配置可能な数字が同じ２つの数字に限られる３マスがつながっていることよりも，ある数字が配置可能なマスが２つに限られる領域のつながりから考えたい理由が２つあります。
理由の一番目は，超難問ナンプレＡＡＡシリーズで表題が 浜田ロジック Simple Coloring となっていることです。 そして説明文でも ある１つの数字がいくつかの列やブロック内で配置可能なマスが二者択一．．．となっています。 説明例題でも，テクニックが成り立つためのマスでは配置可能な数字はたまたま同じ２つの数字のみになっていますが， その他の数字が配置可能なマスにも印がついています。
もう一つの理由は，世界文化社はペンシルマークの利用を積極的には行わないからです （ペンシルマークを利用した説明は 末っ子の甘え排除[XY-Wing, 数字の三つ巴]のみです。リニア新幹線排除[Remote Pair, ペアの不在証明]もペンシルマークでは説明していません]）。
ペンシルマークを使わない場合は，ある数字がある領域で配置可能なマスが２つに限られることの方が見つけやすくなります （ある数字がある領域で配置可能なマスが１つに限られるかな（一人っ子［Hidden Single］，２つに限られるかな（姉妹排除［Hidden Pair］）と調べていきます）。
ペンシルマークを積極的に利用した場合は，配置可能な数字が２つに限られるマスが見つけやすくなります （一気にペンシルマークを作成して，配置可能な数字が１つのマスはないか（お山の大将［Naked Single］，２つに限られるマスに何らかの関連があるかどうか（二都物語排除［Naked Pair］など）と調べていきます）。
なお，世界で一番美しくて難しいナンプレの説明の例題では，すでに７つのマスが埋まっている領域で，配置可能なマスが２つのマスに限られるた領域のみの重なりから検討を開始しています。狭義の浜田ロジックとします。 各シリーズには数問の狭義の浜田ロジックで解ける問題が出題されています（難問ナンプレに挑戦 は未確認）。
世界文化社のナンプレ本では 浜田ロジックに関しては ナンプレ超上級編（第２７巻には説明がありますが第３１巻では説明がなくなっています），超難問ナンプレＡＡＡ，世界で一番美しくて難しいナンプレ，難問ナンプレに挑戦（ナンプレ超上級編と同じ説明） の４つのシリーズで説明しています。
このうち ナンプレ超上級編，世界で一番美しくて難しいナンプレ，難問ナンプレに挑戦 の３シリーズでは，３ないし４つのマスで配置可能な数字が 同じ２つの数字 に限られることから説明が始まります。 本サイトを含め 浜田ロジックに関する説明の多くは，これを元にしていると思われます。 これらの３ないし４マスのうちの１つのマスは他の２つのマスと同じ領域（行，列または大マス）にあるという位置関係にあります。
別の見方として，これらのマスのうちの２マスを持つ領域では どちらの数字に関しても，その領域で配置可能なマスが２マスに限られるとも解釈できます（定員確定の法 もしくは すでに７マスが埋まっている）。 配置可能な数字が同じ２つの数字に限られる３マスがつながっていることよりも，ある数字が配置可能なマスが２つに限られる領域のつながりから考えたい理由が２つあります。
理由の一番目は，超難問ナンプレＡＡＡシリーズで表題が 浜田ロジック Simple Coloring となっていることです。 そして説明文でも ある１つの数字がいくつかの列やブロック内で配置可能なマスが二者択一．．．となっています。 説明例題でも，テクニックが成り立つためのマスでは配置可能な数字はたまたま同じ２つの数字のみになっていますが， その他の数字が配置可能なマスにも印がついています。
もう一つの理由は，世界文化社はペンシルマークの利用を積極的には行わないからです （ペンシルマークを利用した説明は 末っ子の甘え排除[XY-Wing, 数字の三つ巴]のみです。リニア新幹線排除[Remote Pair, ペアの不在証明]もペンシルマークでは説明していません]）。
ペンシルマークを使わない場合は，ある数字がある領域で配置可能なマスが２つに限られることの方が見つけやすくなります （ある数字がある領域で配置可能なマスが１つに限られるかな（一人っ子［Hidden Single］，２つに限られるかな（姉妹排除［Hidden Pair］）と調べていきます）。
ペンシルマークを積極的に利用した場合は，配置可能な数字が２つに限られるマスが見つけやすくなります （一気にペンシルマークを作成して，配置可能な数字が１つのマスはないか（お山の大将［Naked Single］，２つに限られるマスに何らかの関連があるかどうか（二都物語排除［Naked Pair］など）と調べていきます）。
なお，世界で一番美しくて難しいナンプレの説明の例題では，すでに７つのマスが埋まっている領域で，配置可能なマスが２つのマスに限られるた領域のみの重なりから検討を開始しています。狭義の浜田ロジックとします。 各シリーズには数問の狭義の浜田ロジックで解ける問題が出題されています（難問ナンプレに挑戦 は未確認）。