＜＜色分け法(Coloring)＞＞
色分け法（Coloring）は X-Chain の特別な形で，ある一つの数字が ”配置可能なマスが２つに限られる領域”のみ で領域・マスをつなげていき，数字が配置できないマスを見つけるテクニックです。
一つの領域で配置可能な ２マス のうち，片方のマスをある１つの色，もう片方のマスを別の色で塗り分けていくため，”色分け法(Coloring)” とよばれます。
（X-Chain では，配置可能なマスが２つに限られる２つの領域をつなぎ合わせる２つのマスは同じ領域にあれば十分でしたが， 色分け法（Coloring） では，検討している数字は，そのつなぎ合わせの領域でも 配置可能なマスが つなぎ合わせに使われる２つのマスのみに限られます（つなぎ合わせに使用される領域自体もつなぎ合わされる領域になります））
ある一つの数字が配置可能なマスが２つに限られる ２つの領域のつなぎ合わせ は，その２つの領域でその数字が配置可能な共通のマスが存在するときに行います。 ある領域に関してつなぎ合わせが可能な領域が２つあるときには，その両方とつなぎ合わせて枝分かれします。 全体のつながりは，鎖（チェーン）というよりも 樹枝状 の構造となります。
最初の領域でのその数字が配置可能な２マスを２色で塗り分け，つなぎ合わされていく領域でその数字が配置可能な２マスを同じ色にならないようにその２色で塗り分けていくと， つながりの中のその数字が配置可能なすべてのマスは 一意に２色で塗り分けることができます。 つながりは，検討している数字が配置可能なマスが２つに限られる領域のつながりと考えるだけでなく，検討している数字が配置可能なマスのつながりと考えることもできます。 このつながりを 系列 と呼びます。
”配置可能なマスが２つに限られる領域”だけを利用してつなぎ合わせていくことに加え， 塗り分けによる視覚的効果によっても，X-Chain よりも容易に つながりの有無を確認し，検討することができます。
１つの塗り分けの系列だけを利用する色分け法（Coloring）を Simple Colors， 複数の塗り分けの系列を利用する色分け法を Multi Colors といいます。
このページでは，最初に 色分け法について説明します。後半では，色分け法が X-Chain としてどのように解釈できるかを説明します。
色分け法を X-Chain として解釈することは，X-Chain を理解するためにも，また 論理的思考能力を向上させるためにも有効です。
色分け法（Coloring）は X-Chain の特別な形で，ある一つの数字が ”配置可能なマスが２つに限られる領域”のみ で領域・マスをつなげていき，数字が配置できないマスを見つけるテクニックです。
一つの領域で配置可能な ２マス のうち，片方のマスをある１つの色，もう片方のマスを別の色で塗り分けていくため，”色分け法(Coloring)” とよばれます。
（X-Chain では，配置可能なマスが２つに限られる２つの領域をつなぎ合わせる２つのマスは同じ領域にあれば十分でしたが， 色分け法（Coloring） では，検討している数字は，そのつなぎ合わせの領域でも 配置可能なマスが つなぎ合わせに使われる２つのマスのみに限られます（つなぎ合わせに使用される領域自体もつなぎ合わされる領域になります））
ある一つの数字が配置可能なマスが２つに限られる ２つの領域のつなぎ合わせ は，その２つの領域でその数字が配置可能な共通のマスが存在するときに行います。 ある領域に関してつなぎ合わせが可能な領域が２つあるときには，その両方とつなぎ合わせて枝分かれします。 全体のつながりは，鎖（チェーン）というよりも 樹枝状 の構造となります。
最初の領域でのその数字が配置可能な２マスを２色で塗り分け，つなぎ合わされていく領域でその数字が配置可能な２マスを同じ色にならないようにその２色で塗り分けていくと， つながりの中のその数字が配置可能なすべてのマスは 一意に２色で塗り分けることができます。 つながりは，検討している数字が配置可能なマスが２つに限られる領域のつながりと考えるだけでなく，検討している数字が配置可能なマスのつながりと考えることもできます。 このつながりを 系列 と呼びます。
”配置可能なマスが２つに限られる領域”だけを利用してつなぎ合わせていくことに加え， 塗り分けによる視覚的効果によっても，X-Chain よりも容易に つながりの有無を確認し，検討することができます。
１つの塗り分けの系列だけを利用する色分け法（Coloring）を Simple Colors， 複数の塗り分けの系列を利用する色分け法を Multi Colors といいます。
このページでは，最初に 色分け法について説明します。後半では，色分け法が X-Chain としてどのように解釈できるかを説明します。
色分け法を X-Chain として解釈することは，X-Chain を理解するためにも，また 論理的思考能力を向上させるためにも有効です。
Ⅰ 色分け法
色分け法では，ある１つの数字に関して，
・ ”配置可能なマスが２つに限られる領域”のみ をつなげていきます。
２つの領域は，その数字が配置可能な共通のマスが存在するときにつなぎ合わされます
つながりは，領域のつながりと見ることも，その数字が配置可能なマスのつながりと見ることもできます
・ その数字が配置可能なマスは，同じ領域の２マスが異なる色になるように ２色のみを使用して 塗り分けます。
・ 検討している数字が 配置できないマス を見つけるには，その数字が
どちらかの色に塗られたすべてのマスに配置され，
それと異なる色に塗られたすべてのマスに配置されない
ことを 利用します。
１－１） Simple Colors
ある１つの数字に関して，マスが 上記の方法で２色に塗り分けられると，次の２つの形で，配置できないマス を見つけることができます。
① Color Trap：異なる色で塗られた２つのマスの両方と同じ領域にあるマスには，その数字を配置できません
下図 数字１ に関して，配置可能なマスが２つに限られる領域をつなげていきます。
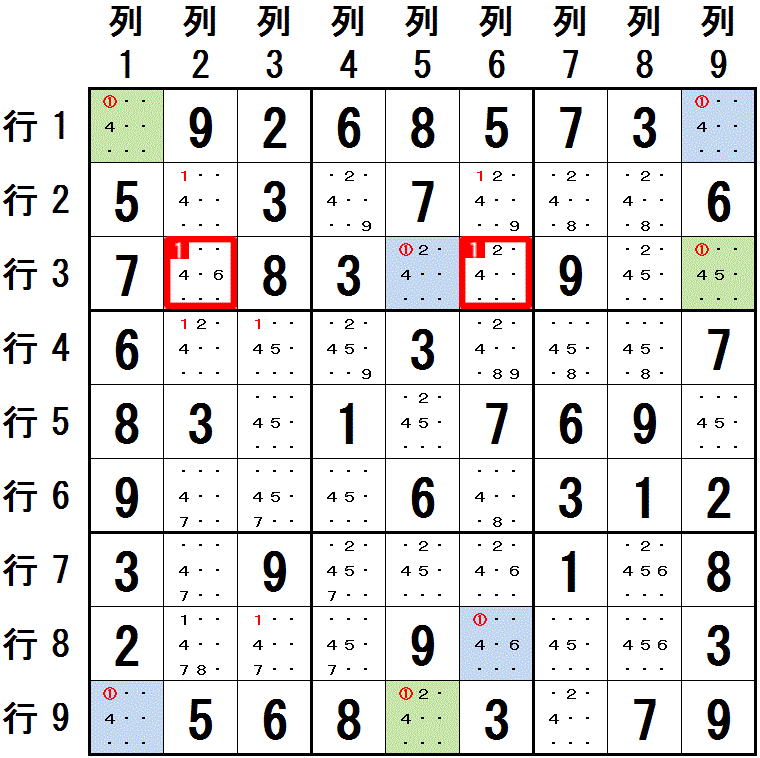
行３列９→行１列９：列９
行１列９→行１列１：行１
行１列１→行９列１：列１
行９列１→行９列５：行９
行９列５→行３列５：列５
〃 →行８列６：大マス８
最初に 行３列９ を 薄緑色，行１列９ を 水色で塗ります。 つなぎ合わされていくマスを，薄緑色，水色の順に塗っていくと，左図のようになります。
行３列５（水色） と 行３列９（薄緑色） は 異なる色に塗られています。
行３列５ と 行３列９ の両方と同じ領域（行３）にあるマス 行３列２，行３列６ には，数字１ を配置できません。
説明）数字１ は
すべての水色のマスに配置される（薄緑色のマスには配置されません） か
すべての薄緑色のマスに配置される（水色のマスには配置されません）
か のどちらかです。
数字１ は，異なる色で塗られた 行３列５ と 行３列９ のどちらかに，必ず配置されます。
その両方のマス（行３列５ と 行３列９）と同じ領域にあるマス（行３列２，行３列６）に，数字１ は配置できません。
上の説明で利用した２マスとは別に，次に示す組み合わせの 異なる色に塗られた２マス の両方と同じ領域にあると解釈しても，数字１が配置できないことがわかります。
行１列１（薄緑色）－行３列５（水色）：数字１ は 行３列２ に配置できません （Skyscraper と解釈することもできます）。
行８列６（水色）－行３列９（薄緑色）：数字１ は 行３列６ に配置できません。
また，例図には上に示したものの他に ２つの 数字１ が，配置可能なマスが２つに限られた領域のつなぎ合わせがあります（このつながりでマスを塗り分けても，数字１が配置できないマスは見つかりません）。
行４列２ －（行４）－ 行４列３ －（列３）－ 行８列３
行２列２ －（行２）－ 行２列６
（Color Trap の X-Chain としての解釈については ここ をクリックしてください）
② Color Wrap：同じ色に塗られた２つのマスが同じ領域にあると，その色で塗られたすべてのマスにその数字は配置できません
下図 数字１ に関して，配置可能なマスが２つに限られる領域をつなげていきます。
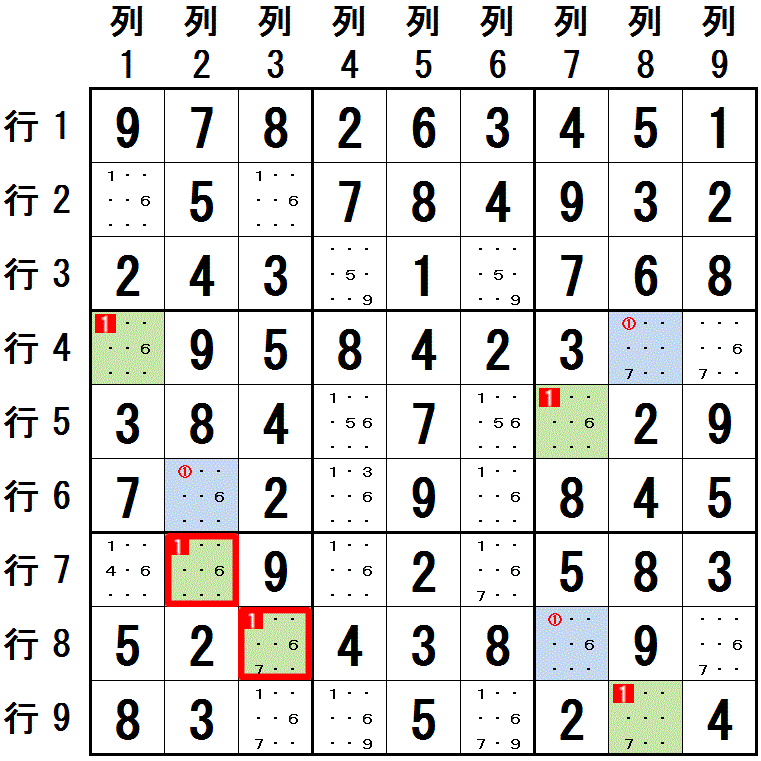
行７列２→行６列２：列２
行６列２→行４列１：大マス４
行４列１→行４列８：行４
行４列８→行９列８：列８
〃 →行５列７：大マス６
行９列８→行８列７：大マス９
行５列７→ 〃 ：列７
行８列７→行８列３：行８
最初に 行７列２ を 薄緑色，行６列２ を 水色で塗ります。 つなぎ合わされていくマスを，薄緑色，水色の順に塗っていくと，左図のようになります。
同じ薄緑色に塗られた 行７列２ と 行８列３ が 同じ 大マス７ に存在します。
薄緑色に塗られたすべてのマス に 数字１ が配置できないことがわかります。
説明）
薄緑色に塗られた 行７列２ と 行８列３ は 同じ 大マス７ に存在します。
同じ薄緑色に塗られた 行７列２ と 行８列３ は どちらにも 数字１ が配置されるか， どちらにも 数字１ が配置されないか のどちらかです。
同じ 大マス７ に存在する 行７列２ と 行８列３ の両方のマスに 数字１ が配置されることはないので 行７列２ にも 行８列３ にも 数字１ が配置されないことがわかります。
薄緑色に塗られたすべてのマスにも 数字１ が配置されないことがわかります。
（すべての 水色に塗られたマスに 数字１ が配置されることが確定します）
（Color Wrap の X-Chain としての解釈については ここ をクリックしてください）
ある１つの数字に関して，マスが 上記の方法で２色に塗り分けられると，次の２つの形で，配置できないマス を見つけることができます。
① Color Trap：異なる色で塗られた２つのマスの両方と同じ領域にあるマスには，その数字を配置できません
下図 数字１ に関して，配置可能なマスが２つに限られる領域をつなげていきます。
行３列９→行１列９：列９
行１列９→行１列１：行１
行１列１→行９列１：列１
行９列１→行９列５：行９
行９列５→行３列５：列５
〃 →行８列６：大マス８
最初に 行３列９ を 薄緑色，行１列９ を 水色で塗ります。 つなぎ合わされていくマスを，薄緑色，水色の順に塗っていくと，左図のようになります。
行３列５（水色） と 行３列９（薄緑色） は 異なる色に塗られています。
行３列５ と 行３列９ の両方と同じ領域（行３）にあるマス 行３列２，行３列６ には，数字１ を配置できません。
説明）数字１ は
すべての水色のマスに配置される（薄緑色のマスには配置されません） か
すべての薄緑色のマスに配置される（水色のマスには配置されません）
か のどちらかです。
数字１ は，異なる色で塗られた 行３列５ と 行３列９ のどちらかに，必ず配置されます。
その両方のマス（行３列５ と 行３列９）と同じ領域にあるマス（行３列２，行３列６）に，数字１ は配置できません。
上の説明で利用した２マスとは別に，次に示す組み合わせの 異なる色に塗られた２マス の両方と同じ領域にあると解釈しても，数字１が配置できないことがわかります。
行１列１（薄緑色）－行３列５（水色）：数字１ は 行３列２ に配置できません （Skyscraper と解釈することもできます）。
行８列６（水色）－行３列９（薄緑色）：数字１ は 行３列６ に配置できません。
また，例図には上に示したものの他に ２つの 数字１ が，配置可能なマスが２つに限られた領域のつなぎ合わせがあります（このつながりでマスを塗り分けても，数字１が配置できないマスは見つかりません）。
行４列２ －（行４）－ 行４列３ －（列３）－ 行８列３
行２列２ －（行２）－ 行２列６
（Color Trap の X-Chain としての解釈については ここ をクリックしてください）
② Color Wrap：同じ色に塗られた２つのマスが同じ領域にあると，その色で塗られたすべてのマスにその数字は配置できません
下図 数字１ に関して，配置可能なマスが２つに限られる領域をつなげていきます。
行７列２→行６列２：列２
行６列２→行４列１：大マス４
行４列１→行４列８：行４
行４列８→行９列８：列８
〃 →行５列７：大マス６
行９列８→行８列７：大マス９
行５列７→ 〃 ：列７
行８列７→行８列３：行８
最初に 行７列２ を 薄緑色，行６列２ を 水色で塗ります。 つなぎ合わされていくマスを，薄緑色，水色の順に塗っていくと，左図のようになります。
同じ薄緑色に塗られた 行７列２ と 行８列３ が 同じ 大マス７ に存在します。
薄緑色に塗られたすべてのマス に 数字１ が配置できないことがわかります。
説明）
薄緑色に塗られた 行７列２ と 行８列３ は 同じ 大マス７ に存在します。
同じ薄緑色に塗られた 行７列２ と 行８列３ は どちらにも 数字１ が配置されるか， どちらにも 数字１ が配置されないか のどちらかです。
同じ 大マス７ に存在する 行７列２ と 行８列３ の両方のマスに 数字１ が配置されることはないので 行７列２ にも 行８列３ にも 数字１ が配置されないことがわかります。
薄緑色に塗られたすべてのマスにも 数字１ が配置されないことがわかります。
（すべての 水色に塗られたマスに 数字１ が配置されることが確定します）
（Color Wrap の X-Chain としての解釈については ここ をクリックしてください）
１－２） Multi Colors
Simple Colors と同じく X-Chain の特殊形です。
ある１つの数字に関して，配置可能なマスが２つに限られる領域のみで領域・マスをつなげ， その数字が配置可能なマスを，同じ領域では別の色になるように２色で塗り分けることは Simple Colors と同様です。
Multi Colors では，この領域・マスをつなげた系列［以下，マスのつながりと表示します］を複数本扱います。
最初は，マスをつなげた系列を２本扱う場合に限定して説明します（塗り分けは４色で行います）。
（最後に マスをつなげた系列を３本以上扱う場合を補足説明します）
◎ マスをつなげた系列を２本扱うの場合の Multi Colors
以下の2つの場合に 検討している数字が配置できないマスが見つかります。
① type１（Color Wing）：２本のそれぞれの系列に属する１つずつのマス２つが同じ領域にあるとき， その領域でそれぞれの系列のマスを着色するのに使われた色と異なる色で塗られた２つのマスの両方と同じ領域にあるマスには，その数字を配置できません
下図 数字１ に関して，配置可能なマスが２つに限られる領域をつなげていきます。
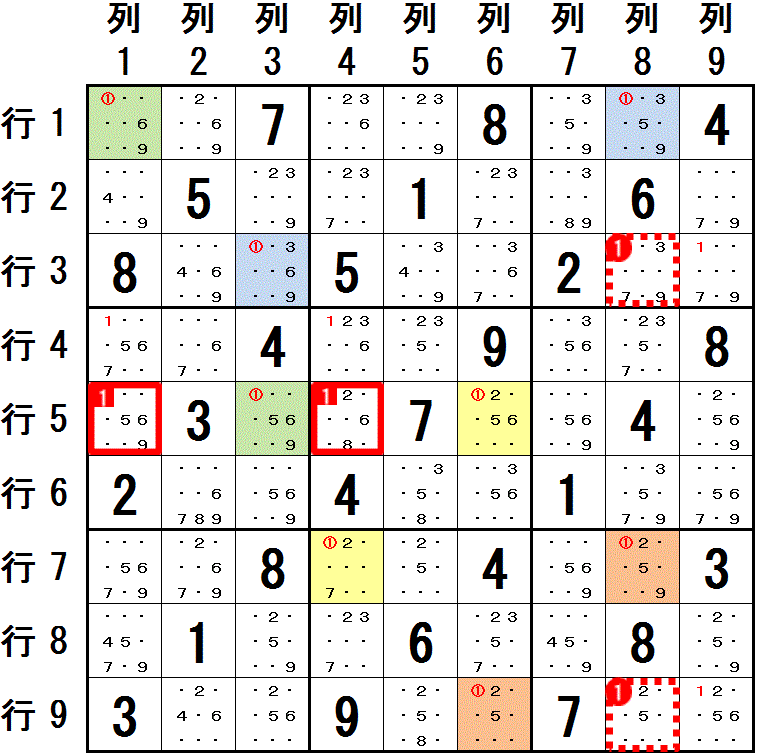
行５列３→行３列３：列３
行３列３→行１列１：大マス１
行１列１→行１列８：行１
最初に 行５列３ を 薄緑色，行３列３ を 水色で塗ります。 つなぎ合わされていくマスを，薄緑色，水色の順に塗っていくと，左図のようになります。
数字１ に関して，配置可能なマスが２つに限られる領域をつなげて作成される系列には以下のものもあります。
行５列６→行９列６：列６
行９列６→行７列４：大マス８
行７列４→行７列８：行７
最初に 行５列６ を クリーム色，行９列６ を だいだい色で塗ります。 つなぎ合わされていくマスを，クリーム色，だいだい色の順に塗っていくと，左図のようになります。
左図のように 塗り分けられました。
水色に塗られた 行１列８ と だいだい色に塗られた 行７列８ が 同じ 列８ に存在します。
水色，だいだい色と それぞれの系列での 反対の色 薄緑色，クリーム色 で塗られたマス，例えば 行５列３ と 行５列６ の両方と 同じ領域（行５）にあるマス 行５列１，行５列４ には 数字１ を配置できません。
説明）
水色に塗られた 行１列８ と だいだい色に塗られた 行７列８ は 同じ 列８ に存在するため， ”両方ともに数字１が配置されること” はありません。
数字１ が，
行１列８ に配置されて，行７列８ に配置されない か，
行１列８ に配置されず，行７列８ に配置される か，
行１列８ に配置されず，行７列８ にも配置されない か
のいずれかになります。
このことを，水色，だいだい色 の反対色 薄緑色，クリーム色 で考えると，薄緑色，クリーム色 のマスの ”両方ともに数字１が配置されないこと” はないことになります。
前述の３行に対応させれば，数字１ が，
薄緑色のマス に配置されず， クリーム色のマス に配置される か，
薄緑色のマス に配置されて， クリーム色のマス に配置されない か，
薄緑色のマス に配置されて， クリーム色のマス にも配置される か，
のいずれかになります。
つまり，薄緑色，クリーム色 のマスのどちらかに 数字１ が必ず配置されることになります。 よって，薄緑色，クリーム色 に塗られたマス，例えば行５列３ と 行５列６ の両方と同じ領域（行５）にあるマス 行５列１，行５列４ には 数字１ は配置されません。
他の 同じ領域にあるマスの組み合わせによっても 数字１ が配置できないマスを見つけることができます。
薄緑色に塗られた 行５列３ と クリーム色に塗られた 行５列６ が 同じ 行５ に存在するため，
それぞれの系列 で 薄緑色，クリーム色の 反対の色 水色，だいだい色 で塗られたマス， 例えば 行１列８ と 行７列８ の両方と同じ領域（列８）にあるマス 行３列８，行９列８ には 数字１ を配置できません。
（Color Wing の X-Chain としての解釈については ここ をクリックしてください）
② type２：一つの系列で同じ色に塗られた２つのマスのうち， １つのマスが もう一つの系列のある色で塗られたマスと同じ領域に属し， もう１つのマスが もう一つの系列の前記とは異なる色で塗られたマスと同じ領域に属しているとき， 最初の系列でその同じ色で塗られたすべてのマスにその数字は配置できません
下図 数字１ に関して，配置可能なマスが２つに限られる領域をつなげていきます。
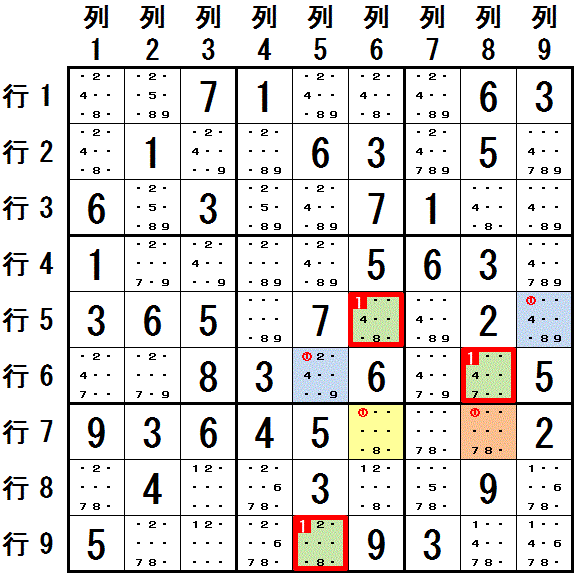
行６列８→行５列９：大マス６
行５列９→行５列６：行５
行５列６→行６列５：大マス５
行６列５→行９列５：列５
最初に 行６列８ を 薄緑色，行５列９ を 水色で塗ります。 つなぎ合わされていくマスを，薄緑色，水色の順に塗っていくと，左図のようになります。
数字１ に関して，配置可能なマスが２つに限られる領域には他に 行７ と 列３ がありますが，このうち 行７ で配置可能なマスを，
行７列６ を クリーム色，行７列８ を だいだい色で塗ります。 左図のように 塗り分けられました。
行６列８ と 行５列６ は同じ薄緑色に塗られていますが， 行６列８ は だいだい色に塗られた 行７列８ と同じ 列８ に存在し， 行５列６ は クリーム色に塗られた 行７列６ と同じ 列６ に存在します。
同じ 薄緑色 に塗られた２つのマスが，もう１本の系列の異なる色（だいだい色とクリーム色）で塗られたマスと同じ領域に属しているので， 薄緑色で塗られたすべてのマス 行６列８，行５列６，行９列５ に 数字１ を配置できません。
（水色に塗られたマスすべてに 数字１ が配置されます）
説明）
同じ薄緑色に塗られた 行６列８ と 行５列６ は どちらにも 数字１が配置されるか，どちらにも数字１が配置されない かのどちらかです。 だいだい色に塗られた 行７列８ と クリーム色に塗られた 行７列６は，どちらかに 数字１ が必ず配置されます。 行６列８ と 行７列８ が同じ領域にあり， 行５列６ と 行７列６ も同じ領域にあるため， 行６列８ と 行５列６ で 行７列８ と 行７列６ のうち数字１が配置されたマスと同じ領域にあるマスには 数字１ が配置されません。 すると，行６列８ と 行５列６ は どちらにも 数字１が配置されるか，どちらにも数字１が配置されない かのどちらかなので， そのどちらにも 数字１ は配置されなくなります。 この２つのマスと同じ 薄緑色に塗られたマスにも 数字１ は配置できません。
注）排除が成り立つ条件は”一つの系列で同じ色に塗られた２つのマスのうち， １つのマスが ・・・， もう１つのマスが ・・・”となっていますが， ”最初の系列の１マス” が もう一つの系列の異なる色で塗られた２マス と同じ領域に属していれば 排除は成立します。
（Multi Colors:type 2 の X-Chain としての解釈については ここ をクリックしてください）
◎ Multi Colors（補足）：マスをつなげた系列を３本以上扱う場合
マスをつなげた系列を３本以上扱う場合も利用する原理は系列を２本まで扱う場合と同じです。
・ １つの系列では，検討している数字は，使用されている２色のうち， 片方の色に塗られたすべてのマスに配置され，もう片方の色に塗られたすべてのマスに配置されません。
・ ２つの系列で ２つの色に塗られたマスの 両方ともには検討している数字が配置できない場合， 各々の系列で，その色の反対の色で塗られたマスのどちらかに 検討している数字が必ず配置されます。
１系列・２系列を扱った場合の最初のタイプ（Color Trap, Color Wing）に対応した ３系列を扱う場合の模式図を示します。
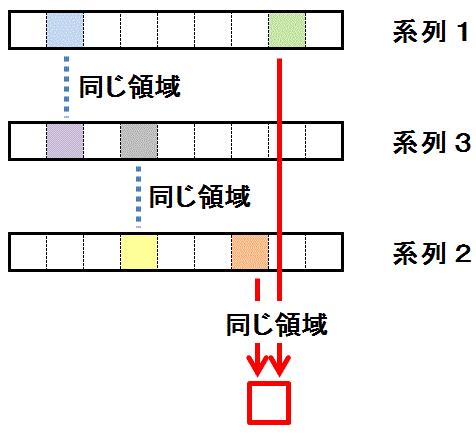２つの系列（系列１・系列２）のマス（水色・クリーム色）が，第３の系列の異なる色（紫色・灰色）に塗られたマスと同じ領域に存在すると，
第１・第２の系列で第３の系列のマスと同じ領域にあるマスと異なる色（薄緑色・だいだい色）に塗られたマスの両方と同じ領域にあるマスには検討している数字を配置できません。説明）第３の系列の異なる色（紫色・灰色）に塗られたマスには，”どちらかの色のマスに検討している数字が必ず配置されます”。 すると，それらの色のマスと同じ領域にある第１・第２の系列のマス（水色・クリーム色）の ”両方共のマスに検討している数字が配置されること” はなくなります。 これは，第１・第２の系列での 水色・クリーム色 と異なる色（薄緑色・だいだい色）の ”両方の色のマスに検討している数字が配置されないこと” はない， つまり ”どちらかの色のマスに検討している数字が必ず配置される” ことを意味します。
第１・第２の系列で 薄緑色・だいだい色 に塗られたマスの両方と同じ領域にあるマス（赤）には検討している数字を配置できません。
３系列を使用した Multi colors の最初のタイプの例題を下に示します。
数字１が配置可能なマスが２つに限られる領域（・そのつながり）を見つけて，数字１が配置可能なマスを着色します。
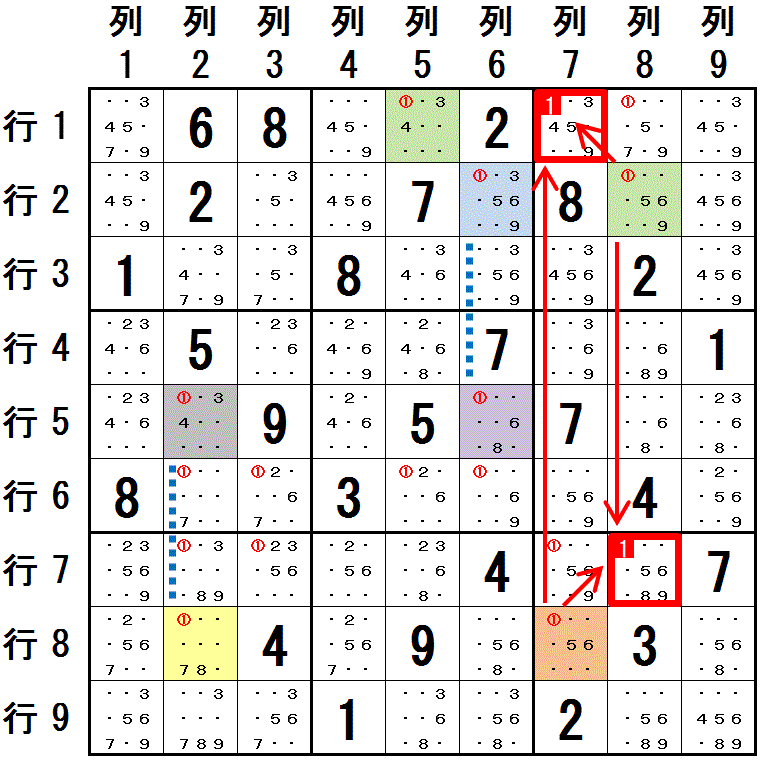第１の系列：行２列８－行２列６－行１列５
第２の系列：
行８列７－行８列２
第３の系列：
行５列６－行５列２
第３の系列の 行５列６ は 第１の系列の 行２列６ と同じ領域にあり， 第３の系列で 行５列６ と異なる色で塗られた 行５列２ は 第２の系列の 行８列２ と同じ領域にあります。
第１，第２ の系列で 行２列６，行８列２ と反対の色に塗られた 行２列８，行８列７ の両方と同じ領域にある 行１列７，行７列８ に 数字１ は配置できません。
系列を４本扱う場合は，系列を３本扱ったときの模式図で，系列３と系列２を切り離して，その間に第４の系列を入れます。
系列１のマス（水色）と同じ領域に系列３のマス（紫色）があり， 系列３で紫色と反対の色（灰色）のマスと同じ領域に系列４のマスがあり， 系列４でそのマスと反対の色のマスと同じ領域に系列２のマス（クリーム色）があれば， 検討している数字は，系列１で水色と反対の色（薄緑色）に塗られたマス と 系列２でクリーム色と反対の色（だいだい色）に塗られたマス の 両方と同じ領域にあるマス には配置できません。
次に １系列・２系列を扱った場合の２番目のタイプ（Color Wrap, Multi Colors type2）に対応した ３系列を扱う場合の模式図を示します。
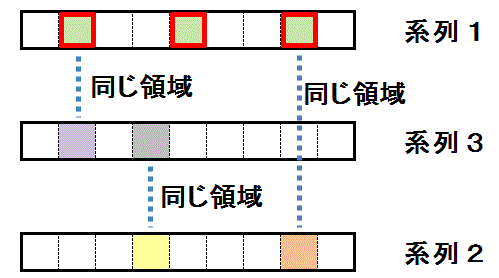１つの系列（系列１）の同じ色（薄緑色）に塗られたマスが，第２・第３の系列（系列２・系列３）のマス（だいだい色・紫色）と同じ領域にあるとき，
第２・第３の系列で，それらの第１の系列のマスと同じ領域にあるマスの色（だいだい色・紫色）と反対の色（クリーム色・灰色）のマス同士が同じ領域にあると，
第１の系列では，第２・第３のマスと同じ領域にあるマスの色（薄緑色）に塗られたすべてのマスに 検討している数字を配置できません。説明）系列２のクリーム色のマス と 系列３の灰色のマス は同じ領域にあるため，”両方共のマスに検討している数字が配置されること” はありません。 これは，それぞれの系列で クリーム色・灰色 の反対の色 だいだい色・紫色 の ”両方の色のマスに検討している数字が配置されないこと” がないこと， つまり ”どちらかの色のマスに検討している数字が必ず配置されること” を意味します。 そのどちらか検討している数字が配置されたマスと同じ領域にある系列１の薄緑色のマスには検討している数字が配置されなくなります。 第１の系列では，検討している数字が すべての薄緑色のマスに配置されるか，すべての薄緑色のマスに配置されないかのどちらかなので，すべての薄緑色のマスに検討している数字が配置されないことがわかります。
３系列を使用した Multi colors の２番目のタイプの例題を下に示します。
数字１が配置可能なマスが２つに限られる領域（・そのつながり）を見つけて，数字１が配置可能なマスを着色します。
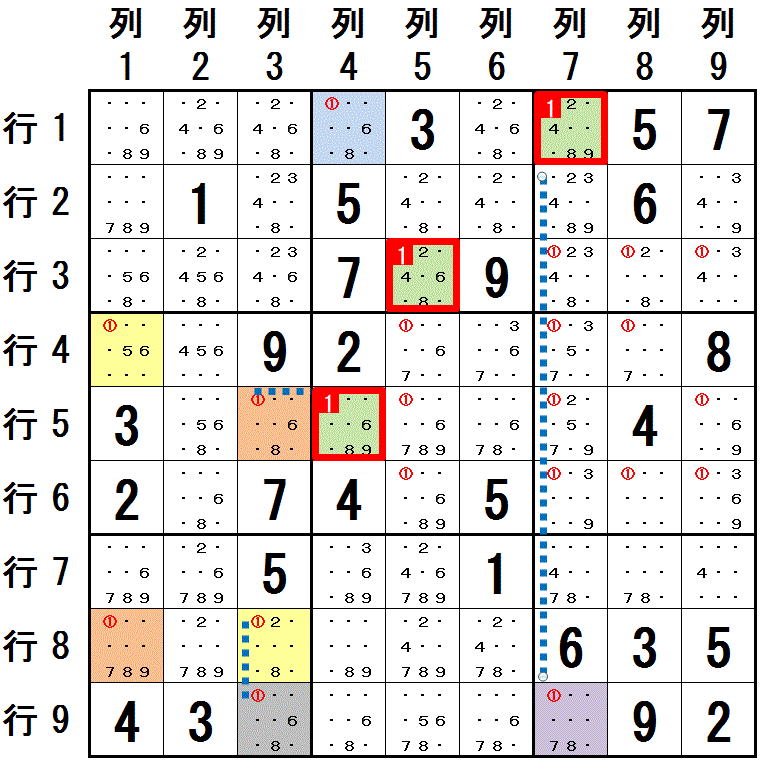第１の系列：行１列４－行１列７
行１列４－行３列５
行１列４－行５列４
第２の系列：
行５列３－行４列１－行８列１－行８列３
第３の系列：
行９列７－行９列３
第１の系列で薄緑色の塗られた 行５列４ は 第２の系列の だいだい色で塗られた 行５列３ と同じ領域にあり， 第１の系列で同じ薄緑色の塗られた 行１列７ は 第３の系列の 紫色で塗られた 行９列７ と同じ領域にあります。
行５列３，行９列７ とその系列で反対の色に塗られた 行８列３ と 行９列３ が同じ領域にあるため， 第１の系列で薄緑色で塗られた 行１列７，行３列５，行５列４ に 数字１ は配置できません。
系列を４本扱う場合は，系列を３本扱ったときの模式図で，系列３と系列２の間に第４の系列を入れます。
系列１で同じ色（薄緑色）に塗られたマスと同じ領域に系列２のマス（だいだい色），系列３のマス（紫色）があり， 系列３で紫色と反対の色（灰色）のマスと同じ領域に系列４のマスがあり， 系列４でそのマスと反対の色のマスと同じ領域に系列２でだいだい色と反対の色（クリーム色）のマスがあれば， 検討している数字は，系列１で 薄緑色に塗られたすべてのマス に配置できません。
Ⅱ 色分け法の Ｘ－Ｃｈａｉｎ としての解釈
色分け法は X-Chain の特殊形です。
色分け法を X-Chain として解釈することは，X-Chain を理解するためにも，また 論理的思考能力を向上させるためにも有効です。
Ⅰ．で説明した色分け法（Coloring）で 扱う系列が２本までの４つの例 （Simple Colors:Color Trap, Color Wrap, Multi Colors:Type1(Color Wing), Type 2）を X-Chain として解釈します。
Color Trap の X-Chain としての解釈
Color Wrap の X-Chain としての解釈
Color Wing の X-Chain としての解釈
Multi Colors:Type2 の X-Chain としての解釈
X-Chain は，
ある一つの数字に関して，その数字をマスに配置すること２つを
・ 強いリンク：同じ領域にある２つのマスに配置する。その領域でその数字が配置可能なマスはその２マスに限られる
（両方の配置が同時に成り立つことはない。どちらかの（マスへの）配置が必ず成り立つ）
・ 弱いリンク：同じ領域にある２つのマスに配置する
（両方の配置が同時に成り立つことはない。どちらの配置も成り立たない可能性もある）
で交互につなげたチェーン（Alternate Inference Chain:AIC）で構成され，
チェーン（鎖）の両端は 強いリンク になります。
関係するマスの数は 偶数個，リンクの数は 奇数個 になります。
X-Chainでは，鎖の両端で，鎖をつなげていくのに利用されなかった 数字の配置は どちらかが必ず成り立ちます。
（両端のマスの 両方と同じ領域にあるマス には その数字 を配置できません）
色分け法を X-Chain として解釈するするときには，強いリンク が 弱いリンク として解釈できることを利用します。
（以下の説明で 強いリンク を 弱いリンク として利用する場合は，リンクを青色の実線 ------→ で表示します）
色分け法で，１つの系列で異なる色に塗られたマス同士は，その２つのマスの間につながりが奇数個あり，関連するマスの数が偶数個であるため，強いリンクと弱いリンクが交互で，両端が強いリンクの鎖（X-Chain）としてつなげることができます。
２－１） Simple Colors の Ｘ－Ｃｈａｉｎ としての解釈
Simple Colors は，”配置可能なマスが２つに限られる領域”で配置可能なマスを色分けしてつなげていきます。 １つの領域だけを考えると，両端のマスは異なる色で塗られます（関連するマスは２個）。 ２つの領域がつながると，両端のマスは同じ色になります（関連するマスは３個）。
これを続ければ，”配置可能なマスが２つに限られる領域”を （枝分かれなく数えて）奇数個 つなげる（関連するマスは偶数個）と両端のマスは 異なる色 に塗られ， 偶数個 つなげる（関連するマスは奇数個）と両端のマスは 同じ色 に塗られることになります。
異なる色で塗られた２つのマス の間には ”配置可能なマスが２つに限られる領域” という条件（強いリンク）が，奇数個 あることになります。 強いリンクは弱いリンクでもあるため，この 奇数個のつながり は，偶数番目の強いリンクを弱いリンクと考えれば， 強いリンク と 弱いリンク が交互で，両端のつながりが 強いリンク であるつながりと解釈することができます。 このつながりは 偶数個のマス で形成されていて X-Chain と解釈できます。
（この解釈は Multi Colors を X-Chain として解釈するときにも使います）
① Color Trap：異なる色で塗られた２つのマスの両方と同じ領域にあるマスには，その数字を配置できません
Color Trap は，上記の 色分け法の X-Chain としての解釈そのものです。 最初のマスから二番目のマスには 強いリンク でつながる とそのまま解釈します。 二番目のマスから三番目のマスへも 強いリンク でつながっていますが，これを 弱いリンク と解釈します。 以降同様に，奇数番目のマスへの （偶数番目の）強いリンク を 弱いリンク と解釈します。
すると，異なる色 で塗られた２つのマス（両者の間には奇数個のつながりがあり，関連するマスは偶数個です） は，
強いリンク と 弱いリンク が交互で，
両端を 強いリンク で
つなぐことができます。
これは X-Chain であり，両端のマスの両方と同じ領域にあるマスには その数字 を配置できないことがわかります。
前章（Ⅰ）で提示した Color Trap の例題図 に 強いリンク と 弱いリンク を記入します（下図）。
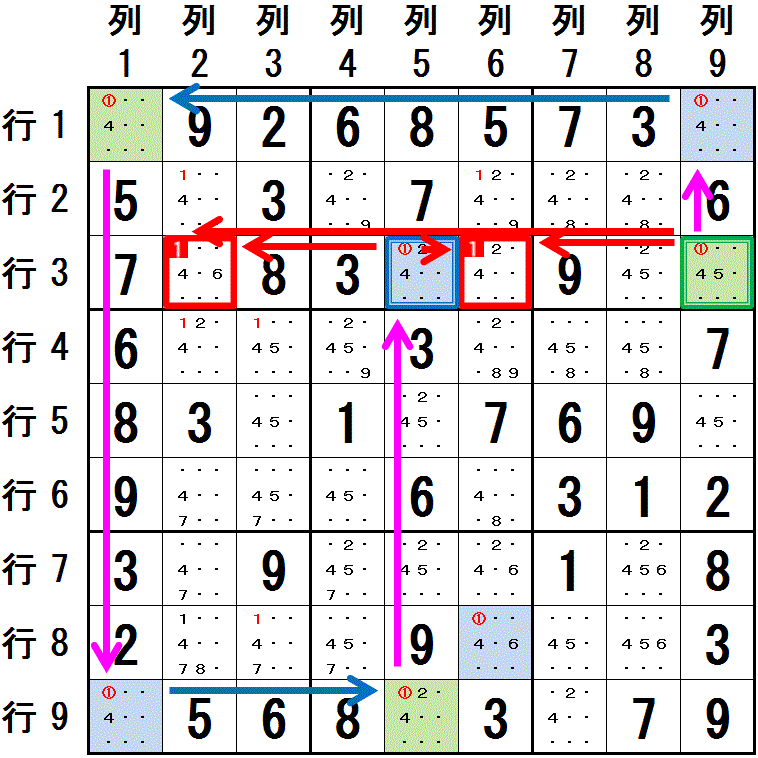
数字１ の配置に関してのリンクを考えます。
マス 行３列９ を始点にして，”配置可能なマスが２つに限られる領域”という条件（強いリンク）でマスをつなげていきます。 強いリンクを，奇数番目の 強いリンク はそのまま 強いリンク（⇒），偶数番目の 強いリンク を 弱いリンク（→） と解釈します。
行３列９⇒行１列９：列９
行１列９→行１列１：行１
行１列１⇒行９列１：列１
行９列１→行９列５：行９
行９列５⇒行３列５：列５
異なる色で塗られた，行３列９ と 行３列５ との間は， 強いリンク と 弱いリンク が交互につながり，鎖の両端は 強いリンク になっています。
これは，X-Chain であり，両端のマス（行３列９，行３列５） の両方と同じ領域にあるマス 行３列３，行３列６ に 数字１ が配置できないことがわかります。
② Color Wrap：同じ色に塗られた２つのマスが同じ領域にあると，その色で塗られたすべてのマスにその数字は配置できません
Color Wrap を X-Chain として解釈するときには，同じ領域にあり同じ色で塗られた２つのマス とともに， その２マスのうちの１マス とは その２マスをつなげる系列の中で”配置可能なマスが２つに限られる領域”という条件によって塗り分けられた 一つ手前のマス にも注目します。
その一つ手前のマス と 前述の同じ領域にあり同じ色で塗られた２つのマスのうちの選択されなかった１マス とは異なる色で塗られているので， この２つのマスの間には ”配置可能なマスが２つに限られる領域” というつながり（強いリンク）が 奇数個 あることになります。 奇数個の強いリンクでつながっているので，偶数番目の強いリンクを弱いリンクと見なせば，この２つのマスは 強いリンク と 弱いリンク で交互に，両端のつながりを 強いリンク としてつなげることができることがわかります， このつながりは X-Chain です。
最初に，同じ領域にあり同じ色で塗られた２つのマスのうちの１マス として選択されたマスは，このチェーンの両端である異なる色で塗られた２マスの両方と同じ領域にあるので，検討している数字を配置できません。 そして，そのマスが塗られている色と同じ色で塗られているマス すべて に その数字を配置できないことがわかります。
前章（Ⅰ）で提示した Color Wrap の例題図 に 強いリンク と 弱いリンク を記入します（下図）。
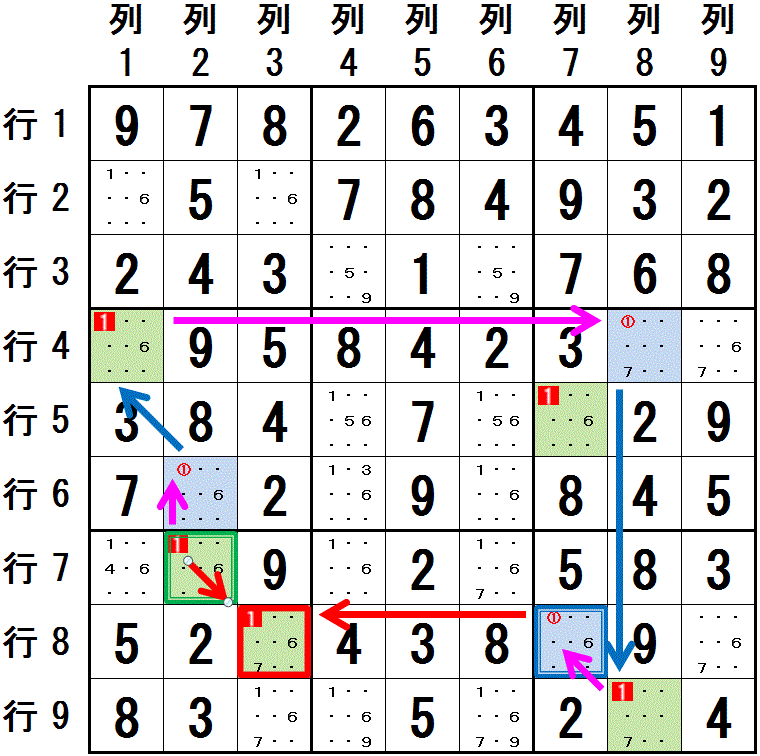
数字１ の配置に関してのリンクを考えます。
行７列２ と 行８列３ は同じ 大マス７ にあり，同じ色 薄緑色 に塗られています。
数字１は 行８ では，この２マスのうちの１マスである 行８列３ ともう一つのマス 行８列７ の２マスにのみ配置可能です。行８列７ は 水色に塗られています。 異なる色に塗られた 行７列２ と 行８列７ の間は，奇数個 の 強いリンク でつながっています。 このつながりを，行７列２ を始点に，奇数番目の強いリンクをそのまま 強いリンク（⇒），偶数番目の強いリンクを 弱いリンク（→） として，強いリンク と 弱いリンク が交互になるようにつないでいきます。 最後の 行８列７ へのリンクは 強いリンクになります。
行７列２⇒行６列２：列２
行６列２→行４列１：大マス４
行４列１⇒行４列８：行４
行４列８→行９列８：列８
行９列８⇒行８列７：大マス９
異なる色で塗られた，行７列２ と 行８列７ とが，X-Chain としてつながりました。 このつながりの両端のマス（行７列２，行８列７） の両方と同じ領域にあるマス 行８列３ に 数字１ が配置できないことがわかります。
行８列３ と同じ 薄緑色に塗られたすべてのマスにも 数字１ は配置できません。
（水色に塗られたすべてのマスに 数字１ が配置されることも確定します）
Simple Colors は，”配置可能なマスが２つに限られる領域”で配置可能なマスを色分けしてつなげていきます。 １つの領域だけを考えると，両端のマスは異なる色で塗られます（関連するマスは２個）。 ２つの領域がつながると，両端のマスは同じ色になります（関連するマスは３個）。
これを続ければ，”配置可能なマスが２つに限られる領域”を （枝分かれなく数えて）奇数個 つなげる（関連するマスは偶数個）と両端のマスは 異なる色 に塗られ， 偶数個 つなげる（関連するマスは奇数個）と両端のマスは 同じ色 に塗られることになります。
異なる色で塗られた２つのマス の間には ”配置可能なマスが２つに限られる領域” という条件（強いリンク）が，奇数個 あることになります。 強いリンクは弱いリンクでもあるため，この 奇数個のつながり は，偶数番目の強いリンクを弱いリンクと考えれば， 強いリンク と 弱いリンク が交互で，両端のつながりが 強いリンク であるつながりと解釈することができます。 このつながりは 偶数個のマス で形成されていて X-Chain と解釈できます。
（この解釈は Multi Colors を X-Chain として解釈するときにも使います）
① Color Trap：異なる色で塗られた２つのマスの両方と同じ領域にあるマスには，その数字を配置できません
Color Trap は，上記の 色分け法の X-Chain としての解釈そのものです。 最初のマスから二番目のマスには 強いリンク でつながる とそのまま解釈します。 二番目のマスから三番目のマスへも 強いリンク でつながっていますが，これを 弱いリンク と解釈します。 以降同様に，奇数番目のマスへの （偶数番目の）強いリンク を 弱いリンク と解釈します。
すると，異なる色 で塗られた２つのマス（両者の間には奇数個のつながりがあり，関連するマスは偶数個です） は，
強いリンク と 弱いリンク が交互で，
両端を 強いリンク で
つなぐことができます。
これは X-Chain であり，両端のマスの両方と同じ領域にあるマスには その数字 を配置できないことがわかります。
前章（Ⅰ）で提示した Color Trap の例題図 に 強いリンク と 弱いリンク を記入します（下図）。
数字１ の配置に関してのリンクを考えます。
マス 行３列９ を始点にして，”配置可能なマスが２つに限られる領域”という条件（強いリンク）でマスをつなげていきます。 強いリンクを，奇数番目の 強いリンク はそのまま 強いリンク（⇒），偶数番目の 強いリンク を 弱いリンク（→） と解釈します。
行３列９⇒行１列９：列９
行１列９→行１列１：行１
行１列１⇒行９列１：列１
行９列１→行９列５：行９
行９列５⇒行３列５：列５
異なる色で塗られた，行３列９ と 行３列５ との間は， 強いリンク と 弱いリンク が交互につながり，鎖の両端は 強いリンク になっています。
これは，X-Chain であり，両端のマス（行３列９，行３列５） の両方と同じ領域にあるマス 行３列３，行３列６ に 数字１ が配置できないことがわかります。
② Color Wrap：同じ色に塗られた２つのマスが同じ領域にあると，その色で塗られたすべてのマスにその数字は配置できません
Color Wrap を X-Chain として解釈するときには，同じ領域にあり同じ色で塗られた２つのマス とともに， その２マスのうちの１マス とは その２マスをつなげる系列の中で”配置可能なマスが２つに限られる領域”という条件によって塗り分けられた 一つ手前のマス にも注目します。
その一つ手前のマス と 前述の同じ領域にあり同じ色で塗られた２つのマスのうちの選択されなかった１マス とは異なる色で塗られているので， この２つのマスの間には ”配置可能なマスが２つに限られる領域” というつながり（強いリンク）が 奇数個 あることになります。 奇数個の強いリンクでつながっているので，偶数番目の強いリンクを弱いリンクと見なせば，この２つのマスは 強いリンク と 弱いリンク で交互に，両端のつながりを 強いリンク としてつなげることができることがわかります， このつながりは X-Chain です。
最初に，同じ領域にあり同じ色で塗られた２つのマスのうちの１マス として選択されたマスは，このチェーンの両端である異なる色で塗られた２マスの両方と同じ領域にあるので，検討している数字を配置できません。 そして，そのマスが塗られている色と同じ色で塗られているマス すべて に その数字を配置できないことがわかります。
前章（Ⅰ）で提示した Color Wrap の例題図 に 強いリンク と 弱いリンク を記入します（下図）。
数字１ の配置に関してのリンクを考えます。
行７列２ と 行８列３ は同じ 大マス７ にあり，同じ色 薄緑色 に塗られています。
数字１は 行８ では，この２マスのうちの１マスである 行８列３ ともう一つのマス 行８列７ の２マスにのみ配置可能です。行８列７ は 水色に塗られています。 異なる色に塗られた 行７列２ と 行８列７ の間は，奇数個 の 強いリンク でつながっています。 このつながりを，行７列２ を始点に，奇数番目の強いリンクをそのまま 強いリンク（⇒），偶数番目の強いリンクを 弱いリンク（→） として，強いリンク と 弱いリンク が交互になるようにつないでいきます。 最後の 行８列７ へのリンクは 強いリンクになります。
行７列２⇒行６列２：列２
行６列２→行４列１：大マス４
行４列１⇒行４列８：行４
行４列８→行９列８：列８
行９列８⇒行８列７：大マス９
異なる色で塗られた，行７列２ と 行８列７ とが，X-Chain としてつながりました。 このつながりの両端のマス（行７列２，行８列７） の両方と同じ領域にあるマス 行８列３ に 数字１ が配置できないことがわかります。
行８列３ と同じ 薄緑色に塗られたすべてのマスにも 数字１ は配置できません。
（水色に塗られたすべてのマスに 数字１ が配置されることも確定します）
２－２） Multi Colors の Ｘ－Ｃｈａｉｎ としての解釈
Multi Colors は，色分けされた系列を複数利用しますが，ここでは２本の系列を利用する例に限定して説明します。 ２本の系列を結びつけるのに，”同じ領域にある”という条件を利用します。これが 弱いリンク になります。
① Multi Colors type１（Color Wing）：２本のそれぞれの系列に属する１つずつのマス２つが同じ領域にあるとき， その領域でそれぞれの系列のマスを着色するのに使われた色と異なる色で塗られた２つのマスの両方と同じ領域にあるマスには，その数字を配置できません
同じ領域にある２つの系列の２つのマスは 弱いリンク でつながっています。 その同じ領域にある２つのマスから，それぞれの系列でそれらのマスと異なる色に塗られたマスまでには 奇数個 のつながり（強いリンク）があります。 奇数個の強いリンクは，偶数番目の強いリンクを弱いリンクと見なして 強いリンク と 弱いリンク が交互で，最初と最後が 強いリンク とすることができます。 このように見なしたそれぞれの２系列を 同じ領域に配置される２系列のマス同士の 弱いリンク でつなげれば， 全体として，同じ領域にあるマスとそれぞれの系統で異なる色で塗られたマス同士が 強いリンク と 弱いリンク が交互につながり，両端が 強いリンク としてつながります。 これは X-Chain であり，その両端のマスの両方と同じ領域にあるマスには その数字が配置できないことがわかります。
前章（Ⅰ）で提示した Multi Colors type１（Color Wing） の例題図 に 強いリンク と 弱いリンク を記入します（下図）。
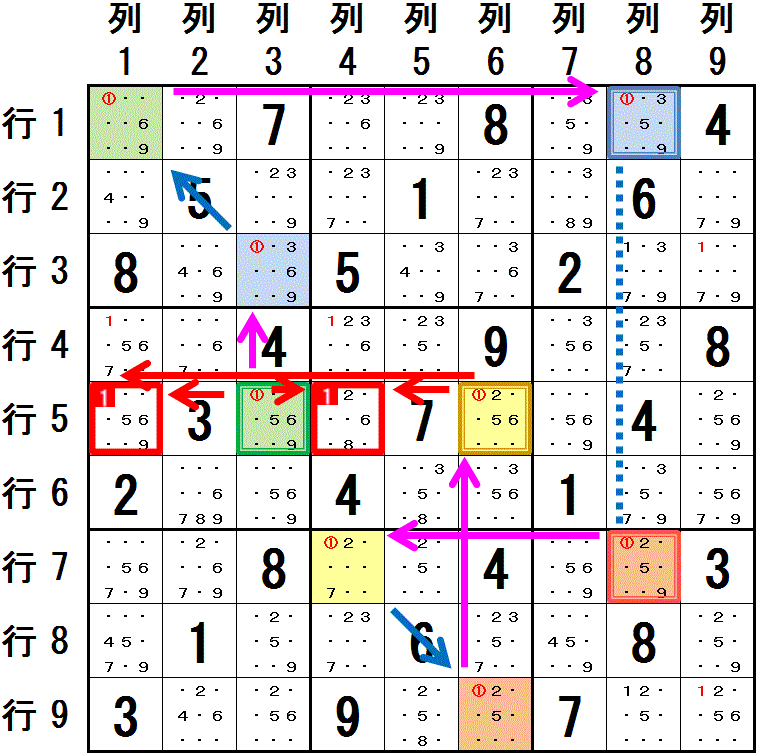
数字１ の配置に関してのリンクを考えます。
水色に塗られた 行１列８ と だいだい色に塗られた 行７列８ は 同じ列８ にあり，両者の間には 弱いリンク があります。
行１列８－行７列８：列８
薄緑色に塗られた 行５列３ から 水色に塗られた 行１列８ までを以下のようにつなげることができます。
行５列３⇒行３列３：列３
行３列３→行１列１：大マス１
行１列１⇒行１列８：行１
一方，だいだい色に塗られた 行７列８ から クリーム色に塗られた 行５列６ までを以下のようにつなげることができます。
行７列８⇒行７列４：行７
行７列４→行９列６：大マス８
行９列６⇒行５列６：列６
この３つをつなげれば，行５列３ から 行５列６ までを
最初と最後を 強いリンク とし，強いリンク と 弱いリンク で交互につなげることができます。
これは X-Chain であり，行５列３ と 行５列６ の両方と同じ領域にある 行５列１，行５列４ に 数字１ を配置できないことがわかります。
② Multi Colors type２：一つの系列で同じ色に塗られた２つのマスのうち， １つのマスが もう一つの系列のある色で塗られたマスと同じ領域に属し， もう１つのマスが もう一つの系列の前記とは異なる色で塗られたマスと同じ領域に属しているとき， 最初の系列でその同じ色で塗られたすべてのマスにその数字は配置できません
あとの系列の異なる色に塗られたマスと同じ領域にある，最初の系列の同じ色に塗られた２つのマスのうちの１つを選びます。 そのマスとは”配置可能なマスが２つに限られる領域”という条件によって塗り分けられた （もう一つの同じ色に塗られたマスへの経路の）一つ手前のマス に注目します（このマスを始点としてリンクを検討します）。
このマスは 最初の２つのマスとは 別の色に塗られています。 このマス（始点） と 最初の系列の２マスのうち選択されなかったマス とは 奇数個 の”配置可能なマスが２つに限られる領域”という 強いリンク でつながります。 奇数個の強いリンクは，偶数番目の強いリンクを弱いリンクと見なして 強いリンク と 弱いリンク を交互につなげ，最初と最後を 強いリンク とすることができます。
このつながりの最後のマス（最初の系列の２マスのうち選択されなかったマス）は，あとの系列で 最初に選択されたマスと同じ領域にあるマス とは異なる色に塗られたマス と同じ領域にあります（弱いリンクがあります）。
あとの系列では，このマス と 最初の系列で選択されたマスと同じ領域にあるマスとは 異なる色に塗られています。 あとの系列でのこの２つのマスは 奇数個 の”配置可能なマスが２つに限られる領域”という 強いリンク でつながります。 最初の系列の場合と同様に，奇数個の強いリンクは，偶数番目の強いリンクを弱いリンクと見なして 強いリンク と 弱いリンク を交互につなげ，最初と最後を 強いリンク とすることができます。
これらの３つのつながりをつなぎ合わせれば，最初の系列で始点としたマス と あとの系列の最後のマス（最初の系列で選択されたマスと同じ領域にあるマス）との間に X-Chain を形成することができます。 最初の系列で同じ色に塗られた２マスのうちの最初に選択されたマスは，この X-Chain の 最初と最後のマスの両方のマスと同じ領域にあります。 よって，このマスに，検討している数字が配置できないことがわかります。 そして，その系列では，その色に塗られたすべてのマスに，検討している数字が配置できないことがわかります。
前章（Ⅰ）で提示した Multi Colors type２ の例題図 に 強いリンク と 弱いリンク を記入します（下図）。
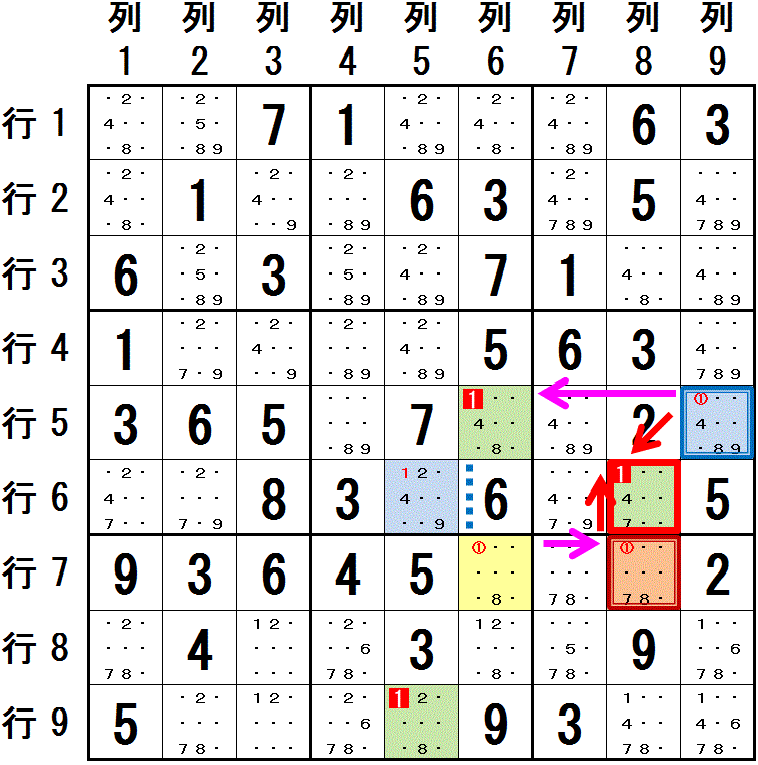
数字１ の配置に関してのリンクを考えます。
同じ薄緑色に塗られた 行５列６ と 行６列８ それぞれは， もう一つの系列で異なる２色，クリーム色に塗られた 行７列６，および，だいだい色に塗られた 行７列８ と同じ領域（列６，列８） にあります。
数字１は，大マス６ では 行６列８ と 行５列９ の２マスにのみ配置可能です。行５列９ は 水色に塗られています。 行５列９ は 行６列８ の一つ手前のマスであり，このマスを始点として検討します。
行５列９ と 行５列６ とは異なる色で塗られているため，この２つのマスの間は 奇数個 の”配置可能なマスが２つに限られる領域”という条件 でつながります。 この例では １つ のつながりとなっています。 強いリンク としてつなげます （３つ以上のつながりの場合は，強いリンク と 弱いリンク を交互に，最初と最後が 強いリンク になるようにつなげます） 。
行５列９⇒行５列６：行６
行５列６ と 行７列６ とは 同じ 列６ にあります。 この２つのマスの間には 弱いリンク が存在します。
行５列６－行７列６：列６
行７列６ と 行７列８ も異なる色で塗られていて，奇数個（１つ） の”配置可能なマスが２つに限られる領域”という条件 でつながり， 強いリンク としてつなげます。
（３つ以上のつながりの場合は，強いリンク と 弱いリンク を交互に，最初と最後が 強いリンク になるようにつなげます）
行７列６⇒行７列８：行７
この３つをつなげれば，行５列９ から 行７列８ までを
最初と最後を 強いリンク とし，強いリンク と 弱いリンク で交互につなげることができます。
これは X-Chain であり，行５列９ と 行７列８ と同じ領域にある 行６列８ に 数字１ を配置できないことがわかります。
行６列８ と同じ 薄緑色で塗られたマスすべてに 数字１ は配置できません。すべての水色に塗られたマスに 数字１ が配置されます。
このページで取り上げた例題は，各テクニックを紹介する目的で選択しています。他のテクニックで簡単に解ける問題も含まれています。
Multi Colors は，色分けされた系列を複数利用しますが，ここでは２本の系列を利用する例に限定して説明します。 ２本の系列を結びつけるのに，”同じ領域にある”という条件を利用します。これが 弱いリンク になります。
① Multi Colors type１（Color Wing）：２本のそれぞれの系列に属する１つずつのマス２つが同じ領域にあるとき， その領域でそれぞれの系列のマスを着色するのに使われた色と異なる色で塗られた２つのマスの両方と同じ領域にあるマスには，その数字を配置できません
同じ領域にある２つの系列の２つのマスは 弱いリンク でつながっています。 その同じ領域にある２つのマスから，それぞれの系列でそれらのマスと異なる色に塗られたマスまでには 奇数個 のつながり（強いリンク）があります。 奇数個の強いリンクは，偶数番目の強いリンクを弱いリンクと見なして 強いリンク と 弱いリンク が交互で，最初と最後が 強いリンク とすることができます。 このように見なしたそれぞれの２系列を 同じ領域に配置される２系列のマス同士の 弱いリンク でつなげれば， 全体として，同じ領域にあるマスとそれぞれの系統で異なる色で塗られたマス同士が 強いリンク と 弱いリンク が交互につながり，両端が 強いリンク としてつながります。 これは X-Chain であり，その両端のマスの両方と同じ領域にあるマスには その数字が配置できないことがわかります。
前章（Ⅰ）で提示した Multi Colors type１（Color Wing） の例題図 に 強いリンク と 弱いリンク を記入します（下図）。
数字１ の配置に関してのリンクを考えます。
水色に塗られた 行１列８ と だいだい色に塗られた 行７列８ は 同じ列８ にあり，両者の間には 弱いリンク があります。
行１列８－行７列８：列８
薄緑色に塗られた 行５列３ から 水色に塗られた 行１列８ までを以下のようにつなげることができます。
行５列３⇒行３列３：列３
行３列３→行１列１：大マス１
行１列１⇒行１列８：行１
一方，だいだい色に塗られた 行７列８ から クリーム色に塗られた 行５列６ までを以下のようにつなげることができます。
行７列８⇒行７列４：行７
行７列４→行９列６：大マス８
行９列６⇒行５列６：列６
この３つをつなげれば，行５列３ から 行５列６ までを
最初と最後を 強いリンク とし，強いリンク と 弱いリンク で交互につなげることができます。
これは X-Chain であり，行５列３ と 行５列６ の両方と同じ領域にある 行５列１，行５列４ に 数字１ を配置できないことがわかります。
② Multi Colors type２：一つの系列で同じ色に塗られた２つのマスのうち， １つのマスが もう一つの系列のある色で塗られたマスと同じ領域に属し， もう１つのマスが もう一つの系列の前記とは異なる色で塗られたマスと同じ領域に属しているとき， 最初の系列でその同じ色で塗られたすべてのマスにその数字は配置できません
あとの系列の異なる色に塗られたマスと同じ領域にある，最初の系列の同じ色に塗られた２つのマスのうちの１つを選びます。 そのマスとは”配置可能なマスが２つに限られる領域”という条件によって塗り分けられた （もう一つの同じ色に塗られたマスへの経路の）一つ手前のマス に注目します（このマスを始点としてリンクを検討します）。
このマスは 最初の２つのマスとは 別の色に塗られています。 このマス（始点） と 最初の系列の２マスのうち選択されなかったマス とは 奇数個 の”配置可能なマスが２つに限られる領域”という 強いリンク でつながります。 奇数個の強いリンクは，偶数番目の強いリンクを弱いリンクと見なして 強いリンク と 弱いリンク を交互につなげ，最初と最後を 強いリンク とすることができます。
このつながりの最後のマス（最初の系列の２マスのうち選択されなかったマス）は，あとの系列で 最初に選択されたマスと同じ領域にあるマス とは異なる色に塗られたマス と同じ領域にあります（弱いリンクがあります）。
あとの系列では，このマス と 最初の系列で選択されたマスと同じ領域にあるマスとは 異なる色に塗られています。 あとの系列でのこの２つのマスは 奇数個 の”配置可能なマスが２つに限られる領域”という 強いリンク でつながります。 最初の系列の場合と同様に，奇数個の強いリンクは，偶数番目の強いリンクを弱いリンクと見なして 強いリンク と 弱いリンク を交互につなげ，最初と最後を 強いリンク とすることができます。
これらの３つのつながりをつなぎ合わせれば，最初の系列で始点としたマス と あとの系列の最後のマス（最初の系列で選択されたマスと同じ領域にあるマス）との間に X-Chain を形成することができます。 最初の系列で同じ色に塗られた２マスのうちの最初に選択されたマスは，この X-Chain の 最初と最後のマスの両方のマスと同じ領域にあります。 よって，このマスに，検討している数字が配置できないことがわかります。 そして，その系列では，その色に塗られたすべてのマスに，検討している数字が配置できないことがわかります。
前章（Ⅰ）で提示した Multi Colors type２ の例題図 に 強いリンク と 弱いリンク を記入します（下図）。
数字１ の配置に関してのリンクを考えます。
同じ薄緑色に塗られた 行５列６ と 行６列８ それぞれは， もう一つの系列で異なる２色，クリーム色に塗られた 行７列６，および，だいだい色に塗られた 行７列８ と同じ領域（列６，列８） にあります。
数字１は，大マス６ では 行６列８ と 行５列９ の２マスにのみ配置可能です。行５列９ は 水色に塗られています。 行５列９ は 行６列８ の一つ手前のマスであり，このマスを始点として検討します。
行５列９ と 行５列６ とは異なる色で塗られているため，この２つのマスの間は 奇数個 の”配置可能なマスが２つに限られる領域”という条件 でつながります。 この例では １つ のつながりとなっています。 強いリンク としてつなげます （３つ以上のつながりの場合は，強いリンク と 弱いリンク を交互に，最初と最後が 強いリンク になるようにつなげます） 。
行５列９⇒行５列６：行６
行５列６ と 行７列６ とは 同じ 列６ にあります。 この２つのマスの間には 弱いリンク が存在します。
行５列６－行７列６：列６
行７列６ と 行７列８ も異なる色で塗られていて，奇数個（１つ） の”配置可能なマスが２つに限られる領域”という条件 でつながり， 強いリンク としてつなげます。
（３つ以上のつながりの場合は，強いリンク と 弱いリンク を交互に，最初と最後が 強いリンク になるようにつなげます）
行７列６⇒行７列８：行７
この３つをつなげれば，行５列９ から 行７列８ までを
最初と最後を 強いリンク とし，強いリンク と 弱いリンク で交互につなげることができます。
これは X-Chain であり，行５列９ と 行７列８ と同じ領域にある 行６列８ に 数字１ を配置できないことがわかります。
行６列８ と同じ 薄緑色で塗られたマスすべてに 数字１ は配置できません。すべての水色に塗られたマスに 数字１ が配置されます。
このページで取り上げた例題は，各テクニックを紹介する目的で選択しています。他のテクニックで簡単に解ける問題も含まれています。