�@�@�s�e�������@��{�`�t
�@�㋉�̃e�N�j�b�N�ł́@�Q�ȏ�̗̈�i�s�C��C��}�X�j�@�̒����������邱�Ƃɂ���ā@�r������鐔���������܂��B
���̃y�[�W�ł́@�e�������n�@�ƌĂ��e�N�j�b�N�̂����́@��{�ƂȂ�e�N�j�b�N�@��������܂��B
�e�������n�̊�{�̃e�N�j�b�N�ł́C�ŏ��Ɂ@����P�̐������z�u�\�ȃ}�X�����ȉ��@�ł���@���̍s�i�܂��͗�j�������܂��B ���́@���̍s�i�܂��͗�j�̒��̓��Y�̐������z�u�\�Ȃ��ׂẴ}�X���܂ށ@���̗�i�܂��͍s�j�����݂���ƁC �����̗�i�܂��͍s�j�ł́C�ŏ��Ɍ������s�i�܂��͗�j�Ɋ܂܂�Ȃ��}�X�ɂ́@���̐������z�u�ł��Ȃ����Ƃ��킩��܂��B
�ȉ��́@k ���@�Q�C�R�C�S�@�̏ꍇ�́@�e�������i��{�`�j�̔r���e�N�j�b�N�@�ł��B
�E�����������r��[X-wing]
�E�O�l�̌����������r��[Swordfish]
�E�l�l�̌����������r��[Jellyfish]
�@���̃y�[�W�ʼn������e�N�j�b�N�Ɂ@�e�������@�̃C���[�W�����͓̂�������m��܂���B �e�N�j�b�N�̓K�����������Ă���Ƃ��Ɂ@���̍��̍\���@�������Ă���̂ł��傤���H ����Ƃ��@���낱�̋K���I�Ȕz��@�������Ă���̂ł��傤���H ��قǐ�������p��𗘗p���āC base sets �ƌĂ��@���Q�@�ɑ� cover sets �ƌĂ��@�ԁ@�𓊂�������@�e�������������@���v�������ׂ�Ƃ悢�����m��܂���B
�i�����������r���@�� X-wing �ƌĂ�܂����C�v�������n�@�ł͂Ȃ��@�e�������n�@�ɕ��ނ���܂��j
�@�㋉�̃e�N�j�b�N�ł́@�Q�ȏ�̗̈�i�s�C��C��}�X�j�@�̒����������邱�Ƃɂ���ā@�r������鐔���������܂��B
���̃y�[�W�ł́@�e�������n�@�ƌĂ��e�N�j�b�N�̂����́@��{�ƂȂ�e�N�j�b�N�@��������܂��B
�e�������n�̊�{�̃e�N�j�b�N�ł́C�ŏ��Ɂ@����P�̐������z�u�\�ȃ}�X�����ȉ��@�ł���@���̍s�i�܂��͗�j�������܂��B ���́@���̍s�i�܂��͗�j�̒��̓��Y�̐������z�u�\�Ȃ��ׂẴ}�X���܂ށ@���̗�i�܂��͍s�j�����݂���ƁC �����̗�i�܂��͍s�j�ł́C�ŏ��Ɍ������s�i�܂��͗�j�Ɋ܂܂�Ȃ��}�X�ɂ́@���̐������z�u�ł��Ȃ����Ƃ��킩��܂��B
�ȉ��́@k ���@�Q�C�R�C�S�@�̏ꍇ�́@�e�������i��{�`�j�̔r���e�N�j�b�N�@�ł��B
�E�����������r��[X-wing]
�E�O�l�̌����������r��[Swordfish]
�E�l�l�̌����������r��[Jellyfish]
�@���̃y�[�W�ʼn������e�N�j�b�N�Ɂ@�e�������@�̃C���[�W�����͓̂�������m��܂���B �e�N�j�b�N�̓K�����������Ă���Ƃ��Ɂ@���̍��̍\���@�������Ă���̂ł��傤���H ����Ƃ��@���낱�̋K���I�Ȕz��@�������Ă���̂ł��傤���H ��قǐ�������p��𗘗p���āC base sets �ƌĂ��@���Q�@�ɑ� cover sets �ƌĂ��@�ԁ@�𓊂�������@�e�������������@���v�������ׂ�Ƃ悢�����m��܂���B
�i�����������r���@�� X-wing �ƌĂ�܂����C�v�������n�@�ł͂Ȃ��@�e�������n�@�ɕ��ނ���܂��j
�@
 �mX-wing�n�@�@���K����
�mX-wing�n�@�@���K����
�Q�̍s�Ł@�Q�Ɍ�����z�u�\�ȃ}�X���@������ɂ���Ƃ��Ɂ@�K���ł���e�N�j�b�N�ł��B
�h��l�̌����������r���h�@�Ƃ��Ăт܂��B
 �m�e�N�j�b�N�n
�m�e�N�j�b�N�n
�ŏ��ɁC�����̐����i�����P�j�Ł@�z�u�\�ȃ}�X���Q�Ɍ�����s�@���������݂��邩�ǂ������m�F���܂��B
���̂悤�ȍs�����݂���ꍇ�C�����̍s�̂����̂Q�̍s�i�s�R�C�s�T�j�Ł@���̐����i�����P�j���z�u�\�ȃ}�X���@�Q�̓�����i��Q�@�Ɓ@��S�j�Ɍ�������̂�������ƁC�ȉ��̐����̂悤��
���̐����i�����P�j�́C�����̗�i��Q�C��S�j�ł́@���������Q�̍s�i�s�R�C�s�T�j�ȊO�́@�}�X�@�ɂ͔z�u�ł��܂���B
�����j�@�ǂ���̗�i��Q�@�܂��́@��S�j�ł��C���������Q�̍s�i�s�R�C�s�T�j�ȊO�́@�}�X�@�Ɂ@���̐����i�����P�j���z�u�����ƁC ���������Q�̍s�i�s�R�C�s�T�j�́@���̗�̃}�X�i�s�R��Q�ƍs�T��Q�@�܂��́@�s�R��S�ƍs�T��S�j�ɂ́@���̐����i�����P�j��z�u�ł��Ȃ��Ȃ�܂��B ����ƁC���̂Q�̍s�i�s�R�C�s�T�j�́@������̗�̃}�X�i�s�R��S�ƍs�T��S�@�܂��́@�s�R��Q�ƍs�T��Q�j�̂ǂ���ɂ��@���̐����i�����P�j���z�u����邱�ƂɂȂ�i�s�R�C�s�T�Ŕz�u�\�ȃ}�X�͂Q�Ɍ����Ă��܂��j�C�������܂��B
�s�@�Ɓ@��@�����ւ��Ă��i���Ȃ킿�@�h�z�u�\�ȃ}�X���Q�Ɍ����Ă���h�@�̂��@�h��h�C�h�z�u�\�ȃ}�X���܂݁@�������r�������h�@�̂��@�h�s�h�j�����������r���@�͐������܂��B
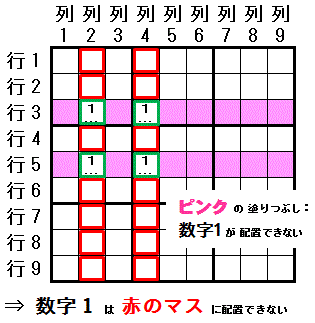
��}�ŁC �����P�@���@��Q�@����с@��S�@���ꂼ��ŁC�����s�i�s�R�@�Ɓ@�s�T�j�ɑ��݂���@�Q�̗̃}�X�i�s�R��Q���s�T��Q�@����с@�s�R��S���s�T��S�j�ȊO�́@�}�X�@�ɔz�u�ł��Ȃ��ꍇ�C �����P�@�́@�s�R�@����с@�s�T�@�ł́@�̃}�X�i�s�R��Q���s�R��S�@����с@�s�T��Q���s�T��S�j�ȊO�́@�}�X�@�ɂ͔z�u�ł��܂���B
�m���́h�����������r���h�̗R���n
�Q�́@������i�s�R�@����с@�s�T�j�Ɂ@���ꂼ��Q���́@�������i�s�R��Q�ƍs�R��S�@����с@�s�T��Q�ƍs�T��S�j���݂����Ă��܂��B ��l�́@�������i�����P�j�́C���ꂼ��́@������@�Ɉ�l���z�u����C�������@����S������@������S���@���Ď����Ă��܂��B �قȂ�@������@�ɐ݂����Ă���@�������i�s�R��Q�ƍs�T��Q�@����с@�s�R��S�C�s�T��S�j�́C���ꂼ��@�Q�{�́@�A���H�i��Q�@����с@��S�j��ɂ���܂��B �����������B�@�́C���ꂼ��قȂ�@�A���H���@�ɂ���@�������@�ɒ��݂��邱�ƂŁC�A���H�S���@���Ď����܂��B �������ȊO�́@�A���H���i�Ԃ��}�X�j�ɂ́C�������@��z�u����K�v�͂Ȃ��Ȃ�܂����B
�m�e�N�j�b�N�h�����������r���h�̔��W�n
�@�@�W����@�s�Ɨ�@�̐�[Swordfish, Jellyfish]
�@�R�ȏ�̍s�i��j�Ł@���鐔�����z�u�ł���}�X���@����̗�i�s�j�Ɍ�����ꍇ���@�r�����������܂��B
�R�̍s�i��j�C�S�̍s�i��j�ɔ��W�������@�����������r���i�e�������@��{�`�j�̃e�N�j�b�N
��O�l�̌����������r��(Swordfish)
��l�l�̌����������r��(Jellyfish)
�͂��̃y�[�W�̎����ȍ~�Ő������܂��B
�T�C�U�C�V�̍s�i�܂��́@��j�ɔ��W�����������������r���i�e�������@��{�`�j�̃e�N�j�b�N�́C���ꂼ�� Squirmbag, Whale, Leviathan �ƌĂ�܂��B ���ۂɖ��������Ƃ��ɂ́C�l�l�̌����������r��(Jellyfish)�܂ł���������Ώ\���ł��B �m�e�N�j�b�N�h�l�l�̌����������r���h�̔��W�n�Ő������܂��B
�A�@�������z�u�\�ȃ}�X���@��̍s�̑�}�X�ɗ]���ɂ���ꍇ�@�Ɓ@���̕ό`
�@�������ߑ��r���iFinned Fish�CSashimi Fish�j�ƌĂ��`�ŁC�����̔z�u���r������邱�Ƃ�����܂��B
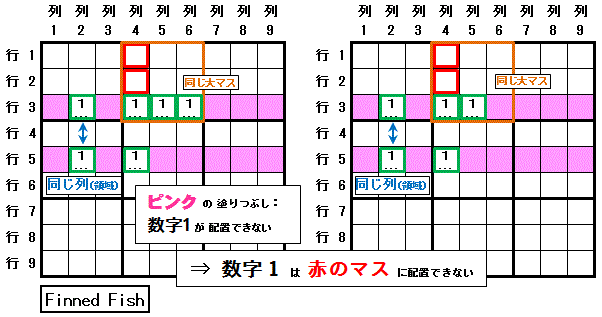
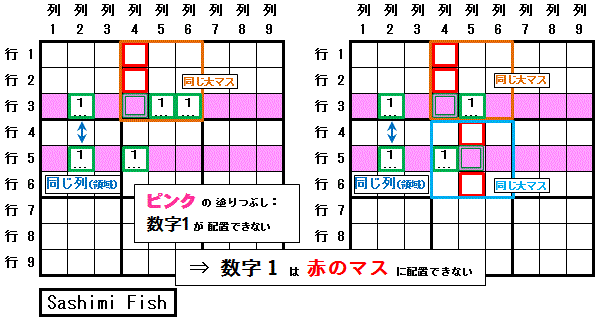

�m�e�N�j�b�N�h�����������r���h�̗�n
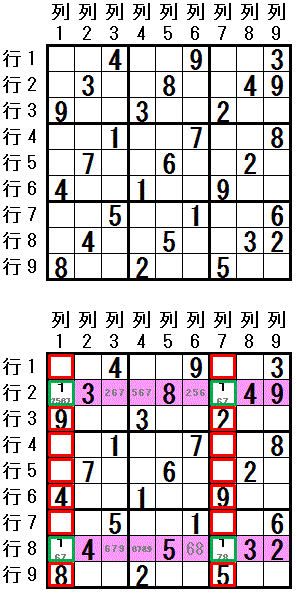
�e�N�j�b�N�h�����������r���h���K���ł�����ł��B
�ŏ��Ɂ@�����̐������@�z�u�\�ȃ}�X���Q�Ɍ�����@�s�C��@�������܂��B
�����P�ł́C�s�Q(1,7)�C�s�T(7,9)�C�s�W(1,7)�@�Ɓ@��T(1,3)
�����Q�ł́C�s�V(1,2)�@�Ɓ@��R(2,6)�C��U(2,6)
�����R�ł́C�s�V(1,5)�@�Ɓ@��V(4,5)
�����S�ł́C�s�R(5,6)�@�Ɓ@��X(5,9)
�����V�ł́C�s�U(8,9)
�����X�ł́C�s�T(3,4)�C�s�W(3,4)�@�Ɓ@��W(7,9)
���C�Y�����܂��B
�J�b�R���̐����́C�z�u�\�ȁ@��i�s�j��\���܂��B
�_�E�����[�h�����������\�t�g�ł́@�������z�u�\�ȃ}�X���Q�Ɍ�����@�s�C��@�̔z�u�\�ȃ}�X�����F���h��Ԃ����@�y���V���}�[�N�@��\���\�ł��B �����P�@�̗�́@�����@���N���b�N���Ă��������B
�����P�@�ɒ��ڂ��܂��B
�����P�@�́C�s�Q�@�Ɓ@�s�W�@�ł́C������̃}�X�@�s�Q��P�C�s�Q��V�@�Ɓ@�s�W��P�C�s�W��V�@�ȊO�ɔz�u�ł��܂���B �����������r���@���������܂��B �����P�@�́@��P�C��V�@�ł́C�Ԃ��}�X�@�ɂ͔z�u�ł��Ȃ����Ƃ��킩��܂��B
�����P�@�́@��V�@�ł́C�s�Q�@�Ɓ@�s�W�@�ɂ����z�u�ł��Ȃ��̂ŁC �s�T��V�@�ɔz�u�ł��܂���B�s�T�@�ł́@�h��l���q�h�@�ɂ��C�s�T��X�@�́@�����P�@���m�肵�܂��B
�_�E�����[�h�����������\�t�g�ł́C
����l�̌����������r���@�r�������� 1�@�s 1�@�� 1
����l�̌����������r���@�r�������� 1�@�s 1�@�� 7
����l�̌����������r���@�r�������� 1�@�s 5�@�� 7
�@�@�r��������
�@�@�@�s 2�C�s 8�@(base sets)�Ŕz�u�\�ȗ�
�@�@�@�� 1�C�� 7�@(cover sets)�Ɍ����Ă���̂�
�@�@�@cover sets �ł� base sets �Ɋ܂܂�Ȃ��}�X�ɂ͔z�u�ł��Ȃ�
�ƁC�\������܂�(�V���ɓ���ꂽ�r�����ȊO�͕\�����܂���)�B
base sets, cover sets �ɂ��ẮC�ʂɐ������܂��B
���̐}�ł́C�����Q���@��R�C��U�ibase sets�j�ŁC�s�Q�C�s�U�icover sets�j�ȊO�ɔz�u�ł��܂��� �i�����@���N���b�N����Ɓ@�����Q�@�ɂ��Ắ@�y���V���}�[�N�@��\�����܂��j�B �����������r���ɂ��@�����Q�@���@�s�U��T�@����r������āC�s�U��T�@�́@�����R�@���m�肵�܂��B
�����X�@�ł��C�����������r���ɂ��r�������}�X��������܂� �i�����@���N���b�N����Ɓ@�����X�@�ɂ��Ắ@�y���V���}�[�N�@��\�����܂��j�B

�@
�m���K���@�h�����������r���h�K���ǖʁn
���}�ɒ��ځ@�e�N�j�b�N�h�����������r���h�@���K���ł��܂��B
���}���N���b�N����ƁC����Ɛ������\������܂��B
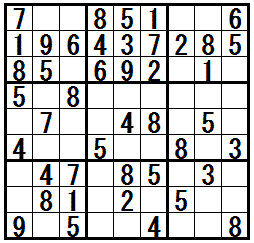
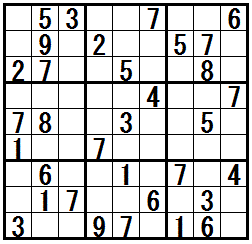
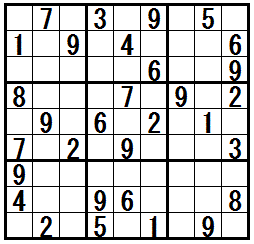
�m���K���@�h�����������r���h�n
�̓r���Ł@�e�N�j�b�N�h�����������r���h�@���K�v�ɂȂ���ł��B
�܂̖��́@�e�N�j�b�N�h�����������r���h�@���S�p���܂��B
��ԉE�̖��́@�e�N�j�b�N�h�����������r���h�@�̑��ɁC�㋉�̃e�N�j�b�N���S��C�����̃e�N�j�b�N���U�p���܂��B
���}���N���b�N����ƁC�����Ǝv�l�ߒ��̗Ⴊ�\������܂��B

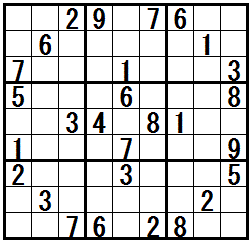
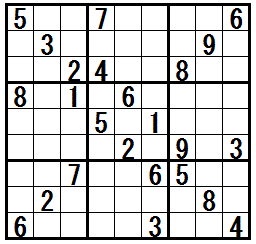

 �mX-wing�n�@�@���K����
�mX-wing�n�@�@���K����
�Q�̍s�Ł@�Q�Ɍ�����z�u�\�ȃ}�X���@������ɂ���Ƃ��Ɂ@�K���ł���e�N�j�b�N�ł��B
�h��l�̌����������r���h�@�Ƃ��Ăт܂��B
 �m�e�N�j�b�N�n
�m�e�N�j�b�N�n�ŏ��ɁC�����̐����i�����P�j�Ł@�z�u�\�ȃ}�X���Q�Ɍ�����s�@���������݂��邩�ǂ������m�F���܂��B
���̂悤�ȍs�����݂���ꍇ�C�����̍s�̂����̂Q�̍s�i�s�R�C�s�T�j�Ł@���̐����i�����P�j���z�u�\�ȃ}�X���@�Q�̓�����i��Q�@�Ɓ@��S�j�Ɍ�������̂�������ƁC�ȉ��̐����̂悤��
���̐����i�����P�j�́C�����̗�i��Q�C��S�j�ł́@���������Q�̍s�i�s�R�C�s�T�j�ȊO�́@�}�X�@�ɂ͔z�u�ł��܂���B
�����j�@�ǂ���̗�i��Q�@�܂��́@��S�j�ł��C���������Q�̍s�i�s�R�C�s�T�j�ȊO�́@�}�X�@�Ɂ@���̐����i�����P�j���z�u�����ƁC ���������Q�̍s�i�s�R�C�s�T�j�́@���̗�̃}�X�i�s�R��Q�ƍs�T��Q�@�܂��́@�s�R��S�ƍs�T��S�j�ɂ́@���̐����i�����P�j��z�u�ł��Ȃ��Ȃ�܂��B ����ƁC���̂Q�̍s�i�s�R�C�s�T�j�́@������̗�̃}�X�i�s�R��S�ƍs�T��S�@�܂��́@�s�R��Q�ƍs�T��Q�j�̂ǂ���ɂ��@���̐����i�����P�j���z�u����邱�ƂɂȂ�i�s�R�C�s�T�Ŕz�u�\�ȃ}�X�͂Q�Ɍ����Ă��܂��j�C�������܂��B
�s�@�Ɓ@��@�����ւ��Ă��i���Ȃ킿�@�h�z�u�\�ȃ}�X���Q�Ɍ����Ă���h�@�̂��@�h��h�C�h�z�u�\�ȃ}�X���܂݁@�������r�������h�@�̂��@�h�s�h�j�����������r���@�͐������܂��B
��}�ŁC �����P�@���@��Q�@����с@��S�@���ꂼ��ŁC�����s�i�s�R�@�Ɓ@�s�T�j�ɑ��݂���@�Q�̗̃}�X�i�s�R��Q���s�T��Q�@����с@�s�R��S���s�T��S�j�ȊO�́@�}�X�@�ɔz�u�ł��Ȃ��ꍇ�C �����P�@�́@�s�R�@����с@�s�T�@�ł́@�̃}�X�i�s�R��Q���s�R��S�@����с@�s�T��Q���s�T��S�j�ȊO�́@�}�X�@�ɂ͔z�u�ł��܂���B
�m���́h�����������r���h�̗R���n
�Q�́@������i�s�R�@����с@�s�T�j�Ɂ@���ꂼ��Q���́@�������i�s�R��Q�ƍs�R��S�@����с@�s�T��Q�ƍs�T��S�j���݂����Ă��܂��B ��l�́@�������i�����P�j�́C���ꂼ��́@������@�Ɉ�l���z�u����C�������@����S������@������S���@���Ď����Ă��܂��B �قȂ�@������@�ɐ݂����Ă���@�������i�s�R��Q�ƍs�T��Q�@����с@�s�R��S�C�s�T��S�j�́C���ꂼ��@�Q�{�́@�A���H�i��Q�@����с@��S�j��ɂ���܂��B �����������B�@�́C���ꂼ��قȂ�@�A���H���@�ɂ���@�������@�ɒ��݂��邱�ƂŁC�A���H�S���@���Ď����܂��B �������ȊO�́@�A���H���i�Ԃ��}�X�j�ɂ́C�������@��z�u����K�v�͂Ȃ��Ȃ�܂����B
�m�e�N�j�b�N�h�����������r���h�̔��W�n
�@�@�W����@�s�Ɨ�@�̐�[Swordfish, Jellyfish]
�@�R�ȏ�̍s�i��j�Ł@���鐔�����z�u�ł���}�X���@����̗�i�s�j�Ɍ�����ꍇ���@�r�����������܂��B
�R�̍s�i��j�C�S�̍s�i��j�ɔ��W�������@�����������r���i�e�������@��{�`�j�̃e�N�j�b�N
��O�l�̌����������r��(Swordfish)
��l�l�̌����������r��(Jellyfish)
�͂��̃y�[�W�̎����ȍ~�Ő������܂��B
�T�C�U�C�V�̍s�i�܂��́@��j�ɔ��W�����������������r���i�e�������@��{�`�j�̃e�N�j�b�N�́C���ꂼ�� Squirmbag, Whale, Leviathan �ƌĂ�܂��B ���ۂɖ��������Ƃ��ɂ́C�l�l�̌����������r��(Jellyfish)�܂ł���������Ώ\���ł��B �m�e�N�j�b�N�h�l�l�̌����������r���h�̔��W�n�Ő������܂��B
�A�@�������z�u�\�ȃ}�X���@��̍s�̑�}�X�ɗ]���ɂ���ꍇ�@�Ɓ@���̕ό`
�@�������ߑ��r���iFinned Fish�CSashimi Fish�j�ƌĂ��`�ŁC�����̔z�u���r������邱�Ƃ�����܂��B



�m�e�N�j�b�N�h�����������r���h�̗�n

�e�N�j�b�N�h�����������r���h���K���ł�����ł��B
�ŏ��Ɂ@�����̐������@�z�u�\�ȃ}�X���Q�Ɍ�����@�s�C��@�������܂��B
�����P�ł́C�s�Q(1,7)�C�s�T(7,9)�C�s�W(1,7)�@�Ɓ@��T(1,3)
�����Q�ł́C�s�V(1,2)�@�Ɓ@��R(2,6)�C��U(2,6)
�����R�ł́C�s�V(1,5)�@�Ɓ@��V(4,5)
�����S�ł́C�s�R(5,6)�@�Ɓ@��X(5,9)
�����V�ł́C�s�U(8,9)
�����X�ł́C�s�T(3,4)�C�s�W(3,4)�@�Ɓ@��W(7,9)
���C�Y�����܂��B
�J�b�R���̐����́C�z�u�\�ȁ@��i�s�j��\���܂��B
�_�E�����[�h�����������\�t�g�ł́@�������z�u�\�ȃ}�X���Q�Ɍ�����@�s�C��@�̔z�u�\�ȃ}�X�����F���h��Ԃ����@�y���V���}�[�N�@��\���\�ł��B �����P�@�̗�́@�����@���N���b�N���Ă��������B
�����P�@�ɒ��ڂ��܂��B
�����P�@�́C�s�Q�@�Ɓ@�s�W�@�ł́C������̃}�X�@�s�Q��P�C�s�Q��V�@�Ɓ@�s�W��P�C�s�W��V�@�ȊO�ɔz�u�ł��܂���B �����������r���@���������܂��B �����P�@�́@��P�C��V�@�ł́C�Ԃ��}�X�@�ɂ͔z�u�ł��Ȃ����Ƃ��킩��܂��B
�����P�@�́@��V�@�ł́C�s�Q�@�Ɓ@�s�W�@�ɂ����z�u�ł��Ȃ��̂ŁC �s�T��V�@�ɔz�u�ł��܂���B�s�T�@�ł́@�h��l���q�h�@�ɂ��C�s�T��X�@�́@�����P�@���m�肵�܂��B
�_�E�����[�h�����������\�t�g�ł́C
����l�̌����������r���@�r�������� 1�@�s 1�@�� 1
����l�̌����������r���@�r�������� 1�@�s 1�@�� 7
����l�̌����������r���@�r�������� 1�@�s 5�@�� 7
�@�@�r��������
�@�@�@�s 2�C�s 8�@(base sets)�Ŕz�u�\�ȗ�
�@�@�@�� 1�C�� 7�@(cover sets)�Ɍ����Ă���̂�
�@�@�@cover sets �ł� base sets �Ɋ܂܂�Ȃ��}�X�ɂ͔z�u�ł��Ȃ�
�ƁC�\������܂�(�V���ɓ���ꂽ�r�����ȊO�͕\�����܂���)�B
base sets, cover sets �ɂ��ẮC�ʂɐ������܂��B
���̐}�ł́C�����Q���@��R�C��U�ibase sets�j�ŁC�s�Q�C�s�U�icover sets�j�ȊO�ɔz�u�ł��܂��� �i�����@���N���b�N����Ɓ@�����Q�@�ɂ��Ắ@�y���V���}�[�N�@��\�����܂��j�B �����������r���ɂ��@�����Q�@���@�s�U��T�@����r������āC�s�U��T�@�́@�����R�@���m�肵�܂��B
�����X�@�ł��C�����������r���ɂ��r�������}�X��������܂� �i�����@���N���b�N����Ɓ@�����X�@�ɂ��Ắ@�y���V���}�[�N�@��\�����܂��j�B

�@
�m���K���@�h�����������r���h�K���ǖʁn
���}�ɒ��ځ@�e�N�j�b�N�h�����������r���h�@���K���ł��܂��B
���}���N���b�N����ƁC����Ɛ������\������܂��B



�m���K���@�h�����������r���h�n
�̓r���Ł@�e�N�j�b�N�h�����������r���h�@���K�v�ɂȂ���ł��B
�܂̖��́@�e�N�j�b�N�h�����������r���h�@���S�p���܂��B
��ԉE�̖��́@�e�N�j�b�N�h�����������r���h�@�̑��ɁC�㋉�̃e�N�j�b�N���S��C�����̃e�N�j�b�N���U�p���܂��B
���}���N���b�N����ƁC�����Ǝv�l�ߒ��̗Ⴊ�\������܂��B




�@
 �mSwordfish�n�@�@���K����
�mSwordfish�n�@�@���K����
�h�����������r���h���@�R�s�R��@�ɔ��W�������e�N�j�b�N�ł��B
 �m�e�N�j�b�N�n
�m�e�N�j�b�N�n
�����̐����i�����P�j�Ł@�z�u�\�ȃ}�X�� �Q�܂��͂R�@�Ɍ�����s�@���R�ȏ㑶�݂��邩�ǂ������m�F���܂��B
���̂悤�ȍs�����݂���ꍇ�C�����̍s�̂����̂R�̍s�i�s�R�C�s�T�C�s�X�j�Ł@���̐����i�����P�j���z�u�\�ȃ}�X���@�R�̓�����i��Q�@�Ɓ@��S�@�Ɓ@��W�j�Ɍ�������̂�������ƁC�ȉ��̐����̂悤��
���̐����i�����P�j�́C�����̗�i��Q�C��S�C��W�j�ł́@���������R�̍s�i�s�R�C�s�T�C�s�X�j�ȊO�́@�}�X�@�ɂ͔z�u�ł��܂���B
�����j�@��l�̌����������Ɠ��l�ł��B�ǂ̗�i��Q�@�܂��́@��S�@�܂��́@��W�j�ł��C���������R�̍s�i�s�R�C�s�T�C�s�X�j�ȊO�́@�}�X�@�Ɂ@���̐����i�����P�j���z�u�����ƁC ���������R�̍s�i�s�R�C�s�T�C�s�X�j�ł́@�z�u���ꂽ��̃}�X�i�s�R��Q�ƍs�T��Q�ƍs�X��Q�@�܂��́@�s�R��S�ƍs�T��S�ƍs�X��S�@�܂��́@�s�R��W�ƍs�T��W�ƍs�X��W�j�ɂ́@���̐����i�����P�j��z�u�ł��Ȃ��Ȃ�܂��B ����ƁC�����R�̍s�i�s�R�C�s�T�C�s�X�j�́@���̐����i�����P�j���z�u���ꂽ��@�ȊO�̂Q��̃}�X�̑g�ݍ��킹�i�m�s�R��Q�ƍs�T��Q�ƍs�X��Q�n�@�Ɓ@�m�s�R��S�ƍs�T��S�ƍs�X��S�n�@�Ɓ@�m�s�R��W�ƍs�T��W�ƍs�X��W�n�@�̂����̂Q�̑g�ݍ��킹�j�Ɂ@���̐����i�����P�j���R�z�u����邱�ƂɂȂ�C�������܂��B
�s�@�Ɓ@��@�����ւ��Ă��C�O�l�̌����������r���@�͐������܂��B
���Y�̐����́@�e�s�̂R�}�X���ׂā@�ɔz�u�ł���K�v�͂���܂���B
�m���́h�O�l�̌����������r���h�̗R���n
�h�����������r���h�̗R���@�Ɠ��l�ł��B ���������K�ɐݒu����Ă���C�O�l�̌����������́C�����g���đ��k���Ē��݂��������������߁C ���������邾���łȂ��C�A���H������������z�u����K�v���Ȃ����܂��B
�@
�m�e�N�j�b�N�h�O�l�̌����������r���h�̔��W�n
�ŏ��� base sets, cover sets �ɂ��Đ������܂��B
�h�����������r���sFish ��{�`�t�h�ŁC���鐔�����z�u�\�ȃ}�X�����肳���s�̏W�܂�� base sets �ƌĂт܂��B �O�l�̌����������r���́m�e�N�j�b�N�n�Ő���������ł́Cbase sets �́@�s�R�C�s�T�C�s�X�@�ƂȂ�܂��B
�����̍s�Ŕz�u�\�ȃ}�X�@���@���ׂĊ܂ޗ�@�̏W�܂�� cover sets �ƌĂт܂��B �m�e�N�j�b�N�n�Ő���������ł́C��Q�C��S�C��W�@�ƂȂ�܂��B
�����������r���sFish ��{�`�t�́C
�hbase sets �Ł@���鐔�����z�u�ł���}�X�@�̂��ׂĂ��Cbase sets �Ɠ������́@cover sets �Ɋ܂܂��ƁC cover sets �ł́Cbase sets �ȊO�̃}�X�ɂ́@���̐�����z�u�ł��Ȃ��h
�Ƃ������ƂɂȂ�܂��B
base sets, cover sets �́C�s�C���łȂ��C��}�X���܂߂��C�ӂ̗̈�̏W�܂�ł��\���܂���B
���̂悤�ȃP�[�X�� Franken Fish�CMutant Fish �ƌĂ�܂��B
�_�E�����[�h�����������\�t�g�ł� Franken Swordfish�CMutant Swordfish �Ɉꕔ�������������@�e�N�j�b�N�h���팫���O�������r���h�@���v���O�������Ă��܂��B �ʂ̃y�[�W�Ő������܂��B
base sets, cover sets �͂��ꂼ��@defining sets, secondary sets �Ƃ��Ă�܂��B

�m�e�N�j�b�N�h�O�l�̌����������r���h�̗�n
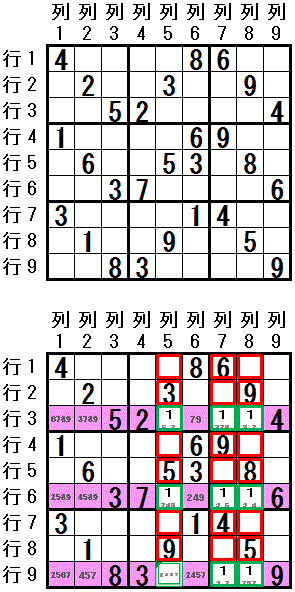 �ŏ��Ɂ@�����̐������@�z�u�\�ȃ}�X���@�R���Q�@�Ɍ�����@�s�C��@�������܂��B
�ŏ��Ɂ@�����̐������@�z�u�\�ȃ}�X���@�R���Q�@�Ɍ�����@�s�C��@�������܂��B
�����P�F�s�R�C�s�T�C�s�U�C�s�X�@�Ɓ@��R�C��S�C��T�C��X
�����Q�F�s�P�@�Ɓ@��U
�����R�F�s�P�C�s�R�C�s�S�C�s�W�@�Ɓ@��Q�C��V�C��W�C��X
�����S�F�s�Q�C�s�T�C�s�W�C�s�X�@�Ɓ@��Q�C��R�C��T�C��W
�����T�F�s�P�C�s�S�C�s�U�C�s�V�C�s�X�@�Ɓ@��P�C��S�C��U�C��V�C��X
�����U�F�s�Q�C�s�R�C�s�W�C�s�X�@�Ɓ@��R�C��S�C��T�C��W
�����W�F�s�Q�C�s�R�C�s�S�C�s�U�C�s�V�C�s�W
�@�@�@�@�@�@�@�@�Ɓ@��P�C��Q�C��S�C��T�C��V�C��X
�����X�F�s�P�C�s�R�C�s�T�C�s�U�C�s�V�@�Ɓ@��P�C��R�C��S�C��U
���C�Y�����܂��B
�_�E�����[�h�����������\�t�g�ł́@�������z�u�\�ȃ}�X���R���Q�Ɍ�����@�s�C��@�̔z�u�\�ȃ}�X�����F���h��Ԃ����@�y���V���}�[�N�@��\���\�ł� �i�������ƂɁC�ŏ��Ɂ@�z�u�\�ȃ}�X���R�Ɍ�����@�s�E��@�ɒ��ڂ��đ��́@�s�E��@��g�ݍ��킹�ā@�O�l�̌����������r�����������邩�ǂ����C���Ɂ@�Q�Ɍ�����@�s�E��@�����̑g�ݍ��킹�Ł@�O�l�̌����������r�����������邩�ǂ����@���������܂��j�B �����P�@�̗�́@�����@���N���b�N���Ă��������B
�����P�@�ɒ��ڂ��܂��B���̐}���Q�Ƃ��Ă��������B
�����P�@�́C�s�R�@�Ɓ@�s�U�@�Ɓ@�s�X�@�ł́C ��T�C�V�C�W�@�̃}�X�@�s�R��T�C�s�R��V�C�s�R��W �@�Ɓ@�s�U��T�C�s�U��V�C�s�U��W �@�Ɓ@�s�X��V�C�s�X��W �@�ȊO�ɔz�u�ł��܂���B �s�X��T�@�ɂ͔z�u�ł��܂��C�O�l�̌����������r���@���������܂��B
�����P�@�́@��T�C��V�C��W�@�ł́C�Ԃ��}�X�@�ɂ͔z�u�ł��Ȃ����Ƃ��킩��܂��B
�����P�@�́@��T�@�ł́C�s�R�@�Ɓ@�s�U�@�Ɓ@�s�X�@�ɂ����z�u�ł��Ȃ��̂ŁC �s�P��T�@�ɔz�u�ł��܂���B�e�N�j�b�N�h���R�̑叫�����h�@�ɂ��C�s�P��T�@�́@�����V�@���m�肵�܂��B
�_�E�����[�h�����������\�t�g�ł́C
���O�l�̌����������r���@�r�������� 1�@�s 1�@�� 5
���O�l�̌����������r���@�r�������� 1�@�s 2�@�� 7
���O�l�̌����������r���@�r�������� 1�@�s 5�@�� 7
���O�l�̌����������r���@�r�������� 1�@�s 1�@�� 8
�@�@�r��������
�@�@�@�s 3�C�s 6�C�s 9�@(base sets)�Ŕz�u�\�ȗ�
�@�@�@�� 5�C�� 7�C�� 8�@(cover sets)�Ɍ����Ă���̂�
�@�@�@cover sets �ł� base sets �Ɋ܂܂�Ȃ��}�X�ɂ͔z�u�ł��Ȃ�
�ƁC�\������܂�(�V���ɓ���ꂽ�r�����ȊO�͕\�����܂���)�B
���̋ǖʂɂ́@�����P�@���R�z�u����Ă��܂��i���z�u���͂U�j�B base sets ���s�ł���@�O�l�̌����������r���@���������Ă���̂ŁCbase sets ����ł���@�O�l�̌����������r���i�U�|�R���R�j�@���������Ă��܂��ibase sets:��R�C��S�C��X�j�B ���̂��Ƃ̘_���́@�����@���N���b�N���Ă��������B
���̋ǖʂł́@�����S�@�ɒ��ڂ��Ă��@�O�l�̌����������r�� �ɂ��@�����S�@���z�u�ł��Ȃ��}�X���S������܂��B �����S�@���z�u�\�ȃ}�X���R���Q�Ɍ�����@�s�C��@�̔z�u�\�ȃ}�X�����F���h��Ԃ����@�y���V���}�[�N�@���Q�l�ɍl���Ă��������B

�@
�m���K���@�h�O�l�̌����������r���h�K���ǖʁn
���}�ɒ��ڃe�N�j�b�N�h�O�l�̌����������r���h���K���ł��܂��B
�܂̖��́C�O�l�̌����������r���@��K���������Ɓ@�����̃e�N�j�b�N���Q�p���ā@���ɔz�u���鐔�������肵�܂��B
��ԉE�̖��́C�O�l�̌����������r���@���@�U�@�K���ł��܂��B
���}���N���b�N����ƁC����Ɛ������\������܂�(�����܂łɂ́@�ق��̒��㋉�e�N�j�b�N���K�v�Ȗ�������܂�)�B
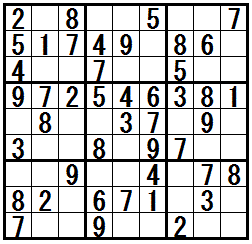
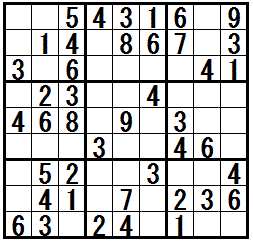
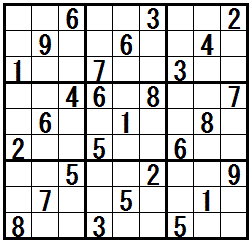
�m���K���@�h�O�l�̌����������r���h�n
�̓r���Ł@�e�N�j�b�N�h�O�l�̌����������r���h�@���K�v�ɂȂ���ł�(�����܂łɂ́@�ق��̒��㋉�e�N�j�b�N���K�v�Ȗ�������܂�)�B
��ԉE�̖��́@�e�N�j�b�N�h�O�l�̌����������r���h�̂ق��ɁC�㋉�̃e�N�j�b�N���@�R��C�����̃e�N�j�b�N���@10��@���p���܂��B
���}���N���b�N����ƁC�����Ǝv�l�ߒ��̗Ⴊ�\������܂��B
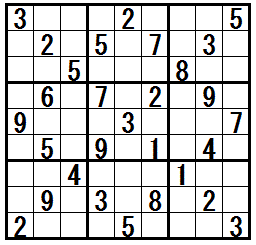
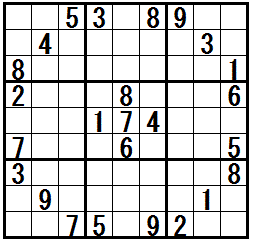
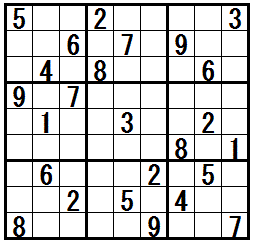

 �mSwordfish�n�@�@���K����
�mSwordfish�n�@�@���K����
�h�����������r���h���@�R�s�R��@�ɔ��W�������e�N�j�b�N�ł��B
 �m�e�N�j�b�N�n
�m�e�N�j�b�N�n�����̐����i�����P�j�Ł@�z�u�\�ȃ}�X�� �Q�܂��͂R�@�Ɍ�����s�@���R�ȏ㑶�݂��邩�ǂ������m�F���܂��B
���̂悤�ȍs�����݂���ꍇ�C�����̍s�̂����̂R�̍s�i�s�R�C�s�T�C�s�X�j�Ł@���̐����i�����P�j���z�u�\�ȃ}�X���@�R�̓�����i��Q�@�Ɓ@��S�@�Ɓ@��W�j�Ɍ�������̂�������ƁC�ȉ��̐����̂悤��
���̐����i�����P�j�́C�����̗�i��Q�C��S�C��W�j�ł́@���������R�̍s�i�s�R�C�s�T�C�s�X�j�ȊO�́@�}�X�@�ɂ͔z�u�ł��܂���B
�����j�@��l�̌����������Ɠ��l�ł��B�ǂ̗�i��Q�@�܂��́@��S�@�܂��́@��W�j�ł��C���������R�̍s�i�s�R�C�s�T�C�s�X�j�ȊO�́@�}�X�@�Ɂ@���̐����i�����P�j���z�u�����ƁC ���������R�̍s�i�s�R�C�s�T�C�s�X�j�ł́@�z�u���ꂽ��̃}�X�i�s�R��Q�ƍs�T��Q�ƍs�X��Q�@�܂��́@�s�R��S�ƍs�T��S�ƍs�X��S�@�܂��́@�s�R��W�ƍs�T��W�ƍs�X��W�j�ɂ́@���̐����i�����P�j��z�u�ł��Ȃ��Ȃ�܂��B ����ƁC�����R�̍s�i�s�R�C�s�T�C�s�X�j�́@���̐����i�����P�j���z�u���ꂽ��@�ȊO�̂Q��̃}�X�̑g�ݍ��킹�i�m�s�R��Q�ƍs�T��Q�ƍs�X��Q�n�@�Ɓ@�m�s�R��S�ƍs�T��S�ƍs�X��S�n�@�Ɓ@�m�s�R��W�ƍs�T��W�ƍs�X��W�n�@�̂����̂Q�̑g�ݍ��킹�j�Ɂ@���̐����i�����P�j���R�z�u����邱�ƂɂȂ�C�������܂��B
�s�@�Ɓ@��@�����ւ��Ă��C�O�l�̌����������r���@�͐������܂��B
���Y�̐����́@�e�s�̂R�}�X���ׂā@�ɔz�u�ł���K�v�͂���܂���B
�m���́h�O�l�̌����������r���h�̗R���n
�h�����������r���h�̗R���@�Ɠ��l�ł��B ���������K�ɐݒu����Ă���C�O�l�̌����������́C�����g���đ��k���Ē��݂��������������߁C ���������邾���łȂ��C�A���H������������z�u����K�v���Ȃ����܂��B
�@
�m�e�N�j�b�N�h�O�l�̌����������r���h�̔��W�n
�ŏ��� base sets, cover sets �ɂ��Đ������܂��B
�h�����������r���sFish ��{�`�t�h�ŁC���鐔�����z�u�\�ȃ}�X�����肳���s�̏W�܂�� base sets �ƌĂт܂��B �O�l�̌����������r���́m�e�N�j�b�N�n�Ő���������ł́Cbase sets �́@�s�R�C�s�T�C�s�X�@�ƂȂ�܂��B
�����̍s�Ŕz�u�\�ȃ}�X�@���@���ׂĊ܂ޗ�@�̏W�܂�� cover sets �ƌĂт܂��B �m�e�N�j�b�N�n�Ő���������ł́C��Q�C��S�C��W�@�ƂȂ�܂��B
�����������r���sFish ��{�`�t�́C
�hbase sets �Ł@���鐔�����z�u�ł���}�X�@�̂��ׂĂ��Cbase sets �Ɠ������́@cover sets �Ɋ܂܂��ƁC cover sets �ł́Cbase sets �ȊO�̃}�X�ɂ́@���̐�����z�u�ł��Ȃ��h
�Ƃ������ƂɂȂ�܂��B
base sets, cover sets �́C�s�C���łȂ��C��}�X���܂߂��C�ӂ̗̈�̏W�܂�ł��\���܂���B
���̂悤�ȃP�[�X�� Franken Fish�CMutant Fish �ƌĂ�܂��B
�_�E�����[�h�����������\�t�g�ł� Franken Swordfish�CMutant Swordfish �Ɉꕔ�������������@�e�N�j�b�N�h���팫���O�������r���h�@���v���O�������Ă��܂��B �ʂ̃y�[�W�Ő������܂��B
base sets, cover sets �͂��ꂼ��@defining sets, secondary sets �Ƃ��Ă�܂��B

�m�e�N�j�b�N�h�O�l�̌����������r���h�̗�n
 �ŏ��Ɂ@�����̐������@�z�u�\�ȃ}�X���@�R���Q�@�Ɍ�����@�s�C��@�������܂��B
�ŏ��Ɂ@�����̐������@�z�u�\�ȃ}�X���@�R���Q�@�Ɍ�����@�s�C��@�������܂��B�����P�F�s�R�C�s�T�C�s�U�C�s�X�@�Ɓ@��R�C��S�C��T�C��X
�����Q�F�s�P�@�Ɓ@��U
�����R�F�s�P�C�s�R�C�s�S�C�s�W�@�Ɓ@��Q�C��V�C��W�C��X
�����S�F�s�Q�C�s�T�C�s�W�C�s�X�@�Ɓ@��Q�C��R�C��T�C��W
�����T�F�s�P�C�s�S�C�s�U�C�s�V�C�s�X�@�Ɓ@��P�C��S�C��U�C��V�C��X
�����U�F�s�Q�C�s�R�C�s�W�C�s�X�@�Ɓ@��R�C��S�C��T�C��W
�����W�F�s�Q�C�s�R�C�s�S�C�s�U�C�s�V�C�s�W
�@�@�@�@�@�@�@�@�Ɓ@��P�C��Q�C��S�C��T�C��V�C��X
�����X�F�s�P�C�s�R�C�s�T�C�s�U�C�s�V�@�Ɓ@��P�C��R�C��S�C��U
���C�Y�����܂��B
�_�E�����[�h�����������\�t�g�ł́@�������z�u�\�ȃ}�X���R���Q�Ɍ�����@�s�C��@�̔z�u�\�ȃ}�X�����F���h��Ԃ����@�y���V���}�[�N�@��\���\�ł� �i�������ƂɁC�ŏ��Ɂ@�z�u�\�ȃ}�X���R�Ɍ�����@�s�E��@�ɒ��ڂ��đ��́@�s�E��@��g�ݍ��킹�ā@�O�l�̌����������r�����������邩�ǂ����C���Ɂ@�Q�Ɍ�����@�s�E��@�����̑g�ݍ��킹�Ł@�O�l�̌����������r�����������邩�ǂ����@���������܂��j�B �����P�@�̗�́@�����@���N���b�N���Ă��������B
�����P�@�ɒ��ڂ��܂��B���̐}���Q�Ƃ��Ă��������B
�����P�@�́C�s�R�@�Ɓ@�s�U�@�Ɓ@�s�X�@�ł́C ��T�C�V�C�W�@�̃}�X�@�s�R��T�C�s�R��V�C�s�R��W �@�Ɓ@�s�U��T�C�s�U��V�C�s�U��W �@�Ɓ@�s�X��V�C�s�X��W �@�ȊO�ɔz�u�ł��܂���B �s�X��T�@�ɂ͔z�u�ł��܂��C�O�l�̌����������r���@���������܂��B
�����P�@�́@��T�C��V�C��W�@�ł́C�Ԃ��}�X�@�ɂ͔z�u�ł��Ȃ����Ƃ��킩��܂��B
�����P�@�́@��T�@�ł́C�s�R�@�Ɓ@�s�U�@�Ɓ@�s�X�@�ɂ����z�u�ł��Ȃ��̂ŁC �s�P��T�@�ɔz�u�ł��܂���B�e�N�j�b�N�h���R�̑叫�����h�@�ɂ��C�s�P��T�@�́@�����V�@���m�肵�܂��B
�_�E�����[�h�����������\�t�g�ł́C
���O�l�̌����������r���@�r�������� 1�@�s 1�@�� 5
���O�l�̌����������r���@�r�������� 1�@�s 2�@�� 7
���O�l�̌����������r���@�r�������� 1�@�s 5�@�� 7
���O�l�̌����������r���@�r�������� 1�@�s 1�@�� 8
�@�@�r��������
�@�@�@�s 3�C�s 6�C�s 9�@(base sets)�Ŕz�u�\�ȗ�
�@�@�@�� 5�C�� 7�C�� 8�@(cover sets)�Ɍ����Ă���̂�
�@�@�@cover sets �ł� base sets �Ɋ܂܂�Ȃ��}�X�ɂ͔z�u�ł��Ȃ�
�ƁC�\������܂�(�V���ɓ���ꂽ�r�����ȊO�͕\�����܂���)�B
���̋ǖʂɂ́@�����P�@���R�z�u����Ă��܂��i���z�u���͂U�j�B base sets ���s�ł���@�O�l�̌����������r���@���������Ă���̂ŁCbase sets ����ł���@�O�l�̌����������r���i�U�|�R���R�j�@���������Ă��܂��ibase sets:��R�C��S�C��X�j�B ���̂��Ƃ̘_���́@�����@���N���b�N���Ă��������B
���̋ǖʂł́@�����S�@�ɒ��ڂ��Ă��@�O�l�̌����������r�� �ɂ��@�����S�@���z�u�ł��Ȃ��}�X���S������܂��B �����S�@���z�u�\�ȃ}�X���R���Q�Ɍ�����@�s�C��@�̔z�u�\�ȃ}�X�����F���h��Ԃ����@�y���V���}�[�N�@���Q�l�ɍl���Ă��������B

�@
�m���K���@�h�O�l�̌����������r���h�K���ǖʁn
���}�ɒ��ڃe�N�j�b�N�h�O�l�̌����������r���h���K���ł��܂��B
�܂̖��́C�O�l�̌����������r���@��K���������Ɓ@�����̃e�N�j�b�N���Q�p���ā@���ɔz�u���鐔�������肵�܂��B
��ԉE�̖��́C�O�l�̌����������r���@���@�U�@�K���ł��܂��B
���}���N���b�N����ƁC����Ɛ������\������܂�(�����܂łɂ́@�ق��̒��㋉�e�N�j�b�N���K�v�Ȗ�������܂�)�B



�m���K���@�h�O�l�̌����������r���h�n
�̓r���Ł@�e�N�j�b�N�h�O�l�̌����������r���h�@���K�v�ɂȂ���ł�(�����܂łɂ́@�ق��̒��㋉�e�N�j�b�N���K�v�Ȗ�������܂�)�B
��ԉE�̖��́@�e�N�j�b�N�h�O�l�̌����������r���h�̂ق��ɁC�㋉�̃e�N�j�b�N���@�R��C�����̃e�N�j�b�N���@10��@���p���܂��B
���}���N���b�N����ƁC�����Ǝv�l�ߒ��̗Ⴊ�\������܂��B




�@
 �mJellyfish�n�@�@���K����
�mJellyfish�n�@�@���K����
�h�����������r���h���@�S�s�S��@�ɔ��W�������e�N�j�b�N�ł��B
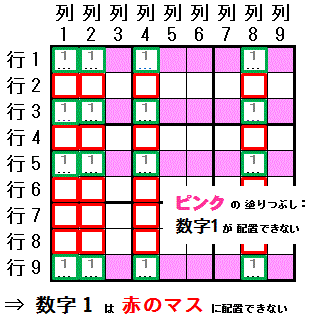 �m�e�N�j�b�N�n
�m�e�N�j�b�N�n
�����̐����i�����P�j���@�S�@�̍s�i�s�P�C�s�R�C�s�T�C�s�X�j���ׂĂŁC �����@�T�@�̗�i�S�̗�@��P�C��Q�C��S�C��W�@�ȊO�̂T��F��R�C��T�C��U�C��V�C��X�j�̃}�X�ɔz�u�ł��Ȃ��Ƃ��Ɂ@���̐����i�����P�j��z�u�ł��Ȃ��}�X��������܂��B
���̐����i�����P�j�́@�S�̗�i��P�C��Q�C��S�C��W�j�ł́@�S�̍s�i�s�P�C�s�R�C�s�T�C�s�X�j�ȊO�́@�}�X�@�ɂ͔z�u�ł��܂���B
�����j�@��l�C�O�l�̌����������Ɠ��l�ł��B�ǂ̗�i��P�@�܂��́@��Q�@�܂��́@��S�@�܂��́@��W�j�ł��C���́@�S�̍s�i�s�P�C�s�R�C�s�T�C�s�X�j�ȊO�́@�}�X�@�Ɂ@���̐����i�����P�j���z�u�����ƁC �S�̍s�i�s�P�C�s�R�C�s�T�C�s�X�j�ł́@���̗�́@�S�̃}�X�i�s�P��P�ƍs�R��P�ƍs�T��P�ƍs�X��P�@�܂��́@�s�P��Q�ƍs�R��Q�ƍs�T��Q�ƍs�X��Q�@�܂��́@�s�P��S�ƍs�R��S�ƍs�T��S�ƍs�X��S�@�܂��́@�s�P��W�ƍs�R��W�ƍs�T��W�ƍs�X��W�j�ɂ́@���̐����i�����P�j��z�u�ł��Ȃ��Ȃ�܂��B ����ƁC�����S�̍s�i�s�P�C�s�R�C�s�T�C�s�X�j�́@���̐����i�����P�j���z�u�����Ɖ��肳�ꂽ��@�ȊO�̂R��̃}�X�@�̑g�ݍ��킹�i�s�P��P�ƍs�R��P�ƍs�T��P�ƍs�X��P�C�s�P��Q�ƍs�R��Q�ƍs�T��Q�ƍs�X��Q�C�s�P��S�ƍs�R��S�ƍs�T��S�ƍs�X��S�C�s�P��W�ƍs�R��W�ƍs�T��W�ƍs�X��W�̂����̂R�̑g�ݍ��킹�j�Ɂ@���̐����i�����P�j���S�z�u����邱�ƂɂȂ�C�������܂��B
��q����悤�ɁC�O�l�̌����������r���@�܂ł𐳂����K�����Ă���C�l�l�̌����������r���@���K���ł��鐔���́C���̋ǖʂɁ@�P�����z�u����Ă��鐔���@���C�S���z�u����Ă��Ȃ������@�����ł��B
���ۂɖ��������Ƃ��ɂ́C�O�l�̌����������r���@�܂ł𐳂����K���������ƂŁC ���̋ǖʂŁC�P���������z�u����Ă��Ȃ����C�S���z�u����Ă��Ȃ������@������C���̐������@�z�u�ł���}�X���@�S�ȉ��̍s�i��j�������ā@�l�l�̌����������r���@���K���ł��邩�ǂ������������܂��B
�s�@�Ɓ@��@�����ւ��Ă��C�l�l�̌����������r���@�͐������܂��B
�O�l�̌����������r���Ɠ��l�ŁC�e�s�ɂ͓��Y�̐������@�S�}�X�@���ׂĂɔz�u�ł���K�v�͂���܂���B
�m���́h�l�l�̌����������r���h�̗R���n
�h�����������r���h�̗R���@�Ɠ����ł��B ���������K�ɐݒu����Ă���C�l�l�̌����������́C�����g���đ��k���Ē��݂��������������߁C ���������邾���łȂ��C�A���H������������z�u����K�v���Ȃ����܂��B
�@
�m�e�N�j�b�N�h�l�l�̌����������r���h�̔��W�n
�T�C�U�C�V�̍s�i�܂��́@��j�ł̌����������r���sFish ��{�`�t�̃e�N�j�b�N�́C���ꂼ�� Squirmbag, Whale, Leviathan �ƌĂ�܂��B
���ۂɖ��������Ƃ��ɂ́C�S�̍s�i����с@��j�܂ł̌����������r���sFish ��{�`�t�j���m���Ɍ�������Ώ\���ł��B
�Ⴆ�C�s�Ł@Squirmbag�i�ܐl�̌����������r���j����������ꍇ�C�����@���Y���������łɂQ�̃}�X�Ŕz�u���m�肵�Ă���ꍇ�C��� X-wing�i��l�̌����������r���j�����藧���܂��B
���łɁ@���̃}�X�Ł@�z�u���m�肵�Ă��鐔���Ɋւ��ẮCbase sets �� ���s�Ł@cover sets ���@����ł́@�����������r���sFish ��{�`�t����������ƁC �����ǖʂŁ@base sets �� �i�X�|���|���j��Ł@cover sets ���@�i�X�|���|���j�s�@�ł́@�����������r���sFish ��{�`�t���������܂��i���������������}�X����r������܂��j�B
�����O�@�Ȃ̂ŁC�s�i��j�ł́@�ܐl�ȏ�̌����������r���@���@��������ƁC��i�s�j�ł́@�l�l�ȉ��̌����������r�����������܂��B
�����@���N���b�N�����������B

�m�e�N�j�b�N�h�l�l�̌����������r���h�̗�n
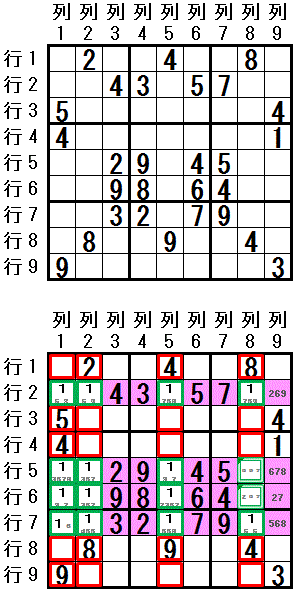
���̖��}�Ł@�P�����z�u����Ă��Ȃ����C�S���z�u����Ă��Ȃ������́@�����P�@�Ɓ@�����U�@�ł��B
�����P�@���S�܂Ŕz�u�\�ȍs�C��́@�z�u�\�ȃ}�X�����F�ɓh��Ԃ����@�y���V���}�[�N�@�́C���������N���b�N����ƕ\������܂� �i�����U�@�ɂ́@�l�l�̌����������r���͓K���ł��܂���j�B
���̃y���V���}�[�N����������ƁC�s�Q�C�s�T�C�s�U�C�s�V�@�� base sets �Ƃ����@�l�l�̌����������r���@�̉\�������邱�Ƃ��킩��܂� �i���Ɂ@��R�C��S�C��U�C��V�@�� base sets �Ƃ��邱�Ƃ��ł��܂��j�B
���Ɏ����@�l�l�̌����������r�����������܂��B
���ۂɂ��̖��������Ƃ��ɂ́C���̑��̒��㋉�̃e�N�j�b�N�𗘗p���Ď��i�߂Ă���C�l�l�̌����������r���@��K�����C���̌�@�l�R�ƃl�Y�~�r���@�𗘗p���āC���ɔz�u���鐔�������肵�܂��B ���}���N���b�N����Ɓ@�l�l�̌����������r���@���K�������ǖʁi�r���}�j�@�Ɓ@����}�@��\�����܂��B
�_�E�����[�h�����������\�t�g�ł́@�r���̕\���ł��B
���l�l�̌����������r���@�r�������� 1�@�s 1�@�� 1
���l�l�̌����������r���@�r�������� 1�@�s 8�@�� 1
���l�l�̌����������r���@�r�������� 1�@�s 3�@�� 2
���l�l�̌����������r���@�r�������� 1�@�s 4�@�� 2
���l�l�̌����������r���@�r�������� 1�@�s 9�@�� 2
���l�l�̌����������r���@�r�������� 1�@�s 3�@�� 5
���l�l�̌����������r���@�r�������� 1�@�s 4�@�� 5
���l�l�̌����������r���@�r�������� 1�@�s 9�@�� 5
���l�l�̌����������r���@�r�������� 1�@�s 3�@�� 8
���l�l�̌����������r���@�r�������� 1�@�s 4�@�� 8
���l�l�̌����������r���@�r�������� 1�@�s 9�@�� 8
�@�@�r��������
�@�@�@�s 2�C�s 5�C�s 6�C�s 7�@(base sets)�Ŕz�u�\�ȗ�
�@�@�@�� 1�C�� 2�C�� 5�C�� 8�@(cover sets)�Ɍ����Ă���̂�
�@�@�@cover sets �ł� base sets �Ɋ܂܂�Ȃ��}�X�ɂ͔z�u�ł��Ȃ�

�@
�m���K���@�h�l�l�̌����������r���h�K���ǖʁn
���}�ɒ��ڃe�N�j�b�N�h�l�l�̌����������r���h���K���ł��܂��B
��ԍ��̖��́C�����܂ł̃e�N�j�b�N�𗘗p����Ή������Ƃ��ł��܂����C�ŏ��ɁC�h�l�l�̌����������r���h�𗘗p���Đ������m�肷��ƁC���̌�͏����̃e�N�j�b�N�݂̂Ő����������܂��B
�܂̖��́C�e�N�j�b�N�h�l�l�̌����������r���h��K���������Ɓ@�����̃e�N�j�b�N���@�P��C�㋉�̃e�N�j�b�N���@�S��@���p���āC���ɔz�u���鐔�������肵�܂��B
��ԉE�̖��́C�Q�̐����ɁC�����p�^�[���́h�l�l�̌����������r���h��K�����ā@���ɔz�u���鐔�������肵�܂��B
���}���N���b�N����ƁC����Ɛ������\������܂��B
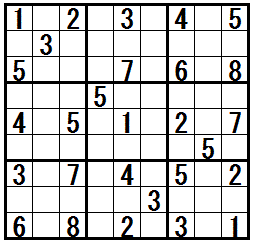
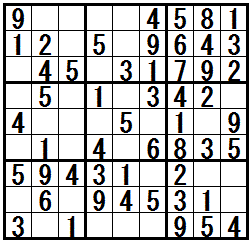
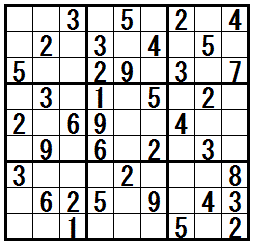
�m���K���@�h�l�l�̌����������r���h�n
�̓r���Ł@�e�N�j�b�N�h�l�l�̌����������r���h�@���K�v�ɂȂ���ł�(�����܂łɂ́@�ق��̒��㋉�e�N�j�b�N���K�v�ł�)�B
���}���N���b�N����ƁC�����Ǝv�l�ߒ��̗Ⴊ�\������܂��B
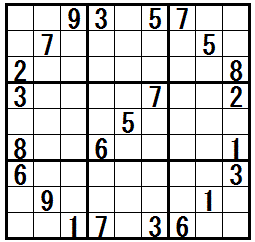
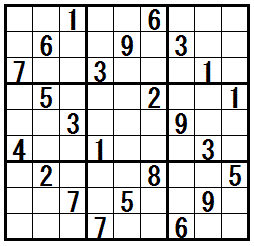
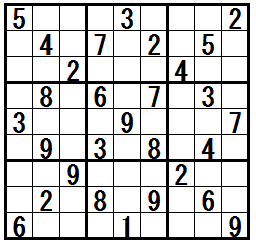

 �mJellyfish�n�@�@���K����
�mJellyfish�n�@�@���K����
�h�����������r���h���@�S�s�S��@�ɔ��W�������e�N�j�b�N�ł��B
 �m�e�N�j�b�N�n
�m�e�N�j�b�N�n�����̐����i�����P�j���@�S�@�̍s�i�s�P�C�s�R�C�s�T�C�s�X�j���ׂĂŁC �����@�T�@�̗�i�S�̗�@��P�C��Q�C��S�C��W�@�ȊO�̂T��F��R�C��T�C��U�C��V�C��X�j�̃}�X�ɔz�u�ł��Ȃ��Ƃ��Ɂ@���̐����i�����P�j��z�u�ł��Ȃ��}�X��������܂��B
���̐����i�����P�j�́@�S�̗�i��P�C��Q�C��S�C��W�j�ł́@�S�̍s�i�s�P�C�s�R�C�s�T�C�s�X�j�ȊO�́@�}�X�@�ɂ͔z�u�ł��܂���B
�����j�@��l�C�O�l�̌����������Ɠ��l�ł��B�ǂ̗�i��P�@�܂��́@��Q�@�܂��́@��S�@�܂��́@��W�j�ł��C���́@�S�̍s�i�s�P�C�s�R�C�s�T�C�s�X�j�ȊO�́@�}�X�@�Ɂ@���̐����i�����P�j���z�u�����ƁC �S�̍s�i�s�P�C�s�R�C�s�T�C�s�X�j�ł́@���̗�́@�S�̃}�X�i�s�P��P�ƍs�R��P�ƍs�T��P�ƍs�X��P�@�܂��́@�s�P��Q�ƍs�R��Q�ƍs�T��Q�ƍs�X��Q�@�܂��́@�s�P��S�ƍs�R��S�ƍs�T��S�ƍs�X��S�@�܂��́@�s�P��W�ƍs�R��W�ƍs�T��W�ƍs�X��W�j�ɂ́@���̐����i�����P�j��z�u�ł��Ȃ��Ȃ�܂��B ����ƁC�����S�̍s�i�s�P�C�s�R�C�s�T�C�s�X�j�́@���̐����i�����P�j���z�u�����Ɖ��肳�ꂽ��@�ȊO�̂R��̃}�X�@�̑g�ݍ��킹�i�s�P��P�ƍs�R��P�ƍs�T��P�ƍs�X��P�C�s�P��Q�ƍs�R��Q�ƍs�T��Q�ƍs�X��Q�C�s�P��S�ƍs�R��S�ƍs�T��S�ƍs�X��S�C�s�P��W�ƍs�R��W�ƍs�T��W�ƍs�X��W�̂����̂R�̑g�ݍ��킹�j�Ɂ@���̐����i�����P�j���S�z�u����邱�ƂɂȂ�C�������܂��B
��q����悤�ɁC�O�l�̌����������r���@�܂ł𐳂����K�����Ă���C�l�l�̌����������r���@���K���ł��鐔���́C���̋ǖʂɁ@�P�����z�u����Ă��鐔���@���C�S���z�u����Ă��Ȃ������@�����ł��B
���ۂɖ��������Ƃ��ɂ́C�O�l�̌����������r���@�܂ł𐳂����K���������ƂŁC ���̋ǖʂŁC�P���������z�u����Ă��Ȃ����C�S���z�u����Ă��Ȃ������@������C���̐������@�z�u�ł���}�X���@�S�ȉ��̍s�i��j�������ā@�l�l�̌����������r���@���K���ł��邩�ǂ������������܂��B
�s�@�Ɓ@��@�����ւ��Ă��C�l�l�̌����������r���@�͐������܂��B
�O�l�̌����������r���Ɠ��l�ŁC�e�s�ɂ͓��Y�̐������@�S�}�X�@���ׂĂɔz�u�ł���K�v�͂���܂���B
�m���́h�l�l�̌����������r���h�̗R���n
�h�����������r���h�̗R���@�Ɠ����ł��B ���������K�ɐݒu����Ă���C�l�l�̌����������́C�����g���đ��k���Ē��݂��������������߁C ���������邾���łȂ��C�A���H������������z�u����K�v���Ȃ����܂��B
�@
�m�e�N�j�b�N�h�l�l�̌����������r���h�̔��W�n
�T�C�U�C�V�̍s�i�܂��́@��j�ł̌����������r���sFish ��{�`�t�̃e�N�j�b�N�́C���ꂼ�� Squirmbag, Whale, Leviathan �ƌĂ�܂��B
���ۂɖ��������Ƃ��ɂ́C�S�̍s�i����с@��j�܂ł̌����������r���sFish ��{�`�t�j���m���Ɍ�������Ώ\���ł��B
�Ⴆ�C�s�Ł@Squirmbag�i�ܐl�̌����������r���j����������ꍇ�C�����@���Y���������łɂQ�̃}�X�Ŕz�u���m�肵�Ă���ꍇ�C��� X-wing�i��l�̌����������r���j�����藧���܂��B
���łɁ@���̃}�X�Ł@�z�u���m�肵�Ă��鐔���Ɋւ��ẮCbase sets �� ���s�Ł@cover sets ���@����ł́@�����������r���sFish ��{�`�t����������ƁC �����ǖʂŁ@base sets �� �i�X�|���|���j��Ł@cover sets ���@�i�X�|���|���j�s�@�ł́@�����������r���sFish ��{�`�t���������܂��i���������������}�X����r������܂��j�B
�����O�@�Ȃ̂ŁC�s�i��j�ł́@�ܐl�ȏ�̌����������r���@���@��������ƁC��i�s�j�ł́@�l�l�ȉ��̌����������r�����������܂��B
�����@���N���b�N�����������B

�m�e�N�j�b�N�h�l�l�̌����������r���h�̗�n

���̖��}�Ł@�P�����z�u����Ă��Ȃ����C�S���z�u����Ă��Ȃ������́@�����P�@�Ɓ@�����U�@�ł��B
�����P�@���S�܂Ŕz�u�\�ȍs�C��́@�z�u�\�ȃ}�X�����F�ɓh��Ԃ����@�y���V���}�[�N�@�́C���������N���b�N����ƕ\������܂� �i�����U�@�ɂ́@�l�l�̌����������r���͓K���ł��܂���j�B
���̃y���V���}�[�N����������ƁC�s�Q�C�s�T�C�s�U�C�s�V�@�� base sets �Ƃ����@�l�l�̌����������r���@�̉\�������邱�Ƃ��킩��܂� �i���Ɂ@��R�C��S�C��U�C��V�@�� base sets �Ƃ��邱�Ƃ��ł��܂��j�B
���Ɏ����@�l�l�̌����������r�����������܂��B
���ۂɂ��̖��������Ƃ��ɂ́C���̑��̒��㋉�̃e�N�j�b�N�𗘗p���Ď��i�߂Ă���C�l�l�̌����������r���@��K�����C���̌�@�l�R�ƃl�Y�~�r���@�𗘗p���āC���ɔz�u���鐔�������肵�܂��B ���}���N���b�N����Ɓ@�l�l�̌����������r���@���K�������ǖʁi�r���}�j�@�Ɓ@����}�@��\�����܂��B
�_�E�����[�h�����������\�t�g�ł́@�r���̕\���ł��B
���l�l�̌����������r���@�r�������� 1�@�s 1�@�� 1
���l�l�̌����������r���@�r�������� 1�@�s 8�@�� 1
���l�l�̌����������r���@�r�������� 1�@�s 3�@�� 2
���l�l�̌����������r���@�r�������� 1�@�s 4�@�� 2
���l�l�̌����������r���@�r�������� 1�@�s 9�@�� 2
���l�l�̌����������r���@�r�������� 1�@�s 3�@�� 5
���l�l�̌����������r���@�r�������� 1�@�s 4�@�� 5
���l�l�̌����������r���@�r�������� 1�@�s 9�@�� 5
���l�l�̌����������r���@�r�������� 1�@�s 3�@�� 8
���l�l�̌����������r���@�r�������� 1�@�s 4�@�� 8
���l�l�̌����������r���@�r�������� 1�@�s 9�@�� 8
�@�@�r��������
�@�@�@�s 2�C�s 5�C�s 6�C�s 7�@(base sets)�Ŕz�u�\�ȗ�
�@�@�@�� 1�C�� 2�C�� 5�C�� 8�@(cover sets)�Ɍ����Ă���̂�
�@�@�@cover sets �ł� base sets �Ɋ܂܂�Ȃ��}�X�ɂ͔z�u�ł��Ȃ�

�@
�m���K���@�h�l�l�̌����������r���h�K���ǖʁn
���}�ɒ��ڃe�N�j�b�N�h�l�l�̌����������r���h���K���ł��܂��B
��ԍ��̖��́C�����܂ł̃e�N�j�b�N�𗘗p����Ή������Ƃ��ł��܂����C�ŏ��ɁC�h�l�l�̌����������r���h�𗘗p���Đ������m�肷��ƁC���̌�͏����̃e�N�j�b�N�݂̂Ő����������܂��B
�܂̖��́C�e�N�j�b�N�h�l�l�̌����������r���h��K���������Ɓ@�����̃e�N�j�b�N���@�P��C�㋉�̃e�N�j�b�N���@�S��@���p���āC���ɔz�u���鐔�������肵�܂��B
��ԉE�̖��́C�Q�̐����ɁC�����p�^�[���́h�l�l�̌����������r���h��K�����ā@���ɔz�u���鐔�������肵�܂��B
���}���N���b�N����ƁC����Ɛ������\������܂��B



�m���K���@�h�l�l�̌����������r���h�n
�̓r���Ł@�e�N�j�b�N�h�l�l�̌����������r���h�@���K�v�ɂȂ���ł�(�����܂łɂ́@�ق��̒��㋉�e�N�j�b�N���K�v�ł�)�B
���}���N���b�N����ƁC�����Ǝv�l�ߒ��̗Ⴊ�\������܂��B








