＜＜チェーン(Chain)＞＞

・　ある１つのマスに　”配置可能な数字が　２つ　に限られる”　こと　と，
・　ある数字が１つの領域（行，列，大マス）で　”配置可能なマスが　２つ　に限られる”　こと
をつなげていくことで情報を得るテクニックを　チェーン(Chain)系のテクニック　と呼びます。
　　　　　　　５）グループ化，命題の一般化，ＡＬＳ，ＡＨＳ　から　この考え方を拡張します。
チェーン　について考察することは，論理的思考能力を向上させる　ために有効です。
（チェーン系のテクニックを積極的に使用することをお勧めする訳では決してありません。ナンプレを楽しみながら論理的思考能力を高めるには，むしろ，名前のついた基本的な中上級のテクニックを理解し，利用することの方が有効です）

１）代表的なチェーン系テクニック
　１−１）X-Chain
　１−２）XY-Chain
　１−３）その他（色分け法 （Simple Colors, Multi Colors）, Remote Pair[リニア]）

２）テクニックのチェーンによる解釈（その１）
　２−１）筋違見張塔排除 （Skyscraper, 2-String Kite, Turbot Fish）
　２−２）賢い見張兵排除（X-Wing）
　２−３）末っ子の甘え排除（XY-Wing）
　２−４）二都物語排除（Naked Pair）

３）チェーン系テクニックの原理
　３−１）強いリンク，弱いリンク
　３−２）ＡＩＣ(Alternate Inference Chain)，チェーン系テクニックの原理

４）テクニックのチェーンによる解釈（その２）
　４−１）ネコとネズミ排除(W-Wing)
　４−２）姉妹排除（Hidden Pair）
　４−３）浜田ロジック

５）グループ化，命題の一般化，ＡＬＳ，ＡＨＳ
　５−１）グループ化
　５−２）命題の一般化
　５−３）ＡＬＳ(Almost Locked Sets)
　５−４）ＡＨＳ(Almost Hidden Sets)

６）テクニックのチェーンによる解釈（その３）
　６−１）信長の野望排除（XYZ-Wing）
　６−２）二守備線見張塔過多排除（Finned・Sashimi X-Wing）
　６−３）三・四都物語排除(Naked Triple・Quadruple)
　６−４）三・四姉妹排除(Hidden Triple・Quadruple)
　６−５）カーブミラー排除（Empty Rectangle）
　６−６）三・四人の賢い見張兵排除(Swordfish・Jellyfish)
　６−７）Ｓｕｅ　ｄｅ　Ｃｏｑ

このページでは，１）代表的なチェーン系テクニック　を説明します。

１）代表的なチェーン系テクニック

１−１） X-Chain

　ある１つの数字に関して　”１つの領域（行，列，大マス）で　配置可能なマスが　２つ　に限られる”領域・マス　をつなぎ合わせていくことによって， その数字が配置できないマスを見つけるテクニックです。

その数字が配置可能なマスが２つに限られる　２つの領域のつなぎ合わせ　は，それぞれの領域の中でその数字が配置可能なマス１つずつが　同じ領域　にあることによって行います。
その数字が配置可能なマスが２つに限られる２つの領域がつなぎ合わされたときに，次のその数字が配置可能なマスが２つに限られる領域への　つなぎ合わせの延長　は， 最初につなぎ合わされた２つの領域のうちのどちらかの領域でそのつなぎ合わせに使われなかったマスが，次の領域でその数字が配置可能なマスのうちの１つのマスと　同じ領域　にあることによって行います。
１つの領域でその数字が配置可能な２つのマス同士　と　領域をつなげるのに使われた２つのマス同士　がつながっていると考えると，一連のマスで　鎖（チェーン）が形成されます。
　　　（文章にすると難解ですが，以下の例図を参照すると理解しやすくなります）

鎖を形成するためにつなげていく単位（node）として，”マス”を考えるのではなく，”ある数字をあるマスに配置すること”を考えると，チェーンを発展的に考察する助けとなります。

このルールによって　その数字が配置可能なマスが２つに限られる領域・マスがつなぎ合わされていくと， 鎖の　最初の領域と最後の領域で　領域をつなぎ合わせていくために使われなかった　それぞれ１つずつのマス　の　両方と同じ領域にあるマス　には　その数字　を配置できません。

下図で　数字１　が配置可能なマスが表示されています。ピンクのマスには　数字１　は配置できません （行１，列１，大マス５　で，数字１　が配置可能なマスが　２つ　に限られています）。
スタートのマスを　行１列９　として，数字１　が配置できるマスが２つに限られる領域をつなぎ合わせて　鎖（チェーン）を作成します。

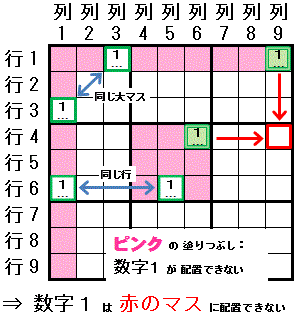行１列９⇒行１列３：行１で配置可能なマスが２つに限られる
行１列３→行３列１：同じ大マス１にある
行３列１⇒行６列１：列１で配置可能なマスが２つに限られる
行６列１→行６列５：同じ行６にある
行６列５⇒行４列６：大マス５で配置可能なマスが２つに限られる
　　　　　　　［終点］

この時，スタートのマス（行１列９）　と　終点のマス（行４列６）の両方 と同じ領域（列９　および　行４）にある　マス（行４列９）　に　数字１　は配置できません。


説明）　もし　数字１　が，行４列９　に配置されると，数字１　は　行１列９　に配置できなくなります。
鎖（チェーン）を順にたどります。
行１　で　数字１　が配置できるマスは，行１列３　と　行１列９　に限られるので，数字１が　行１列９　に配置できないと，行１列３　の　数字１　が確定します。
すると，行１列３　と同じ　大マス１　にある　行３列１　に　数字１　を配置できなくなります。
列１　で　数字１　が配置できるマスは，行３列１　と　行６列１　の２マス　に限られるので，行６列１　の　数字１　が確定します。
すると，行６列１　と同じ　行６　にある　行６列５　に　数字１　を配置できなくなります。
大マス５　で　数字１　が配置できるマスは，行６列５　と　行４列６　の２マス　に限られるので，行４列６　の　数字１　が確定します。
最初に　数字１　を　行４列９　に配置することを仮定していたので，数字１　が　行４　で　行４列６　と　行４列９　の２マスに配置されることになり，矛盾を生じます。 よって，数字１　は　行４列９　に配置できないことがわかります。


＜＜テクニック X-Chain のまとめ＞＞
テクニック X-Chain をまとめます。
・ 一つの数字　に注目する
・ ”同じ領域で配置できるマスが２つに限られる”（強いリンクがある　といいます）　と
　 ”同じ領域にある”（弱いリンクがある　といいます）
　 が　交互に繋がる　鎖（チェーン）：AIC(Alternate Inference Chain)　を見つける
・ 鎖の両端は　”同じ領域で配置できるマスが２つに限られる”（強いリンク）　になっている
　　　　鎖を形成する　マスの数は偶数　になります（任意の偶数で構いません。リンクの数は奇数　になります）
　　　　　　鎖を形成するマスの数を　鎖の長さ（チェーンの長さ）　とします
・ この時，鎖の両端の２つのマスの両方と同じ領域にあるマスには，その数字　を配置できない

強いリンク　は　弱いリンク　として利用できます。その逆は成立しません。




実際のナンプレ局面での　X-Chain を例示します。
　　　強いリンク（同じ領域で配置できるマスが２つに限られる）を
　　　　　　ピンクの実線（鎖を形成していく方向を示す時には　矢印　を付けます------→），
　　　弱いリンク（同じ領域にある）を
　　　　　　青の点線　---→　で表示します。

＜＜X-Chain の例＞＞
下図で，数字１　について　スタートのマスを　行４列８　として，チェーン　を作成します。

　
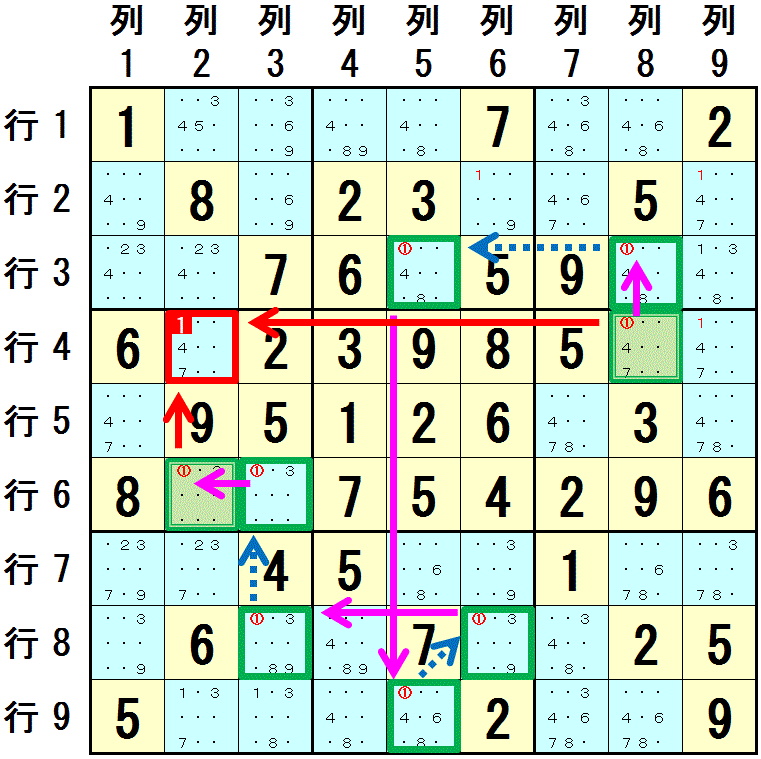
行４列８⇒行３列８
　　：列８で配置可能なマスが２つに限られる
行３列８→行３列５
　　：同じ行３にある
行３列５⇒行９列５
　　：列５で配置可能なマスが２つに限られる
行９列５→行８列６
　　：同じ大マス８にある
行８列６⇒行８列３
　　：行８で配置可能なマスが２つに限られる
行８列３→行６列３
　　：同じ列３にある
行６列３⇒行６列２［終点］
　　：行６で配置可能なマスが２つに限られる








＜＜テクニック X-Chain のまとめ＞＞　と対応させて考えます。
・ 一つの数字（数字１）　に注目した
・ ”同じ領域で配置できるマスが２つに限られる”　と　”同じ領域にある”　が　交互に繋がる　鎖が見つかった
・ 鎖の両端は　”同じ領域で配置できるマスが２つに限られる”　になっている
・ この鎖は　X-Chain であり，鎖の両端の２つのマスの両方と同じ領域にあるマスには，その数字　を配置できない

つまり，スタートのマス（行４列８）　と　終点のマス（行６列２）の両方 と同じ領域（行４　および　列２）にある　マス（行４列２）　に　数字１　を配置できません。

例題のチェーンの構成内容は，冗長さを排除して以下のように記載できます。
行４列８⇒行３列８：列８（強いリンク）
行３列８→行３列５：行３（弱いリンク）
行３列５⇒行９列５：列５（強いリンク）
行９列５→行８列６：大マス８（弱いリンク）
行８列６⇒行８列３：行８（強いリンク）
行８列３→行６列３：列３（弱いリンク）
行６列３⇒行６列２：行６（強いリンク）
矢印の色，形の情報を利用すれば各行最後のリンクに関する記載も不要になります。
　　　（第１行目は，行４列８⇒行３列８　と記載できます）
どの数字に関してのリンクであるかを明示するためには，その数字名を併記します。
　　　（第１行目は，行４列８⇒行３列８：数字１　と記載されます）

１−２） XY-Chain

　”配置可能な数字が　２つ　に限られる”　マスをつなぎ合わせていくことによって， ある数字が配置できないマスを見つけるテクニックです。

配置可能な数字が２つに限られる　２つのマスのつなぎ合わせ　は，それらの２つのマスが　同じ領域　にあり，それぞれのマスで２つに限られた配置可能な数字のうちの　１つが一致　することによって行います。
配置可能な数字が２つに限られる２つのマスがつなぎ合わされたときに，次の配置可能な数字が２つに限られるマスへの　つなぎ合わせの延長　は， 最初につなぎ合わされた２つのマスのうちのどちらかのマスと次のマスが　同じ領域　にあり， 最初につなぎ合わされた２つのマスのうちで次のマスと同じ領域にあるマスで最初のつなぎ合わせに使われなかった数字　と　次のマスで配置可能な数字のうちの　１つが一致　することによって行います。
　　　（以下の例図も参照してください）

このつなぎ合わせのルールにより，配置できる数字が２つに限られるマスの鎖（チェーン）が作成されたときに， 最初のマスで　鎖をつなぎ合わせていくために使われなかった数字　と　 最後のマスで　鎖をつなぎ合わせるために使われていない数字　が同じになると， 最初のマスと最後のマスの　両方と同じ領域のマス　には　その数字　を配置できません。

下図で　配置可能な数字が２つに限られるマス　と　そのマスに配置可能な２つの数字が示されています。
スタートのマスを　行１列５　として，配置できる数字が２つに限られるマス　をつなぎ合わせて　鎖（チェーン）を作成します。


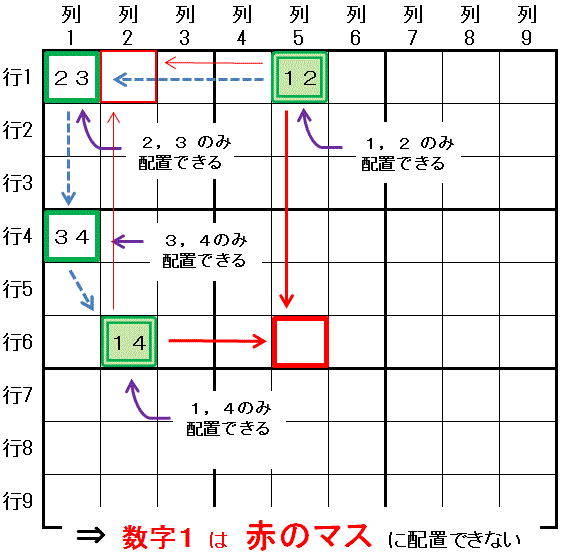
行１列５：配置可能な数字が　数字１，数字２　に限られる
行１列５→行１列１：同じ行１にある
行１列１：配置可能な数字が　数字２，数字３　に限られる
行１列１→行４列１：同じ列１にある
行４列１：配置可能な数字が　数字３，数字４　に限られる
行４列１→行６列２：同じ大マス４にある
行６列２：配置可能な数字が　数字４，数字１　に限られる

スタートのマス（行１列５）と最後のマス（行６列２）　で，鎖を形成するのに利用されない数字は，同じ　数字１　になりました。

この時，スタートのマス（行１列５）と最後のマス（行６列２）の両方と同じ領域（列５　および　行６）にあるマス（行６列５）　にその数字（数字１）は配置できません。
行１列２　にも　数字１　は配置できません。


説明）　もし，数字１　が　行６列５　に配置されると，数字１は　行６列５　と同じ　列５　にある　行１列５　に配置できなくなります。
行１列５　に配置できる数字は，数字１　と　数字２　に限られていますから，行１列５　に　数字１　が配置できないことがわかると，行１列５　に　数字２　が配置されることが確定します。
鎖（チェーン）を順にたどります。
行１列５　に　数字２　が配置されると，行１列５　と同じ　行１　にあるマス　行１列１　に　数字２　が配置できなくなります。
行１列１　に配置できる数字は，数字２　と　数字３　に限られていますから，行１列１　に　数字２　が配置できないことがわかると，行１列１　に　数字３　が配置されることが確定します。
すると，行１列１　と同じ　列１　にあるマス　行４列１　に　数字３　が配置できなくなります。
行４列１　に配置できる数字は，数字３　と　数字４　に限られていますから，行４列１　に　数字３　が配置できないことがわかると，行４列１　に　数字４　が配置されることが確定します。
行４列１　と同じ　大マス４　にあるマス　行６列２　に　数字４　が配置できなくなります。
行６列２　に配置できる数字は，数字４　と　数字１　に限られていますから，行６列２　に　数字４　が配置できないことがわかると，行６列２　に　数字１　が配置されることが確定します。
最初に　数字１　を　行６列５　に配置することを仮定していたので，数字１　が　行６　で　行６列５　と　行６列２　の２マスに配置されることになり，矛盾を生じます。 よって，数字１　は　行６列５　に配置できないことがわかります。



＜＜テクニック XY-Chain のまとめ＞＞
テクニック XY-Chain をまとめます。
・配置可能な数字が　２つに限られる　マスに注目する
・そのマスと同じ領域（行，列　または　大マス）にある　マスで，配置可能な数字が， つなぎ合わせに使われなかった数字（最初に注目したマスからの場合は，２つに限られた配置可能な数字のうちの１つ）　と　もう１つ別の数字　の　２つに限られる　マスを見つける（鎖を延長する，マスをつなげる）
・前項の要領で　鎖（チェーン）を延長していき，鎖の両端のマスで　マスをつなげるのに利用されなかった２つの数字が同じになったら鎖の延長を休止する
・この時，鎖の両端の２つのマスの両方と同じ領域にあるマスには，その（鎖の両端のマスでマスをつなげるのに利用されなかった）数字　を配置できない


　
＜＜XY-Chain の例＞＞
下図で，配置可能な数字が２つ（数字１，数字２）に限られる　マス行１列５　を　スタートのマスとしてチェーンを作成します。


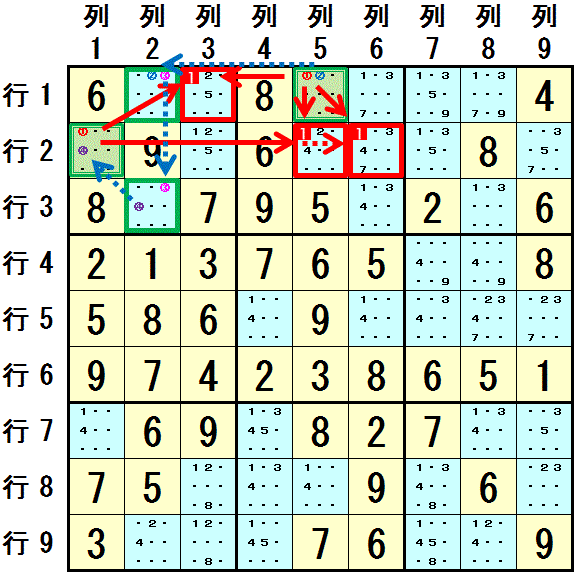
行１列５：数字１，数字２　のみ配置可能
行１列５→行１列２：同じ行１にある
行１列２：数字２，数字３　のみ配置可能
行１列２→行３列２：同じ列２にある
行３列２：数字３，数字４　のみ配置可能
行３列２→行２列１：同じ大マス１にある
行２列１：数字４，数字１　のみ配置可能

スタートのマス（行１列５）と最後のマス（行２列１）　で，鎖を形成するのに利用されない数字は，同じ　数字１　になりました。

この鎖は　XY-Chain です。
スタートのマス（行１列５）と最後のマス（行２列１）の両方と同じ領域（行１　と　大マス１）にあるマス（行１列３）， および，同じ領域（大マス２　と　行２）にあるマス（行２列５，行２列６）　にその数字（数字１）は配置できません。






１つのマスに配置可能な数字が２つに限られる場合，どちらかの数字が必ずそのマスに配置され，両方の数字が同時にそのマスに配置されることはありません。
１つのマスに配置可能な数字が２つに限られる場合，それぞれの数字をそのマスに配置することには　強いリンク　があります。
上の例題の鎖の作成についての解説について説明します。
最初の行，”行１列５：数字１，数字２　のみ配置可能”　を
数字１　を　行１列５　に配置する　⇒　数字２　を　行１列５　に配置する（数字１⇒数字２：マス行１列５（強いリンク））
と解釈します（強いリンクがあります）。
その他の　一つのマスに配置可能な数字が２つに限られる　ことに関する行も　同様に解釈します。
すると，この例題の解説は，
数字１　を　行１列５　に配置する　⇒　数字２　を　行１列５　に配置する（数字１⇒数字２：マス行１列５（強いリンク））
数字２　を　行１列５　に配置する　⇒　数字２　を　行１列２　に配置する（行１列５→行１列２：数字２，行１（弱いリンク））
数字２　を　行１列２　に配置する　⇒　数字３　を　行１列２　に配置する（数字２⇒数字３：マス行１列２（強いリンク））
数字３　を　行１列２　に配置する　⇒　数字３　を　行３列２　に配置する（行１列２→行３列２：数字３，列２（弱いリンク））
数字３　を　行３列２　に配置する　⇒　数字４　を　行３列２　に配置する（数字３⇒数字４：マス行３列２（強いリンク））
数字４　を　行３列２　に配置する　⇒　数字４　を　行２列１　に配置する（行３列２→行２列１：数字４，大マス１（弱いリンク））
数字４　を　行２列１　に配置する　⇒　数字１　を　行２列１　に配置する（数字４⇒数字１：マス行２列１（強いリンク））
と　なります。
強いリンク（同じマスで配置可能なマスが２つに限られる）　と　弱いリンク（同じ領域にある）　が交互に繋がる　鎖（チェーン）になっていて（Alternate Inference Chain:AIC）， チェーンの両端は　強いリンク　になっていること　がわかります。
X-Chain と全く同じ構造をしています。
最初のリンクと最後のリンクで鎖の作成に利用されないのは，数字１を行１列５に配置する　ことと　数字１を行２列１に配置する　ことです。
行１列５　と　行２列１　の両方と同じ領域にあるマスに　数字１　を配置できないことも　X-Chain と同様です。
（チェーンの両端の命題は，どちらかが必ず成立する：チェーン系テクニックの原理）

XY-Chain　をこのように解釈した場合，鎖（チェーン）の長さ　は　鎖に含まれる　ある数字をあるマスに配置する　ことの数とします。
上記の例では　鎖の長さは　８　になります。
あるマスに配置可能な数字が２つに限られることをこのように考えることを理解しておくと，チェーン系のロジックを発展的に考察することができるようになります。

１−３）その他

特別な条件下の　X-Chain, XY-Chain を３つ説明します。 特別な条件が成立する場合にのみ　チェーンを延長　していくため，一般の　X-Chain, XY Chain よりも　チェーンの有無　を容易に見つけることができます。

１−３−１）　Simple Colors
X-Chain の特殊形です。
ある１つの数字に関して，配置可能なマスが　２つに限られる領域のみ　でチェーンをつなげます （X-Chain　では，配置可能なマスが２つに限られる２つの領域をつなぎ合わせる２つのマスは同じ領域にあれば十分でしたが， Simple Colors　では，検討している数字は，そのつなぎ合わせの領域でも　配置可能なマスが　つなぎ合わせに使われる２つのマスのみに限られます）。
１つの領域が２つの領域とつなぎ合わせることができるときは，その両方の領域へ鎖を延長します。 鎖は全体として　樹枝状　の構造になります。
Simple Colors　としての検討するときには，チェーン内のマスは，同じ領域では別の色になるように２色で塗り分けます （色分け法（Coloring）と呼びます。 実際に問題を解く場合は，チェーン　と理解するのではなく，塗り分けられた色の位置関係を利用して解析します）。

次の場合　数字を配置できないマスが見つかります。
・異なる色で塗られた２つのマスの両方と同じ領域にあるマスには，その数字を配置できません：Color Trap
・同じ色に塗られた２つのマスが同じ領域にあると，その色で塗られたすべてのマスにその数字は配置できないことがわかります：Color Wrap

別のページで詳述しますが，最初のケース（Color Trap）の例を示します。


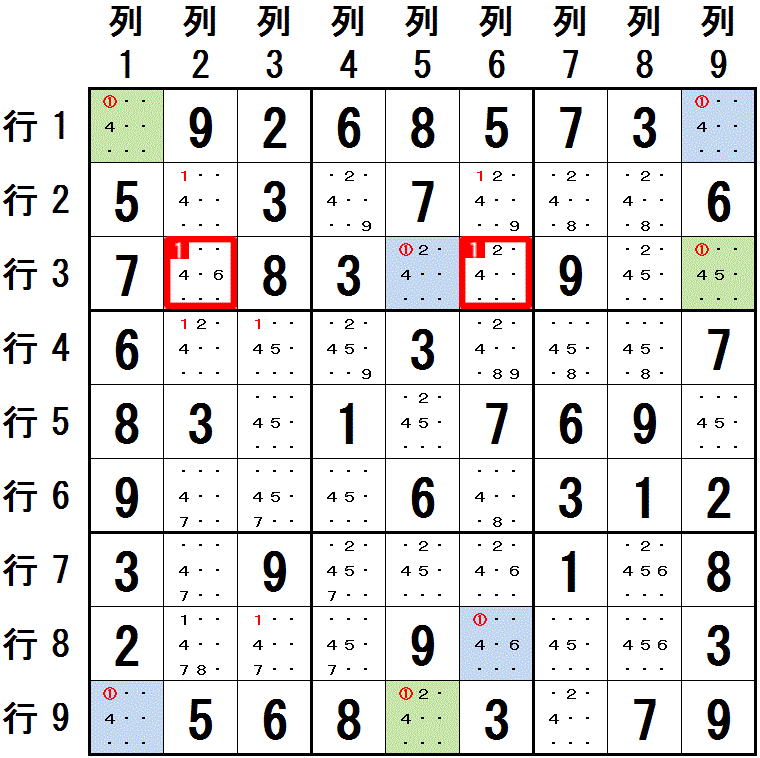
数字１　に関して，配置可能なマスが２つに限られる領域をつなげていき（列９→行１→列１→行９→列５・大マス８），各領域の２つのマスを　薄緑色，水色　で塗り分けています。
行３列９（薄緑色）　と　行３列５（水色）　は　異なる色に塗られています。
行３列９　と　行３列５　の両方と同じ領域（行３）にあるマス　行３列２，行３列６　には，数字１　を配置できません。

数字１　は　すべての薄緑色のマスに配置される（水色のマスには配置されません）　か 　すべての水色のマスに配置される（薄緑色のマスには配置されません）　か のどちらかであるため，行３列９（薄緑色）　と　行３列５（水色）　のどちらかに，必ず配置されるからです。

他の組み合わせの　異なる色に塗られた２マス　の両方と同じ領域にあると解釈しても，数字１が配置できないマスが見つかります （例えば，行１列１　と　行３列５　の両方のマスと同じ領域にある　行３列２　に　数字１　が配置できないことがわかります） 。


Simple Colors　の詳細　と，X-Chain による解釈は　ここ　をクリックしてください。

１−３−２）　Multi Colors
Simple Colors　と同じく　X-Chain の特殊形です（色分け法(Coloring)です）。
ある１つの数字に関して，配置可能なマスが２つに限られる領域のみでチェーンをつなげ， チェーン内のマスを，同じ領域では別の色になるように２色で塗り分けることは　Simple Colors　と同様です。
Multi Colors　では，このチェーンを　複数本　扱います。

２本のチェーンを扱うとき　次の場合　数字を配置できないマスが見つかります。
・２本のそれぞれのチェーンに属する１つずつのマス２つが同じ領域にあるとき， その領域でそれぞれのチェーンのマスを着色するのに使われた色と異なる色で塗られた２つのマスの両方と同じ領域にあるマスには，その数字を配置できません
・１本のチェーンで同じ色に塗られた２つのマスのうち， １つのマスが　もう１本のチェーンのある色で塗られたマスと同じ領域に属し， もう１つのマスが　もう１本のチェーンの前記とは異なる色で塗られたマスと同じ領域に属しているとき， 最初のチェーンでその同じ色で塗られたすべてのマスにその数字は配置できません

Multi Colors　の詳細　と，X-Chain による解釈は　ここ　をクリックしてください。

１−３−３）　リニア新幹線排除［Remote Pair］
XY-Chain の特殊形です。
XY-Chain　と同様に配置可能な数字が　２つ　に限られる　マスをつなぎ合わせてチェーンを作成しますが， Remote Pair　では，その配置可能な数字２つが　つなぎ合わされるマスで　すべて同じ　場合を取り扱います。 同じ領域にある配置可能な２つの数字が同じであるマス同士はすべてつなぎ合わせることができます。
数字が配置できないマスを見つけるときに，XY-Chain　とは異なり，チェーンに含まれるマスの数が　偶数個　であるという制約があります。

配置可能な数字がすべて同じ２つの数字に限られるマスをつなぎ合わせてチェーンを作成すると，チェーンに含まれるマスの数が　偶数個　のとき， チェーンの両端のマスのどちらとも同じ領域にあるマスには，その両方の数字を配置できません。

Remote Pair の例　を提示します。

＜＜Remote Pair の例＞＞
下図で，配置可能な数字が同じ２つ（数字１，数字２）に限られるマスをつなげていきます。 スタートのマスを　行３列８　としてチェーンを延ばしていきます。


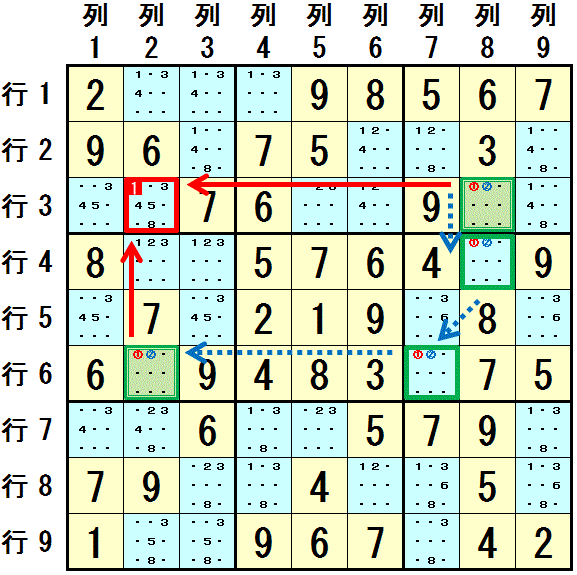
行３列８：数字１，数字２　のみ配置可能
行３列８→行４列８：同じ列８にある
行４列８：数字１，数字２　のみ配置可能
行４列８→行６列７：同じ大マス６にある
行６列７：数字１，数字２　のみ配置可能
行６列７→行６列２：同じ行６にある
行６列２：数字１，数字２　のみ配置可能

行３列８　から　行６列２　まで， 配置可能な数字が　２つの数字（数字１，数字２）　に限られたマス　がつながりました。 チェーンに含まれるマスの数は　４つ（偶数）です。
このチェーンの　両端のマス　行３列８　と　行６列２　のどちらとも同じ領域（行３　と　列２）にあるマス　行３列２　には，数字１　も　数字２　も配置できません。


説明）　もし，行３列８（１番目のマス）　に　数字１　が配置されると，２番目のマス　行４列８　には　数字２　が配置されます。 順番に　数字１，数字２　の配置を確定していくと，偶数番目のマスには　数字２，奇数番目のマスには　数字１　が配置されることになります。 行６列２　は　行３列８　から数えて，偶数番目（４番目）のマスなので，数字２　が配置されます。
一方，行３列８　に　数字２　が配置されると， 行３列８　から数えて，偶数番目（４番目）のマスである　行６列２　には　数字１　が配置されることになります。
行３列８　と　行６列２　は，どちらか一方が　数字１　で，もう一方は　数字２　になります。 行３列８　と　行６列２　のどちらとも同じ領域にあるマス　行３列２　には，数字１　も　数字２　も配置できないことがわかります。

［名称”リニア新幹線排除”の由来］
　数字１　か　数字２　のどちらかしか配置できないマスは　Ｎ極，Ｓ極，Ｎ極，．．．とつながります。 偶数個のマスのつながりでは　両端は　どちらかが　Ｎ極，どちらかが　Ｓ極になります。その両端と同じ領域にあるマスは　Ｎ極にも　Ｓ極にもなれません。
リニア新幹線は名古屋から新大阪まで延長され，さらにその先まで延長されるかも知れません。

リニア新幹線排除［Remote Pair］は　XY-Chain　として解釈することもできます。
スタートのマスを　行３列８　とします。
対象となるマスで配置可能な数字は　数字１，数字２のみなので　マスに配置可能な数字が２つに限られる　という　XY-Chain　の条件は満たされています。
スタートのマス 行３列８ から，数字２　を使って次のマス　行４列８　につなげます（鎖をつなげるのに利用されない数字は　数字１　です）。 行４列８　の次のマスへは　数字１　を利用してつながります。 最初の　行３列８　を１番目のマスとして　そこから数えて　偶数番目のマスへは　数字２　を使い，奇数番目のマスへは　数字１　を利用してつなげることになります。 最後のマス　行６列２　は　最初のマス　行３列８　から数えて　４番目のマスなので，行６列２　へは　数字２　を使ってつながってくることになります。 最後のマス　行６列２　で　鎖を形成するために使われない数字は　数字１　となり，最初のマス　行３列８　で鎖を形成するために使われなかった数字（数字１）と一致します。 XY-Chain　が形成されました。 スタートのマス（行３列８）　と　最後のマス（行６列２）　のどちらとも同じ領域のマス（行３列２）に　数字１　が配置できないことがわかります。
同様に，スタートのマス（行３列８）　から，最初に　数字１　を使ってマスをつなげていけば（鎖をつなげるのに利用されない数字は　数字２）， 最後のマス　行６列２　へは　数字１　を使ってつながってくることになり，鎖を形成するために使われない数字が　数字２　になります。 最初のマス　行３列８　で鎖を形成するために使われなかった数字（数字２）と一致します。 最初のマス（行３列８）と最後のマス（行６列２）の両方と同じ領域にあるマス（行３列２）には　数字２　も配置できないことがわかります。