（おおかたの ナンプレ・ファン は，このページをお読みになる必要はありません）
上級のテクニック（ロジック）
は，中級のテクニックと同じく，排除する数字を見つけるためのテクニックですが，そのなかで，
２つ以上の領域（行，列，大マス）
を検討しなければ適応できるかどうかを確認できないテクニックとします。
このページでは 上級のテクニックを適応できるかどうか を発見することの
容易さ（最初に注目する領域，マス の数）
を元に分類し，説明します。
（上級のテクニックは，排除する数字を見つけるための論理に従って分類するのが一般的です。 上級の各ページでは 論理による分類ごと に説明します）
各項の表題をクリックすると，そのテクニックを詳しく説明したページに移ります（一部工事中）。
◎ 最初に １つのマス または １つの領域 だけ に注目すればよいテクニック
上級のテクニック（ロジック）
は，中級のテクニックと同じく，排除する数字を見つけるためのテクニックですが，そのなかで，
２つ以上の領域（行，列，大マス）
を検討しなければ適応できるかどうかを確認できないテクニックとします。
このページでは 上級のテクニックを適応できるかどうか を発見することの
容易さ（最初に注目する領域，マス の数）
を元に分類し，説明します。
（上級のテクニックは，排除する数字を見つけるための論理に従って分類するのが一般的です。 上級の各ページでは 論理による分類ごと に説明します）
各項の表題をクリックすると，そのテクニックを詳しく説明したページに移ります（一部工事中）。
◎ 最初に １つのマス または １つの領域 だけ に注目すればよいテクニック
１）末っ子の甘え排除 《Wing》
[XY-wing]
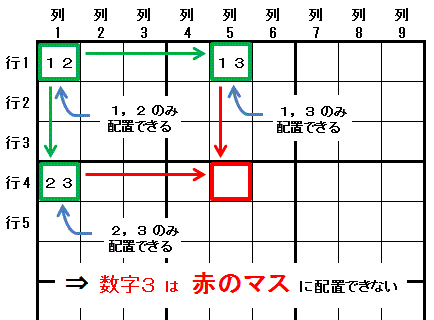最初に 配置できる数字が２つだけ（数字１，数字２）のマス（行１列１）を見つけます。
そのマスと同じ領域にあり，
・片方の数字（数字１）と第三の数字（数字３）の２つだけ，
・もう片方の数字（数字２）と第三の数字（数字３）の２つだけ
しか配置できない２つのマス（行１列５，行４列１）が存在すると，
それら ２つのマスの両方 と同じ領域にあるマス（行４列５）には，
第三の数字（数字３）は配置できません。
[XY-wing]
最初に 配置できる数字が２つだけ（数字１，数字２）のマス（行１列１）を見つけます。そのマスと同じ領域にあり，
・片方の数字（数字１）と第三の数字（数字３）の２つだけ，
・もう片方の数字（数字２）と第三の数字（数字３）の２つだけ
しか配置できない２つのマス（行１列５，行４列１）が存在すると，
それら ２つのマスの両方 と同じ領域にあるマス（行４列５）には，
第三の数字（数字３）は配置できません。
２）信長の野望排除 《Wing》
[XYZ-wing]
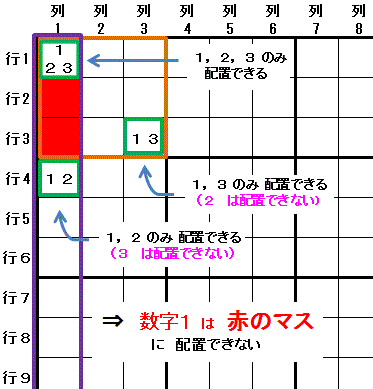最初に 配置できる数字が３つ（数字１，数字２，数字３）のマス（行１列１）を見つけます。・そのマスと同じ行または列（列１）にあり，
第一の数字（数字１）と第二の数字（数字２）の２つだけ，
・そのマスと同じ大マス（大マス１）にあり，
第一の数字（数字１）と第三の数字（数字３）の２つだけ
しか配置できない２つのマス（行４列１，行３列３）が存在すると，
その（行または）列と大マスとの共通部分の（最初のマス以外の）マスには
第一の数字（数字１）は配置できません。
３）ネコとネズミ排除 《Wing》
[W-wing]
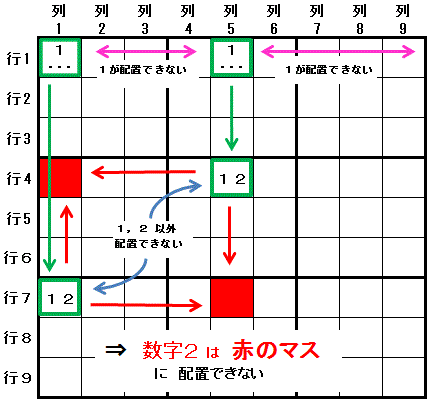最初に ある数字（数字１）が 配置できるマスが２つに限られる領域（行１）を見つけます。その２つのマスそれぞれと同じ領域（列１，列５）にあり，
最初の数字（数字１）と第二の数字（数字２）の２つだけ
しか配置できない ２つのマス（行７列１，行４列５）が存在すると，
それら ２つのマスの両方 と同じ領域にあるマス（行４列１，行７列５） には 第二の数字（数字２）は，配置できません。
４）カーブミラー排除 《Sigle Digit Patterns》
[Empty Rectangle]
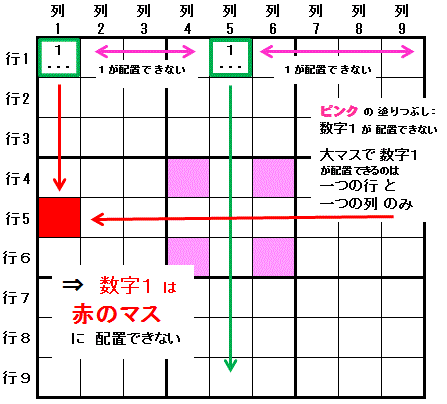最初に ある数字（数字１）が 配置できるマスが２つに限られる領域（行１）を見つけます。
その２つのマスのうちの一つのマス（行１列５）が属する列（列５）と，
一つの行（行５）にのみ 数字１ が配置可能な 大マス（大マス５）が存在すると，
この行（行５）と，最初に配置可能だった２つのマスのうちのもう一つのマス（行１列１）と同じ列（列１）にあるマス（行５列１）には， 数字１を配置できません。
[Empty Rectangle]
最初に ある数字（数字１）が 配置できるマスが２つに限られる領域（行１）を見つけます。その２つのマスのうちの一つのマス（行１列５）が属する列（列５）と，
一つの行（行５）にのみ 数字１ が配置可能な 大マス（大マス５）が存在すると，
この行（行５）と，最初に配置可能だった２つのマスのうちのもう一つのマス（行１列１）と同じ列（列１）にあるマス（行５列１）には， 数字１を配置できません。
◎ 最初に ２つの領域 に注目するテクニック
５）賢い見張兵排除 《Fish》
[X-Wing]
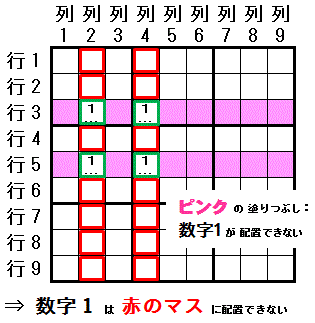最初に，ある一つの数字（数字１）で 配置可能なマスが２つに限られる行 が ２つ（行３，行５） あるものを見つけます。
その配置可能な４つのマス（行３列２，行３列４，行５列２，行５列４）が ２つの同じ列（列２，列４）にあると
その数字（数字１）は，それらの列（列２，列４）では その２つの行（行３，行５）以外の マス には配置できません。
配置可能なマスが２つに限られる行を base set，base set で配置可能なマス をすべて含む列を cover set と呼びます。
賢い見張塔排除は 行 と 列 を入れ替えても成り立ちます。
(三人の賢い見張兵排除（Swordfish）， 四人の賢い見張兵排除（Jellyfish），．．．と発展させることができます。 また，行と列だけでなく，大マスも含めた条件でも排除される数字が見つかることがあります（乱戦賢い三見張兵排除（Franken/Mutant Swordfish））。 これらは ”極上級” とします）
５）賢い見張兵排除 《Fish》
[X-Wing]
最初に，ある一つの数字（数字１）で 配置可能なマスが２つに限られる行 が ２つ（行３，行５） あるものを見つけます。その配置可能な４つのマス（行３列２，行３列４，行５列２，行５列４）が ２つの同じ列（列２，列４）にあると
その数字（数字１）は，それらの列（列２，列４）では その２つの行（行３，行５）以外の マス には配置できません。
配置可能なマスが２つに限られる行を base set，base set で配置可能なマス をすべて含む列を cover set と呼びます。
賢い見張塔排除は 行 と 列 を入れ替えても成り立ちます。
(三人の賢い見張兵排除（Swordfish）， 四人の賢い見張兵排除（Jellyfish），．．．と発展させることができます。 また，行と列だけでなく，大マスも含めた条件でも排除される数字が見つかることがあります（乱戦賢い三見張兵排除（Franken/Mutant Swordfish））。 これらは ”極上級” とします）
６）筋違見張塔排除
《Sigle Digit Patterns》
[Skyscraper, 2-String Kite, Turbot Fish]
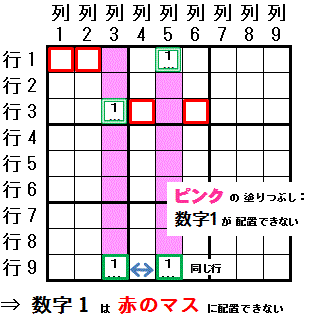最初に，ある一つの数字（数字１）で 配置可能なマスが２つに限られる領域（列） が ２つ（列３，列５） あるものを見つけます。
（Skyscraper:摩天楼 と呼ばれます。そのイメージを出すため，行・列 を他の例図と逆にして説明しています）
そのそれぞれの領域（列）で配置可能な２つマスのうちの１組のマス（行９列３，行９列５）が 同じ領域（行）（行９）にあると，
その数字（数字１）は，残りの２つのマス（行３列３，行１列５）の両者と 同じ領域にあるマス（行１列１，行１列２ および 行３列４，行３列６） には配置できません。
筋違見張塔排除は，それを成立させる領域 （配置可能なマスが２つに限られる領域 と １組のマスが存在する領域）に従って名付けられます。
Skyscraper: ”行”と”列”のみが関係する場合
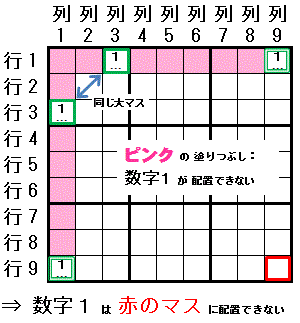
2-String Kite: １組のマスが存在する領域が”大マス”の場合
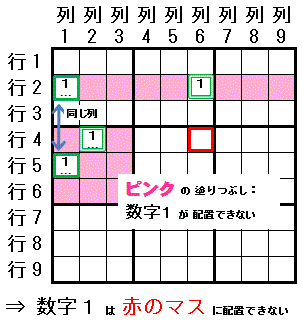
Turbot Fish: 関係する領域が”行”，”列”，”大マス”の任意である場合
・ ある１つのマスに ”配置可能な数字が ２つ に限られる” こと と，
・ ある数字が１つの領域（行，列，大マス）で ”配置可能なマスが ２つ に限られる” こと
をつなげていくことで情報を得るテクニックを チェーン(Chain) と呼びます（定義は拡張されます）。
ここまでに説明したテクニックの多くは，”配置可能な数字（またはマス）が ２つ に限られる”ことを条件にしています。 それらは，チェーンのうち で ”鎖が短く，枝分かれが単純なもの” として説明することができます。
チェーン について考察することは，論理的思考能力を向上させる ために有効です。
（チェーン系のテクニックを積極的に使用することをお勧めする訳では決してありません。ナンプレを楽しみながら論理的思考能力を高めるには，むしろ，名前のついた基本的な中上級のテクニックを理解し，利用することの方が有効です）
詳しくは ここ をクリックしてください。
[Skyscraper, 2-String Kite, Turbot Fish]
最初に，ある一つの数字（数字１）で 配置可能なマスが２つに限られる領域（列） が ２つ（列３，列５） あるものを見つけます。（Skyscraper:摩天楼 と呼ばれます。そのイメージを出すため，行・列 を他の例図と逆にして説明しています）
そのそれぞれの領域（列）で配置可能な２つマスのうちの１組のマス（行９列３，行９列５）が 同じ領域（行）（行９）にあると，
その数字（数字１）は，残りの２つのマス（行３列３，行１列５）の両者と 同じ領域にあるマス（行１列１，行１列２ および 行３列４，行３列６） には配置できません。
筋違見張塔排除は，それを成立させる領域 （配置可能なマスが２つに限られる領域 と １組のマスが存在する領域）に従って名付けられます。
Skyscraper: ”行”と”列”のみが関係する場合
2-String Kite: １組のマスが存在する領域が”大マス”の場合
Turbot Fish: 関係する領域が”行”，”列”，”大マス”の任意である場合
・ ある１つのマスに ”配置可能な数字が ２つ に限られる” こと と，
・ ある数字が１つの領域（行，列，大マス）で ”配置可能なマスが ２つ に限られる” こと
をつなげていくことで情報を得るテクニックを チェーン(Chain) と呼びます（定義は拡張されます）。
ここまでに説明したテクニックの多くは，”配置可能な数字（またはマス）が ２つ に限られる”ことを条件にしています。 それらは，チェーンのうち で ”鎖が短く，枝分かれが単純なもの” として説明することができます。
チェーン について考察することは，論理的思考能力を向上させる ために有効です。
（チェーン系のテクニックを積極的に使用することをお勧めする訳では決してありません。ナンプレを楽しみながら論理的思考能力を高めるには，むしろ，名前のついた基本的な中上級のテクニックを理解し，利用することの方が有効です）
詳しくは ここ をクリックしてください。
◎ 賢い見張兵排除（Fish）で 配置可能なマス が余分にある 場合
７）見張塔過多排除 《Finned/Sashimi Fish》
[Finned/Sashimi X-Wing]
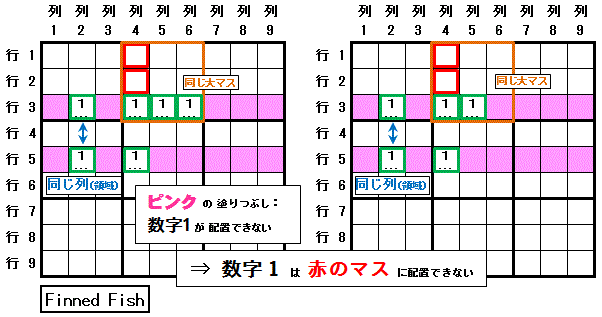(二守備線見張塔過多排除)
賢い見張兵排除(X-Wing)で 見張塔 が余分にある場合です。
余分なマスは Fin（ひれ），排除のテクニックは Finned X-Wing と呼ばれます。
余分な見張塔がある大マスで， 賢い見張兵排除(X-Wing) を成立させるためのマスに当該の数字が配置できない場合は Sashimi Fish と呼ばれます。
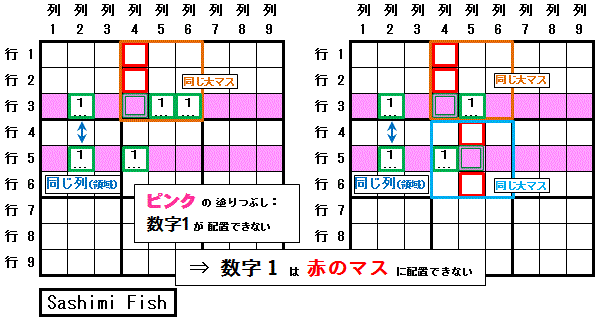
賢い見張塔排除(X-Wing)で 当該の数字（数字１）が配置可能なマスが２つに限定されている２つの行（行３，行５）のうちの片方の行（行３）で， その数字（数字１）が配置可能なマスのうちの一つのマス（行３列４）と 同じ大マス（大マス２）にその数字（数字１）が配置可能なマスが余分にあっても（行３列５，行３列６）， 賢い見張塔排除(X-Wing)で当該の数字（数字１）の配置が排除されるマス（列２，列４で行３，行５にないマス）のうち， その大マス（大マス２）に属するマス（行１列４，行２列４）に 当該の数字（数字１） は配置できません。
排除されるマスは，余分なマスに関与するすべてのマス（行５列４ と 行３列４･行３列５（･行３列６））と同じ領域にあるマスと解釈することができます。
下方の Sashimi Fish の右図は 筋違見張塔排除（Skyscraper）になっています。
配置可能なマスが２つに限られる２つの行が 同じ Floor（横に３つ並んだ大マス）にある場合は，両方の行に余分な見張塔（Fin）があってもその数字が配置できないマスが見つかります。
見張塔過多（Finned/Sashimi）の論理は，以下で説明する 三人の賢い見張塔排除（Swordfish），四人の賢い見張塔排除（Jellyfish）乱戦（Franken/Mutant）でも利用できます （三守備線見張塔過多排除（Finned/Sashini Swordfish），四守備線見張塔過多排除（Finned/Sashini Jellyfish），市街戦狙いうち排除（Finned Franken/Mutant））。
７）見張塔過多排除 《Finned/Sashimi Fish》
[Finned/Sashimi X-Wing]
(二守備線見張塔過多排除)賢い見張兵排除(X-Wing)で 見張塔 が余分にある場合です。
余分なマスは Fin（ひれ），排除のテクニックは Finned X-Wing と呼ばれます。
余分な見張塔がある大マスで， 賢い見張兵排除(X-Wing) を成立させるためのマスに当該の数字が配置できない場合は Sashimi Fish と呼ばれます。
賢い見張塔排除(X-Wing)で 当該の数字（数字１）が配置可能なマスが２つに限定されている２つの行（行３，行５）のうちの片方の行（行３）で， その数字（数字１）が配置可能なマスのうちの一つのマス（行３列４）と 同じ大マス（大マス２）にその数字（数字１）が配置可能なマスが余分にあっても（行３列５，行３列６）， 賢い見張塔排除(X-Wing)で当該の数字（数字１）の配置が排除されるマス（列２，列４で行３，行５にないマス）のうち， その大マス（大マス２）に属するマス（行１列４，行２列４）に 当該の数字（数字１） は配置できません。
排除されるマスは，余分なマスに関与するすべてのマス（行５列４ と 行３列４･行３列５（･行３列６））と同じ領域にあるマスと解釈することができます。
下方の Sashimi Fish の右図は 筋違見張塔排除（Skyscraper）になっています。
配置可能なマスが２つに限られる２つの行が 同じ Floor（横に３つ並んだ大マス）にある場合は，両方の行に余分な見張塔（Fin）があってもその数字が配置できないマスが見つかります。
見張塔過多（Finned/Sashimi）の論理は，以下で説明する 三人の賢い見張塔排除（Swordfish），四人の賢い見張塔排除（Jellyfish）乱戦（Franken/Mutant）でも利用できます （三守備線見張塔過多排除（Finned/Sashini Swordfish），四守備線見張塔過多排除（Finned/Sashini Jellyfish），市街戦狙いうち排除（Finned Franken/Mutant））。
◎ 最初から ３つ以上の領域 に注目するテクニック
”極上級のテクニック”とも呼びます
８）三人の賢い見張兵排除 《Fish》
[Swordfish]
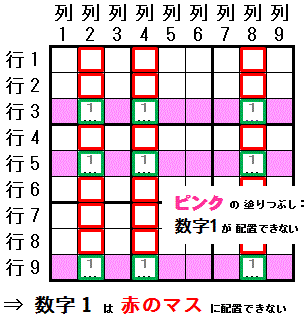関係する 行・列 が３つになった 賢い見張兵排除の発展系です。
ある一つの数字（数字１）で 配置可能なマスが３つか２つに限られる行 が ３つ（行３，行５，行９）あり，
その配置可能なマス（行３列２，行３列４，行３列８，行５列２，行５列４，行５列８，行９列２，行９列４，行９列８）が ３つの同じ列（列２，列４，列８）にあると
その数字（数字１）は，それらの列（列２，列４，列８）では その３つの行（行３，行５，行９）以外の マス には配置できません。
行 と 列 を入れ替えても成り立ちます。
”極上級のテクニック”とも呼びます
８）三人の賢い見張兵排除 《Fish》
[Swordfish]
関係する 行・列 が３つになった 賢い見張兵排除の発展系です。ある一つの数字（数字１）で 配置可能なマスが３つか２つに限られる行 が ３つ（行３，行５，行９）あり，
その配置可能なマス（行３列２，行３列４，行３列８，行５列２，行５列４，行５列８，行９列２，行９列４，行９列８）が ３つの同じ列（列２，列４，列８）にあると
その数字（数字１）は，それらの列（列２，列４，列８）では その３つの行（行３，行５，行９）以外の マス には配置できません。
行 と 列 を入れ替えても成り立ちます。
９）四人の賢い見張兵排除
《Fish》
[Jellyfish]
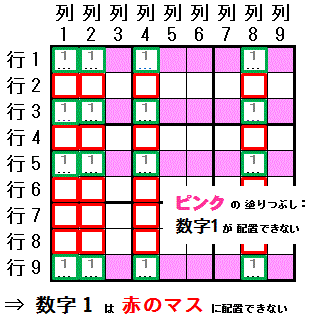関係する 行・列 が４つになった 賢い見張兵排除の発展系です。
ある一つの数字（数字１）で 配置可能なマスが４つ以下に限られる行 が ４つ（行１，行３，行５，行９）あり，
その配置可能なマス（行１列１，行１列２，行１列４，行１列８，行３列１，行３列２，行３列４，行３列８，行５列１，行５列２，行５列４，行５列８，行９列１，行９列２，行９列４，行９列８）が ４つの同じ列（列１，列２，列４，列８）にあると
その数字（数字１）は，それらの列（列１，列２，列４，列８）では その４つの行（行１，行３，行５，行９）以外の マス には配置できません。
行 と 列 を入れ替えても成り立ちます。
[Jellyfish]
関係する 行・列 が４つになった 賢い見張兵排除の発展系です。ある一つの数字（数字１）で 配置可能なマスが４つ以下に限られる行 が ４つ（行１，行３，行５，行９）あり，
その配置可能なマス（行１列１，行１列２，行１列４，行１列８，行３列１，行３列２，行３列４，行３列８，行５列１，行５列２，行５列４，行５列８，行９列１，行９列２，行９列４，行９列８）が ４つの同じ列（列１，列２，列４，列８）にあると
その数字（数字１）は，それらの列（列１，列２，列４，列８）では その４つの行（行１，行３，行５，行９）以外の マス には配置できません。
行 と 列 を入れ替えても成り立ちます。
10）乱戦賢い三見張兵排除
《Franken/Mutant Fish》
[Franken/Mutant Swordfish]
三人の賢い見張兵排除の発展系で，
base set, cover set に 行・列だけでなく，大マスも含まれるもの（Franken），
さらに base set, cover set が 任意の領域である（Mutant）ものです。
ある一つの数字（数字１）で ３つの領域（行１，大マス４，行８：base set）で
配置可能なマス（行１列１，行１列５，行５列２，行６列１，行８列１，行８列２，行８列５）すべてが ３つの領域（列１，列２，列５：cover set）でカバーされると
その数字（数字１）は，それらの領域（列１，列２，列５：cover set）では その３つの領域（行１，大マス４，行８：base set）以外の マス には配置できません。
複数の base set の領域に 同じマスが含まれていても構いませんが，その数字が配置可能なマスは 一つの base set にのみ属します。
１つの base set で その数字が配置可能なマスの数は ３ を超えても構いません（乱戦賢い三見張兵排除の場合）。
[Franken/Mutant Swordfish]
三人の賢い見張兵排除の発展系で，
base set, cover set に 行・列だけでなく，大マスも含まれるもの（Franken），
さらに base set, cover set が 任意の領域である（Mutant）ものです。ある一つの数字（数字１）で ３つの領域（行１，大マス４，行８：base set）で
配置可能なマス（行１列１，行１列５，行５列２，行６列１，行８列１，行８列２，行８列５）すべてが ３つの領域（列１，列２，列５：cover set）でカバーされると
その数字（数字１）は，それらの領域（列１，列２，列５：cover set）では その３つの領域（行１，大マス４，行８：base set）以外の マス には配置できません。
複数の base set の領域に 同じマスが含まれていても構いませんが，その数字が配置可能なマスは 一つの base set にのみ属します。
１つの base set で その数字が配置可能なマスの数は ３ を超えても構いません（乱戦賢い三見張兵排除の場合）。
［補足］
［Brute Force, Reduction to the absurd］
［テクニック］
背理法，仮定法，仮置法 と呼ばれる方法です。 解答に行き詰まった局面で，特定のマスに，配置可能な数字を 仮に配置してみます。 そこから，また問題を解き続けます。 途中で，配置できるマス・数字がなくなってしまったら，仮に配置した マス・数字は 誤りだったと判断します。 数字を仮に配置したマスに 別の配置可能な数字 を再び仮配置して，また問題を解き始めます。これを繰り返します。
完全作（正解が必ずあり，しかも正解は一つである問題）であれば，必ず正解にたどり着けるテクニックです。
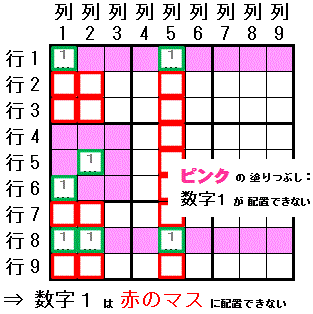
左図は，中級レベルまでのテクニックでは手詰まりとなっています。
大マス９ の 行７列９ には 数字５ と 数字６ しか配置できないことに注目して，
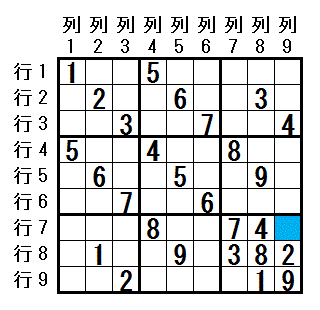
行７列９ に 数字６
を 仮に配置してみます。手を進めていくと，下の図のようになります。
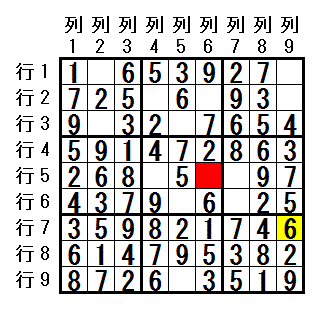行５列６ に配置できる数字がなくなってしまいました。
行７列９ に 数字６ を配置したのは間違いだったと判断し，次は，
行７列９ に 数字５
を仮配置して，再度問題を解き進めます（解答に行き詰まった都度に ナンプレドリーム を試みます）。
［名称”ナンプレドリーム”の由来］
人生でもパズルでも，行き詰まってしまうことは日常茶飯事です。 嘆いていては先はありません。まずは行動を起こしましょう（仮の数字を配置してみましょう）。 夢（ナンプレドリーム）叶い，大成功（正解）を収められるかも知れません。
＜＜背理法についての雑感＞＞
ナンプレ問題を解くときに，様々なテクニックを駆使して正解を得るのを楽しみとする方にとっては，背理法の利用は適しません。
ただし，背理法を使わなければならないかどうかは，問題自体に依るのではなく，解答者が使えるテクニックのレベルに依るのだ ということは，認識しておかなければなりません。
上級のテクニックである”末っ子の甘え排除（XY-Wing）”を利用すれば解ける問題でも，中級のテクニックまでしか利用できない解答者にとっては，背理法が必要な問題になってしまいます。 極端な例を２つ挙げます。
１）今までに発表されているどんなテクニックを利用しても解けず，背理法を利用しなければ解けない問題であったとします。 新たなテクニックが開発されて，そのテクニックに依って解答できるようになれば，その時点から，背理法を利用しなくても解答できる問題になります。
２）一番基本的な”八面楚歌（Full House）”でも，数字の確定をエレガントに証明しようとすれば，背理法が必要になります。
背理法を使わないでナンプレを楽しむためには，その問題を解くために必要なテクニックのレベルが問題に併記されているか あるいは ほのめかされていること が重要になるでしょう。 さもなくば，難問に出くわしたときに 自分の利用できるテクニックをいくら適応しようとしても先へ進めない蟻地獄から這い出せなくなってしまいます。
背理法が必要になった状況の有用さについて説明します。
理解しているテクニックをどのように駆使しても手詰まりになったが，背理法を利用すればなんとか解ける という状況になったとします。 これは，実は 大飛躍の可能性を秘めたときなのです。 今までに発表されているテクニックを再度勉強して，使えるテクニックを新たに習得することができます。
自身で一生懸命思案することによって，新テクニックの発見につながるかも知れません。 ほとんどの 中上級のテクニックも，”数字が特別な条件下に配置されていると，背理法を利用することによって，数字を配置できない情報が得られる”というものです。
背理法の利用は，認知症の初期状態での脳トレに非常に役立ちます。 認知症の初期には，直近の記憶は悪くなりますが，昔から培われてきた知識は保たれます。 ナンプレを解くときに，背理法で仮の数字を配置することは直近の記憶能力で処理されます。 そこから解答を進めるには，認知症の初期には失われていない過去の知識を利用します。 さて，仮数字を配置して解答を進めて，矛盾に陥ったとします。 どこまで逆のぼってどうしたらよいのでしょうか？ これは認知症の初期段階では苦手とされる作業です。 ここに挑戦することは直近の出来事の記銘力低下防止の訓練になります。 仮配置の枝分かれが複雑になればなるほど，良い刺激になります。
（ナンプレの難問を背理法を利用して解くことは その他の認知症の症状（二つ以上のことが重なるとうまく処理できなくなる，計画を立て按配することができなくなる，すべてが面倒に：厚生労働省 認知症の症状－中核症状と行動・心理症状）の予防，改善にも役立ちそうです）
解法のテクニックを利用せずに背理法に頼ってしまうと，筆運に左右されてせっかくの良問がつまらなくなるとされています。 しかし，自分が使うことができる以上のテクニックを要求される問題では，背理法の助けを借りなければ，正解を得るという感動は経験できません。 難易度のわからない問題に挑戦しているときには，正解を得てパズルが楽しめた というためには，背理法も一法でしょう。 ただ，あるマスにある数字を仮置して解答を進めて矛盾なく全８１マスが埋まったとしても，残りの枝分かれがすべて矛盾に陥り，正解が唯一であることだけは，是非確認してください。 万一背理法を誤解されている方がいたらいけないのでの忠告です。背理法と いわゆる 仮置き とは別物です。 ”背理法とは何か”は大学入試でも出題されています。 何らかの仮定を置いて論理を展開すると結論が得られることによって証明する方法 という答えは不正解です。 ナンプレで 背理法という言葉を使う場合 筆運に左右される仮置き と 背理法 とが区別なく使われることが時々ありますが， 背理法は 本来 あるマスに正解以外の数字を配置すると（正解の数字を配置するという命題が 偽 と仮定すると）必ず矛盾に陥る ことによって証明する方法です。 あるマスにある数字を仮置して解答を進めて全８１マスが埋まったから解けたというのは，多分正解が唯一であろう パズル”ナンプレ”が解けたということだけです。 公開される ナンプレ問題が 唯一解を前提としているので 背理法と仮置法が 一致しているだけです。 唯一解であることの証明は 出題者ではなく 解答者に要求されているとすべきでしょう （この考え方を採ると Uniqueness はナンプレテクニックとしては疑問符がつくようになります（Uniqueness を利用すること自体は 大いに 論理的思考の訓練になります））。
since 2011.8.25
頭頭が良くなる 楽しい ナンプレ 数独 ナンバープレイス ドクター中尾 人工知能 無料 フリーソフト ダウンロード 本格的ナンプレソフト 論理的思考能力 理Ⅲ 問題集 難問集 難問 問題解答 問題作成 初期配置指定 テクニック 解き方 解法のヒント テクニック ソルバー 仮置なし 仮置きなし 手詰まり わかりやすい 分かりやすい 分かり易い 手筋
［Brute Force, Reduction to the absurd］
［テクニック］
背理法，仮定法，仮置法 と呼ばれる方法です。 解答に行き詰まった局面で，特定のマスに，配置可能な数字を 仮に配置してみます。 そこから，また問題を解き続けます。 途中で，配置できるマス・数字がなくなってしまったら，仮に配置した マス・数字は 誤りだったと判断します。 数字を仮に配置したマスに 別の配置可能な数字 を再び仮配置して，また問題を解き始めます。これを繰り返します。
完全作（正解が必ずあり，しかも正解は一つである問題）であれば，必ず正解にたどり着けるテクニックです。
左図は，中級レベルまでのテクニックでは手詰まりとなっています。
大マス９ の 行７列９ には 数字５ と 数字６ しか配置できないことに注目して，行７列９ に 数字６
を 仮に配置してみます。手を進めていくと，下の図のようになります。
行５列６ に配置できる数字がなくなってしまいました。行７列９ に 数字６ を配置したのは間違いだったと判断し，次は，
行７列９ に 数字５
を仮配置して，再度問題を解き進めます（解答に行き詰まった都度に ナンプレドリーム を試みます）。
［名称”ナンプレドリーム”の由来］
人生でもパズルでも，行き詰まってしまうことは日常茶飯事です。 嘆いていては先はありません。まずは行動を起こしましょう（仮の数字を配置してみましょう）。 夢（ナンプレドリーム）叶い，大成功（正解）を収められるかも知れません。
＜＜背理法についての雑感＞＞
ナンプレ問題を解くときに，様々なテクニックを駆使して正解を得るのを楽しみとする方にとっては，背理法の利用は適しません。
ただし，背理法を使わなければならないかどうかは，問題自体に依るのではなく，解答者が使えるテクニックのレベルに依るのだ ということは，認識しておかなければなりません。
上級のテクニックである”末っ子の甘え排除（XY-Wing）”を利用すれば解ける問題でも，中級のテクニックまでしか利用できない解答者にとっては，背理法が必要な問題になってしまいます。 極端な例を２つ挙げます。
１）今までに発表されているどんなテクニックを利用しても解けず，背理法を利用しなければ解けない問題であったとします。 新たなテクニックが開発されて，そのテクニックに依って解答できるようになれば，その時点から，背理法を利用しなくても解答できる問題になります。
２）一番基本的な”八面楚歌（Full House）”でも，数字の確定をエレガントに証明しようとすれば，背理法が必要になります。
背理法を使わないでナンプレを楽しむためには，その問題を解くために必要なテクニックのレベルが問題に併記されているか あるいは ほのめかされていること が重要になるでしょう。 さもなくば，難問に出くわしたときに 自分の利用できるテクニックをいくら適応しようとしても先へ進めない蟻地獄から這い出せなくなってしまいます。
背理法が必要になった状況の有用さについて説明します。
理解しているテクニックをどのように駆使しても手詰まりになったが，背理法を利用すればなんとか解ける という状況になったとします。 これは，実は 大飛躍の可能性を秘めたときなのです。 今までに発表されているテクニックを再度勉強して，使えるテクニックを新たに習得することができます。
自身で一生懸命思案することによって，新テクニックの発見につながるかも知れません。 ほとんどの 中上級のテクニックも，”数字が特別な条件下に配置されていると，背理法を利用することによって，数字を配置できない情報が得られる”というものです。
背理法の利用は，認知症の初期状態での脳トレに非常に役立ちます。 認知症の初期には，直近の記憶は悪くなりますが，昔から培われてきた知識は保たれます。 ナンプレを解くときに，背理法で仮の数字を配置することは直近の記憶能力で処理されます。 そこから解答を進めるには，認知症の初期には失われていない過去の知識を利用します。 さて，仮数字を配置して解答を進めて，矛盾に陥ったとします。 どこまで逆のぼってどうしたらよいのでしょうか？ これは認知症の初期段階では苦手とされる作業です。 ここに挑戦することは直近の出来事の記銘力低下防止の訓練になります。 仮配置の枝分かれが複雑になればなるほど，良い刺激になります。
（ナンプレの難問を背理法を利用して解くことは その他の認知症の症状（二つ以上のことが重なるとうまく処理できなくなる，計画を立て按配することができなくなる，すべてが面倒に：厚生労働省 認知症の症状－中核症状と行動・心理症状）の予防，改善にも役立ちそうです）
解法のテクニックを利用せずに背理法に頼ってしまうと，筆運に左右されてせっかくの良問がつまらなくなるとされています。 しかし，自分が使うことができる以上のテクニックを要求される問題では，背理法の助けを借りなければ，正解を得るという感動は経験できません。 難易度のわからない問題に挑戦しているときには，正解を得てパズルが楽しめた というためには，背理法も一法でしょう。 ただ，あるマスにある数字を仮置して解答を進めて矛盾なく全８１マスが埋まったとしても，残りの枝分かれがすべて矛盾に陥り，正解が唯一であることだけは，是非確認してください。 万一背理法を誤解されている方がいたらいけないのでの忠告です。背理法と いわゆる 仮置き とは別物です。 ”背理法とは何か”は大学入試でも出題されています。 何らかの仮定を置いて論理を展開すると結論が得られることによって証明する方法 という答えは不正解です。 ナンプレで 背理法という言葉を使う場合 筆運に左右される仮置き と 背理法 とが区別なく使われることが時々ありますが， 背理法は 本来 あるマスに正解以外の数字を配置すると（正解の数字を配置するという命題が 偽 と仮定すると）必ず矛盾に陥る ことによって証明する方法です。 あるマスにある数字を仮置して解答を進めて全８１マスが埋まったから解けたというのは，多分正解が唯一であろう パズル”ナンプレ”が解けたということだけです。 公開される ナンプレ問題が 唯一解を前提としているので 背理法と仮置法が 一致しているだけです。 唯一解であることの証明は 出題者ではなく 解答者に要求されているとすべきでしょう （この考え方を採ると Uniqueness はナンプレテクニックとしては疑問符がつくようになります（Uniqueness を利用すること自体は 大いに 論理的思考の訓練になります））。
since 2011.8.25
頭頭が良くなる 楽しい ナンプレ 数独 ナンバープレイス ドクター中尾 人工知能 無料 フリーソフト ダウンロード 本格的ナンプレソフト 論理的思考能力 理Ⅲ 問題集 難問集 難問 問題解答 問題作成 初期配置指定 テクニック 解き方 解法のヒント テクニック ソルバー 仮置なし 仮置きなし 手詰まり わかりやすい 分かりやすい 分かり易い 手筋