中級のテクニックは,排除する数字を見つけるときに,1つの領域(行,列または大マス)の中だけを検討します。
そこのけ排除[Locked Candidates],
二都物語系排除[Naked Pairs],
姉妹系排除[Hidden Pairs] の3つのテクニックがあります。
このページでは,二都物語系排除を説明します。
二都物語排除[Naked Pairs]を発展させた, 三都物語排除[Naked Triples], 四都物語排除[Naked Quadruples]についても説明します。
また,都物語排除[Naked Subsets] と 姉妹排除[Hidden Subsets] の関係についても説明します。
このページでは,二都物語系排除を説明します。
二都物語排除[Naked Pairs]を発展させた, 三都物語排除[Naked Triples], 四都物語排除[Naked Quadruples]についても説明します。
また,都物語排除[Naked Subsets] と 姉妹排除[Hidden Subsets] の関係についても説明します。
 [Naked Pairs,n(n=2)国同盟 type 1,定員確定,Disjoint Subsets(DS)] 練習問題へ
[Naked Pairs,n(n=2)国同盟 type 1,定員確定,Disjoint Subsets(DS)] 練習問題へ
 [テクニック]
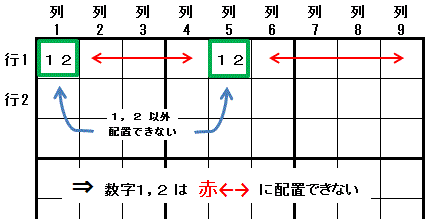
[テクニック]一つの行(または列・大マス)の2つのマスに配置できる数字が2種類(2つ)に限られたときに成立します。
それらの2つの数字は,その行(または列・大マス)の他のマスには配置できません。
行1 で,列1 と 列5 には 数字1 と 数字2 以外の数字が配置できない場合を考えます。
行1 で 列1 と 列5 は,どちらかが 数字1 であり,もう一つのマスが 数字2 になります。 行1 では,数字1 と 数字2 は その他の列(2,3,4,6,7,8,9) には配置できないことがわかります。
[名称”二都物語排除”の由来]
ディケンズの長編小説から名前をとっていますが,排除の考え方は原作のあらすじとは関係ありません。 ある国(行1)には,2つの都[城](行1列1・行1列5)があります。 2つの城には2人の城主候補(数字1・数字2)だけしか城主として居城することができません。 城主候補(数字1・2)は城を守るためそれぞれの城にひとりずつ居城し,鄙[いなか](行1 の 列2,3,4,6,7,8,9)には住むことがありません。
[テクニック”二都物語排除”の発展]
行でなく,同じ列・大マスでも2つのマスに配置できる数字が2種類(2つ)に限られたときに成立します。
同じ領域の3つのマスに配置できる数字が3種類に限られる場合も,それらの数字は同じ領域の他のマスには配置できません (三都物語排除[Naked Triples,3国同盟 type 1,Disjoint Chain(DC)])。 さらに発展させれば,四都物語排除[Naked Quadruples],五都物語排除,六都物語排除,...のテクニックとなります。
 [テクニック”二都物語排除”の例]
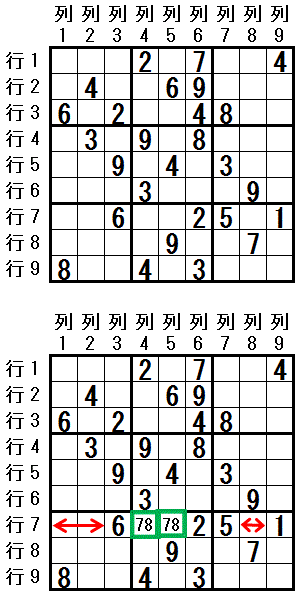
[テクニック”二都物語排除”の例]左図で,配置可能な数字が2つに限られるマスは,
行3列4(数字1,数字5)
行7列2(数字7,数字9)
行7列4(数字7,数字8)
行7列5(数字7,数字8)
行9列8(数字2,数字6)
の 5つがあります。
(ダウンロードいただいたソフトで,配置可能な数字が2つに限られるマス を黄色に塗りつぶした ペンシルマーク を表示可能です。下線部分をクリックしてください)
行7 に注目します。 下図を参照してください。
行7列4 には,数字7,数字8 しか配置できません。
行7列5 にも,数字7,数字8 しか配置できません。
つまり,行7列4 と 行7列5 の,どちらかのマスは 数字7 であり,もう一つのマスは 数字8 になります。 行7のその他のマス には,数字7,数字8 を配置できません。
ダウンロードいただいたソフトでは,
▼二都物語排除( 行 )排除数字▼ 7 行 7 列 1
▼二都物語排除( 行 )排除数字▼ 7 行 7 列 2
▼二都物語排除( 行 )排除数字▼ 8 行 7 列 8
行 7 では 列 4 と 5 には 数字 7 と 8 のみ配置できる
と,表示します(新たに得られた排除情報以外は表示しません)。
数字8が 行5列8 に配置されることがわかります(一人っ子[列])。

[練習問題 ”二都物語排除”適応局面]
問題図に直接テクニック”二都物語排除”が適応できます。
問題図をクリックすると,解説と正解が表示されます。
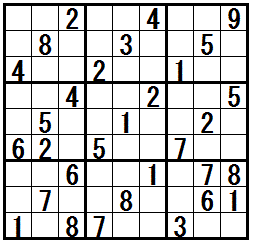
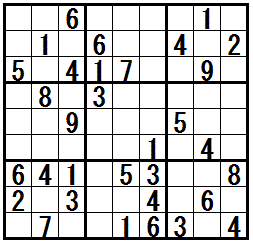
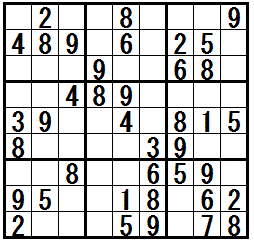
[練習問題 ”二都物語排除”]
解答の途中で テクニック”二都物語排除” が必要になる問題です。
一番右の問題は テクニック”そこのけ排除” と テクニック”二都物語排除” を利用します。
問題図をクリックすると,正解と思考過程の例が表示されます。
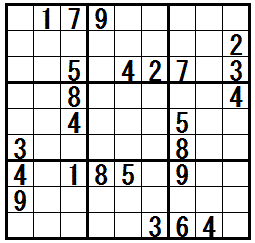



 [Naked Triples,3国同盟 type 1]
[Naked Triples,3国同盟 type 1]
 [テクニック]
[テクニック]二都物語排除 の発展テクニックです。
一つの領域(行,列または大マス)の3つのマスに配置できる数字が3種類に限られたときに成立します。
それらの3つの数字は,その領域の他のマスには配置できません
三都物語排除では 1つのマスに配置できる数字が3つある必要はありません。
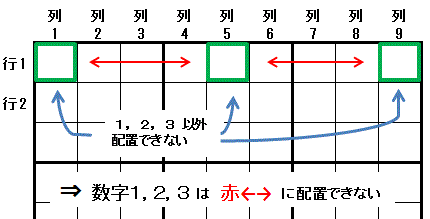
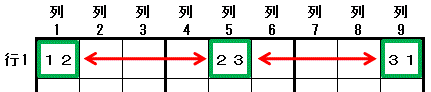 左図のような 緑の3マス に配置できる数字が 数字1,数字2,数字3 の3種類に限られている場合を考えます。
各マスには 数字1,数字2,数字3 の3数字のうち 2つの数字しか配置できませんが,三都物語排除が成立します。数字1,数字2,数字3 は 赤い矢印のマス には配置できません。
左図のような 緑の3マス に配置できる数字が 数字1,数字2,数字3 の3種類に限られている場合を考えます。
各マスには 数字1,数字2,数字3 の3数字のうち 2つの数字しか配置できませんが,三都物語排除が成立します。数字1,数字2,数字3 は 赤い矢印のマス には配置できません。四都物語排除以上でも同様です。
[練習問題 ”三都物語排除”適応局面]
問題図に直接テクニック”三都物語排除”が適応できます。
問題図をクリックすると,解説と正解が表示されます。
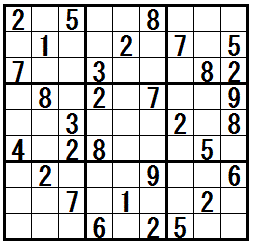

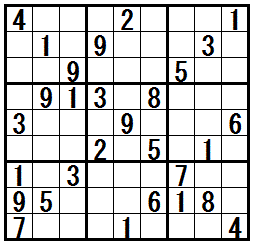
[練習問題 ”三都物語排除”]
解答の途中で テクニック”三都物語排除” が必要になる問題です。
一番右の問題は テクニック”三都物語排除” 以外の中級のテクニック も利用します。
問題図をクリックすると,正解と思考過程の例が表示されます。
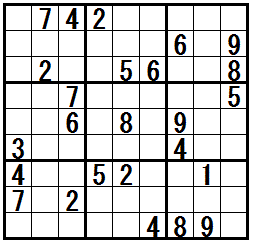
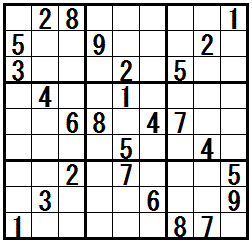
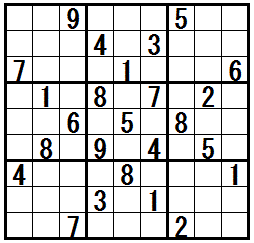
[三都物語排除の補足]
三都物語排除が発見できたら,三都巡りの旅に出かけましょう。 京都・大阪・神戸(奈良)も良いですが,盛岡,青森,秋田を拠点に世界遺産の旅はいかがでしょうか。 初夏には,福島で桃狩り,山形でサクランボ狩りを楽しんで松島湾島巡りです。

 [Naked Quadruples,4国同盟 type 1]
[Naked Quadruples,4国同盟 type 1]
[テクニック]
二都物語排除 の発展テクニックです。
一つの領域(行,列または大マス)の4つのマスに配置できる数字が4種類に限られたときに成立します。
それらの4つの数字は,その領域の他のマスには配置できません。
(三都物語排除と同じで 4つの各マスで 配置できる数字が4つある必要はありません)
[練習問題 ”四(五)都物語排除”適応局面]
(左の問題)問題図に直接テクニック”四都物語排除”が適応できます。
(中央の問題)問題図に,そこのけ排除,三都物語排除を適応した後,”四都物語排除”が適応できます。
(右の問題)問題図に”五都物語排除(三姉妹排除)”を適応したあとに,そこのけ排除を利用します。
問題図をクリックすると,解説と正解が表示されます。
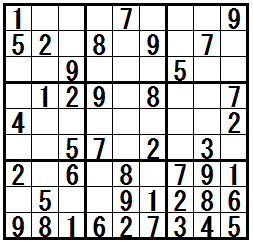
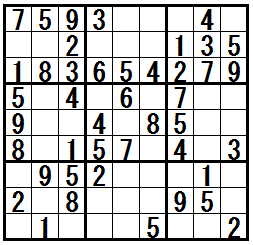
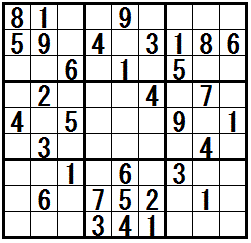
[練習問題 ”四都物語排除”]
解答の途中で テクニック”四都物語排除” が必要になる問題です。
他の 中級のテクニック も利用する問題もあります。
問題図をクリックすると,正解と思考過程の例が表示されます。

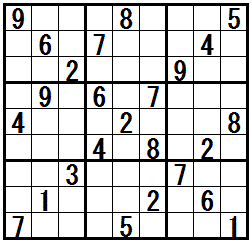
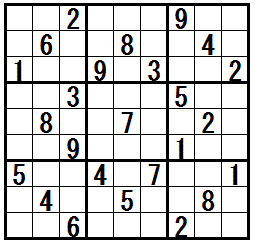

都物語排除[Naked Subsets] と 姉妹排除[Hidden Subsets] の関係
◎ 都物語排除(二都物語系排除) が成立する領域では 姉妹排除(姉妹系排除) が成立する
ある領域で 都物語排除 が成立するときは,その領域の残りのマスでは (別のページで説明する)姉妹排除 が成立し,どちらの排除の方法を使っても,同じ数字が同じマスに配置できないことがわかります。
下図 9つの数字を A,B,C,D,1,2,X,Y,Z とし,行1 では,すべての配置可能な数字が記載されている とします。
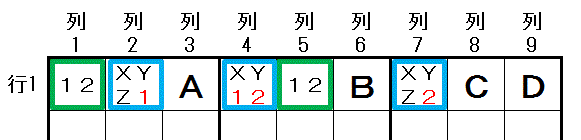 列3,6,8,9 の 数字A,B,C,D はすでに確定しています。
列3,6,8,9 の 数字A,B,C,D はすでに確定しています。緑の2つのマス 行1列1 と 行1列5 には2種類の数字 数字1 と 数字2 しか配置できません。 二都物語排除によって,行1 の他の列にある 数字1(列2,列4),数字2(列4,列7)は 配置できないことがわかります。
一方,3つの 数字X,Y,Z は 青い3つのマス 行1列2,行1列4,行1列7 にだけ配置可能です(緑のマスには数字1,2のみ配置可能です)。 三姉妹排除により,他の 数字1 と 数字2 は,行1列2,行1列4,行1列7 に配置できないことになります。 これは,二都物語排除で排除されたものと同じです。
配置が確定していない数字が N個 である領域で k都物語排除 が成立するときには,残りのマスで (N−k)姉妹排除 が成立します。
都物語排除 と 姉妹排除 が 本質的に同じであることの一般化した説明は, ここ をクリックしてください。
下図は 冒頭に挙げた テクニック”二都物語排除の例” です。これを三姉妹排除で解釈します。
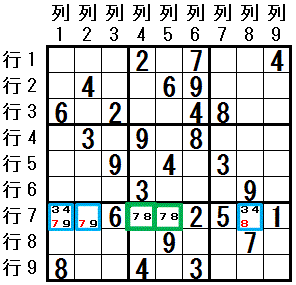 行7 で,
行7 で,3つの数字 数字3,4,9 は,
3つのマス 行7列1,行7列2,行7列8 以外には配置できません (行7列4,行7列5 には 数字7,数字8 しか配置できません)。
三姉妹排除 により,
マス 行7列1,行7列2,行7列8 には,
3つの数字 数字3,4,9 以外の 数字7,数字8 は配置できません。
これは,二都物語排除で排除された マス,数字 と同じです。

◎ 都物語・姉妹排除は 四都物語排除まで と 四姉妹排除まで を検索すれば 十分です
すべてのマスで配置する数字の確定していない領域を考えます。 この領域で,五都物語排除以上 または 五つ子排除以上 が成立する場合 残りのマスで 四姉妹排除(以下) または 四都物語排除(以下) が成立します。 よって,実際に問題を解くときには,四都物語排除まで と 四姉妹排除まで の検索をすれば十分です。
解答者の得手不得手によって 五都物語排除以上,五つ子排除以上 を利用することは問題ありません。
どのマスにも 配置する数字 が確定していない領域で 四都物語排除 と 五つ子排除 が成立する局面を例示します。
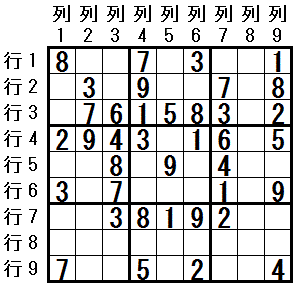 行8 に 四都物語排除が適応できます。
行8 に 四都物語排除が適応できます。
▼四都物語排除( 行 )排除数字▼ 3 行 8 列 8
▼四都物語排除( 行 )排除数字▼ 6 行 8 列 1
▼四都物語排除( 行 )排除数字▼ 6 行 8 列 2
行 8 では 列 4 と 5 と 6 と 9 には
数字 3 と 4 と 6 と 7 のみ配置できる
一方,数字1,2,5,7,8 は
行8では, 列1,2,3,7,8 以外に配置できません。
数字1,2,5,8,9 に関して 五つ子排除 が成立して,
その5つの数字以外の数字(数字3,4,6,9)が 列1,2,3,7,8 に配置できないことがわかります。 上記の 四都物語排除と 同じマス で 同じ数字 が 排除されました。
上記の局面が出現する問題図 と その正解図です。 実際に解く場合は,四都物語排除は使わずに,AIC, NIce Loop などの 超上級テクニック を利用することになります。
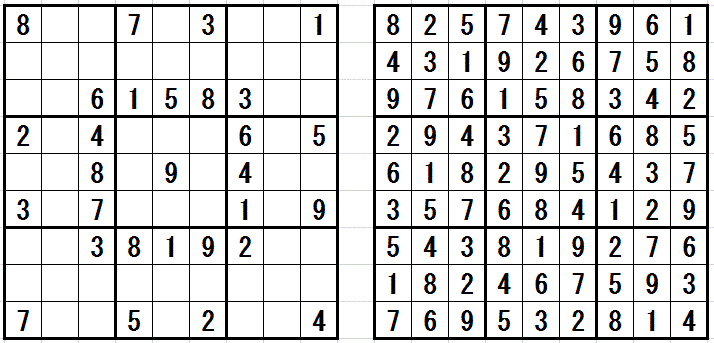

すべてのマスで配置する数字の確定していない領域を考えます。 この領域で,五都物語排除以上 または 五つ子排除以上 が成立する場合 残りのマスで 四姉妹排除(以下) または 四都物語排除(以下) が成立します。 よって,実際に問題を解くときには,四都物語排除まで と 四姉妹排除まで の検索をすれば十分です。
解答者の得手不得手によって 五都物語排除以上,五つ子排除以上 を利用することは問題ありません。
どのマスにも 配置する数字 が確定していない領域で 四都物語排除 と 五つ子排除 が成立する局面を例示します。
 行8 に 四都物語排除が適応できます。
行8 に 四都物語排除が適応できます。▼四都物語排除( 行 )排除数字▼ 3 行 8 列 8
▼四都物語排除( 行 )排除数字▼ 6 行 8 列 1
▼四都物語排除( 行 )排除数字▼ 6 行 8 列 2
行 8 では 列 4 と 5 と 6 と 9 には
数字 3 と 4 と 6 と 7 のみ配置できる
一方,数字1,2,5,7,8 は
行8では, 列1,2,3,7,8 以外に配置できません。
数字1,2,5,8,9 に関して 五つ子排除 が成立して,
その5つの数字以外の数字(数字3,4,6,9)が 列1,2,3,7,8 に配置できないことがわかります。 上記の 四都物語排除と 同じマス で 同じ数字 が 排除されました。
上記の局面が出現する問題図 と その正解図です。 実際に解く場合は,四都物語排除は使わずに,AIC, NIce Loop などの 超上級テクニック を利用することになります。






