<<命題のグループ化・一般化,ALS,AHS>>
・ ある1つのマスに ”配置可能な数字が 2つ に限られる” こと と,
・ ある数字が1つの領域(行,列,大マス)で ”配置可能なマスが 2つ に限られる” こと
をつなげていくことで情報を得るテクニックを チェーン(Chain)系のテクニック と呼びます。
5)グループ化,命題の一般化,ALS,AHS(このページ) から この考え方を拡張します。
チェーン について考察することは,論理的思考能力を向上させる ために有効です。
(チェーン系のテクニックを積極的に使用することをお勧めする訳では決してありません。ナンプレを楽しみながら論理的思考能力を高めるには,むしろ,名前のついた基本的な中上級のテクニックを理解し,利用することの方が有効です)
1)代表的なチェーン系テクニック
1−1)X-Chain
1−2)XY-Chain
1−3)その他(色分け法 (Simple Colors, Multi Colors), Remote Pair)
2)テクニックのチェーンによる解釈(その1)
2−1)筋違見張塔排除 (Skyscraper, 2-String Kite, Turbot Fish)
2−2)賢い見張兵排除(X-Wing)
2−3)末っ子の甘え排除(XY-Wing)
2−4)二都物語排除(Naked Pair)
3)チェーン系テクニックの原理
3−1)強いリンク,弱いリンク
3−2)AIC(Alternate Inference Chain),チェーン系テクニックの原理
4)テクニックのチェーンによる解釈(その2)
4−1)ネコとネズミ排除(W-Wing)
4−2)姉妹排除(Hidden Pair)
4−3)浜田ロジック
5)グループ化,命題の一般化,ALS,AHS
5−1)グループ化
5−2)命題の一般化
5−3)ALS(Almost Locked Sets)
5−4)AHS(Almost Hidden Sets)
6)テクニックのチェーンによる解釈(その3)
6−1)信長の野望排除(XYZ-Wing)
6−2)二守備線見張塔過多排除(Finned・Sashimi X-Wing)
6−3)三・四都物語排除(Naked Triple・Quadruple)
6−4)三・四姉妹排除(Hidden Triple・Quadruple)
6−5)カーブミラー排除(Empty Rectangle)
6−6)三・四人の賢い見張兵排除(Swordfish・Jellyfish)
6−7)Sue de Coq
このページでは,5)グループ化,命題の一般化,ALS,AHS を説明します。
・ ある1つのマスに ”配置可能な数字が 2つ に限られる” こと と,
・ ある数字が1つの領域(行,列,大マス)で ”配置可能なマスが 2つ に限られる” こと
をつなげていくことで情報を得るテクニックを チェーン(Chain)系のテクニック と呼びます。
5)グループ化,命題の一般化,ALS,AHS(このページ) から この考え方を拡張します。
チェーン について考察することは,論理的思考能力を向上させる ために有効です。
(チェーン系のテクニックを積極的に使用することをお勧めする訳では決してありません。ナンプレを楽しみながら論理的思考能力を高めるには,むしろ,名前のついた基本的な中上級のテクニックを理解し,利用することの方が有効です)
1)代表的なチェーン系テクニック
1−1)X-Chain
1−2)XY-Chain
1−3)その他(色分け法 (Simple Colors, Multi Colors), Remote Pair)
2)テクニックのチェーンによる解釈(その1)
2−1)筋違見張塔排除 (Skyscraper, 2-String Kite, Turbot Fish)
2−2)賢い見張兵排除(X-Wing)
2−3)末っ子の甘え排除(XY-Wing)
2−4)二都物語排除(Naked Pair)
3)チェーン系テクニックの原理
3−1)強いリンク,弱いリンク
3−2)AIC(Alternate Inference Chain),チェーン系テクニックの原理
4)テクニックのチェーンによる解釈(その2)
4−1)ネコとネズミ排除(W-Wing)
4−2)姉妹排除(Hidden Pair)
4−3)浜田ロジック
5)グループ化,命題の一般化,ALS,AHS
5−1)グループ化
5−2)命題の一般化
5−3)ALS(Almost Locked Sets)
5−4)AHS(Almost Hidden Sets)
6)テクニックのチェーンによる解釈(その3)
6−1)信長の野望排除(XYZ-Wing)
6−2)二守備線見張塔過多排除(Finned・Sashimi X-Wing)
6−3)三・四都物語排除(Naked Triple・Quadruple)
6−4)三・四姉妹排除(Hidden Triple・Quadruple)
6−5)カーブミラー排除(Empty Rectangle)
6−6)三・四人の賢い見張兵排除(Swordfish・Jellyfish)
6−7)Sue de Coq
このページでは,5)グループ化,命題の一般化,ALS,AHS を説明します。
最初に AIC を復習します(3−2) AIC(Alternate Inference Chain))
ナンプレで利用するチェーンは,強いリンク と 弱いリンク が交互につながったチェーンで(AIC:Alternate Inference Chain), 以下に示すような 最初 と 最後 が 強いリンク になったチェーンでは, 『最初の命題P0 と 最後の命題Pn のどちらかが必ず成立します』。
命題P0⇒命題P1(強いリンク)
命題P1→命題P2(弱いリンク)
命題P2⇒命題P3(強いリンク)
・・・
命題Pn-2→命題Pn-1(弱いリンク)
命題Pn-1⇒命題Pn(強いリンク)
ここまでは,ナンプレ で使用する命題は,”ある数字をあるマスに配置する”というものです としてきました。
しかし,このリンク・チェーンに関する知見は論理学的な事実であり,命題はどんなものでも構いません。
2つの例を説明します。
5−1) グループ化
例えば,”数字1 をマス 行1列1 に配置する または 数字1 を マス 行1列2 に配置する” も 一つの命題になります。グループ化 と呼びます。 下図で説明します。
数字1 を 行5列5 に配置する ことをスタートとして,チェーンを考えます,
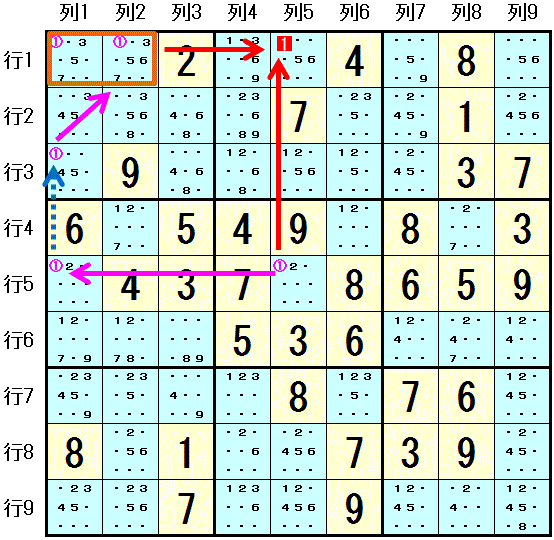
数字1を行5列5に配置する
⇒ (強いリンク(行5))
数字1を行5列1に配置する
→ (弱いリンク(列1))
数字1を行3列1に配置する
ここでチェーンは途切れてしまいます。 しかし,”数字1を行1列1に配置する または 数字1を行1列2に配置する”という命題を考えると, 大マス1 で この命題と,数字1を行3列1 に配置するという命題との間には,
どちらか片方が成り立つ
同時に両方が成り立つことはない
という関係が成り立ちます。つまり,両命題の間には 強いリンク がある ということになります。
上でに示したチェーンはこの関係を利用して延長することができます。
⇒ (強いリンク(大マス1))
数字1を行1列1に配置する または 数字1を行1列2に配置する
両端が 強いリンク である AIC(Alternate Inference Chain) になりました。
両端で チェーンをつなげるのに使われない命題はどちらか一方が必ず成り立ちます。
つまり,
”数字1を行5列5に配置する”
と
”数字1を行1列1に配置する または 数字1を行1列2に配置する”
はどちらか一方が必ず成り立ちます。
すると,数字1 はこの3マス 行5列5,行1列1,行1列2 のいずれかに配置されることになり, この3マス全てと同じ領域にある 行1列5 に 数字1 が配置できないことがわかります。
この例は 長さ4 のチェーン(筋違見張塔排除[2-String Kite])ですが,任意のチェーンで グループ化 は利用することができます。

5−2) 命題の一般化
ナンプレで利用する命題は,さらに一般化された命題,複雑に論理式を組み合わせた命題でも構いません。
一般化された命題の例としては ”N個のマスに配置可能な数字がN個に限られる”というものがあります。 次の項 5−3)ALS(Almost Locked Sets) で説明します。
複雑に論理式を組み合わせた命題は 6−3)三都物語排除(Naked Triple) で例示します。
このあたりから先の議論は,論理学的には深みを増しますが, パズルとしては,複雑すぎる・見つけるのは不可能に近い,場合によってはおもしろみがなくなる と感じる方もたくさん出てくると思います。 ”頭が良くなる楽しい”と冠しているのに恐縮ですが, パズルとしては楽しくないとお感じの方でも, 論理思考が好きな方の中には 頭が良くなりそうで楽しい と思ってくださる方もいるものとして ご容赦ください。 もちろん 読み飛ばされても構いません。
チェーン系テクニックの説明の冒頭に チェーン系テクニックを積極的に利用するよりも 名前のついた基本的テクニックを利用する方が論理的思考能力の向上に有効であると記載しましたが, ここから先に説明するチェーン系テクニックは,その適応を検討するときに かなりの論理的能力を使います。論理的思考能力の向上に有効です。 ここまでに説明した比較的簡単なチェーン系テクニックを 機械的に適応して何らかの情報を得たときでも, その裏にある論理を都度確認すれば 論理的思考能力の向上に役立ちます。
5−3) ALS(Almost Locked Sets)
都物語排除(Naked Subsets) を検索しているときに, あと少しで 排除の前提条件(ある領域(行・列 または 大マス)で N個のマスに配置可能な数字がN個に限られる)が成立する状態が見つかることがあります。 ”ある領域(行・列 または 大マス)で N個のマスに配置可能な数字がN+1個に限られる” という状態です。 ALS(Almost Locked Sets)と呼びます。 ALS 単独では何らの知見も得られません。しかし,これを 強いリンク がある2つの命題と解釈することができます。すなわち
命題P:そのN個のマスのどれかに ある数字 が配置される
命題Q:そのN個のマスに配置可能な数字が その数字を除いたN個に限られる(Naked Subsets)
この2つの命題は,どちらか一方が必ず成り立ち,同時に成立することはありません。 つまり 命題P と 命題Q の間には 強いリンク があります。これを,チェーンに組み込んで AIC を作ることができます。
以下で これを利用した 4つのテクニック を説明します。
1)ALS−XZ
2)ALS Chain
3)Death Blossom
4)Doubly Linked ALS−XZ
再確認:ある領域(行・列 または 大マス)で N個のマスに配置可能な数字がN個に限られる(Naked Subsets)ときには, それらの数字は,その領域では 他のマスには配置できない(N個のマスのどこかに配置される)。
1)ALS−XZ
最初に2つの ALS を組み合わせます。2つのALSをつなぎ合わせるための数字(RCC)を定義します。
両方のALSどちらにも含まれる数字があり,その数字が2つのALSで配置可能なマスがすべて同じ領域にある ときに,
その数字を RCC(Restricted Common Candidate) と呼びます。
注意:2つのALSに共通のマスがある場合,そのマスに配置可能な数字は RCC とはしません
2つのALS(ALS1, ALS2)に RCC が存在すると(X とします),
RCCではない数字で 2つのALSのどちらにも含まれる数字は,
2つのALSでその数字が配置可能なマスの全てと同じ領域にある 両ALS以外のマス には 配置できません(数字を Z とします)。
説明)AIC として説明します。
RCCは その定義から ALS1 と ALS2 の両方に配置されることはありません。つまり, RCC が ALS1 に配置されることと RCC が ALS2 に配置されること の間には弱いリンクがあります。以下の AIC が成立します。
ALS1 が RCC を除いた Naked Subset になっている ⇒ RCCがALS1のマスに配置される(強いリンク)
RCCがALS1のマスに配置される → RCCがALS2のマスに配置される(弱いリンク)
RCCがALS2のマスに配置される ⇒ ALS2 が RCC を除いた Naked Subset になっている(強いリンク)
最初と最後の命題
ALS1 が RCC を除いた Naked Subset になっている
ALS2 が RCC を除いた Naked Subset になっている
はどちらかが必ず成り立ちます。 RCCではない どちらのALSにも含まれる数字は, 最低どちらかのALSの1マスに配置されるので
両ALS内でその数字が配置可能な全てのマスと同じ領域にある 両ALS以外のマス には配置できません。
ALS−XZ は 長さ4のAIC と考えることができます。後述する ALS Chain では 長さが2 と考えることもできます。
実際の問題で説明します。
図のペンシルマークに 行4列7 に 数字1 を配置できない情報を追加して ALS−XZ の説明に入ります。
この情報は 大マス6 では 数字2 と 数字3 は 行4列7 と 行6列9 の2マスにしか配置できないので,姉妹排除(Hidden Pair)が成立することから得られます。
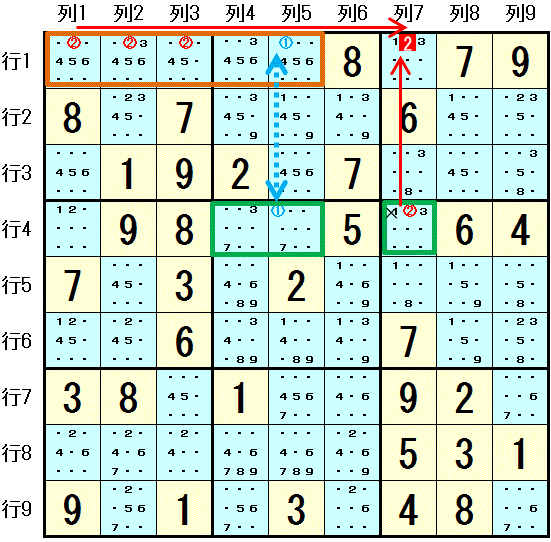
1つめの ALS1 は 行1 の 行1列1,行1列2,行1列3,行1列4,行1列5 の 5マス で, この5マスには 6つの数字 数字1,数字2,数字3,数字4,数字5,数字6 しか配置できません。
2つめの ALS2 は 行4 の 行4列4,行4列5,行4列7 で, この3マスには 4つの数字 数字1,数字2,数字3,数字7 しか配置できません。
両方のALSに含まれる 数字1 が配置可能なマスは,ALS1 では 行1列5 のみであり, ALS2 では 行4列5 のみです。 両マスは 同じ列5 にあります。
数字1 は RCC になります。
両ALSに含まれ RCCではない 数字2 は 両ALS で配置可能なマスが, 行1列1,行1列2,行1列3 および 行4列7 です。数字2 は これら全てと同じ領域にあり,両ALS には含まれないマス 行1列7 に配置できないことがわかります。
(ALS−XZ の別の解釈)
Naked Subsets は,本来,ある領域で N個のマス に配置できる数字が N個 に限られると, その領域では それらの数字はそれらのマス以外のマスには配置できないという排除のロジックでした。
ALS−XZ の例から得られた結論をこの形で表現すると,”RCC以外のALS1の数字は ALS1 以外のその領域のマスには配置できない” または ”RCC以外のALS2の数字は ALS2 以外のその領域のマスには配置できない” のどちらかが成り立つ となります。
これを利用してチェーンを延ばしていくこともできます。 すぐに結論を得られる例としては, 両ALSに含まれる RCC 以外の数字で 両ALSが属する領域の ALS以外のマス と同じ領域にある共通のマスがあり, その数字がそれらの領域で配置可能なマスが その共通マスとそのALS以外のマスの2つに限られる場合 その数字はその共通マスに配置される というものがあります。 文章にすると難解なので,上の問題を少し変形してこの解釈を説明します (初級の問題になっていて 実戦では ALS−XZ を必要とはしません)。
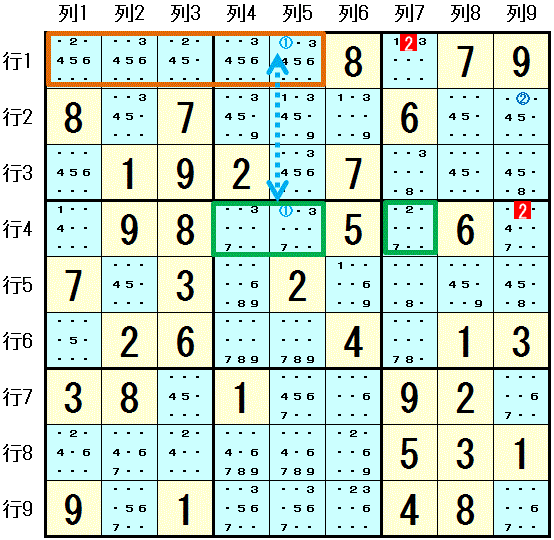
1つめの ALS1 は 行1 の 行1列1,行1列2,行1列3,行1列4,行1列5 の 5マス で 6つの数字 数字1,数字2,数字3,数字4,数字5,数字6 しか配置できません。
2つめの ALS2 は 行4 の 行4列4,行4列5,行4列7 で 4つの数字 数字1,数字2,数字3,数字7 しか配置できません。
数字1 は RCC になります。
ALS1 が 数字1以外の数字の Naked Subset である と ALS2 が 数字1以外の数字の Naked Subset である のどちらかが成立します。
Naked Subset になった ALS ではそれが属する領域で ALS以外のマスには RCC以外の数字を配置できないので,例えば RCCではない 数字2 で
行1列7 に配置できない と
行4列9 に配置できない
のどちらか一方は必ず成り立ちます。
行2列9 は この2マス(行1列7,行4列9)と同じ領域(大マス3,列9)にあります。
数字2 が 大マス3 で配置可能なマスは 行1列7 と 行2列9 の2つのみであり, 列9 で配置可能なマスは 行4列9 と 行2列9 の2つのみであり, この両者には 行2列9 が共通しています。 数字2 が 行2列9 に配置されることが確定します。
このことは,もしそのような共通のマス(行2列9)に,RCC以外のある数字(数字2)が配置されないと, 両ALS が含まれる領域のALS以外のマス(行1列7 および 行4列9)に そのRCC以外の数字(数字2)が配置されることが確定し, 両ALS が RCCを含む Naked Subsets となり 矛盾を生じる(両方のALSに含まれるRCCは1つの領域にあるので同時に両ALSには配置されない) ことからもわかります。

2)ALS Chain
ALS−XZ は AIC ですから,既存の ALS と 新たな ALS との間に RCC が存在すれば つなげていくことができます。
注意:この時 最後の RCC と次につなげるための RCC は異なる数字でなければなりません。
AIC で説明します。
ALS1 と ALS2 が RCC1 でつながっているとします。
ALS1 が RCC1 を除いた Naked Subset になっている⇒RCC1がALS1のマスに配置される(強いリンク)
RCC1がALS1のマスに配置される→RCC1がALS2のマスに配置される(弱いリンク)
RCC1がALS2のマスに配置される⇒ALS2 が RCC1 を除いた Naked Subset になっている(強いリンク)
ここで利用した RCC1 とは 別のRCC(RCC2) で ALS3 がつながれば ALS2 が RCC1 を除いた Naked Subset になっている と ALS2 が RCC2 を除いた Naked Subset になっている は同時には成り立たないので
ALS2 が RCC1 を除いた Naked Subset になっている
⇒
ALS2 が RCC2 を除いた Naked Subset になっている(弱いリンク)
という 弱いリンクを介して
ALS2 が RCC2 を除いた Naked Subset になっている⇒RCC2がALS2のマスに配置される(強いリンク)
RCC2がALS2のマスに配置される→RCC2がALS3のマスに配置される(弱いリンク)
RCC2がALS3のマスに配置される⇒ALS3 が RCC2 を除いた Naked Subset になっている(強いリンク)
とつながり AIC となります。 ALS をつなげていくときの 最初と最後の ALS のどちらか一方が Naked Subsets になります。
もちろん つながりのなかの 任意の2つの ALS でも,どちらか一方が Naked Subsets になります。
ALS−XZ の時のように ”両端のALSにあり 両端のRCC以外の数字で その数字が両ALS内で配置可能な全てのマスと同じ領域にある両端のALS以外のマスが存在すると その数字は そのマス には配置できません” とまで議論を進めるのが一般的ですが,このまま(どちらか一方が Naked Subsets になる)にしておくほうが汎用性が増します(次の例で示します)。
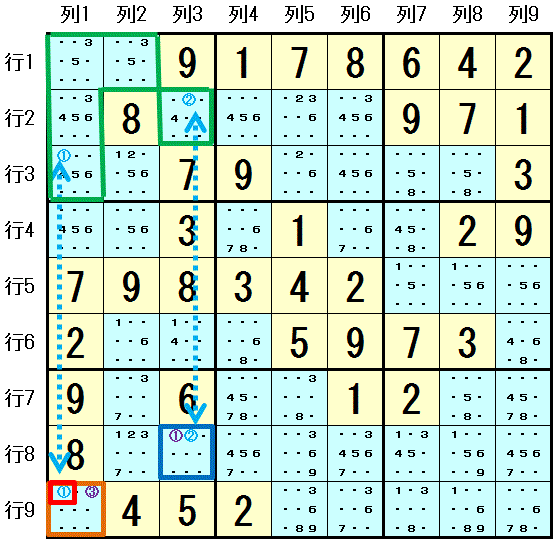
最初の ALS−XZ を説明します。
1つめの ALS1 は 行9列1 の 1マス に 2つの数字 数字1,数字3 しか配置できないというものです。このような形でも ALS になっています。
2つめの ALS2 は 大マス1の 行1列1,行1列2,行2列1,行2列3,行3列1 の5マスで この5マスには 6つの数字 数字1,数字2,数字3,数字4,数字5,数字6 しか配置できません。
この2つのALS で 数字1 が RCC になっています。
次の ALS−XZ は ALS2 と 3つめの ALS3(行8列3 の 1マス に 2つの数字 数字1,数字2 しか配置できない)とが 数字2 を RCC としてつながっているというものです。
このつながりで ”両端のALSにあり 両端のRCC以外の数字で その数字が両ALS内で配置可能な全てのマスと同じ領域にある両端のALS以外のマスが存在すると その数字は そのマス には配置できません”と解釈するのには無理があるので, その前段階の 両端の命題はどちらか一方が必ず成り立つ という結論を利用します。 つまり, ALS1 が RCC(数字1)を除いた Naked Subset になっている か ALS3 が RCC(数字2)を除いた Naked Subset になっている のどちらか一方が必ず成り立つという結論を利用します。 これらはそれぞれ 行9列1 が 数字3 である, 行8列3 が 数字1 である ことを表しています。 この2つのうちのどちらか一方が成り立つので 行9列1 に 数字1 は配置できないことがわかります。
この例は 長さ3の ALS Chain となります(長さ8 のAICになっています)。 長さ3の ALS Chain を ALS−XY−Wing と呼びます。

3)Death Blossom
ALS Chain は ALS をつなげて延ばしていきましたが, 1つのマス にいくつかの ALS が関連するときにも排除される数字を見つけることができる場合があります。
1つのマス(幹)に配置可能な数字全てに対し,その数字を RCC とする ALS(花びら) が存在すると, それらALSで 幹に配置可能な数字以外のある数字が配置可能なマス全てと同じ領域のマスには その数字は配置できません。
幹 のマスにはいずれかの数字が配置されるので,それに対応する 花びらの ALS はいずれかが必ず Naked Subset になるからです。
幹に配置可能な数字が3つ以上の時には 幹のマス は ALS になっていませんが,幹のマスにその数字を配置すること と その数字を除くとALSが Naked Subset になっていることの間に 強いリンク があるので RCC という言葉を借用します。
実際の問題で説明します。
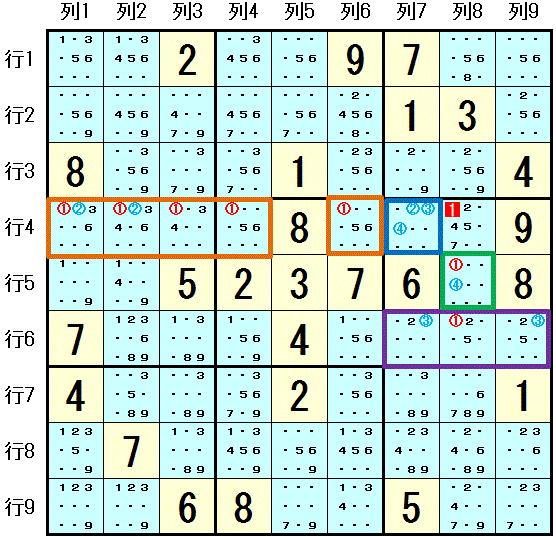
行4列7 が 3つの数字 数字2,数字3,数字4 が配置可能な 幹 になります。 幹 との間には幹に配置可能な3つの数字を RCC とする 次の 3つの花びら ALS が存在します。
数字2 を RCC とする 行4 の 6つの数字 数字1,数字2,数字3,数字4,数字5,数字6 だけが配置可能な 5つのマス 行4列1,行4列2,行4列3,行4列4,行4列6
数字3 を RCC とする 大マス6 の 4つの数字 数字1,数字2,数字3,数字5 だけが配置可能な 3つのマス 行6列7,行6列8,行6列9
数字4 を RCC とする 大マス6 の 2つの数字 数字1,数字4 だけが配置可能な 1つのマス 行5列8
これら3つの ALS のどれか一つが必ず RCCを除いた数字の Naked Subset になります。
全ての ALS に属し,RCC ではない 数字1 が ALSで配置可能なマス全てが 行4列8 と同じ領域にあるので
数字1 が 行4列8 に配置できないことがわかります。
幹 に配置可能な数字が 2つ の場合は ALS−XY−Wing となります。

4)Doubly Linked ALS−XZ
2つの ALS の間に 2つの RCC がある場合です。RCC が1つである ALS−XZ よりも 多くの排除の情報 が得られます。
それぞれの ALS で RCC以外の数字は そのALSの領域のALS以外のマスには 配置できなくなります。 両方のALSとも 2つのRCCのうちの1つのRCCを除いた 2つの Naked Subset のうちどちらかが必ず存在するからです。
2つのALS を ALS1,ALS2 とし,2つのRCC を RCC1,RCC2 とします。 ALS1 に関して,
ALS1 が RCC1 を除いた Naked Subset になっている⇒RCC1がALS1のマスに配置される(強いリンク)
RCC1がALS1のマスに配置される→RCC1がALS2のマスに配置される(弱いリンク)
RCC1がALS2のマスに配置される⇒ALS2 が RCC1 を除いた Naked Subset になっている(強いリンク)
ALS2 が RCC1 を除いた Naked Subset になっている と ALS2 が RCC2 を除いた Naked Subset になっている は同時には成り立たないので
ALS2 が RCC1 を除いた Naked Subset になっている
⇒
ALS2 が RCC2 を除いた Naked Subset になっている(弱いリンク)
という 弱いリンクが存在します。これを利用してして ALS1 に戻ります。
ALS2 が RCC2 を除いた Naked Subset になっている⇒RCC2がALS2のマスに配置される(強いリンク)
RCC2がALS2のマスに配置される→RCC2がALS1のマスに配置される(弱いリンク)
RCC2がALS1のマスに配置される⇒ALS1 が RCC2 を除いた Naked Subset になっている(強いリンク)
ALS1 が RCC1 を除いた Naked Subset になっている と ALS1 が RCC2 を除いた Naked Subset になっている はどちらか一方が必ず成り立ちます。
これは ALS1 で RCC1,RCC2 以外の数字を含んだ Naked Subsets が必ず成り立つことを意味するので, ALS1 の領域で ALS1以外のマスには RCC1,RCC2 以外の数字を配置できないことがわかります。
ALS2 に関しても同様です。
以下の例で説明します。
数字4 は 列7 では 大マス6 にしか配置できないので,大マス6 で 列7以外の列には配置できません(そこのけ排除[Locked Candidate])。
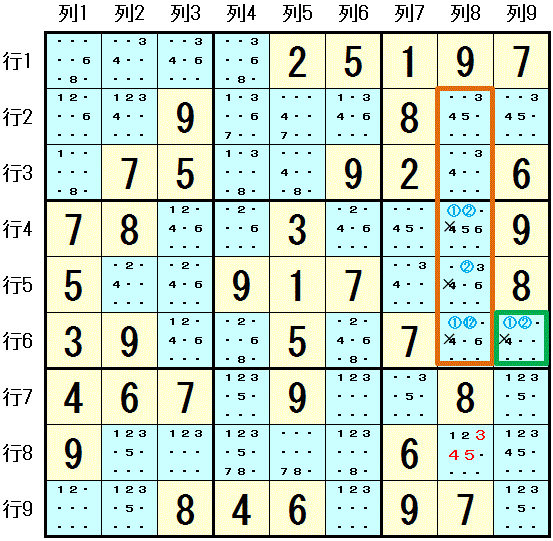
1つめの ALS1 は 列8 の 行2列8,行3列8,行4列8,行5列8,行6列8 の 5マス で この5マスには 6つの数字 数字1,数字2,数字3,数字4,数字5,数字6 しか配置できません。。
2つめの ALS2 は 行6列9 で このマスには 2つの数字 数字1,数字2 しか配置できません。
数字1 と 数字2 の2つの数字が RCC になります。
列8 の ALS1 はRCCである 数字1,2 のうちのどちらか1つの数字 と 数字3,数字4,数字5,数字6 の Naked Subset に 必ずなるので, 数字3,数字4,数字5 は 列8 の ALS1 以外のマス に配置できないことになります。
数字3,数字4,数字5 が 行8列8 に配置できないことがわかります。 (数字4 は この ALS1 に配置されますが 大マス3 にしか配置できないので 行2列9 に配置できないこともわかります)。

5−4)AHS(Almost Hidden Subsets)
ALS は Naked Subsets を見つけようと検索しているときに もう少しで Naked Subsets になりそうな マス,数字の組み合わせとして見つかるもので,前項では それを利用して何らかの情報を得るテクニックを説明しました。
Hidden Subsets を見つけようと検索しているときにも もう少しで Hidden Subsets になりそうな マス,数字の組み合わせは見つかります。
ある領域で N個の数字が配置可能なマスが N+1個に限られるとき それを AHS(Almost Hidden Subset)と呼びます。ALS と同じような論理を展開できます。
2つの AHSを考えます。この2つのAHSのどちらかが必ず Hidden Subset になる条件を考えます。
2つの AHS をつなぎ合わせるのに ALS で利用した RCC は導入できません。 つまり RCC として 2つのAHSどちらにも含まれる数字であり,その数字が2つのAHSで配置可能なマスがすべて同じ領域にある とはできません。 なぜなら まず そのような RCC が 片方のAHS に配置されると,そのRCC をもう片方のAHSに配置できなくなります。 さらに AHSの数字は AHS を含む領域では AHS のマスにしか配置できないので RCC がその領域に全く配置できなくなってしまうからです。
両方のAHSのマスを含む領域で,両方のAHSの数字ではない数字k個 が,その領域で AHS に含まれないマスで, 配置可能なマスの数が K−1個以下であるものが存在する と どちらかの AHS が Hidden Subset になります(その領域に両AHSの共通のマスがあってはいけません)。
この条件で 2つの AHS が結びつけられた場合,
2つの AHS のどちらにも含まれる数字が 両者を結びつけるのに利用された領域以外で配置可能なマス全てと同じ領域にあるマスに その数字は配置できません。
筋違見張塔排除[Skyscraper, 2-String Kite, Turbot Fish]は, ある領域で1個の数字が配置可能なマスが2つに限られ,その数字が同じである2つのAHSが結びつけられたものと解釈できます。 AHS による排除 を理解するために 2-String Kite で説明した例を取り上げます。
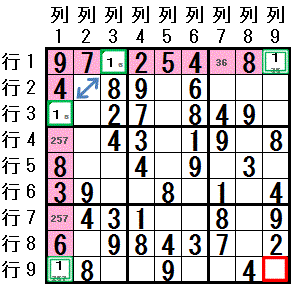
AHS1 は 行1 で,1つの数字 数字1 は 2つのマス 行1列3,行1列9 にしか配置できません。
AHS2 は 列1 で,1つの数字 数字1 は 2つのマス 行3列1,行9列1 にしか配置できません。
AHS1 のマス 行1列3 ,AHS2のマス 行3列1 が属する 大マス1 では, 3つの数字 数字3,数字5,数字6 は AHS 以外のマスでは 2つのマス 行2列2,行3列2 にしか配置できません。
2つの AHS が結びつけられました。 どちらかの AHS が必ず 両者を結びつけるのに利用された領域(大マス)に含まれる1マスを除いた Hidden Subset になります。
数字1 は 大マス1 以外で 配置可能なAHSのマス 行1列9 と 行9列1 のどちらかに必ず配置されます。
その2マスと同じ領域(列9 および 行9)にあるマス 行9列9 には 数字1 を配置できません。
もう少し複雑な AHS を模式図で説明します。
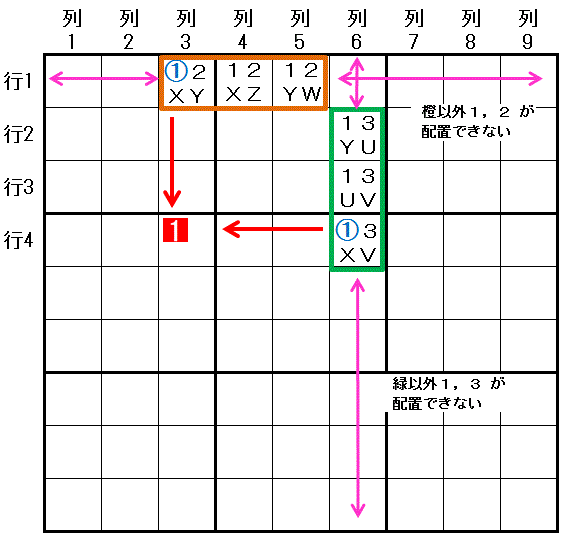
行1 では 2つの数字 数字1,数字2 は 行1列3,行1列4,行1列5 の3マスにしか配置できません(AHS1)。
列6 では 2つの数字 数字1,数字3 は 行2列6,行3列6,行4列6 の3マスにしか配置できません(AHS2)。
数字1〜3 以外の6つの数字は X,Y,Z,W,U,V で表しています。
両方のAHSのマスを含む 大マス2 では 6つの数字 数字X〜V は AHS以外のマスで配置可能なマスは 最大5つです(それらのいくつかは配置が確定していても構いません)。
大マス2 では 数字X〜V のどれか1つの数字は AHS のマスに配置されることになります。 すると AHS1 と AHS2 のどちらか一方は Hidden Subset になります。
AHS1で 両者を結びつけるのに利用された領域以外のマス 行1列3 に 数字1 または 数字2 が配置される と
AHS2で 両者を結びつけるのに利用された領域以外のマス 行4列6 に 数字1 または 数字3 が配置される
は どちらか一方が成り立ちます。 数字1 は 大マス2 で 両方のAHS には配置されないので
行1列3 に 数字1 が配置される と
行4列6 に 数字1 が配置される
のどちらか一方が成り立ちます(行1列3 に 数字2 が配置され かつ 行4列6 に 数字3 が配置される ことはないからです)。
行4列3 に 数字1 が配置できないことがわかります。
ALS と同じように AHS を もう少しで Hidden Subset になるものとしての別解釈を説明します。
上記の模式図では,
数字X,数字Y が 行1列3 に配置されない
数字X,数字V が 行4列6 に配置されない
のどちらか一歩が成り立ちます。
もし 数字X が 列3 および 行4 で配置可能なマスが 共通のマス 行4列3 と 行1列3,行4列6 の2つに限られていれば, 数字X が 行4列3 に配置されることが確定します。
別解釈の例をやはり筋違見張塔排除(2-String Kite)で示します。
行8 の 2つのマス 行8列1,行8列7 で配置可能な数字は 数字7,数字9 の2つのみなので, 数字7,数字9 は 行8列2 に配置できません(二都物語排除[Naked Pair])。
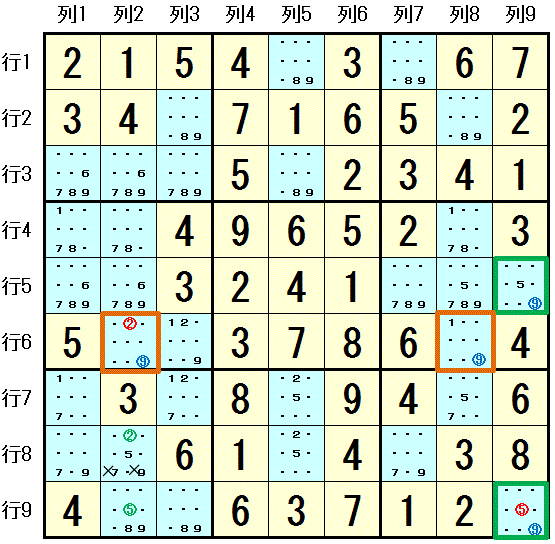
AHS1 は 行6 で,1つの数字 数字9 は 2つのマス 行6列2,行6列8 にしか配置できません。
AHS2 は 列9 で,1つの数字 数字9 は 2つのマス 行5列9,行9列9 にしか配置できません。
AHS1 のマス 行6列8,AHS2 のマス 行5列9 が属する 大マス6 では, どちらのAHSにも含まれない 4つの数字 数字1,数字5,数字7,数字8 は 大マス6 では AHS のマス行6列8,行5列9を除いた 3つのマス 行4列8,行5列7,行5列8 にしか配置できません。 2つの AHS のどちらか一方は Hidden Subset になります。
数字2 が 行6列2 に配置できない
数字5 が 行9列9 に配置できない
のどちらかが成り立ちます。
数字2 が 列2 で配置可能なマスは2つのみであり
数字5 が 行9 でも配置可能なマスも2つのみなので,
数字2 が 行8列2 に配置される
数字5 が 行9列2 に配置される
のどちらかが成り立ちます。
いずれの場合でも
数字2 が 行8列2 に配置され,数字5 が 行9列2 に配置されることになります。
AHS はチェーンとして延長することができます (2つのAHS両方のマスを含む領域で AHS以外の数字k個が AHS以外で配置可能なマスがk−1個以下という条件でつないでいきます) 。
Death Blossom に対応するテクニックも存在します (1つの領域にいくつかのAHSのマスが含まれる場合で AHS以外の数字が その領域で AHS 以外で配置可能なマスの数を条件とします) 。
Doubly Linked ALS−XZ に対応するのは,
両方のAHSのマスを含む領域(その領域に両AHSの共通のマスがあってはいけません)で,両方のAHSの数字ではない数字k個 が,その領域で AHS に含まれないマスで, 配置可能なマスの数が K−2個であるものが存在する
となります(共通の領域以外のAHSのマスにはAHS以外の数字を配置できません)。





