＜＜テクニックのチェーンによる説明（１）＞＞
・ ある１つのマスに ”配置可能な数字が ２つ に限られる” こと と，
・ ある数字が１つの領域（行，列，大マス）で ”配置可能なマスが ２つ に限られる” こと
をつなげていくことで情報を得るテクニックを チェーン(Chain)系のテクニック と呼びます。
５）グループ化，命題の一般化，ＡＬＳ，ＡＨＳ から この考え方を拡張します。
チェーン について考察することは，論理的思考能力を向上させる ために有効です。
（チェーン系のテクニックを積極的に使用することをお勧めする訳では決してありません。ナンプレを楽しみながら論理的思考能力を高めるには，むしろ，名前のついた基本的な中上級のテクニックを理解し，利用することの方が有効です）
１）代表的なチェーン系テクニック
１−１）X-Chain
１−２）XY-Chain
１−３）その他（色分け法 （Simple Colors, Multi Colors）, Remote Pair）
２）テクニックのチェーンによる解釈（その１）
２−１）筋違見張塔排除 （Skyscraper, 2-String Kite, Turbot Fish）
２−２）賢い見張兵排除（X-Wing）
２−３）末っ子の甘え排除（XY-Wing）
２−４）二都物語排除（Naked Pair）
３）チェーン系テクニックの原理
３−１）強いリンク，弱いリンク
３−２）ＡＩＣ(Alternate Inference Chain)，チェーン系テクニックの原理
４）テクニックのチェーンによる解釈（その２）
４−１）ネコとネズミ排除(W-Wing)
４−２）姉妹排除（Hidden Pair）
４−３）浜田ロジック
５）グループ化，命題の一般化，ＡＬＳ，ＡＨＳ
５−１）グループ化
５−２）命題の一般化
５−３）ＡＬＳ(Almost Locked Sets)
５−４）ＡＨＳ(Almost Hidden Sets)
６）テクニックのチェーンによる解釈（その３）
６−１）信長の野望排除（XYZ-Wing）
６−２）二守備線見張塔過多排除（Finned・Sashimi X-Wing）
６−３）三・四都物語排除(Naked Triple・Quadruple)
６−４）三・四姉妹排除(Hidden Triple・Quadruple)
６−５）カーブミラー排除（Empty Rectangle）
６−６）三・四人の賢い見張兵排除(Swordfish・Jellyfish)
６−７）Ｓｕｅ ｄｅ Ｃｏｑ
このページでは，２）テクニックのチェーンによる解釈（その１） を説明します。
・ ある１つのマスに ”配置可能な数字が ２つ に限られる” こと と，
・ ある数字が１つの領域（行，列，大マス）で ”配置可能なマスが ２つ に限られる” こと
をつなげていくことで情報を得るテクニックを チェーン(Chain)系のテクニック と呼びます。
５）グループ化，命題の一般化，ＡＬＳ，ＡＨＳ から この考え方を拡張します。
チェーン について考察することは，論理的思考能力を向上させる ために有効です。
（チェーン系のテクニックを積極的に使用することをお勧めする訳では決してありません。ナンプレを楽しみながら論理的思考能力を高めるには，むしろ，名前のついた基本的な中上級のテクニックを理解し，利用することの方が有効です）
１）代表的なチェーン系テクニック
１−１）X-Chain
１−２）XY-Chain
１−３）その他（色分け法 （Simple Colors, Multi Colors）, Remote Pair）
２）テクニックのチェーンによる解釈（その１）
２−１）筋違見張塔排除 （Skyscraper, 2-String Kite, Turbot Fish）
２−２）賢い見張兵排除（X-Wing）
２−３）末っ子の甘え排除（XY-Wing）
２−４）二都物語排除（Naked Pair）
３）チェーン系テクニックの原理
３−１）強いリンク，弱いリンク
３−２）ＡＩＣ(Alternate Inference Chain)，チェーン系テクニックの原理
４）テクニックのチェーンによる解釈（その２）
４−１）ネコとネズミ排除(W-Wing)
４−２）姉妹排除（Hidden Pair）
４−３）浜田ロジック
５）グループ化，命題の一般化，ＡＬＳ，ＡＨＳ
５−１）グループ化
５−２）命題の一般化
５−３）ＡＬＳ(Almost Locked Sets)
５−４）ＡＨＳ(Almost Hidden Sets)
６）テクニックのチェーンによる解釈（その３）
６−１）信長の野望排除（XYZ-Wing）
６−２）二守備線見張塔過多排除（Finned・Sashimi X-Wing）
６−３）三・四都物語排除(Naked Triple・Quadruple)
６−４）三・四姉妹排除(Hidden Triple・Quadruple)
６−５）カーブミラー排除（Empty Rectangle）
６−６）三・四人の賢い見張兵排除(Swordfish・Jellyfish)
６−７）Ｓｕｅ ｄｅ Ｃｏｑ
このページでは，２）テクニックのチェーンによる解釈（その１） を説明します。
２）テクニックのチェーンによる解釈（その１）
”ある領域（行，列，または，大マス）で配置可能なマスが２つに限られる”や ”１つのマスに配置可能な数字が２つに限られる” という条件をつなげて，数字が排除されるマスを見つけるテクニックは，チェーン系の考え方で解釈することができます。 ここでは，チェーン系テクニックの代表である X-Chain，XY-Chain で簡単に解釈できるテクニックについて説明します。
２−１） 筋違見張塔排除（Skyscraper, 2-String Kite, Turbot Fish）
筋違見張塔排除 は 鎖の長さが ４ の X-Chain です。
＜＜2-String Kite＞＞
下左側に 筋違見張塔排除(2-String Kite) の説明 に利用した図を示します。 その右側に示す X-Chain の説明 に利用した図と似ています。 X-Chain を説明するときに使った図（右）は，筋違見張塔排除(2-String Kite) の説明に使った図（左）を拡張したものです。
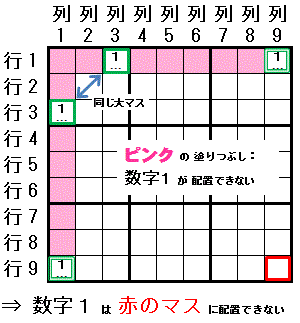
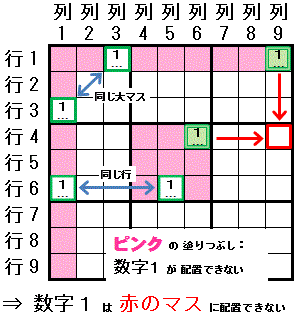
左：筋違見張塔排除(2-String Kite) 数字１は，行１で配置可能なマスは 行１列３と行１列９ の２マスに限られます。 列１でも配置可能なマスは 行３列１，行９列１ の２マスに限られます。 行１列３と行３列１ は同じ 大マス１ に存在します。 この時，数字１は 行１列９と行９列１ のどちらのマスとも同じ領域にある 行９列９ に配置できません。
下の図は，上左側の 筋違見張塔排除(2-String Kite) の説明図を，スタートのマスを 行１列９ とし， 配置可能なマスが２つに限られる（強いリンク）ことを ピンクの矢印（------→）， 同じ領域にある（弱いリンク）ことを 青い点線の矢印（---→）で表現して書き換えたものです。 数字１ に関してチェーンを作成します。
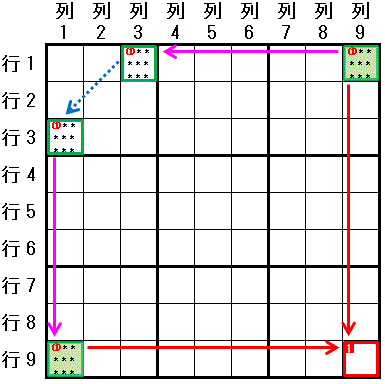
行１列９⇒行１列３：強いリンク（行１）
行１列３→行３列１：弱いリンク（大マス１）
行３列１⇒行９列１：強いリンク（列１）
［終点］
スタートのマス（行１列９） と 終点のマス（行９列１）が， 強いリンク と 弱いリンク が交互で（Alternate Inference Chain:AIC）， 両端が 強いリンク でつながりました。X-Chain です。
スタートのマス（行１列９） と 終点のマス（行９列１）の両方 と同じ領域（列９ および 行９）にある マス（行９列９） に 数字１ を配置できないことがわかります。
筋違見張塔排除(2-String Kite) は 鎖の長さが ４（チェーンに含まれるマスが４つ，リンクの数は３つ） の X-Chain と解釈することができます。
2-String Kite と同様に その他の筋違見張塔排除(Skyscraper, Turbot Fish) も 鎖の長さが ４ の X-Chain と解釈することができます。
筋違見張塔排除として説明した図（図をクリックすると，テクニックを説明するページを表示します）と X-Chain として解釈する図を対比して示します。
＜＜Skyscraper＞＞
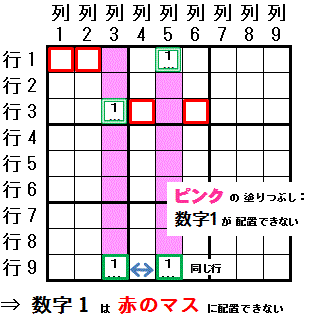数字１は，列３で配置可能なマスは 行３列３と行９列３ の２マスに限られます。
列５でも配置可能なマスは 行１列５，行９列５ の２マスに限られます。
行９列３と行９列５ は同じ 行９ に存在します。
この時，数字１は 行３列３と行１列５ のどちらのマスとも同じ領域にある 行１列１，行１列２，行３列４，行３列６ に配置できません。
下図で 数字１に関して，スタートのマスを 行３列３ として作成したチェーンを示します。
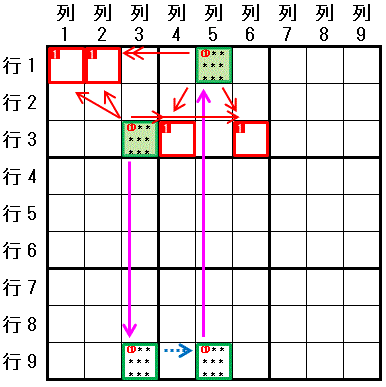行３列３⇒行９列３：強いリンク（列３）
行９列３→行９列５：弱いリンク（行９）
行９列５⇒行１列５：強いリンク（列５）
［終点］
スタートのマス（行３列３） と 終点のマス（行１列５）が， 強いリンク と 弱いリンク が交互で（Alternate Inference Chain:AIC）， 両端が 強いリンク でつながりました。X-Chain です。
スタートのマス（行３列３） と 終点のマス（行１列５）の両方 と同じ領域（大マス１と行１ および 行３と大マス２）にある マス（行１列１，行１列２，行３列４，行３列６） に 数字１ を配置できないことがわかります。
＜＜Turbot Fish＞＞
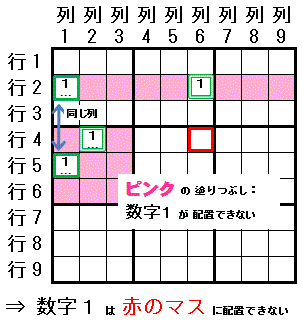数字１は，行２で配置可能なマスは 行２列６と行２列１ の２マスに限られます。
大マス４でも配置可能なマスは 行５列１，行４列２ の２マスに限られます。
行２列１と行５列１ は同じ 列１ に存在します。
この時，数字１は 行２列６と行４列２ のどちらのマスとも同じ領域にある 行４列６ に配置できません。
下図で 数字１に関して，スタートのマスを 行２列６ として作成したチェーンを示します。
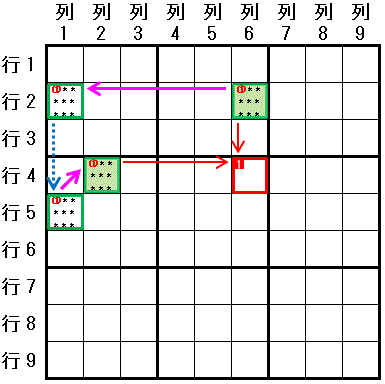行２列６⇒行２列１：強いリンク（行２）
行２列１→行５列１：弱いリンク（列１）
行５列１⇒行４列２：強いリンク（大マス４）
［終点］
スタートのマス（行２列６） と 終点のマス（行４列２）が， 強いリンク と 弱いリンク が交互で（Alternate Inference Chain:AIC）， 両端が 強いリンク でつながりました。X-Chain です。
スタートのマス（行２列６） と 終点のマス（行４列２）の両方 と同じ領域（列６ および 行４）にある マス（行４列６） に 数字１ を配置できないことがわかります。
”ある領域（行，列，または，大マス）で配置可能なマスが２つに限られる”や ”１つのマスに配置可能な数字が２つに限られる” という条件をつなげて，数字が排除されるマスを見つけるテクニックは，チェーン系の考え方で解釈することができます。 ここでは，チェーン系テクニックの代表である X-Chain，XY-Chain で簡単に解釈できるテクニックについて説明します。
２−１） 筋違見張塔排除（Skyscraper, 2-String Kite, Turbot Fish）
筋違見張塔排除 は 鎖の長さが ４ の X-Chain です。
＜＜2-String Kite＞＞
下左側に 筋違見張塔排除(2-String Kite) の説明 に利用した図を示します。 その右側に示す X-Chain の説明 に利用した図と似ています。 X-Chain を説明するときに使った図（右）は，筋違見張塔排除(2-String Kite) の説明に使った図（左）を拡張したものです。
左：筋違見張塔排除(2-String Kite) 数字１は，行１で配置可能なマスは 行１列３と行１列９ の２マスに限られます。 列１でも配置可能なマスは 行３列１，行９列１ の２マスに限られます。 行１列３と行３列１ は同じ 大マス１ に存在します。 この時，数字１は 行１列９と行９列１ のどちらのマスとも同じ領域にある 行９列９ に配置できません。
下の図は，上左側の 筋違見張塔排除(2-String Kite) の説明図を，スタートのマスを 行１列９ とし， 配置可能なマスが２つに限られる（強いリンク）ことを ピンクの矢印（------→）， 同じ領域にある（弱いリンク）ことを 青い点線の矢印（---→）で表現して書き換えたものです。 数字１ に関してチェーンを作成します。
行１列９⇒行１列３：強いリンク（行１）
行１列３→行３列１：弱いリンク（大マス１）
行３列１⇒行９列１：強いリンク（列１）
［終点］
スタートのマス（行１列９） と 終点のマス（行９列１）が， 強いリンク と 弱いリンク が交互で（Alternate Inference Chain:AIC）， 両端が 強いリンク でつながりました。X-Chain です。
スタートのマス（行１列９） と 終点のマス（行９列１）の両方 と同じ領域（列９ および 行９）にある マス（行９列９） に 数字１ を配置できないことがわかります。
筋違見張塔排除(2-String Kite) は 鎖の長さが ４（チェーンに含まれるマスが４つ，リンクの数は３つ） の X-Chain と解釈することができます。
2-String Kite と同様に その他の筋違見張塔排除(Skyscraper, Turbot Fish) も 鎖の長さが ４ の X-Chain と解釈することができます。
筋違見張塔排除として説明した図（図をクリックすると，テクニックを説明するページを表示します）と X-Chain として解釈する図を対比して示します。
＜＜Skyscraper＞＞
数字１は，列３で配置可能なマスは 行３列３と行９列３ の２マスに限られます。
列５でも配置可能なマスは 行１列５，行９列５ の２マスに限られます。
行９列３と行９列５ は同じ 行９ に存在します。
この時，数字１は 行３列３と行１列５ のどちらのマスとも同じ領域にある 行１列１，行１列２，行３列４，行３列６ に配置できません。下図で 数字１に関して，スタートのマスを 行３列３ として作成したチェーンを示します。
行３列３⇒行９列３：強いリンク（列３）行９列３→行９列５：弱いリンク（行９）
行９列５⇒行１列５：強いリンク（列５）
［終点］
スタートのマス（行３列３） と 終点のマス（行１列５）が， 強いリンク と 弱いリンク が交互で（Alternate Inference Chain:AIC）， 両端が 強いリンク でつながりました。X-Chain です。
スタートのマス（行３列３） と 終点のマス（行１列５）の両方 と同じ領域（大マス１と行１ および 行３と大マス２）にある マス（行１列１，行１列２，行３列４，行３列６） に 数字１ を配置できないことがわかります。
＜＜Turbot Fish＞＞
数字１は，行２で配置可能なマスは 行２列６と行２列１ の２マスに限られます。
大マス４でも配置可能なマスは 行５列１，行４列２ の２マスに限られます。
行２列１と行５列１ は同じ 列１ に存在します。
この時，数字１は 行２列６と行４列２ のどちらのマスとも同じ領域にある 行４列６ に配置できません。下図で 数字１に関して，スタートのマスを 行２列６ として作成したチェーンを示します。
行２列６⇒行２列１：強いリンク（行２）行２列１→行５列１：弱いリンク（列１）
行５列１⇒行４列２：強いリンク（大マス４）
［終点］
スタートのマス（行２列６） と 終点のマス（行４列２）が， 強いリンク と 弱いリンク が交互で（Alternate Inference Chain:AIC）， 両端が 強いリンク でつながりました。X-Chain です。
スタートのマス（行２列６） と 終点のマス（行４列２）の両方 と同じ領域（列６ および 行４）にある マス（行４列６） に 数字１ を配置できないことがわかります。
２−２） 賢い見張兵排除（X-wing）
賢い見張兵排除（X-wing）は，２本の X-Chain と解釈できます。
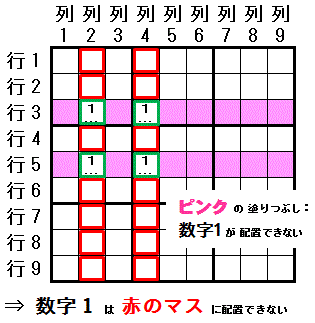左図は 賢い見張兵排除 の説明 に利用した図です。数字１は，行３で配置可能なマスは 行３列２，行３列４ の２マスに限られます。 行５でも配置可能なマスは 行５列２，行５列４ の２マスに限られます。 行３列２と行５列２ は同じ 列２ に存在し，行３列４と行５列４ は同じ 列４ に存在します。 この時，数字１ は 列２ と 列４ では，行３，行５で配置可能なマス（行３列２，行３列４，行５列２，行５列４）以外のマスには配置できません。
下図で 数字１に関して，スタートのマスを 行３列２ としてチェーンを作成します。
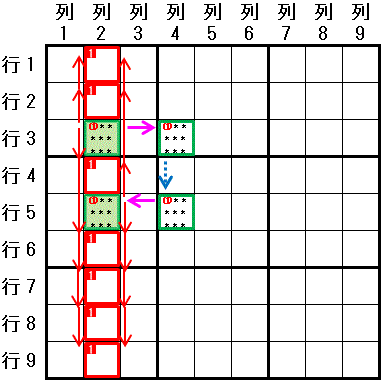行３列２⇒行３列４：強いリンク（行３）行３列４→行５列４：弱いリンク（列４）
行５列４⇒行５列２：強いリンク（行５）
［終点］
スタートのマス（行３列２） と 終点のマス（行５列２）が， 強いリンク と 弱いリンク が交互で（Alternate Inference Chain:AIC）， 両端が 強いリンク でつながりました。X-Chain です。
数字１ は，スタートのマス（行３列２） か 終点のマス（行５列２）の どちらかのマスに必ず配置されるので， 列２ では，その２つのマス以外のマス（行１列２，行２列２，行４列２，行６列２〜行９列２） には配置できません。
同様に，スタートのマスを 行３列４ として X-Chain（行３列４⇒行３列２→行５列２⇒行５列４）が作成され， 数字１ が，スタートのマス（行３列４） か 終点のマス（行５列４）の どちらかのマスに必ず配置されることから， 列４ では，その２つのマス以外のマス（行１列４，行２列４，行４列４，行６列４〜行９列４） には配置できないことがわかります。
賢い見張兵排除（X-wing）が X-Chain で解釈できました。
２−３） 末っ子の甘え排除（XY-wing）
下左側に 末っ子の甘え排除（XY-wing） の説明 に利用した図を示します。 その右側に示す XY-Chain の説明 に利用した図と似ています。 XY-Chain を説明するときに使った図（右）は，末っ子の甘え排除（XY-wing） の説明に使った図（左）を拡張したものです。
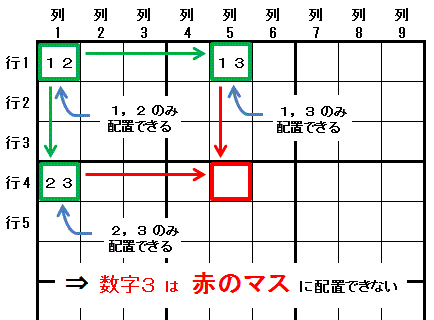
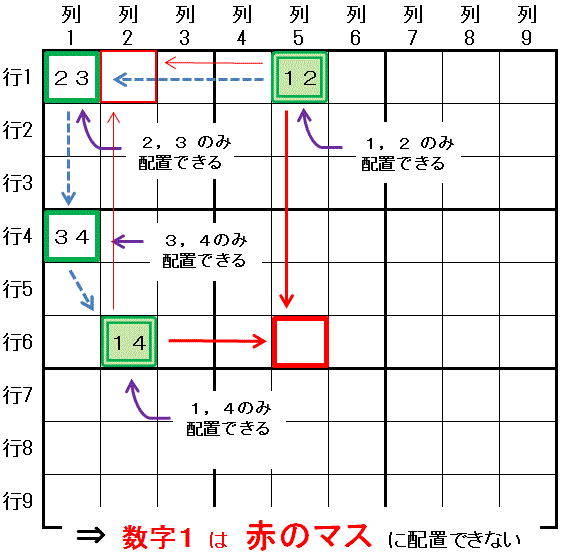
左：末っ子の甘え排除（XY-wing） 行１列１ には 数字１ と 数字２ の２つの数字しか配置できません。 行１列１ と同じ 行１ にある 行１列５ には 数字１ と 第三の数字 数字３ の２つの数字しか配置できません。 行１列１ と同じ 列１ にある 行４列１ には 数字２ と 第三の数字 数字３ の２つの数字しか配置できません。 この時，行１列５ と 行４列１ の両方と同じ領域にある（列５ と 行４） 行４列５ には 数字３ を配置できません。
下の図は，上左側の 末っ子の甘え排除（XY-wing） の説明図を，スタートのマスを 行１列５ とし， 同じ領域にある（弱いリンク）ことを 青い点線の矢印（---→）で表現して書き換えたものです。 この図の XY-Chain としての解釈を示します。
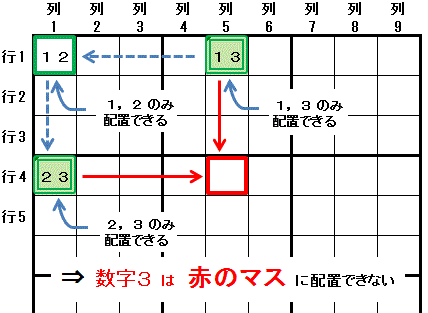行１列５：配置可能な数字が 数字３，数字１ に限られる行１列５→行１列１：同じ行１にある
行１列１：配置可能な数字が 数字１，数字２ に限られる
行１列１→行４列１：同じ列１にある
行４列１：配置可能な数字が 数字２，数字３ に限られる
スタートのマス（行１列５）と最後のマス（行４列１） で，鎖を形成するのに利用されない数字は，同じ 数字３ になりました。
この時，スタートのマス（行１列５）と最後のマス（行４列１）の両方と同じ領域（列５ および 行４）にあるマス（行４列５） にその数字（数字３）は配置できません。
末っ子の甘え排除（XY-wing）が XY-Chain として解釈できました。
１つのマスに配置可能な数字が２つに限られる場合，どちらかの数字が必ずそのマスに配置され，両方の数字が同時にそのマスに配置されることはありません。
１つのマスに配置可能な数字が２つに限られる場合，それぞれの数字をそのマスに配置することには 強いリンク があります。
上の 末っ子の甘え排除（XY-wing）を XY-Chain として解釈することの説明 にこの考え方を導入します。
最初の行，”行１列５：配置可能な数字が 数字３，数字１ に限られる” を
数字３ を 行１列５ に配置する ⇒ 数字１ を 行１列５ に配置する（数字３⇒数字１：マス行１列５（強いリンク））
と解釈します（強いリンクがあります）。
その他の 一つのマスに配置可能な数字が２つに限られる ことに関する行も 同様に解釈します。
すると，上記の説明は，
数字３ を 行１列５ に配置する ⇒ 数字１ を 行１列５ に配置する（数字３⇒数字１：マス行１列５（強いリンク））
数字１ を 行１列５ に配置する ⇒ 数字１ を 行１列１ に配置する（行１列５→行１列１：数字１，行１（弱いリンク））
数字１ を 行１列１ に配置する ⇒ 数字２ を 行１列１ に配置する（数字１⇒数字２：マス行１列１（強いリンク））
数字２ を 行１列１ に配置する ⇒ 数字２ を 行４列１ に配置する（行１列１→行４列１：数字２，列１（弱いリンク））
数字２ を 行４列１ に配置する ⇒ 数字３ を 行４列１ に配置する（数字２⇒数字３：マス行４列１（強いリンク））
と なります。
強いリンク（同じマスで配置可能なマスが２つに限られる） と 弱いリンク（同じ領域にある） が交互に繋がる 鎖（チェーン）になっていて（Alternate Inference Chain:AIC）， チェーンの両端は 強いリンク になっています。
最初のリンクと最後のリンクで鎖の作成に利用されないのは，数字３を行１列５に配置する ことと 数字３を行４列１に配置する ことです。
この形のチェーンでは，この２つの配置のどちらかが必ず成立します。 行１列５ と 行４列１ の両方と同じ領域にあるマス（行４列５）に 数字３ を配置できません。
鎖（チェーン）の長さ は 鎖に含まれる ある数字をあるマスに配置する ことの数とします。 この例では 鎖の長さは ６ になります。
あるマスに配置可能な数字が２つに限られることをこのように考えることを理解しておくと，チェーン系のロジックを発展的に考察することができるようになります。
２−４） 二都物語排除（Naked Pairs, ２国同盟(type1), 定員確保）
二都物語排除（Naked Pairs）は 一番短い（関連するマスが２つだけの）XY-Chain あるいは Remote Pair と考えることができます。最初に 二都物語排除の説明をします。
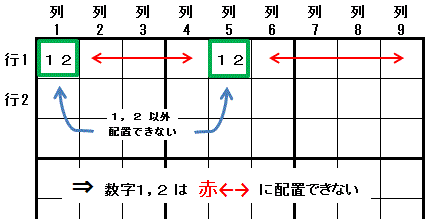二都物語排除：１つの領域（行，列 または 大マス：左図では行１）で２つのマス（左図では，行１列１ と 行１列５）に配置可能な数字が２種類（２つ）だけに限られると（左図では，数字１ と 数字２），
それらの数字（数字１，数字２）は その領域（行１）では それらのマス（行１列１ と 行１列５）以外のマスには配置できない。２種類の配置可能な数字１つ毎に直接 XY-Chain または Remote Pair を適応すれば，それらの数字はその領域では 配置可能な数字がその２種類の数字に限られたマス 以外のマスに配置できないことがわかります。
ここでは，前項（末っ子の甘え排除）の最後に示した 数字をあるマスに配置すること を単位として考えたチェーンによって配置できないマスが見つかることを説明します。
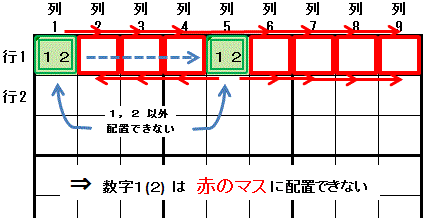最初に 数字１ を考えます。数字１ を 行１列１ に配置する ⇒ 数字２ を 行１列１ に配置する（数字１⇒数字２：マス行１列１（強いリンク））
数字２ を 行１列１ に配置する ⇒ 数字２ を 行１列５ に配置する（行１列１→行１列５：数字２，行１（弱いリンク））
数字２ を 行１列５ に配置する ⇒ 数字１ を 行１列５ に配置する（数字２⇒数字１：マス行１列５（強いリンク））
強いリンク と 弱いリンク が交互につながり（Alternate Inference Chain:AIC），両端は 強いリンク になっています。 このチェーンの両端である ”数字１ を 行１列１ に配置する” と ”数字１ を 行１列５ に配置する” は，どちらかが必ず成り立ちます。数字１は 行１では 行１列１，行１列５ 以外に配置できないことがわかります。 同様に 数字２ について考えれば，数字２が 行１では 行１列１，行１列５ 以外に配置できないことがわかります。