�@�@�s�v�������t
�@�㋉�̃e�N�j�b�N�ł́@�Q�ȏ�̗̈�i�s�C��C��}�X�j�@�̒����������邱�Ƃɂ���ā@�r������鐔���������܂��B ���̃y�[�W�ł́@�v�������n�@�ƌĂ��e�N�j�b�N�̂����̑�\�I�ȁ@�R�̃e�N�j�b�N
�E�����q�̊Â��r��[XY-wing]
�E�M���̖�]�r��[XYZ-wing]
�E�l�R�ƃl�Y�~�r��[W-wing]
��������܂��B
�@�v�������n�̃e�N�j�b�N�ł́C������������@�P�̃}�X�@�܂��́@�P�̗̈�ɑ�����Q�̃}�X�@�ɒ��ڂ��܂��B ���́i�����́j�}�X���N�_�Ƃ��ā@�����L����悤�Ɂ@���́i�����́j�}�X��������Q�̗̈���������܂��B ���̂Q�̗̈悻�ꂼ��̒��ɓ���̏��������}�X�����݂���ƁC���̓���̏������������̃}�X�Ɠ����̈�ɂ���}�X�Ɂ@�����@��r�����邱�Ƃ��ł���}�X�������邱�Ƃ�����܂��B �ڂ����́C�e�e�N�j�b�N�̐������������������B
�Ȃ��C�����������r��[X-wing]�@�́@�v�������n�@�ł͂Ȃ��@�e�������n�@�ɕ��ނ���܂��B
�@�㋉�̃e�N�j�b�N�ł́@�Q�ȏ�̗̈�i�s�C��C��}�X�j�@�̒����������邱�Ƃɂ���ā@�r������鐔���������܂��B ���̃y�[�W�ł́@�v�������n�@�ƌĂ��e�N�j�b�N�̂����̑�\�I�ȁ@�R�̃e�N�j�b�N
�E�����q�̊Â��r��[XY-wing]
�E�M���̖�]�r��[XYZ-wing]
�E�l�R�ƃl�Y�~�r��[W-wing]
��������܂��B
�@�v�������n�̃e�N�j�b�N�ł́C������������@�P�̃}�X�@�܂��́@�P�̗̈�ɑ�����Q�̃}�X�@�ɒ��ڂ��܂��B ���́i�����́j�}�X���N�_�Ƃ��ā@�����L����悤�Ɂ@���́i�����́j�}�X��������Q�̗̈���������܂��B ���̂Q�̗̈悻�ꂼ��̒��ɓ���̏��������}�X�����݂���ƁC���̓���̏������������̃}�X�Ɠ����̈�ɂ���}�X�Ɂ@�����@��r�����邱�Ƃ��ł���}�X�������邱�Ƃ�����܂��B �ڂ����́C�e�e�N�j�b�N�̐������������������B
�Ȃ��C�����������r��[X-wing]�@�́@�v�������n�@�ł͂Ȃ��@�e�������n�@�ɕ��ނ���܂��B
�@
 �mXY-wing�n�@�@���K����
�mXY-wing�n�@�@���K����
 �m�e�N�j�b�N�n
�m�e�N�j�b�N�n
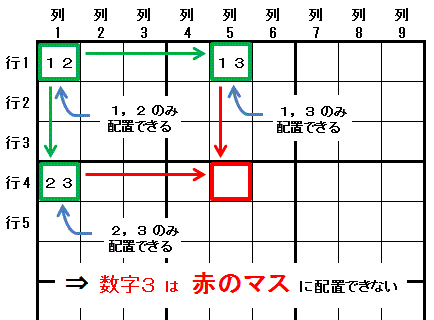
�ŏ��ɁC�Q�̐����i�����P�C�����Q�j�����z�u�ł��Ȃ��}�X�i�s�P��P�j�������܂��B
�E�s�P��P�@�Ɠ����s�ɑ����C�����P�@�Ɓ@��O�̐����@�����R�@�����z�u�ł��Ȃ��}�X�i�s�P��T�j
�ƁC
�E�s�P��P�@�Ɠ�����ɑ����C�����Q�@�Ɓ@��O�̐����@�����R�@�����z�u�ł��Ȃ��}�X�i�s�S��P�j
�����݂���ꍇ�C
�����Q�̃}�X�i�s�P��T�C�s�S��P�j�Ɠ����̈�ɑ�����}�X�i�s�S��T�j�@�ɂ́@��O�̐����@�����R �@�͔z�u�ł��܂���B
�����j�@�����C�s�S��T�@�Ɂ@�����R�@���z�u�����ƁC�s�P��T�@�́@�����P�@�� �s�S��P�@�́@�����Q�@���m�肵�C�s�P��P�@�ɔz�u�ł��鐔�����Ȃ��Ȃ�܂��B����āC�s�S��T�@�Ɂ@�����R�@�͔z�u�ł��܂���B
�m���́h�����q�̊Â��r���h�̗R���n
�@�s�P��P�@�́@�{���@�ŁC���q�i�����P�j�Ɓ@���q�i�����Q�j�������Z��ł��܂��B ���q�@�́@�{���@�Ɠ����̈�́@�s�P��T�@�Ɂ@���q�̕����@�����āC ���q�@���@�{���@�Ɠ����̈�́@�s�S��P�@�Ɂ@���q�̕����@�����Ă܂��B ��l�ƍ̗��ꂽ�Â���V�́@�����q�i�����R�j�́@���q�̕����@�Ɓ@���q�̕����@�ɓ���т���� �i���q�̕����@�ɂ́@���q�i�����P�j�Ɓ@�����q�i�����R�j�������Z�ނ��Ƃ��ł��C���q�̕����@�ɂ́@���q�i�����Q�j�Ɓ@�����q�i�����R�j�������Z�ނ��Ƃ��ł��܂��j�C �@�����q�̕����@�Ƃ��ė\�肵�Ă����@�s�S��T�@�ɂ͋����Ȃ��Ȃ��Ă��܂��܂����B
�m�e�N�j�b�N�h�����q�̊Â��r���h�̔��W�n
�@�@�z�u�ł��鐔�����Q�Ɍ����� �R�̃}�X�̈ʒu�W
�@�e�N�j�b�N�̍��Ő��������@�����s�E������ɑ�����@�Ƃ�������́C��}�X�������ā@�����̈�i�s�C��C��}�X�j�ɑ������@�Ƃ�������Ɍ��������Ă��r�����������܂��B ��}�X���W����ƁC��葽���̃}�X���琔����r���ł���\�����łĂ��܂��B
�e�N�j�b�N�̍��ł́@�����Q�@�Ɓ@�����R�@�݂̂��z�u�ł���}�X���@�ŏ��ɒ��ڂ����}�X�Ɓ@������@�ɑ����Ă��܂������C�����̂Q�̃}�X���@������}�X�@�ɑ������������܂��B
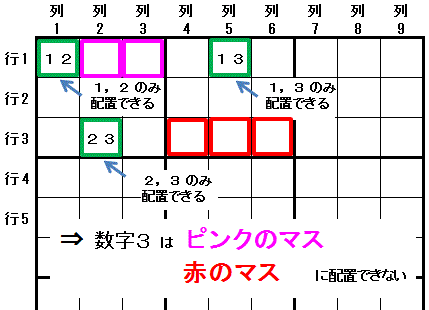 �s�P��P�@�ɂ́C�Q�̐����i�����P�C�����Q�j�����z�u�ł��܂���B
�s�P��P�@�ɂ́C�Q�̐����i�����P�C�����Q�j�����z�u�ł��܂���B
�s�P��P�@�Ɠ����s�ɑ�����}�X�@�s�P��T�@�ɂ́C�����P�@�Ɓ@��O�̐����@�����R�@�����z�u�ł��܂���B
�s�P��P�@�Ɓi������ł͂Ȃ��j������}�X�ɑ�����}�X�@�s�R��Q�ɂ́C�����Q�@�Ɓ@��O�̐����@�����R�@�����z�u�ł��܂���B
�����q�̊Â��r���̏�������������܂����B
�}�X�@�s�P��T�@�Ɠ����s�ɑ����C�s�R��Q�@�Ɠ�����}�X�i������j�ɑ�����}�X�@�s�P��Q�C�s�P��R�@�ƁC
�}�X�@�s�P��T�@�Ɠ�����}�X�i������j�ɑ����C�s�R��Q�@�Ɠ����s�ɑ�����}�X�@�s�R��S�C�s�R��T�C�s�R��U
�ɂ́@��O�̐����@�����R�@�͔z�u�ł��܂���B
�����C�s���N�@���́@���@�̃}�X �Ɂ@�����R�@���z�u�����ƁC�s�P��T�@�́@�����P�@�� �s�R��Q�@�́@�����Q�@���m�肵�C�s�P��P�@�ɔz�u�ł��鐔�����Ȃ��Ȃ邩��ł��B
�����q�̊Â��r���@�Ŕz�u����鐔�����Q�Ɍ�����@�R�̃}�X�@�̈ʒu�W�Ɋւ��Ắ@�����@���N���b�N���Ă��������B �����̈ʒu�W�ł́C�����q�̊Â��r���@�𗘗p���Ȃ��Ă��C�����܂ł̃e�N�j�b�N�@�𗘗p����C�r������鐔��������ł��܂��B
�A�@�ŏ��ɒ��ڂ���}�X�� �R�ȏ�̐������z�u�\
�@�ŏ��ɒ��ڂ���}�X�ɔz�u�\�Ȑ������R�ȏ�@���݂��Ă��C���ʂȏŁ@�z�u�ł��Ȃ������@����������ꍇ������܂��B �ŏ��ɒ��ڂ���}�X�ɔz�u�\�Ȑ����� �R�� �̏ꍇ���@�M���̖�]�r���mXYZ-wing�n�@�ƌĂсC���̍��Ő������܂��B

�m�e�N�j�b�N�h�����q�̊Â��r���h�̗�n
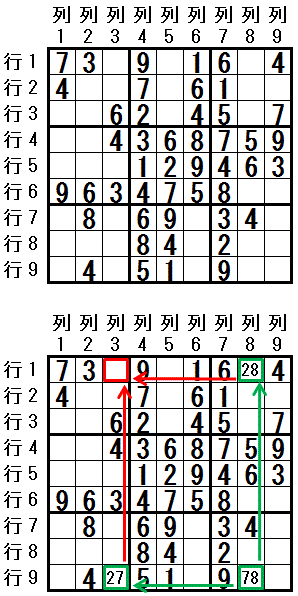 ���}�Ł@�z�u�\�Ȑ������Q�Ɍ�����}�X����܂��B
���}�Ł@�z�u�\�Ȑ������Q�Ɍ�����}�X����܂��B
�s�P��T�i�����T�C�W�j�@�@�s�P��W�i�����Q�C�W�j
�s�Q��X�i�����Q�C�W�j
�s�R��P�i�����P�C�W�j�@�@�s�R��Q�i�����P�C�X�j
�s�R��T�i�����R�C�W�j
�s�S��P�i�����P�C�Q�j�@�@�s�S��Q�i�����P�C�Q�j
�s�T��P�i�����T�C�W�j�@�@�s�T��Q�i�����T�C�V�j
�s�U��W�i�����P�C�Q�j�@�@�s�U��X�i�����P�C�Q�j
�s�V��U�i�����Q�C�V�j�@�@�s�V��X�i�����P�C�T�j
�s�W��U�i�����R�C�V�j�@�@�s�V��W�i�����P�C�V�j
�s�X��R�i�����Q�C�V�j�@�@�s�X��W�i�����V�C�W�j
�s�X��X�i�����U�C�W�j
�h�����q�̊Â��r���h�̓K������������Ƃ��ɂ́C�ŏ��Ɂ@�z�u�\�Ȑ������Q�Ɍ�����}�X�@�������܂��B
�_�E�����[�h�����������\�t�g�ł́C�z�u�\�Ȑ������Q�Ɍ�����}�X�����F�œh��Ԃ����@�y���V���}�[�N�@��\���\�ł��B
���ꂽ�}�X�@�̂����Ł@�s�X��W�@�ɒ��ڂ��܂��B
�s�X��W�i�{�Ɓj�@�ɂ́C�����V�i���q�j�@�Ɓ@�����W�i���q�j�@�����z�u�ł��܂���B
�s�X��W�i�{�Ɓj�@�Ɠ����s�ɂ���@�s�X��R�i���q�̕��Ɓj�@�ɂ́@�����V�i���q�j�@�Ɓ@�����Q�i�����q�j�@�����z�u�ł��܂���B
�s�X��W�i�{�Ɓj�@�Ɠ�����ɂ���@�s�P��W�i���q�̕��Ɓj�@�ɂ́@�����W�i���q�j�@�Ɓ@�����Q�i�����q�j�@�����z�u�ł��܂���B
�����q�̊Â��r�����K���ł�����������Ă��܂��B�����q�̊Â��r���ɂ��C
�s�X��R�i���q�̕��Ɓj �Ɠ�����@���@�s�P��W�i���q�̕��Ɓj�@�Ɠ����s�@�́@�s�P��R�i�����q�̕��Ɨ\��n�j�@�ɂ́@�����Q�i�����q�j�@�͔z�u�ł��܂���B
�_�E�����[�h�����������\�t�g�ł́C
�������q�̊Â��r���@�@�@�r�������� 2�@�s 1�@�� 3
�@�@�r���������z�u������
�@�@�@�@�s 9�@�� 3�@�̐��� 7�@��
�@�@�@�@�s 1�@�� 8�@�̐��� 8�@�Ƃ��m�肵
�@�@�@�@�s 9�@�� 8�@�ɐ������z�u�ł��Ȃ��Ȃ�
�ƁC�\������܂��B

�@
�m���K���@�h�����q�̊Â��r���h�K���ǖʁn
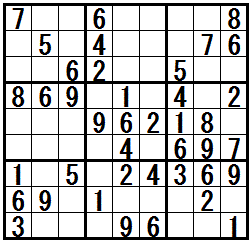
���}�ɒ��ڃe�N�j�b�N�h�����q�̊Â��r���h���K���ł��܂��B
��ԉE�̖��́@�����̂��r���@��K���������ƁC�e�N�j�b�N�h�����q�̊Â��r���h�@�𗘗p���܂��B
���}���N���b�N����ƁC����Ɛ������\������܂��B

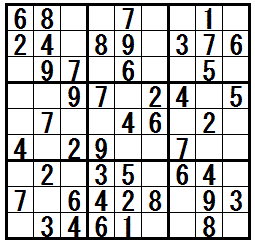
�m���K���@�h�����q�̊Â��r���h�n
�̓r���Ł@�e�N�j�b�N�h�����q�̊Â��r���h�@���K�v�ɂȂ���ł��B
�^�̖��́@�e�N�j�b�N�h�����q�̊Â��r���h�@���R�p���p���܂��i�����̃e�N�j�b�N�����p���܂��j�B
��ԉE�̖��́@�����̃e�N�j�b�N���U��K���������ƁC�e�N�j�b�N�h�����q�̊Â��r���h�@���Q�p���܂��B
���}���N���b�N����ƁC�����Ǝv�l�ߒ��̗Ⴊ�\������܂��B
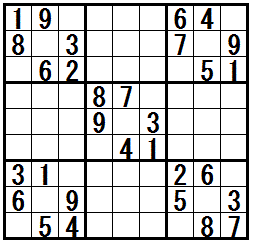
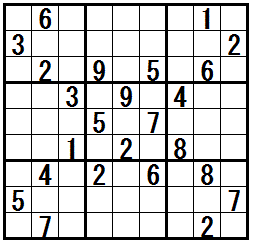
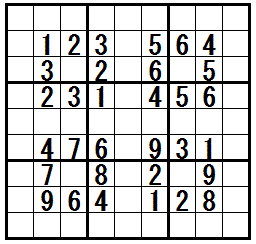

 �mXY-wing�n�@�@���K����
�mXY-wing�n�@�@���K����
 �m�e�N�j�b�N�n
�m�e�N�j�b�N�n�ŏ��ɁC�Q�̐����i�����P�C�����Q�j�����z�u�ł��Ȃ��}�X�i�s�P��P�j�������܂��B
�E�s�P��P�@�Ɠ����s�ɑ����C�����P�@�Ɓ@��O�̐����@�����R�@�����z�u�ł��Ȃ��}�X�i�s�P��T�j
�ƁC
�E�s�P��P�@�Ɠ�����ɑ����C�����Q�@�Ɓ@��O�̐����@�����R�@�����z�u�ł��Ȃ��}�X�i�s�S��P�j
�����݂���ꍇ�C
�����Q�̃}�X�i�s�P��T�C�s�S��P�j�Ɠ����̈�ɑ�����}�X�i�s�S��T�j�@�ɂ́@��O�̐����@�����R �@�͔z�u�ł��܂���B
�����j�@�����C�s�S��T�@�Ɂ@�����R�@���z�u�����ƁC�s�P��T�@�́@�����P�@�� �s�S��P�@�́@�����Q�@���m�肵�C�s�P��P�@�ɔz�u�ł��鐔�����Ȃ��Ȃ�܂��B����āC�s�S��T�@�Ɂ@�����R�@�͔z�u�ł��܂���B
�m���́h�����q�̊Â��r���h�̗R���n
�@�s�P��P�@�́@�{���@�ŁC���q�i�����P�j�Ɓ@���q�i�����Q�j�������Z��ł��܂��B ���q�@�́@�{���@�Ɠ����̈�́@�s�P��T�@�Ɂ@���q�̕����@�����āC ���q�@���@�{���@�Ɠ����̈�́@�s�S��P�@�Ɂ@���q�̕����@�����Ă܂��B ��l�ƍ̗��ꂽ�Â���V�́@�����q�i�����R�j�́@���q�̕����@�Ɓ@���q�̕����@�ɓ���т���� �i���q�̕����@�ɂ́@���q�i�����P�j�Ɓ@�����q�i�����R�j�������Z�ނ��Ƃ��ł��C���q�̕����@�ɂ́@���q�i�����Q�j�Ɓ@�����q�i�����R�j�������Z�ނ��Ƃ��ł��܂��j�C �@�����q�̕����@�Ƃ��ė\�肵�Ă����@�s�S��T�@�ɂ͋����Ȃ��Ȃ��Ă��܂��܂����B
�m�e�N�j�b�N�h�����q�̊Â��r���h�̔��W�n
�@�@�z�u�ł��鐔�����Q�Ɍ����� �R�̃}�X�̈ʒu�W
�@�e�N�j�b�N�̍��Ő��������@�����s�E������ɑ�����@�Ƃ�������́C��}�X�������ā@�����̈�i�s�C��C��}�X�j�ɑ������@�Ƃ�������Ɍ��������Ă��r�����������܂��B ��}�X���W����ƁC��葽���̃}�X���琔����r���ł���\�����łĂ��܂��B
�e�N�j�b�N�̍��ł́@�����Q�@�Ɓ@�����R�@�݂̂��z�u�ł���}�X���@�ŏ��ɒ��ڂ����}�X�Ɓ@������@�ɑ����Ă��܂������C�����̂Q�̃}�X���@������}�X�@�ɑ������������܂��B
 �s�P��P�@�ɂ́C�Q�̐����i�����P�C�����Q�j�����z�u�ł��܂���B
�s�P��P�@�ɂ́C�Q�̐����i�����P�C�����Q�j�����z�u�ł��܂���B�s�P��P�@�Ɠ����s�ɑ�����}�X�@�s�P��T�@�ɂ́C�����P�@�Ɓ@��O�̐����@�����R�@�����z�u�ł��܂���B
�s�P��P�@�Ɓi������ł͂Ȃ��j������}�X�ɑ�����}�X�@�s�R��Q�ɂ́C�����Q�@�Ɓ@��O�̐����@�����R�@�����z�u�ł��܂���B
�����q�̊Â��r���̏�������������܂����B
�}�X�@�s�P��T�@�Ɠ����s�ɑ����C�s�R��Q�@�Ɠ�����}�X�i������j�ɑ�����}�X�@�s�P��Q�C�s�P��R�@�ƁC
�}�X�@�s�P��T�@�Ɠ�����}�X�i������j�ɑ����C�s�R��Q�@�Ɠ����s�ɑ�����}�X�@�s�R��S�C�s�R��T�C�s�R��U
�ɂ́@��O�̐����@�����R�@�͔z�u�ł��܂���B
�����C�s���N�@���́@���@�̃}�X �Ɂ@�����R�@���z�u�����ƁC�s�P��T�@�́@�����P�@�� �s�R��Q�@�́@�����Q�@���m�肵�C�s�P��P�@�ɔz�u�ł��鐔�����Ȃ��Ȃ邩��ł��B
�����q�̊Â��r���@�Ŕz�u����鐔�����Q�Ɍ�����@�R�̃}�X�@�̈ʒu�W�Ɋւ��Ắ@�����@���N���b�N���Ă��������B �����̈ʒu�W�ł́C�����q�̊Â��r���@�𗘗p���Ȃ��Ă��C�����܂ł̃e�N�j�b�N�@�𗘗p����C�r������鐔��������ł��܂��B
�A�@�ŏ��ɒ��ڂ���}�X�� �R�ȏ�̐������z�u�\
�@�ŏ��ɒ��ڂ���}�X�ɔz�u�\�Ȑ������R�ȏ�@���݂��Ă��C���ʂȏŁ@�z�u�ł��Ȃ������@����������ꍇ������܂��B �ŏ��ɒ��ڂ���}�X�ɔz�u�\�Ȑ����� �R�� �̏ꍇ���@�M���̖�]�r���mXYZ-wing�n�@�ƌĂсC���̍��Ő������܂��B

�m�e�N�j�b�N�h�����q�̊Â��r���h�̗�n
 ���}�Ł@�z�u�\�Ȑ������Q�Ɍ�����}�X����܂��B
���}�Ł@�z�u�\�Ȑ������Q�Ɍ�����}�X����܂��B�s�P��T�i�����T�C�W�j�@�@�s�P��W�i�����Q�C�W�j
�s�Q��X�i�����Q�C�W�j
�s�R��P�i�����P�C�W�j�@�@�s�R��Q�i�����P�C�X�j
�s�R��T�i�����R�C�W�j
�s�S��P�i�����P�C�Q�j�@�@�s�S��Q�i�����P�C�Q�j
�s�T��P�i�����T�C�W�j�@�@�s�T��Q�i�����T�C�V�j
�s�U��W�i�����P�C�Q�j�@�@�s�U��X�i�����P�C�Q�j
�s�V��U�i�����Q�C�V�j�@�@�s�V��X�i�����P�C�T�j
�s�W��U�i�����R�C�V�j�@�@�s�V��W�i�����P�C�V�j
�s�X��R�i�����Q�C�V�j�@�@�s�X��W�i�����V�C�W�j
�s�X��X�i�����U�C�W�j
�h�����q�̊Â��r���h�̓K������������Ƃ��ɂ́C�ŏ��Ɂ@�z�u�\�Ȑ������Q�Ɍ�����}�X�@�������܂��B
�_�E�����[�h�����������\�t�g�ł́C�z�u�\�Ȑ������Q�Ɍ�����}�X�����F�œh��Ԃ����@�y���V���}�[�N�@��\���\�ł��B
���ꂽ�}�X�@�̂����Ł@�s�X��W�@�ɒ��ڂ��܂��B
�s�X��W�i�{�Ɓj�@�ɂ́C�����V�i���q�j�@�Ɓ@�����W�i���q�j�@�����z�u�ł��܂���B
�s�X��W�i�{�Ɓj�@�Ɠ����s�ɂ���@�s�X��R�i���q�̕��Ɓj�@�ɂ́@�����V�i���q�j�@�Ɓ@�����Q�i�����q�j�@�����z�u�ł��܂���B
�s�X��W�i�{�Ɓj�@�Ɠ�����ɂ���@�s�P��W�i���q�̕��Ɓj�@�ɂ́@�����W�i���q�j�@�Ɓ@�����Q�i�����q�j�@�����z�u�ł��܂���B
�����q�̊Â��r�����K���ł�����������Ă��܂��B�����q�̊Â��r���ɂ��C
�s�X��R�i���q�̕��Ɓj �Ɠ�����@���@�s�P��W�i���q�̕��Ɓj�@�Ɠ����s�@�́@�s�P��R�i�����q�̕��Ɨ\��n�j�@�ɂ́@�����Q�i�����q�j�@�͔z�u�ł��܂���B
�_�E�����[�h�����������\�t�g�ł́C
�������q�̊Â��r���@�@�@�r�������� 2�@�s 1�@�� 3
�@�@�r���������z�u������
�@�@�@�@�s 9�@�� 3�@�̐��� 7�@��
�@�@�@�@�s 1�@�� 8�@�̐��� 8�@�Ƃ��m�肵
�@�@�@�@�s 9�@�� 8�@�ɐ������z�u�ł��Ȃ��Ȃ�
�ƁC�\������܂��B

�@
�m���K���@�h�����q�̊Â��r���h�K���ǖʁn
���}�ɒ��ڃe�N�j�b�N�h�����q�̊Â��r���h���K���ł��܂��B
��ԉE�̖��́@�����̂��r���@��K���������ƁC�e�N�j�b�N�h�����q�̊Â��r���h�@�𗘗p���܂��B
���}���N���b�N����ƁC����Ɛ������\������܂��B



�m���K���@�h�����q�̊Â��r���h�n
�̓r���Ł@�e�N�j�b�N�h�����q�̊Â��r���h�@���K�v�ɂȂ���ł��B
�^�̖��́@�e�N�j�b�N�h�����q�̊Â��r���h�@���R�p���p���܂��i�����̃e�N�j�b�N�����p���܂��j�B
��ԉE�̖��́@�����̃e�N�j�b�N���U��K���������ƁC�e�N�j�b�N�h�����q�̊Â��r���h�@���Q�p���܂��B
���}���N���b�N����ƁC�����Ǝv�l�ߒ��̗Ⴊ�\������܂��B




�@
![�M���̖�]�r��](image/logo99.gif) �mXYZ-wing�n�@�@���K����
�mXYZ-wing�n�@�@���K����
�@��̃}�X�ɔz�u�ł��鐔�����@�R�@�̏ꍇ�ł��C���̃}�X���܂ށ@�s�i�܂��́@��j�Ƒ�}�X�@�̒��̃}�X�Ɣz�u�\�Ȑ����@�����̏��������ƁC �r������鐔�����������邱�Ƃ�����܂��B
![�M���̖�]�r���@��@�R��](image/nobunaganoyabouhaijosanto.gif) �m�e�N�j�b�N�n
�m�e�N�j�b�N�n
�ŏ��ɁC�z�u�ł��鐔�����@�R�i�����P�C�����Q�C�����R�j�Ɍ�����}�X�i�s�P��P�j�������܂��B
�E���̃}�X�i�s�P��P�j�Ɓ@������i��P�j�ɑ����C �����P�@�Ɓ@�@�����Q�@�����z�u�ł��Ȃ��i�����R�@�͔z�u�ł��Ȃ��j�}�X�i�s�S��P�j�@�ƁC
�E�ŏ��Ɍ������}�X�i�s�P��P�j�Ɓ@������}�X�i��}�X�P�j�ɑ����C �����P�@�Ɓ@�@�����R�@�����z�u�ł��Ȃ��i�����Q�@�͔z�u�ł��Ȃ��j�}�X�i�s�R��R�j�@�����݂���ƁC
�Q�̗̈�i��P�C��}�X�P�j�̋��ʕ����ɑ��݂����i�ŏ��Ɍ������}�X�ȊO�́j�}�X�i�s�Q��P�C�s�R��P�j�ɂ́C �@�����P�@��z�u�ł��܂���B
�����j �����@�s�Q��P�@�܂��́@�s�R��P�@�Ɂ@�����P�@���z�u�����ƁC �s�S��P�@�́@�����Q�@�ƁC �s�R��R�@�́@�����R�@���m�肵�܂��B ����ƁC�s�P��P�@�ɔz�u�ł��鐔�����Ȃ��Ȃ��Ă��܂��܂��B ����āC�����P�@�́@�s�Q��P�C�s�R��P�@�ɔz�u�ł��Ȃ����Ƃ��킩��܂��B
�ŏ��Ɍ�����}�X�i�s�P��P�j�Ɂ@�����P�@���z�u�s�\�ȏꍇ�́C�e�N�j�b�N�h�����q�̊Â��r���h�̓���`�ƂȂ�܂��B �h�M���̖�]�r���h������������̃}�X���琔����r���ł���\��������܂��B
���̃}�X�i�s�S��P�j�܂��́@��O�̃}�X�i�s�R��R�j���C�����̗̈�i��P�C��}�X�P�j�̋��ʕ����ɑ�����ꍇ�ɂ́C�h�O�s����r���h�ƂȂ�C��͂�C �h�M���̖�]�r���h������������̃}�X���琔����r���ł���\�����o�Ă��܂��B
�m���́h�M���̖�]�r���h�̗R���n
�����P�@�́@�D�c�M���C�����Q�@�́@�H�ďG�g�C�����R�@�́@���q���G�@�ł��B
�s�P��P�@�́@���y���C�s�S��P�@�́@�����������C�s�R��R�@�́@�O�g�T�R���@�ł��B
���y��Ɣ����������@�̊ԁC���y��ƒO�g�T�R���@�Ƃ̊ԁ@�ɂ͊X��������܂��B�����������@�Ɓ@�O�g�T�R���@�Ƃ͒��ڍs�������邱�Ƃ͂ł��܂���B
�@ �����S�`�X�@�́@���@�ł���C�O���@�ɂ͗������邱�Ƃ��ł��܂���B
�����������@�ɐ��͂����̂́C�퓬���Ă���@�G�g�@�ƁC�ڂ����点�Ă���@�M���@�ł��B���G�@�̐��͂͋y��ł��܂���B
�O�g�T�R���@�ɐ��͂����̂́C���邵�Ă���@���G�@�ƁC�ڂ����点�Ă���@�M���@�ł��B�G�g�@�̐��͂͋y��ł��܂���B
���y���@�ɂ́C�틵����邽�߂Ɂ@�G�g�@�Ɓ@���G�@�̐Ȃ��݂����Ă��܂� �i�M���@������͂��ł����C���Ȃ������m��܂���F���y���@�́@�M���̉e�����@�ɔC����Ă��邩���m��܂���m�h�����q�̊Â��r���h�̓���`�n�j�B
�e�N�j�b�N�h�M���̖�]�r���h�@�̏������������܂����B
���̂悤�Ɂ@�퓬�\�͂̃o�����X���Ƃꂽ��Ԃł́C�M���@�́@�{�\���i�s�Q��P�@�܂��́@�s�R��P�j�ɏ����̏������]���������Ői�R����K�v�͂���܂���ł����i�r���̐����j�B
�M���@���@���G�@�Ɂ@�����������@�ŋ�킵�Ă����@�G�g�@�̌��ւ̉��R�Ƃ��Ă̏o�w�𖽂������߁@��͂̋ύt������܂��� �i���G�@�̐��͂��@�����������@�ɋy�т܂����j�B �M�����g�@���@�{�\���@�ɐw��C�{�\���̕ρ@���N���Ă��܂��܂����B �M���@���@���G�@�̖d�����@�m���C�@�G�g�@�Ɂ@�O�g�T�R���@���U�߂�悤�ɖ����Ă��@�M���@�ɂ͓��l�̔߉^���҂��Ă��������m��܂���ˁB
�m�e�N�j�b�N�h�M���̖�]�r���h�̔��W�n
�S�ȏ�̐������W���Ă��Ă��C���̏��������������C�h�M���̖�]�r���h���������܂��B
���ۂɖ��������Ƃ��ɂ́C�S�ȏ�̐������W����h�M���̖�]�r���h���������邩�ǂ������m�F���邱�Ƃ́C����߂Ď�̂������ƂɂȂ�Ǝv���܂��B �_�E�����[�h�����������\�t�g�ł��C�S�ȏ�̐������W����h�M���̖�]�r���h�̃��W�b�N��g�ݍ���ł��܂���B
�h�M���̖�]�r���h�̃��W�b�N�̌����𗝉����邽�߂ɁC���ʕ�������������Ƒ�}�X�ɑ�����@�T�̃}�X�@�Ł@�z�u�\�Ȑ������T�@�Ɍ�����ꍇ�́h�M���̖�]�r���h��Ꭶ���܂��B
![�M���̖�]�r���@�T��](image/nobunaganoyabouhaijogoto.gif) �Q�̗̈�i��P�C��}�X�P�j�ɑ�����T�́@�̃}�X�@�ɔz�u�ł��鐔���́@�\������Ă���T�̐����i�����P�`�T�j�Ɍ�����Ƃ��܂��B
���̔z�u�ł́C�����P�@�́@�Ԃ̃}�X�i�s�Q��P�C�s�R��P�j�ɔz�u�ł��Ȃ����Ƃ��킩��܂��B
�Q�̗̈�i��P�C��}�X�P�j�ɑ�����T�́@�̃}�X�@�ɔz�u�ł��鐔���́@�\������Ă���T�̐����i�����P�`�T�j�Ɍ�����Ƃ��܂��B
���̔z�u�ł́C�����P�@�́@�Ԃ̃}�X�i�s�Q��P�C�s�R��P�j�ɔz�u�ł��Ȃ����Ƃ��킩��܂��B
�����j �Ԃ̃}�X�i�s�Q��P�C�s�R��P�j�@�Ɂ@�����P�@���z�u�����ƁC�����P�@�͂��ׂẮ@�̃}�X�@�ɔz�u�ł��Ȃ��Ȃ�܂��B �����P�@�ȊO�́@�S�̐����i�����Q�`�T�j���ꂼ��́C�Q�̗̈�i��P�C��}�X�P�j�́@�Q�̔ʕ����@�̂����́@�ǂ��炩����ɂ����z�u�\�Ȃ̂ŁC �S�̐����i�����Q�`�T�j�́C�Q�̗̈�i��P�C��}�X�P�j�́@�Q�̔ʕ����ɑ��݂���@�S���̃}�X�@�̂����Q�����ȏ�ɂ͔z�u�ł��܂���B �܂�C�S���̃}�X�@�ɂ́@�S�̐����i�����Q�`�T�j������z�u����邱�ƂɂȂ�܂��B ����ƁC�Q�̗̈�i��P�C��}�X�P�j�́@���ʕ����ɑ��݂���̃}�X�i�s�P��P�j�@�ɔz�u�ł��鐔�����Ȃ��Ȃ�@�������܂��B
�h�M���̖�]�r���h�̈�ʌ`�@�͈ȉ��̂悤�ɂȂ�܂��B
���ʕ��������@�s�i�܂��͗�j�Ƒ�}�X�@�̒��ɑ��݂���@���̃}�X�@�ɔz�u�\�Ȑ������@���@�Ɍ����Ă���ꍇ���l���܂��B ���̎��C���̍s�i�܂��͗�j�Ƒ�}�X�@�̂Q�̔ʕ����̂ǂ���ɂ��z�u�\�ȃ}�X�����݂��鐔�����@�P�Ɍ�����i�c��̐����́C�ǂ��炩��̔ʕ����ɂ́@�z�u�\�ȃ}�X�@�����݂��܂���j�ƁC ���̂P�Ɍ���ꂽ�����́C���ʕ����̒��ŁC�ŏ��ɏ����Ŏw�肵���@���̃}�X�ȊO�̃}�X�@�ɂ͔z�u�ł��܂���B

�m�e�N�j�b�N�h�M���̖�]�r���h�̗�n
![�N���b�N����Ɛ�����\�����܂� �M���̖�]�r���@���](image/nobunaganoyaboureidai.gif)
�z�u�\�Ȑ������@�R�i�����P�C�����T�C�����V�j�Ɍ�����@�}�X�i�s�P��Q�j�ɒ��ڂ��܂��B
���̋ǖʂŁ@�z�u�\�Ȑ������@�R�Ɍ�����}�X�́@�Q�Q�}�X�@������܂��B �h�M���̖�]�r���h���K���ł��邩�ǂ����́C�z�u�\�Ȑ������@�R�Ɍ�����}�X�@�Ɓ@�Q�Ɍ�����}�X�@�ɒ��ڂ���Ɗm�F���₷���Ȃ�܂��B
�_�E�����[�h�����������\�t�g�ł́C�z�u�\�Ȑ������@�R�@����с@�Q�Ɍ�����}�X���@��ʂ��Ē��F�����@�y���V���}�[�N�@��\���\�ł��B
�ŏ��ɔz�u�\�Ȑ������R�Ɍ�����}�X�Ɠ�����}�X�̒��ɁC���̂R�̐����̂����́@�Q�̂݁@���z�u�\�ȃ}�X�����邩�ǂ������������܂��B�����C���̂悤�ȃ}�X�����݂�����C�ŏ��̃}�X�Ɠ����s�܂��͗�̒��Ɂ@���̂Q�̐����̂ǂ��炩��@�Ɓ@������̐����@�̂Q�̐����̂ݔz�u�\�ȃ}�X�����݂��邩�ǂ������m�F���܂��B ���̂悤�ȃ}�X�����݂���C�h�M���̖�]�r���h����������O���������������܂��B
�s�P��Q�@�Ɠ�����}�X�i��}�X�P�j�ɑ�����}�X�@�s�Q��P�@�ɂ́@�����P�C�����V�@�̂ݔz�u�\�ł� �i�����T�@�͔z�u�ł��܂���j�B
�s�P��Q�@�Ɠ����s�܂��͗�̒��ɁC�����P�@���@�����V�@�̂ǂ��炩��Ɓ@�����T�@�̂Q�݂̂��z�u�\�ȃ}�X��T���ƁC�s�P�@�ɑ�����}�X�@�s�P��V�@��������܂��i�����P�C�����T�@�̂Q�����݂̂��z�u�\�ł� �i�����V�@�͔z�u�ł��܂���j�j�B
�M���̖�]�r�����������āC�����P�@�́C�Q�̗̈�i�s�P�@����с@��}�X�P�j�̋��ʕ����̂����@�s�P��Q�@�ȊO�̃}�X�i�s�P��R�j�ɂ͔z�u�ł��Ȃ����Ƃ��킩��܂��B
�_�E�����[�h�����������\�t�g�ł́C
���M���̖�]�r���@�@�@�@�r�������� 1�@�s 1�@�� 3
�@�@�r���������z�u������
�@�@�@�@�s 2�@�� 1�@�̐��� 7�@��
�@�@�@�@�s 1�@�� 7�@�̐��� 5�@�Ƃ��m�肵
�@�@�@�@�s 1�@�� 2�@�ɐ������z�u�ł��Ȃ��Ȃ�
�ƁC�\������܂��B

�@
�m���K���@�h�M���̖�]�r���h�K���ǖʁn
���}�ɒ��ڃe�N�j�b�N�h�M���̖�]�r���h���K���ł��܂��B
�܂̖��́C�h�M���̖�]�r���h���Q������܂����C�V���ɔz�u�ł��鐔����������̂́C�Е��̔r���݂̂ł��B
��ԉE�̖��́C�h�M���̖�]�r���h��K�����Ď��i�߂�ƁC������x�h�M���̖�]�r���h��K������ǖʂ�����܂��B
���}���N���b�N����ƁC����Ɛ������\������܂��B
![�N���b�N����Ɖ���Ɛ�����\�����܂� �M���̖�]�r���K���ǖʐ}�P](image/nobunaganoyaboutekioukyokumen1.gif)
![�N���b�N����Ɖ���Ɛ�����\�����܂� �M���̖�]�r���K���ǖʐ}�Q](image/nobunaganoyaboutekioukyokumen2.gif)
![�N���b�N����Ɖ���Ɛ�����\�����܂� �M���̖�]�r���K���ǖʐ}�R](image/nobunaganoyaboutekioukyokumen3.gif)
�m���K���@�h�M���̖�]�r���h�n
�̓r���Ł@�e�N�j�b�N�h�M���̖�]�r���h�@���K�v�ɂȂ���ł��B
�܂̖��́C�����̃e�N�j�b�N�@�Ɓ@�h�����q�̊Â��r���h��K���������ƁC���i�߂ā@�h�M���̖�]�r���h�@�𗘗p���܂��B
��ԉE�̖��́C�h�M���̖�]�r���h�̂ق��Ɂ@�����̃e�N�j�b�N���V��C�h�����q�̊Â��r���h���Q�p���܂��B
���}���N���b�N����ƁC�����Ǝv�l�ߒ��̗Ⴊ�\������܂��B
![�N���b�N����Ɛ����Ǝv�l�ߒ��̗��\�����܂� �M���̖�]�r�����}�P](image/nobunaganoyaboumondaizu1.gif)
![�N���b�N����Ɛ����Ǝv�l�ߒ��̗��\�����܂� �M���̖�]�r�����}�Q](image/nobunaganoyaboumondaizu2.gif)
![�N���b�N����Ɛ����Ǝv�l�ߒ��̗��\�����܂� �M���̖�]�r�����}�R](image/nobunaganoyaboumondaizu3.gif)

![�M���̖�]�r��](image/logo99.gif) �mXYZ-wing�n�@�@���K����
�mXYZ-wing�n�@�@���K����
�@��̃}�X�ɔz�u�ł��鐔�����@�R�@�̏ꍇ�ł��C���̃}�X���܂ށ@�s�i�܂��́@��j�Ƒ�}�X�@�̒��̃}�X�Ɣz�u�\�Ȑ����@�����̏��������ƁC �r������鐔�����������邱�Ƃ�����܂��B
![�M���̖�]�r���@��@�R��](image/nobunaganoyabouhaijosanto.gif) �m�e�N�j�b�N�n
�m�e�N�j�b�N�n�ŏ��ɁC�z�u�ł��鐔�����@�R�i�����P�C�����Q�C�����R�j�Ɍ�����}�X�i�s�P��P�j�������܂��B
�E���̃}�X�i�s�P��P�j�Ɓ@������i��P�j�ɑ����C �����P�@�Ɓ@�@�����Q�@�����z�u�ł��Ȃ��i�����R�@�͔z�u�ł��Ȃ��j�}�X�i�s�S��P�j�@�ƁC
�E�ŏ��Ɍ������}�X�i�s�P��P�j�Ɓ@������}�X�i��}�X�P�j�ɑ����C �����P�@�Ɓ@�@�����R�@�����z�u�ł��Ȃ��i�����Q�@�͔z�u�ł��Ȃ��j�}�X�i�s�R��R�j�@�����݂���ƁC
�Q�̗̈�i��P�C��}�X�P�j�̋��ʕ����ɑ��݂����i�ŏ��Ɍ������}�X�ȊO�́j�}�X�i�s�Q��P�C�s�R��P�j�ɂ́C �@�����P�@��z�u�ł��܂���B
�����j �����@�s�Q��P�@�܂��́@�s�R��P�@�Ɂ@�����P�@���z�u�����ƁC �s�S��P�@�́@�����Q�@�ƁC �s�R��R�@�́@�����R�@���m�肵�܂��B ����ƁC�s�P��P�@�ɔz�u�ł��鐔�����Ȃ��Ȃ��Ă��܂��܂��B ����āC�����P�@�́@�s�Q��P�C�s�R��P�@�ɔz�u�ł��Ȃ����Ƃ��킩��܂��B
�ŏ��Ɍ�����}�X�i�s�P��P�j�Ɂ@�����P�@���z�u�s�\�ȏꍇ�́C�e�N�j�b�N�h�����q�̊Â��r���h�̓���`�ƂȂ�܂��B �h�M���̖�]�r���h������������̃}�X���琔����r���ł���\��������܂��B
���̃}�X�i�s�S��P�j�܂��́@��O�̃}�X�i�s�R��R�j���C�����̗̈�i��P�C��}�X�P�j�̋��ʕ����ɑ�����ꍇ�ɂ́C�h�O�s����r���h�ƂȂ�C��͂�C �h�M���̖�]�r���h������������̃}�X���琔����r���ł���\�����o�Ă��܂��B
�m���́h�M���̖�]�r���h�̗R���n
�����P�@�́@�D�c�M���C�����Q�@�́@�H�ďG�g�C�����R�@�́@���q���G�@�ł��B
�s�P��P�@�́@���y���C�s�S��P�@�́@�����������C�s�R��R�@�́@�O�g�T�R���@�ł��B
���y��Ɣ����������@�̊ԁC���y��ƒO�g�T�R���@�Ƃ̊ԁ@�ɂ͊X��������܂��B�����������@�Ɓ@�O�g�T�R���@�Ƃ͒��ڍs�������邱�Ƃ͂ł��܂���B
�@ �����S�`�X�@�́@���@�ł���C�O���@�ɂ͗������邱�Ƃ��ł��܂���B
�����������@�ɐ��͂����̂́C�퓬���Ă���@�G�g�@�ƁC�ڂ����点�Ă���@�M���@�ł��B���G�@�̐��͂͋y��ł��܂���B
�O�g�T�R���@�ɐ��͂����̂́C���邵�Ă���@���G�@�ƁC�ڂ����点�Ă���@�M���@�ł��B�G�g�@�̐��͂͋y��ł��܂���B
���y���@�ɂ́C�틵����邽�߂Ɂ@�G�g�@�Ɓ@���G�@�̐Ȃ��݂����Ă��܂� �i�M���@������͂��ł����C���Ȃ������m��܂���F���y���@�́@�M���̉e�����@�ɔC����Ă��邩���m��܂���m�h�����q�̊Â��r���h�̓���`�n�j�B
�e�N�j�b�N�h�M���̖�]�r���h�@�̏������������܂����B
���̂悤�Ɂ@�퓬�\�͂̃o�����X���Ƃꂽ��Ԃł́C�M���@�́@�{�\���i�s�Q��P�@�܂��́@�s�R��P�j�ɏ����̏������]���������Ői�R����K�v�͂���܂���ł����i�r���̐����j�B
�M���@���@���G�@�Ɂ@�����������@�ŋ�킵�Ă����@�G�g�@�̌��ւ̉��R�Ƃ��Ă̏o�w�𖽂������߁@��͂̋ύt������܂��� �i���G�@�̐��͂��@�����������@�ɋy�т܂����j�B �M�����g�@���@�{�\���@�ɐw��C�{�\���̕ρ@���N���Ă��܂��܂����B �M���@���@���G�@�̖d�����@�m���C�@�G�g�@�Ɂ@�O�g�T�R���@���U�߂�悤�ɖ����Ă��@�M���@�ɂ͓��l�̔߉^���҂��Ă��������m��܂���ˁB
�m�e�N�j�b�N�h�M���̖�]�r���h�̔��W�n
�S�ȏ�̐������W���Ă��Ă��C���̏��������������C�h�M���̖�]�r���h���������܂��B
���ۂɖ��������Ƃ��ɂ́C�S�ȏ�̐������W����h�M���̖�]�r���h���������邩�ǂ������m�F���邱�Ƃ́C����߂Ď�̂������ƂɂȂ�Ǝv���܂��B �_�E�����[�h�����������\�t�g�ł��C�S�ȏ�̐������W����h�M���̖�]�r���h�̃��W�b�N��g�ݍ���ł��܂���B
�h�M���̖�]�r���h�̃��W�b�N�̌����𗝉����邽�߂ɁC���ʕ�������������Ƒ�}�X�ɑ�����@�T�̃}�X�@�Ł@�z�u�\�Ȑ������T�@�Ɍ�����ꍇ�́h�M���̖�]�r���h��Ꭶ���܂��B
![�M���̖�]�r���@�T��](image/nobunaganoyabouhaijogoto.gif) �Q�̗̈�i��P�C��}�X�P�j�ɑ�����T�́@�̃}�X�@�ɔz�u�ł��鐔���́@�\������Ă���T�̐����i�����P�`�T�j�Ɍ�����Ƃ��܂��B
���̔z�u�ł́C�����P�@�́@�Ԃ̃}�X�i�s�Q��P�C�s�R��P�j�ɔz�u�ł��Ȃ����Ƃ��킩��܂��B
�Q�̗̈�i��P�C��}�X�P�j�ɑ�����T�́@�̃}�X�@�ɔz�u�ł��鐔���́@�\������Ă���T�̐����i�����P�`�T�j�Ɍ�����Ƃ��܂��B
���̔z�u�ł́C�����P�@�́@�Ԃ̃}�X�i�s�Q��P�C�s�R��P�j�ɔz�u�ł��Ȃ����Ƃ��킩��܂��B�����j �Ԃ̃}�X�i�s�Q��P�C�s�R��P�j�@�Ɂ@�����P�@���z�u�����ƁC�����P�@�͂��ׂẮ@�̃}�X�@�ɔz�u�ł��Ȃ��Ȃ�܂��B �����P�@�ȊO�́@�S�̐����i�����Q�`�T�j���ꂼ��́C�Q�̗̈�i��P�C��}�X�P�j�́@�Q�̔ʕ����@�̂����́@�ǂ��炩����ɂ����z�u�\�Ȃ̂ŁC �S�̐����i�����Q�`�T�j�́C�Q�̗̈�i��P�C��}�X�P�j�́@�Q�̔ʕ����ɑ��݂���@�S���̃}�X�@�̂����Q�����ȏ�ɂ͔z�u�ł��܂���B �܂�C�S���̃}�X�@�ɂ́@�S�̐����i�����Q�`�T�j������z�u����邱�ƂɂȂ�܂��B ����ƁC�Q�̗̈�i��P�C��}�X�P�j�́@���ʕ����ɑ��݂���̃}�X�i�s�P��P�j�@�ɔz�u�ł��鐔�����Ȃ��Ȃ�@�������܂��B
�h�M���̖�]�r���h�̈�ʌ`�@�͈ȉ��̂悤�ɂȂ�܂��B
���ʕ��������@�s�i�܂��͗�j�Ƒ�}�X�@�̒��ɑ��݂���@���̃}�X�@�ɔz�u�\�Ȑ������@���@�Ɍ����Ă���ꍇ���l���܂��B ���̎��C���̍s�i�܂��͗�j�Ƒ�}�X�@�̂Q�̔ʕ����̂ǂ���ɂ��z�u�\�ȃ}�X�����݂��鐔�����@�P�Ɍ�����i�c��̐����́C�ǂ��炩��̔ʕ����ɂ́@�z�u�\�ȃ}�X�@�����݂��܂���j�ƁC ���̂P�Ɍ���ꂽ�����́C���ʕ����̒��ŁC�ŏ��ɏ����Ŏw�肵���@���̃}�X�ȊO�̃}�X�@�ɂ͔z�u�ł��܂���B

�m�e�N�j�b�N�h�M���̖�]�r���h�̗�n
![�N���b�N����Ɛ�����\�����܂� �M���̖�]�r���@���](image/nobunaganoyaboureidai.gif)
�z�u�\�Ȑ������@�R�i�����P�C�����T�C�����V�j�Ɍ�����@�}�X�i�s�P��Q�j�ɒ��ڂ��܂��B
���̋ǖʂŁ@�z�u�\�Ȑ������@�R�Ɍ�����}�X�́@�Q�Q�}�X�@������܂��B �h�M���̖�]�r���h���K���ł��邩�ǂ����́C�z�u�\�Ȑ������@�R�Ɍ�����}�X�@�Ɓ@�Q�Ɍ�����}�X�@�ɒ��ڂ���Ɗm�F���₷���Ȃ�܂��B
�_�E�����[�h�����������\�t�g�ł́C�z�u�\�Ȑ������@�R�@����с@�Q�Ɍ�����}�X���@��ʂ��Ē��F�����@�y���V���}�[�N�@��\���\�ł��B
�ŏ��ɔz�u�\�Ȑ������R�Ɍ�����}�X�Ɠ�����}�X�̒��ɁC���̂R�̐����̂����́@�Q�̂݁@���z�u�\�ȃ}�X�����邩�ǂ������������܂��B�����C���̂悤�ȃ}�X�����݂�����C�ŏ��̃}�X�Ɠ����s�܂��͗�̒��Ɂ@���̂Q�̐����̂ǂ��炩��@�Ɓ@������̐����@�̂Q�̐����̂ݔz�u�\�ȃ}�X�����݂��邩�ǂ������m�F���܂��B ���̂悤�ȃ}�X�����݂���C�h�M���̖�]�r���h����������O���������������܂��B
�s�P��Q�@�Ɠ�����}�X�i��}�X�P�j�ɑ�����}�X�@�s�Q��P�@�ɂ́@�����P�C�����V�@�̂ݔz�u�\�ł� �i�����T�@�͔z�u�ł��܂���j�B
�s�P��Q�@�Ɠ����s�܂��͗�̒��ɁC�����P�@���@�����V�@�̂ǂ��炩��Ɓ@�����T�@�̂Q�݂̂��z�u�\�ȃ}�X��T���ƁC�s�P�@�ɑ�����}�X�@�s�P��V�@��������܂��i�����P�C�����T�@�̂Q�����݂̂��z�u�\�ł� �i�����V�@�͔z�u�ł��܂���j�j�B
�M���̖�]�r�����������āC�����P�@�́C�Q�̗̈�i�s�P�@����с@��}�X�P�j�̋��ʕ����̂����@�s�P��Q�@�ȊO�̃}�X�i�s�P��R�j�ɂ͔z�u�ł��Ȃ����Ƃ��킩��܂��B
�_�E�����[�h�����������\�t�g�ł́C
���M���̖�]�r���@�@�@�@�r�������� 1�@�s 1�@�� 3
�@�@�r���������z�u������
�@�@�@�@�s 2�@�� 1�@�̐��� 7�@��
�@�@�@�@�s 1�@�� 7�@�̐��� 5�@�Ƃ��m�肵
�@�@�@�@�s 1�@�� 2�@�ɐ������z�u�ł��Ȃ��Ȃ�
�ƁC�\������܂��B

�@
�m���K���@�h�M���̖�]�r���h�K���ǖʁn
���}�ɒ��ڃe�N�j�b�N�h�M���̖�]�r���h���K���ł��܂��B
�܂̖��́C�h�M���̖�]�r���h���Q������܂����C�V���ɔz�u�ł��鐔����������̂́C�Е��̔r���݂̂ł��B
��ԉE�̖��́C�h�M���̖�]�r���h��K�����Ď��i�߂�ƁC������x�h�M���̖�]�r���h��K������ǖʂ�����܂��B
���}���N���b�N����ƁC����Ɛ������\������܂��B
![�N���b�N����Ɖ���Ɛ�����\�����܂� �M���̖�]�r���K���ǖʐ}�P](image/nobunaganoyaboutekioukyokumen1.gif)
![�N���b�N����Ɖ���Ɛ�����\�����܂� �M���̖�]�r���K���ǖʐ}�Q](image/nobunaganoyaboutekioukyokumen2.gif)
![�N���b�N����Ɖ���Ɛ�����\�����܂� �M���̖�]�r���K���ǖʐ}�R](image/nobunaganoyaboutekioukyokumen3.gif)
�m���K���@�h�M���̖�]�r���h�n
�̓r���Ł@�e�N�j�b�N�h�M���̖�]�r���h�@���K�v�ɂȂ���ł��B
�܂̖��́C�����̃e�N�j�b�N�@�Ɓ@�h�����q�̊Â��r���h��K���������ƁC���i�߂ā@�h�M���̖�]�r���h�@�𗘗p���܂��B
��ԉE�̖��́C�h�M���̖�]�r���h�̂ق��Ɂ@�����̃e�N�j�b�N���V��C�h�����q�̊Â��r���h���Q�p���܂��B
���}���N���b�N����ƁC�����Ǝv�l�ߒ��̗Ⴊ�\������܂��B
![�N���b�N����Ɛ����Ǝv�l�ߒ��̗��\�����܂� �M���̖�]�r�����}�P](image/nobunaganoyaboumondaizu1.gif)
![�N���b�N����Ɛ����Ǝv�l�ߒ��̗��\�����܂� �M���̖�]�r�����}�Q](image/nobunaganoyaboumondaizu2.gif)
![�N���b�N����Ɛ����Ǝv�l�ߒ��̗��\�����܂� �M���̖�]�r�����}�R](image/nobunaganoyaboumondaizu3.gif)

�@
 �mW-wing�n�@�@���K����
�mW-wing�n�@�@���K����
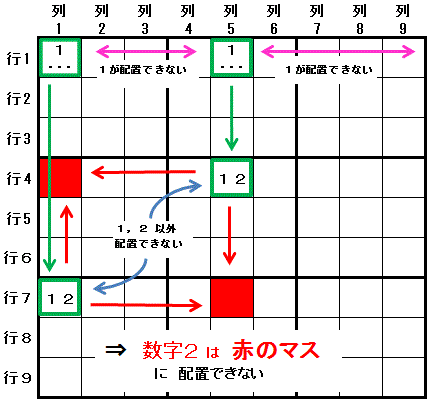
�z�u�\�ȃ}�X���Q�Ɍ����鐔�������݂���̈�ɒ��ڂ��āC���̂Q�̃}�X����L���闃�i�̈�j���������ā@�r���̉\�����m�F����e�N�j�b�N�ł��B
 �m�e�N�j�b�N�n
�m�e�N�j�b�N�n
�ŏ��ɁC�z�u�\�ȃ}�X���Q�i�s�P��P�C�s�P��T�j�Ɍ����鐔���i�����P�F���̐����j�����݂���̈�i�s�P�j�������܂��B
�����Q�̃}�X�i�s�P��P�C�s�P��T�j���ꂼ��Ɓ@�����̈�i��P�@����с@��T�j�ɂ����āC �z�u�\�Ȑ������@���̐����i�����P�j�Ƒ��̐����i�����Q�j�́@�Q�̐����Ɍ��肳���}�X�i�s�V��P�@����с@�s�S��T�j�����݂���ƁC
�����Q�̃}�X�i�s�V��P�@�Ɓ@�s�S��T�j�̗����̃}�X�Ɠ����̈�ɂ���}�X�i�s�S��P�@����с@�s�V��T�j�ɂ� ���̐����i�����Q�j�͔z�u�ł��܂���B
�����j�@�����C�s�S��P�@�܂��́@�s�V��T�@�Ɂ@�����Q�@���z�u�����ƁC �s�V��P�@����с@�s�S��T�@�́@�����P�@���m�肵�C �s�P��P�@����с@�s�P��T�Ɂ@�����P�@���z�u�ł��Ȃ��Ȃ�܂��B ����ƁC�s�P�@�Ɂ@�����P�@���z�u�ł��Ȃ��Ȃ�@�������܂��B
�m���́h�l�R�ƃl�Y�~�r���h�̗R���n
�@�䏊�i�s�V��P�j�@�Ɓ@�H���i�s�S��T�j�ɂ́@�`�[�Y�̃u���b�N�@���u���Ă���܂��B �l�Y�~�i�����Q�j�́C�l�Y�~�̑��i�s�S��P�@����с@�s�V��T�j�ƒ��ڂȂ����Ă��� �@�䏊�@�Ɓ@�H���@���s�������ă`�[�Y���ނ��ڂ�܂��B �l�R�i�����P�j�́@�䏊�@�Ɓ@�H���@�ɏo�v����@�l�Y�~�@��ǂ������܂��B �������C�o�����i�s�P��P�ƍs�P��T�j���Q�����́@�L���i�s�P�j��ʂ�Ȃ��� �@�䏊�@�Ɓ@�H���@�̊Ԃ��s�����ł��Ȃ��̂� �@�Ȃ��Ȃ��@�l�Y�~�@��߂܂����܂���B �l�Y�~�@�́@�l�R�@�����炩���̂��y������ �@�����̑��@�ɋ����ɂ�����܂���B
�m�e�N�j�b�N�h�l�R�ƃl�Y�~�r���h�̔��W�n
�m�e�N�j�b�N�n�̍��� �@�h�z�u�\�ȃ}�X���Q�Ɍ����鐔�������݂���@�̈��h�@�� �@�h�����Q�̃}�X���ꂼ��Ɓ@�����@�̈��h �@�Ɛ��������@�̈��@�́C�s���@�����ł͂Ȃ��C��}�X�@�ł����Ă��C �e�N�j�b�N�h�l�R�ƃl�Y�~�r���h�͐��藧���܂��B
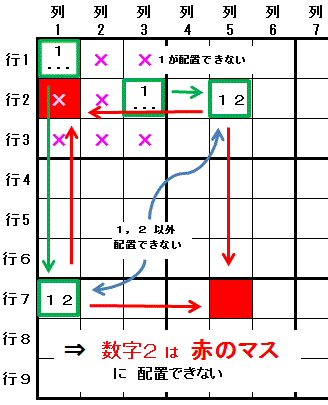 �l�R�ƃl�Y�~�r���@�𐬗�������@�̈�@���@���ʂȗ�ł��B
�l�R�ƃl�Y�~�r���@�𐬗�������@�̈�@���@���ʂȗ�ł��B
��}�X�P�@�ŁC�����P�@���z�u�\�ȃ}�X�́@�s�P��P�C�s�Q��R�@�Ɍ����܂��B
�s�P��P�@�Ɠ�����ɂ���@�s�V��P�@��
�s�Q��R�@�Ɠ����s�ɂ���@�s�Q��T
�ɔz�u�\�Ȑ������C�����P�@�Ɓ@���̐����i�����Q�j�́@�Q�̐����Ɍ��肳���ƁC
�����Q�̃}�X�i�s�V��P�@�Ɓ@�s�Q��T�j�̗����̃}�X�Ɠ����̈�ɂ���}�X�i�s�Q��P�@����с@�s�V��T�j�ɂ�
���̐����i�����Q�j�͔z�u�ł��܂���B

�m�e�N�j�b�N�h�l�R�ƃl�Y�~�r���h�̗�n
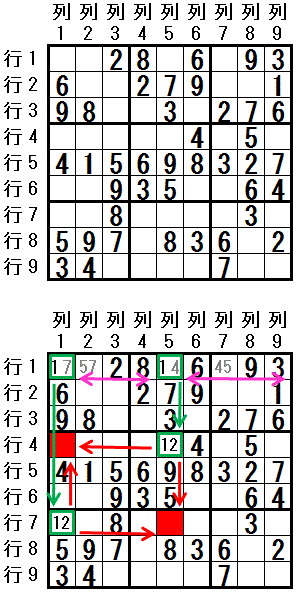 ���}�ŁC�����P�@���z�u�\�ȃ}�X���@�Q�̃}�X�@�Ɍ�����̈�́C
���}�ŁC�����P�@���z�u�\�ȃ}�X���@�Q�̃}�X�@�Ɍ�����̈�́C
�s�P�C�s�U�C�s�W�C
��P�C��R�C��W�C
��}�X�P�i�C��}�X�U�j�C��}�X�V
�� ���v�W�̈�@���݂��܂��i�s�E��̏ꍇ�Ɠ����Q�}�X�ɂȂ��}�X�̓J�b�R�ŕ\�����C���v�����珜�O���Ă��܂��j�B
�_�E�����[�h�����������\�t�g�ł́C�����P�@���z�u�\�ȃ}�X���@�Q�̃}�X�@�Ɍ�����̈�ł̔z�u�\�ȃ}�X�����F���h��Ԃ����@�y���V���}�[�N�@��\���\�ł��B
�i�����Q�`�X�@�ł́C�z�u�\�ȃ}�X���@�Q�̃}�X�@�Ɍ�����̈�́C���ꂼ�� �R�C�Q�C�W�C�U�C�V�C�T�C�V�C�S�@�̈摶�݂��܂��j
�����P�@���@�s�P�@�Ŕz�u�\�ȃ}�X�́@�s�P��P�@�Ɓ@�s�P��T�@�Ɍ����܂��B
�s�P��P�@�Ɓ@�����@��P�@�ɂ���@�s�V��P�@�ɔz�u�\�Ȑ����́C�����P�@�Ɓ@���̐����@�����Q�@�̂Q�Ɍ����܂��B
�s�P��T�@�Ɓ@�����@��T�@�ɂ���@�s�S��T�@�ɔz�u�\�Ȑ������C�����P�@�Ɓ@���̐����@�����Q�@�̂Q�Ɍ����܂��B
�l�R�ƃl�Y�~�r�������������������������܂����B
�Q�̃}�X�@�s�V��P�@�Ɓ@�s�S��T�@�̗����̃}�X�Ɠ����̈�ɂ���}�X�@�s�S��P�@����с@�s�V��T�@�ɂ�
���̐����@�����Q�@�͔z�u�ł��܂���B
�_�E�����[�h�����������\�t�g�ł́C
���l�R�ƃl�Y�~�r���@�@�@�r�������� 2�@�s 4�@�� 1
���l�R�ƃl�Y�~�r���@�@�@�r�������� 2�@�s 7�@�� 5
�@�@�r���������r���}�X�ɔz�u������
�@�@�@�s 7�@�� 1�@�Ɓ@�s 4�@�� 5�@�̐��� 1�@���m�肷��
�@�@���� 1�@�́@�@�s�@�P�@�ł�
�@�@�@�s 1�@�� 1�@���@�s 1�@�� 5�@�̂����ꂩ�ɔz�u����邽�߁@��������
�ƁC�\������܂��B
�h�l�R�ƃl�Y�~�r���h�́C��ɁC�z�u�\�Ȑ������@�Q�@�Ɍ�����}�X�ɒ��ڂ��Ă��K�����������邱�Ƃ��ł��܂��i�y���V���}�[�N�F�z�u�\�Ȑ������Q�Ɍ�����}�X�����F�ɓh��Ԃ��Ă��܂��j�B
�z�u�\�Ȑ������Q�Ɍ�����}�X�̂����@�����������z�u�\�ł���}�X�̑�[��L���i�ȉ����l�j�F�s�V��P�C�s�S��T�C�����P�C�����Q]�ɒ��ڂ��܂��B ���ɁC���̑ł���Q�̃}�X���ꂼ��ŁC���̃}�X�Ɠ����̈�[��P�C��T]�ɂ���C�����̐����̂����̂ǂ��炩���������[�����P]���z�u�\�ȃ}�X���l���܂��B �����̂����C�ɂ����}�X���ꂼ�ꂩ�瓱���o���ꂽ����̂Q�}�X���C�����̈�[�s�P]�ɂ���C���̗̈�ł͂��̐������z�u�\�ȃ}�X�����̂Q�}�X�ȊO�ɂ͂Ȃ��@�ꍇ�C�h�l�R�ƃl�Y�~�r���h�̏�������������܂��B �ŏ��ɒ��ڂ����ɂȂ�Q�̃}�X�̗����Ɠ����̈�ɂ���}�X�Ŕr�����������邩�ǂ������m�F���܂��B
 �@
�@
�m���K���@�h�l�R�ƃl�Y�~�r���h�K���ǖʁn
���}�ɒ��ڃe�N�j�b�N�h�l�R�ƃl�Y�~�r���h���K���ł��܂��B
�܂̖��́C�h�l�R�ƃl�Y�~�r���h��K�����Ď��i�߂�ƁC������x�h�l�R�ƃl�Y�~�r���h��K������ǖʂ�����܂��B�����̃e�N�j�b�N�����p���܂��B
��ԉE�̖��́C�h�l�R�ƃl�Y�~�r���h���S�p���܂��B�����̃e�N�j�b�N�����p���܂��B
���}���N���b�N����ƁC����Ɛ������\������܂��B
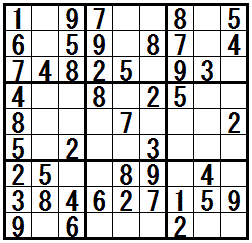

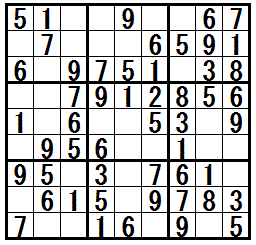
�m���K���@�h�l�R�ƃl�Y�~�r���h�n
�̓r���Ł@�e�N�j�b�N�h�l�R�ƃl�Y�~�r���h�@���K�v�ɂȂ���ł��B
�܂̖��́C�h�l�R�ƃl�Y�~�r���h�C�h�����q�̊Â��r���h�C�h�l�s����r���h�C�h��s����r���h�𗘗p���܂��B
��ԉE�̖��́C�h�l�R�ƃl�Y�~�r���h���R��@�Ɓ@�h�M���̖�]�r���h�C�h�����q�̊Â��r���h�C����Ɂ@�h�l�s����r���h���܂߂Ē����̃e�N�j�b�N���U��@���p���܂��B
���}���N���b�N����ƁC�����Ǝv�l�ߒ��̗Ⴊ�\������܂��B
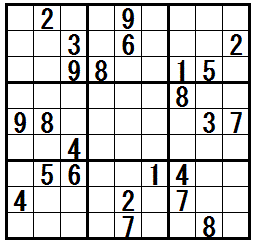
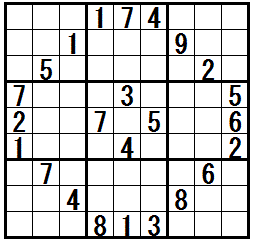
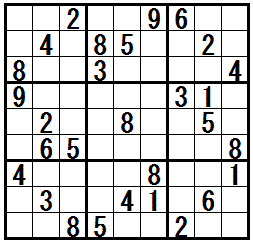

 �mW-wing�n�@�@���K����
�mW-wing�n�@�@���K����
�z�u�\�ȃ}�X���Q�Ɍ����鐔�������݂���̈�ɒ��ڂ��āC���̂Q�̃}�X����L���闃�i�̈�j���������ā@�r���̉\�����m�F����e�N�j�b�N�ł��B
 �m�e�N�j�b�N�n
�m�e�N�j�b�N�n�ŏ��ɁC�z�u�\�ȃ}�X���Q�i�s�P��P�C�s�P��T�j�Ɍ����鐔���i�����P�F���̐����j�����݂���̈�i�s�P�j�������܂��B
�����Q�̃}�X�i�s�P��P�C�s�P��T�j���ꂼ��Ɓ@�����̈�i��P�@����с@��T�j�ɂ����āC �z�u�\�Ȑ������@���̐����i�����P�j�Ƒ��̐����i�����Q�j�́@�Q�̐����Ɍ��肳���}�X�i�s�V��P�@����с@�s�S��T�j�����݂���ƁC
�����Q�̃}�X�i�s�V��P�@�Ɓ@�s�S��T�j�̗����̃}�X�Ɠ����̈�ɂ���}�X�i�s�S��P�@����с@�s�V��T�j�ɂ� ���̐����i�����Q�j�͔z�u�ł��܂���B
�����j�@�����C�s�S��P�@�܂��́@�s�V��T�@�Ɂ@�����Q�@���z�u�����ƁC �s�V��P�@����с@�s�S��T�@�́@�����P�@���m�肵�C �s�P��P�@����с@�s�P��T�Ɂ@�����P�@���z�u�ł��Ȃ��Ȃ�܂��B ����ƁC�s�P�@�Ɂ@�����P�@���z�u�ł��Ȃ��Ȃ�@�������܂��B
�m���́h�l�R�ƃl�Y�~�r���h�̗R���n
�@�䏊�i�s�V��P�j�@�Ɓ@�H���i�s�S��T�j�ɂ́@�`�[�Y�̃u���b�N�@���u���Ă���܂��B �l�Y�~�i�����Q�j�́C�l�Y�~�̑��i�s�S��P�@����с@�s�V��T�j�ƒ��ڂȂ����Ă��� �@�䏊�@�Ɓ@�H���@���s�������ă`�[�Y���ނ��ڂ�܂��B �l�R�i�����P�j�́@�䏊�@�Ɓ@�H���@�ɏo�v����@�l�Y�~�@��ǂ������܂��B �������C�o�����i�s�P��P�ƍs�P��T�j���Q�����́@�L���i�s�P�j��ʂ�Ȃ��� �@�䏊�@�Ɓ@�H���@�̊Ԃ��s�����ł��Ȃ��̂� �@�Ȃ��Ȃ��@�l�Y�~�@��߂܂����܂���B �l�Y�~�@�́@�l�R�@�����炩���̂��y������ �@�����̑��@�ɋ����ɂ�����܂���B
�m�e�N�j�b�N�h�l�R�ƃl�Y�~�r���h�̔��W�n
�m�e�N�j�b�N�n�̍��� �@�h�z�u�\�ȃ}�X���Q�Ɍ����鐔�������݂���@�̈��h�@�� �@�h�����Q�̃}�X���ꂼ��Ɓ@�����@�̈��h �@�Ɛ��������@�̈��@�́C�s���@�����ł͂Ȃ��C��}�X�@�ł����Ă��C �e�N�j�b�N�h�l�R�ƃl�Y�~�r���h�͐��藧���܂��B
 �l�R�ƃl�Y�~�r���@�𐬗�������@�̈�@���@���ʂȗ�ł��B
�l�R�ƃl�Y�~�r���@�𐬗�������@�̈�@���@���ʂȗ�ł��B��}�X�P�@�ŁC�����P�@���z�u�\�ȃ}�X�́@�s�P��P�C�s�Q��R�@�Ɍ����܂��B
�s�P��P�@�Ɠ�����ɂ���@�s�V��P�@��
�s�Q��R�@�Ɠ����s�ɂ���@�s�Q��T
�ɔz�u�\�Ȑ������C�����P�@�Ɓ@���̐����i�����Q�j�́@�Q�̐����Ɍ��肳���ƁC
�����Q�̃}�X�i�s�V��P�@�Ɓ@�s�Q��T�j�̗����̃}�X�Ɠ����̈�ɂ���}�X�i�s�Q��P�@����с@�s�V��T�j�ɂ�
���̐����i�����Q�j�͔z�u�ł��܂���B

�m�e�N�j�b�N�h�l�R�ƃl�Y�~�r���h�̗�n
 ���}�ŁC�����P�@���z�u�\�ȃ}�X���@�Q�̃}�X�@�Ɍ�����̈�́C
���}�ŁC�����P�@���z�u�\�ȃ}�X���@�Q�̃}�X�@�Ɍ�����̈�́C�s�P�C�s�U�C�s�W�C
��P�C��R�C��W�C
��}�X�P�i�C��}�X�U�j�C��}�X�V
�� ���v�W�̈�@���݂��܂��i�s�E��̏ꍇ�Ɠ����Q�}�X�ɂȂ��}�X�̓J�b�R�ŕ\�����C���v�����珜�O���Ă��܂��j�B
�_�E�����[�h�����������\�t�g�ł́C�����P�@���z�u�\�ȃ}�X���@�Q�̃}�X�@�Ɍ�����̈�ł̔z�u�\�ȃ}�X�����F���h��Ԃ����@�y���V���}�[�N�@��\���\�ł��B
�i�����Q�`�X�@�ł́C�z�u�\�ȃ}�X���@�Q�̃}�X�@�Ɍ�����̈�́C���ꂼ�� �R�C�Q�C�W�C�U�C�V�C�T�C�V�C�S�@�̈摶�݂��܂��j
�����P�@���@�s�P�@�Ŕz�u�\�ȃ}�X�́@�s�P��P�@�Ɓ@�s�P��T�@�Ɍ����܂��B
�s�P��P�@�Ɓ@�����@��P�@�ɂ���@�s�V��P�@�ɔz�u�\�Ȑ����́C�����P�@�Ɓ@���̐����@�����Q�@�̂Q�Ɍ����܂��B
�s�P��T�@�Ɓ@�����@��T�@�ɂ���@�s�S��T�@�ɔz�u�\�Ȑ������C�����P�@�Ɓ@���̐����@�����Q�@�̂Q�Ɍ����܂��B
�l�R�ƃl�Y�~�r�������������������������܂����B
�Q�̃}�X�@�s�V��P�@�Ɓ@�s�S��T�@�̗����̃}�X�Ɠ����̈�ɂ���}�X�@�s�S��P�@����с@�s�V��T�@�ɂ�
���̐����@�����Q�@�͔z�u�ł��܂���B
�_�E�����[�h�����������\�t�g�ł́C
���l�R�ƃl�Y�~�r���@�@�@�r�������� 2�@�s 4�@�� 1
���l�R�ƃl�Y�~�r���@�@�@�r�������� 2�@�s 7�@�� 5
�@�@�r���������r���}�X�ɔz�u������
�@�@�@�s 7�@�� 1�@�Ɓ@�s 4�@�� 5�@�̐��� 1�@���m�肷��
�@�@���� 1�@�́@�@�s�@�P�@�ł�
�@�@�@�s 1�@�� 1�@���@�s 1�@�� 5�@�̂����ꂩ�ɔz�u����邽�߁@��������
�ƁC�\������܂��B
�h�l�R�ƃl�Y�~�r���h�́C��ɁC�z�u�\�Ȑ������@�Q�@�Ɍ�����}�X�ɒ��ڂ��Ă��K�����������邱�Ƃ��ł��܂��i�y���V���}�[�N�F�z�u�\�Ȑ������Q�Ɍ�����}�X�����F�ɓh��Ԃ��Ă��܂��j�B
�z�u�\�Ȑ������Q�Ɍ�����}�X�̂����@�����������z�u�\�ł���}�X�̑�[��L���i�ȉ����l�j�F�s�V��P�C�s�S��T�C�����P�C�����Q]�ɒ��ڂ��܂��B ���ɁC���̑ł���Q�̃}�X���ꂼ��ŁC���̃}�X�Ɠ����̈�[��P�C��T]�ɂ���C�����̐����̂����̂ǂ��炩���������[�����P]���z�u�\�ȃ}�X���l���܂��B �����̂����C�ɂ����}�X���ꂼ�ꂩ�瓱���o���ꂽ����̂Q�}�X���C�����̈�[�s�P]�ɂ���C���̗̈�ł͂��̐������z�u�\�ȃ}�X�����̂Q�}�X�ȊO�ɂ͂Ȃ��@�ꍇ�C�h�l�R�ƃl�Y�~�r���h�̏�������������܂��B �ŏ��ɒ��ڂ����ɂȂ�Q�̃}�X�̗����Ɠ����̈�ɂ���}�X�Ŕr�����������邩�ǂ������m�F���܂��B
 �@
�@�m���K���@�h�l�R�ƃl�Y�~�r���h�K���ǖʁn
���}�ɒ��ڃe�N�j�b�N�h�l�R�ƃl�Y�~�r���h���K���ł��܂��B
�܂̖��́C�h�l�R�ƃl�Y�~�r���h��K�����Ď��i�߂�ƁC������x�h�l�R�ƃl�Y�~�r���h��K������ǖʂ�����܂��B�����̃e�N�j�b�N�����p���܂��B
��ԉE�̖��́C�h�l�R�ƃl�Y�~�r���h���S�p���܂��B�����̃e�N�j�b�N�����p���܂��B
���}���N���b�N����ƁC����Ɛ������\������܂��B



�m���K���@�h�l�R�ƃl�Y�~�r���h�n
�̓r���Ł@�e�N�j�b�N�h�l�R�ƃl�Y�~�r���h�@���K�v�ɂȂ���ł��B
�܂̖��́C�h�l�R�ƃl�Y�~�r���h�C�h�����q�̊Â��r���h�C�h�l�s����r���h�C�h��s����r���h�𗘗p���܂��B
��ԉE�̖��́C�h�l�R�ƃl�Y�~�r���h���R��@�Ɓ@�h�M���̖�]�r���h�C�h�����q�̊Â��r���h�C����Ɂ@�h�l�s����r���h���܂߂Ē����̃e�N�j�b�N���U��@���p���܂��B
���}���N���b�N����ƁC�����Ǝv�l�ߒ��̗Ⴊ�\������܂��B








