|
�@
�E�c�o�i�̃g�b�v�y�[�W�@�A�C���V���^�C���̑��ΐ����_
���x���ٕM���X�V�����̂ŁA�R���g���[���L�[�������Ȃ���e�T�������Ă�������
�@
�i�P�j�u�����A�����A�����f�v�Ȃ��Ȓ��p�O�p�`
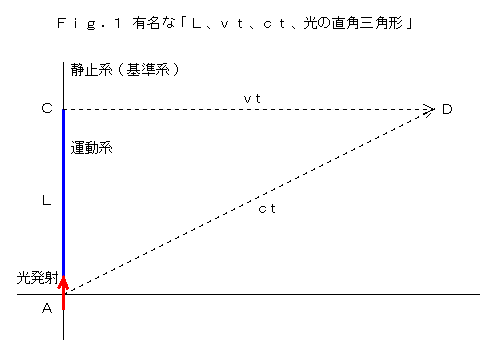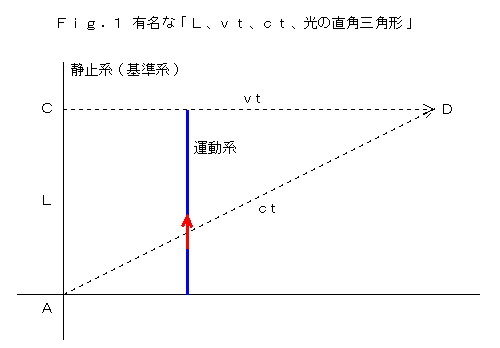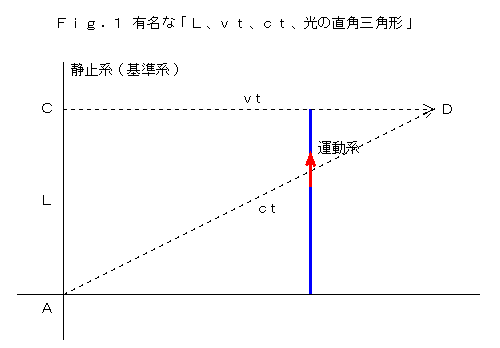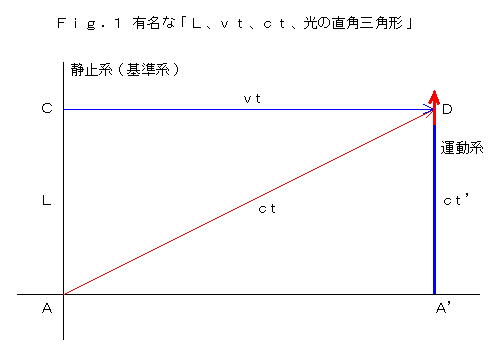
�@�}�C�P���\���E���[���[�̎�����͂ɗp����ꂽ�A���̐}���u���ꑊ�ΐ������v�Ɓu�����x�s�ς̌����v�Ƃ���
�Q�̉���݁A�A�C���V���^�C���̓��ꑊ�ΐ����_�̏o���_�ɂȂ������Ƃ́A�F����悭�������Ǝv���܂��B
�@
�@����ɁA���̎O�p�`�̓��p�̘a���P�W�O�x�ł͂Ȃ����[�}���w�ɉ����i�߂��̂���ʑ��ΐ����_�ł���܂��B
�@�A�C���V���^�C���͈ꐶ�A�������p�O�p�`�������痣��Ȃ������悤�ł��B�A�C���V���^�C�����v�����X�g����w���A�ǂ����̍u���ŁA�������p�O�p�`�����ɕ`���ă��[�����c���q���o���Ă��郂�m�N���ʐ^���������Ƃ�����܂��B
�@
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�`�f�c
�ł��B
�@���[�����c�ƃ|�A���J���̓}�C�P���\���E���[���[�̎����̉����� ���� ���k�߂�Ύ���������o����Ɖ��肵���̂ɁA�A�C���V���^�C���͂Ȃ�Əc�����Ƀ��[�����c���q���g�����̂ł��B���⏑�������ǂ��Ȃ��B�����ł͂Ȃ��A�A�C���V���^�C�����Q�T�̎��ɍl�����͎̂O�����̒藝�̏c�����̒����� A'D=ct' �Ƃ����̂ł��B��������Ƌ��R�Ƀ��[�����c���q���o�ė��܂����B�㎮���������������B����͌��݂̓��{�̋��烌�x���ł͒��w���ȏ�Ȃ�v�Z�ł��܂��B
�@
�@���̌��ʂ͎O�����̒藝���O���O�Ƃ����������ƂȂ�܂��B���ꂪ���ꑊ�ΐ����_�̊�b�������ł��B�����Ď��Ԃ� ���f �Ƃ��āu���Ԃ͒x���̂��v�Ƃ�����̂ł��B
�@
�@���̎��͎O�����̒藝����o�Ă����̂ňꌩ�������悤�ȍ��o���N�����܂��B���������_�Ƃ��Ċm��������ɂ͕s�\���ȓ��e�ł��B���Ƃ��A�悭����� �`���c �������� ���A�`'���c �������� �� �ł��B����͖��炩�ɖ������Ă��܂��B
�@�����ŁA�u�������Ⴄ�̂ɁA���� �� �ł͍���B�`'���c �̌��͂���������Ƃɂ��悤�B��������Γ��� �� �ŁA���Ԃ� ���f�ŗǂ��B���Ԃ͒x���̂��v�Ƃ�����̂ł��B���ꂪ�u�����x�s�ς̌����v�����肵���n�܂�ł��B
�@
�@�����Đ}������ƕ�����܂����A���̂𓊂������̂悤�Ɍ������ł��܂��ˁB���ꂪ�u���ꑊ�ΐ������v�����܂ꂽ���R�ł��B�������āA�����Q�� �g�����h �ƂO���O�Ȃ������������ꑊ�ΐ����_���a�����܂����B�g�����h �Ə̂���܂����A����͓��{�ƃA�����J���炢�ŁA�����̌����ł�assumption�i����j�Ə�����Ă��܂��B
�@����ȑ�������Q�́g�����h�Ə̂���鉼�肩�琳�������_���\�z����܂����H
�@
�@���ʂ̐l�Ȃ�M�����Ȃ��b�ł��B�O�����̒藝���O���O�ɂȂ��Ȃ�ĐM�����Ȃ��ł��傤�B�����f �� ���f �Ƀ��[�����c���q���������Ă��܂�����A�F�l�A�v�Z���Ă݂Ă��������B�{���ɂO���O�ɂȂ��Ă��܂��B�A�C���V���^�C���͂���Ȋ�Ȏ��ɋC���t���Ȃ������̂ł��傤���B�܂����A�Ǝv���̂ł����B
�@���݂ł͓��ꑊ�Θ_�͓��퐶���ɂ͎g���Ă��܂��A�V���w�ł͎���ƂȂ��Ďg���Ă��܂��B
����ǎ҂���u����Ȏ��͂Ȃ��I�f�o�r�ł��g���Ă���Iyahoo�m�b�܂ɍڂ��Ă����I�v�Ƃ̔��_������܂������A���������̂��g�����h���Č�����ł��B
�@
�@�w�҂��܂݈�ʂ̓ǎ҂ɁA�{�e���u�i�R�P�j���{��o�[�W�����v�ɁA�_���Ƃ��� �����f �Ƃ����̂͑��݂����Ȃ��A�Ӗ��������A�Ƃ������Ƃ��ڍׂɐ}�ʂƐ����ŏؖ����Ă���܂��B���ǂ݂������鎖��ɂ��肢�v���܂��B
�@
�i�Q�j���Θ_�ɑ��闝�_
�@���ꑊ�ΐ����_�͊Ԉ���Ă��܂��B�Ԉ���Ă���Ȃ�A����ɑ��闝�_���Ȃ��Ƃ����܂���B�S�O�Ή߂������̎��ɁA���̊��������x���P���Ă����̂��v���o���܂��B
�g���[�����c�ϊ��h �̑���ɂȂ鎟����̗��_ ���|���Ecos�� �����Ɏ����܂��B
�@
�@�F�l�ɖ��������グ�܂��傤�B��}�e�����D1 �́u�^���n�i���x���j������ �� ���ϑ�����ƁA�ǂ̈ʂɂȂ�܂����H�v
�m���F�c�ŏՓ˂��Ă���̂�����K������ł��܂��B���̊ϑ��l����������̌����ł��B���f�ƕ\�L���܂��n
���R�A�A�C���V���^�C���́u�ϑ��⑪�������K�v�͂Ȃ��B�g�v�l�����h �ŗǂ��B�����x�s�ς̌����ɂ���� �� ���v�Ɠ����܂����A�����ł͂���܂���B
������ ���f�� ���|���Ecos���ł��B�}���� ���f���R×�P�O�W�m���^���n �|�Q�D�U�S×�P�O�W�m���^���n×�������i���^�V�j���O�D�U�Q×�P�O�W�m���^���n �ł��B
�@���Ȃ� ���f���x���ł��ˁB�Ȃ����Ƃ����ƁA���̐}�̉^���n�͌��ĕ�����قǑ����āA���� �� �ɋ߂��قǑ�������ł��B���ꂪ�[�I�Ɍv�Z�ɕ\��Ă���̂ł��B�}�̂����ł��B
�@���Ȃ݂Ɍ�q�́i�P�R�j�e�����D�R���Ƃ��^�Q���傫���̂ŁA���f���� �ƂȂ��Ă��܂��B
�@
�@���݂͐�łƂȂ��Ă��܂����A�w������葬���� �A�C���V���^�C���ɒ��ގႫ�Ȋw�҂̕���x �W���A�I�E�}�Q�C�W�����^�،O��^�m�g�j�o�Łinhk-book�j�Ƃ����{���Q�O�N�قǑO�ł������A�ǂ��Ƃ�����܂��B
�@���̒��҂̌��� �g������葬�����h �ƁA���̔������� ���f �Ƃ͑S�R�Ⴄ�̂ŁA�����A���̒�����ǂ��̂���l�͍������Ȃ��ł��������B
�@
�i�R�j�}�C�P���\���E���[���[�̎������
�@�}�C�P���\���E���[���[�̎����ł́A�w���������i�^�Q�j���O �ɒ�������Ă��܂��B�����犱�Ȃ��w�Ǐo�Ȃ������̂ł��B
�������A�C���V���^�C���́A���̎����ɂ͌덷���o��̂����m�Ȓ��p�O�p�`�ɂ͂Ȃ�Ȃ��̂ɁA���p�O�p�`����O�����̒藝���g���Ă��܂����̂ł��B���̌��͂��Ƃŏڍׂ��q�ׂ܂��B
�@
�i�S�j���Θ_����̐E�ƂƂ���Ă���搶����
�@�A�C���V���^�C���́u���������^���͐�ΐÎ~�Ƌ�ʏo���Ȃ��v�ƍl�������Ƃ����킹�ė������܂��傤�B���ɏd�v�ł��B�����g�b�v�y�[�W�����`��§�Q�Q �́A���Гǔj���Ă��炢�����ł��B
�@�����A���Θ_����̐E�ƂƂ���Ă���搶���ɂ́A�����̃e���g���[��Ƃ���Ă���̂ŁA�C���������A������������X���ɂ���܂��B�C�����͕�����܂����A���܂ł��A�����������ł͎���Ɏ��c����܂��B�w������
�u ���|�ucos�� ��������Ă��������v�ƌ����āu�킵��m���v�ł͍���܂��B�����Ƃ��āA���Θ_�� ���|�ucos�� �������A���̐��藧������u�`�����鎖�ł��B�����Ċw�������� �g�l��������h �̂ł��B
�@�Ⴆ�Ύ��̖����w���ɂ�点�Ă݂Ă��������B�L�����i���{���j�� �� �ɂȂ邵�A�i���|���j�� �� �ɂȂ�Ƃ����A�C���V���^�C�����m�� �g���x�̉��@���h �̍��Z���o�[�W�����ł��B
�@�@�@�T�͒萔�ł���B�Q�͕ϐ��ł���B����āi�T�{�Q�j���T�ł���B�܂��i�T�|�Q�j���T�ł���B
�E�E�E�E�E�E�E�E�A�C���V���^�C�����m
�萔�T�ƃx�N�g���Q�̂Ȃ��p�x�����Ƃ���A�T�|�Q���������ł���B �E�E�E�E�E�E�E�E�E�E�E�E�E�E �E�c�o�i
���F�T���Q�̂Ȃ��p�x�����̏ꍇ�A�����V
���F�T���Q�̂Ȃ��p�x���O�̏ꍇ�A�����R
���F�T���Q�̂Ȃ��p�x���^�Q�̏ꍇ�A�����T
�������D
�@
�@����F�l����A��L�̏��w���`���Z���o�[�W�����̎��₪���܂����B���̎���ł��B
�u���Θ_�͊Ԉ���Ă���Ɩ^���Ɍ�������A�^���́w���Θ_�͐������B�Ԉ���ĂȂ��B�Ȃ��Ȃ瑊�Θ_�ŁA���������Ƃ��ؖ��ł��邩�炾�x�ƌ����܂����B������ĕςł��ˁB�Ԉ���Ă��鑊�Θ_�𐳂������_�������Θ_���ؖ��o�����ł����H�v
�E�c�F�ł��܂��ˁB���Ƃ��i�T�|�Q�j���R���Ə��w�Z�ŏK���܂����A�A�C���V���^�C���̑��x�̉��@���ł͓������T�ł��B
����̓A�C���V���^�C���⑊�Θ_�����w�҂ɂƂ��Ă͐������̂ł��B���ʂ̐l�X�͏��w���̕����������ƌ����܂��B
�@�Ȃ����x���\���܂����A�A�C���V���^�C���̑��x�̉��@���́w���ꑊ�ΐ������ƌ����x�s�ς̌����Ƃ����Q�̑������鉼������ѕt���鎮�ŁA���w�����K���ɕ����x�ł��B
�@�����璆�w���́A���̔ɕ������������Ƃ��ł���̂ŁA��L���̓����́u�T�܂����R�v�Ɠ����܂��B
�@���Z���ɂȂ�Ƒ��Θ_�ɋ^������悤�ɂȂ�̂ŁA��L���̓����́u�R�ł��傤�A�T�Ȃ�Ă���������v�ƌ��@���܂��B
�@�����������_�̑�w�����ŁA�������A������A���̖�肪�o����u�T�v�Ə����Ȃ��ƃy�P�ɂȂ�܂��B�����Q�T�O�N�@�͂�����ł��傤���A���|�ucos�� �������̋��ȏ��ɍڂ�悤�ɂȂ�����A�u���w���̕��������������v�ƂȂ�ł��傤�B
�@
�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\
�@
�����{�����o�ŋ���u�G���N�g���j�N�X���C�t���v�M�Ґٍe�F�P�X�X�R�N�R�����`�T�����A��
�����ԏ��X�u�A�C���V���^�C���̑��ΐ����_�͊Ԉ���Ă����v�P�X�X�R�N�^�ْ�
�����ԏ��X�u���Θ_�͂�͂�Ԉ���Ă����v�P�X�X�S�N�^��w�㓡�w������Ƌ���
�����ԏ��X�u�Ȋw�̓A�C���V���^�C�����x����Ă����̂��v�P�X�X�U�N�^�㓡�w�����A�x�E�g�E�W���[������Ƌ����@�@�ق�
�i�Ȃ��A�ْ��L���ɂ͂������̍Z���~�X��L�q�~�X�����邱�Ƃ�[�����l�ђv���܂��B������Ԃŏ��������߂̂Ȃ���ƂƂ��Ă����������邱�Ƃ�ɂ��肢�������܂��B���̌�J�݂��܂����{�z�[���y�[�W�ł́A���̓����ْ̐��̃~�X�𐳂��āA����̖����悤�A�����ċC����V�A���������āA������Ղ��L�q���܂����j
�@
�i�T�j�ً}�lj�
�m�ً}�lj��Q�O�Q�S�N�P�Q���R�P���n�F�{���̈�������ɂ߂ďd�v�ȁA�����ċM�d�Ȃ����ӂՂ������܂����B���̕��͈ȑO�ɂ����[�������������Ƃ�����A���̗��_������������Ă��邨�l�ł��B
�u�E�E�E�r�����E�E�E�ڎ�������� �g���Ό����x ���|�ucos���h �Ə����Ă��鍀������܂��ˁB���̏������͂��������ł��B
���|�ucos�� ���@�g�Q�̍��W���֘A�����鐔�w�h �ł���A���Θ_�������A�h�邬�Ȃ����x�ȗ��_�ł��B���Θ_�Ƃ͑S�R�قȂ���̂ŁA���݁A���Θ_�́A�ǂ�Ȓ����ɂ��ڂ��ĂȂ������ł��B����� �g���Ό����x�h �Ə̂���̂́A�f���ċ����܂���B�g���h �Ƃ����̂̓A�C���V���^�C���� �g�����h�i�H�j�ł���B��߂ĉ������E�E�E�v
�@���Ƃ͏ȗ������đՂ��܂��B�܂��o�邲�w�E�ł��B�����폜���܂����A�����ɂ����邩���m��܂���B�����폜���Ă����܂��B
�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\
�@
�i�U�j�V���̂��ē�
���V���̂��ē��F�q�J�������h�Ёu���ΐ����_�͋[���Ȋw�������^�P�O�O�N�ȏ�N���C�Â��Ȃ������ӓ_�v2022.12.2�����@�ڍׂ́@�E�c�o�i�@���`�@��§�Q�Q���������������B
�@
�@2023�N1��21���NjL�F����ǎ҂����u�O���O�Ƃ����������̒��Ɏ��Ԃ��k�ގ��������Ă����̂������̂͌E�c�����߂Ăł��B�{���R�O���͉i���ɗ��j�Ɏc��܂��v�Ƃ������[�������܂����B
�A���肪�Ƃ��������܂��B2022�N�x�̃m�[�x���܂��������ȏ�̑����ŐM���̕ω����e�����y�ڂ������b��ɂȂ�܂����B�ʎq�_�Ƒ��Θ_�̑Ό��ŗʎq�_���������ł��ˁB
�@
�B���̓ǎ҂��F�u�lj����܂��BYahoo�m�b�܂ɁA���E�c�̓G�[�e���ɂ�������Ă���n�������Ƃ����̂�����܂����B�E�c�搶�̗��_��S�R�������ĂȂ��l�̂悤�ł��B���������ɂȂ��Ă��C�ɂ��Ȃ��ł��������B�v
�@�E�c�F���肪�Ƃ��������܂��B�����o�J�ɂ���l�X�͑������܂��B���͉��Ƃ��v���Ă��܂���B�K�Ȕ��_�Ȃ�Q�l�ɂ��܂����A�^�������痝�_�I�ɍU�߂Ă���l�͂��Ȃ��ł��B
�@���܂ɕ����w�ғ��m���Ԃ��荇���āA����������Ă���搶�� ���|�ucos�� ���u�唭�����v�ƌ����A���Θ_�ɌŎ����Ă�����搶�́u���[�����c�ϊ������ׂĂ��v�Ƌ��܂��B
�@�܃A�A�킽���I�ɂ�120�N�ȏ�̂ɃG�[�e�����Ń}�C�P���E���[���[�̎���������������_�����A���|�ucos�� �̕����K�ł͂Ȃ����A�Ǝv���Ă��܂��B
���̏͂́�(15)�d��ȃ}�C�P���\���E���[���[�̎����̗��Ƃ������̍����A����n���ɂ���Yahoo�m�b�܂̕ҏW���ɓǂ�ŖႢ�����B���e�����l�����A������f�ڂ����ҏW���̕��ɓǂ�ŖႢ�����ł��B
�@
�C�Q�O�Q�R�N�P���Q�U���ǎ҂��烁�[���F�u�E�E�E�O���O�Ƃ������������Ĉ�̂ȂA�Ǝv���Ė{������Ŗ{�����āA�ŏ����R�O�ł��J���Ĉ��R�Ƃ��܂����B���[�����c���q�������Ȃ�I���ꑊ�ΐ����_���Ă���ȃg���b�N���������Ƃ́I�S���E�̐l�X���A����ȃg���b�N���P�O�O�N�ȏ��x����Ă����Ƃ͉����鎖���B�E�c����͉��\�N�����Θ_�ɋ^��������Ă���ꂽ�̂ł����A����Ɖ������܂����ˁB���߂łƂ��������܂��I�v
�E�c�F���肪�Ƃ��������܂��B�{���̒E�e�͍�N�̃m�[�x���ܔ��\�O�ł����̂ŁA�ЂƂ���������ɐs���܂��B
�����A���̗ʎq�_�Ƒ��Θ_�̑Ό��ŗʎq�_�����������ɂ���{���̒��������Ȃ���Ȃ�Ȃ���������������܂��B���ꂪ�C�ɂȂ��Ă���܂��B<(_ _)>
�@
�i�V�j���͔��˃|�C���g����`������
�e�����D�Q���������������B
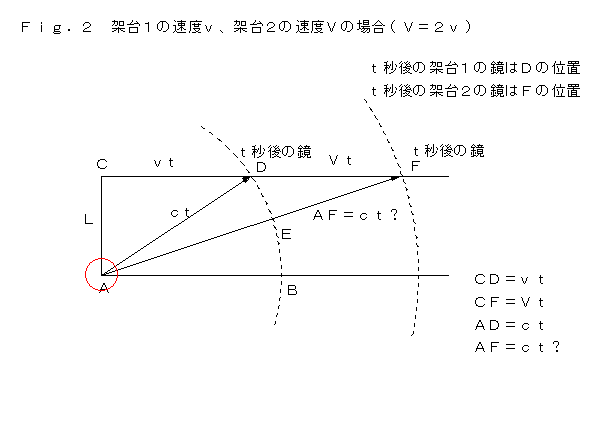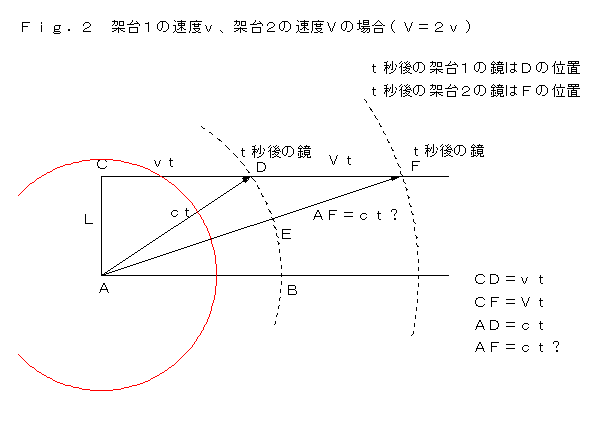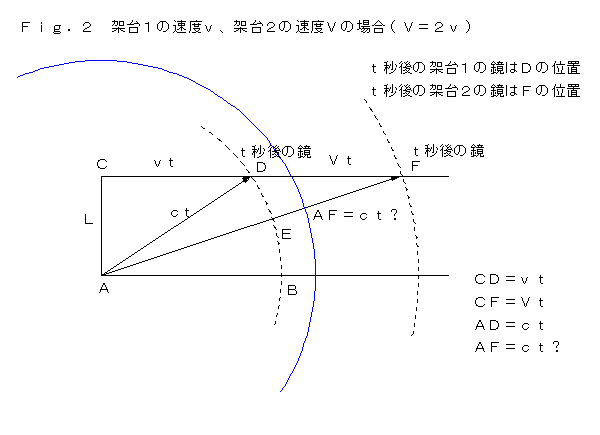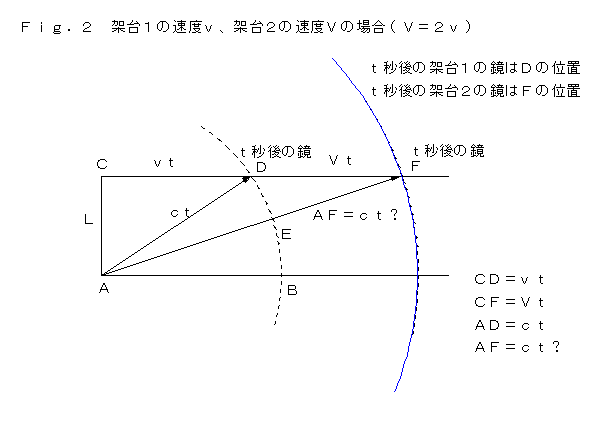
�@�ˑ䂪�Q����A��Ƃ��� �u���Q�� �̏ꍇ�̐}�������܂������A����߂Ċ�Ȑ}�ł��B
�u�k�A�����A�����A���̒��p�O�p�`�v���������A
�u�k�A�u���A�����A���̒��p�O�p�`�v�����������Ƃ͂��蓾�܂���B�@�@�@�@�@�@�@�@�@�@�@�@
�@
�@����ɑ��锽�_�͑������A���ΐ����_�͐�ɐ������Ƃ�������̂��̂ŁA�u�ˑ�P�Ɖˑ�Q�ł́A���Ԃ̐i�ݕ����قȂ�A�u �̕������������Ă���̂ŁA���Ԃ͂�����荏�ނ��炻��ŗǂ��̂��B���Ԃ� �� �� ���f �ɂȂ�̂��B�����Ƒ����ˑ�R������A���̎��Ԃ� ���h �ƂȂ�A����ɂ�����莞�Ԃ����ނ̂��B
�@���ԂƋ�Ԃ̊T�O��ς����j��ő�̑�V�˃A�C���V���^�C�����m���Ԉ���Ă���͂��͂Ȃ��v
�Ƃ������̂ł��B
�@
�@���́A���̔��_�͔��_�ɂȂ��Ă��Ȃ��Ƃ��Ă��܂��B���f �Ƃ����̂́A���ꑊ�ΐ����_�ł́A�e�����D�P�Ɏ������悤�ɁA�^���n �`�f�c �̎��Ԃł��B�e�����D�Q�� �`�e �ł̎��Ԃł͂���܂���B
�@
�e�����D�Q�ɂ��ẮA�A�C���V���^�C���͂���Ȑ}�͖��ɂ��v�������͂Ȃ��ł��傤�B�����̓ǎҁi�w�҂��܂ށj���A�u����Ȑ}�͌������Ƃ��Ȃ��I�ڂ��炤�낱�I�v�ƁA�т����肵�����ւ���R���Ղ��܂����B
�@
�@���ڂ��ׂ��́A����a��m�̋L���ł��B���̃A�^�}�̒����͂����茩�������������Ă���܂��B�u���͔��˂����|�C���g��������Ŕ��ł����i�e�����D�P�͈꒼���A�e�����D�Q�͋��ʔg�j�ƁA�E�c���͍l���������B�v
�u�A�C���V���^�C���͂����l���ĂȂ��B���͕��̂𓊂����悤�ɔ�Ԃƍl���Ă���B�Ȃ̂Ɉ���� �g�����x�s�ς̌����h �ƕ��C�Ŗ����������������Ă���B�v
�@
�i�W�j�A�C���V���^�C���P�X�O�T�N�̎G�����e�L��
�@�A�C���V���^�C��1905�N�̎G�����e�L���̖`���ɂ��錈��I�ȊԈႢ�����A�����ł��Љ�Ă����܂��傤�B
�@����G���L���̖`���� �g�����́i�v�l�I�j���������ɂ��h �Ə����Ă���܂����A����͔��ɔ����ȏ������ł��B
�g�|�A���J���̘_���������˂�h �Ƃ͏����Ȃ��̂ŁA�g�����́i�v�l�I�j���������ɂ��h �Ə������̂ł��B
���́A����G���Ƃ����̂́w�A�i�[�����E�f�A�E�t�B�W�[�N����P�V���W�P�P�y�[�W�x�^�P�X�O�T�N �ł��B
���̌���A�C���V���^�C���͋C��ǂ������̂��A�|�A���J���̒����w�V�̗͊w�̐V�������@�x����ʑ��ΐ����_�Ƃ��ē��e���܂����B�܂�����܂��B���̂P�X�O�T�N�̓A�C���V���^�C���͖�p�����ɑ��l�̔������������w��̗L���Ȏ����A�������������������悤�ɂ��ĎG�����e���~�߂܂���ł����B
�@�L���Ȃ̂��O�N�̂P�X�O�S�N�Ƀ}���R�[�j������Ђ̌ږ�����Ă����t���~���O���Q�Ɋǂ����ē��������܂������A���̓����̒��� �g�M�h �� �g���h �ɂ��āu���d���ʁv�Ƃ��Ĕ��\���A�m�[�x���܂��l���B���̎��A�m�[�x���܈ψ���͑��Θ_�ɂ��܂�^���悤�Ƃ��܂������A�j�[���X�E�{�[�A�ȂǃR�y���n�[�Q���w�h���u����ȗ��_�͗��_�ł͂Ȃ��v�Ɩҗ�ɔ����ď܂͎������ꂽ�o�܂�����܂��B������A���A�l�����Θ_�ɑ��ċ^�`��\�����Ă�����e�ȂǁA�P�Q�O�N�ȏ�̂Ƀj�[���X�E�{�[�A�Ȃǂ́A�Ƃ����ɗ������Ă����Ǝv���܂��B
�@
�@�b�𑊑Θ_�ɖ߂��܂��B�A�C���V���^�C���́u���������^���͐�ΐÎ~�Ƌ�ʂ͂��Ȃ��v�ƍl���ē��ꑊ�ΐ����_��������̂ł����A���ꂪ���̐}�ł��B
�@
�@�@�@�@�@�@�@�@�@�@�@�@�@�������` �������������a�@���
�@�@�@�@�@�@�@�@ �@�@�@�`�n�_�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�a�n�_�@�˓��������^����
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�������f�`��������ɔ���
�@
�@�L���Ȏ����@���a �| ���` �� ���f�` �| ���a �ł��B���Ă�������Ǝv���܂����A�O�̂��ߐ������Ă����܂��ƁA�A�C���V���^�C���́u������Ԃɗv���鎞�Ԃ� �`���a �� �a���` �������ŕω��Ȃ��B���ꂪ�����x�s�ς̌������v�Ƃ����咣�ł��B
�@���̎����ʼnY�H�Ƒ�w��w�@�ōu�`�������A�w���B�ɘb������A�u����Ȏ��͂Ȃ��B���a �| ���` �� ���f�` �| ���a ���v
�Ƒ��U�œ����܂����B
�@�ǎ҂̊F�l�͂ǂ����l���ɂȂ�܂����H
�w���B�̕����������ł��ˁB������P�Q�O�N�ȏ�̂ɂ͑��݂��Ȃ����������O���[�U�[�W���C�����A���̌��������p���Ă��邩��ł��B���݂̃W�F�b�g�퓬�@��F���T���@�ɂ͕K�����ڂ���Ă��� �g�����O���[�U�[�W���C���h�B�ʏ�͒����R���ɂR��ڂ���Ă��܂��B
�@����̐i���͑��Θ_���ǂ̂悤�ȖڂŌ��ĒQ���Ă���ł��傤���B�E�E�E�E�E
�����Ŕ��ɏd�v�ȓ_��������Ă����܂��B���������l c ��299,792,458�m��/s�n���Ƃ����̂̓}�b�N�X�E�F���d���͊w���瓾������̂Łi�������A�n���ƌ��̊Ԃ̂悤�Ȑ^�̌����j�A���p�͈͂����ɍL���ł��B
������ �g�����O���[�U�[�W���C���h �i�����O�̒��͐^��ɂȂ��Ă��܂��j�Ȃǂɉ��p����Ă���̂ł��B
�@���݂ł̓i�m�e�N����ɂȂ��Ă��āA���͌����́A�����������x�ł͂Ȃ��̂ł��B�P�i�m�b�ł������� �R�O���� �����i�݂܂���B���ꂪ�A�����w��H�w�̎���ɂ��Ȃ��Ă��܂��B�g�����O���[�U�[�W���C���h ���܂��ɁA���̃i�m�e�N�Z�p�Ȃ̂ł��B
�@����ȁu�P�i�m�b�ł������� �R�O���� �����i�܂Ȃ��v���x�����̒��ōō����x���Ɖ��肷�鑊�Θ_�̂ǂ����������̂��A�ƌ��������ł��B
�@��q�̂悤�ɁA���� �R�O�����^ns �Ƃ����̂� �g�^�h �ł̘b�ł���A��C���␅�A�F����Ԃ̃A�����j�A�K�X���Ȃǂł́A�����ƒx���Ȃ鎖�͂������ł��ˁB�s�ϒl�ł͂Ȃ��̂ł��B�����͔}���̗U�d���Ɠ���������Č��܂���̂ł��B
�@������A���V�������Ŕ�юU�������������A���̑��̑f���q�͌����ȏ�ƂȂ��Ă���\���͏\���ɍl�����܂��B
�@�X�� �g�ʎq����h ���F���ɉ��p����ƁA�启�Ɣ����� �g�ʎq����h ��ԂɂȂ��Ă���Ƃ������܂��B
�@
�@�b����L �g�����x�̕ω��h �ɖ߂��܂��B���f�� ���|���Ecos�� �ŁA���̖��������Ǝ��̂悤�ɂȂ�܂��B
�@�@�����̉��i�`���a�j�́A���f�� ���|���Ecos�� �� ���|���Ecos�� ���{��
�@�@�����̕��i�a���`�j�́A���f�� ���|���Ecos�� �� ���|���Ecos�O�� ���|��
�@�@ ���������āA���a �| ���` �� ���f�` �| ���a �ƂȂ�܂��B
�@��}�͌����꒼���ɔ��ł���ȒP�Ȑ}�ł����A�`�n�_�A�a�n�_�͂����Ȃ�����ɂ��낤�Ƃ��A���f�� ���|���Ecos�� �Ōv�Z���鎖���ł��܂��B����������������܂��B��n �� �ƁA����ɑ���^���n�� �� �ɂ͊֘A�����K�v�ł��B
��L�i�Q�j�ŏq�ׂ��悤�� �� �� �� �Ɋ֘A���Ȃ�������A���f �͑��݂��锤�͂���܂���B
�@���Θ_�����w�҂��ł��������镔���ł��B
�@
������������������������������������������������������������
�@
�i�X�j�e����.�Q�ւ��ǎ҂̔��_
�@���� �� �ɂ��āA���锽�_�҂��u�e�����D�Q�� �� �͂��������B���`�c�b�� ���P�@�C���`�e�b�� ���Q �ƕ`���Ȃ��Ƃ����Ȃ��v�Ƃ̂��ւ肪����܂����B�������Ƃ��Ȏ��ł��B����Ȏ��͕���������b�ł��B
�@�����q�ׂĂ���̂́A��̊�n���W�̒��ɁA��̈قȂ����^���n��`���������ł��B���ꑊ�ΐ����_�ł́A��ł��O�ł��A�����ł��`�������\�ł��B����ȎO�p�`�͂��蓾�Ȃ��ƁB
�@�����Ċ�n���W�͂P�b�ԂɂR�O�������Ƃ��������̖ڐ���ŁA�^���n�̂k�̓}�C�P���\���E���[���[�̎���(1887�N)�ł́A�P�b�ԂɁA�P�R�O�O����]���̉������˂��J��Ԃ��Ă��銱�Ȏ����̉ˑ�̒�����P�P���ł��B
�ǂ����āA����Ȑ}���`���܂����H
�@��ɕ`����킯���Ȃ��̂ł��B����𗝉����ĖႤ���߂Ɋ����� �g�`�����h �̂ł��B
�@���̔��_�҂������悤�Ɂ@���P �Ɓ@���Q �ɂ��܂��傤���B�P�X�O�T�N�̃A�C���V���^�C�����ɏ����ƁA
�i�����P�j�Q���i�����P�j�Q�{�k�Q
�i�����Q�j�Q���i�u���Q�j�Q�{�k�Q
�ƂȂ�܂��B��������ƁA�i�����P�j�Q �|�@�i�����P�j�Q���i�����Q�j�Q �|�i�u���Q�j�Q�@�ł�����A���� �� �����߂�ƁA
�� �����i ���P �C���Q�@�C���C�u �j���S�̊��ɂȂ�܂��B����Ō����x�s�ς̌����ł����H������S�̕ϐ����ǂ������l�ɂ���� c ��299,792,458�m��/s�n�ɂȂ�܂����H���́u����Ȓ��p�O�p�`�͕����w�ł����w�ł��Ȃ��v�Əq�ׂĂ���̂ł��B
�@
�i�P�O�j���ւ̍U���͓ڍ����Ă���
�ǔ��V���S���ł̒����P�ʂ̒����Ɂw�A�C���V���^�C���ɂ��A�����ňړ����Ă���������炻�̑O���ɔ��˂������͌����Ŕ�ԏo���x�ƌ����x�s�ς̌������������Ă��܂����B���ւ̍U���ł��傤�B������āA�̂����������Θ_�ł͂��蓾�Ȃ��������R�Əq�ׂĂ��܂��ˁB�u�����Ō�������������A�����͂ǂ��Ȃ�H�v�B�����̓y�`�����R�ɂȂ�A���Ԃ̓[���ƂȂ�A�����͖�����̎��ʂɂȂ�܂���B�悭���܁`�A����Ȍ�������������яo������ł��ˁB
�@
�@�Ԉ���Ă��闝�_����́A�Ԉ�����������ł�������T�^�I�ȗ�ł��B�u����������A��������݂���v�A�u����������A�������������v�Ə�ɘb���͂��炩���āA�������������������Ă���悤�ɂ��閂�p�����Θ_�ł��B
�@
�@�{����������āA���̐V���L���ւ́A���̂悤�ɂ��������Ă����܂��B�w���������ňړ����Ă������������A���̑O���ɔ��˂������͌�������o���Ȃ��̂Ō������̌����x�͋ɓx�ɏ㏸���A�����͔�������x�ƁB
�@����ɑ��Ė^�Ȋw�҂̃R�����g�́w���������_���Ȏ��g���̏ꍇ�͌E�c���͓K�Ő������B���ʂ͔������邾�낤�B�P����g���̌��i���[�U�[�Ȃǁj�ł͌������Ō��͑ł�������̂ŁA�����͂��Ȃ����O�ɂ͏o�ė��Ȃ��x�Ƃ̎��ł��B
�@����́A�h�C�c�̃_�����V���^�b�g��w�̃Q�I���O�E�n�C���c�F���m��̌����`�[���ł����A���[�U�[���ŕs�����Ȍ�������U�����ɂ��Č����̒��Ɍ����P���Ԏ~�߂�ꂽ�Ƃ����L�^��B�����Ă��܂��B���ꂪ�����ɂȂ��Ă��锭���ł��傤�B���������ł��B�Ȃ��A���̎����ł́A�P����Ɍ����́u��ꂽ�v�����ł��B�������Ȃ��Ă悩�����B
�@
2024�N11��23���NjL�F���̌��� ���f�� ���|�ucos�� ������č����x�M���̃R���s���[�^�[�������o���邱�Ƃ��������Ă���悤�Ɏv���܂��B��������ꂽ�Ƃ����̂��P���Ƃ����������ԁA��������߂�����ŁA�������ɒZ�����ԁA�� �𐧌䂵�� on�^off ���J��Ԃ��Ώo�� ���f �͂���ɓ������������锤�ł��B�����܂ł��Ȃ��A����̓R���s���[�^�[�̐M���`�B���̂��̂ł��B
�@��̓I�Ɍ����܂��ƁA�u �Ƃ����̂́A���̏ꍇ�n���̉^���ł�����A���̕ω��� on�^off �ɑΉ�������̂ł��B
����� cos�� �𐧌䂷�邱�Ƃœ����܂��B�Ɓ��O �̏ꍇ�� ���f�����|�u �ł��B�Ɓ��^�Q�̏ꍇ�� ���f���� �ł��B
�������� �u �̕ω��� on�^off �ɑΉ�������̂ł��B�u�̕ω��͑傫���ł�����A���݂̃R���s���[�^�[���P���{�A�Q���{�ȏ�̍����x�M���̃R���s���[�^�[�����ł͂Ȃ��Ȃ�܂��B
�@
�i�P�P�j���Θ_�͖ʔ����Ċy�����������w�ł͂Ȃ�
�@�Ƃ�����A�A�C���V���^�C���̑��ΐ����_��
�u�}�C�P���\���E���[���[�̎������u�͉��������n���̉^���ɂ���ďk��ł���Ƃ��Ď�����������A�嗝�_�ƂȂ����v�A
�u�^�����鎞�v�͂������i�ށB�������A�A�C���V���^�C���ɂ��A���̎��v�͌̏Ⴕ�Ă���̂ł͂Ȃ��v�A
�u�^�����鎞�v�͐i�s�����ɏk�ށB�k��ł����v�͌̏Ⴕ�Ȃ��v�A
�u�������ʼnF�����s����Ɣ�s�m�͍����Ȃ����A�n���ɖ߂�ƈ�u�ɂ��Ēn�����ԂɂȂ�����Ƃ����A�C���V���^�C���̉Y�����Y���ʁv�A
�u�n�����a������ꡂ����P�R�W���N�O�Ƀr�b�O�o���ɂ���ĉF�����a�������u�Ԃ��玞�ԂƋ�Ԃ��n�܂����B���݂���Ԃ͐L�тāA���Ԃ͏k��ł���B�ԕ��Έڂ����[�����c���q�Ōv�Z���Ă���̂ŁA�P�R�W���N�O���A�Q�O�O���N�O���A�]���������B�������قljF���̑傫���͑傫���Ȃ��Ă����B�����ď�ɉF���̒��S�͒n���ł���B���l�ɂd�s���ɏZ��ł���d�s���l�͉F���̒��S�́A��X�̏Z��ł���d�s�����I�v
�ȂǁA����߂Ċ�ȁA�l�X�̋����������錋�_�ɂȂ��Ă���̂ł���܂��B
�@�����������Ƃ͂��蓾�Ȃ��A�ʔ����������w�ł͂Ȃ��A�Ƃ����̂��A���̎w�E�ł��B
�C�O�̔����ł�http://worknotes.com/Physics/SpecialRelativity/TwinParadox/htmlpage9.aspx�@�Ɂu�P�X�X�O�N��ɓ����ē˔@�Ƃ��đ��Θ_�̕��n�܂����v�A�u���Θ_�̓W���[�N���v�Ȃǂ�����܂����B���̍�����m�[�x���ܕ����w����ł͑��Θ_�ɋ^��������n�߂��̂����m��܂���B�ł���Ηʎq�_�ɌX���͓̂��R�̐���s���Ƃ��l�����܂��B
�@
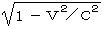 �����Ŗ����o���܂��B���}�ł��B �����Ŗ����o���܂��B���}�ł��B
�@�̌����x�͂�����ł��傤���B
�A�̌����x�͂�����ł��傤���B
�B�͓ˑR�o�����p�Ɍ������Č����������ɕ��˂��ꂽ�̂ŁA�ϑ��ҁi�^�]��j�͑��U�ŁA����𑨂��āA���̌����̑��x���v�Z���܂����B�p�|�C���g�ŏo������̂Ōv�Z�o�����̂ł��B����ȊO�̏ꏊ�ł͌v�Z�ł��Ȃ����A���Ӗ��ł��B���āA������ƂȂ����ł��傤���B
���̎����Ԃ͖����Ԑ��ŁA�����x�ő����Ă��܂��B
���������҂��܂����A
�@
�@
�����A�F�{���̈������炨�ւ肪����܂����B����͑S�����f�ڂ��܂��i��������ɏ����ρj
�u�E�c�搶�A���炭�ł����B�����C�ł�����̗l�q�A�������q�ǂ��Ă���܂��B�g���Ό����x�h �̌��A�����폜����Ă���̂��m�F���܂����B�搶�̂��Ή��Ɋ��Ӓv���܂��B
�@����͏�L�ɖʔ�����肪�f�ڂ���Ă��āA�������킵�܂����B�搶�̖�肻�̂��͕̂�����܂��āA�ǂ������̂ł����A�܂��܂��ꌾ�ł��B�\�������܂���B�����Θ_�ł́A�ǂ��Ȃ邩���Ƃ����ٖ�ł��B�q�ǂ��܂��ƁA�܂��������ٖ⁄�ł��B���Θ_�͖{���ɐْt�ȗ��_�ł��B�������A���̎������܂�ɂ��������߂��Ă��܂��B�搶�̂��l�����^����悤�ȕ��ʂ�����ł��܂��B����͂�߂Ă��������B���h����搶�������̐l�X���猙����̂�z������Ɩ����������Ȃ��Փ��ɋ���܂����B�X�������z���̂قǂ����肢���܂��B�h��v
�@
�@���肪�������w�E�ł��B�����폜���܂����B�����ׂ��͐M���o����F���Ƃ悭�����܂��B�������Ď����g����������̂ł��B���ʂ܂Ő��������������ł��B�L���������܂����B�Q�O�Q�T�N�R���P�Q��
�@
�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\
�@
�i�P�Q�j���Ɖ^���n������
�@���́A�����͈�肾����A�^���n�ɂƂ��āA���̌����x�͌�������ω������Ƃ��Ă��܂��B
���̑傫���� ���f�� ���|�ucos�� �ł��邱�Ƃ���L�ْ��A�{�z�[���y�[�W�ȂǂŁA���̓��o�������Ă��܂��B�����Q�̍��W���֘A�����鐔�w�́A���w�҂͂������ł����A���Θ_�����w�҂͂������Ȃ��ł��B
�@
�@���ꂪ�؋��Ɏ��͂s�u�Ō�����������̂ł��B�A�X�y�N�g��S�F�R����̌Â��b�ł����猻�݂͂ǂ���������܂��A���L���Ȋw�Ґ搶���u�A�C���V���^�C���̌����x�s�ς̌����͐������̂��v�ƕ��R�Əq�ׂĂ��܂����B���Ӑ[���O����Ă���ƁA�u�}�b�N�X�E�F���d����������������x�͈��ł��邱�Ƃ������o����邩�炾�v�ƁA�������Ă��܂����B
�@���́u�Ȃ�قǁA�����ɑ傫�ȕǂ�����v�Ǝv�����u�Ԃ������B����ȑ�Ȋw�҂��A�}�b�N�X�E�F���d�����������瓾��������x����ƁA�A�C���V���^�C���̉������ł������x�͕s�ς��A�Ƃ�����ʂ��t���ĂȂ��̂�����A���ȂS�~�݂����Ȃ��ƁB
�@
�@���͌��݁i2025.7.13�L�j�ł��A��L�u�}�b�N�X�E�F���d�����������瓾��������x����ƁA�A�C���V���^�C���̉������ł������x�͕s�ς��A�Ƃ�����ʂ��t���ĂȂ��Ȋw�҂����܂��B�č��J���t�H���j�A��w�o�[�N���[�Z�����m���ł��B
���̂悤�ȋL�������t���܂����B
�@�����Ɂw95���̉F���@�𖾂���Ă��Ȃ� �g��h ��ǂ݉����F������x�����邪�A�l�X�̉F���ς�傫���ς����A�C���V���^�C���́u���ΐ����_�v�ɂ��ĉ������A�Ƃ����L���ł��B
�@���̑����Ō���ǂ���������ǂ��Ȃ�H
�l�X�̉F���ς�傫���ς������ΐ����_�Ƃ́A�ǂ��������̂Ȃ̂ł��傤���B�܂��A1905�N�ɔ��\���ꂽ���ꑊ�ΐ����_����ȒP�ɐ������܂��B
���ꑊ�ΐ����_�̒��z�́A�A�C���V���^�C����16�̂Ƃ��ɔ������Ƃ����u���̑����Ō���ǂ���������ǂ��Ȃ�̂��낤���v�Ƃ����^�₩�甭���Ă��܂��B
�i�E�c�F�A�C���V���^�C���̓��_���l�ł���`�L�ɂ́A16�̎��A����Ȏ����l�����Ƃ͏�����Ă��܂���B�A�C���V���^�C���ꑰ�ɂ͐��_�ُ�҂������A�A�C���i��̂Ƃ����Ӗ��j�A�V���^�C���i����Ƃ����Ӗ��j�Ƃ������O��t�����͕̂�e�ł��B�A�C���V���^�C���͎q���̍����瓐�Ȃ�����A���l�̐H�ׂĂ��镨�������Ɖ���肵�ĉB��ĐH�ׂ�A�Ƃ����L����N���Ɋo���Ă��܂��B
�@�j�[���X�E�{�[�A���w�A�C���V���^�C���Ƃ̘_���x�ɂ́A�u�A�C���V���^�C�������l�̘_���������˂Ă��A���邱�Ƃ͍T���悤�v�Ƃ����S���������������q�ׂ��Ă��܂��B���R�̓��_���l�𔗊Q���邱�ƂɌq�����Ă͂����Ȃ��A�Ƃ����Љ�I�Ȋ�Ղ�����������ł��B
�@���ꑊ�ΐ����_��1905�N�ȑO�Ƀ|�A���J�������ɘ_�����\���Ă������̂ł��B�j
�@
���������o���������I�Ȋ��o�ōl���Ă����ƁA���Ɠ������x�Ō���ǂ���������A���͑��x0�̏�ԁA�܂�~�܂��Č�����ł��傤�B
�i�E�c�F���͎~�܂��Č����邱�Ƃ͂Ȃ��ł��B���͂d�Ƃg�����݂ɃG�l���M�[�ϊ����Ȃ�������Ŕ��ł���g�g���h�ł���B
�����郏�P�Ȃ��ł��傤�B������Ɏ����Č��Ă����B���͐��������܂����H��C�R���f���T�[�ɓd�����|����Ɠd�ꂪ�����܂����A���̓d�ꂪ�����܂����H
�@���͔g���ł��ˁB���������l�����܂����H�B
�@�}�b�n�P�̑��x�ʼn���ǂ���������A���̉����~�܂��ĕ�������́H�������܂���B
�u���H�v�Ǝv��ꂽ��A���ۂɃW�F�b�g�퓬�@�ɏ���đ��c���Ă���l�ɕ����Ă����A�u�}�b�n�P�ȏ�ɂȂ�Ƃ��Ռ��g���������ăo�[���Ƌ���ȉ������܂����A���c���Ă���l�́A�������܂����H�v�ƁB�u�������܂���B�v������Ȃ��ƁA���}�b�n�P������������܂���v�Ɠ����܂���B�j
�@
�A�C���V���^�C�������ꑊ�ΐ����_�̍\�z�Ɏ��g�����ɂ́A�d���C�w�̕���Ō��̑�������̓I�Ɍv�Z����Ă��܂����B�A�C���V���^�C���͂�����āA���̑��x�͏�Ɉ��ł���Ƃ����u�����x�s�ς̌����v�𒌂ɂ��ē��ꑊ�ΐ����_�����肠���Ă������ƂɌ��߂܂����B
�i�E�c�F�d���C�w�Ō����x�͈��ł��邱�Ƃ��ăA�C���V���^�C���́u�����x�s�ς̌����v�𒌂ɂ��ē��ꑊ�ΐ����_��������A�̂ł͂���܂���B���ɔ��\����Ă����|�A���J���̘_���������˂āA������P�X�O�T�N�ɁA����G���ɓ��e�����̂ł��B���́A����G���Ƃ����̂́w�A�i�[�����E�f�A�E�t�B�W�[�N�����P�V���W�P�P�Łx�^�P�X�O�T�N �ł��B
�j�[���X�E�{�[�A�u�A�C���V���^�C���Ƃ̘_���v��u�A�C���V���^�C���A���ꑊ�Θ_������肷��^�W�����E���f�B�b�N���^�[��m���^�ۑP�v�A�uJustin Manning Jacobs�� "Relativity of light " �v�Ȃǂ����ǂ݂��������B�j
�@
���̌������̗p����Ƃ����̂́A�ƂĂ���_�Ȍ��f�ł��B�Ȃ��Ȃ�A�Ⴆ����l���猩�Č�����99���̑����œ����Ă���l�������Ƃ��āA���̓����Ă���l���猩�Ă��A�����͓������Ƃ����̂ł�����B
�i�E�c�F���͌����Ȃ��ł��B����������ȏŌ����������ł��鎖�ȂǑ���o���Ȃ��ł��B�j
�@�ȏ�́A���̒����̈ꕔ�ł����A���������Ԉ�������_�ʼnF�����𖾂����Ȃ��蓾�Ȃ��ł��B��������݂���Ă���̂ł��B
�@�X�Ɏ��̒��q�ɂ����ڂ��܂��傤�B
�@
�u���̑����v�Ƃ����̂́A�����莞�ԓ��Ɍ����i�����Ƃ����Ӗ��Ȃ̂ŁA�����N���猩�Ă������ɂ��邽�߂ɂ́A���Ԃ��ԂƂ������T�O�̕����A����l�ɂ���ĕς��Ȃ���Ȃ�܂���B
�܂�A�j���[�g���ɂ���Ύ��ԂƐ��ԂƂ����l�������C������K�v���o�Ă��܂��B
�i�E�c�F�u�����N���猩�Ă������ɂ��邽�߂ɂ́A���Ԃ��ԂƂ������T�O�̕����A����l�ɂ���ĕς��Ȃ���Ȃ�܂����v�ł����āH ���͌����Ȃ��̂ɁA�Ȃ� �g�����Ȃ����Ԃ��ԁh �̊T�O��ς��Ȃ���Ȃ�Ȃ��̂ł����H
�����������ԂƂ���ԂƂ����͕̂����w�ł͂Ȃ��̂ł��B���w�ł��B���ԂƂ����͎̂����Ǝ����̊Ԃ̎��ł��B�������w�肳��ĂȂ������玞�Ԃ͖����ł��B���ł��B��Ԃ����l�ł��B���w�ł͋�Ԃ͑�ȊT�O�ł����A�����w�ł͖��ł��B���̋�ԂɐF��ȕ���������A�F�����`�����Ă���̂ł��B
�@�������͂悭 �g�F����ԁh �Ƃ��������g���܂����A����͖��̋�Ԃɐ���_�A���̑������̕������݂��i�̎��ł��B�l�ލő�̔����͂O�i�[���j�Ƃ��������ł��ˁB��Ԃ͂܂��Ƀ[���i���j�ł��B
�@�Ȃ��A�j���[�g���͐�Ύ��ԂƂ����ԂȂǂƂ����l���͂��Ă��܂���B�j
�@
���ہA���ꑊ�ΐ����_�ׂ�ƁA���ʂ������̂͌����̋߂��܂ʼn������邱�Ƃ͂ł��Ă��A�����ɒB���邱�Ƃ͂ł��Ȃ��Ƃ������Ƃ��킩��܂��B
�i�E�c�F�ǂ�����āA�������������̂�������Ă��܂��A�����דd���q�������V���N���g�����ʼn�������̂ł���A�Ȃ������ȏ�ɂȂ�Ȃ����͊ȒP�ł���B�d����ʼn������Ă��邩��ł��B�d����̑��ݍ�p�̓}�b�N�X�E�F���d���͊w���番����悤�� �g�����h ������ł��B����������ȏ�ɂ͂Ȃ�Ȃ��̂ł��B
2022�N�x�̃m�[�x���ܕ����w�����R�����Ă��������B�����ȏ�ő��ݍ�p���錻�ۂ��������̂ł���B
�@�X�ɂ��߉������q�ׂ�ƁA�A�C���V���^�C���́u���ꑊ�ΐ������v�B����́u���͕��̂𓊂����悤�ɔ�ԁv�Ƃ�������ł��ˁB���̉���ɂ��A�ȒP�Ɍ��͌����ȏ�̃X�s�[�h�Ŕ�ׂ鎖�ɂȂ�܂��B�A�C���V���^�C���̑��x�̉��@���ł��B
�@���́u���ꑊ�ΐ������v�A�u���x�̉��@���v�ɂ��ẮA�����ǂ͈͂ł͈ꌾ���G��Ă��Ȃ������B�u�����x�s�ς̌����v�Ɩ�������̂ŁA�킴�Ə����Ȃ������̂ł����H�j
�@
�܂��AE = mc^2�̎��́A����c���A�ʏ펄�������g���Ă���P�ʂŔ��ɑ傫�Ȓl�i�b����30���L�����[�g���j����邱�Ƃ���A�ƂĂ������ȕ��̂ł��A�������̎��ʂ��G�l���M�[�ɕϊ����邱�Ƃ��ł���A����ȃG�l���M�[���ɂȂ邱�Ƃ��Ӗ����Ă��܂��B���̎����́A��Ɍ��q���e�̊J���Ɏg���Ă������ƂɂȂ�܂��B
�i�E�c�F�S���̃f�^�������悭�����܂��ˁB���q���e�J���̌��_�͗ʎq�_�ł��B�E�����̌��q�j��j��ƁA�c��Ȕj�ꂽ�f���q�̉^���G�l���M�[�����o����邾�낤�A�Ƃ����̂͗ʎq�͊w�҂����Q�����E���̎n�܂�ȑO������ɘ_���Ƃ��Ĕ��\���Ă��āA���{�͂��Ƃ�萢�E���̉Ȋw�҂��m���Ă��܂����B
�@���e�ł��q�ׂ��悤�Ɋj����̔������P�X�R�W�N�ŁA����܂ł͌��q�j�͉i���s�łƐM�����Ă��܂����B�������A���q�j�͂��͕���B����������ȃG�l���M�[����o���Ȃ���B����������Ŋm���߂��̂́A�킸���U�N�W�P������P�X�S�T�N�V���P�U���̃g���j�e�B�����ł��B�A�����J�j���[���L�V�R�B�̍����̒n��ɓS�������ĂāA���̏㕔�ōs�Ȃ����j�㏉�̊j���������ł��B���̔����̈З͂͑z����₷��傫�Ȃ��̂ŁA�S���͐Ռ`���Ȃ��A�n��ɑ傫�Ȍ����Ă����B�j���e��������Ȋw�҂̒N������������ŁA�u����Ȕ��e��푈�Ɏg���ȁI�v�Ɛ�債�������ł��B�����Ɋւ�����w�ǂ̗L���ȉȊw�ҁi�ʎq�͊w�j���A���̌㎫�ނ��������ł��B�������A���̎��_�ł͊j����Ő�������ː��A���˔\�ɑ��Ă̔F���͖w�ǂȂ������B���̂��߁A���������܂������A�J�����}���⒲�������L��ȍ����������������߁A�̂��ɔ����a���̑��ŁA���X�Ɏ��S�������͗L���Ȏ����ł��B
�@�S�����S���������̂ł����A�Q�x�ڂ̎����̓v���g�j�E���j���ǂ̒��x�̈З͂����邩��m�邽�ߍL�����ōs�Ȃ����i���̑��G�l���M�[�͒n�k�̃G�l���M�[�Ɋ��Z����ƃ}�O�j�`���[�h�U�j�B
�R�x�ڂ̎����͖�i�̓S�H����̗\�肾�����̂ł����A�V�C�������_�ŕ����Ă����̂ŁA�����̈З͂��B�e�o���Ȃ��Ɣ��f�����̂ŁA��͑��D���̂��钷��ɂȂ����B
�@���̌���I��̑O���܂ŁA���{�e�n�ŁA�����\���e�������ς��D����C�ɔ���������������s�Ȃ����B�����́A�O�����ĕČR���u���O���E�����߂ł͂Ȃ��B�����������������e�𗎂Ƃ�����A�����Ă��������v�ƃr�����T���Ă����̂ŁA�w�ǂ̐l�X�͉����ɓ����Ă����̂ŁA�������������ł���B�������N�������A����V�l�̏،������X�����B�u�߂��Ă�����A�Ɖ��A�ƒ{�A�c�┨�Ȃlj������������I�v
�@�A���R�̗\��ł́A����ł��푈���~�߂悤�Ƃ��Ȃ��̂Ȃ�A�w��B�ɂT�O���l�A�Z������ɂT�O���l�A�֓�����ɂT�O���l�A�v�P�T�O���l�̕��m���㗤���āA���{����ł�����x�Ƃ����v�悾���������ł��B
�@
�@�d�������Q �Ƃ������͕����w�ł͂Ȃ��A�A�C���V���^�C�����L�̗L���Ȏ��������˂����ł��āA�^���G�l���M�[
�d�������Q �^�Q �����������x���ɂ��ċU�����������ł��B�f�B�����V�����������Ȃ̂ŁA���E���̐l�X���܂�܂��x����Ă���̂ł��B���ꂪ�؋��ɁA�����̐��{������}�X�R�~�̑O�Œ�������E�E�E�E�E�B�ȉ��ȗ����܂��B
�@
�@���͒��w�R�N���̎��A�A�C���V���^�C���̓`�L��ǂ�ŁA���̐����������āA���Θ_�Ƀn�}�b�čs������l�ł��B���̍������������B�������g�����i���Ɓj�������v���B
�@
�|�|�|�|�|�|�|�|�|�|�|�|�|�|�|�|�|�|�|�|�|�|�|�|�|
�@
�@���߂ēǎ҂̊F����͎��̌����������͈�肾���灄�́A���}�b�N�X�E�F���d�����������瓾���������聄�̎����ƃA�^�}�ɓ���Ă����Ă��������B�A�C���V���^�C���́u�����x�s�ς̌����v�ł͂���܂���B�u�����x�s�ς̌����v�́i���{���j�����ɂ�����A�i���|���j�����ɂ��āA�� ��r������Ԉ�������w�ł��B
�@
������ǎ҂���u���f �������ł����H�����x�ł����H�v�Ƃ��������Ȏ��₪���܂����B�{���ɔ����ł�(*^_^*)�B
�� ����ɂ��Čv�Z����ꍇ�́u�����v�ł��ˁB�������u�ƁA���Ȃ�p�x��L���Ă��܂�����A���̈Ӗ����猾���Ɓu�����x�v�ƂȂ�܂��B����u�����l�ł��B�P�Ƃł́u�����v�ł����A���ƁA���Ȃ�p�x��L���Ă���̂ŁA�u����ɂ��Čv�Z����ꍇ�́u���x�v�ł��ˁB�ucos�� �͖��炩�Ɂu���x�v�ł��B�����𑍍��I�ɍl����Ɓu���f�͌����ł������x�ł��ǂ��v�Ǝv���܂��B
�@
�@���f�� ���|�ucos�� �̓}�b�N�X�E�F���d���͊w�ɉ�����u�g�����v�ƃj���[�g���͊w�́u���̂̉^���u�v���������ɂȂ��Ă��܂��B�ʎq�_�����l�A�}�b�N�X�E�F���d���͊w�ɉ�����u�g���v�ƃj���[�g���͊w�́u���q�v���������̂ł��B
�@�A�i���O�ƃf�W�^���̈Ⴂ�͂���ɂ���A�A�v���[�`�̊�{�͓����ł��B
�@
�@���f�� ���|�ucos�� �̖��̂ɂ��܂��ẮA����̕����w�̔��W�ɔC���܂��B���� �� �� �u �𐔊w�I�Ɋ֘A������Ƃ����v�����甭���������ł��̂ŁA�K�Ȗ��̂������Ȃ��B
�@���������̂��P�X�X�Q�N�̓~�ł������A���\�����̂͗��P�X�X�R�N�̏t�ł����B�Ȃ��P�N���x�ꂽ�̂������`�ɏڍׂ������Ă������܂��B�E�E�E�����̒��������w�Ґ搶�ɁA�K���s�K���������ꂽ����ł��B�܃A�A�w�Ґ搶�����炷��A���Θ_������Ă��܂����ł��̂ŁA�M�������Ȃ��������낤���A���邢�́A���̎��Ӗ���������Ȃ������̂����m��܂���B������҂ł��傤�B
�@����E�E�E��`���l����Ǝ��`�ɂ������܂������A���{�̉Ȋw�҂͐l�̔��z������肷��悤�Ȏ��͂��Ȃ��A�Ƃ�������������̌��ʂ��낤�Ƃ��v���܂��B
�@
���f�� ���|�ucos�� �̉��p�ɂ̓h�b�v���[���ʁA�����O���[�U�[�W���C���̌����A�u���b�h���[�̌��s���̌��ہA���̐��i�P���A�f���A���̉q���Ȃǂ��ׂĂ̐��j�������Ă�����̑��x�A�}�C�P���\���E���[���[�̎����̌v�Z�Ȃǂ�����܂��B
�@�����ȊO�ɂ����p�͂���Ǝv���܂��B
�@
�@�́A�Ⴂ���A���鏑���Łu�����w�̊�{�@���͒P���Ȃ��̂��A�������͒P���ȂقǗǂ��v�Ƃ������ʂɏo�������������܂��B�j���[�g���̖@�����ɏo���Đ�������Ă��܂����B�l���Ă݂�ƃ}�b�N�X�E�F���d���͊w�����l�ł��ˁB�d�Ƃg�����̗��_���甜��ȕ������ۂ�����o���Ă���̂ł��B�i���F���m�ɂ́A���̂Q�����ł͂���܂���j
�@
�i�P�R�j�ȏ���v���o���ĉF�����n���������悤�� �g�P���h ���낤�Ǝv���悤�ɂȂ����B�i�Q�O�Q�T�N�R���Q�S���L�j
�ŋ߂̉F���_�̔��W���Ȋw���œǂނƁA�������̉F���͋���ȋ��̏�ł���A�S�̂��������ɉ�]���Ă��邻�����B����͒n���̎��]�Ɠ������B������]���ɑ��Ď߂ɂȂ��Ă���A�n���̒n���Ɠ����悤�ȌX�������鎖�ɂȂ�B
�@�����ău���b�N�z�[���Ƃ����̂͑䕗�̖ڂɑ������邾�낤�B�n���P�[���ɂ��ڂ�����B���������u���b�N�z�[���������Ă��s�v�c�ł͂Ȃ��B
�@����ɋ�͂̉�]���E���̂��̂ƍ����̂��̂�����Ɣ��\����Ă���B���ڂ��ׂ��́A�ϑ��q���̈ʒu��]�����̕����ɂ���āA����炪�قȂ邻���ł���B�F�����n���������悤���i�A�Ǝv��������B
�@
���u���b�N�z�[���͌������z�����ނ��獕���������A�Ƌ������Ă��邪�A����͂Ƃ�ł��Ȃ�������B�u���b�N�z�[���̓����ɂ͑f���q�⌴�q�A���q�Ȃǂ̗��q�ŏ[�����Ă���B������ �g���F�h �Ɍ�����̂��B�����A�u���b�N�z�[���̌������������邭�Ă������� �g���F�h �Ɍ�����B����͗ʎq�_�������Δ���B
�@
�@�ʎq�_���o�����łɁu�F���͗ʎq�_���v�Ə�����l���Ă��鎖���q�ׂĂ��������B����� �g�ʎq����h �̌��ł��B
�P�X�R�T�N�ɁA�����͂܂� �g�ʎq����h �Ƃ������t�͂Ȃ������̂ł����A�ʎq�_�ŁA����Ȍ��ۂ����邱�Ƃ͔�������Ă��܂����B���̎��̃A�C���V���^�C���̗L���Ȍ��t�u�s�C���ȉ��u��p�v�B
�@2022�N�x�̃m�[�x���ܕ����w����Łu��������Ă��Ă��u���ɉe�����y�ڂ����� �g�ʎq����h �̔����v���������B
����͉F���ł͐���_�Ȃǂ��A�ʎq�����ԂɂȂ鎖���������Ă���̂ł͂Ȃ����낤���B
�@���݂̓V���w�̎���͖��L���͂ƌ����x�s�ς̌����A���ꑊ�ΐ����_�ɂ�鋗������ԕ��ΈڂȂ��ł��邪�A�s�v�c�Ȍ��ۂ��R�قǂ���B������ �g�ʎq����h �������Ă���Ɖ�R���e���ς���Ă���B
�@�A�C���V���^�C�����A���������Ă���A�u�j�[���X�E�{�[�A���w�A�C���V���^�C���Ƃ̘_���x�ɏ����Ă���悤�ɁA�A�C���V���^�C���̓O�[�̍����o�Ȃ����낤�B
�@���b��ɂȂ��Ă���w1�����N���ꂽ�A���n�Ŕ��F����������}���ɋz�����A���V�������̉\������������Ă���x�ikangnamtimes ���j������B���̔��F��Ə��^�����͂P���N�O�A�ʎq������ԂɂȂ����̂ł͂Ȃ����낤���B
�@�������msn���w�E�H�[���b�N��w�i�C�M���X�j��Snehalata Sahu����M���Ƃ��錤���`�[���́A�w���N���X���̕�����260���N��̔��F��uWD 1647+375�v�ɁA���z�n�ł����Ζ������̂悤�ȓV�̂̔j�Ђ����������\�����������������ʂ\���܂����x������B��������F��ƁA���̏��^�������ʎq������ԂɂȂ��Ă����̂ł͂Ȃ����ƁA�킽���͐��@���Ă��܂��B�i2025.9.25�j
�@
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
�@
�@���ݒn���ɂ͔N�Ԗ��T�Q�O�O�g���ɂ�����ԉF���o�i����ee�炵���j���~�蒍���ł���B�F���͍L�傾�B���o��_�o�����łȂ��A�e�핪�q�╨���������ɑ��݂���B����炪�F���錹��Ȃ̂��B���`��§�P�S���Q�Ƃ��ꂽ���B
�@
�@�u���b�N�z�[���͉����N������Ώ����Ė����Ȃ邾�낤�B�������傫����������̂����邾�낤�B�䕗�̖ڂƓ������B
�@���łɏ������Ȃ��ď����鐡�O�̃u���b�N�z�[���͔�������ĂȂ��̂��낤���B�傫�ȑ䕗�̖ڂ�T�������łȂ��A�k�����ď����Ă����u���b�N�z�[�����T���Ă��������ƓV���w�҂ɂ��肢�������B
�@
�@�N��F�Q�O�Q�T.�O�R.�Q�W�t���Łu�n���������O�v�ƌĂ��u���b�N�z�[���̖�����̓V�� �f�`�k�|�b�k�t�r�|�O�Q�Q�O�T�Ws ���������ꂽ�ƁA�l�b�g�ɍڂ��Ă��܂����B�����������O�i�ցj�Ƃ����̂́A�������Ăѕ��ł͂Ȃ��Ǝv���܂��B
�������ł�����o���o���Ɂ��������i�Ƃ낯���j��Ԃ̐��_�ł��傤(*^_^*)�B���̂����S�A�I�X�~�E���A�j�b�P���ȂǏd�������𒆐S���Ɏc���Ĕ������A�F����ԂɎU�킷��Ɨ\�z�ł��܂��B�����ĉ����N�ォ�ɍ��x�̓u���b�N�z�[���ł͂Ȃ��A�ʏ�̍P���ɐ��܂�ς�邩���m��Ȃ��B
�@���邢�͗����̂悤�Ȍ`��������u�����_�v�i�M�Ҍď́j�ɂȂ鎖���l�����܂��B
�@
�@�����A�n������̋����ɂ��ẮA���ꑊ�ΐ����_�ɂ��ԕ��Έ����Ōv�Z���Ă���̂ŁA���̊��҂���悤�ɂ͂Ȃ�Ȃ����O������B�X���u���b�N�z�[���̓����ɑ����̋�͂������ƁA�l�b�g�Ɏʐ^����ōڂ��Ă����B�������n������̋����̌v�Z������Ă����̂ŁA�����Ȃ��Ă��܂��B�u�u���b�N�z�[���̓����ɑ����̋�͂������v�Ȃ�ĐM�����܂����B
�@
���̒�o���� �Ɂ��i�P�^���j�E�i�����^�Q�d�j �� ���f�� ���|�ucos�� �����ȏ��ɍڂ�悤�ɂȂ�̂́A�z���g���R�T�O�N�ォ�A
�߂����B
�@
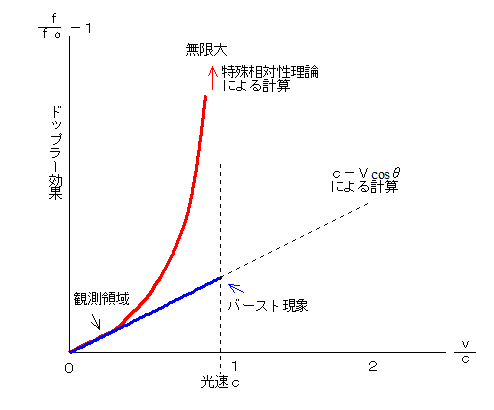 ���}�Ɍ��݉F���_�Ŏg���Ă���h�b�v���[���ʂƁA���̎��ɂ��h�b�v���[���ʂ̈Ⴂ�������Ă���܂��̂ŁA�������������B�F���_�����̎��������̖�S�O���قǂ܂ł́A�w�Ǖς��܂��A����ȏ�ɂȂ�ƈ�C�ɕς���Ă��܂��B ���}�Ɍ��݉F���_�Ŏg���Ă���h�b�v���[���ʂƁA���̎��ɂ��h�b�v���[���ʂ̈Ⴂ�������Ă���܂��̂ŁA�������������B�F���_�����̎��������̖�S�O���قǂ܂ł́A�w�Ǖς��܂��A����ȏ�ɂȂ�ƈ�C�ɕς���Ă��܂��B
�@���̎��ł̓��j�A�ł����A���Θ_�ł͋}���Ɏw�����I�ɏ㏸���Ă��܂��B�����̕����ׂĂ݂܂��ƁA���݂͂܂��n���Ƃ̑��Ό����x���S�O���ȏ�ɂȂ�悤�ȓV�͔̂�������Ă��܂���B���������ُ�Ȑԕ��Έڂ������V�̂���������āA�]�������ł́A���蓾�Ȃ��Ƃ������ԂɂȂ�����A���̎����g���Ă݂Ă��������B
�w�F���͖c�����Ă���̂ł͂Ȃ��x�Ƃ����̂��A���̎��_�ŏؖ������ł��傤�B
�@
�@�Ȃ��}���̃o�[�X�g���ۂƂ����̂́A���̂��K�ł͂Ȃ������m��Ȃ��ł����A���̗\�z�����u��������u�Ԃ̕����̔����v�̎��ł��B�����ɂ������Ă���܂����A���Ȃ�̍l�����\�z�ł��B�ْ���g�o�ɂ�2002�N1��25���Ə����Ă���܂��B���̔����̏u�Ԃ͂��܂��܂ȑf���q�������A�����A�����Ȃǂ̂ق��A����ȑ����̓d���g�����o�����ł��傤�B���݂͂܂��A������������ϑ��͓����Ă��܂���B
�i2025.9.14.�^�T�C�g������������I�ɕ��o����Ă���P�������t�������A�Ƃ����L�����������̂ŁA�ڍׂ�ǂ����Ƃ���ƁA�����̃T�C�g�͊댯�ł����Ƒ傫�Ȏ������o�Ă��ăp�\�R���������I�Ƀ_�E�����Ă��܂����I�j�B��͂���S���Đ��m�ȏ���ǂނɂ�msn�������ł��B�����ĉ��B�҂��ǂ��B
�@
�@�������f���q���m�̏Փ˂ł́A���̔j�Ђ͌����ȏ�Ŕ�юU�邾�낤�Ɨ\�������̂����������Ⴊ����܂��B
�@
�Q�O�P�P�N�X���Q�S���e�V���ő�X�I�Ɏ��グ���b�肪�������� �g�j���[�g���m�h �����B���É���w�Ȃǂ̍��ی����O���[�v�����\�����u������葁����j���[�g���m�v�B�X�C�X�E�W���l�[�u�x�O�̂b�d�q�m�F���E�ő�K�͂̑f���q�����w�̌����������\���܂����B�������A���̒���A�d�i��c�̂��猃����������H����āA��������������u���߂�Ȃ����A�Ԉ���Ă��܂����v�ƒ����̐������o����܂����B�����̑Ή��͌����ł��B���z�̊�t���Ă���s����A�������E����̂��ǂ��ł��B
�@�����̉Ȋw�҂��A���̎����͐����������̂��A�Ƃ����F�����������Ȃ̂ŁA�S�z�ɂ͋y�т܂���B���ɓ��{��t�����X�Ȃǎ��R�ȗ���ɂ��鍑�X�ł́A�����̑f���q�̒����� �g�j���[�g���m�h �Ɍ��肵�Ď��g�����Ƃ��Ă��܂��B
�@
�@�������A�����Ɏ����Ă��A�܂��A�C���V���^�C���̗\������ �g�d�͔g�h �����o���悤�Ɗ撣���Ă��鍑������܂��B���{�ł��B�d�͔g�͒��V�������Ő����邾�낤�Ƃ���Ă������ԂƋ�Ԃ̐U�������������ʼnF������ł���g�������ł��B
�@
�imsn�u�ߋ��̊Ԉ�����Ȋw���_�v���F�A�C���V���^�C���� �g�d�͔g�h ��\�����Ă͂��Ȃ��A�Ƃ̂��Ƃł��B�d�͔g�͂̂��̉Ȋw�҂̍��b�ł���A���s�������̈�ł��B
�@�A�C���V���^�C���̈�ʑ��ΐ����_�ł́A�F���͉i�v�ɐÎ~������Ԃɂ���A���k���c�������Ă��炸�A����������Ċg�債�Ȃ����Ƃ��咣���Ă��邪�A���݂ł͑S���s���m�ȉF�����f�����Ƃ���Ă���A�Ƃ̎��ł��B
�@�����ȊO�ɂ����ڂ������L��������܂����B�u1929�N�ɃG�h�E�B���E�n�b�u�����ԕ��Έڂ����A�F���͈��̑��x�ŊO���ɖc�����Ă���Ǝ咣�������v�A����ɔ����āu�������̓V�̐��͂��F���̒��S�ł���A�������͉F���̒��S�ɋ���A�Ƃ������B�����͌��݂ł͊��S�ɔے肳��A�������̓V�̐��͍͂L��ȉF���̐��X�̋�͂��炷��Ώ����ȓ_�قǂ��v�ȂǁB2025�N8��8���Ǎe�j
�@
�@�������̂�T�� �g�d�͔g���o�h�B���z�̗\�Z���l�����Ă����������� �g�������I���o�����I�h �Ɣ��\���Ȃ��Ɗi�D���t���Ȃ��B�n��ʼn��M�����ɗ��Ƃ������̐U���ł��L���b�`�o����n���Q�O�O���ɂ��鋐�呕�u������A���̂����傫�ȃj���[�X�Ŏ��グ���邾�낤���A���͐M�p���܂���B�d�͔g�Ƃ������͖̂����Ǝv���Ă��܂��B
�@�Ȃ��A��̔\�o�������̑�n�k(2024.1.1)�ŁA���̑��u����ꂽ�̂��C�����邻���ł��B�ߏ��̒��w���ɂ������������ł��B�g�������I���o�����B�g���͂������܌v�Z���I�h �ƂȂ�͖̂ڂɌ����Ă��܂��B
�@�]�v�ȓ˂����݂����m��Ȃ��ł����A�d�͔g�]�����Ƃ����̂�����܂��ˁB�����{���ɏd�͔g������̂�������A��L�̂悤�ȋ��呕�u�Ȃ��K�v�͂Ȃ��ł��傤�B���́u�d�͔g�]�����v�Ŋς�����ł���B
�@���́A���́u�d�͔g�]�����v�Ƃ����̂́A�V�̂���o�钴���g�d���g��l�Ԃ̉����ɒ��{���Ċς���悤�ɂ��Ă��鑕�u�ł��B�������g�d���g�h ���A�����҂͌���������̓��j�[�N�Ȗ��̂Ƃ��āu�d�͔g�]�����v�Ɩ��t���������ł��B
�@
�@�G���N�g���j�N�X���͂��� �g�H�w�h �͖��ɗ����Ȃ����͎̂̂Ă��āA���̒��ɖ𗧂��m�����������c��X���ɂ���܂��B�������A�g�����w�h �ɂ͗��_�̗��s������܂��B���������Ԉ���Ă��邩�͓�̎��B���̎��ǂ��ɍ��킹�āu���ꂪ����v�Ƃ������ɕz������܂��B�̂͂���Ȏ��͂Ȃ������B�D�G�ȉȊw�҂� �g�_���h �Ƃ����}�̂ŐT�d�ɕ����w�W�����܂����B
�@�Ƃ��낪���݂͂��������ł͂Ȃ��̂ł��B
��Ⴊ��L�� �g�d�͔g�h �ł��B���ԂƋ�Ԃ��g�ƂȂ��ē`�������ł����āB�M�����Ȃ��͎̂��������낤���B
2025.9.17.�^�������̔��\�ŁA�u�A���o�[�g�E�A�C���V���^�C���̈�ʑ��ΐ����_�ƃX�e�B�[�����E�z�[�L���O���m�̗\�����������I�v�ƁA�d�͔g�̔�����傫�����Ă��܂����B�Q�̃u���b�N�z�[�������̂����ہA���ɔ��ׂŁA�������Ȏ��ԂƋ�Ԃ̐U�����g�ɂȂ��Ēn���ɓ͂����A�ƌ������Ƃł��B�����̌������̓z�[�L���O���������A�z�[�L���O�����璼�ړd�b������A�b�����̂��ؖ��o�����Ǝ��������ɏ����Ă���܂����B
�@
�@msn�̔��\�����������A���̌������̔��\�����������B�����S�O�Ȃ�msn�̔��\�̕����������Ǝv���Ă��܂��B
�@
�@�A���e�n�̍� ���Q�l�ɂȂ����Ă��������B�����w�ɂ͂Q�̌n��������܂��B��́����ʂ̕����w�i�j���[�g���͊w�A�}�b�N�X�E�F���d���͊w�A�ʎq�_�j���ŁA������������Θ_�����w������̓A�C���V���^�C���͍l�������Ȃ����������A�C���V���^�C���̖��O���g���Ă���Ă���w�⁄�ł��B
�@
�ԊO�҂Ƃ��āAhttps://www7b.biglobe.ne.jp/~kubota-takashi/wen.html�@�Ɍf�ڂ��������w�����ȊO�ɂ��A�茳��
Silvan S. Schweber�uRELATIVISTIC QUANTUM FIELD THEORY�v1964������܂��B�������������Θ_�I�ʎq�_�Ƃ������Θ_�Ɨʎq�_���~�b�N�X�����w�p�������s������������܂����B���ǁA���Θ_�Ɨʎq�_�͑��e��Ȃ����_�\�������Ă���̂ŁA�G�Ȍ������ł����A�g���ܕʂ�h �ɂȂ����悤�ł��B����̗���ł��B
���̖{���X�O�O�ňȏ゠�镪�������̂ł����A���������R�́wThe Klein-Gordon Equation�x�̍�������������ł��B
�ق��ɂ́wThe Dirac Equation�x�ƁwThe Zero Mass Equations�x������܂��B����͌��݂ł̓j���[�g���m�̂��Ƃł��B
�@
���F2025�N12��23���L�F�{���A���Θ_�Ɨʎq�_���~�b�N�X���ĐV�������_�����Ƃ����w�҂��Љ�Ă���T�C�g������܂����B
�E�c�F���������������Ă����ʁB�Ƃ����̐̂ɑ����̉Ȋw�҂ɂ���Č�������Ă��܂��B��Ⴊ�d�q�̐��̂ł��B���Θ_�ł́A�d�q�� �g�_�h �ł��B�������A�g�_�h �ł��Ǝ��ȃG�l���M�[�͖�����ƂȂ�܂��B�����Ń��[�����c�́A���̏��I�ɂ���A���̗L���Ȓ����A�d�q�_�wH.A.Lorentz�uThe Theory of electrons�v1909�N�^DOVER PUB.�x�ŁA�d�q�͑傫���������Ƃ��v�Z����Ă��܂��B�̂��ɁA������ؖ������̂� �g�ʎq�_�h �ł��B
�@���[�����c�̓A�C���V���^�C�����ꡂ��ɗD�ꂽ�����w�҂������i1902�N�m�[�x�������w�ҁj�B�ʏ�̓}�C�P���\���E���[���[�̎�������������Ƃ���� �g���[�����c�ϊ��h ���L���ł��B
�@���Ȃ݂ɁA���̃��[�����c���q�̓A�^�}�̗ǂ����[�����c�����̋C�Ȃ��ɂӂƎv���t�������莮�ł��āA����ŃA�b�Ƃ����ԂɃ}�C�P���\���E���[���[�̎���������o���Ă��܂����̂ŁA���E���ő唏�肾�����̂ł��B���[�����c�̊�{�I�͍l���́w�������u�̉������̓G�[�e���ɂ���ĉ�����Ă���̂ŏk�ށx�Ƃ����̂����[�ł��B
�@���݂͉F����ԂɃG�[�e���͖����Ƃ���Ă��܂��B���āA�ǂ��Ȃ��Ă���ł��傤���B�����w�̔��W���P�Q�O�N�ȏ�̃X�p��������܂��B�߂����ł����A���ꂪ�����Ȃ̂ł��B�A�C���V���^�C���̗��_����q�̂悤�Ɋ��ɔp����������Ă��܂��B
�@
�g�j���[�g���m�h �̘b�ɖ߂��܂��B����͂������̂悤�ɒn����y���Ȃǂ̐��X�Ƃ����Ȃ��Ŋђʂ���f���q���ł����������q�ł��B���̔��x��m�邱�Ƃ͕����w��傫�����W�����錹��ƂȂ�܂��B�j���[�g���m�̔����͎�Ƃ��Ď��R�E�ł͒��V�������ɂ����̂��w�ǂł��B
�@���������āA�Ⴆ����ϑ����u�Ńj���[�g���m���ϑ������Ƃ��܂��B���̃j���[�g���m�̔��������A�@���łɉ������O�̒��V�������ɂ����̂������̂��A�A�j���[�g���m���ϑ�������ŁA���V���������A�ǂ������ŋN�������A�Ƃł͎��ԍ����t�]����ł��傤�B������҇A��������A�j���[�g���m�̔��x�͌�����葬���������ƂɂȂ�܂��B
�@�������A���̊ϑ��͍�����ɂ߂܂��B�Ƃ����̂́A���V�������͉F���̂ǂ����ŁA�قږ����A����P���ɂQ�ȏ�ɂ��Ȃ�p�x�Ŕ������Ă�������ł��B�]���������B�������قǁA���̔����͑����Ȃ��Ă��܂��B���Ƀn�b�u���F���]�����̌�p�Ƃ����W�F�C���Y�E�E�F�b�u�F���]�����ł̔����͑z����₷�鐔�̐V�V�̂ŁA���̒��ɂ͒��V���������܂܂�Ă��܂��B
�@��������O�ɑO�G�ꌻ�ۂ�����̂ŁA������������Ȃ��Ŋϑ���������ł����A���������B
�@�������������������ɂ́A��͂�n����ł̎����A�b�d�q�m�⍂���V���N���g�����Ȃǂɗ���̂��ǂ��ł��傤�B
�@
�d�v�Ȓlj��F�����ȏ�ő��ݍ�p����������������� �g�ʎq����h �ł́A�Q�O�Q�Q�N�x�̃m�[�x���ܕ����w���傪����܂��B
�R�l��܂��܂����B�l�b�g�̌��o���ő傫���w�A�C���V���^�C����ے肵����m�[�x���܁I�x�ƍڂ��Ă����̂���ۓI�ł����B�ŋ߂̃m�[�x���ܕ����w����ł́u�����Ŋm���ꂽ���́v�ɑ��đ�����悤�ɂȂ��Ă��܂��B
�@
�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\
�@
�i�P�S�j���Ԃ͐i�ނ̂��A�x���̂�
�����ׂĂ̑��Θ_�����w�҂Ɏ��̖����o���܂��B�e�����D�R�̉^���n�� ���� ���f �͐i�ނ̂ł����H�x���̂ł����H
�@�@�i���̉^���n�͌����̖�R�S���A�b�� �u ���P�O���Q�炋���A�� ���P�O�W° �ʼnE�����ɓ��������^�����Ă��܂��j
�@
�@���ւ肪����܂����^2021.04.05�^���Θ_�����w�҂���ʂ̕����s���ł��B�j�b�N�l�[���̂悤�ł��B�S���Ɨ������Ղ��������z�ւ̕ԐM���lj����Č��J���Ă����܂��B
�u�O���B���Θ_�͋[���Ȋw�ł��B�y���������^�����镨�̂͐i�s�����ɏk���z�ȂǂƂ������Ƃ͂��蓾�Ȃ��B�y���������^�����鎞�v�͎��Ԃ��x����z�ȂǂƂ������Ƃ͂��蓾�Ȃ��B
�@�� �͉��}�ɉ����Ăn���o���A�n�f���o�f �������ł���B��������f �ȂǑ��݂��Ȃ��B
���̐}�͈�ʐ}�ł���A�^���n�������Ȃ�����ɁA�����Ȃ�p�x�ňړ����Ă����藧���A���f �� ���|�u��������
�Ő����o����B�|�A���J���͖{���̌�������299,792,458�m��/s�n�ƁA�������㑖����� ���f �̋�ʂ��t���Ȃ������B
�܂��́A�����ꂵ�悤�Ƃ������A���s���ċ[���Ȋw�ƂȂ��Ă����B�ȏ�A�ٕ��ɂĎ���v
�@
�E�c���F������L���������܂��B���f �̌v�Z���Ȃ������̂ŁA�G�z�ł����A���L�Ɏ����Ă����܂��B
�@���f �� �R×�P�O�W�m��/���n�|�P�O�D�Q���m����/���n×�������P�O�W° �� �R�D�R ×�P�O�W [��/��] �ƂȂ�܂��ˁB
���̒ʂ�A�w�� �͂n���o���A�n�f���o�f �������ł���B���f �ȂǑ��݂��Ȃ��x�̂������������w�ƌ����܂��B�}�ʂŕ�����悤�ɁA�n�f���o�f �̌��_�̈ړ��͌��� �� ��茩�����������ł��B
�@
�e�����D�R
�@
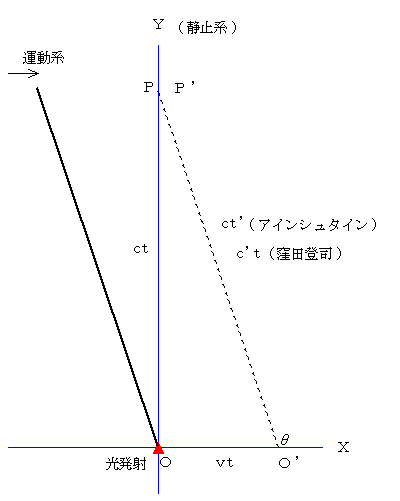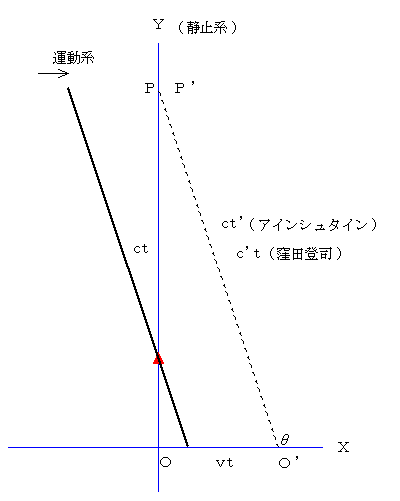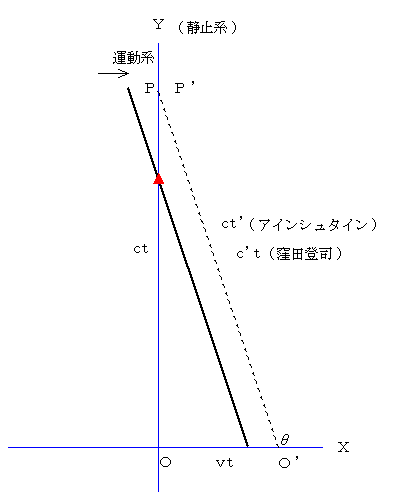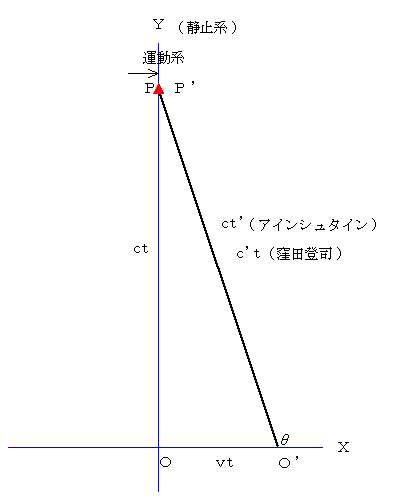
�@�F�l����u�����W�J�͗����ł����̂ł����A�� �͂Ȃ� �����f�n�f�� �Ȃ�ł����H�����Ă��������v�Ƃ��܂����B�e�����l�Ȃ̂ŁA���́i���j�}�������Đ������܂����B�����Ԏ������āA�u���A�������B���������B�v����Ƀx�N�g���͑傫���ƕ���������B���̑傫���� �� �ŁA�����͐}�̂悤�� �� �ɂȂ�v�Ə��}�[�N��t���Ă��܂����B�ǎ҂̊F�l���A���̂�������T�����i�܂Â����j�����m��܂���B
�i�Q�O�Q�S�N�P�P���L�j
�@
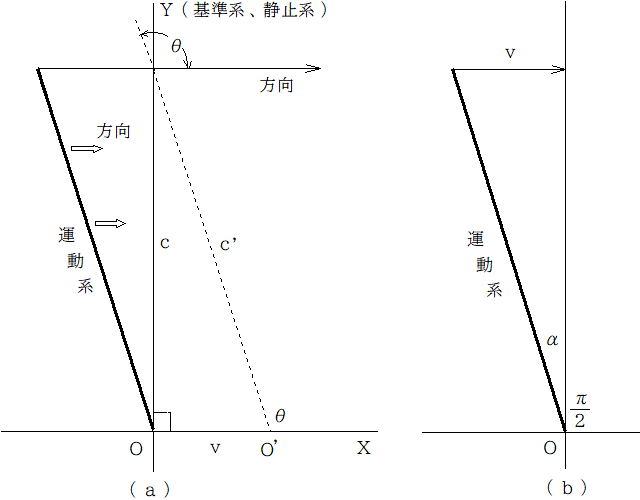
�����w������u�l�͉^���n�̌X�����d������ �������{�^�Q �ƍl���܂����i���j�}�ł��B����ł��ǂ��ł���ˁv�Ƃ������ւ肪����܂����B
�������ł��B��������ʂ̎��_�ŋ��߂�_��ɋ����܂��B
���̐}�́i���j�}�ƍ��킹�邽�߂Ɏ����`���܂����B
�@
�Q�T�̐N�A�C���V���^�C���͎O�����̒藝�����m��Ȃ������ƈ����Ă��܂�����A�����������Q�̍��W�𐔊w�I�Ɋ֘A�t�����@�͎v�����˂�Ȃ������̂ł��傤�B
�@
�@
�@
�@
�@
�@
�@
�@
�i�P�T�j�d��ȃ}�C�P���\���E���[���[�̎����̗��Ƃ���
�}�C�P���\���E���[���[�̎����͑��u���قڒ��p�ɂ��Ă���̂ŁA�� �� ���^�Q�ł�����Acos�i ���^�Q�j�� �O�ƂȂ�܂��B����� ���f�� �� �ƂȂ花�Ȃ͋ɏ��ƂȂ�܂��B
�@�������A���x�������Ȃ�Ȃ�ق� ���f�� �� �ɋ߂��Ȃ�܂����A�����̋����g�p���āA���̉������ˋ��������Ă���̂Łi��P�P���^�P�b�Ԃ��P�C�R�O�O����]�̉��������j�A�����Đ��m�� cos�i���^�Q�j�ɂ͂Ȃ�܂���B�K�� �����Ȋp�x �� �̌덷��L���Ă��܂��B
�A�C���V���^�C���́A���������Ȋp�x���̌덷�̑��݂ɋC���t���Ȃ������̂��A���p�ɂ͂Ȃ�Ȃ��̂��g���p�O�p�`����h�}�C�P���\���E���[���[�̎�����������܂����B�傢�Ȃ鎸�s�ƌ����܂��B����ȂƂ��납����ꑊ�Θ_�����܂ꂽ�̂ł�����c�O�ł��B
�@
�@�����ŁA���������v�Z�ł͂Ȃ��A�V�������_�̓W�J�����������̂����`��§�Q�O�ʼnY�H�Ƒ�w��w�@�ōu�`�������e�ł��B
�u���̉������ϑ��x�v�Ƃ����T�O�Ŋw���B�ɐ��������̂ł��B
����͌��݁A���Θ_�����w�҂͂������Ȃ��v�Z�ł��B�m���Ă�����A�Ƃ����̐̂Ƀ}�C�P���\���E���[���[�̎������A����Ő������Ă������ł��B�����ē��ꑊ�Θ_�Ƃ������_�́A���̐��ɑ��݂��Ȃ������ł��B
�@
�@���͂��́u���̉������ϑ��x�v�� ���|�ucos�� �Ɛe�ʊW������悤�ł��B���͂��Ƃ����Q�̍��W�i��n�Ɖ^���n�j���֘A�����鐔�w�ŁA�܂菃���Ȑ��w�Ŕ����������Ȃ̂ł����A��L�u�����Ȋp�x �� �̌덷��L���锽�ˋ��v�ւ̌��� �� �ƁA�n���̑��x�u��������A���|�u�E�i�u�^���j���i���Q�[�u�Q�j�^�� �ƂȂ�A����͕�����Ȃ��u���̉������ϑ��x�v���̂��̂ł��B
�@
�i�P�U�j���|�ucos�� �̉��p
�@���|�ucos�� �̉��p�͎��ɑ���ɓn���Ă��܂��B(10)�Î~�n�Ɖ^���n�ɂ��� �ɂ������Ă������܂��B
���ɒ��ڂ���Ă���̂́A�u���b�h���[���ϑ����瓾�����s���̎��𗝘_�I�ɏؖ��������ł��B
�@
�u���Θ_�͋[���Ȋw�ł���v�͎��������ł������܂��B�����ԏ����� ���f�� ���|�ucos�� ���[���Ȋw���Ɣl�|�E��������Ă��܂������A�t�]�������Ɉ��g���Ă���܂��B
�@
�@�������A���́A���̖{���Ƃ��܂��ẮA���������������̔��_�҂������Ă����̎��Ȍ[�ւ��������Ɋ��ӂ��Ă���܂��B���_������������A���Ȓ��S�Ɋׂ��ĂƂ�ł��Ȃ������ɒĂ��čs���������m��Ȃ��̂ł��B���_�ɑ��Đ[�����o�������A�����Ē�����������ǂ��Ɣ��f������f���ɁA����ɏ]�������B�{�g�b�v�y�[�W�́i�S�j�ɂ������̍��̎��̃~�X�ɂ��ď����Ă������܂��B�����̌�w�E�����݂̎����ƁA�S��葽���̔��_�҂Ɍ��\���グ�����B
�@
�@���̌�͑S���ւ���V���ȏオ�A���̍l���́u�����������ɂ���v�Ƃ�����܂��ł����̂ŁA�^���h�i���Θ_�ȊO�̊w�Ґ搶���܂݂܂��j�̕��X�ւ̎��̋C�����͐}�肫��Ȃ����i�Ɍq���������Ƃ��L���Ă����܂��B�L���������܂����B�Q�O�Q�T�N�P���Q�T���^�E�c�o�i
�@
�|�|�|�|�|�|�|�|�|�|�|�|�|�|�|�|�|�|�|�|�|�|�|�|
�@
�i�P�V�j�ǎ҂Ƃ̉�b
2025�N7��26���^8��1���^���̑��lj��ҏW�F����ǎ҂��玟�̎��₪���܂����̂ŁA�x����Ȃ���A�����Ő������Ă����܂��B�����������������̂��A�܂Ƃ߂܂����B�C�y�ɂ��ǂ݂��������B
�@
����ҁF�w�l�ލő�̔����͂O�i�[���j�Ƃ��������ł��B��Ԃ͂܂��Ƀ[���i���j�ł��x�Ə����ꂽ��������܂����B�E�c�搶�͐����������l���ɂȂ�Ƃ����h�����Ă���܂��B���̂悤�Ȏ҂ɂ�������悤�ɁA���̌������������Ă���܂��B����������F�B�Ɏ����������ł��B�i�j
�E�c�F���₢��A����������ł͂���܂���B(*^_^*)
�@���w�Z�̐��w�̎��ƂŁA�����A�����������āA���̌�_���O�i�[���j�Ə����܂��ˁB���̂O�Ƃ����̂́A�ǂ������Ӗ��ł����H
�����ł��A�[���ł��i�j�B���������Ƃ����Ӗ��ł��B��`�Ƃ��Č��_�������Ă��邾���ŁA������Q������Ԃƌ����܂��B
�@���l�ɂ��A���A�����łR������Ԃ��`�ł��܂��B�����̋�Ԃ͒�`���������ʼn��������ł��B���O�ł��薳���ł��B
���́������̂R������Ԃɐ��P�ł��ӂ���Ă�����A������Ԃł͂Ȃ��ł��B����� �g�F���h �ł��B
�@
�@���ƃA�C���V���^�C���ł͍l�����ɁA���̐����Ⴂ�����邱�ƂɋC���t���܂������H�}�ˌE�c�ƓV�˃A�C���V���^�C���̑Ό����A���� �g�O�i�[���j�܂薳�̋�ԁh ����n�܂����̂ł��B
�i���`�����Z�������ǂ�ł݂Ă��������B���h���Ă������w�̔n��搶�̂Ђƌ����l�̐��U�����߂��̂������j
�@
����ҁF��Ԃ��j���[�g���m�����ł����A�Ƃ����������͍\��Ȃ��ł����H
�E�c�F�����ł���B���ʂ��������ꍇ�́u�F����Ԃ��j���[�g���m�����ł����v�Ƃ������܂��ˁB���n���痎�n��
�Ƃ��A���ꔑ���܂聄�ɂȂ��Ă��܂��܂���(*^_^*)�A�u�F����Ԃ�T�����P�b�g�����ё����Ă���v�Ƃ��A�悭�����܂��̂łˁB
����ҁF������܂����`�B�v����ɌE�c�搶�́A�{������ԁ��Ɓ��F�����Ƃ͈قȂ���̂��A�Ƃ̂��l���ł��ˁB���̕ӂ��l�ɂ́A�悭�������ĂȂ������悤�ł��B
�E�c�F���肪�Ƃ��������܂��B�g����h �Ƃ������t���{�������w�ł͂Ȃ��ł���B����͐��w�p��ł��B
����ҁF�͂��A�������Ă��܂��B��ʂ̋L���ɍڂ��Ă��܂����B���ԂƂ����͎̂����Ǝ����̊Ԃ̎��ł���ˁB�������ݒ肳��ĂȂ������玞�Ԃ̓[���ł��B������ �g����h �Ƃ����̂̓[���ƃ[���̊|�������B�����w�Ŏg���錾�t�ł͂Ȃ��ł��B
�E�c�F�悭�������Ă���܂����B�������v���܂��B�����̐l�X�� �g����h �Ƃ����̂́u����v�܂�u���݂�����́v���ƁA���Θ_���狳�����Ă���悤�ł����A�����w�I�ɂ́A�����������̂� �g�����h �̂ł��B�[���Ȃ�ł��B
�@
�@�l�b�g�ɁA�w�ǖ����u����̘c�݂ɂ��A�C���V���^�C���̏d�̓����Y�ɂ�����^�A�C���V���^�C�������O�ɂ�������X�v�������܂��B�����ł͂Ȃ��u�F����ԂɎU�݁A�������͉_�̂悤�ɏd�͂ɂ���ďW�܂��Ă���K�X�W�c�ɂ����܍�p�ɂ���āA���_�̌��������ς���Ă���̂��v�Ƃ̍l�������Ȃ��o���Ȃ��̂��ƁA���͔߂����v���Ă��܂��B
�@������S���������ꂽ���_���㉺�ɂQ�ʐ^�Ɏʂ��Ă��܂������A����́u�A�C���V���^�C���̏d�̓����Y�ɂ����̂��v�Ə����Ă���܂����B����ȉˋ�̘b�����Ȃ��Ă��A�]�����̉������Y�Ɠʃ����Y�ɂ�锽�˂ŏo����S�[�X�g���Ƃ͍l���Ȃ��̂�����B�Ƃɂ����A�g�A�C���V���^�C���h �̖��O�����g���ΑS�`���������ł��Ă��܂������w�A��Ȃ��B
�@���̍l�����ɂ͈�т������������鎖�ɋC���t���܂������H
�@
����ҁF���������܂��B�搶�͂��� �g���R���ہh �Ƃ��đ����܂����B�ł��w�Ґ搶�́A�����ł͂Ȃ��A
�g�A�C���V���^�C���ɂ���āh �������ł��B
�E�c�F�ł���ˁB����͏��������ł͂Ȃ������A�Ƃ������_��ϑ�������ꂽ���A�u�����̂����ł͂Ȃ��B�A�C���V���^�C���̂������v�ƊȒP�ɓ����鎖���o���邩��ł��B
�@�ł��ˁA���̊w�Ґ搶�͂��̐������w�����ӂʼn��ł�������Ⴂ�܂�����A���������͎����ł͐��������Ƃ�����Ă���ƁA�v�����ޏꍇ�������B���������ǂ́u����͉��\�N���̂ɗ��s���������ł���A�����̊w�҂����g��ł�������Ɠ������I�v�ƋC���t���P�[�X������܂��B��������Ɓu�����̂�������͖��ʂ������v�ƂȂ�A��x�������������l���̔߂��������ɂȂ�܂��B
�@
�@���w�ł́A�ǂ�ȋ�Ԃł����܂��B���s���͖������Ōq����Ƃ������[�}����ԁA���ꑊ�ΐ����_���S�����Ɋg�������~���R�t�X�L�[�̂S��������A��ʑ��ΐ����_�̑���������A�ʔ�����Ԃł̓��r�E�X�̗ցA������ĕ�����������܂�����ˁB�����̋�Ԃ͐��w�ł�����A�D���Ȃ悤�ɃO�j���b�ƋȂ��邱�Ƃ��o���܂��B
�@�L���ȃz�[�L���O���m�́u��ʑ��ΐ����_�̉F���ʂɂ���ƁA�����Ȃ�v�ƒ������������ׂĂ��܂����B
�@
�@�ł��A�����������w�ō������ԂɌ���A�L�A�l�Ԃ��Z�߂܂����H���Ɖ��M�ŏ�������Ԃɂ͏Z�߂Ȃ��ł��B
�@���͓����s�̑�R�Ƃ����F���̕Ћ��ɏZ��ł��܂��B
����ҁF���I�F���ɕЋ��������ł����H
�E�c�F����Ǝv���܂���B�F���͂�����������������Ǝv���܂��B�����ċ�Ԃ͖����ł�����B�������āg���肪�����h�Ə����܂��B�����A�F���͓r�Q���Ȃ��ł���������A�ׂ̉F������Əo����Ƃ͂Ȃ��ł��傤�ˁB�����猻��̓V���w�ł́A�������̐���ł���F���������Ƃ��Ă���̂ł��B���̕����F���_���\�����₷���B
�������̕��̉F���͊ϑ��o���Ȃ����B�Ћ����Č����܂������A�s��������A���������������ł��B<(_ _)>�B
�@���݂̉F���_�ł́w��Ԃ̂���P�_�Ŕ������ĉF�����o�����x�Ƃ����r�b�O�o���F���_���A���s���Ă��܂����A
�i��ԍŏ��̒̓A�����J�̃K���t�̘_���j�A�u���������P�_�Ƃ͉����H�v�ƌ�������ƁA�u�����ł��ǂ��v�ƂȂ��Ă��܂��B����́u�F���͉�X�̋���F���������B�ق��ɉF���͖����v�Ƃ������_������ł��B�����ĉF���͂ǂ�����Ēa���������A�Ƃ����N����������邽�߂ɐ��܂ꂽ���_�ł��B
����ҁF������Ƒ҂��āB�n������V�̂��ϑ�����ƁA�n���𒆐S�ɂ��āA����������ɉ��������Ă���ƂȂ��Ă��܂�����B������A�F���̒��S�͒n���ł͂Ȃ��̂ł����H
�E�c�F����́A���t�̃A���Ƃ������̂ł��B�ΐ��œV�̂��ϑ�����ƁA�ΐ��𒆐S�ɓV�͉̂��������Ă���Ƃ���܂��B������A�O�Ɍ������u��Ԃ̂���P�_�Ŕ������ĉF�����o�����B���̂P�_�Ƃ͉����ł��ǂ��v�Ɠ��������ł��B���݂̉F���_�͓V�����ł���A�ǂ��ɂł����߂ł���Ԉ�������_�ł��B
�@
�ȏ�̕��ʁA���̕��s���ł����B���݂̉F���_�ł́A�F���ɂ͒��S������A�Ƃ��������L�͂ł��B����́����k�E�c���J��Ԃ������ł��āA�r�b�O�o���F���ł͂���܂���B���_���̑����݂��̈��͂ň����������k���k����A�z�����鋅��Ɉ��k����A���ɏ�Ԃ���唚������B�����čĂіc������Ƃ����z���ŁA���݂̎������͖c���̓r��ɂ���A������͖c�����~�܂�A�₪�Ă͍Ăь݂��̈��͂Ŏ��k�Ɍ������Ƃ����z���F�����Ƃ�����ł��B���̍l�����͎����^���ł��B�Ƃ����̂́A���̍l�����ł��ƁA�F���͋�Ԃɂ������݂邱�ƂɂȂ�܂��B���ݗׂ̉F���i�Ƃ����Ă�ꡂ������ޕ��ł��傤���j�͎��k�������m��܂���B���������Ӗ�������F���͑傫�����́A���������̂̍��݂��l�����܂��B�܂������������������_���̑��̕����ƂȂ�̂�����A�������R�ȍl�������Ǝv���܂��B2026.2.8
�@
����ҁF��L�ԕ����̕����ǂ݂܂����B�������R�ȍl�����ł��ˁB�r�b�O�o���F���ȂǓ˔��q���Ȃ��l���Ƃ́A�S�R�Ⴄ�B�F���͉i�����ƌE�c�搶�͂悭�����܂����A���̈Ӗ����ǂ�������܂����B
�E�c�F���肪�Ƃ��������܂��B�Q�O���I�ɗ��s�������r�b�O�o���F�����A���łɉߋ��̂��̂ɂȂ�܂����ˁB�F���͖����̉ߋ����疳���̖����܂ʼni���ɑ��������k�E�����J��Ԃ����B�����������������ƁA�u��ԍŏ��͂ǂ��������̂��H�v�Ƃ悭���ɂ��܂��B���͏��Ȃ���u����Ȏ��A�n���l�������锤�Ȃ��v���ē����Ă��܂��B
�@
����ҁF�����ł��B�E�E�E�b��߂��܂����A�搶�� �Ɂ��i�P�^���j�E�i�����^�Q�d�j ���x������w�҂��������ł��ˁB
�E�c�F�͂��B���̊w�Ґ搶�͓V���w�҂ł͂Ȃ��ł��B�H�w���m�ł��B�Ɂ��i�P�^���j�E�i�����^�Q�d�j �́A�������\�N���̂���d�g�ʐM�H�w�Ŏg���Ă��鎮�ł����A�V���w�҂͎g�����Ƃ��܂���B���ΐ����_�⌻��V���w�������ꂷ�邩��ł��B
����ҁF�L���������܂����B��ԂƉF���̈Ⴂ����F���_�܂Řb�������Ƃ͎v�������܂���ł����B�r�b�O�o���F���Ȃ�ĂȂ��Ǝv���܂��B�����X�J�b�Ƃ��܂����B
�@
�E�c�F����A�Ō�ɖl����̎���ł��B��L �Ɂ��i�P�^���j�E�i�����^�Q�d�j �ɂ��ƁA�V�̂����������痣��čs���Ȃ��Ă��A���̓V�̂�������Ή����قǎ���G�l���M�[�͏������̂ŁA�ԕ��ΈڂƂȂ�̂��ƂȂ��Ă��܂��ˁB�ł͐��Έڂ��Ă���H
����ҁF����Ǝv���܂���B�搶�̕��͂��t���܂ɓǂ߂����̂ł́H�w�V�̂����������痣��čs���Ȃ��ŁA�߂Â��Ă���Ό��̃G�l���M�[�͑傫���Ȃ�̂ŁA����͐��ΈڂƂ��Ċϑ������x�ł͂Ȃ��ł����B
�E�c�F������`(*^_^*)�B�ł�������ēV�����ł��ˁB
�w�V�̂͂����Ƃ��Ă��āA�������ϑ��҂��߂Â��čs���x�ł������ł��傤�B����͒n�����ł��B�n�����Ō����Ɋϑ�����Ă���Ⴊ�����ł��B�������̓V�̐��͂̂��ɂ���A���h�����_��́B������ēV�̐��͂��ꡂ��ɑ傫���āA���͂��ׂ�ڂ��ɑ傫���̂ŁA�������̋�͂������Ă��܂��B��������ΈڂƂ��Ċϑ�����Ă���̂ł��B
�i����������������l����ƌ��݂̎������̉F���́A������~�܂肩���Ă���r�ォ���m��܂���B�O�q�̉F���_�A�����E���k�J��Ԃ����j
�@
���Ȃ݂ɃA���h�����_��͂܂ł̋����͂����炩�m���Ă��܂����H
����ҁF�l�b�g�Œ��ׂ�����Q�T�O�����N�Ə����Ă���܂����B
�E�c�F�ł��ˁB�l�����w���̎��͖��P�T�O�����N���ƁA���ȏ��ɂ��A�ǂ̖{�ɂ��ڂ��Ă��܂����B����͎O�p�@�Ƃ�����@�ő��肵�����̂ŁA���̕����������Ǝv���Ă��܂��B���Z1�N���̎��A���s�̉ԎR�V����ɍ��h�ōs�������A�V����ŃA���h�����_���_�������Ă���܂������A���̎��̊w�p���̐搶���u�����͖��P�T�O�����N���v�Ƌ����Ă���܂����B
����ҁF���`�I���Ⴀ�A�Q�T�O�����N�Ƃ����̂́A�ǂ�����A�����Ȃ��ł����H
�E�c�F���ꑊ�Θ_�ɂ��ԕ��Έڒl������̌v�Z�ł��B���Θ_�͊Ԉ���Ă���̂ŁA�V�̂܂ł̋������Ԉ���Ă��܂����A�w�Z�̋��ȏ����Q�T�O�����N�ƂȂ��Ă���A�N���������o���Ĉ���Ă����܂��B
�@�����A��������ċL�����������A�l�b�g�ɍڂ��Ă���l�����̂܂����Ă��܂��B�P�T�O�����N�Ə����Ǝ��̋L���S�����ԈႢ���ƒf�肳��Ă��܂������m��Ȃ��̂ŁA�����͉䖝�̂��ǂ���ł��B
�@
�@�V�̂܂ł̋����ɂ��ẮA���̋�̓I�ȗ\�z�������܂��Ɓu�������Ă��鋗�������߂����낤�v�ł��B�Ⴆ�ΐ�قnj��������A���h�����_��͂܂ł̋������́A�u��͂���P�T�O�����N�������v�ƁB
����ҁF�Ƃ������Ƃ́A�F���̑傫���͌������Ă����菬�����Ȃ�܂��ˁB
�E�c�F�����ł��B�ł����_���}�����͂Ȃ��ł��B�R�T�O�N�͑҂��܂��傤�B
����ҁF�C���ł��B���ꑊ�Θ_�͊Ԉ���Ă��鎖��搶�͏ؖ������ł͂Ȃ��ł����I
�E�c�F�����w���������܂��B
����ҁF���݂ł������w�͍������Ă��܂��B���Θ_�Ɨʎq�_�̐킢�́A�ʎq�_���������̂ɁA�V���w�͑��Θ_�Ɏ�������B
�E�c�F�����ł��ˁB���������݂̓V���w�͓V�����ł�����B
����ҁF�V�����͕������ׂ��ł��B�搶�� �Ɂ��i�P�^���j�E�i�����^�Q�d�j �͎���G�l���M�[�ɂ����̂ł�����n�����ł��B�V���w�҂� �Ɂ��i�P�^���j�E�i�����^�Q�d�j ���g��Ȃ��̂� �g�l�퍷�ʁh �ł��I
�E�c�F�g�l�퍷�ʁh �ł���(-_-;)�B�l�����ʂ���|�����t�ł��ˁB
�@
�|�|�|�|�|�|�|�|�|�|�|�|�|�|�|�|�|�|�|�|�|�|�|�|
�@
�i�P�W�j����F���_
�@�����ꌏ�A���������Ă��鎖���q�ׂ����Ă��������B����͑����̊w�Ґ搶����w�E�c�̓r�b�O�o���F���a������ے肵�Ă��邻�������A�ł́A�ǂ�����ĉF���͒a�������̂��H�x�Ƃ������̂ł��B
�@���̓����͒P���ł��B�u�����̉ߋ����疳���̖����܂ő����Ă��镡���̉F���ɋN���ȂǕ����낤�����Ȃ��v���Ă��Ƃł��B
���̕����̉F���Ƃ����̂��A�̂��w�Ґ搶�ɂ̓s���Ƃ��Ȃ��ł��傤�ˁB�F���͂����̐���ł���F����������A�ƐM���Ă�����悤�ł�����B�����̋�ԂɁA������������������̉F����������čl�����ق������������̂ł́H
�����Ċ뜜���ׂ��́A�w�Ґ搶�� �g��ԁh �� �g�F���h ���������Ă���t�V������܂��B��Ԃ́w���i�[���j�ł���A���͖̂����x�ł��B��Ԃɐ���_�������i���F���ł��B
�@�������A�p��ł� �g��ԁh �� �g�F���h ���A�ǂ����space�ƂȂ��Ă��܂��B���ꂪ�n���l�̌��t�̔��B�r��Ǝv���܂��B���������{��ł͋�ʂ����Ă��܂��B�p�����͂Q�U�����ō\������܂����A���{��͂S�W�����ł��B���̍��͂��ɑ傫���B�\���̎d���Ɉ��|�I�ȍ��������܂��B
�@
�@��Ƃ��āA��Ԃ⎞�Ԃ�N�w�Ƒ�����w�Ґ搶�������܂����A����͎v���߂��B�w��Ԃ͖��x�A�w���Ԃ͎����Ǝ����̊Ԃ̎ړx�̎��ł���A�{���͖��x�ł��B���̏q�ׂĂ��鎖�A��������ɂȂ�܂����H(��)�E�E�E
�@���ꂪ�؋��ɁA����l�����܂ꂽ�̂́u�����̉��������ƋL�^����A�����͉����̉��������v�Ƃ���҂��L�^���܂��B����� �g�����̋L�^�h �ł��B�����āu���������Ԑ������v�Ƃ����̂́A���́u�����Ǝ����̊Ԋu�v�̎��ł��B
�@
�@���Θ_�ł͎��ԂƋ�Ԃ��Ȃ������Ƃ��A�k�Ƃ��A�ʔ����ĊF����т܂����A����͐��w���y����ł��邾���ŕ����w�ł͂Ȃ��ł��B���Θ_�������w�ł͂Ȃ����͈ȑO�ɓd�q�̑傫���̌��ŏ����܂����B���Θ_�ł͓d�q�̑傫���� �g�_�h �ł��B �g�_�h �łȂ������玩�ȃG�l���M�[�͖�����ɂȂ邩��ł��B��������������̂��A���̗L���ȃ��[�����c�ł��B���[�����c�͓d�q�̑傫�����v�Z���܂����B�̂��ɁA������ؖ������̂��ʎq�_�ł��B���[�����c�̒����u�d�q�_�v�͎��̏��I�ɂ���܂��B�ʐ^�͎��̎��`§�P�Vhttps://www7b.biglobe.ne.jp/~kubota-takashi/seikatsu.html
�ɍڂ��Ă��܂��B
�@
�@�F���̓r�b�O�o���ɂ���āA�n�����ԂŌ����ƁA138���N�O�̉��������̉����������b�̍X�ɏ����ȏu�Ԃɉ�������Ԃ̂P�_����a�������A�����Č��݂̉F���Ɏ����Ă���Ƃ����A������������n���l�ނ� �g遂�h �ƌ����܂��B
�g遂镽�Ƃ͋v�����炸�h �ƌ����܂��B����͎~�܂��Ă��܂���B�Ⴂ����̉Ȋw�҂����X�������d�˂Ă��܂��B
���̓����A�����������͖Y�ꋎ���āA�V���������䓪���܂��B
�@���̐����������̂��ƌ����Ă���̂ł͂���܂����B���͒P�Ɂu�F���͖����̉ߋ����疳���̖����܂ŕ������݂���v�Ǝ咣���Ă��邾���ł��B������ǂ�����ĉF�����a���������ȂǕ����낤�����Ȃ��A�ƌ����Ă���̂ł��B
�@����Ȑ��w���g���ĉF���̐��藧�������������Ă�����搶�����������܂����A����͂����܂ł� �g���w�h �ł��B�g�����w�h �ł͂Ȃ��ł��B
�@
�@�lj��F2025�N8��2���imsn���j�F�ʔ����L�������t���܂����B�u138���N�O�ɒa��������X�̉F���͉i���ɖc����������v�Ƃ���Ă������A�A�����J�E�R�[�l����w�ƒ����̏�C��ʑ�w�̌����ɂ��A�u195���N��ɉF���͓˔@�P�_�Ɏ��k���A�Ԃ�ĐՌ`���Ȃ����ł���v�̂������ł��B
�@���̌����ɂ��A���ɉ�X�̉F���͒a����138���N�o�߂��Ă���̂ŁA����57���N�̎����Ƃ����킯�ł��B
��u�ɂ��Ēa�������F�����A���x�͈�u�ɂď��ł���Ƃ����嗝�_�ł��B�ڍׂ͏�Lmsn���������������B
�@��ޓ��e�̒����������\����܂����B�i2025�N8��18���j�F�u�F���̎�����333���N�B����138���N�c���������Ă����̂ŁA195���N��ɉF���͓˔@�Ƃ��ĂP�_�Ɏ��k���Ċ��S�ɏ��ł���v�Ƃ������_�������ł��B���̗��_�́u�F���̑傫���̖�70���ɁA�Í��G�l���M�[���[�����Ă���v�Ƃ������݂̓V���w�ɂ����̂ł��B�́A�F���ɂ̓G�[�e�����[�����Ă���Ƃ���Ă��܂������A���݂̓G�[�e���̑���Ƀ_�[�N�}�^�[�i�Í������j������A�Ƃ���Ă��܂��B
�@�����āA�����_�[�N�}�^�[��R���Ƃ��Đ����a�����Ă����A�Ƃ̘_��������܂����B
���Ȃ݂Ɏ��� �g�Í������h �Ȃ����Ǝv���Ă��܂��B
�@�A���X�e���_����w��Erik Verlinde�������A�g�Í������h�i�_�[�N�}�^�[�j�͑��݂��Ȃ��Ǝ咣���Ă��܂��B
�u�ǂ�ȂɊϑ����Ă��A�Í������́A�����������t����Ȃ��v�ƁB
�@
�@��1���I�ɂ킽���ē�ɕ�܂�Ă����_�[�N�}�^�[���A���ɂ��̎p��������������܂���B������w�̌˒J�F���������ANASA�̃t�F���~�K���}���F���]�����̊ϑ��f�[�^����A�_�[�N�}�^�[�̒��ړI�ȏ؋��ƂȂ�K���}�������o�����Ɣ��\���܂����B2025.11.30.�@
�E�c�F�K���}���͔g���̒Z���d���g�Ŏ��݂�����̂ł��B����A�_�[�N�}�^�[�͉F�������ˋ�̕����������ł��B���̊W������́H
�@�K���}���F���]�����ŃK���}����������������A�_�[�N�}�^�[�̒��ړI�ȏ؋��ƂȂ�́H
�u�_�[�N�}�^�[�͂���v�Ƃ���������w�h�ƁA�u�_�[�N�}�^�[�͖����v�Ƃ����A���X�e���_����w�h�̑Ό��ɂȂ�܂����ˁB�P�Q�O�N�オ�y���݂ł��B
�@
�@msn�ҏW�����s�������^�������ɓ����������L�������t���܂����B�u�_�[�N�}�^�[�����t����ƁA�����������̂��v�ƁB
�^�������͎��̂悤�ɓ����Ă����B�u��]���Ă����͂��Ȃ����Ȃ��̂��������邩�炾�B�~�܂鎖������葱����ɂ̓_�[�N�}�^�[���K�v���v�ƁB���ʂ������ł͂Ȃ��ł����A�����������e�ł����B
�@���̓����͓I���˂Ă��܂���B��]���Ă���Q������͂́A������~�܂�܂��B�����Ă��イ���イ�Ɏ��k���đ唚�����N�����āA�ꐶ���I���܂��B
�@����ɁA�W�F�C���Y�E�E�F�b�u�F���]�����̊ϑ��Łu�Q����͂��~�܂肩���Ă���Œ����Q�ɕ������āA�A���̂悤�Ɍ݂��ɑ���̈��͂ʼn��n�߂��A�����_�ƂȂ����v�����Ă��܂��B����̓_�[�N�}�^�[�͖������Ƃ��ؖ������ϑ����������ɂȂ�܂��B�����_�[�N�}�^�[����������A����ȘA�����_�͐��܂�Ȃ��B
�@
�B�B�B�B�B�B�B�B�B�B�B�B�B�B�B�B�B�B�B�B�B�B�B�B�B�B�B�B�B�B
�@
�i�P�X�j����̐V�����F���_�Ɋ��҂�����
�@����̉F���_�� �g����h �����邱�ƂȂ� �g�ϑ��h ���d�����A����Ɠ������� �g�F���͊w�h �̑n�݂��K�v�Ǝv����B
���݂͉F���͊w�Ƃ�������͂Ȃ��B�����Ƃ�������F���������͊w�͖����ł��낤���A�����I�ł��u���̌��ۂ͂������v�ƌ�����͊w�Ő����ł���w��Ɋ��҂������B
�@���̏ꍇ�A�P�Q�O�N�ȏ���́A���肩����ꂽ���Θ_�͊Ԉ���Ă��邵�A�j�]���Ă���̂ʼnF���͊w�ɓ����Ă͂Ȃ�ʁB��x�Ƃ��������s����`�̊ԈႢ���N�����ʂ悤�A�S���V�����F���͊w�����݂��ĖႢ�����B
��������A�g�ʎq����h �����ڂ����悤�ɂȂ邾�낤�B
�����āA�����A�����ق����V�������Ŕ�юU�����f���q�������ȏ�ł��������Ƃ������o����悤�ɂȂ�B
�E�c�o�i�^�Q�O�Q�T�D�P�O�D�P�R�^�W�T�Βa����
�@
�i�Q�O�j�A�C���V���^�C���ɂ����ݕt���Ă��錻��F���_
�ً}�lj��F�Q�O�Q�T�N�P�O���P�S���F�{���u�A�C���V���^�C�������O��V���ɔ��������v�Ƃ����j���[�X������܂����B
�ٕM�g�o��https://www7b.biglobe.ne.jp/~kubota-takashi/bk-kubota.html �̃��X�g�Ɂw���{�̋C�ے��A�C���V���^�C���x�Ƃ����^�C�g���������t���������O���f�ڂ��܂����B���̃����O�͉�]���Ă��܂���B
��������ɂȂ�܂���(*^_^*)�B�����������B
�@
�@���̉F���ɃA�C���V���^�C�������O�Ȃ���܂���B�͊w�I�ɁA�����ė��_�I�ɂ����������̂��������܂���B�����O�ł��Ǝ��Ȉ��͂ɂ���ĂԂ�Ă��܂�����ł��B�K����]���ĂȂ��ƈ���ɂ͂Ȃ�܂���B
�������ǂ����Ă� �g�A�C���V���^�C���h �̖��O��t�������Ȃ��A���ׂ��A�C���V���^�C���Q�������_���A�������́A
�����ƈ���ȓ����ł́��ׂ��A�C���V���^�C�������_���ł��傤�B
�@�{���i2025.12.02�j���u�A�C���V���^�C�������O�����I�v�Ƒ傫�Ȍ��o���Ńl�b�g�ɍڂ��Ă��܂����B�ϑ��҂͂����Ɨ͊w������邱�Ƃ����߂܂��B�u�������܂��B���A�C���V���^�C���Q�������_���������I�v�ƁB���̂����A�����ƍ������x�̊ϑ��ɂ���ā��A�C���V���^�C�������_���������ƂȂ邩���m��܂���B����A����������Ȃ灃kubota�����_type1���Ɩ��t���ĖႢ�����ł��B
�@
�@�����őS���E�̓V���w�҂Ɏ��₵������������܂��B���̃A�C���V���^�C�������O�Ƃ����̂́A�{���ɐ��E���̓V����œ��������O���������̂ł����H�����č��ł�������̂ł����H�A����������V����ƌ����Ȃ��V���䂪����A���S�Ƀ~�X���Ă��鎖���ؖ����ꂽ���ɂȂ�܂��B����͓V���䑤�ɖ�肪���邩��ł��B
�@�ŋ߂͖]�����Ƃ����Ă���Őڊ���Y���̂�������ł݂�̂ł͂Ȃ��A������f�b-�l�n�r����̐M�����f�B�X�v���[�ɉf���o���Ċϑ�����̂��嗬�ƂȂ��Ă��܂��B�ǂ����ŃS�[�X�g���������Ă���Ƃ����ϑ����u���̂��̂ɖ�肪�����Ă���\�������ɍ����ł��B�d�g�]�����ł��ƁA�d�g�̉�܍�p�������O��Ɏʂ�\���͂����ƍ����ł��B
�@�]�v�Șb�ŋ��k�ł����A����G�����m�̘_���ɂ͊ԈႢ������̂��ŋߔ�������Ă��܂��ˁB
�V���w�ł����l�ł��B�����̓V����� �g�{���ɃA�C���V���^�C�������O���H�h �Ƃ����m���߂�p������Ǝv���܂��B
�@
���F�Q�O�Q�T�N�P�O���Q�O���Asorae�@�Ƃ����T�C�g���v��������u�A�C���V���^�C�������O�B��ʑ��ΐ����_�ɂ���āB���ԂƋ�Ԃ��Ȃ����āB���X�v�𑽐��̎ʐ^���ڂ��đ��`���Ă��܂����B���z�ȂقǃA�C���V���^�C���ɂ����݂��Ă����B
�@���Ԃ��Ȃ���A��Ԃ��Ȃ�����āA����Ȏ����M�����܂��H
���w�Ȃ玞��Ƃ����T�O�͏펯�I�ɂ����ċȂ��鎖�͊ȒP�ł����A���݂��鎄�����̉F���ɁA����Ȏ��ۂ����݂���Ɩ{���ɐM���Ă���́H�݂�Ȃ�������������A�������u�E�֕킦�v�ł͂Ȃ��ł����H
�@
������_�F�{������߂āF2025.12.03�F�A�C���V���^�C���̏d�̓����Y�B�܂����̊��ɋy��Łu�d�̓����Y�Ő��̌����Ȃ��Ă���̂��ϑ������v�Ɩ^�T�C�g�Ō��܂����B
�@���͂Ƃ����̐�(1994�N)�ɁA�u����Ȏ��͂Ȃ��B�����Ȃ���̂͏d�͂ŏW�܂������o��_�o�ɂ����܍�p�ł��v�Ɛ}�ʂ␔���Ŕ��\���Ă��܂��B����ɂ��Ƌ��܊p�͔}���̑w�ɂ���Đ��̓����ɋȂ邩�A�O�����ɋȂ邩�������ł��܂��B
�@�����A����ɔ��_�����Ȋw�҂����܂����B�u�d�̓����Y�ɂ͓ʃ����Y�A�������Y������I�v�ƁB��L2025.12.03�̊ϑ��ł͓ʃ����Y�������́H�A�������Y�������́I
�@�̂���d���w�œd�g���Ȃ��邱�Ƃ��m���Ă��܂��ˁB����͓V���w�ɂ��A���̂܂ܒʗp���܂��B���������Ɠd���g�ł͔g�����S�R�قȂ�̂ŁA�����悤�ɋȂ���ƍl���Ă͂����܂����B
�@�����̂��̂ł����̎��F�Œm���Ă���悤�ɁA�F�ɂ���ċ��܊p�͈Ⴂ�܂��B
���F���S�����킳��Ɣ��F�����F���A�ǂ��炩�Ɍ����܂��B����͗ʎq�_�������Ɨ����ł��܂��B�i�O�̂��߁j�B
�@�A�C���V���^�C�����u���z�̈��͂ɂ���Đ��̌��������ɋȂ�v�Ɨ\�����āA������������ƃC�M���X�̃G�f�B���g�����iSir Arthur Stanley Eddington�i1882�\1944�j���s���_���\���A���A�C���V���^�C���͖����̎G�����e�}�j�A�����V�˂Ƃ��ꂽ���͒N�����m���Ă��܂��B���ꂪ�܂����������Ă���Ƃ͏�Ȃ��ƌ����ق��Ȃ��ł��B
�@����ȏ����ȑ��z�̈��͂Ō����Ȃ���Ȃ�i���P�j�A�V�̂ɂ͖����Ƃ�������Q�������_������܂����A�����̂悤�Ȃ��ꂢ�ȉQ�����ɂ͂Ȃ�Ȃ��ł���B�����ꒃ������_���ȉF���ɂȂ��Ă��܂��܂��I
���P�F�����ɂ���Ắu���͒��i���Ă��邪�A��Ԃ��Ȃ����Ă��邩�炻��������̂��v�Ƃ����̂�����܂����B
���z�̎���͋�Ԃ��Ȃ����Ă���́H�������ꂪ�{���Ȃ�A���������ϑ����Ă���F���͋Ȃ��肭�˂��Ă��܂��ˁI
���Q�F�P���̎��ȕ���Ƃ����̂�����܂��B����͏�q�̌��Ƃ͖��W�ł��B���_�̈ꕔ��������Ĕ�яo���Ă���ʐ^���������Ƃ�����܂��B������县�ʍP���̎��ȕ���̈��ł��傤�B��q�́������Ȃ��遄�Ƃ͖��W�ł��B
�@
�i�Q�P�j�����Ȃ���͔̂}���ɌX������ꏊ
�@�����Ȃ���̂́A�����܂ł��}���ɌX������ꏊ�̋��܍�p�ł��B�n���ƌ��̊Ԃɂ͌���d�g��W����悤�Ȕ}���������̂łقڒ��i���܂��B�g�قځh �Ə������̂́A���m�Ȓ��i�͖���������ł��B�ǂ����Ă�������܂����B�n�������������ȗ����^�������Ă��邩��ł��B������ؖ�����ȒP�Ȏ���������܂��B
�@���[�U�[�Ō��܂ł̋������Q�S���ԑ��肵�Ă����B�P���Ԃ����Q�S��ł����ł�����O���t�p���Ƀv���b�g���Ă����Ȃ����B�u�����I�v�Ƃт����肵�܂���B���� �g�т�����h ���Ȋw�҂́u���͐��m�ȉ~��Œn���̎��������Ă��Ȃ����炾�B�ȉ~�����炾�v�ƌ����Ǝv���܂����A���̃f�[�^�����Ƃɗ����^���Ȃ�ǂ��Ȃ邩���v�Z���Ă����B
�u������I�Q�S���ԑ��肵���̂��Q�S���ԂɂȂ�Ȃ��v�ƁA������� �g�т�����h ���܂��B
�@
�B�B�B�B�B�B�B�B�B�B�B�B�B�B�B�B�B�B�B�B�B�B�B�B�B�B�B�B�B�B
�@
�i�Q�Q�j�ŐV�̓V�̊ϑ�
�Q�O�Q�T�N�P�O���R�O���Asorae�T�C�g���A�n�b�u���F���]���������������Q�����NGC�S�T�V�P�̎ʐ^���f�ڂ��Ă��܂����B���̋�͂́u�Q�������̍H��v�Ƃ��Ă���U�O�O�O�����N��̋�͂ŁA�V���Ȑ������������܂����قȋ�͂������ł��B
�@�^���ʏォ��̎ʐ^�ƂȂ��Ă��܂����A�������̋�͂������ł��߂Ɏʂ���Q�����L�тĂ��遄�A�܂藆����ɂȂ��Ă���Ƒz���ł��܂��B
�@�u�n�������Q�̉Q����́vNGC�R�Q�T�U����������Ă��邻���ł��B�f�G�Ȏʐ^�L��������܂����B�z�b�Ƃ��܂��B
�@
�y�ً}�lj��z�F�u���z��10���{���邢���县�ʃu���b�N�z�[���̃t���A���ۂ��ϑ����ꂽ�B�v
Image:Caltech/R. Hurt�iIPAC�j �V���w�҂�͑��z�n���� ��100�����N ���ꂽ�ꏊ�ɑ��z��10�����̌�����������ۂ��ϑ������BGadget Gate�B
������ʐ^������ƒ��S���ƁA���̎��͂͗�����ɐ���オ���Ă��܂��I�����������ɐ���オ�葱���āA�����N�ォ���������N�����āA���肶��̋�͂��������܂�邾�낤�B�����ʐ^�ł��B
�@�����ōl���Ă݂܂��傤�B�u�F���a���c�����I�v�B�����{���Ɂu�F���̓r�b�O�o���ɂ����138���N�O�ɒa�����A���݂����ԂƋ�Ԃ͖c���������Ă���B������Ή����قǑ����n�����痣��Ă���v���������Ȃ�A��L�̂悤�Ȏʐ^�͎B��Ȃ������B�ʐ^���B�ꂽ�Ƃ������Ƃ́u�F���a���c�����I�v�ɂ͋^�₪����A�Ƃ������ł��B2025.11.16
�@
�B�B�B�B�B�B�B�B�B�B�B�B�B�B�B�B�B�B�B�B�B�B�B�B�B�B�B�B�B�B
�@
�i�Q�R�j�A�C���V���^�C���̑���Ƀz�[�L���O���o��
�@�G�[�e�����ے肳�ꂽ��A���̑���_�[�N�}�^�[�Ƃ����������F���ɂ͖�W�T���[�����Ă���Ɖ��肳�ꂽ���͊F����悭�������Ǝv���܂����A�ŋ߂͈Í��d�q�A�Í��d�ׂȂǂ��F���ɂ͑��݂���Ɗϑ�����Ă��邻���ł��B
�@���͂���� �g�Í��h �Ȃ�Ė��̂�t���Ȃ��Ă� �g�d�q�h �� �g�d�ׁh �͖����ɑ��݂��鎖�͉F���ł͓��R���Ǝv���Ă��܂����B
�@�������A���̋L�����悭�ǂނƈÍ��d�q�A�Í��d�ׂƂ����̂́A�r�b�O�o���Ő��܂ꂽ�F���̖�P�b��ɁA�����ꔭ���܂ꂽ���n�u���b�N�z�[���ɂ����̂��Ƃ̎��B���̌��n�u���b�N�z�[�������˂��Ă���G�l���M�[�̂��Ƃ��z�[�L���O���\�������̂ŁA�����Í��d�q�A�Í��d�ׂ��z�[�L���O���˂ƌ����̂������ł��B
�@����͌��݂ł��P�O�N���P�x�A�n���ɍ~�蒍���ł���Ƃ̂��Ƃł��B
�@�P�R�W���N���̐̂ɒa�������ƌ�����F���̏����G�l���M�[�i�z�[�L���O���ˁj���A�����P�O�N���P�x�͒n���ɍ~�蒍���ł���炵���B�A�C���V���^�C���̑���Ƀz�[�L���O���o�ꂵ�܂����B���ꂪ�ŐV�̉F���_�ł��B�i2026.2.7�j
�ăo���_�[�r���g��w�̕����w�҃��o�[�g�E�V�F���[���́u����Ȃ��͎̂��ۂɂ͑��݂��Ȃ��B�v�Əq�ׂĂ��܂��B
(2026.2.15�j
msn��Bright Side Japan�Ɏ��̃^�C�g���̋L�����ڂ��Ă��܂����B
�u�Ȋw�҂ɂ��A�F���͐M���Ă����@����j���Ă���v�Ƃ����^�C�g���̋M�d�ȋL���ł��B���̋L�����ɋC�ɂȂ镶�ʂ�����܂����B�u�E�E�E��������ׂĂ��Ԉ���Ă���Ƃ̈Ӗ��ł͂���܂��A�E�E�E�v�Ƃ������ʂł��B�������q�ׂ܂��Ɓu���ׂ����v�Ƃ������ł��B����́A���݂̓V���w�̏o���_�́u�r�b�O�o���v�܂�u�����Ȃ����̋�Ԃ̂����_����A�u�Ԃɔ������ĉF�����o�����B���݂́A���̎��_�����P�R�W���N�o�߂��Ă���v�Ƃ����K���t�̘_������a���������̂�����ł��B�����M���邩�A�M���Ȃ����ʼnF���_�͊��S�ɕς���Ă��܂��B�@ �i2026.2.20�j
�B�B�B�B�B�B�B�B�B�B�B�B�B�B�B�B�B�B�B�B�B�B�B�B�B�B�B�B�B�B
�@
�i�Q�S�j���R�E�����i�M�Ҍď́j
�Ō�ɏd�v�Ȏ����q�ׂĂ��������B����̓����O��Ƃ��A�ȉ~��́A���̎��R���E�ɂ͂Ȃ��Ƃ��������B�j���[�g���ɂ͎��炾���A���z�̎����ȉ~��ɘf��������Ă���̂ł͂Ȃ��B�������������ĉ���Ă���B���ՓI�Ɍ���ƈ�����ȉ~�ƂȂ��Ă��邾�����B���ꂪ�؋��ɒn���ɂ͂S�N�Ɉ�x�P�N���R�U�U���ɂ��ĂP���������� �g���邤�N�h ������B�p��ł� �gleap year" �ł���B����͒n�������z�̎�����������Ƃ������^���̂��ߎ��Ԃ��|�����Ă��邩�炾�B�f���ɂƂ��ė����^�����ł�����ȓ����Ȃ̂��B��L �g�F���͊w�͗�������n�܂�h �ƌ����č����x���Ȃ����낤�B
�@���͒n���̎�����~��ɉ���Ă���悤�Ɍ����邪�A���ۂɂ͏����ȗ����^�������Ă���B���̂��ߌ��͏��X�ɒn
�@�����痣��Ă���B
�@�ؐ��̑�Ԕǂ�������Ɏ��������Ă���B���ꂪ�ł�����Ńo���o���ɂȂ�Ȃ������ł��邩�炾�B
�@�䕗��������ł���B�����O��䕗�Ȃ��������Ȃ��B�n���P�[�������l���B
�@���_���������B�Q������A�����Ă��ꂪ������ɂȂ��Ĕ��Ε������Q�L�тĂ��鐯�_���d�g�]�����Ŕ��������
�@����B
�@����͈ȑO�Ɂu�����_�v�Ɨ\�z���ďq�ׂ��̂Ɠ������B�������_���Ɨ\������ΓK���������낤�B
�@���w�]�����ł̓u���b�N�z�[���̒��S����㉺�ɃK�X���꒼���ɕ����o���Ă���悤�Ɍ�����ʐ^�����������A
�@�K�X�͗�����ɂȂ��Ă���B�꒼���ł͓r���ŃK�X�͎U�킷��B
�@
�@���͂��ׂė����ł���B
�@�ł����������̂ł͌��q�j�̎����d�q���_�̂悤�ɒ�ݔg�Ԋu�ʼn���Ă��邪�A�����������ɂȂ��Ă���B
�@�c�m�`�͓�d������ɂȂ��Ă���B�ł����ʂ������Ȃ�\��������ł���B
�@����̂�����Ă����Ȃ����B������ɂȂ��Ă���B����͕��Ȃǂɂ���ėh���Ă��܂�Ȃ����߂��B
�@���͔�тȂ���Ԃ̖����z�������o����B����͌�����������ɂȂ��Ă��邩�炾�B
�@���L�̊k�͗�����ɂȂ��Ă���B�k�����łɂ��Ď�������邽�߂��B
���R�E�̒m�b�͐l�Ԃ̒m�b���ꡂ��ɗD��Ă���B��������� �g���R�E�����h�iThe Principle of Nature�j �Ɩ��t�����B�E�c�o�i�i2025.11.19�j
�@
�ǎ҂���u���R�E�����͏�L �g�F���h ���܂ނ̂ł��ˁv�Ƃ������₪����܂����B������͂��̂���ł��B
�@
�g���邤�N�h �ɂ��Ă͌��݁A�g���R�E�����h�i�������_�j�ɂ��v�Z�͖����B
���̒n��������Q�S���Ԃƒ�߂Čv�Z����ȂǁA�l�ɂ���āA�܂����ɂ���Ă܂��܂��ł��荬�����݂���B
�������_�ɂ��n���K�͂̓��ꂪ��������̂�҂��ɂ��悤�B
���͊����W�T�̘V�l�ł��邽�ߎQ�^�o���Ȃ����Ƃ����l�т��܂��B�w�҂ł��Ȃ����B���Θ_�ɖҐi�������̌��C���Ȃ��B
�@
���͒n���ɑ���̈��͕ϓ���^���Ă��邪�i��F�C�̖������j�A���͌��Ȃ�̗����^�������Ă���̂ŁA�n���̗����^���ɂ͊W�Ȃ��Ƃ���Ηǂ��B�����������X�[�p�[�R���s���[�^�[�ɂ���Čv�Z���A�����ȉe��������ƂȂ����ꍇ�́A����Ȃ�̕������Ηǂ����낤�B
�@
�y�ǎ҂���z�F�E�c�搶�́u�l�퍷�ʂ���Ă���v�Ƃ�����b������܂��ˁB�܂��搶�����g����L�Ɂu�w�҂ł��Ȃ����v�Ɣډ�����Ă��܂��B���ꂪ�����Ȃ���ł��B���M�������Ă��������B
�l�̎���̗F�l�͌E�c�搶�̎��� �g���w�ҁh �ƌĂ�ł��܂��B�g���R�E�����h�i�������_�j�͖l����^���ł��B
�E�c�搶�I���M�������Ă��������I���M�������Ƃ��l����L���ɂ��܂��I
�E�c�o�i�F�L���������܂��B�̂ɖ����܂��B
�@
�|�|�|�|�|�|�|�|�|�|�|�|�|�|�|�|�|�|�|�|�|�|�|�|
�@
�i�Q�T�j���f�� ���|�ucos�� �̕\�L�ƁA�g�p���Ă���p�\�R���ɂ���
�@�Ȃ��A�]�v�Ȏ��ł����A���|�u�������ƁA���|���Ecos�ƁA���|�ucos�ƁA���|�ucos�� ���X���ꂳ��Ă��܂���ˁB�\����܂���B���ׂē��������ł��B�p�\�R���Ń|���|���ł�����ł��邽�߁A����ȂɂȂ��Ă��܂����B
�@���|�ucos�� ���O���ł悭�����Ă��܂��ˁB
�@
�@��̃z�[���y�[�W�ɁA�������̂o�b��\�t�g���g������ł���̂ŁA��ςł��B
�@
�i�Q�U�j���̃g�b�v�y�[�W���I���ɂ������āE�E�E��Ƃ̖��E�E�E�@�@�@�@�@�@�@�@�@�@�@�Q�O�Q�U�N�Q���P�O��
�@���̒�o�������A�Ɂ��i�P�^���j�E�i�����^�Q�d�j �� ���f�� ���|�ucos�� �������̉Ȋw�҂ɂ���ĔF�߂���ɂ́A�R�T�O�N�͂�����ł��傤�B
�@�Ȃ����ƌ����܂��ƁA�P�Ɂw���Θ_�͊Ԉ���Ă����x�����łȂ��A�w���݂̉F���_�����ꂩ������Ă��܂��x
�̂ŋ��ȏ����������邩��ł��B
�@�K�����I�E�K�����[���n�����\���āA�w�_���n������F�߂��x�̂́A�v��A�����R�T�O�N����P�X�X�Q�N�ł����B
���Ղ͎����Ĕ���c�����ƈ����܂��B�S����ɉ������u�ꂿ���ʂ�������v�ƕ��A���̐�����V���������w�������܂��B
�@
�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\
�@
���ΐ����_�͊Ԉ���Ă��܂�
�@
�@�A�C���V���^�C���Ǝ��̌����x�̈Ⴂ���ꗗ�\�Ɏ����Ă����܂��B���f�� ���|�ucos�� �i�P�X�X�R�N�Q�����L�G���ɔ��\�j�́A���݁A�ǂ̕����w���ɂ��Ȃ��̂ŁA���̂ɂ��Ă͍���̕����w�̔��W�ɔC���܂��B
�@
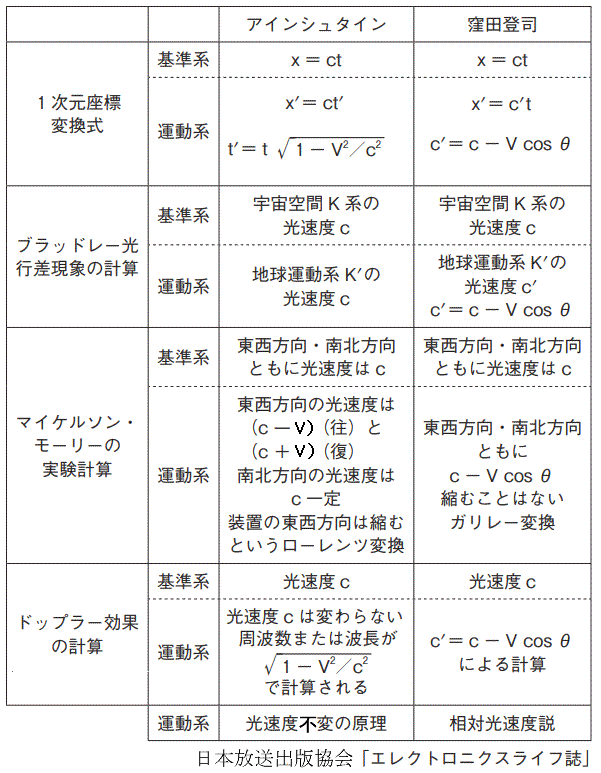 c t' �� ���f�� �������_�ƂȂ�܂� c t' �� ���f�� �������_�ƂȂ�܂�
�@�@
�@�@�@�@�@���{�����o�ŋ���w�G���N�g���j�N�X���C�t���x1993�N3�����`5�����A��
�i�t���[�F�Ȋw�Z�p�^�G���N�g���j�N�X�Z�p���C�^�[�j
�@���ӌ��A���ւ�̈���F��203-0033 �����s���v���Ďs��R�S�|�P�O�|�P�P�@�@�E�c�o�i
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@Email�Fkubota-takashi@outlook.jp
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@ or�Fdover.worldpress@gmail.com
�@
�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\
�@
�ڎ�
�@
(01)�g�b�v�y�[�W�@�A�C���V���^�C���̑��ΐ����_�@�E�E�����w�̊v���́A���̈������B�R�T�O�N�オ�y���݂ł��B
�@
(02)�}�b�N�X�E�F���ƃA�C���V���^�C���̘_���@�E�E�E�ʼnY�H�Ƒ�w�w�� �����l�������|�Ă������������́B
�@
�@
(04)�}�C�P���\���E���[���[�̎����ɂ��ā@�p�[�g�Q�@�@�E�E�E �ǂ݉����̂���y�[�W�ł��B
�@
�@
�@
�@
�@
�@
(10)�Î~�n�Ɖ^���n�ɂ����@�E�E�E���̋L���͂����Ȏ����������̂Ŗʔ����B
�@
(11)���ꑊ�Θ_�̗��_�\���@�E�E�E����ɁA�g�܂ɔG�ꂽ�{�h �����݂�����܂��B�ʐ^���f�ڂ��܂����B
�@
(12)���ꑊ�ΐ����_�̃~�X�̏o���_�E�㔼�ɕΔ������������o�Ă���̂Ŕ���l�����ł����A�O���͗������₷���B
�@
�@
�@
�@
�@
�@
�@
�@
(20)���s���̌��ۂɂ����@�E�E�E�E�E�E�E�ʼnY�H�Ƒ�w�w�� �����l�����������L���������Ă����������B
�@
�@
�@
(23)���ΐ����_�͊Ԉ���Ă��� ���|�u�������Ƃ̔����B�ڍׂ������Ă���܂����A�i31�j���{��o�[�W�����̕�������₷���B
�@
�@
�@
�@
�@
(28)���Θ_�͐��������Ԉ���Ă��邩 �E�E�Ԉ���Ă��鎖�𗝉��ł����l�͓��]�����B�A�C���V���^�C���͌������B
�@
(29)�j�[���X��{�[�A�u�A�C���V���^�C���Ƃ̘_���v �R�y���n�[�Q���w�h�̓A�C���V���^�C���ɋ^��������Ă����B
�@
�_���F����ȉp���̂��߁A���{��ɖ|�Ȃ��ł��������B
�@
(31)���{��o�[�W���� (Japanese version 3/23.2004)�@�_���F�u �����f �͈Ӗ����Ȃ��v���Ƃ��ؖ����Ă���܂��B
�@
�@
(33)���҉Ȋw�����u�ΐ����Łv�@ �E�E�E���X�g�V�[���͕|���I�ƁA�����̓ǎ҂̊��z�B
�@
(34)�t�@���^�W�b�N���ҏ����u�����R�r�̐�N���[�v�v�@�E�E�EHistorical Story �ł��B
�@
(35)�Z�ҏ����u�ł����߂āv �@�����̓ǎ҂���A�u��l���͒N�H�v�������B�킽�����I�ɂ� �g���c���}�q�h �ł��B
�@
(36)���_�u�ƒ�p�R�c�e���r�͂��܂ő������v�@ �E�E���e������߂ČÂ��I�J�������D���Ȑl�͎Q�l�ɂȂ邩���B
�@
�@
�@
�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\
�@
���ē��FEdge��Google Chrome�ł����l�ł����A�{��������ێ�����ƂȂ��Ă��āA�Â����ʂ��\������邱�Ƃ�����܂��B��ɐV�����g�o��\������ɂ́uCtrl�R���g���[���L�[���������܂�F�T�������v�ƁA�p�b�ƍŐV�ɂȂ�܂��B�V�������ʂ�lj�������A�Z���~�X�ȂǏC����������������ꍇ�A�L���ł��B����͂ǂ̍��ڂ��A�J������A���̎��_�ōs���܂��B������K���ɂ��Ă����Ɨǂ��ł��ˁB
�@���̂g�o�����łȂ���ʓI�ȑ���ł��B
�@
�@�@���̃g�b�v�y�[�W����
�i�P�j�u�����A�����A�����f�v�@�Ȃ��Ȓ��p�O�p�`
�i�Q�j���Θ_�ɑ��闝�_
�i�R�j�}�C�P���\���E���[���[�̎������
�i�S�j���Θ_����̐E�ƂƂ���Ă���搶����
�i�T�j�ً}�lj�
�i�U�j�V���̂��ē�
�i�V�j���͔��˂����|�C���g����`������
�i�W�j�A�C���V���^�C���P�X�O�T�N�̎G�����e�L��
�i�X�j�e�����D�Q �ւ̓ǎ҂̔��_
�i�P�O�j���ւ̍U���͓ڍ����Ă���
�i�P�P�j���Θ_�͖ʔ����Ċy�����������w�ł͂Ȃ�
�i�P�Q�j���Ɖ^���n������
�i�P�R�j�F�����n���������悤��
�i�P�S�j���ꑊ�Θ_�� ���f�� ���|�u�������� �̔�r�}
�i�P�T�j���Ԃ͐i�ނ̂��x���̂�
�i�P�U�j���f�� ���|�u�������� �̉��p
�i�P�V�j�ǎ҂Ƃ̉�b
�i�P�W�j����F���_
�i�P�X�j����̐V�����F���_�Ɋ��҂�����
�i�Q�O�j�A�C���V���^�C���ɂ����ݕt���Ă��錻��F���_
�i�Q�P�j�����Ȃ���͔̂}���ɌX������ꏊ
�i�Q�Q�j�ŐV�̓V�̊ϑ�
�i�Q�R�j�A�C���V���^�C���̑���Ƀz�[�L���O���o��
�i�Q�S�j���R�E�����i�M�Ҍď́j
�i�Q�T�j���f�� ���|�u�������� �̕\�L���g�p���Ă���p�\�R���ɂ���
�i�Q�U�j���̃g�b�v�y�[�W���I���ɂ������āE�E�E��Ƃ̖E�E�E
�@
�@
�@
|