|
�@
���[�����c�ϊ��̐���
�X�V�����̂�Ctrl�R���g���[���L�[���������܂܂e�T�������Ă�������
�@
�@���[�����c�ϊ��͖��@�̂悤�ɑ��Θ_�̒��Ŋ��܂����A�܂��Ƀ��[�����c�ϊ��� �g���@�̏�h �ł��B
���̃y�[�W�ł́A�P�O�O�N�ȏ㒷���N���̊ԁA�N���C���t���Ȃ��������[�����c�ϊ��̃��J�j�Y����������܂��傤�B
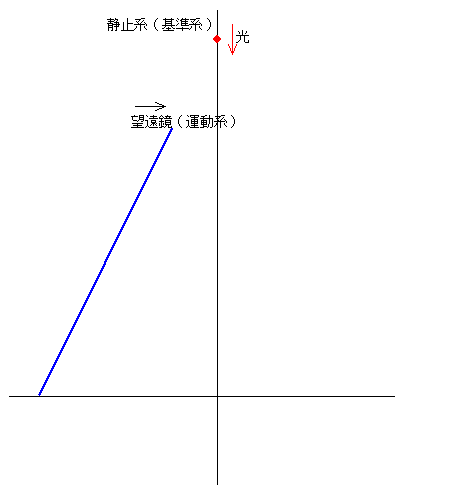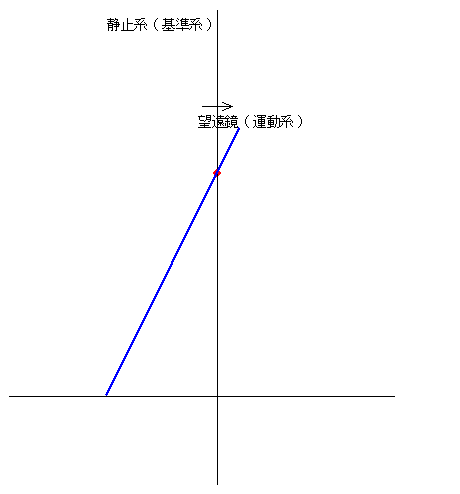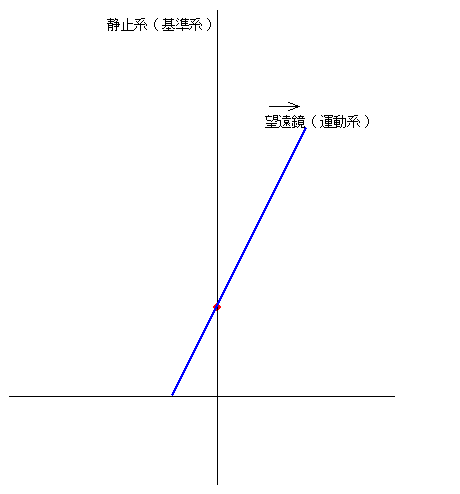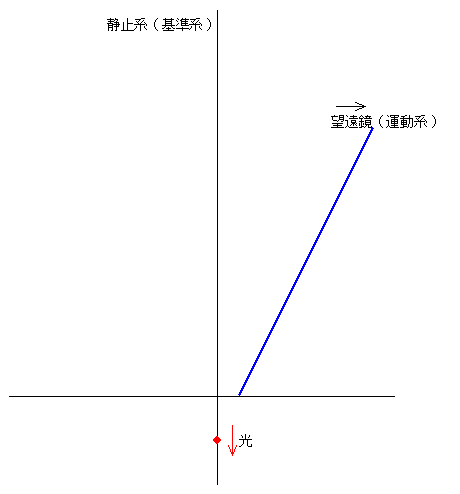
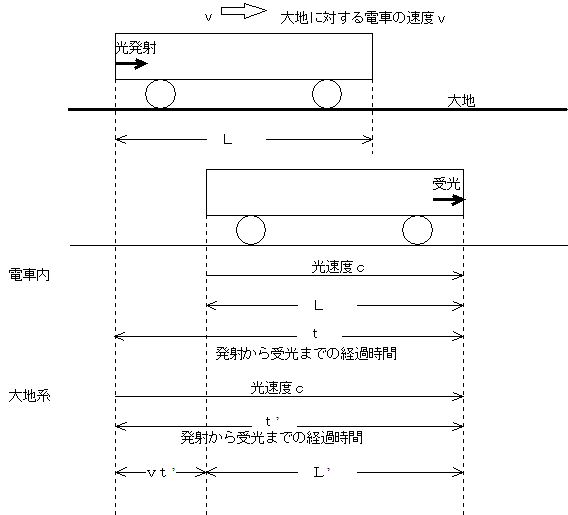 �@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@���}�͑�n�̏�������^�����Ă���d�Ԃ́A�d�ԓ��Ƒ�n�n�� �g���ΐ��h ���_���������L���Ȑ}�ł��B��������l���Ă݂܂��傤�B �@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@���}�͑�n�̏�������^�����Ă���d�Ԃ́A�d�ԓ��Ƒ�n�n�� �g���ΐ��h ���_���������L���Ȑ}�ł��B��������l���Ă݂܂��傤�B
�@�܂��A�d�ԓ��̊ϑ��҂́u�����x �� �v���ǂ̂悤�ɂ��đ��肷��ł��傤���B�Q�O���I�����w�ł͓d�ԓ��̐l�͊O�����Ȃ���A���������͓����Ă���̂��Î~���Ă���̂����ʂł��Ȃ��ƂȂ��Ă���̂Łi�����鑊�Θ_�̌����u���������^���͐�ΐÎ~�Ƌ�ʂł��Ȃ��v�Ƃ������Ɓj�ł�����A���R�A�����k�^���@�i�P�j���Ƃ��܂��ˁB
�@
�@���ɁA��n�n�̊ϑ��҂́u�����x �� �v���ǂ̂悤�ɂ��đ��肷��ł��傤���B���R�A�}���炷��������悤�ɁA
�����i�����f�{�k�f�j�^���f�����{�k�f�^���f�@�i�Q�j���ł��B
�@
�@�����ő�Ȃ��Ƃ́i�����������w�ł� �������f �̂͂��ł����j�A���ꑊ�ΐ����_�ł͓d�ԓ��̎��� �� �Ƒ�n�n�̎��� ���f �̓��[�����c�ϊ��ɂ���Č����Ƃ��Ă��邱�Ƃł��B���̏�ŁA�i�P�j���Ɓi�Q�j���͓������A�܂�u�����x�s�ς̌������v�Ƃ��Ă���̂����ꑊ�ΐ����_�ł��B
�@
�@�����ŁA�d�v�Ȏ����l���Ă݂܂��傤�B�i�P�j���́u�����x �� �v�̒P�ʂ͉��ł��傤�B�����A�y���^���z�ł��ˁB
�ł́A�i�Q�j���́u�����x �� �v�̒P�ʂ͉��ł��傤�B�������A�y���^���z�ł͂���܂���B��n�n�̒P�ʁA���Ƃ��_�b�V���u �f�v��t���āA�y ���f�^���f �z�ł��B�Ȃ��Ȃ瑼�̊����n�i�����ł͑�n�n�j�͒������A���Ԃ��ς��Ƃ����̂����ꑊ�ΐ����_�ł�����B
�@�����u�����x �� �v�̒P�ʂȂ̂ɁA�i�P�j���Ɓi�Q�j���ł͈قȂ邱�Ƃɒ��ڂ��Ă��������B�����ŁA���ɐ���ȕ����w�����E���Ă邱�ƂɋC���t���܂��B
�@
�@���ɁA���Α��x �� �̒P�ʂ͉��ł��傤�B�����A�y ���f�^���f �z�ł��ˁB�����I�ɂ����Ȃ��Ă��܂����A���Α��x�ł�����A�d�Ԍn�ł���n�n�ł������łȂ�������܂���B���������łɖ����������Ă��܂��B
�@�����̖���������u�����x�s�ς̌����v���܂���ʂ�܂��B
�@
�@�ȏ�́A�g���[�����c�ϊ��h �Ƃ������w�I�ȃg���b�N�Ȃ�ł��B�ȒP�ɐ������邱�Ƃ��\�ł��B����Ă݂܂��傤�B
�k �� �k�f �̓��[�����c�ϊ��ɂ��A
�@
�k�f��
�@
�ł���A�� �� ���f �͏�}�̏ꍇ�A�ȒP�Ȍv�Z����A
�@
���f �����i�P�{���^
�@
�ł�����A�������i�P�j���Ɓi�Q�j���ɑ������A
�� �����{�i���|���j�� ��
�ƂȂ�܂��B�����Ɂu�����x�s�ς̌����v�ł��B
�@
�@���̃g���b�N�͊����n�݂͌��� �g���ΓI�Ɂh �����⎞�Ԃ͈قȂ�A�����x�̐��l �Q�X�X�V�X�Q�S�T�W �͕ς��Ȃ��A�Ƃ��邱�Ƃɑ��Ȃ�܂���B
�@�����Ƌ�̓I�Ɍ����Ȃ�A�P�ʂ�����ɕω������� �g�L�����h �܂��� �g���̐��l�h ��s�ςɂ������̂����ꑊ�ΐ����_�ł��B
�@������ �g�L���h �͒n���l�̍l�����C�ӂ̂��̂ł���A���l�Q�X�X�V�X�Q�S�T�W�����萸�x�������Ες����̂ł���A�U�d���ⓧ�������ς��ǂ�Ȓl�ɂ��Ȃ�l�ނ��X��g�p���Ă���A���r�A�����ł��B
�����x �����R�S�O�y ���^���z���R�S�O�y ���f�^���f �z�Ƃ���A�����x�s�ς̌����ł��B
�@���ꂪ�{���̕����w�ł��傤���B���w�I�ȃg���b�N�Ƀn�}���Ă͂��܂��H
�@
�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\
�@
���Q�l�܂ł�
�@
�@���ꑊ�ΐ����_�ł́A�����n���ƂɎ��Ԃ͕ς��ƂȂ��Ă��܂��ˁB�Ⴆ�A�����n�P�Ɗ����n�Q�����Α��x �� �ʼn^�����Ă���ꍇ�A�u�����n�P����ɂ���Ɗ����n�Q�̎��Ԃ͒x���v�ƂȂ��Ă��܂��B�������u�����n�Q����ɂ���Ɗ����n�P�̎��Ԃ͒x���v�ł��ˁB�i�����n�Ƃ͓��������^�����Ă���n�̂��Ƃł��j
�@�Ƃ���ŁA���́u���Ԃ��x���v�Ƃ͂ǂ����������������ł����H
����͂ł��ˁA�u�����P�b�ł��A�����n�P�Ɗ����n�Q�ł͈قȂ�v�Ƃ������ƂŁA�ǂ��炩����ɂ���Ƒ�����̕����x���A�Ƃ������ƂȂ̂ł��B
�@���̃A�j���́u�����n�P����ɂ����Ƃ��A�����n�Q�̎��Ԃ��x���v���Ƃ����������ł��B
�@
 �@�@�@�@�@�@�@�@�@�@�@�@�@�@�@ �@�@�@�@�@�@�@�@�@�@�@�@�@�@�@
�����n�P�̂P�b�Ԋu�@�@�@�@�@�@�@�@�@�@�����n�Q�̂P�b�Ԋu
�@
�@�A�C���V���^�C���̓��ꑊ�ΐ����_�́A���̂悤�Ɏ��Ԃ̊T�O�������I�ȕ����w�����E�������̂ł��B
�@
�g���ԁh �͂ǂ̌n�������ł��邱�Ƃ��A���̃u���b�h���[�̌��s���̌��ۂɎ����Đ������܂��B�{���̃u���b�h���[�̌��s���̌��ۂ́A���̐}���t���܂ɂ����悤�ɂȂ��Ă��܂��B��]�����ɐ��̌��͓����ė���̂�����B�{���̏I�Ղɖ{���̖]�����̕����������Ă���܂��̂ł������������B�n�f ���Ε������Y�A�o�f ���ڊ���Y�ł��B
�@
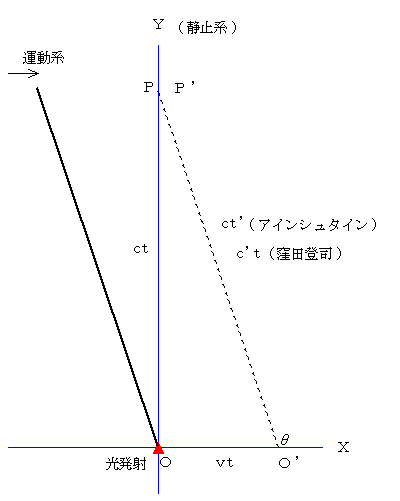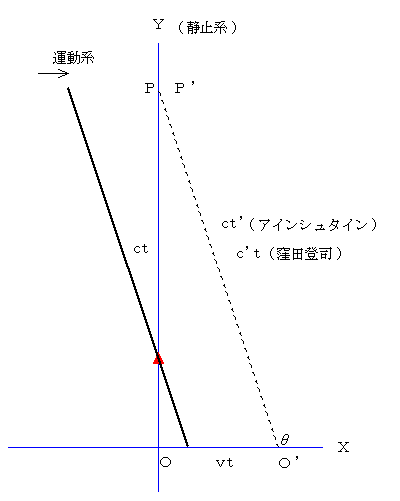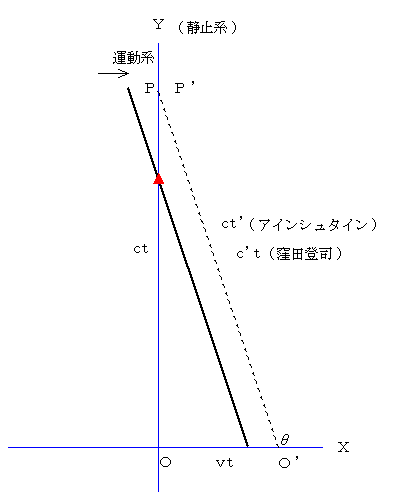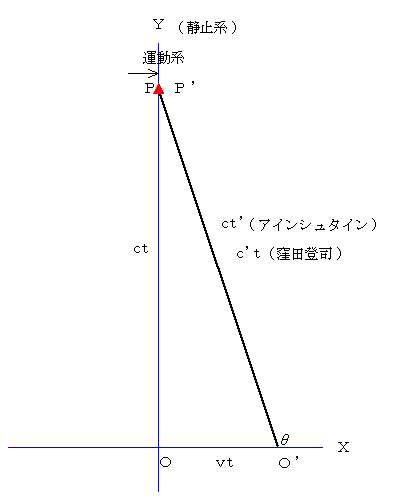
�@�A�C���V���^�C���̌����x�s�ς̌����Ƃ����̂́A���ׂĂ̍��W�n�Ō����x�͈��ł���Ƃ�������ł��B
�@���Ȃ킿�A��}�ɂ����܂��āA�^���n�ł������x�� �� �A�Î~�n�ł������x�� ���A �����Ď��Ԃ��قȂ�̂��Ƃ��āA
�n�o ������
�n�f�o�f �������f
���Ƃ���āA���������Ȑ��w���E�ɓ����čs���A���[�����c�ϊ��ŏ�������܂��B
�@
�@����ɑ��Ď����P�X�X�R�N�ɂm�g�j�o�Łu�G���N�g���j�N�X���C�t���v�R�����`�T�����A�ڂɂĔ��\�������̂́A���Ԃ͂ǂ̌n�������ŁA��������̌����� ���f �� ���|���Ecos�� �ɂȂ�̂��Ƃ������ł��B����ɂ��A�Q�̌n�A
�n�o ������
�n�f�o�f �����f ��
�̓K�����[�ϊ��Ō���܂��B
���f �͕����Ƒ傫���������Ă���̂ŁA�g�����x�h ���������������ł͂Ȃ����Ƃ̂��ӌ�������܂������A�����������Ȃ��ꍇ���i��F��=�O�j�A���̎��͐��藧�̂ŁA�ǂ���ł��\��Ȃ��Ǝv���܂��B���ꂾ�����p�͈͂��L���Ɖ��߂�������ǂ��Ǝv���܂��B
�@
�@�b�����ɖ߂��܂����A�A�C���V���^�C���̍l�������������A���̍l���̕��������I���́A��}������Ε�����Ǝv���܂��B�d�v�Ȏ��́A���H�͂P�{�������Ƃ������Ƃł��B
�@
�@���ꑊ�ΐ����_�ɂ��A��}�́A
�@�n�o�������x�� �� �A�n�f�o�f �������x�� �� �A���������āu�^���n�ł��������� �n�f�o�f �������x �� �Ŕ�Ԃ��玞�Ԃ͐i���v�B���ʂ͎��Ԃ�������A�ƌ����܂��B�܂莞�Ԃ��f ���傫���ł��B
�A(10)�Î~�n�Ɖ^���n�ɂ����̔��_�҂̌��������o���܂����A�u�^���n�ł��Z�������n�f�o�f �������x �� �Ŕ�Ԃ��玞�Ԃ͒x����v�B���ʂ͎��Ԃ͒Z���Ă�������A���Ԃ͂�����Ȃ��A�ƌ����܂��B�܂莞�Ԃ��f ���������ł��B
�h�C�c�����{��ɖƂ��A���̇@�A�A�́u�傫���A�������v�́u�i�ށA�x���v�Ƃ���̂ł��ˁB�@�̏ꍇ�͎��Ԃ��f�@�� �g�傫���h �� �g�����ς����v�͓����̂Ői��ł���h �ƂȂ�A�A�̏ꍇ�͎��Ԃ��f �� �g�������h �� �g���܂莞�v�͓����Ȃ��̂Œx��Ă���h �ƂȂ邱�Ƃł��ˁB��ꂽ���v���Ⴀ��܂����B
�@�ȏ�̂悤�ɁA���ꑊ�ΐ����_�ł́u�^���n�ɂ���āA���Ԃ͐i�ގ������邵�A�x��邱�Ƃ�����v���ƂɂȂ�܂��B�ł��}�����Ă����B�n���o �� �n�f���o�f ������ �� �ł��傤�B���f���Đ��̒��ɂ���́H
�@
�@�Ɠ��ɁA���̘b��������u��₱����������Ȃ��ŁI�v�Ɠ{���܂����B(^_^)
�@
�@���� �n�f�o�f �Ƃ����ߕ����ɔ�킯�ł͂���܂���B�����������H�͑��݂��Ȃ��̂ł��B���H�� �n�o �̂P�{�����ł��B
�@������ �g���ԁh �͊�n���^���n������ �� �ł��B���Θ_�̐���́A���̕����������ł��邩�ǂ����ɂ������Ă��܂��B���̒����܂�����ɂ��āA��L�@�A�A�����l�����������B�u��₱����������Ȃ��ŁI�v�Ɠ{��Ȃ��ʼn�����(^_^)�B
�g���ԁh �̗���͂ǂ̌n�������ł���Ƃ����̂����������R���ۂł͂���܂��B
�@
�@��}�̏ꍇ�A�� �Ƃ����X�����l���āA�^���n�́A��������̌����x���l���邱�Ƃ����͎w�E���Ă��܂��B���ꑊ�ΐ����_�Ɛ^��������Η�����l�����ł��B
�@���̐}�� �g�^���n�h �������̖�R�S���A�b����P�O���Q�炋���A�Ɓ��O�D�U�� �ʼn^�����Ă����ł��B�����猩����������x�� �� ��菭�������Ȃ��Ă��܂��B
���f �� ���|��cos�Ƃ���v�Z����ƁA���f�� �R�D�R×�P�O�W���^���ł��B
�@���x���\���܂����A�^�̌����x���ω������̂ł͂���܂���B�����܂ł��^���n�����肵����������̌����x���A���̂悤�ɂȂ��Ă���Ƃ������ł��B
�@
�@�Ȃ��A�V�k�S�Ȃ���t�������܂����A��}�ɂ����܂��āA�g���p�O�p�`�h ������ƌ����āA�g�O�����̒藝�h�������Ă��āA
�i�����j�Q �{�i�����j�Q �|�i�����f �j�Q ���O
�܂��́A�^���n�̎��Ԃ����f�Ƃ��āA
�i�����j�Q �{�i�����f�j�Q �|�i�����f �j�Q ���O
�ƌv�Z���Ă͂����Ȃ����͂�������ɂȂ�܂��ˁB
�@�������ł����A�i�����j�Q �{�i�����j�Q �|�i���f�� �j�Q ���O �Ƃ��鎖���ł��܂���B
�@
�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\
�@
�y�X���̂l����ւ��������܂��B�Q�O�O�Q�N�R���P�W���z
�����������w�I�ȊԈႢ������Ă͂����܂���B�A�C���V���^�C����������̂��������Ă����Ƃ����@�͂���܂���B
�@��}�̗�ŁA
�i�����j�Q �{�i���� �j�Q ���i�����f �j�Q�@����v�Z���āA���f ���P�D�O�T�U�Q�� �Ƃ��A
�i�����j�Q �{�i�����f �j�Q ���i�����f �j�Q�@����v�Z���āA���f ���P�D�O�U�R�R�� �Ƃ��A
�i�����j�Q �{�i���� �j�Q ���i���f�� �j�Q�@����v�Z���āA���f ���P�D�O�T�U�Q��
�ȂǂƂ��Ă͂����܂���B
���f ���P�D�P�P�U�Q�W�� �������ł��B
�@
�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\
�@
�y���Ɍ��̊�J���玟�̂悤�Ȏ��₪���܂����B�}�ʂŎ����܂��̂ł��l�����������B
�Q�O�O�Q�N�R���Q�Q���^�E�c�o�i �z
�u�E�E�E�E���ΐ����_�������_�\���ɒv���I�Ȍ��ׂ����邱�Ƃ͖����ɂȂ����Ǝv���܂��B
�@�Ƃ���ŁA��̃A�j���� �g�u���b�h���[�̌��s���̌��ہh �ł���悤�ɏ�����Ă��܂����A�ڂ��̕���������ɂ����āA�����ł͂Ȃ��悤�Ɏv����̂ł����B
�E�E�E�i�ȉ��ڂ�����������Ă��܂����A�����ł͏ȗ������Ă��������܂��j�v
�@
�@���w�E�̓��e�͂��̒ʂ�ł��B��قǏq�ׂ��悤�ɁA�}���t���܂ɂ��������ł�(*^_^*)�B
�@
�@
�@�u���b�h���[�̌��s���̌��ۂ́A���y�[�W�ł��q�ׂĂ���悤�ɁA���R��Ԃ����͒��i���邽�߁A�]�������X���Ȃ���Ȃ�Ȃ����ł��ˁB
�@��}�͋ɒ[�ɖ]�������X���Ă��܂����A������₷�����邽�߂ł��B���̗�͖]�������b����P�S���V�炋���Ƃ��������ʼn^�����Ă��܂����A���ۂ̒n���̉^���͘f�����ϑ�����ꍇ�A��R�O�����^���������x�ł��B
�@
�@�����}�C�P���\���E���[���[�̎�����͂ɂ��̌��s���̌��ۂ����p�����̂́A�Ƃ���Ȃ����� �g���̒��i���h �������̂ł��B�u������������ꂽ���́A�����̉^���ɂ͈ˑ����邱�ƂȂ����i����v�Ƃ����_�������̂ł��B
�@������A���w�E�̃A�j���́A�g�{���́h �u���b�h���[�̌��s���̌��ۂ��̂��̂ł͂Ȃ��ł��ˁB�������s�\���������ł����A�u�^���n�̉��[�n�f ���玆�ʂŐ�������Ɍ��˂��Ă���v�}�ł��B
�@�����Ė����ɂn�f�o�f ��ʉ߂��čs���ɂ́A�^���n�̑��x �� �ƌX�� �� ����`�I�Ɍ��܂�Ɛ��������̂ł��B
�@
�@�A�C���V���^�C���̓��ꑊ�ΐ����_�́A�����m�̂悤�ɌX�� �� �ɂ͈�ؖ��W�ɁA�ǂ�ȑ��x�� �� �ł��낤�Ƃ����́u�n�f ����o�f �����ɔ��˂���A���ꂪ�n�f�o�f ����ł����v�ƂȂ��Ă��܂��ˁB
�u�����X���Ȃ��Ă��ǂ��̂��B�ق��Ƃ��Ă� �� �ɉ����������Ɍ��͔��ŏo�čs���̂��v�ƁA�j��w�l�����w���_�����́A���̒����Ŏ��ɔ������Ă��܂����A�����������͕�����Ȃ��ԈႢ�ł��B
�@
�@�������ł��傤���B�ȏ�̐����Ō���͉����Ă��ꂽ�ł��傤���B
���͈ȑO�ɁA�u�E�c�̓u���b�h���[�̌��s���̌��ۂƃ}�C�P���\���E���[���[�̎������������Ă����n���҂��I����ȈႢ���m��Ȃ��ŃA�C���V���^�C�����Ԉ���Ă���ƌ����Ă�����炠���ꂽ���̂��v�ƚ}���ꂽ��������܂��B
�@���̓}�C�P���\���E���[���[�̎������l�������q���g�ɂȂ����̂��A���̒��i���������u���b�h���[�̌��s���̌��ۂ������̂ł����A�����K�ɐ������Ȃ��������Ȃ��Ă��܂��B���݂ł� ���|���Ecos�� �Ńu���b�h���[�̌��s���̌��ۂ𗝘_�I�ɐ����ł����Ƃ��Ē��ڂ���Ă��܂��B
�Q�O�O�Q�N�R���Q�Q��
�@
�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\
�@
�@�L����w�̂��镨���w����������������ւ肪����܂����B�Q�O�O�Q�N�P�O���P�R��
�w�E�c����̍l���̕������炩�ɐ����I�ł��B�Ȃ��Ȃ�A�E�c����͉�������≼�������Ă��܂���B���ɑ��Ă����̂ɑ��Ă����ʂ������_�\�������Ă��邩��ł��B���ɑ��Ă����̂ɑ��Ă����W�ϊ��̓K�����[�ϊ��ƂȂ闝�_�ł��B���Θ_�����Ă������ł����������p���������x
�@
�E�c�F�g����h �ł����Ƃ������Ⴂ�܂����A�g����h �ł͂Ȃ��A�{���ɂ���������Ă���Ǝv���܂��B�������A���̗��_�����y��ł���A�C���V���^�C���̗v���i����j�ɋ^��������Ȃ������̂�����܂��Ƃ���ł������܂��B����^����������ł����������m��܂���B�����A�Ȃ��Ȃ��A�C���V���^�C���ɗ������������Ƃ��o���Ȃ������̂ł͂Ȃ��ł��傤���B
�@���͎��R�̐g�ł��̂ŁA�ǂ�Ȃɔl�|�A��������Ă��r�N�Ƃ����܂���B���\�N�������Ă������ʂ��Y�o�b�Əq�ׂĂ��邾���ł��B���ւ�L���������܂����B�@�@�@�@�@�@�@�@�@�@�Q�O�O�Q�N�P�O���P�R���i�U�Q�Βa�����j
�@
�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\
�@
�ڎ��̂���g�b�v�y�[�W�́@������ ���̃T�C�g�͑��܂Ƃ߂Ƃ���������e�ł��B���ЂƂ��ǔj���Ē��������Ɗ���Ă��܂�
�@
�@
|