トップページ (2電子原子も含む正確な新ボーア模型)
電子スピンは存在しない。単なる数学上の産物。
古いボーアモデルのヘリウムと古典的原子模型。
もし あなたがたが 癌やその他の不治の病を治そうと思い立ったとしよう。そのとき最初に考えることは 正常な細胞と がん細胞をミクロのレベルで正確に見分けられる ナノマシーン や ナノ分子装置 などであろう。
これらの治療を正確に実行するには、原子、分子内の電子や原子核間の様々な相互作用を把握し操作しなければならない。
もちろん、これら ナノテクノロジー は 他の物理学や化学の分野においても非常に重要である。
しかし、もし実際に 量子力学や量子化学を勉強し始めたとしたら、現在の量子化学は あなたがたが思い描いていた姿と大きくかけ離れていることに唖然とするだろう。
これらの 曖昧かつ非常に非効率的な量子化学が 私が 量子力学を疑い始めた主要な要因の1つなのである。
そのため ぜひとも あなたがたには 現在の量子化学の現状を知って欲しいのである。
( 残念なことに、通常の教科書には 水素原子のことのみ頻繁に扱っているだけで ヘリウムなどの多電子原子に関しては ほとんど触れられていない。なぜなのだろうか?)
(Fig.1) "数式のみの" シュレディンガー方程式 vs. "リアルな" ボーア模型。

ご存じのとおり、私たちは シュレディンガーの波動関数が 実際何を意味しているのかまったく知らない。
また、電子スピンや パウリの排他原理の 実際の姿も分からない。
そのため、私たちは どんなに複雑な原子、分子においても、シュレディンガー方程式を ただ信じて それを解くしか手段を知らない。
( もちろん、多電子原子は解くことは不可能なため、何らかの近似に頼らなければならない。)
要するに、私たちが 量子力学に拘束されているかぎり、もっと有用かつ柔軟な方法を 様々な原子間の相互作用に使用することができないのである。
(Fig.2) 量子力学のヘリウムは不安定?
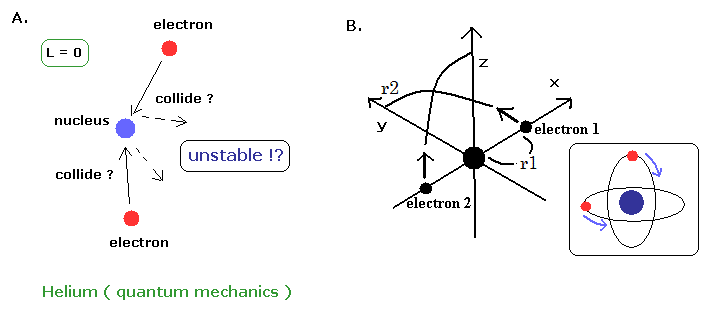
量子力学によれば、ヘリウムの2つの電子とも 角運動量はゼロ ( L = 0 ) である。
これはつまり、これら2つの電子は ヘリウムの原子核に頻繁に衝突し かつそこから跳ね返っているのだろうか ?? (Fig.2A)
あなたがたは、この量子力学的なヘリウムが 安定になり得ると思われるだろうか?(私はそうは思わない。)
ところで 量子力学における ヘリウムの具体的な構造は何なのだろうか?
私たちは 教科書で 頻繁に水素原子の構造を見かける。しかし ヘリウムの構造に関してはまったく見かけることができない。なぜなのだろうか?
(Eq.1)
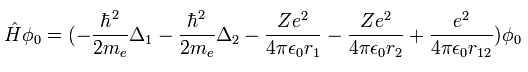
Z=2 のとき、Eq.1 は ヘリウム原子のハミルトニアンを意味している。( Δ = ∇2 )
もし ヘリウムの基底状態のエネルギーの正確な値を知ろうとすると、次のように 1000以上にもわたる変分関数を使用しなければならない。
(Eq.2)
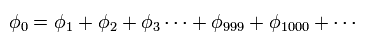
もちろん 私たちは Eq.2 の数式の羅列から 何も ヘリウムの実際の姿を知ることができない。
また この計算結果は -79.015 eV で これは 実験値 -79.0051 eV と少し異なる。
一方で トップページに示した 新しいボーア模型のヘリウム原子は -79.0035 eV という より正確な値をだすことができる。
( この -79.0035 eV と -79.0051 eV のわずかな差は いわゆる相対論効果と呼ばれるものである。このページも参照のこと。)
重要な点は、新しいボーア模型の方法では 内殻の 1S 軌道の2つの電子における 明白な原子構造と電子軌道の半径を知ることができるということである。
そのため 私たちは これらのボーア模型を 他の原子や分子に容易にかつ正確に 利用することができる。
一方で 単なる数式の項の羅列である Eq.2 は 完全に役に立たない。
私たちは これら無数の無意味な項を 他の原子や分子に応用することができない。
これはつまり 現在の量子力学的な手段が "ナノ装置" として役に立たないことを意味している。
(Fig.3) 量子力学と相対論の関係。

1920 年代、ボーア模型は ヘリウムの正確な原子模型を示すことができなかった。
なぜなら ヘリウム (もしくは 他の原子や分子) は いわゆる3体問題であり、それを計算するには コンピューターが必須だったからである。
一方で、量子力学的な変分法は ヘリウムの基底状態のエネルギーの近似的な値をだすことができた。
( しかし 上で述べたとおり、これらの量子力学的な手法は 具体的な原子模型を示すことができない。)
もし ヘリウム原子 (= 内殻の2つの電子 ) の構造が定義できなければ、その時点で すべての物理、化学の発展はストップしてしまっただろう。
そのため 私たちは 奇妙な量子力学と量子化学を受け入れるしか他に道がなかったのである。
1920 年代から コンピューターの使用が一般的になる 1980 から 1990 年代までの間に、ボーア・ゾンマーフェルト模型の微細構造が 相対論的なディラック方程式に すり替わった。
また この非常に影響力のある ディラック方程式 (+ マクスウェル方程式 ) を基にして、QED (1930s ) と 標準模型 (1960s) が作られた。
もちろん、ディラック方程式は 特殊相対論をベースにしているため、これらすべての理論は 特殊相対論が基になっていることは言うまでもない。
そして これらの理論の最終形が 奇妙な 10次元の ひも理論なのである。
そのため、もし ボーア・ゾンマーフェルト模型に戻ろうとするならば、これらすべての理論を見直さなければならない。
また 真空の何かしらの”エーテル”を認めない限り、私たちは 永久に "非実在"の仮想粒子に頼らなければならない。
率直に言えば、これらの非常に影響力が大きい基本的な理論である場の量子論や相対論が 本当のサイエンスの発展の妨げになっていると 私は思う。
( トップページから これらの理論の全改定を見ることができる。)
重要な点は 一般の方々が これら非常に込み入った 数学のみと化した物理の現状をよく知らないということである。
これは非常に深刻な問題であると私は思う。
( 複雑な場の量子論や QED に関しては、直接その分野に関わっていない物理学者 (もちろん化学者)でさえ よく知らないのである。)
テレビや 専門書でない一般の本が与える 様々な物理のイメージは 真実ではない。
密度汎関数法 (DFT) や 分子軌道法などの 現在の量子化学は ハートリー・フォック法がベースになっている。
もちろん、これらすべての方法は つまるところ シュレディンガー方程式とパウリの排他原理に頼っている。
これらの理論では、n 電子を含む ハミルトニアン (= H ) は、
(Eq.3)
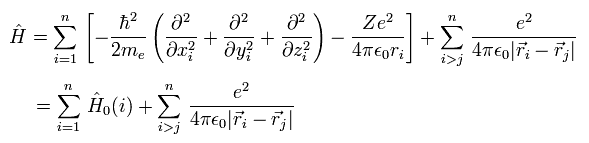
ここで 最初の行の最初の項は 電子の運動エネルギーを意味している。
2番目の項は 電子 (= -e ) と 原子核 (= Ze ) のクーロンエネルギーを表している。
そして 3番目の項は 電子間のクーロン反発力を意味する項である。
ここでは 次の表記を使用している。
(Eq.4)
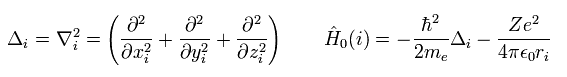
ご存じのとおり、シュレディンガー方程式は 1電子の水素原子を除いて 完全に解くことができない。
そのため 何らかの近似に頼らなければならない。
多電子原子においては、通常 1電子近似を使用する。つまり波動関数は、
(Eq.5)
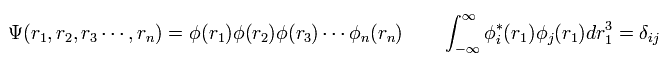
ここで、各波動関数は 正規直交系の関係にあるとしている。
( これは計算を容易にするためである。)
もちろん、Eq.5 の波動関数は真実ではない。単なる1電子近似だからである。
( Eq.5 のように 各電子の波動関数がきれいに分離できて並べられる状態を 1電子近似という。)
さらに パウリの排他原理も考えればさらに複雑になる。
Eq.3 のハミルトニアンの期待値 (= E ) は、
(Eq.6)
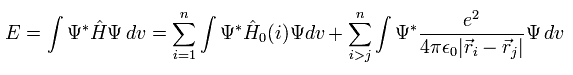
Eq.5 と 正規直交系を使用すると、 次の全エネルギーの期待値を得ることができる。
(Eq. 7)
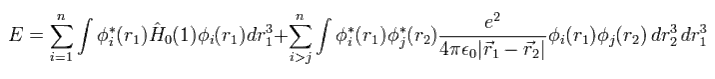
つまり、正確な値を知るためには、次のすべてのシュレディンガー方程式を解く必要がある。
(Eq. 8)
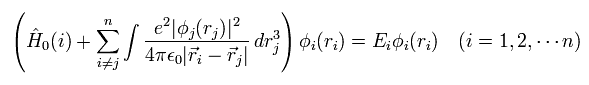
しかし Eq.8 を解くには、最初に 各波動関数 (= φi) の初期状態 を知る必要がある。
なぜなら Eq.8 は 電子間の相互作用演算子として これらの φ を使用しているからである。
そのため ある試行関数を φi として選んで Eq.8 を 解くのである。
( もちろん、この計算は非常に難しい。)
そして 新しい波動関数 φ の結果が得られたら、今度は それらの新しい波動関数を Eq.8 に使用してまた解く。
その複雑で難解な計算を正確な波動関数を得るまでリピートするのである。
これを 自己無撞着(つじつまの合う場, SCF)の方法という。
この SCF の方法は 密度汎関数法 (DFT) においても使用されている。
あなたがたは これら非常に込み入った非効率的な方法を 例えば分子生物学やナノテクノロジーなどの様々な分野で応用したいと思われるだろうか?
もちろん、Eq.5 は完全ではない。
パウリの排他原理によれば、各状態は 2つより多くの電子を含むことができない。
例えば リチウム原子では 3番目のイオン化エネルギーは 他の2つの内殻の電子のよりも かなり小さい。
2つのスピン状態 (= α と β ) を考慮して、
(Eq.9)
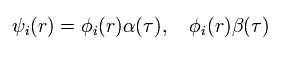
Eq.5 の全波動関数は、
(Eq.10)
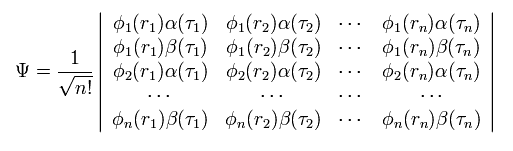
ここで 全波動関数 Ψ は 行列式として表される。
ご存じのとおり、行列式では 任意の2つの行または列が同じとき、この行列式は ゼロになる。
彼らは この行列式の性質を パウリの排他原理として利用しているのである。
しかし この非常に込み入った行列式のために、私たちは 容易に 現在の量子化学を他の分野に応用することができない。
これはつまり 現在の量子力学の範疇で 私たちは自ら 自分たちの科学の発展を妨げているのである。
例えば、2電子の場合 行列式は
(Eq.11)
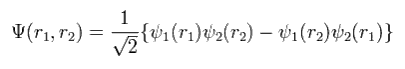
ここで
(Eq.12)
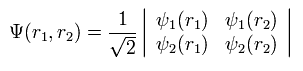
もし ψ1 = ψ2 のとき、 Eq.11 はゼロになる。
Eq.11 で r1 と r2 を交換したとき、 Eq.11 の 全波動関数の符号は逆になる。
このことから 彼らは 行列式は 電子などのフェルミ粒子の反対称の性質を示していると主張しているのである。
しかし このページに示したように、反対称の性質は もともと 相対論的なディラック方程式から得られたものである。( シュレディンガー方程式とは何の関係もない。)
また フェルミ粒子の反交換の関係式は もとのド・ブロイ理論に反している。
これら非常に曖昧な性質に頼る代わりに、もし ド・ブロイ波の干渉に基ずく パウリの排他原理に対するクリアな解釈を使用すると、計算がぐっと簡単になる。
( どうしてヘリウムは化合物を形成しないのか? や 奇妙なスピンのページも参照のこと。 )
(Fig.4) 2つの電子のド・ブロイ波が互いに干渉 (interference) している。
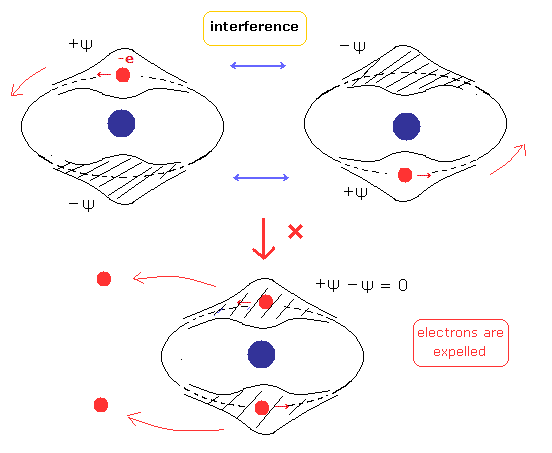
(Fig.5) 安定 かつ 互いに独立したド・ブロイ波 (= 垂直交差 )
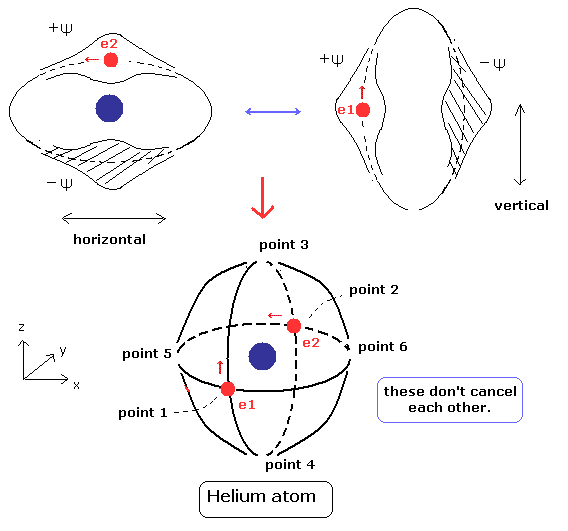
Eq.10 を用いると、期待値は
(Eq.13)
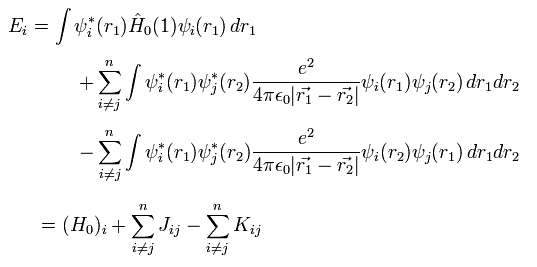
ここで J の項は 電子間の通常のクーロン反発エネルギーである。
また K の項は 交換積分でパウリの排他原理を表している。
重要な点は この交換積分 K は 同じスピン状態 ( αα もしくは ββ ) のみを含んでいることである。
異なったスピン状態 (= αβ ) は α と β の直交性でゼロになる。
例えば、ヘリウム原子では、Eq.13 の H0 と J の項のみ残る。
( このケースは 2つの電子が同じ状態なため許される。)
しかし 多電子原子では 異なったスピン状態を含む異なった状態が存在する。
Eq.18 は 非常に込み入っている割には これらの多電子原子の状態を正確に表せないのである。
完全配置間相互作用 (CI) 法 や ab initio 分子軌道法などは このカテゴリーに属する。
しかし 基本的には 使用できる基底関数系に制限があるため、正確な値を得ることは不可能である。
そのため、現在の量子化学は限界にきているため できるだけすみやかに他のもっとシンプルかつ効率的な方法に移る必要がある。
現在は、 密度汎関数法 (DFT) が その簡単な計算のために 量子化学の世界で主要な地位を築いている。
しかし まず 密度汎関数法は 単なる近似の1つにすぎないということである。
さらに 結局のところ DFT もシュレディンガー方程式を解く必要があり、自己無撞着な方法 (SCF) を使用しているのである。
そのため 基本的には DFT においても状況は何ら変わっていないのである。
このセクションでは 2つの粒子間の距離を次のように表す。
(Eq.14)
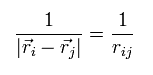
各波動関数は 正規直交条件を満たす。
(Eq.15)
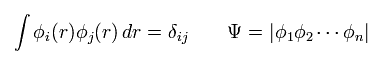
ここで Ψ は 上で述べたように行列式でなければならない。
全電子密度 ρ(r) は 次のように表せる。
(Eq.16)
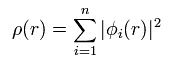
これはつまり 電子密度 ρ(r) は 波動関数 φ の 2乗 となる。
Eq.13 のように、 密度 ρ(r) を使うと、ハミルトニアンの期待値は、
(Eq.17)
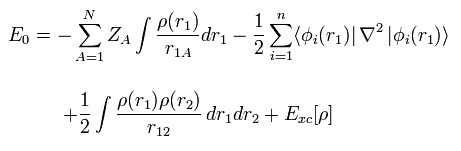
ここで 係数 1/4πε や h, m などは省略した。
ここでは N 個の 正電荷 (+Ze) の原子核が存在しているとする。
Eq.17 の最初の項は 原子核と電子間のクーロン引力を意味している。
Eq.17 の2番目の項は 運動エネルギーを意味している。
Eq.17 の3番目の項は クーロン反発エネルギーである (Eq.13 の J のような)。
最後の項 Exc は 交換相関エネルギーと呼ばれるもので K や 他の相互作用が含まれている。
密度 ρ が 各波動関数の 2乗 (Eq.16) であることを考慮すると、エネルギー期待値 E の ρ に対する 汎関数微分は、
(Eq.18)
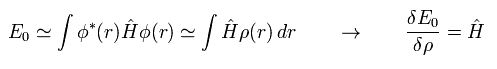
汎関数微分は 積分の内部の関数に作用する。
同じように、 運動エネルギーの項の汎関数微分 (= Eq.17 の2項目 ) は、
(Eq.19)
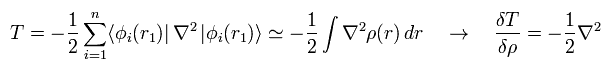
原子核と電子間のクーロン引力の項 (= Eq.17 の1番目の項 ) の汎関数微分は、
(Eq.20)
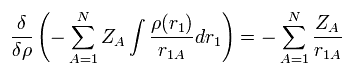
電子間のクーロン反発の項 (= Eq.17 の3番目の項 ) の汎関数微分は、
(Eq.21)
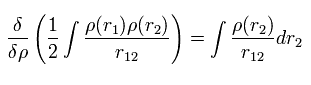
Eq.17、 Eq.18、 Eq.19、 Eq.20、 Eq.21 から、ハミルトニアンとその固有関数は、
(Eq.22)
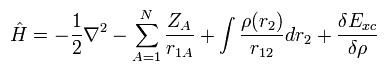
(Eq.23)
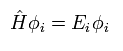
つまり 結局 密度汎関数法 においても Eq.22 と Eq.23 の非常に込み入ったシュレディンガー方程式を解かなければならないのである。
もちろん 最も難しい項 Exc は 不明のままである。
近似の1つとして、局所密度近似 (LDA) というのがある。
LDA では、正電荷と負電荷の密度が 1様でかつ 互いに等しい(= 中性)と仮定したものである。
この非常に特殊な状況では、ハミルトニアンは 次のように運動エネルギーの項のみ残す。
(Eq.24)
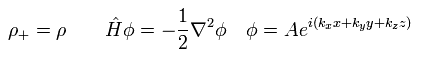
交換相関エネルギー Exc は次のように分離できる。
(Eq.25)
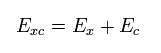
ここでは
(Eq.26)
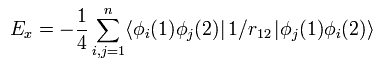
Eq.26 は Eq.13 の K のような交換積分を意味している。
上で述べたように 同じスピン状態のみ残る。
そのため 閉殻原子では 1/4 が付加されている。
Eq.24 の自由粒子様の波動関数を Eq.26 に代入して それを解く。 すると次の近似式を得る。
(Eq.27)
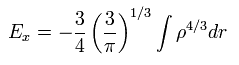
さらに 均一密度のシュレディンガー方程式を解いて E0を計算する。
これらの計算結果をもとに、次の関係式から Ec を知ることができる。
(Eq.28)
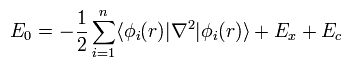
最初に 次のような近似の関数を選ぶ必要がある。
(Eq.29)
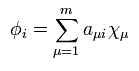
Eq.27 と Eq.29 を使って、Eq.22 と Eq.23 を解いて 新しい波動関数を得る。
これらの新しい波動関数を使って、Eq.22 と Eq.23 の計算を繰り返していく・・。
(= つじつまの合う方法。 )
つまり 密度汎関数法 においても 混沌とした状況は一向に変わってないのである。
また、密度汎関数法は ここで示したとおり、単なる近似なため、本当の値を得ることはできない。
これら古い混沌とした量子力学的手法に頼るよりも、私たちは 計算をより効率 かつ リアルなものにするために 新しいボーア模型による手法を使うべきだと思われる。
新しいボーア模型では、私たちは クーロン力と 整数倍のド・ブロイ波 (+ その干渉) を考慮するだけでいい。
ボーア模型の利点は 対象となる原子や分子の具体的なイメージを把握できるため、そこから 様々な効率的かつ 具体的な手法を考え 試すことができる点である。
一方で シュレディンガー方程式+パウリの排他原理に基づく方法は それらの実態が何か分からないままなので、単にその式をルールに従って解くという手法から逃れることができないのである。
つまり 数学上のシュレディンガー方程式と奇妙なスピンを信じて進むしか他に道がないのである。
( シュレディンガー方程式はボーア・ゾンマーフェルト模型の間違いバージョン?も参照のこと。 )
(Fig.6) "クーパー対" は 実在するのか??
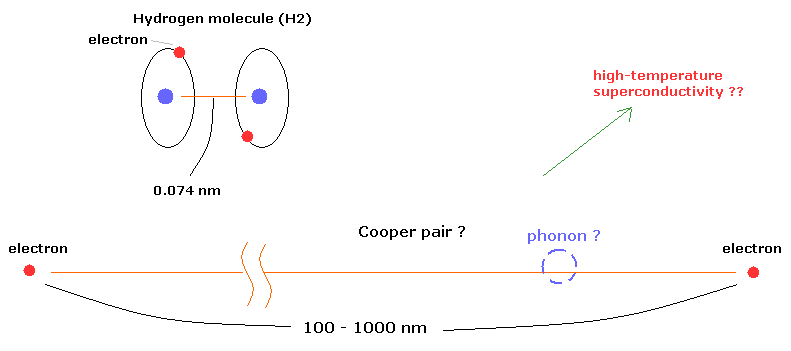
現在の物性物理学によれば、クーパー対は 低温状態において 非常に曖昧な存在である "フォノン" というものを介して結合するとされている。
驚くことに クーパー対の2つの電子間の距離は 何と 100 - 1000 nm (ナノメーター) もあるのである。
例えば、水素分子 (H2) の 核間距離は 約 0.073 nm である。
どうやって、これら2つの電子は 超伝導体の中で 安定して結合できるのだろうか?非常に奇妙である。
標準的な解釈によれば、正電荷の原子核などが これら非常に長い結合に 準粒子 フォノン として関わっているそうである。
( しかし、私はこの長すぎる結合が 非常に不自然に思われてならない。あなたがたはどう思われるだろうか?)
BCS 理論によれば、非常に低温において 超伝導体中に クーパー対が形成されるとされる。
そのため 現在の BCS 理論は 高温超伝導を説明することができない。
このページ (Eq.15 - Eq.18)に示したように、もし 通常のボーア模型と ド・ブロイ波の整数倍の考えを用いれば、奇妙なクーパー対を使用せずとも 磁束量子の現象を説明することが可能となる。
もちろん、クーパー対なるものが最初から存在しなければ 高温超電導における問題も生じない。
おそらく クーパー対なる概念は ボゾン様の性質 (= フェルミ粒子+フェルミ粒子 ) と 超伝導体における磁束量子を説明するために導入されたものであろう。
しかし あなたがたは 最初から 奇妙な電子スピンなど存在しないと思わないだろうか? ( このページも参照のこと。)
外磁場を物質にあてて、それを冷やして超伝導体にすると、その超伝導体内部の磁場はゼロになる。
現在の物性物理学の標準的な解釈によると、このゼロの磁場は もともと質量ゼロの光子が 質量を得ることによって起こるとされている。
なぜなら 質量のある光子によって生じる力は遠くまで届かないからである。
( 相対論によれば クーロン力などは エーテルではなく奇妙な”仮想光子”によって起こるとされている。)
しかし このメカニズムは マクスウェルの古典的な電磁気学によって説明できると思われる。
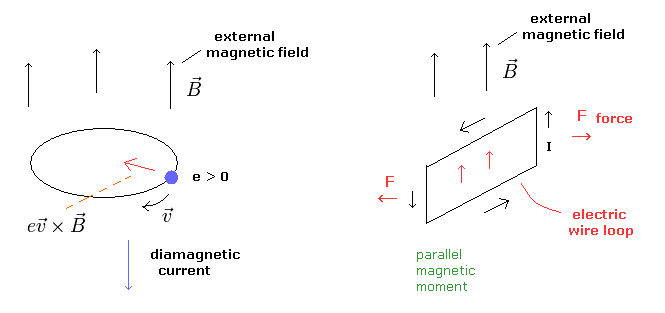
なぜなら 外磁場によるローレンツ力は 外磁場を打ち消す方向の円運動を起こすからである (= Fig.7 左図 )
超伝導体でない物質で 各荷電粒子の個々の運動が 全体的なドブロイ波よりも影響力が強いとき、これらの円運動によって生じる磁気モーメントは 外磁場に平行になろうとする ( Fig.7 右図 )。
現在の量子力学によれば、荷電粒子は "スピン" を持つ必要がある。
そのため 反磁性による磁場ゼロ状態を説明するためには 上記の非常に長いペアによって これら奇妙なスピンを消去する必要があったと思われる。
なぜなら スピンは外磁場に平行になって安定になろうとするからである。
ところで 質量のある光子の "具体的な"状態とはいったい何なのだろうか?
(Fig.7) 反磁性 (= diamagnetism ) と強磁性 (= parallel )。
物性物理学のような 非相対論的な場の量子論においてすら 生成消滅演算子や 自発的対称性の破れのような非常に曖昧な概念を用いている。
もともと 現在の場の量子論が非常に抽象的なものになった原因は 相対論の非常に厳しい制限が原因である。
つまり 非相対論的な物理学まで この曖昧な場の量子論の概念を持ち込む必要がないと思われる。
例えば、電子とフォノンの相互作用は次のように表される。
(Eq.30)

また 対称性の破れでは 次のような”数学的な”表現が用いられる。
(Eq.31)
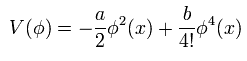
あなたがたは 非常に低温での これら自発的な対称性の破れが 通常の古典力学的な視点から 自然に説明できると思われないだろうか?
非常に低温状態では 各粒子の独立した動きが 不活発になる。
そのため 非常に低温では 全体的なド・ブロイ波効果が より強くなるのは自然なことである。
つまり 強磁性や超伝導などの様々な現象は 通常の古典力学+ド・ブロイ理論で説明可能と思われる。
質量ゼロのディラック粒子なるものがあるが、いくら準粒子と言えども これはオリジナルの理論に矛盾してないだろうか?
また、スピノン (スピンを運ぶもの?)、オービトン (軌道的性質を運ぶもの?)、ホロン (電荷を運ぶもの?) などの準粒子の実在的な性質についても再検証する必要があると思われる。

2012/7/27 updated This site is link free.