トップページ (2電子原子も含む正確な新ボーア模型)
スピンは存在しない。単なる数学上の産物。
現在の物理の説明が分かりにくい理由。
水素結合と立体障害の本質 (13/6/7)
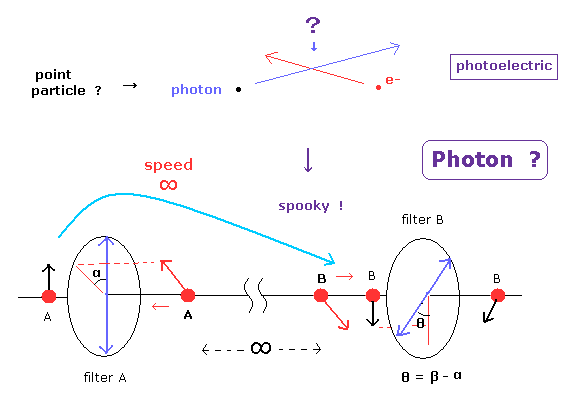
(Fig.1) 光電効果 → 光子? → 不気味なリンク。

通常の教科書は よく 光電効果は 光子が波ではなく 粒子であることの証拠であると 説明している。
しかし ご存じのとおり、光の "振動数" というのは c / 波長 と同じ意味であり、これは 完全に 粒子でなく 波の性質であることは言うまでもない。
ボーア模型の加速する電子の電磁波放射のように、現在の物理の教科書は 本当の真実を捻じ曲げてしまい 一般人を 一種の マインドコントロールのように 間違った事実のほうに向けさせようとしている感がある。
このページに示したように、超光速の不気味なリンクは "光子" という 架空の粒子によって生じたと言っていい。
もちろん、量子もつれに関する何らかの実験が アインシュタインの生存時に行われていたとしたら 彼は絶対に 光子という粒子を認めなかっただろうと思われる。
(Fig.2) 仮想光子は 特殊相対論に反する。
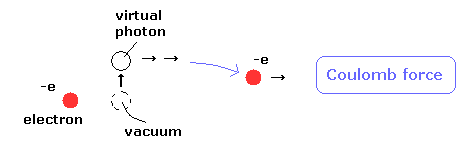
実際に エーテルを否定して "光子" を認めたとしたら、相対論に反する超光速の
仮想光子を認めなければならなくなる。
もちろん、アインシュタインが 場の量子論や 量子電磁力学を決して認めなかったことは言うまでもない。
彼は 本音では 光子という量子を認めたくなかったのでは と思われる。
リー スモーリンの「迷走する物理学」 によれば、量子力学を頑なに認めなかった アインシュタインは その後 物理界から 完全に無視された存在だったらしい。
本の中で フリーマン・ダイソンとのエピソードが 非常に印象的である。
アインシュタインに憧れていたダイソンは 彼の量子力学に依存しない統一理論の論文をみて 愕然とした。
そして その後ずっと アインシュタインを避けることを決心したそうである。
この 現実は 非常に苦痛だった アインシュタインの人生だったにも関わらず、どうして 彼は 現在の物理界で "神格化" された存在になってしまったのだろうか?
(Fig.3) いつ、どうして アインシュタインは "神格化"されるようになったのか ?
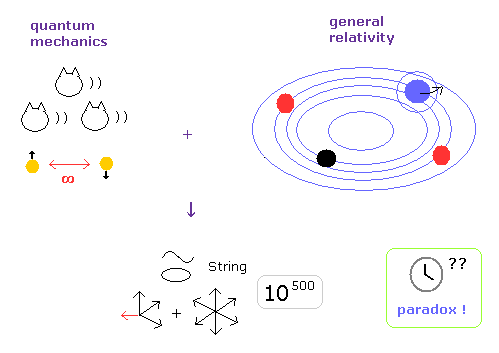
主要な原因は 現在唯一の 量子力学と相対論の統一理論である 10 次元の ひも理論にあると言っていい。
彼らは 非現実的な ひも理論を 一般人や 学生達に信じさせるために アインシュタインを 神格化する必要があったといえる。
それに追従するかのように 様々なメディアや ポピュラーサイエンス本などが その傾向を助長させた。
特殊相対論の致命的なパラドックスのために ひも理論、QED、一般相対論、標準模型などの 相対論的な理論が リジェクトされるのは 後は 時間の問題 と言える。
( おそらく アインシュタイン自身は これらのパラドックスや 量子力学、リアリティーの狭間で苦しみ続けたと思われる。)
問題は 今のねじれた状態を悠長に長引かせればするほど、 より多くの新しい学生達や それを目指そうとする人達の その後の彼らの人生が狂わされてしまうことになる。
それでも これらの重要なパラドックスを隠し続ける彼らに その責任を取ることができるのだろうか?
非常に心配である。
(Fig.4) 一般相対論は 本当に"すべて"のテストをパスしてきたのか?
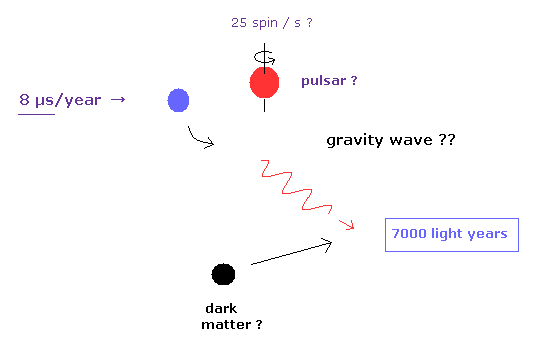
私達は しばしば "量子力学と一般相対論は 今までの ありとあらゆるテストをパスして すべての実験結果に合致してきた" というコメントを見かける。
しかし 本当にそうだろうか?
例えば あるトップジャーナルでは、地球から 7000 光年も離れた 白色矮星が 想像上の重力波を放出して エネルギーを消失させ、その軌道周期をほんのわずかだけ変化させるとしている。
しかし よくよく見ると この変化量が 1年で たったの 8 μs なのである。
あなたがたも感じだとおり、この非常にわずかな量を 7000 年もはるかかなたからくる光の情報だけで判断することは はっきりいってやりすぎである。
良く分かっていない ダークマターや 他の無数の星の重力の 7000 年もの道筋に対する 影響を正確に知ることは不可能である。
地球上のことでさえ、7000 年前の 些細な出来事を知ることは不可能なのにである。
現在の研究者達が 一般相対論が 絶対的に正しいという 前提条件のもとで 実験を行っているという いい証拠である。
(Fig.5) 分数電荷 -1/3、 +2/3 は 実在するのか?
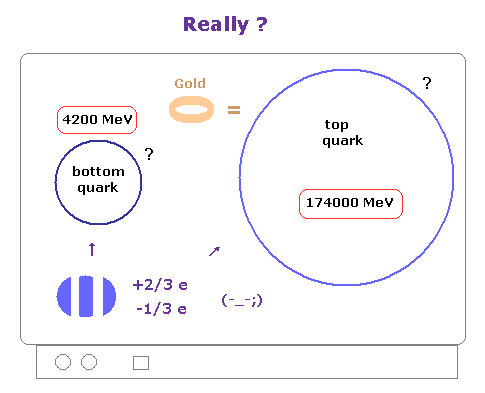
あなたがたは しばしば 標準模型は 最も成功した理論の1つであるという コメントを目にすることだろう。
しかし 例えば、 -1/3e や +2/3e などの分数電荷自体は 今まで見つかっておらず、そもそも彼ら自身 クォークやグルーオンは 絶対に単離できないと主張しているぐらいである。
( それに "1/3" や "2/3" などの値は ちょっと出来すぎだと思われないだろうか? どうして "2/5e" や "4/7e" ではだめなのだろうか? )
もちろん、これらの非現実的なクォークが実在しなければ、標準模型は その時点で 崩壊する。
つまり このケースにおいても、想像上の分数電荷が存在するという 非常に限定された前提条件の元でのみ、彼らは標準模型の実験を行っているにすぎない。
これらの前提条件が もし変われば もちろん これらの理論はすべて書き変わることになる。
(Fig.6) どうして 量子もつれの実験は ワンパターンなのか?

残念ながら 量子もつれ (= エンタングルメント ) に関する実験は 見るからに 何の進展もない状態である。
彼らは "あるループホールを閉じる" だとか "3光子、4光子のをもつれさせた" だとか 毎度同じワンパターンの実験を繰り返しているだけである。
あなた方も感じられたと思うが、私達が最も知りたいことは 超光速の不気味なリンクが 各粒子に どう作用しているかという具体的なメカニズムそのものである。
しかし 彼らは 肝心なこの部分のこととなると ただ "Shut up and calcualte !" と言って 口を閉ざしていしまう。
この理由は おそらく 実験家である彼ら自身 量子もつれというのが ただの幻想で 光子というのが 単なる古典的な電磁波であることに すでに気づいているからだと思われる。
このセクションに示したように、同時刻に存在しない もつれた光子対も 結局は "光子" というワードを用いた結果である。
(Fig.7) 現在の反粒子に関する実験もワンパターンである。
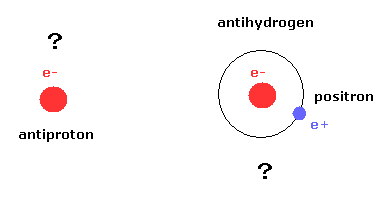
結論から言って、現在の一般相対論、量子もつれ、素粒子物理学は 単に ワンパターンの実験を繰り返しているだけで 実質的に何にも進展していないように思われる。
もし 一般相対論にそれほどの自信があるなら、”想像上”の重力子が 具体的に どういうメカニズムで 奇妙な時間の遅れを引き起こしているのかを 真っ先に調べるべきであろう。
また これらの重力子と 仮想粒子などの具体的な関係などについても 実際の実験で明らかにすべきである。
反クォークも含めた 反粒子の実在性について それほどの自信があるなら、少なくとも その反粒子を 重金属を使わずに 真空そのものから 発生させる必要がある。
なぜなら 重金属への衝突に頼るということは これらの現象が 単に 電子、陽子、中性子捕獲と 何ら変わらないことを示しているにすぎないからである。
( 実際に 疑わしき陽電子の磁気モーメントは 電子と同じである。)
一般に 生じた反粒子の量は 非常に少なく、それらのほとんどは無数のノイズである。
彼らは 最終産物である 光から それらの存在を推定しているにすぎない。
(Fig.8) ネオン (= Ne ) の本当の電子分布。
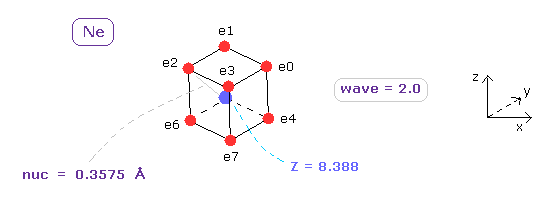
ここでは このプログラムを用いて 本当の原子半径 (= nuc ) と 中心電荷 Z を計算する。
このプログラムのテキストを "twoion.java" としてセーブしてコンパイルしてほしい。 "--Xlint: unchecked ---" などの注意は無視して実行できる。
このプログラムの操作方法は このページのと ほぼ同じである。
本当の原子半径の計算方法は このページのと同じ方法である。
このプログラムでは、各電子に作用する トータルの力 (F) を元に、
次のように "仮想" の半径 (r1) を定義する。
(Eq.1)
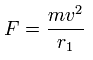
これはつまり 遠心力が F に等しいとしている。
"v" は 電子の速度で 各運動エネルギーから得られる。
これらの値から 次のように 1軌道に含まれるドブロイ波 ( wn ) を求めることができる。
(Eq.2)
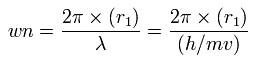
App. 1に示したように、ネオンの 1-8th のイオン化エネルギーは 953.614 eV である。
ビリアル定理を用いれば、全ポテンシャルエネルギー (= tV ) は -953.614 × 2 = 1907.228 eV になる。
全 V が ほぼ 1907.228 eV で 1軌道のドブロイ波 (= Waves ) が 2.0 のとき、 各電子と Ne 原子核の距離 (= nuc ) は 0.3575 Å、 中心電荷 Z は +8.388 になる。
( ここでは 新しい単位 1 MM = 1.0 × 10-14 meter を使っている。 )
"Ne" を スクロールバーから選んで、 "Atom A" ボタンをクリックする。
右下の "A-tV" は A atom 内のみで計算した 全ポテンシャルエネルギーである。
"nuc" や "charge Z" などを変えて この A-tV を ほぼ 1907.228 eV にするように調整することができる。
( 指定のテキストボックス内にある値をいれて、"nuc" と "charge Z" ボタンをクリックする。)
(Fig.9) フッ素 (= F ) の本当の電子分布。
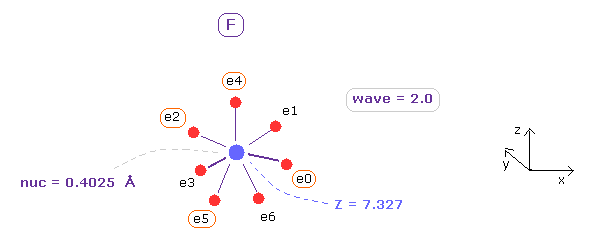
次に "F" を スクロールバーの中から選んで "Atom A" ボタンをクリックする。
App. 1 に示したように、フッ素の 1-7th のイオン化エネルギーは658.836 eV である。
つまり ビリアル定理によれば、全ポテンシャルエネルギー (= A-tV ) は ほぼ 658.836 × 2 = 1317.672 eV になる必要がある。
1軌道の 平均のドブロイ波 (= ave ) が2.0 のとき、 各価電子と F 原子核の距離 (= nuc ) は 0.4025 Å (= 4025 MM )、 中心電荷 Z = +7.327 となる。
"A nuc" ボタンをクリックすると、A atom 内のみで計算したときの A 原子核 (= F ) に作用する力が表示される。
このケースでは、 ( FX, FY, FZ ) = ( 3, 2, 3 ) は ほぼゼロで、 F 原子核は 安定である。
"+X (MM)" ボタンをクリックすると、電子 0, 2, 4, 5 のみの座標を変えることができる。
( 電子 1、 3、 6 は 電子 0, 2, 5 の座標を元に自動的に変わる。 )
"nuc"、 "charge Z"、各座標を調整して、 最も対称的 (= 最も低い tV ) な F 電子の配置を見つけられる。
(Fig.10) PDB データバンク - カリウムチャネル。
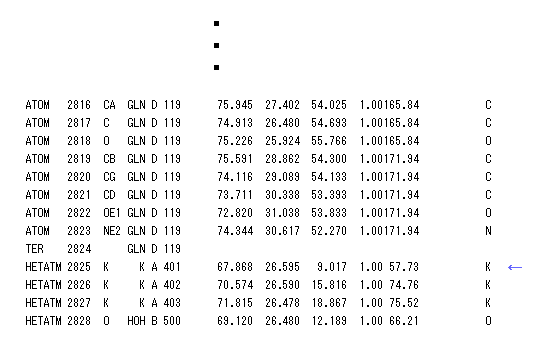
カリウムチャネルが カリウムイオン (= K+ ) のみを通し、それより小さい ナトリウムイオン (= Na+ ) を ブロックする話は有名である。
この理由について PDB のデータ (= K-O の距離 ) と 上記のプログラムを用いて調べることにする。
PDB (= タンパクデータバンク ) は その3次元タンパク構造を可視化するフリーソフト RasMol との組み合わせで 非常に便利で有用なツールである。 ( 一度試されるといいと思う。 )
PBD のサイトで "1BL8" (= K+ チャネル PDB id ) で検索して、 Display File ボタンをクリックし、その PDB data をセーブして RasMol を使って表示する。
(Fig.11) K+ イオンと 酸素原子 (= 電子対共与体 )。
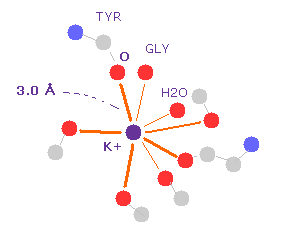
K+ チャネルの "401" 番目の残基が カリウムイオンである ( Fig.10 も参照のこと )。
ここで "select" コマンドを用いて K+ イオンから 5.0 Å 以内の距離の原子のみ表示させる。
K+ と その周囲の酸素原子の1つをクリックすると、 K-O の距離が 約 3.0 Å であることが分かる。
K+ イオンのみが カリウムチャネルの 9つの酸素と相互作用できると言われている。
一方で より小さい Na+ イオンは 相互作用できない。
しかし 非現実的な量子化学では 各電子の具体的な位置関係を示せず、かつ 他の粒子に対する "力" という概念がない。
そのため 量子化学を用いて 何が起こっているのかを知ることはできない。
(Fig.12) O 原子核に作用する力。
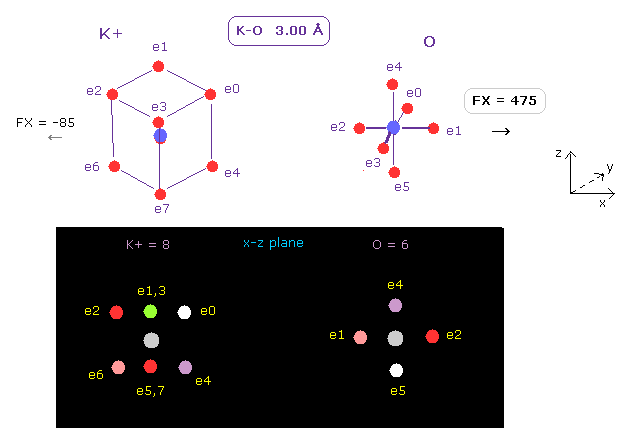
このプログラムを実行後、 A、B atom として それぞれ K+ (= カリウムイオン ) と O (= 酸素 ) を選択する。
そして 核間距離を 3.00 Å ( internuc = 30000 MM ) にする。
カリウムイオン (= K+ ) は Ar のように 8つの価電子を持つ。
上記と同様に、App.1 の 2-9th のトータルのイオン化エネルギーを用いて K+ の電子軌道半径 (= 0.5970 Å ) と その中心電荷 (= 10.44 ) を計算する。
Fig.12 に示したように、各原子核に作用する反発力は それぞれ FX = 475 と FX = -85 である。
(Fig.13) O-H 間の反発力。
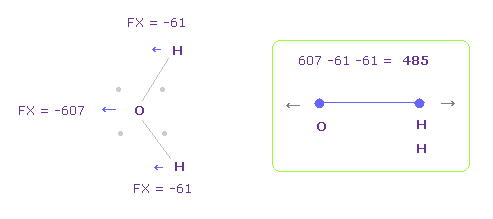
このページ (Fig.28) に示したように、K-O 間の反発力は H2O のものと ほぼ同じである。
| 分子 : | H2O | OF2 | OCl2 | OFH |
|---|---|---|---|---|
| Repulsive force: | 586 | 564 | 576 | 582 |
さらに Fig.12 の K-O における 全反発力は 475 + 85 = 560 で、これは 他の H2O-様分子とほぼ同じである。( このページの Table 6 参照のこと。 )
正電荷による反発力によって 酸素原子の 負の電子 ( 例えば Fig.12 の e4 と e5 ) を H などの他の原子に打ち勝って 十分に引きつけることができる。
(Fig.14) Na+ イオンの力は小さい。
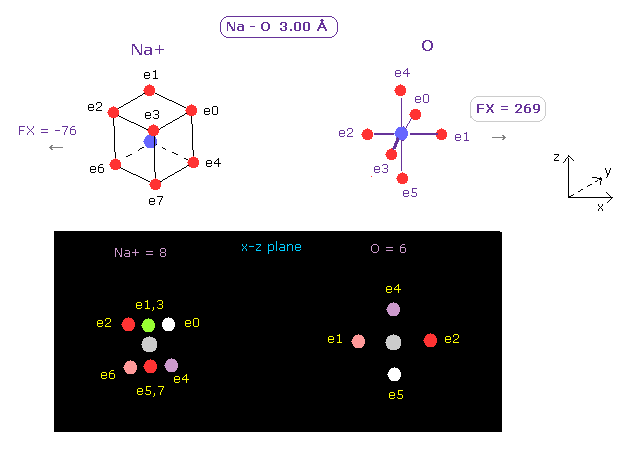
次に A atom として Na+ イオンを選ぶ ( Na+ をスクロールバーから選んで "Atom A" ボタンをクリックする。)
このケースでは、O 原子核に作用する力は 小さくなる ( FX = 269 )。
これはつまり Na+ イオンは 酸素の電子を十分に引きつけることができず、Na+ イオン水和物が 自身の H2O 結合分子を離して 狭い K+ チャネルを通過することができないことになる。
基本的に Na+ や K+ イオンは 体内で "水和物" として存在しており、狭いチャネルの孔を通過するには これらのくっついた H2O を 手放す必要がある。
K+ イオンのケースでは、K+ が 孔の酸素と十分に相互作用できて H2O を放すことができる。
(Fig.15) [Na (H2O)]+ 水和物。
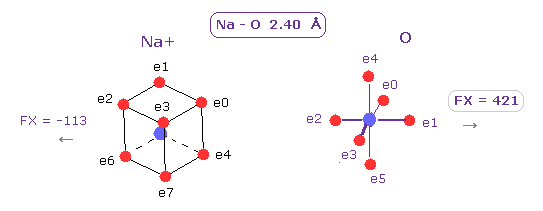
通常の [ Na+ - (H2O) ] 水和物では、 Na-O 結合長は 約 2.40 Å である。
この距離では、 Na+ イオンの O 原子核に対する力は 酸素の電子と引きつけるのに十分なもの (= 421 ) になる。
K+ と Na+ イオンは それぞれ 1.33 Å と 0.95 Å の半径を持つとされている。
しかし 量子力学は 明白な電子の位置を示すことが できない。
そのため これらの半径は 本当の電子の分布状態を意味していない。
単に核間距離から推定したものである。
明白な電子分布を持たないということは 量子力学には
クーロン力のような概念がないことになる。
クーロン力は 明らかに 様々な結合状態を決定する 主要なファクターの1つにも関わらずだ。
(Fig.16) 力 = 1000.
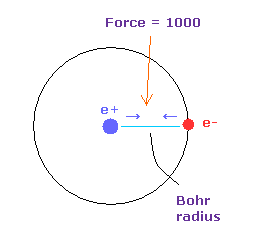
このページの 力の単位を Fig.16 に示した。
水素原子の基底状態の 電子と原子核間の力を "1000" と定義した。
つまり 電子と +e の原子核間の距離が ボーア半径のとき、その力は1000 になる。
例えば、 1468 の力は 基底状態の H 原子の 1.468 倍ということになる。
(Fig.17) K-O は 共有結合でない。
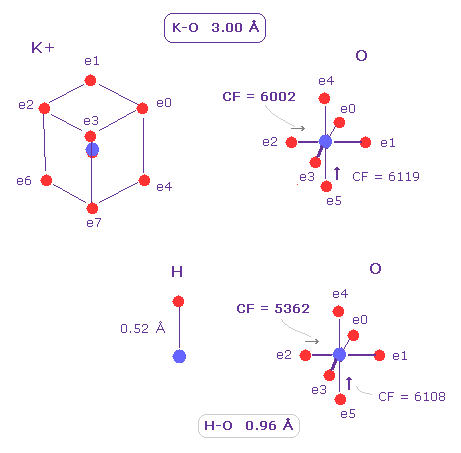
K+ イオンでは その価電子が広く分布している (= 3 ドブロイ波長の軌道 ) ため、その正電荷の原子核が さらけだした状態になっている。
そのため K-O の距離が 3.00Å と長くても 酸素原子核と相互作用できる。
しかし 通常の O-H 結合と異なり、酸素の価電子 (= e2 ) に直接作用する力は 小さい。
CF = 6002 ( = O 原子核方向への力 ) は O-H の共有結合 (= 5362 ) よりも大きい。
これはつまり K+ の影響力は O-H 結合のケースよりも 小さい。
もし K+ イオンが カリウムチャネルの孔と強固に結合してしまうと、その孔が ふさがって通れなくなってしまう。
よって 3.0 Å の K-O 長は 生体システムにとって適切な距離と言える。
(Fig.18) PDB データバンク - ミオグロビン。

ミオグロビンは ヘモグロビンのように 中心に 鉄イオン ( Fe2+ ) があるポルフィリン体 からなる 酸素結合蛋白である。
そのため 強力な酸素に攻撃されても Fe2+ を持つミオグロビンの構造は 安定でなくてはならない。
PDB サイトで "1MBN" (= ミオグロビン PDB ID ) を検索して、 Display File をクリックし、その PDB データをセーブして、通常の RasMol を用いて可視化する。
155 番目の残基が Fe 原子である。"select" コマンドを用いて Fe2+ イオンから 4.0 Å 以下の部分を表示させる。
他の値は 各原子の ( x, y, z ) 座標 (= Å ) である。
(Fig.19) Fe2+ イオンと N、 O 原子。
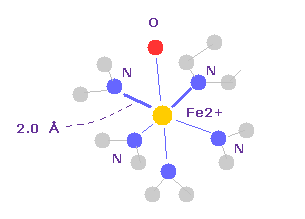
Fe2+ は 6つの価電子を持ち、他の 5つの 窒素原子 と 酸素原子 とで 八面体構造を形成する。
八面体構造は 金属錯体では 非常に頻繁に登場する構造である。
これはつまり 架空の s, p, d 軌道の代わりに、古典的なクーロン力が 常に重要な役割を果たしていることを意味している。
1つの Fe と その周囲の窒素原子の1つをクリックすると、N-O の距離が 約 2.0 Å であることがわかる。
(Fig.20) 窒素の e3 に作用する力。
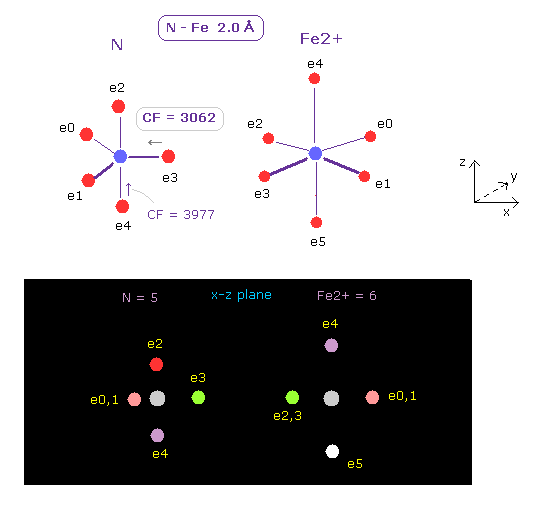
このプログラムを実行後、 A,B原子として それぞれ N (= 窒素 ) と Fe2+ (= 鉄イオン ) を選択する。
そして 核間距離を 2.00 Å ( internuc = 20000 MM ) にする。
鉄イオン (= Fe2+ ) は 6つの価電子を持つ。
上記と同様に、Fe2+ の電子軌道の半径 (= 0.8264 Å ) と その中心電荷 (= 11.91 ) を App. 1 の 3-8th のイオン化エネルギーを用いて求める。
Fig.20 に示すように、 Fe2+ の正電荷による力は 非常に強いため CF (= e3 電子に作用する力の N 原子核方向への力 ) は 3062 に減少する。
(Fig.21) 窒素の e3 に作用する力の比較。
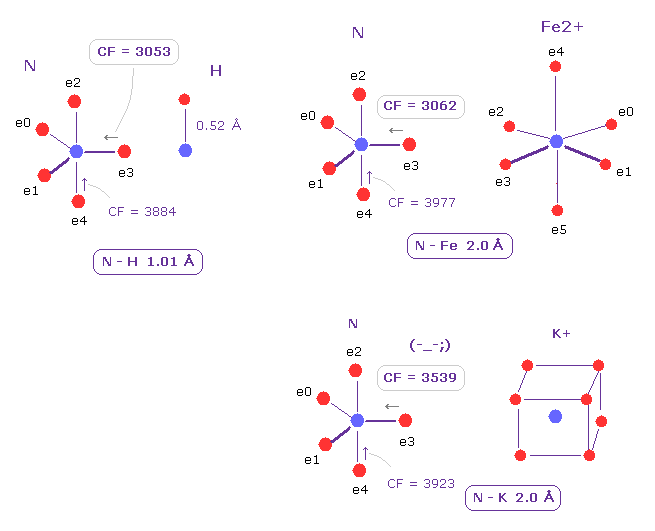
A、B atom として ( N,H )、 ( N, Fe2+ )、 ( N, K+ ) を選んで 窒素の価電子 e3 に対する 影響を調べた。
Fig.21 に示したように、 N-Fe2+ 結合は e3 に作用する CF に関して 通常の N-H 結合と ほぼ 同じである ( それぞれ CF = 3062, 3053 )。
これはつまり Fe2+ は 窒素と "固い" 共有結合をして 非常に安定だということを表している。
一方で Fe2+ を K+ イオンに変えると、 e3 電子に対する影響力は 弱くなる。
つまり Fe2+ は その 大きな正電荷のために 蛋白の形態に 非常に大きな 影響力を持っている。
(Fig.22) 酸素の "e1" 電子に作用する 力 (= CF )。
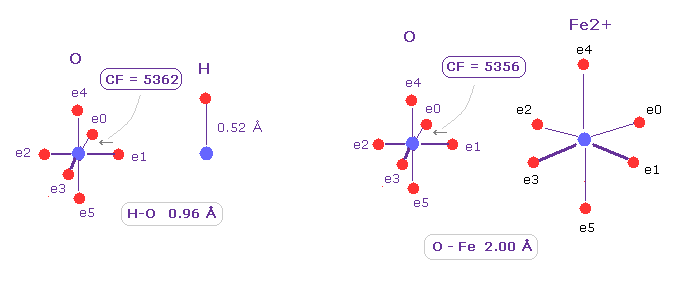
酸素との結合においても、 Fe-O は 共有結合様である。
A, B atom として、 ( O,H )、 ( O Fe2+ ) を選んで、 O 原子を x-y 平面上で 45°回転させる。
Fig.22 に示したように、酸素の価電子 e1 に作用する力は O-H、O-Fe 結合で ほぼ同じである ( それぞれ 5362, 5356 )。
結論からして、 Fe2+ イオンは ミオグロビン や ヘモグロビン において 窒素や酸素原子と タイトな共有結合を形成し、他の酸素から攻撃されても 安定していられる。
(Fig.23) 酸素の "e1" 電子に作用する力 (= CF ) の比較。
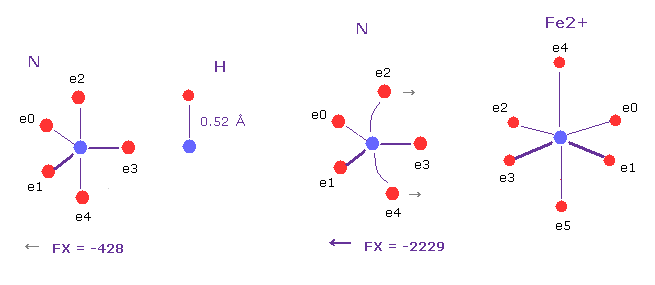
基本的に 大きな正電荷をもつ 金属イオンは タンパク質全体の形態に 大きな影響力を与えている。
上記のケースでは Fe2+ は N の原子核に 大きな正電荷の力を及ぼしている。
( FX =-2229 と N-H 結合の -428 を 比較するように )。
結果的に 電子 e2 と e4 は Fe2+ のほうへ 少し 引きつけられ、他の原子に影響を及ぼす。 ( 試しに それを移動させてみるといい。 )
量子力学は N と O が 非結合電子対を持つため 電子共与体として働くとしている。
しかし Fig.23 を見て分かる通り、電子 e2 と e3 は 明らかに N の原子核を挟んで 反対側にある。
つまり 非常に曖昧な 電子対という概念は ミスリーディングの部分を含んでいるといえる。
基本的に、鉄イオンは 体内では Fe2+ である。
Fe3+ は 他の原子と タイトな結合を形成して 不活性である。
( 例えば Fe2O3 は 非常に安定で 不溶性である。 )
Fe2+ の価電子に作用する力 CF は ほぼ "4000" であり、もう1つ電子を除去する余裕が少しある。
(Fig.24) カルモジュリン - Ca2+ 複合体。
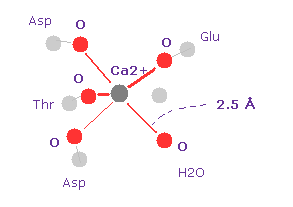
カルモジュリンは カルモジュリン結合タンパク質で カルシウムイオンを結合し 形態変化を起こすことで カルシウムシグナルを伝達することができる。
Fig.24 は カルモジュリンにおける Ca2+ イオン 結合タンパク質である ( PDB id = 1CLL )。
Ca2+ と 酸素原子の距離は 約 2.5 Å である。
このプログラムを実行後、A, B atom として O と Ca2+ 原子を選択する。
核間距離を 2.5 Å (= 25000 MM ) として、酸素を x-y 平面上で 45°回転させる。
(Fig.25) Ca2+ は "中間の" 影響力を持つ。
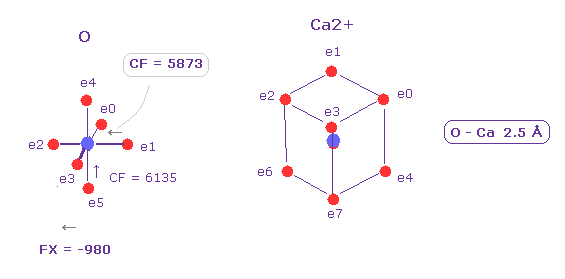
Ca2+ は 8つの価電子を持ち、"3" ドブロイ波長である。
同様に、 全イオン化エネルギーから その半径 (= 0.5277 Å ) と 中心電荷 (= 11.494 ) を計算する。
Fig.25 に示したように、 Ca2+ イオンは K+ と Fe2+ イオンの 中間の影響力を持つと言える。
他の O 原子核に作用する力は FX = 980 で、これは 475 (= K+, Fig.12) と 2000 (= Fe2+, Fig.23) の中間である。
e1 の価電子に作用する CF は 5873 で、これは 6002 (= K+, Fig.17 ) と 5356 (= Fe2+, Fig.22 ) の間ぐらいである。
つまり カルシウムイオンは 共有結合を形成するだけの力は ない ( 閉殻性の 8 電子も考慮して ) が、タンパク質の形態を 変化させ、迅速な シグナル伝達を生じさせると言える。
もし それらが酸素にくっついて 共有結合を形成してしまったら、それは シグナル伝達できない。
(Fig.26) クロロフィルの Mg2+ イオン。
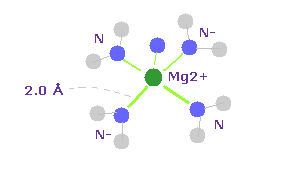
マグネシウムシオン (= Mg2+ ) は クロロフィルで使用され、 光を吸収して 光合成を起こす。
Fig.26 に示したように、 Mg2+ イオンと 周囲の N 原子の距離は 約 2.0 Å である ( PDB id= 2BHW )。
Mg は 2つの価電子を持ち、それらは 周囲の 窒素原子によって 容易に引きはがされる。
結果的に Mg2+ は ネオンのように 8つの価電子を持つ。
この イオン化エネルギーを用いて 軌道半径などを計算している。
(Fig.27) Mg2+ イオンによる影響力。
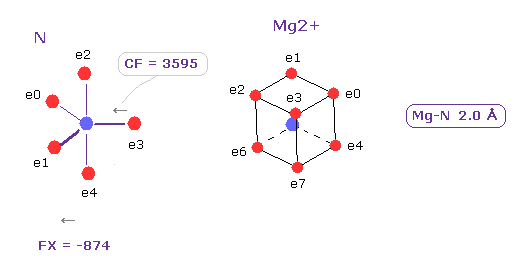
このプログラムを実行して、 A、B atom として N と Mg2+ を選択し、核間距離を 2.0 Å (= 20000 MM ) にする。
Mg2+ の影響力は 通常の共有結合よりも弱い。
CF = 3595 を Fe2+ (= 3062, Fig.21 ) と比較してみるといい。
実際に Mg-N 結合は 不安定で、 ある状況下で Mg は 容易に 他の原子に置き換わってしまう。
(Fig.28) どうしてマグネシウムなのか?
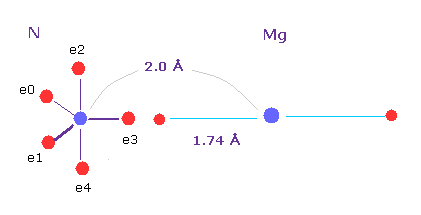
中性の "Mg" を選ぶと、Mg 原子核と その価電子間の距離は 1.74 Å で、それは Mg-N 距離 (= 2.0 Å ) と ほぼ同じである。
マグネシウムの2つの価電子は Mg から 容易に離れて これらの電子は 光合成における エネルギー伝達に使用される。
結果的に、Mg2+ の中間的な力、2つの緩い結合、光の吸収 などを考慮して Mg が クロロフィルとして選べばれたと 思われる。
(Fig.29) ジンクフィンガーにおける Zn2+ イオン。
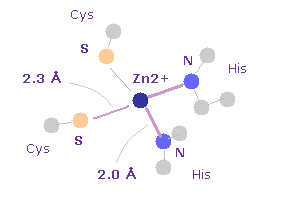
基本的に 小さいタンパク質は 他のタンパク質を用いて 疎水性部分を覆うことができないため、非常に不安定である。
ジンクフィンガータンパク質は 非常に小さいにも関わらず、それらは非常に安定である。なぜなら 亜鉛イオンが それらの形体を安定に保つ役割をはたしているからである。
Fig.29 に示したように、 Zn2+ イオンと 周囲の N 原子との距離は 約 2.0 Å ( PDB id= 1ZAA ) である。
Zn は 12 の価電子を持つため、 Zn2+ は 10 の価電子を持つことになる。
これらの イオン化エネルギーを用いて 軌道半径を計算する。
(Fig.30) Zn2+ イオンによる影響力。
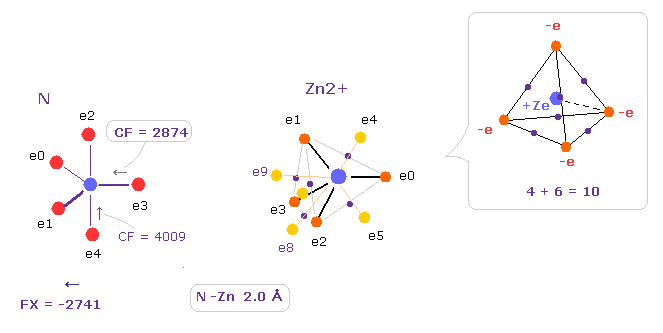
このプログラムを実行後、 A,B atom として N と Zn2+ を選択し、核間距離を 2.0 Å (= 20000 MM ) にする。
10 の価電子は 正四面体の 4つの頂点と 6つの各辺の中点を延長させたところに配置させる。
Zn+ の影響力は Fe2+ イオンよりも強い。
CF = 2874 を Fe2+ (= 3062, Fig.21 ) のと比較するといい。
これはつまり 窒素の e3 電子は Fe2+ よりも Zn2+ に より引きつけられていると言える。
(Fig.31) Zn2+ イオンの 硫黄に対する力。
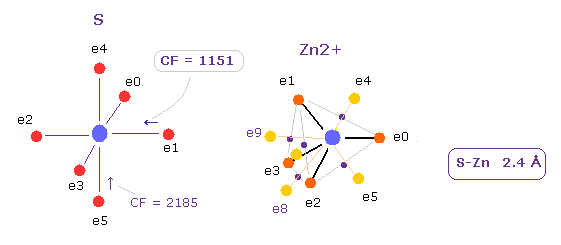
S と Zn2+ 間の距離は 2.4 Å である。
このケースでは e1 電子に作用する力の S 原子核方向への成分は CF = 1151 となる。
この値は Zn2+ イオンの引きつけ力が 非常に強いことを意味している。
(Fig.32) N=C、 S=C 2重結合。
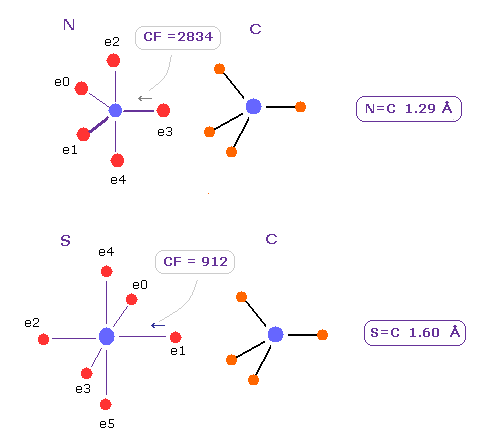
Zn2+ イオンの 窒素と硫黄に作用する力は N=C、S=C の 2重結合に 似ている。
N=C の CF は 2834 で、 これは Fig.30 の N-Zn 結合の 2874 に近い。
S=C の CF は 912 で、 これも Fig.31 の S-Zn における 1151 に近い。
それらの違いは Zn2+ イオンが 大きな正電荷を持つため、その影響力が 広範囲に及び、タンパク質全体の構造変化を生じさせるという点である。
つまり、亜鉛金属の 引きつけ力は 様々な厳しい状況下においても 小さな亜鉛結合タンパク質の構造を保つ キープレイヤーと言える。
(Fig.33) ヘモシアニンにおける Cu。
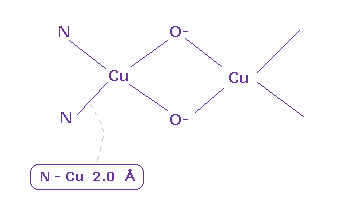
ヘモシアニンは 非脊椎動物などで 酸素を体内で運搬する役目を果たしている。
基本的に 銅は Cu+ として存在し、酸素が それに結合すると Cu2+ イオン になる。
タンパク質の構造データ ( PBD id = 1LNL ) によると、 平均の Cu-N (= 窒素 ) 結合長は 2.0 Å である。
(Fig.34) Cu+ イオンの 窒素に対する力。
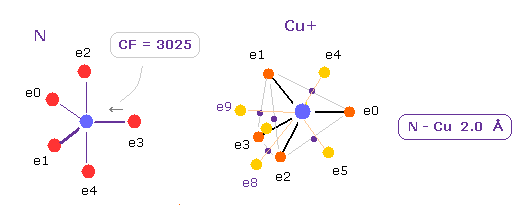
Cu は 11 の価電子を持つため、 Cu+ イオンは 10 の価電子があることになる。
おそらく この "10" という数は 対称的で安定な ( Fig.30 参照のこと ) 電子配置に関係していると思われる。
Fig.34 に示したように、e3 電子に作用する力 CF は Cu2+ の引きつけ力のために CF= 3025 に減少している。
この 3025 の値は Fe2+ のケースの CF= 3062 に非常に似ている ( Fig.21 も参照のこと )。
つまり Cu+ は Fe2+ イオンと ほぼ同じ性質があることになる。
もし Cu+ を Cu2+ に変えると、 この CF は 2950 に少し減少する。
(Fig.35) 様々な金属イオン。
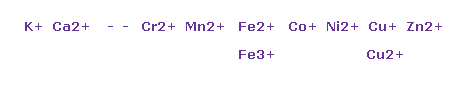
金属では "+2" イオンが 最もポピュラーなイオン形態である。
基本的に "4" 周期の原子では 中心電荷による 価電子を引きつける力は 弱くなる。なぜなら その軌道半径が 長い からである (= "4" ドブロイ波長 )。
そのため 各原子は これらの弱い結合力のために 2つの価電子ぐらいまで 放出することが可能である。
3、もしくは 4つの価電子まで 引き放つことは それらの大きな正電荷のため 難しくなる。
銅は Cu+ イオン、Zn は Zn2+ イオンになる傾向がある。
これらは Fig.30 に示したように "10" の電子の 対称的な構造に関係しているからと言える。
マンガン (= Mn )、 ニッケル (= Ni )、セレン (= Se ) なども SOD や ウレアーゼなどの 様々な酵素で使用されている。
上記のプログラムを用いて これらの機能を調べてみるといい。
8つより多くの価電子があるとき、"ele No" ボタンをクリックすると、9番目以上の電子情報がテキストに表示される。
"+X (MM)" ボタンをクリックすると、操作できる 電子が 制限される。
"ele" のワードがついた電子のみ 操作でき、他の電子は それを元に 対称的な位置に移動する。
"A nuc" ボタンをクリックすると、各原子核に作用する力の表示されている値が変化する。
基本的に表示されている力の成分 (= FX, FY, FX ) は A と B の原子両方の核と電子を考慮した結果の値である。
"A only" のときは、A 原子内のみの 電子と核のみを考慮したときの A 原子核に作用する力成分である。
"x-y and"、 "x-z ang"、 "y-z ang" ボタンを押すと、 x-y、 x-z、 y-z 平面上で 指定された角度だけ 原子を回転させる。
"A-tV" と "B-tV" は それぞれ A 原子内のみ もしくは B 原子内のみ で計算したときの 全ポテンシャルエネルギーである。
"AB change" ボタンをクリックすると、 A と B 原子 どちらをテキストに表示させるか変更できる。
他の方法は このページと同じである。
| 原子 | 1st | 2nd | 3rd | 4th | 5th | 6th | 7th | 8th | 9th | 10th | 11th | 12th | Total |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| H | 13.606 | - | - | - | - | - | - | - | - | - | - | - | 13.606 |
| Be | 9.323 | 18.211 | - | - | - | - | - | - | - | - | - | - | 27.534 |
| B | 8.298 | 25.155 | 37.931 | - | - | - | - | - | - | - | - | - | 71.384 |
| C | 11.260 | 24.383 | 47.888 | 64.494 | - | - | - | - | - | - | - | - | 148.025 |
| O | 13.618 | 35.121 | 54.936 | 77.414 | 113.899 | 138.120 | - | - | - | - | - | - | 433.108 |
| F | 17.423 | 34.971 | 62.708 | 87.140 | 114.243 | 157.165 | 185.186 | - | - | - | - | - | 658.836 |
| Ne | 21.565 | 40.963 | 63.45 | 97.12 | 126.21 | 157.93 | 207.276 | 239.100 | - | - | - | - | 953.614 |
| Na | 5.139 | - | - | - | - | - | - | - | - | - | - | - | 5.139 |
| Na+ | - | 47.286 | 71.62 | 98.91 | 138.4 | 172.18 | 208.50 | 264.25 | 299.864 | - | - | - | 1301.01 |
| Mg | 7.646 | 15.035 | - | - | - | - | - | - | - | - | - | - | 22.681 |
| Mg2+ | - | - | 80.144 | 109.266 | 141.27 | 186.76 | 225.02 | 265.96 | 328.06 | 367.50 | - | - | 1703.98 |
| Al | 5.986 | 18.829 | 28.448 | - | - | - | - | - | - | - | - | - | 53.263 |
| Al3+ | - | - | - | 119.992 | 153.825 | 190.49 | 241.76 | 284.66 | 330.13 | 398.75 | 442.00 | - | 2161.607 |
| Si | 8.152 | 16.346 | 33.49 | 45.142 | - | - | - | - | - | - | - | - | 103.13 |
| P | 10.487 | 19.77 | 30.202 | 51.444 | 65.025 | - | - | - | - | - | - | - | 176.928 |
| S | 10.36 | 23.338 | 34.79 | 47.222 | 72.595 | 88.053 | - | - | - | - | - | - | 276.358 |
| Cl | 12.968 | 23.814 | 39.61 | 53.465 | 67.8 | 97.03 | 114.196 | - | - | - | - | - | 408.883 |
| 原子 | 1st | 2nd | 3rd | 4th | 5th | 6th | 7th | 8th | 9th | 10th | 11th | 12th | Total |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| K | 4.341 | - | - | - | - | - | - | - | - | - | - | - | 4.341 |
| K+ | - | 31.63 | 45.806 | 60.91 | 82.66 | 99.4 | 117.56 | 154.88 | 175.817 | - | - | - | 768.663 |
| Ca | 6.113 | 11.872 | - | - | - | - | - | - | - | - | - | - | 17.985 |
| Ca2+ | - | - | 50.913 | 67.27 | 84.50 | 108.78 | 127.2 | 147.24 | 188.54 | 211.275 | - | - | 985.718 |
| Ti | 6.828 | 13.576 | 27.492 | 43.267 | - | - | - | - | - | - | - | - | 91.163 |
| Cr | 6.767 | 16.486 | 30.96 | 49.16 | 69.46 | 90.635 | - | - | - | - | - | - | 263.468 |
| Cr2+ | - | - | 30.96 | 49.16 | 69.46 | 90.635 | - | - | - | - | - | - | 240.125 |
| Mn | 7.434 | 15.64 | 33.668 | 51.2 | 72.4 | 95.6 | 119.203 | - | - | - | - | - | 395.145 |
| Mn2+ | - | - | 33.668 | 51.2 | 72.4 | 95.6 | 119.203 | - | - | - | - | - | 372.071 |
| Fe | 7.902 | 16.188 | 30.652 | 54.8 | 75.0 | 99.1 | 124.98 | 151.06 | - | - | - | - | 559.682 |
| Fe2+ | - | - | 30.652 | 54.8 | 75.0 | 99.1 | 124.98 | 151.06 | - | - | - | - | 535.592 |
| Fe3+ | - | - | - | 54.8 | 75.0 | 99.1 | 124.98 | 151.06 | - | - | - | - | 504.94 |
| Co | 7.881 | 17.084 | 33.50 | 51.3 | 79.5 | 102.0 | 128.9 | 157.8 | 186.13 | - | - | - | 764.095 |
| Co+ | - | 17.084 | 33.50 | 51.3 | 79.5 | 102.0 | 128.9 | 157.8 | 186.13 | - | - | - | 756.214 |
| Ni | 7.640 | 18.169 | 35.19 | 54.9 | 76.06 | 108 | 133 | 162 | 193 | 224.6 | - | - | 1012.559 |
| Ni2+ | - | - | 35.19 | 54.9 | 76.06 | 108 | 133 | 162 | 193 | 224.6 | - | - | 986.75 |
| Cu | 7.726 | 20.292 | 36.841 | 57.38 | 79.8 | 103 | 139 | 166 | 199 | 232 | 265.3 | - | 1306.339 |
| Cu+ | - | 20.292 | 36.841 | 57.38 | 79.8 | 103 | 139 | 166 | 199 | 232 | 265.3 | - | 1298.613 |
| Cu2+ | - | - | 36.841 | 57.38 | 79.8 | 103 | 139 | 166 | 199 | 232 | 265.3 | - | 1278.321 |
| Zn | 9.394 | 17.964 | 39.723 | 59.4 | 82.6 | 108 | 134 | 174 | 203 | 238 | 274 | 310.8 | 1650.88 |
| Zn2+ | - | - | 39.723 | 59.4 | 82.6 | 108 | 134 | 174 | 203 | 238 | 274 | 310.8 | 1623.522 |

2013/6/3 updated This site is link free.