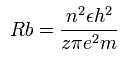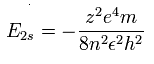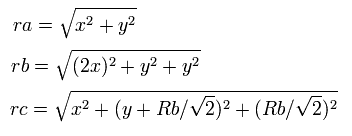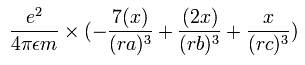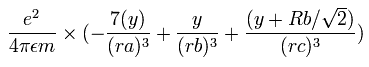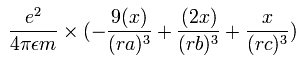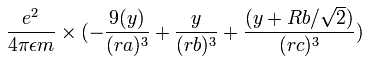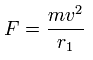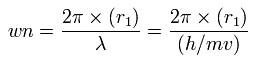新しいボーア模型によるフッ素と窒素( F, N )
トップページ (2電子原子も含む正確な新ボーア模型)
電子スピンは実在しない
我々の新しいボーア模型によって、ヘリウム原子の基底状態エネルギーの計算で、量子力学的な変分法よりも正確な結果をだすのに成功した。(トップページ参照のこと)。
この成功した新ボーア模型では、ヘリウム原子 (He) の2つの電子は、ちょうど1ド・ブロイ波長の互いに垂直な軌道上を運動している。
また、この新しい原子模型は、パウリの排他原理の現象も正確に説明できる。なぜなら、この新しいボーアの2電子原子には、3つめの電子が入りこむスペースがないからだ。
驚くべきことに、この新しいボーアのヘリウム構造は、他の2電子原子(イオン)である、リチウムイオン (Li+)、ベリリウムイオン (Be2+)、ホウ素イオン (B3+)、炭素イオン (C4+) にも正確にあてはめることができた。
(このページを参照のこと。)
さらに、3電子原子である、リチウム原子 (Li) のイオン化(基底状態の)エネルギーも、近似的なボーア模型の”2S”軌道を使用して、計算することができた。(このページも参照のこと。)
ボーア模型の窒素イオン (N 4+)
ここでは、、3電子原子である窒素イオン (N4+) を使って、窒素の3番目の電子が2 × ド・ブロイ波長の軌道に入ることを確かめることにする。
窒素イオン (N4+) は、1S軌道に2つの電子と、2S軌道に1つの電子をもっている。
1Sの2つの電子は、7e+ の原子核に強くひきつけられているため、2S の電子に比べてかなり原子核に距離的に近いところにある。
つまり、近似的に、我々は2S電子が、 +5e 原子核 (+7e - 2e = +4e) の周りの2ド・ブロイ波長の円軌道を回っているとみなすことができる。
(これは、我々が2S電子において、近似的に水素原子の式を使えることを意味する。)
ボーア模型によれば、n × ド・ブロイ波長の軌道の半径 (Rb) は、次のように なる。
(Eq.1)
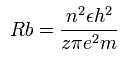
( z = 1 と n = 1 のとき、 Rb はいわゆる”ボーア半径”となる。)
N4+ の 2S 電子では、原子核の陽電荷 z は、5+ と近似的にみなすことができ(上を参照)、また、n は 2 である。
計算すると、この Rb は 4/5 × ボーア半径 ( = 0.4233 × 10-10 meter ( = 4233 MM ) となる。
(ここでは、便宜のため次のような新しい単位を使う。 1 MM = 10-14 meter, 1 SS = 10-22 second, 1 MM/SS = 108 m/s.)
水素様原子のエネルギー準位は、
(Eq.2)
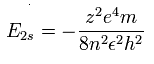
N4+ の 2S 電子では、n=2 と z=5 をこの式に代入する。
そのため、窒素イオン (N4+) の原子模型をつぎのように仮定できる。
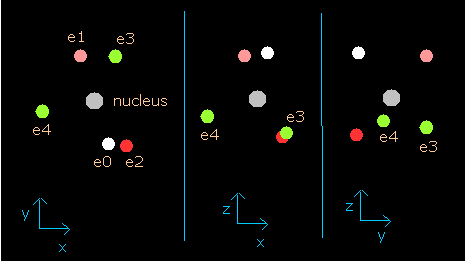
Fig. 1. 窒素イオン (N4+) 模型
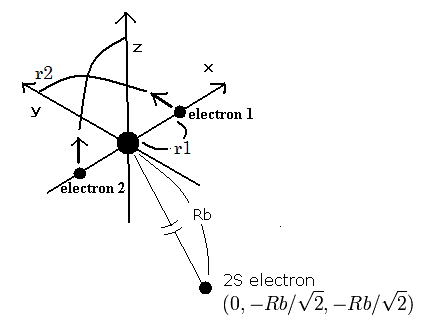
1Sの2つの電子はなるべく2S電子を避けるように運動する。そこで、我々は2S電子を Fig. 1. に示すように ( 0, - Rb / √2, - Rb / √2 ) に固定する。
(Fig.1 は3つの電子の相対的な位置関係を示している。実際は、この2Sの電子は1Sの電子よりもゆっくりと核の周りを周回している。)
このページのように、電子1が、(x, y, 0) にあるとき、電子2は、 (-x, 0, y) にある。
つまり、各粒子間の距離は、
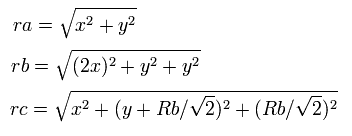
となる、ここで、ra は電子1と核の距離、rb は2つの 1S 電子間の距離、rc は電子1と 2S の電子の距離である。
電子1の加速度 (m/sec2) の x成分は、
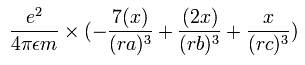
となる。
同様に、電子1の加速度 (m/sec2) の y成分は、
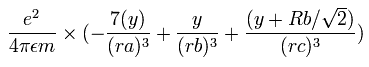
となる。
また、他の2電子原子のときのように、1S 軌道の 1/4 周に含まれるド・ブロイ波の数を計算する。
サンプルJAVAプログラム (N4+)
中に示すプログラムをメモ帳などのテキストエディタにコピーして貼り付ければ、簡単にコンパイルして実行できる。
このクラスファイル名は、MathMethod なので、このテキストエディタを "MathMethod.java" として保存してコンパイルするといい。
Table 1. Ionization energies of the nitrogen atom (eV).
(Experimental values.)
| Name | 1st | 2nd | 3rd | 4th | 5th | 6th | 7th |
|---|
| Nitogen (N) | 14.53 | 29.60 | 47.45 | 77.47 | 97.89 | 552.07 | 667.046 |
窒素イオン (N4+) の基底状態エネルギーは、5-7th のイオン化エネルギーの和である。
(-97.89 - 552.07 - 667.046 = - 1317.0 eV)
Table 2 は、N4+ において、 last VY (電子1が 1/4 周した後の速度の y 成分)がゼロに一番近い時の結果を示す。
Table.2. last VY がゼロのときの r1 と WN の結果 (N4+)。.
| E (eV) | r1 (MM) | WN | WN x 4 |
|---|
| -1300.0 | 800.0 | 0.25151 | 1.00604 |
| -1305.0 | 796.0 | 0.25099 | 1.00396 |
| -1310.0 | 793.0 | 0.25048 | 1.00192 |
| -1314.5 | 790.0 | 0.25000 | 1.00000 |
| -1320.0 | 786.5 | 0.24945 | 0.99780 |
| -1325.0 | 783.5 | 0.24894 | 0.99576 |
| -1330.0 | 780.0 | 0.24844 | 0.99376 |
この結果は、N4+ イオンの基底状態エネルギーが -1314.5 eV のとき、軌道の長さがド・ブロイ波長の ちょうど 1.00000 倍になることを示している。
窒素イオン (N4+) エネルギーの実験値は -1317.0 eV である。
つまり、計算誤差は、わずか 2.5 eV ( 0.19 % ) である。
(この小さな計算誤差は、おそらく、”近似的な”2S電子軌道を用いたことによると考えられる。)
このことは、窒素イオン (N4+) の3つの電子が、 Fig.1 に示すように運動していると言ってほぼ間違いないということを意味する。
ボーア模型のフッ素イオン (F 6+)
次に、3電子原子であるフッ素イオン (F6+) を使って、フッ素の3番目の電子が2 × ド・ブロイ波長の軌道に入ることを確かめることにする。
上のセクションのように、F6+ の 2S 電子が +7e の核 ( +9e - 2e = +7e ) の周りの2ド・ブロイ波長の円軌道を回っているとみなすことができる。
(これは、我々が2S電子において、近似的に水素原子の式を使えることを意味する。)
F6+ の 2S 電子では、原子核の陽電荷 z は、+7 と近似的にみなすことができ(上を参照)、また、n は 2 である。
Eq.1 で計算すると、Rb は 4/7 × ボーア半径 ( = 0.3024 × 10-10 meter ( = 3024 MM ) となる。
また、z=7 と n=2 を Eq.2 に代入すると、F6+ の 2S 電子の近似的なエネルギーを知ることができる。
また3電子のフッ素イオン (F6+) でも Fig.1 の模型を使うことができる。
このページのように、電子1が、(x, y, 0) にあるとき、電子2は、 (-x, 0, y) にある。
つまり、各粒子間の距離は、
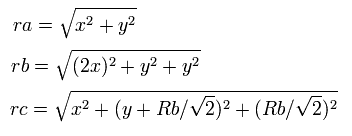
となる、ここで、ra は電子1と核の距離、rb は2つの 1S 電子間の距離、rc は電子1と 2S の電子の距離である。
電子1の加速度 (m/sec2) の x成分は、
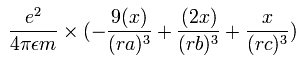
となる。
同様に、電子1の加速度 (m/sec2) の y成分は、
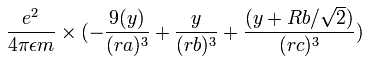
となる。
また、他の2電子原子のときのように、1S 軌道の 1/4 周に含まれるド・ブロイ波の数を計算する。
サンプルJAVAプログラム (F6+)
中に示すプログラムをメモ帳などのテキストエディタにコピーして貼り付ければ、簡単にコンパイルして実行できる。
このクラスファイル名は、MathMethod なので、このテキストエディタを "MathMethod.java" として保存してコンパイルするといい。
Table 3. Ionization energies of the fluorine atom (eV).
(Experimental values.)
| Name | 1st | 2nd | 3rd | 4th | 5th | 6th | 7th | 8th | 9th |
|---|
| Fluorine (F) | 17.42 | 34.97 | 62.71 | 87.14 | 114.24 | 157.16 | 185.18 | 953.91 | 1103.12 |
フッ素イオン (F6+) の基底状態エネルギーは、7-9th のイオン化エネルギーの和である。
(-185.18 - 953.91 - 1103.12 = - 2242.2 eV)
Table 4 は、F6+ において、 last VY (電子1が 1/4 周した後の速度の y 成分)がゼロに一番近い時の結果を示す。
Table.4. last VY がゼロのときの r1 と WN の結果 (F6+)。.
| E (eV) | r1 (MM) | WN | WN x 4 |
|---|
| -2225.0 | 613.0 | 0.25083 | 1.00332 |
| -2230.0 | 611.0 | 0.25052 | 1.00208 |
| -2235.0 | 610.0 | 0.25023 | 1.00092 |
| -2238.7 | 608.5 | 0.25000 | 1.00000 |
| -2245.0 | 607.0 | 0.24958 | 0.99832 |
| -2250.0 | 605.5 | 0.24931 | 0.99724 |
| -2255.0 | 604.0 | 0.24898 | 0.99592 |
この結果は、F6+ イオンの基底状態エネルギーが -2238.7 eV のとき、軌道の長さがド・ブロイ波長の ちょうど 1.00000 倍になることを示している。
フッ素イオン (F6+) エネルギーの実験値は -2242.2 eV である。
つまり、計算誤差は、わずか 3.5 eV ( 0.15 % ) である。
(この小さな計算誤差は、おそらく、”近似的な”2S電子軌道を用いたことによると考えられる。)
このことは、フッ素イオン (F6+) の3つの電子が、 Fig.1 に示すように運動していると言ってほぼ間違いないということを意味する。
ボーア模型の窒素 (N) の5つの価電子の配置
中性の窒素 (N) 原子においては、5つの外殻電子はどのように運動しているのだろうか?
窒素原子は7つの電子をもち、そのうちの2つの 1S 電子は核にとても近づいている。(上の N4+ の項を参照のこと。)
つまり、近似的我々はこれらの5つの電子は1つの +5e の中心核 (+7e-2e = +5e) の周囲を周っていると仮定できる。
(ここでは、5つの価電子の全エネルギーは -266.94 eV = 1-5th のイオン化エネルギーの和 と仮定できる。)
炭素原子模型では、我々は 炭素のページに示すように、”正四面体”の構造を用いて表現するのに成功した。
このプログラムでは、微小時間 (1 SS) ごとに、電子群と原子核の間のクーロン力を計算し、それに基づき各速度ベクトルを変化させていく。
また、各電子において、微小区間に含まれるド・ブロイ波の数を計算し足していく。
中心の正電荷が +4.0e (= + 6e - 2e) のとき、外殻電子の軌道長が 1.9 になる。
しかし、炭素の2つの 1S 電子は約 930 MM ほど +6e の炭素原子核から離れている。(それらは核にくっついていない。)
つまり、4つの価電子に影響を与える "実質的"正電荷は +4.0eよりも少し大きい。
そのためこの中心の正電荷を +4.0e よりも少し大きい +4.25e に変化させた。
(イオン化されて価電子が減るにつれて、残った価電子はより +6.0e の原子核に近づく。つまりこの効果は特に炭素の 3rd や 4th のイオン化エネルギーの値に含まれる。)
軌道長がちょうど 2.0 ド・ブロイ波長になったとき、炭素の4つのすべての価電子は次に示すようにほぼ元の位置に戻ることができる。
Fig. 2. 波が wn = 0.0 と wn = 2.0 における炭素の電子 ("実質的"電荷 = +4.25e)
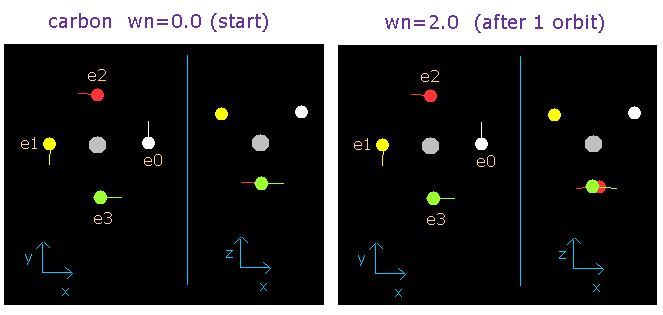
さらに、ビリアル定理を用いてこのことを証明できた。
Fig. 3. 炭素の価電子 ("実質的"電荷 = +Ze)
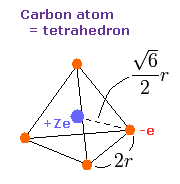
Z = +4.0 のとき、この wn は 1.87 (ほぼ 1.9) になった。
また、Z = +4.25 のとき、この wn は ちょうど 2.02 となった。
窒素原子では、炭素原子のように電子の運動をイメージ化することは 非常に難しい。
窒素は 5つの価電子を持つため、炭素(正四面体)、酸素(正八面体)、ネオン(正六面体)のようないわゆる”正多面体”で表現することができない。
そこで、我々は、次に示すサンプルプログラムを使って窒素の5つの価電子の”対称的な”配置を探すことにする。
サンプル JAVA プログラム (N の価電子の配置)
このプログラムは少し長いので、中に示すソースプログラムをコピーして、テキストエディタ(メモ帳など)にそのまま貼り付けて、コンパイルすれば簡単に実行できる。
このプログラムの class file name は Nit なので、このデキストエディタを "Nit.java" のファイル名で保存してコンパイルしてほしい。
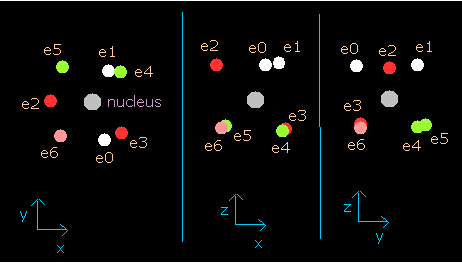
Fig.4 窒素における5つの価電子の配置 (中心電荷 = +5.25e)
窒素原子 (N) においても、2つの 1S 電子は N の +7e の核から少し離れている。
そのため、この図の”実質的”中心電荷は +5e ( = +7e -2e ) よりも少し大きい。
(ここでは炭素の場合のように +0.25e だけ大きい +5.25e を使う。)
このプログラムでは、窒素原子核は灰色の円で示してある。
ここでは、新しい単位として ( 1 MM = 10-14 meter) を使っている。
テキストボックス内の電子の各座標 (+X (MM), +Y (MM), +Z (MM)) は、この原子核からの”相対的な”位置座標を示している。
"nuc (MM)" は各電子と核の距離を意味している。(すべての価電子で同じになるようにしてある。)
(このテキストボックス内に値を入力して、エンターキーを押せば自由にこれら の値を変更できる。)
V (eV) と T (eV) は各電子の位置と運動エネルギーを意味している。
CF は各電子に作用する力の核方向の成分の量を表している。
(fx, fy, fz) は各電子に作用する力から、上の CF を除いた残りの力の各成分を表している。
最後の行の (FX, FY, FZ) は核に作用する力の各成分を表している。
(力の単位は、+e の原子核と -e の電子がボーア半径離れているときに、その間に働く力の大きさを 1000 としている。)
最後の行の tV は全位置エネルギー (eV) を意味する。
Waves (wn) は 各電子の 1 軌道に含まれるド・ブロイ波の数を表している。
ビリアル定理によれば、”平均的な”全位置 (V) と 運動 (T) エネルギーは次の関係式を満たす。
< V > = -2 × < T > , E = V + T
窒素の5つの価電子の全エネルギーは -266.94 eV ( = 1-5th のイオン化エネルギーの和) であるため、この位置エネルギー (V) は 2 × -266.94 = -533.88 eV となる。
核の周囲に 対称的に配置されるためには、すべての価電子において、電子と核との距離がそろう必要がある。
このプログラムでは、各電子に作用する力 (F) を CF (核方向の成分) と (fx,fy,fz) に分離する。
つまり (fx, fy, fz) は CF を除いた残りの力であり、これはなるべく小さくなる必要がある。
我々はこれらの座標や nuc の値を変化させながら、これらの条件を満たすことを目指す。
この各電子に働く力 (F) の値を元に、我々は次のように "仮の"半径 (r1) を定義する。
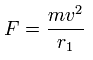
(これは、”仮の”遠心力が F と等しいことを意味する。)
ここで、m は電子の質量、v は各運動エネルギーを基に導かれる電子の速度である。
これらの値を基に、各電子の1軌道に含まれるド・ブロイ波の値 (wn) を次のように導く。
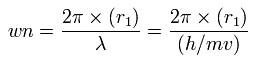
Table 5 に示すように、窒素の価電子の全位置エネルギー (tV) が - 533.89 eV のときに各電子の wn (Waves) は、ほぼ 2.0 となる。
Table.5. 窒素の価電子の各パラメーター (tV=-533.89 eV).
| eNo. | +X (MM) | +Y (MM) | +Z (MM) | nuc (MM) | CF | fx | fy | fz | Waves |
|---|
| ele 0 | 1128 | -3324 | 4013 | 5332 | 3759 | 5 | 11 | 7 | 1.995 |
| ele 1 | -904 | 3746 | 3684 | 5332 | 3750 | -11 | 0 | -2 | 1.985 |
| ele 2 | 2260 | -3618 | -3198 | 5332 | 3746 | -7 | 4 | -9 | 1.98 |
| ele 3 | 2439 | 3754 | -2895 | 5331 | 3761 | 11 | 0 | 9 | 1.997 |
| ele 4 | -5019 | -629 | -1686 | 5332 | 3783 | -2 | 2 | 7 | 2.02 |
これらの座標 (+X, +Y, +Z) や nuc (MM) は自由に変更できる。
(nuc が変化すると、すべての電子のこれらの値 (nuc) は自動的に同じにそろう。)
試しにこれらの値を変化させてみると分かるが、全位置エネルギーが -533.89 eV のとき、ド・ブロイ波 (Waves) はほぼ 2.0 となることがわかる。
この結果は、窒素の5つの価電子すべてが 2ド・ブロイ波長の軌道上を運動していることを示している。
この場合では、核に作用する力の各成分は、(FX, FY, FZ) = (-89, -66, -76) でこれらの値は小さい。
(力の単位は、+e の原子核と -e の電子がボーア半径離れているときに、その間に働く力の大きさを 1000 としている。)
もちろん、各電子の (fx, fy, fz) は平衡状態ではとても小さくなる必要がある。
(このプログラムを実際に実行して、よりふさわしい電子の配置状態(構造)を誰か見つけてくれると非常にうれしいが・・。)
ボーア模型のフッ素 (F) における7つの価電子の配置
中性のフッ素 (F) においては、7つの外殻電子はどう動いているのだろうか?
中性のフッ素は9つの電子を持ち、そのうちの2つの 1S 電子は核にとても近づいている。(上の F6+ の項を参照のこと。)
つまり、近似的に我々はこれらの7つの電子は1つの +7e の中心核 (+9e-2e = +7e) の周囲を周っていると仮定できる。
(ここでは、7つの価電子の全エネルギーは -658.835 eV = 1-7th のイオン化エネルギーの和 と仮定できる。)
フッ素原子においても、電子の運動をイメージ化することは 非常に難しい。
フッ素は 7つの価電子を持つため、炭素(正四面体)、酸素(正八面体)、ネオン(正六面体)のようないわゆる”正多面体”で表現することができない。
そこで、我々は、次に示すサンプルプログラムを使ってフッ素の7つの価電子の”対称的な”配置を探すことにする。
サンプル JAVA プログラム (F の価電子の配置)
このプログラムは少し長いので、中に示すソースプログラムをコピーして、テキストエディタ(メモ帳など)にそのまま貼り付けて、コンパイルすれば簡単に実行できる。
このプログラムの class file name は Fus なので、このデキストエディタを "Fus.java" のファイル名で保存してコンパイルしてほしい。
Fig.5 フッ素における7つの価電子の配置 (中心電荷 = +7.3e)
フッ素原子 (F) においても、2つの 1S 電子は F の +9e の核から少し離れている。
そのため、この図の”実質的”中心電荷は +7e ( = +9e -2e ) よりも少し大きい。
(ここでは酸素のページ場合のように +0.3e だけ大きい +7.3e を使う。)
Fig. 6. 波が wn = 0.0 と wn = 2.0 における酸素の電子運動 ("実質的" 電荷 = +6.3e)
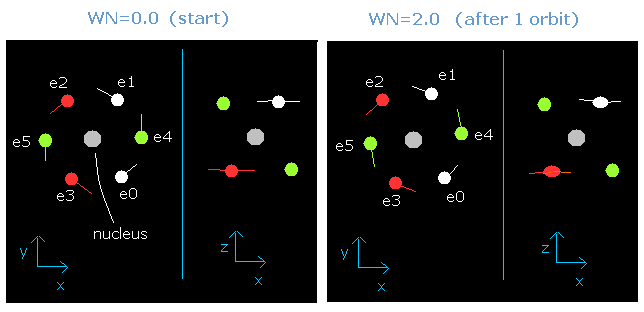
さらに、我々は酸素において、ビリアル定理を用いてこのことを証明できた。
Fig. 7. 酸素の価電子 ("実質的" 電荷 = +Ze)
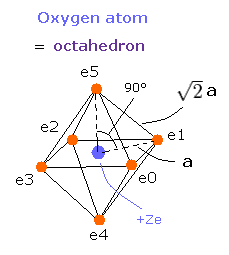
酸素のページに示したように、Z = +6.0 のときに、この wn は 1.88 (ほぼ 1.9) となる。
また、Z = +6.3 のときに、この wn はちょうど 2.01 となった。
+0.3e ( = +6.3e - 6.0e ) は炭素の +0.25e ( = +4.25e - 4.0e ) よりも少し大きい。
価電子がイオン化されて減るにつれて、残りの価電子は +8e の酸素の原子核により近づく。
(そのため、この増加効果は特に酸素の 4-6th のイオン化エネルギーに含まれる。)
おそらく、酸素の電子は、より強い力によって、炭素のよりも核に近づくためと考えられる。
このプログラムでは、フッ素の原子核は灰色の円で示してある。
ここでは新しい単位を使う。( 1 MM = 10-14 meter )。
他の操作や方法は上の窒素のケースと同じである。
ビリアル定理によれば、”平均的な”全位置 (V) と 運動 (T) エネルギーは次の関係式を満たす。
< V > = -2 × < T > , E = V + T
フッ素の7つの価電子の全エネルギーは -658.835 eV ( = 1-7th のイオン化エネルギーの和) であるため、この位置エネルギー (V) は 2 × -658.835 = -1317.67 eV となる。
Table 6 に示すように、フッ素の価電子の全位置エネルギー (tV) が - 1317.77 eV のときに各電子の wn (Waves) は、ほぼ 2.0 となる。
Table 6. フッ素の価電子の各パラメーター (tV=-1317.77 eV).
| eNo. | +X (MM) | +Y (MM) | +Z (MM) | nuc (MM) | CF | fx | fy | fz | Waves |
|---|
| ele 0 | 1003 | -2774 | 2707 | 4004 | 8834 | -8 | 0 | 2 | 1.993 |
| ele 1 | 1656 | 2376 | 2763 | 4003 | 8853 | -1 | 0 | 0 | 2.001 |
| ele 2 | -3137 | 252 | 2475 | 4003 | 8825 | 1 | 0 | 1 | 1.988 |
| ele 3 | 2567 | -2408 | -1907 | 4004 | 8804 | 0 | -1 | 1 | 1.979 |
| ele 4 | 2552 | 2277 | -2081 | 4004 | 8796 | -4 | 0 | -5 | 1.975 |
| ele 5 | -2256 | 2721 | -1879 | 4004 | 8833 | -3 | 1 | 6 | 1.992 |
| ele 6 | -2416 | -2451 | -2045 | 4004 | 8854 | 3 | 0 | -3 | 2.001 |
これらの座標 (+X, +Y, +Z) や nuc (MM) は自由に変更できる。
(nuc が変化すると、すべての電子のこれらの値 (nuc) は自動的に同じにそろう。)
試しにこれらの値を変化させてみると分かるが、全位置エネルギーが -1317.77 eV のとき、ド・ブロイ波 (Waves) はほぼ 2.0 となることがわかる。
この結果は、フッ素の7つの価電子すべてが 2ド・ブロイ波長の軌道上を運動していることを示している。
この場合では、核に作用する力の各成分は、(FX, FY, FZ) = (-96, -18, -100) でこれらの値は小さい。
(力の単位は、+e の原子核と -e の電子がボーア半径離れているときに、その間に働く力の大きさを 1000 としている。)
もちろん、各電子の (fx, fy, fz) は平衡状態ではとても小さくなる必要がある。
(このプログラムを実際に実行して、よりふさわしい電子の配置状態(構造)を誰か見つけてくれると非常にうれしい。)

2010/11/5 updated This site is link free.