トップページ (2電子原子も含む正確な新ボーア模型)
電子スピンは現実には存在しない。
特殊相対論は間違い。
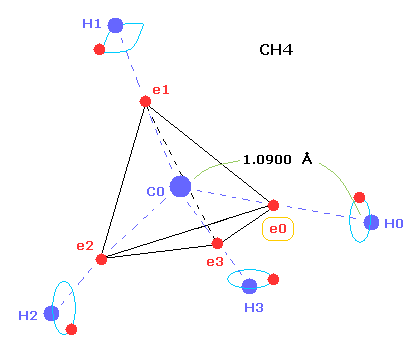
(Fig.1) メタン ( CH4 ) の C-H 結合長。

このページに示したように、メタンの C-H 結合長が どうして 1.09 Å (= 1.09 × 10-10 meter ) になるのかを ボーア軌道を軸とした 分子模型で説明することができた。
量子力学と量子化学の弱点は どんなに複雑な分子でも シュレディンガー方程式を解くという手法から逃れることができないということである。
さらに、このシュレディンガーの波動関数や 反対称のパウリの排他原理そのものの本当の性質を聞こうとすると、彼らはただ "Shut up and calculate !" と言って そのようなことを考えることは諦めるように と繰り返すだけである。
お気づきのとおり、量子力学のこれらの姿勢は 強い好奇心で 自然界の本当の性質を知りたいと願う 人々や学生たちを 殊更に 排除し続けている。
これらの悲惨な状況を改めない限り、私たちの科学は これからも発展が止められ、かつ 真実が知りたいという好奇心の強い人々が特に 物理そのものから離れていく傾向が続いていくと思われる。
(Fig.2) 水素が炭素に近づきすぎると、 メタン ( CH4 ) は 不安定になる。
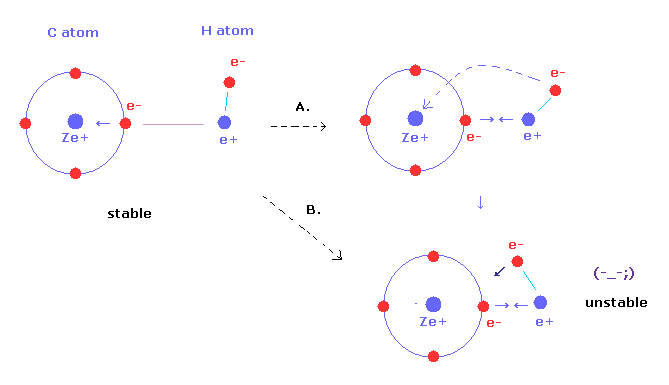
メタンの C-H 結合長が短くなるにつれて、その結合は強くなっていく。
しかし メタンの水素の原子核が 炭素の価電子に引きつけられすぎてしまう。
また 水素の電子に対する 炭素原子核の引力も強くなる (= Fig.2B)。
結果的に 水素の原子核と電子が 自身の安定位置を保てなくなる。
(Fig.3) もし C-H 結合長が短くなると・・。
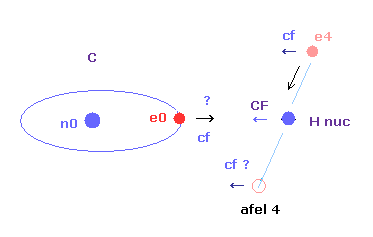
また 炭素の価電子 ( e0 ) も 水素原子核に強く引きつけられすぎてしまい、その軌道が 伸びきって不安定になる。
( 炭素の電子 e0 に作用する この力 "cf" は 後で説明するが 分子結合の鍵になる存在である。 )
結果的に、メタンの C-H 結合長が 実験値よりも短くなると、電子と原子核の両方が その安定な位置 ( もしくは 軌道 ) を保てなくなる。
これが メタンの C-H 結合長が 実験値 (= 1.09 × 10-10 meter ) よりも短くなれない理由である。
(Fig.4) どうして エタンの C-C 結合長が 1.54 Åなのか?
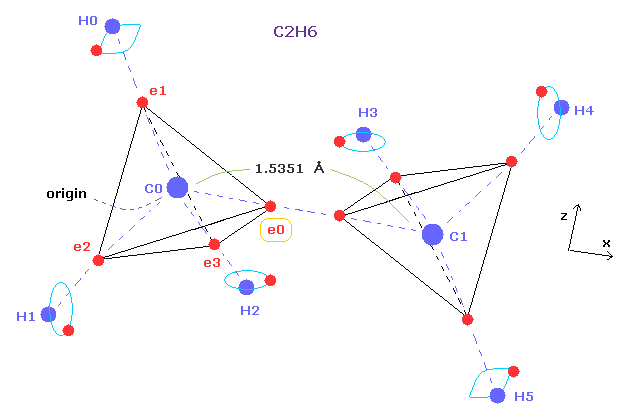
Fig.1 と Fig.4 を比較すると、メタンとエタンは ほぼ共通の構造を持っていることが分かる。
メタンの 1つの 水素原子を CH3 に置き換えると、メタンから エタンになる。
このページや 上記で述べたように、炭素の電子 ( e0 ) と 水素原子核間に働く力は メタンの結合長を決定する際の 重要な鍵となる。
もし エタンの炭素の価電子も クーロン力と ドブロイ波の法則に 従うとすると、その炭素の価電子 (= e0 ) に働く力が メタンのと ほぼ同じになる必要がある。
(Fig.5) メタンの価電子 (= e0 ) に働く "force 1"。
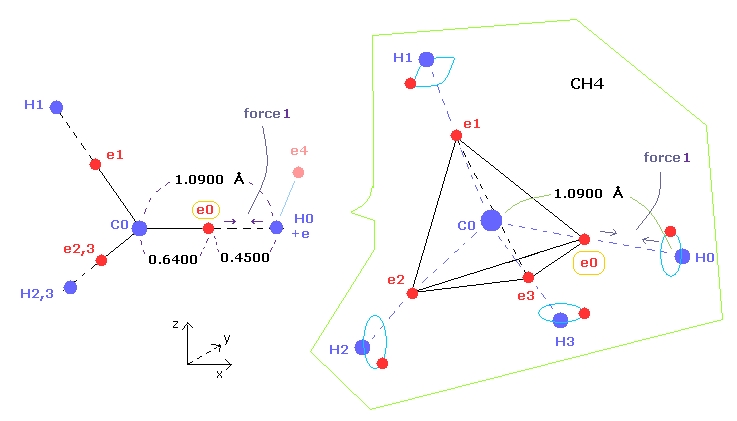
このページや このページ (Fig.22) に示したように、炭素の 1-4 のイオン化エネルギーの合計と "2" ドブロイ波長の軌道を考慮すると、
炭素の4つの価電子の回転半径は 約 0.6400 × 10-10 meter (= 6400 MM ) になる。
( ここでは 新しい単位 1 MM = 1 × 10-14 meter を使用している。 )
結果的に 価電子 e0 が 水素原子核に最も近づいたとき、それらの距離は 約0.4500 Å (= 1.0900 - 0.6400 ) になる。
この地点において ( クーロン力の ) "force 1" が e0 と H0 原子核間に働いている。
(Fig.6) エタン ( CH3-CH3 ) の 周期的な運動。
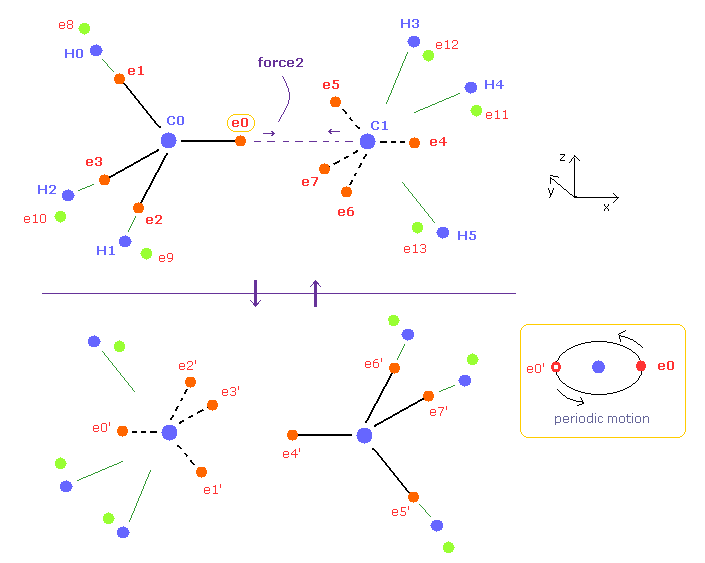
炭素の4つの価電子は それらの対称的な分布を考慮すると、正四面体状に配置されているとみなせる。
各電子は 各中心の炭素原子核の周囲を 実際に回っている。
つまり、もし エタンの "リアルな" 運動パターンを知ろうとするならば、Fig.6 の上下のパターンが 周期的に繰り返されていることになる。
(Fig.7) エタンにおける 価電子 (= e0 ) に作用する力 "force 2"。
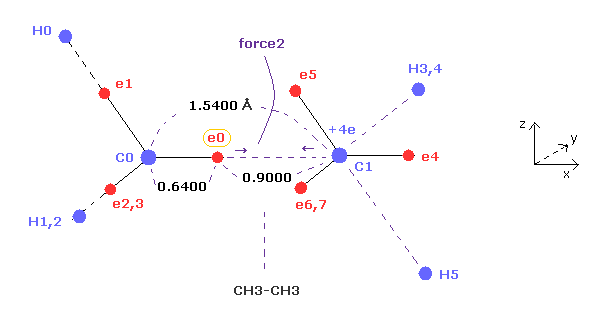
Fig.7 は Fig.6 の上図の x-z 断面図である。
エタンの C-C 結合長は 約 1.5400 Åであり、メタンのように "2" ドブロイ波長の軌道を考慮すると、 価電子 e0 と C0 原子核の距離は 約 0.6400 Å である。
結果的に e0 と 他の炭素原子核 C1 の距離は 約 0.9000 Å (= 1.5400 - 0.6400 ) となる。
また 中心の炭素の電荷は 2つの 1s 電子の効果を差し引けば 約 +4e ( +6e - 2e ) である。
(Fig.8) メタンとエタンにおける力 force 1, 2 は ほぼ同じである。
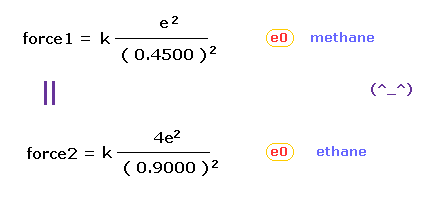
Fig.5 (= メタン ) と Fig.7 (= エタン ) から、e0 価電子と 他の原子核 ( H0 もしくは C1 原子核 ) の間に働くクーロン力を知ることができる。
クーロンの逆2乗の法則を用いれば、メタンの "force 1" が エタンの "force 2" と ほぼ同じであることがわかる。
これはつまり 価電子 e0 に作用する力は 結合長を決定する際の 鍵となる存在であることを意味している。
Fig.8 の結果は メタンとエタンの両方において、クーロンとドブロイの関係が 非常に重要であることを示している。
-----------------------------------------------------------------
(Fig.A-1) O-H、 O-C 結合における 力 force 1, 2.
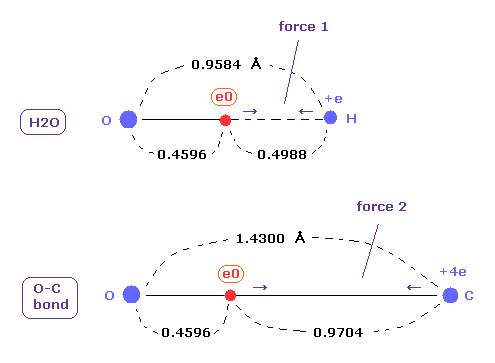
このページ ( Eq.8 - Eq.12 ) もしくは このプログラムを実行すると、酸素の価電子の 軌道半径 (= nuc ) が、 酸素の 1-6 の全イオン化エネルギー、2ドブロイ波長の軌道を考慮すれば、約 0.4596 Å になることが分かる。
水の O-H 結合長は 0.9584 Å で、平均のシングルの O-C 結合長は 1.4300 Å であることが知られている。
これらの結合長から 軌道半径 0.4596 を引くと、電子と他の原子核の間に働くクーロン力 ( force 1,2 ) を知ることができる。
(Fig.A-2) O-H、O-C 結合における force 1, 2 は ほぼ同じである。
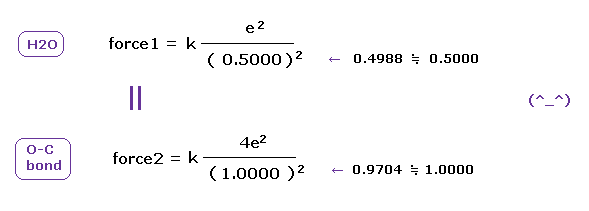
H 原子核は +e で、 C 原子核は 2つの 内殻の 1s 電子を引くと 約 +4e (= +6e - 2e ) である。
結果的に 電子と他の原子核間に働く クーロン力 ( force 1, 2 ) は O-H、O-C 結合両者で ほぼ同じになる。
( もちろん、酸素と電子間の力も同じであることはいうまでもない。)
これらの結果は O-H と O-C 結合における 酸素の価電子が 共通の物理法則に従って 運動していることを示している。
また 分子中の O-H と O-C 結合において クーロンと ドブロイの関係式が重要な役割を果たしていることも示している。
-------------------------------------------------------------------
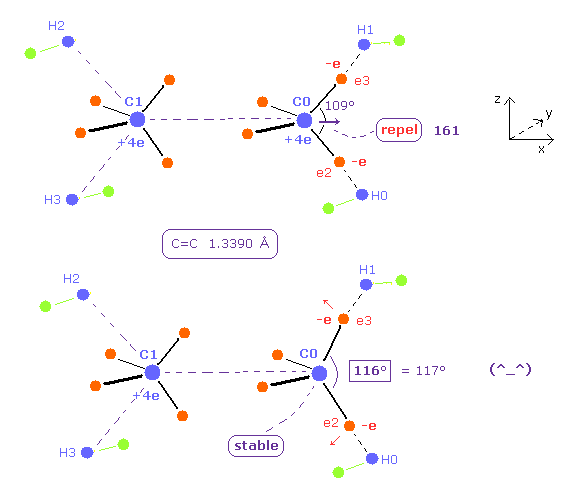
(Fig.9) 結合長と結合角は エチレンの安定性にとって重要である
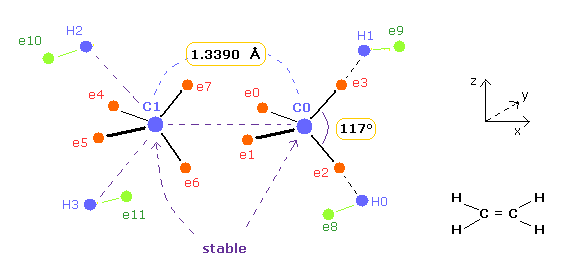
エチレン ( CH2=CH2 ) の結合長の実験値は 1.3390 Å である。
また エチレンの H-C-H の角度は 117°である。
後半のセクションで、この結合長 1.3390 と 結合角 117°が エチレンの原子核の安定性にとって必要であることを 古典的な軌道を用いて示す。
(Fig.10) エチレンにおける 結合長と結合角の関係。
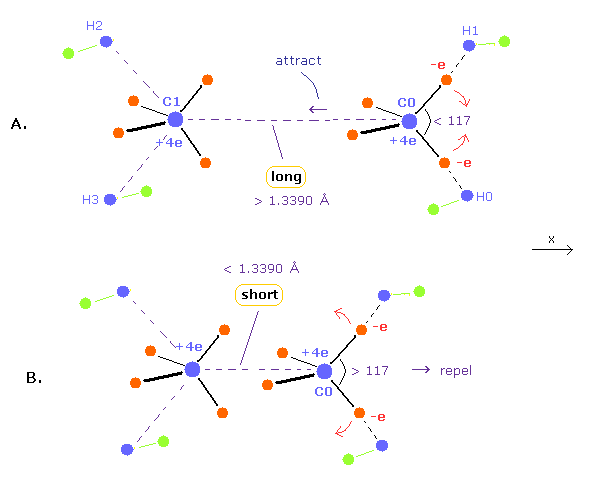
結合長が 1.3390 Å (= 実験値 ) よりも 長いとき、もう1つの炭素原子核による反発力は 弱くなる。
( これはつまり C0 原子核が Fig.10A に示すように その価電子によって C1 原子核方向へ 引きつけられることを意味する。)
この引力をキャンセルするために、H-C-H 角は 117°よりも 小さくなる必要がある。
H-C-H 角が小さいとき、C0 は 電子によって +x 方向へ引き寄せられるため 上記の力をキャンセルできる。
逆に、結合長が 1.3390 Å よりも短いとき、他の C 原子核による反発力が強くなる。
結果的に H-C-H 角は 炭素原子核を安定にするために 広くなる必要がある ( Fig.10B )。
なぜなら H-C-H 角が大きくなると 価電子による +x 方向への引力が弱くなるからである。
後半のセクションで コンピュータープログラムを用いて 実際にこれらの関係を正確に示すことにする。
(Fig.11) エタン ( CH3-CH3 ) のリアルな動き。

対称的な構造を考慮して 各炭素の 4つの価電子が Fig.11 に示したように 正四面体状に分布していると仮定する。
各電子は 各中心の炭素原子核の周囲を実際に回っているため、エタンでは Fig.11 の上下のパターンが 周期的に繰り返されていることになる。
(Fig.12) 炭素の外殻電子の平均位置。
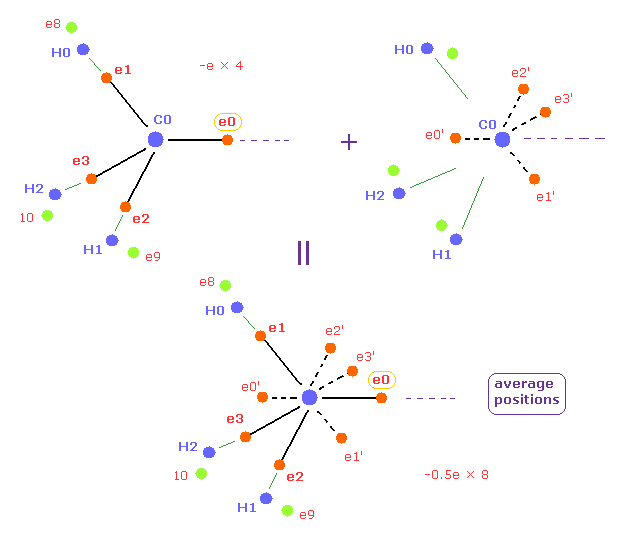
このページに示したように メタンにおいて 4つの価電子の平均的な分布を用いた。
この平均的な配置では、4つの外殻電子を Fig.12 に示すように 8つの 半荷電粒子として対称的に配置した。
( 全電荷は -e × 4 = -0.5e × 8 で もちろん同じである。 )
各半荷電粒子は Fig.12 に示すように 炭素原子核を挟んだ反対位置に位置している。
(Fig.13) C0 と C1 における 電子の対称的な平均分布位置。
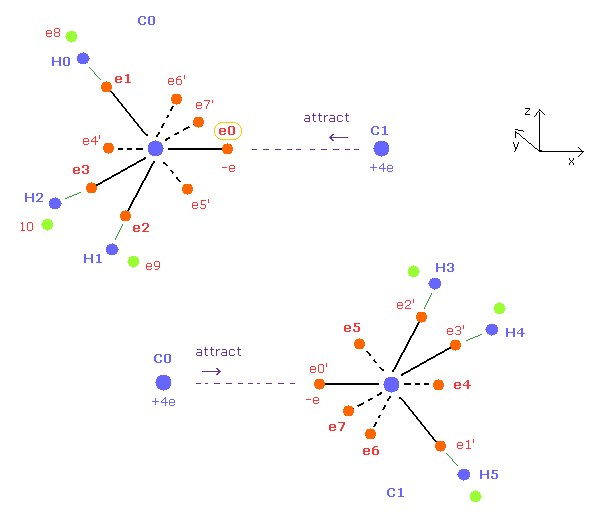
Fig.11 の エタンの C0 と C1 の炭素は 互いに対称的である。
そのため 例えば C0 原子核周囲では e0'、 e1'、e2'、e3' の代わりに e4、e5、e6、e7 の対称的な位置を用いる。
C1 原子核も C0 原子核と同じ平均的な電子分布を持つ。
そのため C0 原子核が 電子 0' に引きつけられるとき、C1 原子核も 電子 0 に引きつけられる。
( e0 の位置を x 方向に移動させると、その対称的な e0' も同様に マイナス x 方向へ移動する。)
もちろん、電子 0-7 そのものの間の相互作用を計算する際は もとの電荷を用い、半電荷を使ってはいけない。
なぜなら e0 が e0' を反発するというあり得ないことがおきるからである。
e0'、e1'、.... は e0-7 と e8-13 の間、e0-7 と 各原子核の間の平均の相互作用を考慮する際の 仮の電子である。
エタンのサンプル JAVA プログラム。 ( ビリアル定理。 )
プログラム中で使われている方法は このページのものと ほぼ同じである。
(Fig.14) プログラム中の エタン ( CH3-CH3 ) の構造。
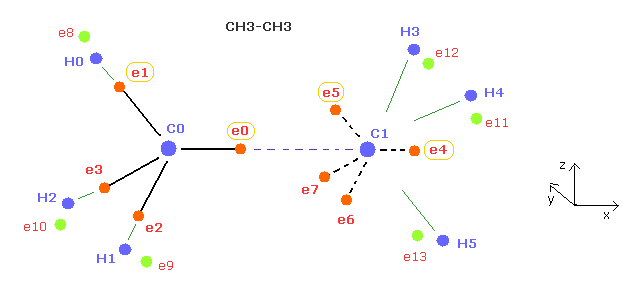
プログラムを実行した後、Fig.14 の 電子 0、1、4、5 (= ele0, ele1, ele4, ele5 ) の座標のみ変更できる。
電子 e2 と e3 は e1 の座標に基づいて 対称的な位置に自動的に配置される。
電子 e6 と e7 は e5 の座標に基づいて 対称的な位置に自動的に配置される。
Fig.13 で説明したように、例えば 炭素 0 の e1 の座標を変更すると、炭素 1 の 対称的な e1' の座標も変化する。
( Fig.13 で e0 を x 方向へ移動すると、e0' が マイナス x 方向へ移動する。 )
なぜなら 対称的な平均の電子分布を考慮しているからである。
同様に Fig.13 で e4 を x 方向へ移動させると、e4' も マイナス x 方向へ移動する。
(Fig.15) Fi.14 の 断面図 ( x-z 平面 )。
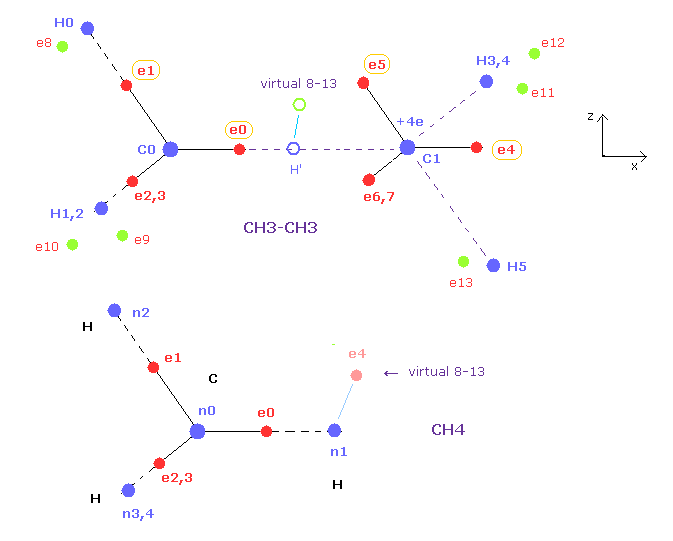
Fig.15 は Fig.14 のエタンの断面図である。
電子 e0、 e1、 e4、 e5 と 原子核 C0、 C1、 H0、 H5 は すべて x-z 平面上にある。
また e1, e2, e3 ( もしくは e5, e6, e7 ) の x 座標は同じである。
このページのメタンでは、水素の e4 の座標のみ変更することができた。
この e4 は x-z 平面に属じているため その位置がイメージしやすい。
エタンでは "virtual 8-13" 電子が メタンの この e4 にあたるものである。
この virtual 8-13 電子の ( virtual ) H' に対する相対的な x、z 座標を変化させると、水素のすべての電子 e8-e13 が メタンのように 自動的に対称的な位置に配置される。
エタンのすべての結合 ( 6 × C-H + C-C ) を切断するのに、2826.1 kJ/mol (= 29.29 eV) のエネルギーが必要である。
そのため、エタンの基底状態エネルギー ( 8つの炭素原子の価電子+6つの水素原子 ) は、-29.29 -148.024 × 2 -13.606 × 6 = -406.974 eV となる。
(148.024 eV は炭素原子の 1-4th のイオン化エネルギーの合計である。)
ビリアル定理によれば、全位置エネルギー (tV) は、2 × -406.974 = -813.948 eV である。
C-C と C-H 結合長は それぞれ 15351 MM と 10940 MMである。 (1 MM = 10-14 meter).
また C-C-H 角は 111.7°である。
| eNo | +X (MM) | +Y (MM) | +Z (MM) | nuc | V | cforce | rforce | Waves |
|---|---|---|---|---|---|---|---|---|
| C0 ele 0 | 6549 | 0 | 0 | nuc 6549 | V -76.23 | cf 1505 | rf 0 | wn 2.026 |
| -- ele 1 | -2157 | 0 | 5990 | nuc 6366 | V -76.23 | cf 1531 | rf 0 | wn 1.991 |
| C1 ele 4 | 6303 | 0 | 0 | nuc 6303 | V -76.23 | cf 2432 | rf 0 | wn 1.975 |
| -- ele 5 | -2098 | 0 | 6098 | nuc 6448 | V -76.23 | cf 2229 | rf 0 | wn 2.008 |
| Virtual 8-13 | 468 | 0 | 4138 | - | - | - | - | - |
| C0 nuc | C1 nuc | H0 nuc | total V | avewave 0-3 | avewave 4-7 | 0,4 ave | avewave 8-10 |
|---|---|---|---|---|---|---|---|
| force = 0 | force = 0 | force = -1 | -817.22 eV | wave 2.0 | wave 2.0 | 2.0 | wave 1.0 |
Table 1 では、C0、C1、H0、H3 原子核に作用する 力が ゼロになる 電子座標を見つける。
( プログラムでは、 "FX" が 原子核に作用する力の x 方向への成分で、 "CF" が 中心方向への成分である。 )
また ele0-3、 ele4-7 軌道における 平均的なドブロイ波は 2.0近くなる必要がある。
"0,4 ave" は e0 と e4 (= e0 の対称的な位置 ) の平均のドブロイ波で、これも 2.0 になる必要がある。
また ele8-10、 ele11-13 の平均のドブロイ波は 1.0 近くになるべきである。
Table 1 の値を プログラム実行後に テキストボックスへ入力して これらの値がでることを確かめてほしい。
ポテンシャルエネルギー -817.22 は 実験値 -813.9 eV とほぼ同じである。
最も重要な点は C0 原子核周囲の ele 0 と ele 1 に作用する力 "cf" が ほぼ同じ値であるという点である。
( ele 0 は 力 cf が 1505、 ele 1 は cf が 1531 である。 )
(Fig.16) 力 = 1000.
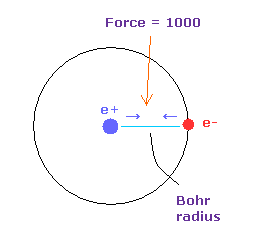
このページのように、水素原子の基底状態における 電子と原子核間の力を "1000" と定義する。
つまり 電子と +e の原子核の間の距離が ボーア半径のとき、その力は 1000 になる。
また "cf" は 各電子に作用する力の 中心の C 原子核方向への力である。
(Fig.17) C-C 結合長が実験値のとき、e0、 e1 に作用する力は ほぼ同じ。
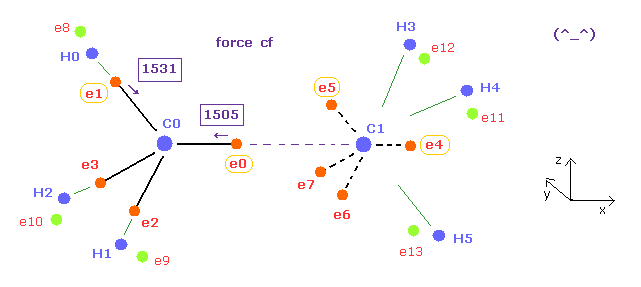
炭素周囲の電子が 同じ周期で周回するとき、それらに作用する力は ほぼ同じになる必要がある。
幸いなことに、エタンの C-C 結合長が 実験値 (= 15351 MM ) のとき、これらの力は 互いに等しくなる ( 1505 = 1531 )。
ここでは 新しい単位 1 MM = 1 × 10-14 meter, を使用している。
(Fig.18) メタンにおける e0、 e1 に作用する力。
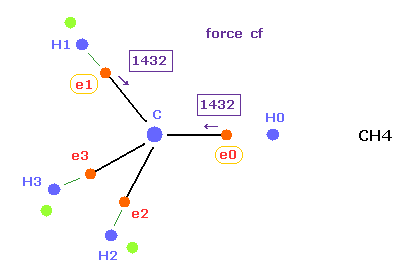
Fig.17 と Fig.18 を比較すると、エタンにおいて e0 に作用する力 ( cf 1503 ) は メタンの e0 に作用する力 ( cf 1432 ) とほぼ同じである。
つまり この結果は エタン分子においても クーロン と ドブロイの関係式が成り立っていることを示している。
プログラムでは "afel" は 作用する力によって動いた後の電子を意味し、メタンのときと意味は同じである。
( プログラム中では、 電子 0, 4, 8, 11 の値のみ表示した。 )
ele 8 と afel 8 の "cf" を見ると、水素の電子 ( e8-e13 ) の動きは エタンにおいても 安定であることを示している。
( e8 cf = 254 で、 afel8 cf = -232 であり、それらの符号は逆で 絶対値は ほぼ同じである。)
| eNo | +X (MM) | +Y (MM) | +Z (MM) | nuc | V | cforce | rforce | Waves |
|---|---|---|---|---|---|---|---|---|
| C0 ele 0 | 6579 | 0 | 0 | nuc 6579 | V -76.44 | cf 1191 | rf 0 | wn 2.032 |
| -- ele 1 | -2165 | 0 | 5980 | nuc 6359 | V -76.44 | cf 1551 | rf 0 | wn 1.990 |
| C1 ele 4 | 6273 | 0 | 0 | nuc 6273 | V -76.44 | cf 2455 | rf 0 | wn 1.970 |
| -- ele 5 | -2098 | 0 | 6109 | nuc 6459 | V -76.44 | cf 2191 | rf 0 | wn 2.010 |
| Virtual 8-13 | 456 | 0 | 4125 | - | - | - | - | - |
| C0 nuc | C1 nuc | H0 nuc | total V | avewave 0-3 | avewave 4-7 | 0,4 ave | avewave 8-10 |
|---|---|---|---|---|---|---|---|
| force = 0 | force = 0 | force = 0 | -820.0 eV | wave 2.0 | wave 2.0 | 2.0 | wave 1.0 |
次に スクロールバーの中から "14500" を選んで C-C (MM) ボタンをクリックする。
Table 2 に示したように、C-C 結合長が 実験値より短くなると、e0 は もう1つの C1 原子核に より引き寄せられることになる。
結果的に e0 の力 cf は 炭素の他の電子のよりも 弱くなりすぎてしまう ( 1191 < 1551 )
これはつまり 4つの価電子の 同じだった回転周期が壊れてしまうことを意味している ( Fig.19 )。
(Fig.19) C-C 結合長が短くなると、e0 に作用する力が小さくなりすぎる。
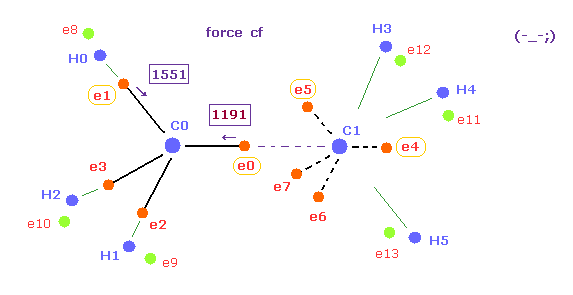
Fig.19 は Table 2 に示したように C-C 結合長が 実験値よりも短くなった (= 14500 MM ) ときの結果である。
もちろん、Fig.19 の 1191 の値は メタンの 1430 の値 ( Fig.18 ) と完全に異なっている。
| eNo | +X (MM) | +Y (MM) | +Z (MM) | nuc | V | cforce | rforce | Waves |
|---|---|---|---|---|---|---|---|---|
| C0 ele 0 | 6529 | 0 | 0 | nuc 6529 | V -76.04 | cf 1764 | rf 0 | wn 2.023 |
| -- ele 1 | -2162 | 0 | 5996 | nuc 6373 | V -76.04 | cf 1512 | rf 0 | wn 1.992 |
| C1 ele 4 | 6303 | 0 | 0 | nuc 6303 | V -76.04 | cf 2436 | rf 0 | wn 1.979 |
| -- ele 5 | -2120 | 0 | 6090 | nuc 6448 | V -76.04 | cf 2256 | rf 0 | wn 2.007 |
| Virtual 8-13 | 473 | 0 | 4145 | - | - | - | - | - |
| C0 nuc | C1 nuc | H0 nuc | total V | avewave 0-3 | avewave 4-7 | 0,4 ave | avewave 8-10 |
|---|---|---|---|---|---|---|---|
| force = 0 | force = 0 | force = 0 | -815.1 eV | wave 2.0 | wave 2.0 | 2.0 | wave 1.0 |
(Fig.20) C-C 結合長が長くなると、e0 に働く力は強くなりすぎる。
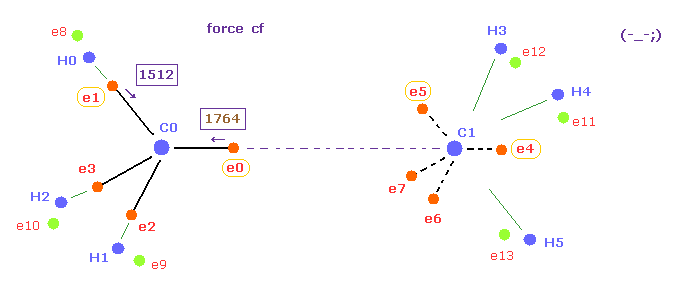
次に スクロールバーの中から "16500" を選んで C-C (MM) ボタンをクリックする。
Table 3 に示すように、C-C 結合長が 実験値よりも長くなると、e0 に対する C1 原子核の引力が弱くなる。
結果的に e0 の C0 原子核方向への力 "cf" が 炭素の他の電子のよりも 強くなりすぎる
( 1764 > 1512 )。
そのため このケースでも 4つの価電子のそろった回転周期が 壊れてしまうことになる ( Fig.20 )。
さらに 全ポテンシャルエネルギーは 15351 MM のときよりも高くなる。
(Fig.21) C 原子核を安定にする ( FX = 0 ) 方法。
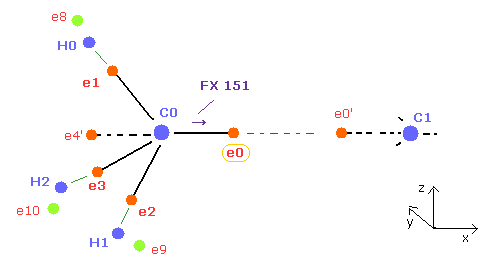
プログラム実行後、C0 と C1 原子核は 他の原子核の電子 0 もしくは 0' に 引きつけられた状態になっている。そのため C0 nuc FX が 151 で、C1 nuc FX が -151 の数値になっている。
ここでは "FX" は 各 C 原子核に作用する力の x 方向への成分である。
なぜなら Fig.12 と Fig.13 で述べたように、C 原子核周囲の平均の電子分布を考えているからである。
そのため C0 原子核が e0' 電子 (= e0 に対称的な電子 ) に引き寄せられているとき、C1 原子核も e0 電子に引き寄せられる傾向にある。
FX = 151 をゼロに近付けるには、e0 の電子を x 方向へ移動させる必要がある ( つまり e0' は マイナス方向へ移動 )。
なぜなら e0 が x 方向へ移動すると、e0 と C0 原子核の間の距離が長くなるため C0 に作用する力の x 方向の成分が弱くなるからである。
(Fig.22) C 原子核を安定にする ( FX = 0 ) 方法。
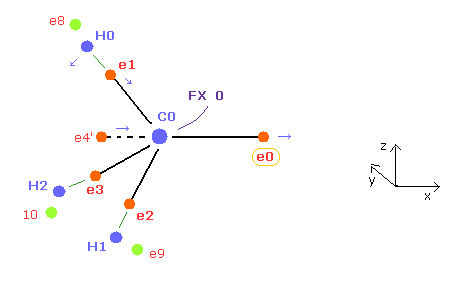
また e0 と e4' は C0 原子核周囲の1つの軌道を構成するものであるため、 e4' が C0 のほうへ近づくことになる ( これはつまり e4 も 対称的に C1 に近づく )。
結果 電子 0 と 4 の平均のドブロイ波も 2.0 に保たれる ( 0,4ave = 2.0 )。
また e0 が C0 から離れるにつれて、e1、e2、e3 の電子は C0 原子核に近づく傾向になる。
( もちろん、この e1-e3 が C0 原子核に近づきすぎると e1 と e0 のそろった回転周期が壊れてしまうので、できる限りそれらの C0 原子核との距離はそろえる必要がある。)
C-C 結合長が短くなると、C-C-H 結合角が大きくなる。
そのため e1 電子は x、-z の方向へ移動する傾向になる。
これらの効果と 平均のドブロイ波 = 2.0 を考慮すると、Table 1-3 の結果を得ることができる。
e0 と C0 原子核の距離は C1 原子核の引力のために メタン (= 6415 MM ) に比べて 少し長くなっている (= 約 6500 MM )。
(Fig.23) エチレン ( CH2=CH2 ) の古典的軌道

エチレン (= エテン) のすべての結合を切断するのに ( 4 × C-H + C=C ) 2253.1 kJ/mol (= 23.35 eV) のエネルギーが必要である。
そのため、エチレンの基底状態のエネルギー (8つの炭素の価電子+4つの水素原子) は、-23.35 -148.024 × 2 -13.606 × 4 = -373.822 eV となる。
C=C と C-H 結合長は それぞれ、13390 MMと 10870 MM でなる。(1 MM = 10-14 meter).
また、H-C-H 角は 117°であり、これは重要である。
エチレンの サンプル JAVA プログラム ( ビリアル定理 )
(Fig.24) プログラム中の エチレン ( CH2=CH2 ) 模型。
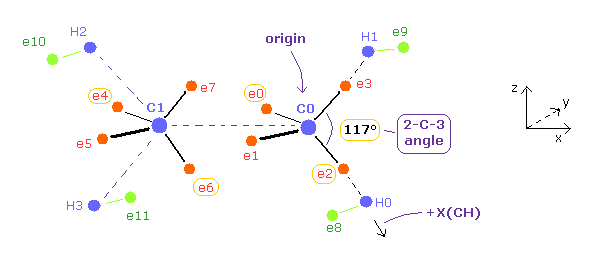
このプログラムでは 原子核 C0 (= 原点 )、C1、H0-H3 と 電子 e2、 e3、 e6、 e7 は 同じ x-z 平面上にある。
電子 e0、 e1、 e4、 e5 は x-y 平面上にある。
テキストボックス中の ele 0、 2、 4、 6、 8 の座標のみ変更できる。
ele8 の +X(CH) は C0 → H0 方向への座標である ( Fig.24 参照のこと )。
これらの入力値を元に、他の電子の座標が 自動的に配置される。
エタンのときのように、このプログラムは C0 原子核に対する e0、 e1、 e2、e3 の対称的な電子を e4'、 e5'、 e6'、e7' と定義して 平均の電子分布を使用している。
( 各 C 原子核周囲で -e × 4 = -0.5e × 8 に分布させている。 )
| eNo | +X (MM) | +Y (MM) | +Z (MM) | nuc | V | cforce | rforce | Waves |
|---|---|---|---|---|---|---|---|---|
| C0 ele 0 | -3703 | 5237 | 0 | nuc 6413 | V -76.56 | cf 2196 | rf 0 | wn 1.978 |
| C0 ele 2 | 3357 | 0 | -5465 | nuc 6413 | V -75.56 | cf 1430 | rf 0 | wn 2.021 |
| C1 ele 4 | -3703 | 5237 | 0 | nuc 6413 | V -75.56 | cf 2349 | rf 0 | wn 2.0 |
| C1 ele 6 | 3703 | 0 | -5237 | nuc 6413 | V -75.56 | cf 2189 | rf 0 | wn 2.0 |
| H0 ele8 | 496 | -3957 | 0 | nuc 3987 | V -35.62 | cf 270 | rf 1672 | wn 0.884 |
| C0 nuc | C1 nuc | H0 nuc | total V | e0-7 avewave | avewave 8 | nospilt wave | 2-C0-3 angle |
|---|---|---|---|---|---|---|---|
| force = 0 | force = 0 | force = 0 | -747.01 eV | wave 2.0 | wave 0.934 | wave 0.982 | 116 degree |
エタンのときと異なり、他の原子核側へ 大きく突き出た e0 の電子 (= Fig.17 ) は エチレンでは存在しない。
( Fig.17 と Fig.23 の e0 を比較するように )。
そのため プログラムを実行直後は C0 と C1 の原子核は 互いに反発しあう傾向にある。
C0 nuc FX は 161 であるため、 C0 の原子核は Fig.24 と Fig.25 では、x 方向へ反発力を受けている。
(Fig.25) C 原子核の安定のためには H-C-H の結合角は 116°になる。
この炭素原子核間の反発力をキャンセルするために、他の電子の正四面体状の配置を保ったまま ele2 ( と ele8 ) のみの座標を変化させることとする。
プログラム実行後に Table 4 の 赤い文字の部分を 各テキストボックスに入力してみてほしい。
Table 4 に示したように、ele2-C0-ele3 の結合角が 116°( ほぼ 117° ) のとき、各原子核に作用する力は ちょうどゼロになる。
これはすなわち 結合長 13390 MM と H-C-H 結合角 117°が ボーア軌道をベースにした模型で説明できたことを意味している。
Table 4 に示したように、ポテンシャルエネルギーが実験値 (= -747 eV ) のとき、水素の電子 (= e8 ) の 平均のドブロイ波は 1.0 より少し小さくなる。
これは エタンに比べて エチレンでは 水素原子が少なくなったせいである。
つまり エチレンでは 他の水素原子核に結合する代わりに、C 原子核と より結合し、それに応じて すばやく振動していることになる。
( もし 電子 0-7 を 半荷電粒子に分離せずに e8 のドブロイ波を計算すると その値は 0.982 となる。)
| eNo | +X (MM) | +Y (MM) | +Z (MM) | nuc | V | cforce | rforce | Waves |
|---|---|---|---|---|---|---|---|---|
| C0 ele 0 | -3703 | 5237 | 0 | nuc 6413 | V -75.64 | cf 2181 | rf 0 | wn 1.963 |
| C0 ele 2 | 3107 | 0 | -5620 | nuc 6421 | V -75.64 | cf 1435 | rf 0 | wn 2.035 |
| C1 ele 4 | -3703 | 5237 | 0 | nuc 6413 | V -75.64 | cf 2353 | rf 0 | wn 2.0 |
| C1 ele 6 | 3703 | 0 | -5237 | nuc 6413 | V -75.64 | cf 2181 | rf 0 | wn 2.0 |
| H0 ele8 | 490 | -3980 | 0 | nuc 4010 | V -35.35 | cf 267 | rf 1655 | wn 0.883 |
| C0 nuc | C1 nuc | H0 nuc | total V | e0-7 avewave | avewave 8 | nospilt wave | 2-C0-3 angle |
|---|---|---|---|---|---|---|---|
| force = 0 | force = 0 | force = 0 | -746.52 eV | wave 2.0 | wave 0.934 | wave 0.985 | 122 degree |
次に スクロールバーの中から "12500" を選んで C=C ボタンをクリックする。
そして Table 5 の 赤い数値を 画面上の各テキストボックスに入力する。
Table 4 と同じドブロイ波の条件 ( e0-7 平均の波 = 2.0 と e8 波 = 0.934 ) を目指す。
(Fig.26) C 原子核の安定のためには、 H-C-H 角が 122°になる必要がある。
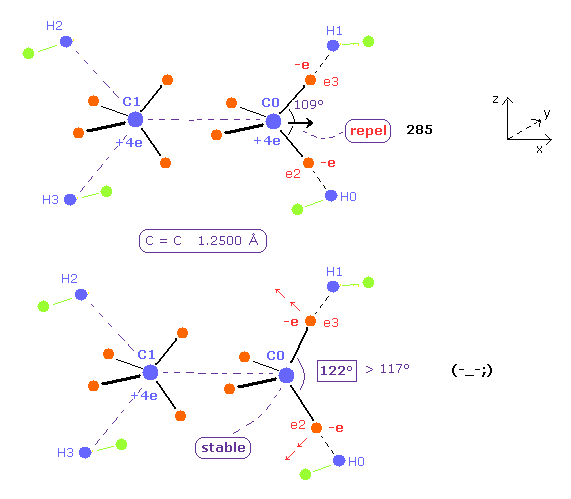
C=C 核間距離が 短くなるにつれて、他の C 原子核による反発力も 強くなる。
この反発力をキャンセルするために、H-C-H 角は 実験値よりも広くなる必要がある。
C=C 結合長が 12500 MM のとき、H-C-H 角は 122°になる必要があり、これは 実際の値 117°よりも大きい。
さらに、全ポテンシャルエネルギー -746.52 eV は Table 4 (= -747.01 eV ) よりも 高くなる。
つまり エチレンそのものが このケースでは 不安定になる。
| eNo | +X (MM) | +Y (MM) | +Z (MM) | nuc | V | cforce | rforce | Waves |
|---|---|---|---|---|---|---|---|---|
| C0 ele 0 | -3703 | 5237 | 0 | nuc 6413 | V -75.43 | cf 2215 | rf 0 | wn 1.992 |
| C0 ele 2 | 3572 | 0 | -5327 | nuc 6413 | V -75.43 | cf 1440 | rf 0 | wn 2.008 |
| C1 ele 4 | -3703 | 5237 | 0 | nuc 6413 | V -75.43 | cf 2345 | rf 0 | wn 2.0 |
| C1 ele 6 | 3703 | 0 | -5237 | nuc 6413 | V -75.43 | cf 2204 | rf 0 | wn 2.0 |
| H0 ele8 | 480 | -3945 | 0 | nuc 3974 | V -35.83 | cf 264 | rf 1685 | wn 0.885 |
| C0 nuc | C1 nuc | H0 nuc | total V | e0-7 avewave | avewave 8 | nospilt wave | 2-C0-3 angle |
|---|---|---|---|---|---|---|---|
| force = 0 | force = 0 | force = 0 | -746.82 eV | wave 2.0 | wave 0.934 | wave 0.979 | 112 degree |
次の スクロールバーの中から "14500" を選んで C=C ボタンをクリックする。
そして Table 6 の赤の文字を 画面上の各テキストボックス内に入力する。
Table 4 と同じドブロイ波の条件 ( e0-7 平均 = 2.0 と e8 の波 = 0.934 ) を目指す。.
(Fig.27) C 原子核を安定のために H-C-H は 112°になる必要がある。
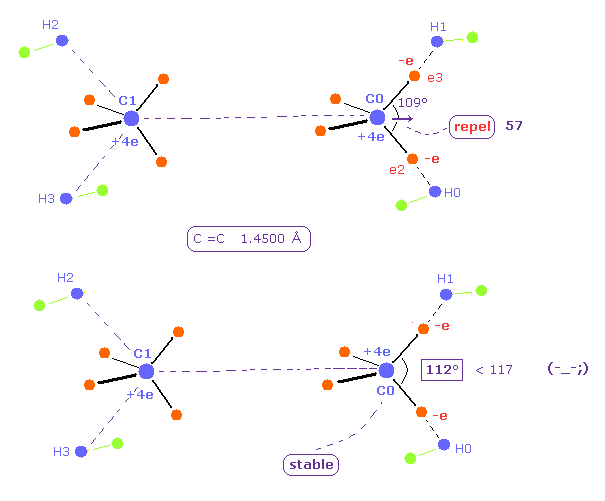
C=C の 核間距離が 長くなるにつれて、もう1つの C 原子核による反発力は 弱くなる。
そのため H-C-H 角は そんなに大きくなる必要がない。
C=C の結合長が 14500 MM のとき、 H-C-H 角は 112°になり、これは 実際の 117°の値よりも 小さくなる。
さらに、全ポテンシャルエネルギー -746.82 eV は Table 4 (= -747.01 eV ) のときの値よりも高くなる。
3つの正の原子核 C1、 H0、 H1 は 三角形状に配置する傾向になる (= H-C-H 角は 約 120° )。
そのため この 112° は 原子核の 三角形状の分布と 矛盾している。
| C = C 結合 | e2 +X | e2 +Y | e2 +Z | e8 CH | e8 +Y | V (eV) | Waves | H-C-H angle |
|---|---|---|---|---|---|---|---|---|
| 12000 | 2929 | 0 | -5730 | 476 | -4000 | V -745.72 | 0.934 | 125 degree |
| 12500 | 3107 | 0 | -5620 | 490 | -3980 | V -746.53 | 0.934 | 122 degree |
| 13390 | 3357 | 0 | -5465 | 496 | -3957 | V -747.01 | 0.934 | 116 degree |
| 14500 | 3572 | 0 | -5327 | 480 | -3945 | V -746.82 | 0.934 | 112 degree |
| 15000 | 3630 | 0 | -5278 | 473 | -3949 | V -746.55 | 0.934 | 110 degree |
| C0 nuc | C1 nuc | H0 nuc | e0-7 avewave | avewave 8 |
|---|---|---|---|---|
| force = 0 | force = 0 | force = 0 | wave 2.0 | wave 0.934 |
Table 7 は e8 のドブロイ波が 0.934 で、各原子核が安定のときの ele2 と 8 の 座標を示したものである。
全ポテンシャルエネルギー V = -747 eV は 上で述べたように 実験値である。
Table 7 に見られるように、C=C 結合長が 13390 MM (= 1.3390 Å、 実験値 ) のとき、 ポテンシャルエネルギーが 最も低くなり、かつ H-C-H 角 (= 116°) が 実験値 (= 117°) に最も近づく。
| C = C 結合 | e2 +X | e2 +Y | e2 +Z | e8 CH | e8 +Y | V (eV) | nosplit wave | H-C-H angle |
|---|---|---|---|---|---|---|---|---|
| 12000 | 2929 | 0 | -5734 | 471 | -3979 | V -746.40 | 0.982 | 125 degree |
| 12500 | 3107 | 0 | -5620 | 487 | -3969 | V -746.92 | 0.982 | 122 degree |
| 13390 | 3357 | 0 | -5465 | 496 | -3957 | V -747.01 | 0.982 | 116 degree |
| 14500 | 3572 | 0 | -5327 | 485 | -3958 | V -746.34 | 0.982 | 112 degree |
| 15000 | 3630 | 0 | -5278 | 473 | -3949 | V -746.05 | 0.982 | 110 degree |
| C0 nuc | C1 nuc | H0 nuc | e0-7 avewave | nosplit 8wave |
|---|---|---|---|---|
| force = 0 | force = 0 | force = 0 | wave 2.0 | wave 0.982 |
電子 0-7 を 半電荷に分離してない状態で 電子 8 のドブロイ波を計算したものが "Nospilit" である。
C 原子核周囲の 電子の平均的な分布を考慮して Fig.12 と Fig.13 のエタンのように エチレンにおいても 炭素の4つの価電子を 8つの対称的な 半電荷に分離した。
ここでは もとの4つの価電子のままでのドブロイ波を計算した。
Table 8 の状態においても、C=C 結合長が 実験値 (= 13390 MM ) のとき、 全ポテンシャルエネルギーは 最も低くなり、 H-C-H 結合角は 117° に 最も近くなる。
これらの結果は 通常のクーロンとドブロイの関係式によって、 ( 2重結合も含めた ) 分子結合を 正確に説明できることを示している。
人類の科学が非常に発展した現在でさえ
私達は シュレディンガーの波動関数が何なのかを知ることができず、それが何かを問うことを諦めている。
現在の量子化学による計算手法が 不完全 かつ 非常に問題が多いにも関わらずである。
さらに、このページに示したように、たとえ 相対論的な場の量子論を勉強したとしても ミステリアスなパウリの排他原理が何なのか知ることができない。
基本的な物理に関するこれらの態度が 私たちの科学の発展を 明らかに阻害している。
とくに 多電子原子や分子において シュレディンガー方程式 (+ 複雑な行列式 ) を解くことは不可能である。
(Fig.29) 1 × ドブロイ波長 = 水素の基底状態。

このページに示したように、シュレディンガーの水素原子も ドブロイ波長の整数倍の条件を満足する。
これが シュレディンガーの水素原子が すべてのエネルギー準位で ボーア模型と完全に同じ結果を与える理由である。
Fig.29 に示すように、水素原子の基底状態では ボーア模型は 接線方向のドブロイ波で シュレディンガーの水素 ( rR ) は 動径方向のドブロイ波で構成されている。
( 確率密度 |rR|2 のグラフを見ても このことを容易に理解できる。)
(Fig.30) 非実在の "s" 状態 ( 角運動量ゼロ )。
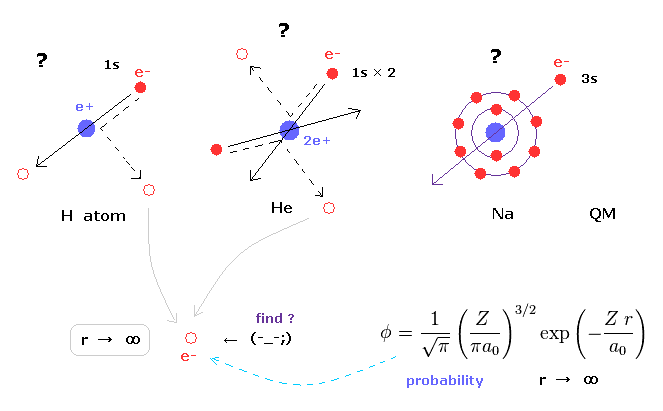
ヘリウムや水素分子なども含めた 様々な原子、分子における シュレディンガーの波動関数は 必ず 無限大まで広がっている。
また 量子力学的な模型のすべてのエネルギー準位において 必ず 角運動量ゼロの 非実在の "s" 状態を含んでいる。
これらの 非実在の "s" 状態が 様々な分子において 実際の電子分布を思い浮かべることを阻害しており もっと役に立つかもしれないシンプルな手法を探す障害になっている。
例えば、ナトリウムやカリウムで 実際 3s や 4s の価電子が 非常に強いクーロン反発力を避けて 内殻の電子群を貫いていくことは はっきり言って不可能である。
多電子分子などでは、分子動力学法 (= MD ) がよく用いられている。なぜなら 非常に込み入った波動関数で これらの分子を取り扱うことは不可能だからである。
しかし MD 法は 電子そのものを用いておらず、仮想的な力 というものに頼っている。
そのため、もし ボーア軌道をベースとした電子分布を このような理論と組み合わせれば、現在の分子計算法は 非常に簡単かつ正確なものに発展していくと思われる。
人気のある密度汎関数法 ( DFT ) は 単なる近似であり、これによって様々な分子における 真の性質を知ることはできない。
ボーア軌道のような 具体的な電子分布を用いて より簡潔かつ正確な方法を発展させない限り、現在の分子計算やナノテクノロジーは 決して これ以上発展することはないだろうと思われる。

2013/3/20 updated This site is link free.