トップページ (2電子原子も含む正確な新ボーア模型)
電子スピンは現実には存在しない。 単なる数学上の産物
ボーア模型の水素分子(H2)
特殊相対論は間違っている。
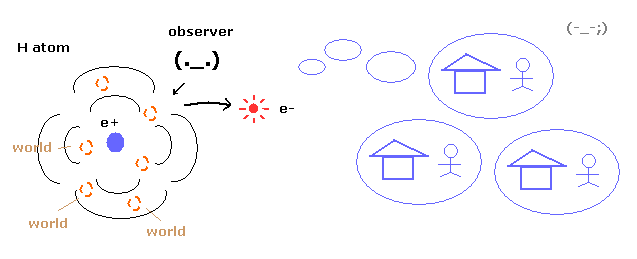
(Fig.1) 重ね合わせ = 非現実的な多世界 !

ご存じのとおり 量子力学は 電子の具体的な運動をまったく示すことができない。
それは 水素原子における 電子の確率密度のみを示すだけである。
そのため 波動関数の 収縮 (収束) を説明するためには、非現実的な多世界を必要とする。
(Fig.2) 1 × ドブロイ波長 = 水素の基底状態。

このページに示したように、シュレディンガーの水素原子も ドブロイ波長の整数倍の条件を満足する。
これが シュレディンガーの水素原子が ボーア模型と完全に同じ結果を与える理由である。
Fig.2 に示すように、水素原子の基底状態では ボーア模型は 接線方向のドブロイ波で シュレディンガーの水素 ( rR ) は 動径方向のドブロイ波で構成されている。
( 確率密度 |rR|2 のグラフを見ても このことを容易に理解できる。)
実際に、水素原子の基底状態の確率密度は ボーア半径周囲で もっとも高い。
問題は シュレディンガーの動径方向の波動関数は 必ず ゼロから無限大に広がっていなければならない。
また 1s のドブロイ波は 線状なため、それらの逆位相どうしが 重なり合って互いに打ち消しあってしまう。
(Fig.3) シュレディンガーの波動関数は 必ず無限大まで広がっている。
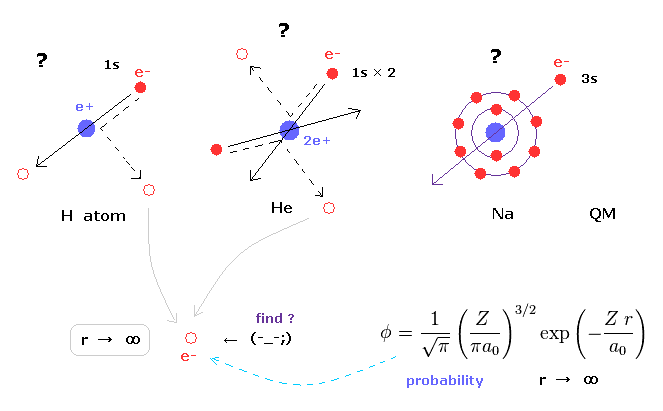
ヘリウムや水素分子なども含めた 様々な原子、分子における シュレディンガーの波動関数は 必ず 無限大まで広がっている。
これはつまり 非常に安定なヘリウムの 基底状態の電子でさえ、無限遠の近くで見つけることができるという意味である。
もちろん こんなことはあり得ないので 量子力学(化学)は 様々な原子や分子のリアルな状態を説明できる能力がないことになる。
ヘリウム原子のシュレディンガー方程式は解くことができないが、その変分関数は 必ず無限大まで広がっている。
(Fig.4) シュレディンガーの 2P の "動径方向" の波動関数 ( 角運動量 = 1 )。
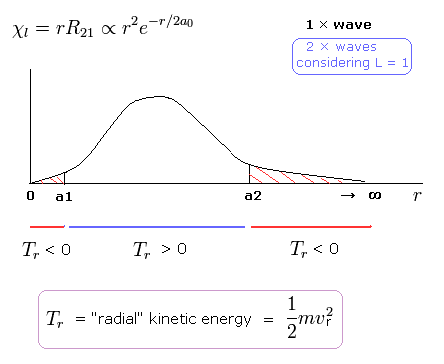
例えば、シュレディンガーの 2P の状態では、Fig.4 に示すように 動径方向の運動エネルギー (= 1/2mv2 ) が 両サイドで マイナスになる。
( 2P 状態では、 エネルギー準位は n = 2 で 角運動量は L = 1 である。 )
この奇妙な状態は いわゆるトンネル効果とは何の関係もない。
なぜなら Fig.4 の 0 から a1 の領域では、位置エネルギーは 全エネルギーよりも低いからである。
接線方向の運動エネルギーの増加をキャンセルするために、動径方向のエネルギーが マイナスにならなければならないのである。
これらの不合理な状態が シュレディンガーの水素原子が 間違いであることを示している。
(Fig.5) 量子力学のヘリウムは カオスになり不安定である。
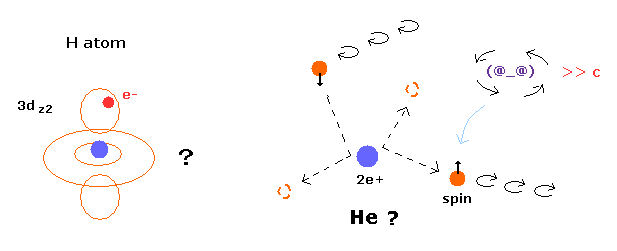
量子化学では もし 水素原子の 1s の波動関数を使用すると、ヘリウムの近似的な基底状態のエネルギーを得ることができる。
お気づきのとおり、1s の状態は 角運動量がゼロである。
この状態では ヘリウムの2つの状態は カオス状態になり、それらの間のクーロン反発力のため 非常に不安定になる。
つまり 量子力学のヘリウムは リアルなヘリウム原子とは まったく異なるものである。
(Fig.6) 量子力学のヘリウム。
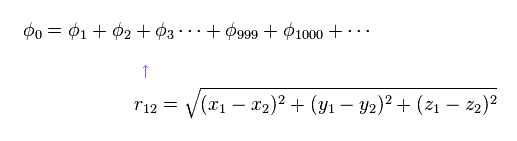
シュレデインガー方程式を用いて ヘリウム ( もしくは 水素分子 ) などの 正確な基底状態を得るためには Fig.6 に示すように 千以上の変分関数を使用しなければならない。
(Fig.7) ヘリウム もしくは H2 の確率密度 ?
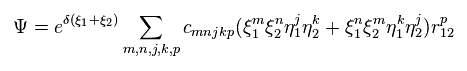
これらの変分関数は 2電子間の距離を表す変数 (= r12 ) を含まなければならない。
そのため 定常な水素原子と異なり、ヘリウム (もしくは H2 ) の電子 1 を発見する確率密度は 電子 2 の位置に応じて絶えず変化していることになる。
つまり このヘリウムの変分関数は 曖昧な確率密度波の点からも 2つの電子が実際に動いていることを示している。
(Fig.8) 換算質量 = 電子と原子核は実際に動いている。
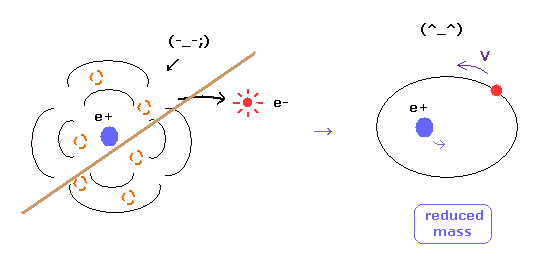
ご存じのとおり、電子の換算質量を用いると、水素原子においても より正確な エネルギー準位の値を得ることができる。
この事実は 明確に電子と原子核が互いに相互作用しながら実際に動いていることを示している。
もちろん、電子の分数電荷は 実際に見つかっていないため、ヘリウムの2つの電子のリアルな動きを直に示す必要がある。
このページに示したように、量子力学では ガイド波 (ボーム) 理論でさえ 2電子のヘリウムを説明できない。
(Fig.9) 換算質量を用いた計算結果は より正確になる。
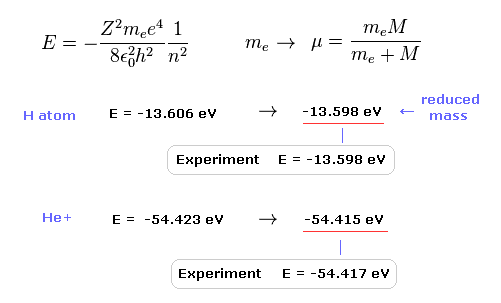
水素原子の基底状態エネルギーの実験値は -13.598 eV である。
この基底状態のエネルギーをシュレディンガー方程式 ( もしくは ボーア模型 ) を用いて計算すると、
それは -13.606 eV になる。
原子核の運動を考慮して 通常の電子質量を 換算質量に置き換えると、この計算結果は より正確になる (= 13.598 eV )。
この結果は 明らかに 原子内の電子と原子核が 実際に動いていることを示している。
He+ イオンにおいても、換算質量を用いると、より正確な値 (= -54.415 eV ) を得ることができる。通常の電子質量だと -54.423 eV となる。
He+ の実験値は -54.417 eV である。
(Fig.10) 2電子原子モデル ( He, Li+, Be2+, B3+, C4+ ... )
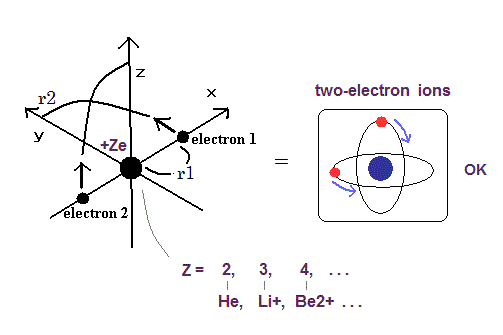
トップページに示したように、もし 2つのドブロイ波 (= 1 × 波長 ) が 互いに重なりあっているとすると、それらの逆同士の位相は干渉で打ち消し合う。
( この電子のドブロイ波の打ち消し合いは ダビッソン・ガーマーの実験で確認されている。)
そのため 2つの電子軌道は 打ち消し干渉を避けるために 互いに垂直にならなければならない。
| 原子 | r1 (MM) | WN x 4 | 同一円軌道 | 計算結果 (eV) | 実験結果 (eV) | 誤差 (eV) |
|---|---|---|---|---|---|---|
| He | 3074.0 | 1.000000 | -83.335 | -79.0037 | -79.0051 | 0.001 |
| Li+ | 1944.5 | 1.000000 | -205.78 | -198.984 | -198.093 | -0.89 |
| Be2+ | 1422.0 | 1.000000 | -382.66 | -373.470 | -371.615 | -1.85 |
| B3+ | 1121.0 | 1.000000 | -613.96 | -602.32 | -599.60 | -2.72 |
| C4+ | 925.0 | 1.000000 | -899.67 | -885.6 | -882.1 | -3.50 |
| N5+ | 788.0 | 1.000000 | -1239.8 | -1223.3 | -1219.1 | -4.20 |
| O6+ | 685.3 | 1.000000 | -1634.38 | -1615.44 | -1610.70 | -4.74 |
| F7+ | 607.3 | 1.000000 | -2083.3 | -2062.0 | -2057.0 | -5.00 |
| Ne8+ | 544.5 | 1.000000 | -2586.7 | -2563.0 | -2558.0 | -5.00 |
Table 1 に示すように、これらの2電子原子模型は 様々な原子における 実際のエネルギー状態を完全に再現することが可能である。
このヘリウムの基底状態エネルギー ( -79.0037 eV ) は 量子力学的な変分法 ( -79.015 eV ) よりも より正確な値を出すことができた。
なぜなら 量子力学のヘリウムは 原子核の動き (換算質量) を正確に扱えないからである。
具体的な計算プログラムに関しては このページを参照のこと。
(Fig.11) 新しいボーア模型のヘリウム (= A.) は 電気的に分極していない。
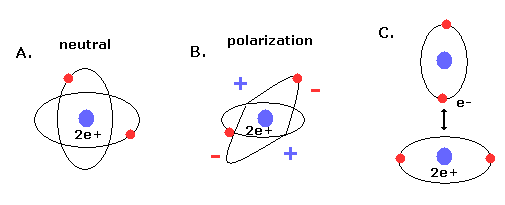
さらに このヘリウム模型は ヘリウムが最も安定な原子で かつ 他の原子 もしくは 自分自身と化合物を形成しない という事実と ちょうど一致する。
なぜなら 2つの軌道が 互いに垂直だと、2e+ 原子核の周囲の空間は 電子の均等分布のため ちょうど中性になるからである。
また ドブロイ波の安定性を考慮すると、Fig.10 のヘリウムには 3番目の電子が入っていく空間は残っていない。(= パウリの排他原理 )。
もし 3番目の電子が そこに入っていくと ドブロイ波どうしで 打ち消し合うものがでてきて 不安定になってしまうからである。
(Fig.12) "数学上の" シュレディンガー方程式 vs. "リアルな" ボーア模型。
私達は シュレディンガーの波動関数が何なのかを知ることができず、それが何かを問うことを諦めている。
さらに、このページに示したように、たとえ 相対論的な場の量子論を勉強したとしても ミステリアスなパウリの排他原理が何なのか知ることができない。
彼らは 数学上の演算子の反交換性が パウリの排他原理を意味しているという主張しかできない。
このページに示したように、私たちは この非常に制限された 曖昧な条件のもとでは より簡単で有用な方法を試して発展させることができない。
この役になっていない現在の量子化学を 分子生物学や ナノテクノロジーなどの他分野に 応用することができないため、それらの発展は 分子レベルにおいて 現在 すべてストップしている。
(Fig.13) 密度汎関数法 = 近似。
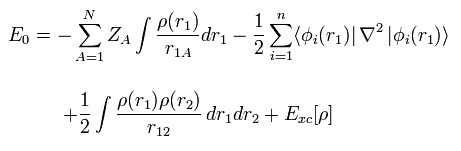
最初に、現在頻繁に使用されている 密度汎関数法 (= DFT ) は 単なる近似 であり、第一原理 ( ab-initio 方法 ) ではないということである。
DFT は 半経験的な手法の1つである。
実験結果に合わせるため LDA などの様々な近似方法を 人為的に選択しているだけにすぎない。
つまり 現在人気がある DFT そのものは 真の理論ではない。
(Fig.14) 量子力学の水素分子イオン ( H2+ ) ?
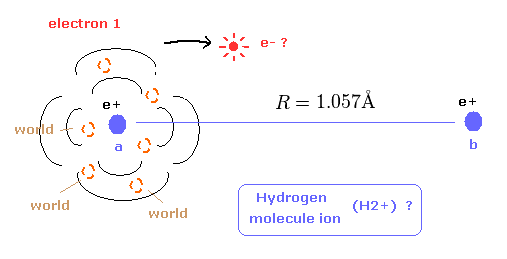
最初に 量子力学的手法による 水素分子イオン (H2+) の計算についてい知る必要がある。
水素原子と異なり、H2+ 分子イオンの波動関数そのものは 電子のリアルな確率密度を意味していない。
そのため この量子力学的な H2+ 分子イオンから 電子のリアルな状態を知ることはできない。
(Eq.1) H2+ 分子イオンのハミルトニアン。
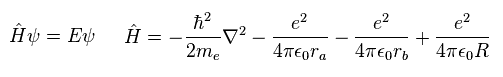
Eq.1 は 電子の運動エネルギーと 1電子と2原子核 ( a と b ) の間のクーロン相互作用から成る。
H2+ の核間距離は 非常に長い (= 1.057 × 10-10 m )。
そのため 1原子核周囲の 電子の確率密度は 水素原子とほぼ同じであると考えるのは自然である。
そのため 彼らは H2+ の波動関数を 水素原子の 1s 波動関数を用いて 次のように定義した。
(Eq.2) H2+ 分子イオンの波動関数。
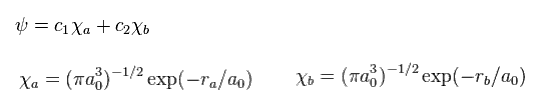
ここで a0 は ボーア半径である。
c1 と c2 は 変分パラメーターである。
Eq.1 と Eq.2 を 次のエネルギーの式に代入して、
(Eq.3)
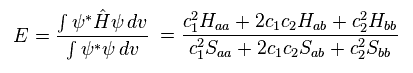
ここでは
(Eq.4)
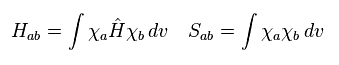
これを 重なり積分と呼ぶ。
Eq.3 を解いて、楕円体座標を用いると
(Eq.5)
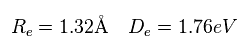
Re は 核間距離、 De は H2+ の解離 ( 結合 ) エネルギー である ( H2+ → H + H+ )。
Eq.5 の計算結果は 次の実験結果と異なる。
(Eq.6) H2+ の実験結果。
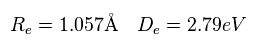
そのため 彼らは Eq.2 の波動関数を次のように変化させ、変分パラメーターの数を増やした。
( しかし この操作は 実験結果に近づけるための人為的なものに思えるが。 )
(Eq.7)
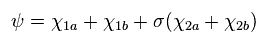
ここでは
(Eq.8)
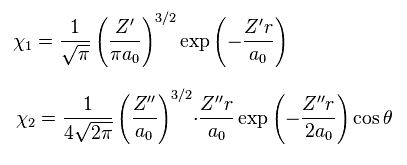
Eq.8 では、χ1 は 1s の水素原子の波動関数、 χ2 は 水素原子の 2p の波動関数である。
σ、 Z'、 Z'' 変分パラメーターである。
彼らは 2p の波動関数により 2つの核間の電子の分布を自然に説明できると主張している。
しかし 彼らは この 2p が ( 異なった Z の ) 1s や 2s などの他の関数ではだめなのか 説明すべきと思われる。
Eq.7 に基づく計算結果は
(Eq.9)
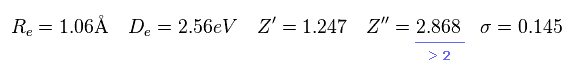
この結果は Eq.6 の実験値により近い。
しかし Eq,9 を見てわかるとおり、2p の波動関数の正電荷は 2.868 である。
もちろん、 H2+ 分子イオンは たった 2つの原子核しか持たない。そのため Z'' = 2.868 は あり得ない値である。
つまり 彼らの どうして 2p の波動関数を用いたのかという理由に正当性がないのである。
また 角運動量の保存則を考慮すれば、2p から 1s の変化は起こり得ない。
結果的に Eq.7 は 本当の H2+ 分子イオンの電子状態を意味していないのである。
( どうして この奇妙な Z'' = 2.868 が得られたのかという理由は 変分法の真実を参照のこと。 )
(Fig.15) H2+ 分子イオンの2つの原子核。
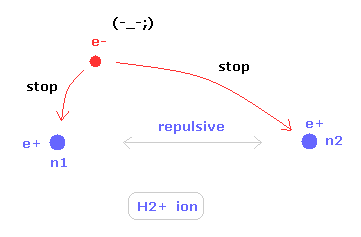
ある特殊な状況下で、不安定な 水素分子イオン (H2+) が存在できる。
水素分子イオンは 2つの正の原子核と 1つの負の電子をもつ。
2つの原子核の位置を安定にするには、この唯一の電子が 水素分子よりも 活発に動き回る必要がある。
つまり、H2+ 分子イオンは 電子が自身の運動のみで 2つの原子核を安定に保つ必要があるため ヘリウム原子とは完全に異なるものなのである。
よって H2+ イオンでは 余計な運動 (= 歳差運動など) が非常に重要になってくる。
(Fig.16) H2 分子の2つの原子核。
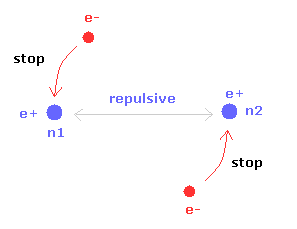
H2+ 分子と異なり、H2 分子は 2つの電子を持つ。
そのため 各電子は 2つの原子核の どちらか一方のみをメインに保つように運動している。
2つの原子核のうち片方が安定になると、もう1つの原子核は 対称的な構造のために 自動的に安定になる。
結果的に H2 分子の電子は H2+ 分子イオンのように 激しく揺れ動く必要がない。
すべての安定な分子の結合は 特殊な H2+ イオンよりも 水素分子 (H2) をベースにしている。
そのため 分子結合の本当の性質が知りたいならば 水素分子 (H2) のページ をご覧になるように。
(Fig.17) ボーア模型の H2+ イオン。

ここで Fig.17 と 次のプログラムを用いて 1軌道に含まれるドブロイ波の数を計算する。
H2+ イオンの サンプル JAVA プログラム。
H2+ イオンの C 言語プログラム。
ここでは 1 MM = 1 × 10-14 meter という新しい単位を使用している。
このサンプルプログラムでは、実行すると、最初に H2+ の核間距離 ( MM ) を入力する。
その後、電子1の y座標 "r" ( MM )、x 座標 "a" ( MM ) を 入力する。
(Fig.18) 最初に 原子核 2 をストップする。
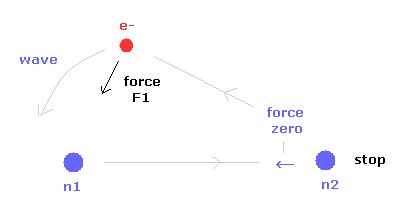
最初に 原子核 2 (= n2 ) がストップする 電子の位置を見つける。
( n2 に作用する力の x 成分が ゼロのとき。)
つまり このケースでは n2 に作用する 電子と n1 からの力の比 が ちょうど1.000 になる。
F1 は 電子に作用する力の 原子核 1 (= n1 ) 方向の力である。
入力値 ( a, r, nuc ) から、全位置エネルギー V を計算する。
ビリアル定理を用いて、エネルギー E = 1/2 V と 運動エネルギー T = -1/2 V を得る。
この運動エネルギーから 電子の速度 (= v ) と ドブロイ波長 (= h/mv ) を得る。
(Eq.10)
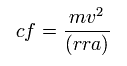
非常に長い核間距離を考慮して、電子は 主に 原子核 1 の周囲を周っていると仮定して、遠心力 (cf) を計算する。
また 電子 1 に作用する 全力の 原子核 1 方向の力 (F1) を次のように計算する。
(Eq.11)
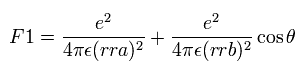
最初の項は 原子核1 (n1) と 電子間のクーロン力であり、2番目の項は 原子核 2 (n2) によるクーロン力である。
この θ は rra と rrb の間の角である ( Fig.17 を参照のこと。)
驚くことに、原子核 2 が止まると、F1 と 遠心力 (= cf ) の比が ちょうど 1.000 ( Eq.10 = Eq.11 ) になる。
そのため この円軌道に含まれる ドブロイ波の数 (W1) を 次のように計算する。
( しかし 実際には 電子はもっと複雑に運動している。)
(Eq.12)
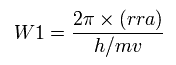
h は プランク定数、 h/mv ドブロイ波長である。
n1 周囲の この円軌道のために 原子核1は 安定になる。
2つの電子を持つ水素分子では この過程を省略できる。
(Fig.19) x 軸周囲の歳差運動。
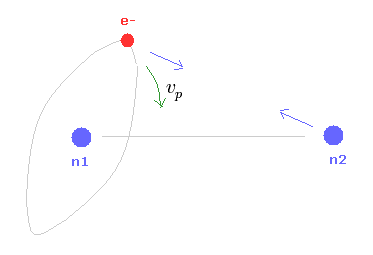
さらに 原子核2からの クーロン力の y成分から生じる x軸周囲の歳差運動を考える。
遠心力がクーロン力に等しいことより、運動方程式は
(Eq.13)
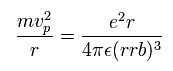
ここで r は 電子と x 軸の距離、 vp は x 軸周囲の 電子の歳差運動の速度である。
この歳差運動が 原子核 2 によって生じることを考慮して Eq.13 の右辺は 原子核 2 からの力の y 成分にしてある。
原子核 1 周囲を回る時間周期は T = 2 π × (rra) / v である。
この時間の間に、電子は x 軸周囲を T × vp 進む。
そのため この余計な進行部分のドブロイ波を上記に追加する。
この余分なドブロイ波 (W2) は、
(Eq.14)
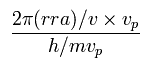
Eq.12 と Eq.14 の合計が トータルのドブロイ波である。
Table 2 は 様々な核間距離 (= nuc ) のとき n2 に作用する力がゼロで 全ドブロイ波が 1.000 のときの 結果である。
"n2 force" は n2 に作用する 電子と n1 からの力の比の意味である。
この比が 1.000 のとき、n2 に作用する力は 釣り合っている。
| nuc (MM) | r (MM) | a (MM) | Energy (eV) | centrifugal | n2 force | total waves | new waves |
|---|---|---|---|---|---|---|---|
| 8000 | 3707 | 1537 | 4.998 | 1.000 | 1.000 | 1.000 | 0.996 |
| 9000 | 3940.5 | 1507 | 3.964 | 1.000 | 1.000 | 1.000 | 0.998 |
| 10000 | 4136 | 1460 | 3.196 | 1.000 | 1.000 | 1.000 | 0.999 |
| 10570 | 4237 | 1436 | 2.826 | 1.000 | 1.000 | 1.000 | 1.000 |
| 11000 | 4304 | 1415 | 2.592 | 1.000 | 1.000 | 1.000 | 1.000 |
| 11500 | 4381 | 1390 | 2.332 | 1.000 | 1.000 | 1.000 | 1.001 |
| 12000 | 4448 | 1370 | 2.112 | 1.000 | 1.000 | 1.000 | 1.001 |
エネルギーは H2+ イオンの結合エネルギーである。
"centrifugal" は F1 (= Eq.11) と n1 周囲の遠心力 (= Eq.10 ) の比である。
Table 2 に示すように、核間距離が 小さくなるにつれて、結合エネルギーは小さくなる。
(Fig.20) x 軸周囲の 歳差運動。
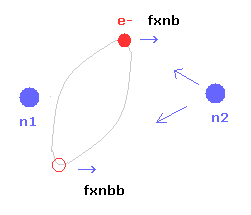
全ドブロイ波を計算するとき、n2 からの x 方向への引力を無視した。
そのため 2つの端点 ( x 軸の上と下 ) において この力の影響を付け加えて 新たにドブロイ波 ( new waves ) を計算する。
Table 2 に示すように、核間距離が短くなるにつれて ( 10570 MM よりも )、この new waves は 1.000 よりも短くなる。
H2 + イオンの実験値は
(Eq.15) H2+ の実験値。
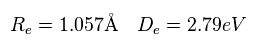
つまり 実験値の nuc = 10570 MM 近くで、 全ドブロイ波が ちょうど 1.000 になり、結合エネルギーが 実験値に近づく。
しかし 水素分子と異なり、単一電子が 同時に 2つの原子核の世話をしなければならない。
(Fig.21) H2+ 分子イオンの2つの原子核。

つまり この電子の運動は 単純な回転ではなく、不安定な H2+ イオンでは 非常に活発に 電子は動きまわる必要がある。
しかし 電子は 明らかに量子化された (= 分離してない ) 粒子であり、また 変分法では Eq.9 に示す 非現実的な電荷を与える。
(Fig.22) 推定される リアルな水素分子イオン (H2+)
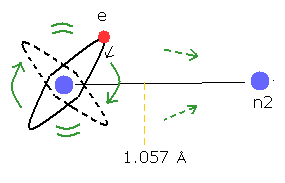
この不安定な H2+ イオンは 他の安定な分子に比較して 非常に複雑である。
そのため 誰か (専門家も含めて) H2+ イオンに関する もっと正確 かつ リアリティー のある構造を見つけてくれると 非常に喜ばしい。

2013/2/12 updated This site is link free.