トップページ (2電子原子も含む正確な新ボーア模型)
電子スピンは実在しない
ボーアの2重結合 (C=C, O=O)
我々の新しいボーア模型によって、ヘリウム原子の基底状態エネルギーの計算で、量子力学的な変分法よりも正確な結果をだすのに成功した。(トップページ参照のこと)。
この成功した新ボーア模型では、ヘリウム原子 (He) の2つの電子は、ちょうど1ド・ブロイ波長の互いに垂直な軌道上を運動している。
さらに、我々は炭素の4つの価電子と酸素の6つの価電子の運動のイメージ化に成功した。
(炭素のページ と 酸素のページ を参照のこと。)
このページでは、水素分子 (H2) における具体的な電子軌道を計算した。
ここでは、ビリアル定理 (Virial theorem) を用いて、水素分子 (H2) の2つの電子がちょうど1ド・ブロイ波長の軌道上を運動していることを証明してみることにする。
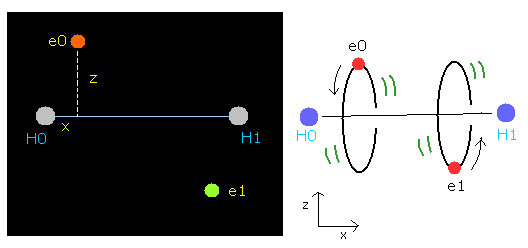
水素分子 (H2) は、2つの陽子 (H0, H1) と、2つの電子 (e0, e1) より成る。
その結合エネルギーは、4.7467 eV である。
つまり、H2 の基底状態エネルギーは、- 27.212 ( H × 2 ) - 4.7467 = - 31.9587 eV となる。
平衡核間距離 ( = nleng ) は、0.7414 × 10-10 m. ( = 7414 MM) であり、これはボーア半径 (5292 MM) よりも 少し長い。
(ここでは、新しい便利な単位、1 MM = 10-14 meter を使う。)
Fig. 1. 水素分子 ( H2 )

ビリアル定理によれば、平衡状態の2電子分子は次の関係式を満たす。
2 < T > + < V > = 0
E = < T > + < V >
T は”平均の”運動エネルギー、V は”平均の”位置エネルギーである。
H2 の基底状態エネルギー (= E) は、-31.9587 eV である。
つまり、平衡状態では、位置エネルギーは、-31.9587 eV × 2 = - 63.9174 eV である。
ここでは、次のサンプル JAVA プログラムを使って、水素分子の軌道長がド・ブロイ波のちょうど1になることを示すことにする。
このプログラムは少し長いので、中に示すソースプログラムをコピーして、テキストエディタ(メモ帳など)にそのまま貼り付けて、コンパイルすれば簡単に実行できる。
このプログラムの class file name は hydd なので、このデキストエディタを "hydd.java" のファイル名で保存してコンパイルしてほしい。
このプログラムでは、原子核は灰色の円で示してある。
テキストボックス内の電子の各座標 (+X (MM), +Z (MM)) は、これらの原子核からの”相対的な”位置座標を示している。
(ele 0 は水素原子核 0 (H0), ele1 は H1 からの座標である。)
"nuc (MM)" はこれらの核と電子の距離である。
tV (eV) は全位置エネルギーである。
(FX, FZ) は各粒子(電子や核)に作用する力の成分を意味する。
(力の単位: 1000 = ボーア半径離れた +e の核と -e の電子の間に働く力。)
Waves (wn) は1軌道に含まれるド。ブロイ波の数を示している。
電子の座標 (+X, +Z) と核間距離は自由に変更できる。
(テキストボックス内に数値を入力して、Enter キーを押せばいい。)
各運動エネルギー (T) をもとに各電子の速度 ( = v (m/s) ) を計算する。
この速度 (v) と各電子に働く力 (F) を使って、次のように遠心力がこの力 (F) に等しくなると仮定する。
(Eq.1)
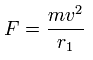
この r1 は、この式で出現する”仮の”半径である。
この r1 を使って、次のように1軌道に含まれるド・ブロイ波を計算することができる。
(Eq.2)
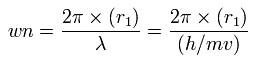
驚くべきことに、電子の位置が安定している (FX = 0) とき、ド・ブロイ波 (wn) は、Table 1 と 2 に示すようにちょうど 1.0 となる。
| tV (eV) | X (MM) | Z (MM) | FX | FZ | nleng | Waves(wn) |
|---|---|---|---|---|---|---|
| -60.0 | 1154 | 4984 | 0 | -1077 | 7414 | 1.037 |
| -62.0 | 996 | 4816 | 0 | -1154 | 7414 | 1.017 |
| -63.91 | 890 | 4665 | 0 | -1227 | 7414 | 1.001 |
| -65.0 | 830 | 4583 | 0 | -1271 | 7414 | 0.991 |
| -67.0 | 740 | 4440 | 0 | -1352 | 7414 | 0.975 |
核間距離 ( = nleng) の実験値は 7414 MM である。
また、全位置エネルギー (tV) が -63.91 eV (=実験値)のとき、ド・ブロイ波の数 (wn) はちょうど 1.001 となる。
Table 2 は次のようにこの距離を変化させてみる。
| nleng (MM) | X (MM) | Z (MM) | FX | FX (nuc) | eleng (MM) | tV (eV) |
|---|---|---|---|---|---|---|
| 6500 | 1275 | 4630 | 0 | 86 | 3950 | -64.76 |
| 7000 | 1025 | 4645 | 0 | 78 | 4950 | -64.34 |
| 7414 | 890 | 4665 | 0 | 74 | 5634 | -63.91 |
| 8000 | 730 | 4677 | 0 | 67 | 6540 | -63.53 |
| 8500 | 628 | 4710 | 0 | 59 | 7244 | -62.94 |
Table 2 に示すように、核間距離 (=nleng) が 7414 MM のときに、全位置エネルギー (tV) は -63.91 eV (= 実験値) になる。
つまり、我々は、H2 分子において、ビリアル定理とともに、Eq.1 と Eq.2 の考えを使えることを意味する。
Table 2 では、核間距離が 長くなるにつれて、全位置エネルギー tV は高くなる。これは H-H 結合はより不安定になる。
一方で、核間距離が短くなるにつれ、H0 核に作用する力 (FX (nuc)) はより強くなる。これは、核の位置が不安定になることを意味する。
また、nleng が 7414 MM (実験値) のとき、2つの電子のx座標の距離 (eleng) は 5634 MM ( = 7414 - 2 × 890) となる。
nleng が 7414 MM よりも短いとき、この eleng はボーア半径 ( = 5292 MM ) よりも短くなる。
つまり、おそらく "7414 MM" は電子と核が安定になる適切な値と言えるだろう。
(注意: 水素原子は たった1つしか電子がないため、核の位置を 1シーンのみで完全に安定にする ( = FX (nuc), FZ (nuc) を完全にゼロにする) ことはほぼ不可能である。このことは、炭素や酸素などの他の原子と違う。)
酸素のページ で示したように、このJAVA プログラムを使うことによって、我々は6つの価電子の運動のイメージ化に成功した。
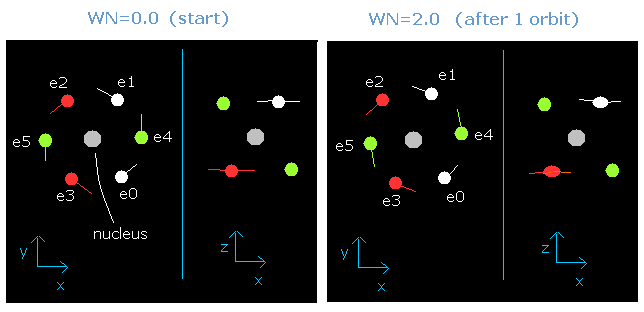
全エネルギーが 1 - 6th のイオン化エネルギーの和 (= -433.103 eV) と仮定したとき、6つの全電子は、1.9 (ほぼ 2.0) ド・ブロイ波長の軌道を進んだとき元の位置に戻ることを示した。
しかし、実際は2つの 1S 電子は +8e の酸素原子核から少し離れている。 そのためこれらの価電子に影響を与える”実質的な”中心電荷は +6e ( = +8e -2e ) よりも少し大きくなる。
この中心電荷を +6e のかわりに +6.3e としたとき、6つの電子すべては ちょうど 2ド・ブロイ波長の軌道を進んだときに元に戻る。
Fig. 2. wn = 0.0 と wn = 2.0 のときの酸素の電子状態 ("実質的な" 中心電荷 = +6.3e)
さらに、この運動は "正八面体"模型と組み合わせることにより、ビリアル定理とリンクしていた。
Fig. 3. 酸素の価電子 ("実質的な" 中心電荷 = +Ze)
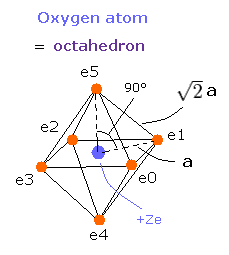
詳細な計算方法については、酸素のページ を参照のこと。
ビリアル定理によれば、6つの価電子の全位置エネルギー (tV) は 2 × -433.103 = -866.206 eV となる。
( 運動エネルギー (T) は 433.103 eV となる。)
これらの tV と T の値を基に、Fig.3 の 長さ a と電子の速度を知ることができる。
もし、Fig.3 の a の値を知ることができれば、我々は各電子に作用する力 (F) を決定することができる。
我々は、次のように 遠心力がこの力 (F) に等しいと仮定する。
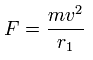
この r1 はこの関係式で出現する "仮の"半径である。
この r1 を使って、次のように1軌道に含まれるド・ブロイ波の数 (wn) を計算することができる。
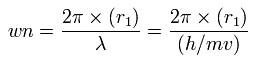
Z = 6.0 のとき、 この wn は 1.88 (ほぼ 1.9) となる。
また Z = 6.3 のとき、 この wn は ちょうど 2.01 となる。
炭素原子においても、”正四面体”模型をビリアル定理とともに使うことができた。(炭素のページ参照のこと。)
上のセクションでは、我々は水素分子の各電子に作用する力 (F) を使うことによって、H2 のド・ブロイ波の計算に成功した。
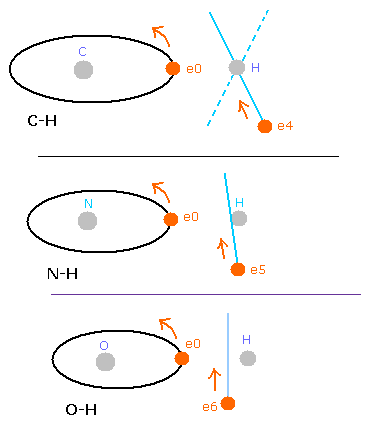
水素分子においては、この力 (F) の方向は H-H の結合線に垂直である。
しかし酸素や炭素原子においては、いくつかの電子 (例えば、Fig.4A の e0, e1 のような) は結合線に 平行である。
Fig. 4. O-H 結合における力の方向。
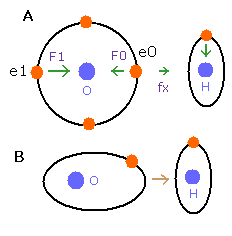
Fig. 4A の e0 や e1 では、上のド・ブロイ波の計算方法を使うことはできない。
酸素 (O) の電子 0 (e0) では、水素原子核からの反対方向の引力 (fx) のため、Fig.4A に示すように 力 F0 は、電子1の力 F1 よりも弱くなる。
つまり、Eq.1 では、e0 の”仮の”半径 r1 は e1 に比べて長く なる。
これは、Eq.1, Eq.2 の計算方法を使うと、e1 (< 2.0) よりもより多くのド・ブロイ波 (> 2.0) が e0 軌道に含まれてしまう。
しかし、もし、1つのみの電子軌道に注目すると (Fig.4B)、ド・ブロイ波の数 ( = 2.0 ) はその軌道の位置や形を変化させることで維持される。
(正の電荷の水素原子核は、この電子軌道を少し平行移動させ、またそれを楕円形に変化させる。)
つまり、われわれは酸素原子のすべての電子軌道の”平均の”ド・ブロイ波を計算しなければならない。
Fig. 5. O-H 結合における”正八面体”の変化。
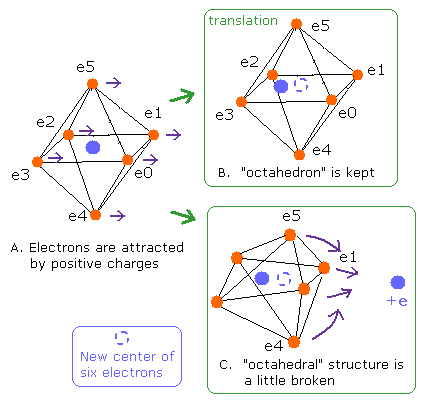
もし酸素のすべての価電子が同じ力で引きつけられるとしたら、すべての軌道は等しく平行移動し、また”八面体”構造は維持される (Fig. 5B)。
Fig.5B の場合は、すべてのド・ブロイ波の数は 2.0 になる必要がある。
しかし、もしこれらの価電子が他の正電荷の核に 不均等に引きつけられるとしたら、”正八面体”構造は壊れる (Fig. 5C)。
これらの違い (Fig.5B と Fig.5C) を我々はどうすれば区別できるのだろうか?
もし、6つの価電子の新しい中心を、原子核と仮定すると、Fig.5B のすべてのド・ブロイ波は Fig.5A のように 2.0 のままである。
しかしFig.5C では、八面体構造の変化により、例えこの新しい中心を核としても、ド・ブロイ波のいくつかは 2.0 と異なる可能性がある。
そこで、我々は下のプログラムの中では、酸素、炭素、窒素の価電子においてこの”新しい中心核”を利用することにする。
(この新しい中心の座標 = noxx[0-2]、この新しい中心をベースにした各電子に働く力の成分 = teqq[el][0-2])
ビリアル定理によれば、平均の位置エネルギー (V) と運動エネルギー (T) は、-1/2 V = T の関係を満たす。
原子の場合は、原子核が1つしかないので、各電子のV を計算するのは簡単だ。
しかし、分子の場合は少し複雑だ。なぜなら V は原子核間の反発する位置エネルギーを含む必要があるからだ。
問題はどのようにこの核間の位置エネルギーを各電子に分配するかである。
例えば、水の O-H 結合では、2つの正電荷の核は、他の核に属する電子によって引きつけられる必要がある。(Fig.6)
Fig. 6. O-H 結合と各位置エネルギーの変化。
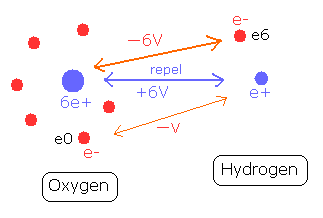
水素原子核 (e+) は、酸素原子の6つの電子に引きつけられる。
水素原子核と酸素の1つの電子 (e0) の間の位置エネルギーは -V である。
一方で、酸素原子核は、水素原子に属する1つの電子 (e6) によって引きつけられる。そのため、酸素原子核とこの電子 e6 の間の位置エネルギーは - 6V となり、この結合力は、上の場合の6倍も強い。
つまり、水素の電子 (e6) の位置エネルギーは O-H 結合で-6V も低くなる。しかし、そのかわり 電子 e6 は、2つの反発する原子核を結合させるのに 多くのしごとをしなければならない。よって、この影響でそれよりかは、少し位置エネルギーは高くなる。
この事実をもとに、このプログラムでは、電子ー電子間、電子ー原子核間の位置エネルギーを計算の後、反発する原子核間の位置エネルギーを各電子に分配する。
例えば、この反発するエネルギーが、+6V のとき、e6 と e0 の分配比は 6 : 1 (= -6V : -V) とする。
酸素は6つの e0 - e5 の電子を持つため、 +6V × 6/(1x6 +6) = +6V / 2 が e6 に分配され、+6V × 1/(1x6+6)= +6V / 12 が e0 に分配される。
(下のプログラムでは、各電子の他の原子核との相互作用 (V = rhp[el][5]) を計算し、この rhp[el][5] に比例するように、核間の反発する位置エネルギーが各電子に分配される。)
その各位置エネルギーをもとに、運動エネルギーが分配される。
基本的に、力の両端には同じ大きさの力がかかる。
水素原子側では、1つの電子 (e6) でしか、対処できないが、酸素原子側では、この被る力が6つの電子に分割されるので、
上記の原理が有効なのである。
メタン (CH4) のすべてのC-H 結合を切断するのに 1663 kJ/mol ( = 17.235 eV ) が必要である。
つまり、メタンの基底状態エネルギー(4つの炭素の価電子+4つの水素原子)は、-148.024 -54.416 -17.235 = 219.675 eV となる。
また、平均の C-H 結合長は 1.09 × 10-10 meter (=10900 MM) である。
Fig. 7. 炭素の価電子 ("実質的な" 中心電荷 = +Ze)
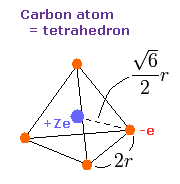
炭素のページで示したように、炭素の価電子の運動は、ビリアル定理とともに、”正四面体”の構造とリンクしている。
ビリアル定理によれば、”平均の”位置エネルギーは (V) は、2 × -148.024 (E) = -296.048 eV となる。
(全運動エネルギー (T) は、148.024 eV となる。)
この V の値をもとに、Fig.7 の 長さ(2r) が決定する。
(この状態では、r は 5260 MM となる。)
もし、2r の値が決まると、各電子に作用する力 (F) の値が分かる。
ここで、次のように遠心力がこの力 (F) に等しいと仮定する。
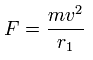
この r1 は 仮の半径で、この式によって初めて現れる。
この r1 を使って、次のように1軌道に含まれるド・ブロイ波の数 (wn) を計算することができる。
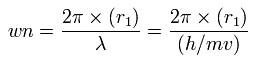
Z = +4.0 のとき、 この wn は 1.87 (ほぼ 1.9) となる。
また、 Z = +4.25 のとき、 この wn は ちょうど 2.02 となる。
(この章では、我々は Z=+4.23を使う。すると、wn は 2.007 (ほぼ 2.0) となる。)
メタン (CH4) の C-H 結合の計算にこの簡単な四面体構造を利用する。
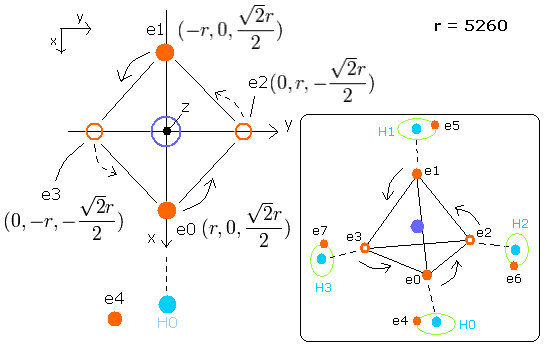
Fig. 8. 推定されるメタン (CH4) 模型。
CH4 のサンプル JAVA プログラム (ビリアル定理)
このプログラムでは、核は灰色の円で、また各粒子は、X-Y (左)、X-Z (中心)、Y-Z (右) 平面上に表示される。
ここでは、電子4 (ele 4) の座標 (+X, +Y, +Z) のみ変更することができる。なぜなら、CH4 では、4つの水素原子核と電子は必ず対称的に配置されるからである。
(ele 4 のテキストボックス内に値を入力して、Enter キーを押せばいい。)
"nuc (MM)" はこれらの核と電子の距離である。
V (eV) と T (eV) は各電子の位置エネルギーと運動エネルギーを示している。
tV (eV) は全位置エネルギーである。
ele 0-3 の CF は、中心方向への力を意味し、ele 4-7 のCF は C-H line 方向への(C-H line に垂直な方向への)力を意味する。
(fx, fy, fz) は CF を除いた残りの力の成分を意味する。
(ここでは、ele0-3 の力の中心として、rpp[el][0-2] という配列変数を使っている。)
rpp[el][0-2] は炭素原子核、4つの水素原子核と 4-7 の4つの電子の合計の力の成分を意味する。
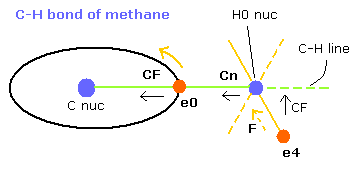
Fig. 9. メタンの C-H 結合 (ビリアル定理)
ビリアル定理によれば、CH4 の全位置エネルギー (tV) は - 219.675 × 2 = 439.3 eV となる。
tV が -439.3 eV で、ド・ブロイ波が 2.0 (炭素) と 1.0 (水素) のとき、メタンの8つの電子はどう配置されるのだろうか?
電子 0 (e0) が Fig.9 の位置にあるとき、それは H0 核に最も近づいているときである。
(C-H の長さが 10900 のとき、e0 と H0 核の距離は 約 4500 MM である。)
そのため、この状態では、e4 は e0 からして H0 を挟んだ逆の位置あたりに存在し、また H0 核を安定させるためには、Cn はできる限り小さくする必要がある。
Fig. 10. CH4 の電子配置 (C-H = 10900 MM, tV= -440.53 eV)
| eNo | X (MM) | Y (MM) | Z (MM) | nuc (MM) | CF | fx | fy | fz | Waves(wn) |
|---|---|---|---|---|---|---|---|---|---|
| ele 0 | 5260 | 0 | 3719 | 6442 | 1249 | -1 | 0 | 1 | 2.007 |
| ele 1 | -5260 | 0 | 3719 | 6442 | 1249 | 1 | 0 | 1 | 2.007 |
| ele 2 | 0 | 5260 | -3719 | 6442 | 1249 | 0 | -1 | -1 | 2.007 |
| ele 3 | 0 | -5260 | -3719 | 6442 | 1249 | 0 | 1 | -1 | 2.007 |
| ele 4 | 1850 | -4152 | 1820 | 4896 | 858 | -481 | 0 | -340 | 0.999 |
| ele 5 | -1850 | 4152 | 1820 | 4896 | 858 | 481 | 0 | -340 | 0.999 |
| ele 6 | 4152 | 1850 | -1819 | 4896 | 858 | 0 | -481 | 340 | 0.999 |
| ele 7 | -4152 | -1850 | -1819 | 4896 | 858 | 0 | 481 | 340 | 0.999 |
Table 3 は 我々がド・ブロイ波の条件と実験値が適切に結合できることを示している。
(Table 3 では、tV は -440.53 eV (実験値 -439.3 eV) でド・ブロイ波は 炭素で2.007 (ほぼ 2.0)、水素で 0.999 (ほぼ 1.0) である。 )
この結果によれば、水素原子核側の電子は Fig.9 の e4 のように歳差運動しながら運動している。
電子 4 は水素原子核の方向にひきつけられ、CF (= C-H line 方向への力)とは異なる。
C-H の長さが 10900 MM のとき、Cn (Fig.9) の最も小さい値は 101 である。
(力の単位: 1000 = ボーア半径離れた +e の核と -e の電子の間に働く力。)
もし、電子 4 (e4) のド・ブロイ波 0.999 を保ったまま、この Cn の 101 の値を減らそうとしようとすると、これ以上減らせないことが分かるだろう。(C-H=10900 MM のとき、101 が最少。)
この Cn (=101) のとき、tV は -440.53 eV になり、これはほぼ実験値と同じである。
Fig.9 では、電子 0 (e0) は、H0 核に最も近づいている。そのため H0 核の Cn はゼロより少し大きいと思われる。
次に、スクロールバーの中から "9500", "10000", "11400" のどれかを選択し、"C-H (MM)" ボタンをクリックする。
自動的に、8つの電子が次の2つの条件 を満たすように配置される。
1. ド・ブロイ波: (C = 2.007, H = 0.999)。
2. Cn が、各核間距離においてなるべく小さくなるようにする。
| C-H (MM) | X (ele4) | Y (ele4) | Z (ele4) | CF (ele0) | Cn (H0) | Wave (ele0) | Wave (ele4) | tV (eV) |
|---|---|---|---|---|---|---|---|---|
| 9500 | 1700 | -2940 | 2070 | -24 | 846 | 2.007 | 0.999 | -498.5 |
| 10000 | 1400 | -3289 | 2500 | 609 | 467 | 2.007 | 0.999 | -471.1 |
| 10900 | 1850 | -4152 | 1820 | 1249 | 101 | 2.007 | 0.999 | -440.5 |
| 11400 | 1600 | -4379 | 2000 | 1462 | -7 | 2.007 | 0.999 | -430.6 |
Table 4 は C-H 結合長が 10900 MM (実験値)のとき、tV が -440.5 eV (ほぼ実験値)になることを示している。
C-H 結合長が 10900 MM よりも短いとき、水素原子核 (H0) は不安定になる。
C-H 結合長が 10000 MM のとき、H0 原子核は 電子 0 に近づく、そのため Cn (H0 原子核に作用する力でC原子核方向の成分)が”不自然に”大きくなる (Cn = 467)。 (Fig. 9 を参照のこと。)
(力の単位: 1000 = ボーア半径離れた +e の核と -e の電子の間に働く力。)
この状態では、電子 0 に作用する力の C 核方向の成分 (CF) は Cn とほぼ同じになっている (CF = 609, Cn=467)。
これはおかしいと言わざるを得ない。
C-H 結合長が 9500 MM のとき、H0 原子核は 電子 0 により近づく。そのため、電子 0 (e 0) はなんと C 原子核のかわりに H0 原子核にひきつけられるという異常事態になる。 (CF(ele0) = -24, Cn(H0) =846) (Fig.9も参照のこと。)
もし、このプログラムを実行し、電子の座標を変化させようとすると、ド・ブロイ波の条件が満たされるときは Cn は減らせないことがわかるだろう。
C-H 結合長が 10900 MM のとき、Cn (H0) は十分に小さく (Cn(H0)=101) 安定し、また CF (ele 0) は C 原子核に引きつけられるぐらい大きい (CF(ele0) = 1249)。
C-H 結合長が 長く (11400 MM) なると、tV は実験値よりも高くなる。(tV = -430.6 eV > - 439.3 eV)
つまり、結合状態は 10900 MM よりも不安定になる。
(水素原子は1つしか電子がない。そのため1つの場面のみで Cn がゼロにならなくても自然と言える。
しかし、Cn が 400-500 以上に極端に大きくなることは不自然と言わざるを得ない。)
次に我々は、ビリアル定理を使って H2O 分子模型に挑戦することにする。
1つの O-H 結合エネルギーの平均は 9.6066 eV (=926.9 kJ/mol) / 2 = 4.8033 eV である。
つまり、H2O の全エネルギーは -433.103 (O) - 2 × 13.606 (H) - 9.6066 (bond energy) = -469.92 eV. となる。
Fig. 11. 推定される 水分子 (H2O) 模型。
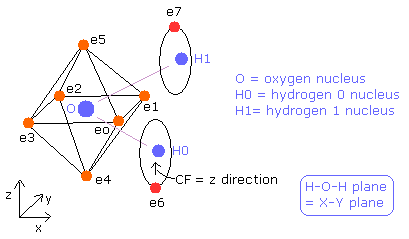
次のプログラムを使って、我々は 水分子 (H2O) の構造を探究することにする。
サンプル JAVA プログラム H2O (ビリアル定理)
このプログラムでは、我々は”中心の”電荷を +6.3 (このとき、Fig.3 でドブロイ波は 2.01 となる。)のかわりに、+6.273 とする。(このとき、Fig.3 のド・ブロイ波は 2.00 となる。)
このプログラムは少し長いので、中に示すソースプログラムをコピーして、テキストエディタ(メモ帳など)にそのまま貼り付けて、コンパイルすれば簡単に実行できる。
このプログラムの class file name は watr なので、このデキストエディタを "watr.java" のファイル名で保存してコンパイルしてほしい。
このプログラムでは、原子核は灰色の円で示してある。
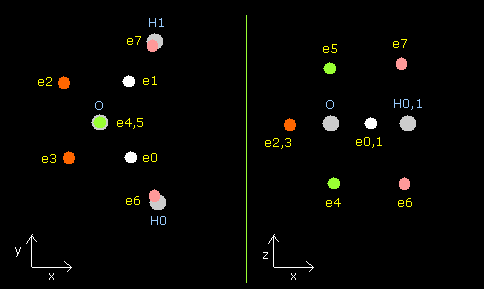
H2O の各粒子は、X-Y 平面(左)、X-Z 平面 (中心)、Y-Z 平面 (右)に表示される。
テキストボックス内の電子の各座標 (+X (MM), +Y (MM), +Z (MM)) は、これらの原子核からの”相対的な”位置座標を示している。
(ele 0-5 は酸素原子核からの、 ele 6 は 水素原子核 0 (H0)からの、ele7 はH1 からの相対座標である。)
すべての電子の座標 (+X, +Y, +Z) は自由に変更することができる。
(テキストボックス内に値を入力して、Enter キーを押せばいい。)
ele 0-5 の CF は、中心方向への力を意味し、ele 6,7 のCF は H-O-H 平面への方向の力 (+z 軸方向) を意味する。
(fx, fy, fz) は CF を除いた残りの力の成分を意味する。
(FX, FY, FZ) は各原子核に作用する力の成分を意味する。
H0, On は H0 核方向、 O 核方向への力の成分を意味する。
Waves (wn) は1軌道に含まれるド。ブロイ波の数を示している。
スクロールバーの中から、O-H 結合長 (MM) を選択して、"O-H (MM)" ボタンをクリックすると、O-H の核間距離が変化する。
また、スクロールバーの中から角度を選択し、”angle” ボタンをクリックすると、H-O-H 角が変化する。
酸素原子の6つの価電子は核の周囲に均等に分布している。
酸素原子では、もし CF が核方向の力と定義すると、CF 以外の力成分 (fx, fy, fz) は、6つの電子が 正八面体状に分布していると、ゼロになる。
しかし、水分子においては、酸素原子に加えて2つの水素原子を考慮する必要がある。
つまり、H2O の CF は酸素原子核に加えて 2つの水素原子核と電子を含むことになる。
(プログラムでは、rpp[el][0-2] という配列変数が、酸素原子核、2つの水素原子核と電子の合計の力である CF 方向への力成分としている。)
Fig. 12. 水分子 (H2O) の構造。
| eNo | X (MM) | Y (MM) | Z (MM) | nuc (MM) | CF | fx | fy | fz | Waves(wn) |
|---|---|---|---|---|---|---|---|---|---|
| ele 0 | 3151 | -3244 | 0 | 4522 | 5586 | 1 | 1 | 0 | 1.989 |
| ele 1 | 3151 | 3244 | 0 | 4522 | 5586 | 1 | -1 | 0 | 1.989 |
| ele 2 | -3290 | 3290 | 0 | 4652 | 5723 | 0 | 0 | 0 | 2.011 |
| ele 3 | -3290 | -3290 | 0 | 4652 | 5723 | 0 | 0 | 0 | 2.011 |
| ele 4 | 0 | 0 | -4557 | 4557 | 6110 | 0 | 0 | 0 | 1.989 |
| ele 5 | 0 | 0 | 4556 | 4556 | 6113 | 0 | 0 | 0 | 1.989 |
| ele 6 | -260 | 319 | -4535 | 4553 | 1232 | 7 | -4 | 0 | 0.995 |
| ele 7 | -260 | -319 | 4535 | 4553 | -1232 | 7 | 3 | 0 | 0.995 |
平衡状態 では、(fx, fy, fz) はなるべく小さくする必要がある。(できれば 10 未満に。)
H2O では、電子 6,7 (ele 6,7) は CH4 よりも酸素に近づいている。そのため、ele 6,7 の (fx, fy, fz) は、ほぼゼロになっている。
(力の単位: 1000 = ボーア半径離れた +e の核と -e の電子の間に働く力。)
Table 5 では、全位置エネルギー (tV) は、-938.18 eV となり、これは実験値 (-469.92 × 2 = -939.84 eV) とほぼ同じである。
もし、酸素原子核を 安定にしようと (FX = -9, FY = 0, FZ= 3 of O nuc となっている)、”正八面体”構造が 少し壊れる。
そのため Table 5 では、電子 0-5 のド・ブロイ波は 2.00 と少し異なる。
(誤差は、± 0.011 である。)
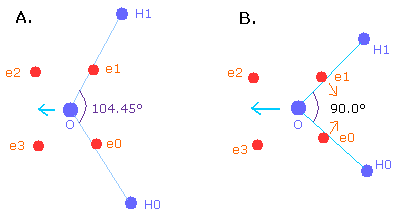
ところで、どうして H-O-H 角は 90°でなく 104.45°なのだろうか?
次に、スクロールバーの中から 90.0 を選択し、”angle”ボタンをクリックする。
自動的に適切な条件 (= ele の (fx, fy, fz) と O nuc の (FX, FY, FZ) が小さくなる) がセットされる。
| eNo | X (MM) | Y (MM) | Z (MM) | nuc (MM) | CF | fx | fy | fz | Waves(wn) |
|---|---|---|---|---|---|---|---|---|---|
| ele 0 | 3214 | -3215 | 0 | 4545 | 5480 | 2 | 2 | 0 | 1.99 |
| ele 1 | 3214 | 3215 | 0 | 4545 | 5480 | 2 | -2 | 0 | 1.99 |
| ele 2 | -3284 | 3293 | -10 | 4650 | 5741 | 2 | 2 | 2 | 2.015 |
| ele 3 | -3284 | -3293 | 10 | 4650 | 5741 | 2 | -2 | -2 | 2.015 |
| ele 4 | 0 | 0 | -4562 | 4562 | 6098 | -9 | -2 | 0 | 1.989 |
| ele 5 | 0 | 0 | 4562 | 4562 | 6098 | -9 | 2 | 0 | 1.989 |
| ele 6 | -162 | 330 | -4435 | 4450 | 1278 | -1 | -3 | 0 | 0.995 |
| ele 7 | -162 | -330 | 4435 | 4450 | -1278 | -1 | 3 | 0 | 0.995 |
H-O-H 角度が 90°のとき、104.45°のときより”正八面体”構造がより壊れる。
そのため、電子 2, 3 のド・ブロイ波が 2.00 より 0.015 異なる。
(104.45°のとき、誤差は 0.011 である。)
角度が 90.0°のとき、酸素原子核は2つの水素原子核に左側にはねのけられる (Fig.13)。
(一方で、電子はそれらにひきつけられる。)
つまり、酸素原子核を安定にするには (= O nuc の FX, FY, FZ が小さい)、104.45°のときよりも、酸素の構造を変化させる必要がある。
Fig. 13. 原子核は互いに反発しあう。
次に スクロールバーの中から、"110.0" を選択し、"angle" ボタンをクリックする。
| eNo | X (MM) | Y (MM) | Z (MM) | nuc (MM) | CF | fx | fy | fz | Waves(wn) |
|---|---|---|---|---|---|---|---|---|---|
| ele 0 | 3138 | -3247 | 0 | 4515 | 5625 | -3 | -3 | -1 | 1.987 |
| ele 1 | 3138 | 3247 | 0 | 4515 | 5625 | -3 | 3 | 1 | 1.987 |
| ele 2 | -3290 | 3290 | -20 | 4652 | 5722 | 0 | 0 | 4 | 2.011 |
| ele 3 | -3290 | -3290 | 20 | 4652 | 5722 | 0 | 0 | -4 | 2.011 |
| ele 4 | 0 | 0 | -4556 | 4556 | 6116 | 1 | -4 | 0 | 1.989 |
| ele 5 | 0 | 0 | 4556 | 4556 | 6116 | 1 | 4 | 0 | 1.989 |
| ele 6 | -260 | 330 | -4650 | 4668 | 1182 | -4 | 2 | 0 | 0.994 |
| ele 7 | -260 | -330 | 4650 | 4668 | -1182 | -4 | -2 | 0 | 0.994 |
110°のときのド・ブロイ波の数は 104.45°のときとほぼ同じである。
しかし、110.0°のときは、全位置エネルギー (tV = -936.85 eV) は、104.45°のとき (-938.18 eV) よりも高くなる。
(実験値は、tV = -939.84 eV である。)
そのため、110°では、結合の強さは弱くなる。
酸素原子核の e0 - O - e1 の角度は”正八面体”構造のため 90°である。
110.0°は、安定した O-H 結合を形成するには 大きすぎる (110 > > 90) と思われる。
次に "104.45" を選択し、"angle" ボタンをクリックする。 (= 元の状態に戻る。)
それから、スクロールバーの中から "9000" を選び、"O-H (MM)" ボタンをクリックする。
| eNo | X (MM) | Y (MM) | Z (MM) | nuc (MM) | CF | fx | fy | fz | Waves(wn) |
|---|---|---|---|---|---|---|---|---|---|
| ele 0 | 3120 | -3240 | 0 | 4497 | 5471 | 0 | 0 | -1 | 1.983 |
| ele 1 | 3120 | 3240 | 0 | 4497 | 5471 | 0 | 0 | 1 | 1.983 |
| ele 2 | -3290 | 3290 | -20 | 4652 | 5720 | -1 | -1 | 4 | 2.010 |
| ele 3 | -3290 | -3290 | 20 | 4652 | 5720 | -1 | -1 | -4 | 2.010 |
| ele 4 | 0 | 0 | -4557 | 4557 | 6113 | 0 | -4 | 0 | 1.990 |
| ele 5 | 0 | 0 | 4557 | 4557 | 6113 | 0 | 4 | 0 | 1.990 |
| ele 6 | -260 | 310 | -4310 | 4328 | 1342 | 0 | 4 | 0 | 0.995 |
| ele 7 | -260 | -310 | 4310 | 4328 | -1342 | 0 | -4 | 0 | 0.995 |
90°のときのように (Fig.13)、O-H 結合長が 9584 MM よりも短いとき、酸素原子核は2つの水素原子核による反発力が強くなる。
そのため、O-H 結合長が 9000 MM のとき、”八面体”構造は酸素原子核の安定のためにはより崩れてしまう。
Table 8 に示したように、電子 0, 1 のド・ブロイ波は 1.983 (誤差は -0.017) になる。
もし電子 0, 1 を 1.983 の値を 2.00 に近づくようと動かそうとすると、電子 2 の値 2.010 は代わりに大きくなってしまう。(例えば、2.016 など。)
そのため、この”壊れた”構造を戻すことはできない。一度試してほしい。
(この場合は、tV は -944.88 eV になり、これは -939.84 eV の実験値よりも低い。 )
次に我々はスクロールバーの中から 10000 を選択し、"O-H" ボタンをクリックする。
| eNo | X (MM) | Y (MM) | Z (MM) | nuc (MM) | CF | fx | fy | fz | Waves(wn) |
|---|---|---|---|---|---|---|---|---|---|
| ele 0 | 3150 | -3245 | 0 | 4522 | 5677 | 5 | 5 | -1 | 1.989 |
| ele 1 | 3150 | 3245 | 0 | 4522 | 5677 | 5 | -5 | 1 | 1.989 |
| ele 2 | -3290 | 3290 | -20 | 4652 | 5724 | 0 | 0 | 4 | 2.011 |
| ele 3 | -3290 | -3290 | 20 | 4652 | 5724 | 0 | 0 | -4 | 2.011 |
| ele 4 | 0 | 0 | -4558 | 4558 | 6104 | 1 | -4 | 0 | 1.989 |
| ele 5 | 0 | 0 | 4558 | 4558 | 6104 | 1 | 4 | 0 | 1.989 |
| ele 6 | -200 | 300 | -4800 | 4813 | 1118 | -7 | 6 | 0 | 0.995 |
| ele 7 | -200 | -300 | 4800 | 4813 | -1118 | -7 | -6 | 0 | 0.995 |
Table 9 のときのド・ブロイ波の数は Table 5 のときとほぼ同じである。
しかし、O-H 結合長が 9584 MM よりも長いとき、tV は高くなってしまう。(tV = -933.66 eV)
これは、結合の力が弱くなることを意味する。
他の組み合わせ (9000 x 90°、9000 x 110°、10000 x 90°、10000 x 110°) も試すことが可能である。
これらの組み合わせでは、自動的には適切な初期条件がセットされないため、自分で電子の座標を調整する必要がある。
各電子の (fx, fy, fz)と O nuc の (FX, FY, FZ) をなるべく小さくするように。(できれば 10 以下に。)
もしこれも試してみれば、Table 5 がもっともよい条件だということがわかるだろう。
メタン (CH4) のときと比べて、H2O の水素の電子 (6, 7) は酸素原子核に より近づく。
(Fig.10 と Fig.12 を参照のこと。)
Fig. 14. C-H 結合と O-H 結合の違い。
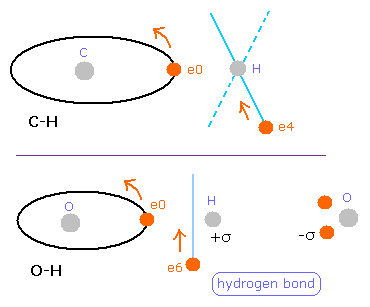
そのため H2O では、Fig.14 に示すように、水素結合が他の分子と形成されると思われる。
次にビリアル定理を使って、NH3 分子構造にトライしてみる。
1つの N-H 結合エネルギーは 4.052 eV (=391 kJ/mol) である。
そのため NH3 の全エネルギーは、-266.94 (N) - 3 × 13.606 (H) - 3 × 4.052 (bond energy) = --319.914 eV. である。
(266.94 eV は 1-5th のイオン化エネルギーの合計である。)
NH3 の N-H 結合長は、10170 MM (= 1.0170 × 10-10 meter) である。
H-N-H の角度は、107.8°で 109.5°(正四面体)よりも少し小さい。
Fig. 15. 推定されるアンモニア (NH3) 模型。
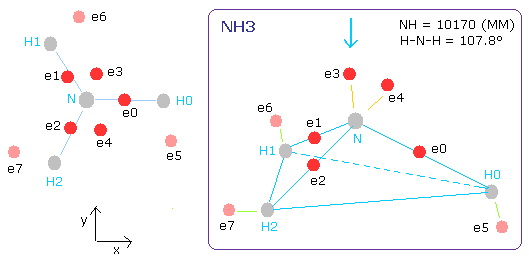
窒素のページでは、窒素 (N) の5つの価電子の軌道がほぼ 2.0 ド・ブロイ波長であることを示した。
このセクションでは、ビリアル定理と、ド・ブロイ波を満たすアンモニア (NH3) 模型を探究することにする。
NH3 のサンプル JAVA プログラム (ビリアル定理)
(このプログラムでは、 中心電荷は +5.25eとしている。)
このプログラムは少し長いので、中に示すソースプログラムをコピーして、テキストエディタ(メモ帳など)にそのまま貼り付けて、コンパイルすれば簡単に実行できる。
このプログラムの class file name は NH3 なので、このデキストエディタを "NH3.java" のファイル名で保存してコンパイルしてほしい。
このプログラムでは、NH3 の各粒子は、x-y 平面(左)、x-z 平面 (中心)、y-z 平面 (右)に表示される。
ここでは、新しい単位として ( 1 MM = 10-14 meter) を使っている。
テキストボックス内の電子の各座標 (+X (MM), +Y (MM), +Z (MM)) は、これらの原子核からの”相対的な”位置座標を示している。
(ele 0-4 は窒素原子核からの、 ele 5 は 水素原子核 0 (H0)からの、ele6 はH1 からの、ele7 は H2 からの相対座標である。)
すべての電子の座標 (+X, +Y, +Z) は自由に変更することができる。
(テキストボックス内に値を入力して、Enter キーを押せばいい。)
tV (eV) は全位置エネルギーである。
ele 0-4 の CF は、中心方向への力を意味し、ele 5,6,7 のCF は 各 N-H line 方向への力(= N-H line に垂直な力)を意味する。
(fx, fy, fz) は CF を除いた残りの力の成分を意味する。
(FX, FY, FZ) は各原子核に作用する力の成分を意味する。
H0 核の Nf は N 核方向への力の成分を意味する。
Waves (wn) は1軌道に含まれるド。ブロイ波の数を示している。
スクロールバーの中から、N-H 結合長 (MM) を選択して、"N-H (MM)" ボタンをクリックすると、N-H の核間距離が変化する。
また、スクロールバーの中から角度を選択し、”angle” ボタンをクリックすると、H-N-H 角が変化する。
”e5,6,7” ボタンをクリックすると、 電子 5, 6, 7が対称的に配置される。
NH3 の CF は窒素原子核に加えて、3つの水素原子核と電子を含んでいる。
(このプログラムでは、配列変数 rpp[el][0-2] が CF 方向への力成分をしめしており、これは窒素原子核と3つの水素原子核と電子を合計したものである。)
Fig. 16. NH3 の分子構造 (control. tV= -639.4 eV).
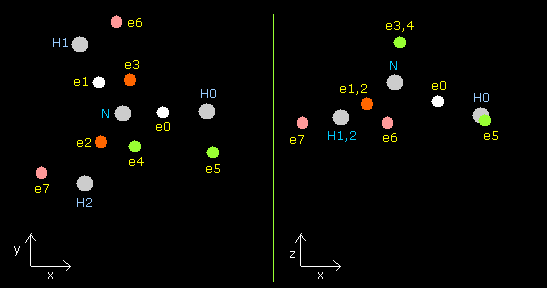
| eNo | X (MM) | Y (MM) | Z (MM) | nuc (MM) | CF | fx | fy | fz | Waves(wn) |
|---|---|---|---|---|---|---|---|---|---|
| ele 0 | 4870 | 0 | -2350 | 5407 | 3000 | 1 | 0 | 2 | 2.002 |
| ele 1 | -2685 | 3685 | -2488 | 5194 | 3508 | 4 | 0 | -3 | 1.988 |
| ele 2 | -2685 | -3685 | -2488 | 5194 | 3515 | 4 | -1 | -2 | 1.988 |
| ele 3 | 595 | 3780 | 3950 | 5499 | 3545 | -13 | -8 | 9 | 2.011 |
| ele 4 | 595 | -3780 | 3950 | 5499 | 3547 | -12 | 8 | 9 | 2.011 |
| ele 5 | 340 | -4380 | -370 | 4408 | 1230 | -190 | 0 | 77 | 0.998 |
| ele 6 | 3790 | 2506 | -400 | 4561 | 1185 | 104 | -183 | 64 | 0.996 |
| ele 7 | -4020 | 1770 | -450 | 4415 | -1228 | 98 | 175 | 116 | 0.996 |
3つの水素原子核の反発力のために、窒素原子核を安定にするためには(= N nuc の FX, FY, FZ が小さい)、ド・ブロイ波は 2.00 と少し異なる必要がある。
Table 10 では、全位置エネルギー (tV) は -639.4 eV であり、これは実験値とほぼ同じである。(= 2 × -319.914 = -639.82 eV)
電子 5-7 は水素原子核の少し 外側にあるため (Fig.16)、電子 5-7 の(fx, fy, fz) は ゼロにならない。
これらは、H2O よりも外側にあるが (Fig.12 参照)、CH4 よりも内側にある (Fig.10 参照)。
Fig. 17. C-H, O-H, N-H 結合の比較。
次に、スクロールバーから ”100.0”を選択し、"angle"ボタンをクリックする。
自動的に適切な初期条件がセットされる。
| eNo | X (MM) | Y (MM) | Z (MM) | nuc (MM) | CF | fx | fy | fz | Waves(wn) |
|---|---|---|---|---|---|---|---|---|---|
| ele 0 | 4820 | 0 | -2510 | 5434 | 2934 | -5 | -1 | -10 | 2.002 |
| ele 1 | -2695 | 3685 | -2570 | 5239 | 3368 | 13 | 2 | -11 | 1.988 |
| ele 2 | -2695 | -3685 | -2570 | 5239 | 3368 | 12 | -2 | -11 | 1.988 |
| ele 3 | 616 | 3780 | 3940 | 5494 | 3565 | -11 | -7 | 9 | 2.022 |
| ele 4 | 600 | -3780 | 3940 | 5492 | 3569 | -10 | 8 | 9 | 2.021 |
| ele 5 | 350 | -4280 | -370 | 4310 | 1279 | -209 | 0 | 83 | 0.996 |
| ele 6 | 3680 | 2500 | -440 | 4470 | 1222 | 119 | -209 | 92 | 0.997 |
| ele 7 | -4000 | 1700 | -450 | 4369 | 1244 | 107 | 186 | 117 | 0.996 |
H-N-H 角が 107.8°よりも小さいとき、3つの水素原子核の上方に反発させる力がより強くなる。(Fig. 15 参照)。
そのため、窒素原子核を安定にさせるためには、窒素の電子 0-4 の対称的な配置は 107.8°のときよりもより壊れることになる。
Table 11 に示すように、電子 3, 4 のド・ブロイ波はより大きくなる。(誤差は +0.022 である。)
もし、この値を 2.022 よりも減らそうとすると、かわりに電子 1, 2 のドブロイ波は 1.988 よりも小さくなってしまう。
そのため この誤差は減らすことができない。これも試してみるといい。
次に、スクロールバーから ”110.0”を選択し、"angle"ボタンをクリックする。
| eNo | X (MM) | Y (MM) | Z (MM) | nuc (MM) | CF | fx | fy | fz | Waves(wn) |
|---|---|---|---|---|---|---|---|---|---|
| ele 0 | 4880 | 0 | -2380 | 5429 | 2990 | 7 | 0 | 14 | 2.003 |
| ele 1 | -2695 | 3685 | -2470 | 5190 | 3538 | -1 | 3 | 6 | 1.989 |
| ele 2 | -2695 | -3685 | -2470 | 5190 | 3556 | -1 | -3 | 6 | 1.989 |
| ele 3 | 650 | 3780 | 3940 | 5498 | 3549 | -19 | -7 | 10 | 2.011 |
| ele 4 | 650 | -3780 | 3940 | 5498 | 3551 | -18 | 7 | 10 | 2.011 |
| ele 5 | 290 | -4400 | -370 | 4425 | 1222 | -172 | -1 | 77 | 0.998 |
| ele 6 | 3820 | 2600 | -350 | 4634 | 1155 | 107 | -186 | 60 | 0.995 |
| ele 7 | -4020 | 1800 | -450 | 4427 | 1225 | 95 | 170 | 117 | 0.995 |
110°の場合は、ド・ブロイ波は Table 10 のコントロールの場合とほぼ同じになる。
しかし、全位置エネルギー (tV) はコントロール (= -639.4 eV) の場合よりも高くなる (= -637.98 eV)。
(実験値の tV は -639.82 eV である。)
そのため、この場合では結合状態がより弱くなっているといえる。
次に、”107.8”を選択し、"angle"ボタンをクリックする。すると元の状態にもどる。
それから "9000" を選択し、"N-H (MM)" ボタンをクリックする。
| eNo | X (MM) | Y (MM) | Z (MM) | nuc (MM) | CF | fx | fy | fz | Waves(wn) |
|---|---|---|---|---|---|---|---|---|---|
| ele 0 | 4800 | 0 | -2160 | 5263 | 2600 | 7 | 0 | 14 | 1.981 |
| ele 1 | -2540 | 3750 | -2400 | 5125 | 3139 | 0 | 5 | 7 | 1.986 |
| ele 2 | -2540 | -3750 | -2400 | 5125 | 3177 | 0 | 0 | 0 | 1.987 |
| ele 3 | 490 | 3800 | 4150 | 5648 | 3337 | -9 | 2 | -1 | 2.025 |
| ele 4 | 450 | -3800 | 4100 | 5608 | 3399 | -5 | 3 | 3 | 2.014 |
| ele 5 | 800 | -4200 | -500 | 4304 | 1236 | -383 | 0 | 139 | 0.998 |
| ele 6 | 3470 | 2480 | -440 | 4287 | 1288 | 159 | -280 | 96 | 0.995 |
| ele 7 | -3700 | 1545 | -450 | 4034 | 1396 | 143 | 254 | 162 | 0.999 |
9000 MM のときは、核の強い反発力のために、窒素の構造はより壊れてしまう。
そのため、Table 10 に比較して、ド・ブロイ波の誤差は大きくなる。(Table 13 においては 電子 3 は +0.025、 電子 0 は -0.019 である。)
この場合は 全位置エネルギーは -655.22 eV であり、これは実験値 (-639.98 eV) よりもかなり小さい。
また、H0 核に作用する N 核方向への力 (= Nf) は大きくなりすぎる。(= 561) これは水素原子核がより不安定になる。
次に 11000" を選択し、"N-H (MM)" ボタンをクリックする。
| eNo | X (MM) | Y (MM) | Z (MM) | nuc (MM) | CF | fx | fy | fz | Waves(wn) |
|---|---|---|---|---|---|---|---|---|---|
| ele 0 | 4870 | 0 | -2300 | 5385 | 3282 | -4 | 0 | -8 | 2.002 |
| ele 1 | -2695 | 3660 | -2550 | 5211 | 3661 | 5 | 0 | -6 | 1.986 |
| ele 2 | -2695 | -3650 | -2560 | 5209 | 3670 | 6 | 0 | -5 | 1.986 |
| ele 3 | 530 | 3740 | 3940 | 5458 | 3588 | -9 | -3 | 4 | 2.006 |
| ele 4 | 520 | -3740 | 3940 | 5457 | 3591 | -9 | 2 | 3 | 2.007 |
| ele 5 | 220 | -4480 | -260 | 4492 | 1222 | -130 | 0 | 50 | 0.994 |
| ele 6 | 3890 | 2400 | -300 | 4580 | 1196 | 69 | -122 | 42 | 0.993 |
| ele 7 | -4000 | 2026 | -300 | 4493 | 1221 | 54 | 97 | 76 | 0.993 |
11000 MM のときは、ド・ブロイ波は比較的安定になる。
しかし、全位置エネルギー (tV) は control (Table 10, tV=-639.4 eV) よりも高くなる (= -635.67 eV)
つまり、11000 MM のときは結合の力が弱くなることを意味する。
他の組み合わせ (9000 x 100°、9000 x 110°、11000 x 100°、11000 x 110°) も試すことが可能である。
これらの組み合わせでは、自動的には適切な初期条件がセットされないため、自分で電子の座標を調整する必要がある。
各電子の (fx, fy, fz)と N nuc の (FX, FY, FZ) をなるべく小さくするように。(できれば 10 以下に。)
もしこれも試してみれば、Table 10 (control) がもっともよい条件だということがわかるだろう。

2010/11/24 updated This site is link free.