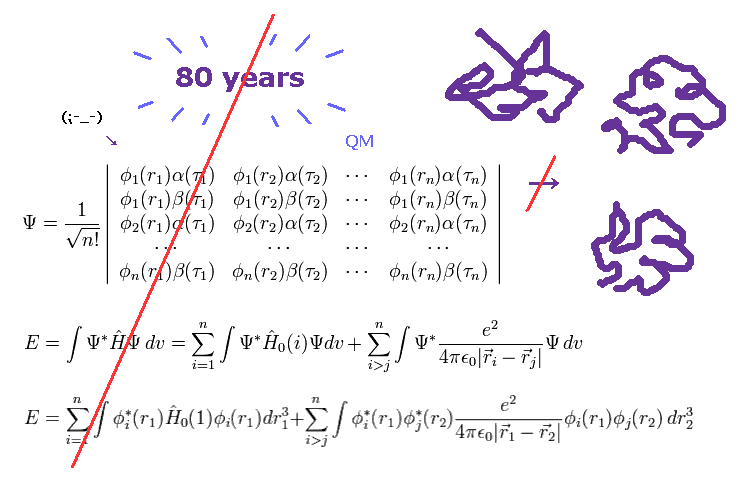
トップページ (2電子原子も含む正確な新ボーア模型)
タンパク質回転と操作のマニュアル。
蛋白質サブユニット、原子間衝突。(13/10/19)
(Fig.1) 80 年以上も経過した。 → 量子力学は役に立たない。
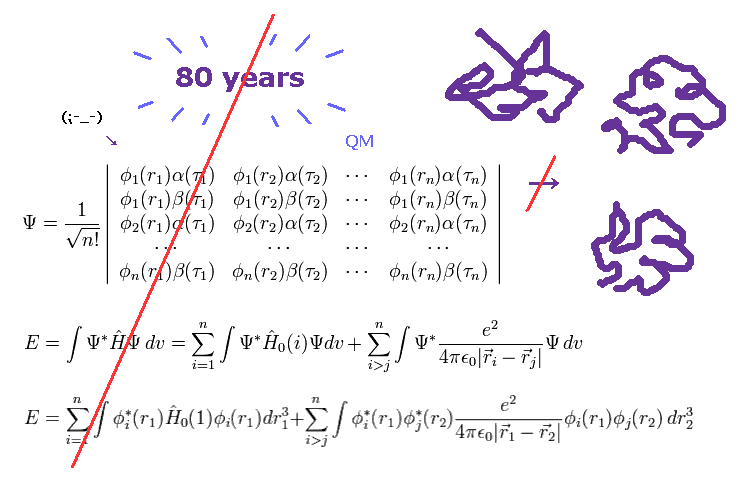
すてに述べたとおり、多原子の波動関数 ( シュレディンガー方程式 ) を解くことは 難しすぎて 実際のタンパク質相互作用計算においては 使い物にならない。
シュレディンガー方程式を用いて マクロの分子を計算するには、人為的に ある有限な数の基底関数を選択する必要がある。
もちろん 小さい基底関数では 正確なエネルギー状態を得ることは不可能であり、異なった基底関数の選択ごとに 様々な異なった誤差が 発生する。
タンパク質相互作用を決定する 水素結合や ファンデルワールス力のエネルギーは 共有結合の 10分の1 以下である。
例えば、単一の酸素原子の 1-6 の全イオン化エネルギーは 433.11 eV で、これは 共有結合 (= 約 3.0 eV ) や 水素結合 (= 約 0.1 eV ) に比べて 非常に大きい。
そのため 異なった基底関数の選択による タンパク質全体におけるエネルギー誤差が これらの小さな結合エネルギーよりも はるかに大きくなってしまう。
密度汎関数法 (= DFT ) は "ab-initio" ではなく、また "LDA" などの かなり粗い近似に頼っているため、様々なタンパク質相互作用に使えない。
私達は 数学と化した量子力学的波動関数を諦めて、もっと実在的な 各価電子や原子核に作用する 実際のクーロン力などを考慮する必要がある。
(Fig.2) 回転が両方向にブロックされている。
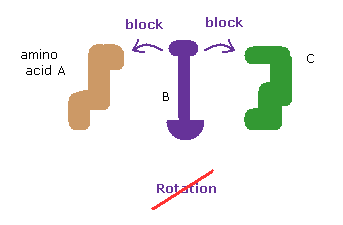
タンパク質の構造は 二面角 (= ねじれ角 ) で決まる。
各回転部位で、アミノ酸は ある範囲に自由に回転できる (= 回転異性体 )。
このウェブサイトでは 2つの 離れたアミノ酸の衝突が これらの回転をブロックして その結果 タンパク質全体の構造が決まることを示す。
つまり タンパク質は 回転する固体のように振舞うと言える。
ここでは タンパク質構造を調べたり 操作するのに 次の サンプル JAVA プログラムを使用する。
操作方法に関しては このページも参照のこと。
サンプル JAVA プログラム ( PDB タンパク質 - 回転 )。
最初に 次のミオグロビンを扱う。
Oxymyoglobin text ( 1MBO.txt ).
また このプログラムは 各アミノ酸側鎖を変化させることができる ( 例えば、 ALA → PHE など )。
そのため 次のテキストファイルを 19 種類のアミノ酸のテンプレートとして使用する。
(Fig.3) セーブフォルダー位置の変更。

このテキストを "C:\sdff" フォルダーの位置に "1MBO.txt" のファイル名でセーブする。
( もしくは PDB ウェブサイトから 直接セーブすることもできる。 )
同じように "tout.txt" のテキストも フォルダーにセーブする。
( 違うフォルダーにセーブした場合は、プログラム内の Fig.3 部分を変更するように。 )
その後、上の サンプル JAVA プログラムを "amic.java" としてセーブしてコンパイルする。
"詳細は、-Xlint: unchecked オプションを指定して再コンパイルしてください。" などの注意は無視してそのまま実行できる。
(Fig.4) すべての角度を回転 → コマンドプロンプト画面。
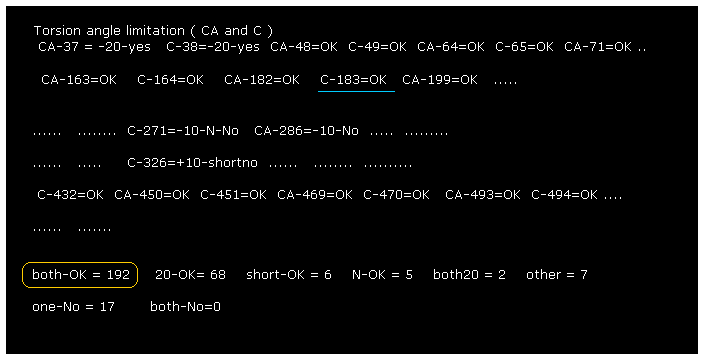
プログラム実行後、 "0" を入力 (= Rotate all angles, yes ) すると、 Fig.4 の結果が表示される。
"C-183" は プログラム原子番号 "183" の炭素前の 二面角の回転結果を示している。 ).
"both-OK" は 両方向 (= ±10 ° ) の回転が ブロックされおり、この状態が 安定であることを意味している。
( このページも参照のこと。 )
この結果は このページの方法が 実際のタンパク質構造を決定する際の 決定的な要因の1つであることを示している。
Fig.4 の結果の意味を "C-183" の部位を例にとって説明することにする。
(Fig.5) 炭素-183 の選択。
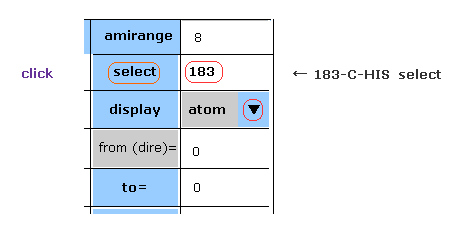
スクロールバー内から "atom" を選択して "183" (= プログラム原子番号 ) を "select" の横に入力して "select" ボタンをクリックする。
そうすると、183 の炭素が 画面中心にくる。
(Fig.6) y と z の幅を狭める。
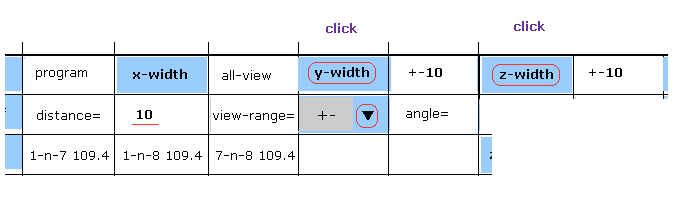
画面上には ミオグロビンのすべての原子が表示されるので ごちゃごちゃして分かりにくい。
そこで 画面に表示される 範囲を 狭めることにする。
スクロールバー内から "+-" を選択して "10" を "distance=" 横のテキストボックス内に入力する。
それから "y-width" と "z-width" ボタンをクリックする。
(Fig.7) タンパク質画像。
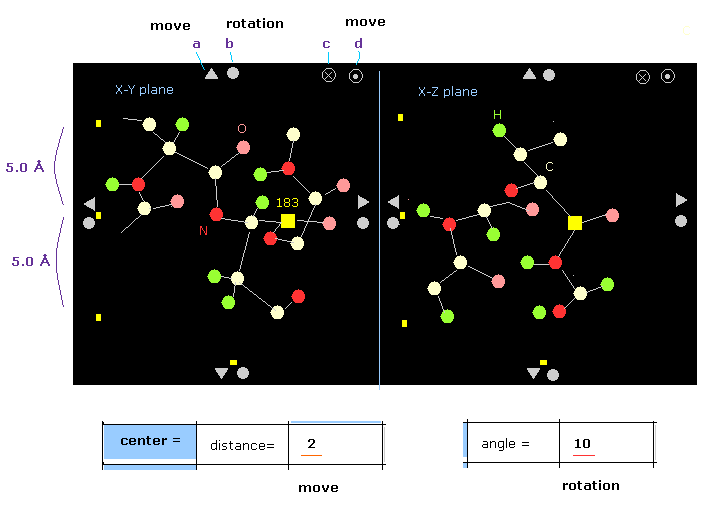
指定された原子は 黄色の四角形で表示される (= 炭素-183 ).
例えば、 x-z 平面上では、y 方向に ±5 Å の範囲内にある原子のみ表示される。
縁にある 各矢印や 円をクリックして タンパク質全体を移動、回転させることができる。
(Fig.8) 二面角 ( ねじれ角 )。
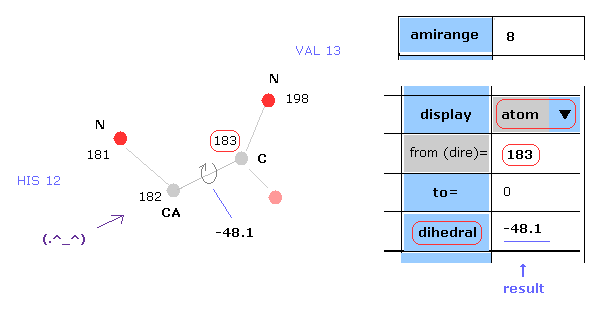
二面角 は それが決まれば タンパク質全体の構造が決まるため 非常に重要な概念である。
二面角は Fig.8 において 平面 A (= 181-182-183 ) と 平面 B ( 182-183-198 ) 間の角度を表している。
スクロールバー内から "atom" を選択して、 "183" の数値を "from (dire)=" の横のテキストボックスに入力して "dihedral" ボタンをクリックすると、ここの二面角 ( 182 と 183 間の ) を得ることができる。
"atom" を選択しているときは プログラム原子番号で指定し、 "PDBat" を選択しているときは PDB 原子番号を指定する。
(Fig.9) "residue" (残基)+ "C" の選択。
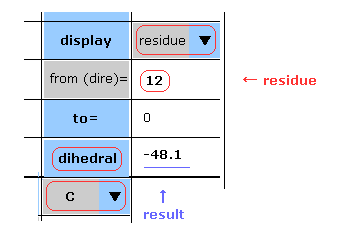
各スクロールバー内から ( N, CA, C, CB, CG, ... ) のどれかと "residue" を選択しても二面角を得ることができる。
この場合、 "C" を選択して PDB の残基番号 (= HIS-12 ) をテキストボックス内に入力して "dihedral" ボタンをクリックする。
( 基本的に ペプチド結合は 二重結合性のため、 "N" の場合は、この角度は -180°近くになる。)
水素原子や酸素原子は 二面角に何も関係がないことを注意しておく。
(Fig.10) 二面角と原子の選択。.
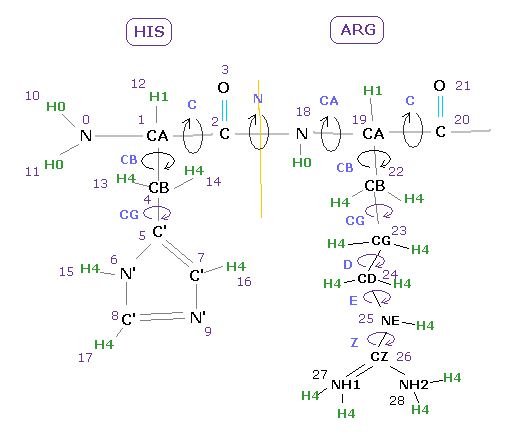
例えば、Fig.10 で CA 直前の 18-19 間の二面角が知りたいときは 原子番号 "19" をテキストボックス内に入力して "dihedral" ボタンをクリックする。
基本的に CA や C の炭素の直前の角度は ラマチャンドランプロットとして知られ、αへリックスやβシートの構造にとって 非常に重要である。
"4" (=CB ) を入力すると、Fig.10 において 平面 0-1-4 と 平面 1-4-5 間の角度を知ることができる。
"26" (=CZ ) を入力すると、平面 24-25-26 と 平面 25-26-27 間の角度を知ることができる。
( もちろん、各スクロールバー内から "residue" と "Z" を選択して、残基番号を入力しても "CZ" の二面角を得ることができる。 )
(Fig.11) 二面角と原子位置。

Fig.11 に示したように、 原子 29 と 46 が "シス" の位置にあるとき、この二面角は "0"°になる。
一方、それらが "トランス"の位置にあるとき、二面角は -180° (もしくは 180°) になる。
Fig.11 の視点 (= 30 → 31 方向の矢印 ) から見て、ベクトル 31-46 は 反時計方向に ある角度 (例えば 30° ) 回転すると、 二面角は 負 ( -30° ) になる。
一方、時計回りに回転すると、その角度は 正 になる。
(Fig.12) C-183 を挟む 原子間の距離。
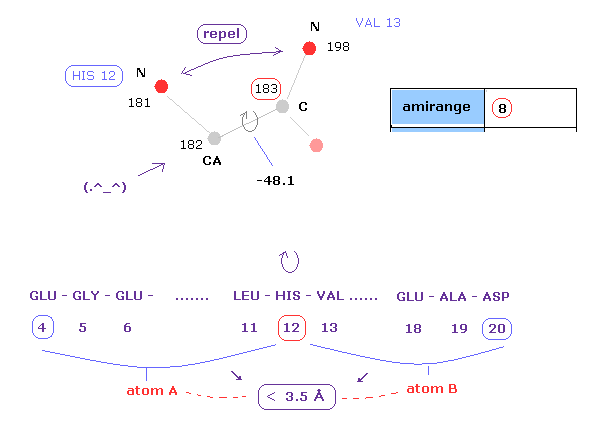
重要なのは 何が 二面角を決定するのか ということである。
ここでは 指定された二面角を挟んだ 両サイドの原子 ( A と B ) の間の 反発相互作用に注目した。
"8" の数値を "amirange" 横のテキストボックス内に入力すると、 このプログラムは 残基 "4" (= 12 - 8 ) と 残基 "20" (= 12+8) の間の 水素原子を除く すべての原子間距離を計算する。
1つの原子 A は 残基 4 から 12 に含まれ、 もう1つの原子 B は 残基 12 から 20 の間に含まれている。
ここで 炭素 182 (=CA ) と 183 (= C ) は この二面角に まったく影響を与えない。
( 例えば、182 と 198 の原子間距離は この二面角の回転で 変化しない。)
そのため このケースでは 原子 182 と 183 は この計算から除外されている。
(Fig.13) 182-183 の両サイドの2つの原子間距離が 3.5 Å 未満のもの。

このプログラムは コマンドプロンプト画面上に 水素原子を除いた
3.5 Å 未満の原子間距離のものをすべて表示させる。
このページに示したように、水素原子は 非常に弱い反発効果しか持たないため、ここでは この効果を無視できる。
例えば Fig.13 では、 酸素原子 (= プログラム番号 130 ) と 窒素 (= 198 ) の間の距離は 3.364 Å である。
この二面角に影響を与えうる 最も短い距離は 2.765 Å で、これは Fig.12 の 窒素 181 と 198 間の距離になる。
重要な点は 立体障害のために、ほとんどすべての原子間距離は
2.8-2.9 Å 以上になる。
( これは タンパク質構造を決定する際の重要な要因である。)
(Fig.14) C-183 後のアミノ酸すべてを 10°回転。
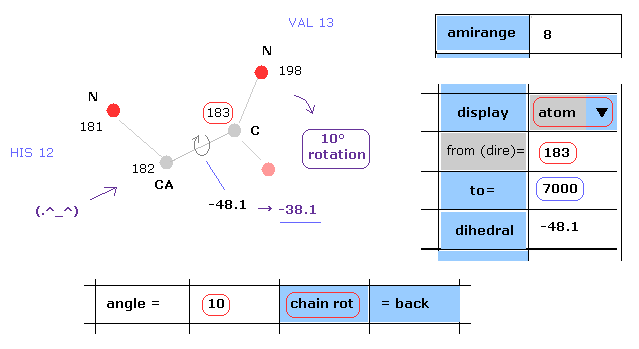
次に 炭素-183 の後のすべてのアミノ酸を 10°回転させる。
"183" と "7000" を "from(dire)=" と "to=" の横のテキストボックス内に入力する。
( ミオグロビンの最後の原子は 2843 であるため、この "7000" の数値は 2843 以上だったら何でもいい。 )
それから "angle=" の隣の テキストボックス内に "10" を入力して "chain rot" ボタンをクリックする。
このミオグロビンは 2843 原子を含んでいるため この場合では 炭素-183 後の すべての原子が 182-183 の原子間を軸として その周囲を 10°回転する。
( つまり この 二面角は -48.1°から -38.1°に変化する。 )
(Fig.15) C-183 後のすべての原子の 10°回転 - 残基指定。
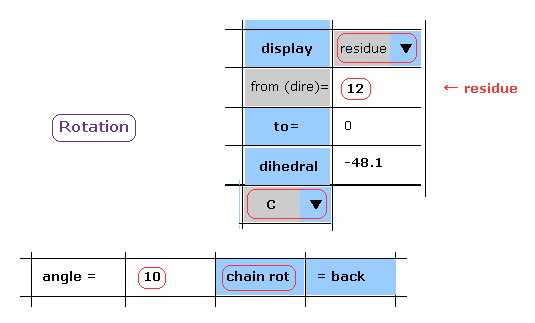
各スクロールバー内で "residue" と "C" を選択しても Fig.14 のように 回転させることができる。
"10" (= 回転角 ) と "12" (= 回転させる場所の 残基番号 ) を 各テキストボックス内に入力して "chain rot" ボタンをクリックする。
このケースでは、 "to" ボタン横の値に関わらず、C-183 移降の すべてのアミノ酸を 10°回転させる。
(Fig.16) 回転後の 原子間距離の変化。

コマンドプロンプト画面で、回転前より 短くなった 原子間距離が 画面に表示される。
Fig.16 に示したように、窒素 181 と 198 間の距離は 短くなりすぎる ( 2.765 Å → 2.690 Å )。
そのため この部分は 強い反発効果を発揮し、立体障害によって この回転を
ブロックする。
Fig.13 に示すように 回転前の 最も短い距離は 2.764 Å である。
そのため この最も短い長さが この回転によって ますます短くなってしまう。
(Fig.16') 最も短い原子間距離が もっと短く → この回転はブロック。
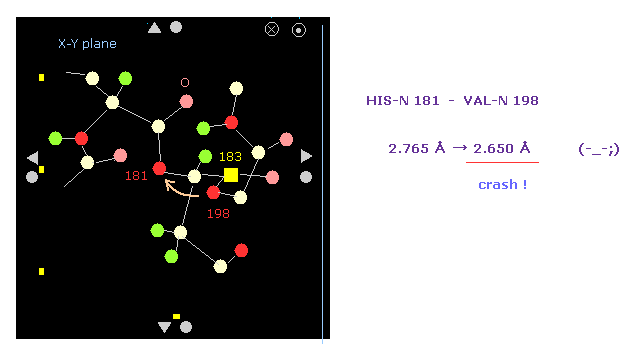
タンパク質の画面上においても 窒素 181 と 198 間の距離が さらに短くなっているのが分かる。
結果的に この +10°の回転後 最も短い原子間距離が さらに短くなる。
これはつまり この回転が 立体障害によってブロックされていることを意味している。
(Fig.17) 回転戻す。 → -10°回転。
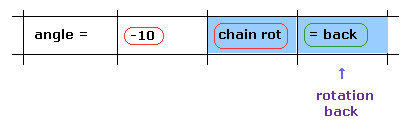
次に 逆方向への回転を調べる。
"=back" ボタンを押して 元の状態に戻る。
"-10" をテキストボックス内に入力して "chain rot" ボタンをクリックする。
このケースでは、炭素-183 後の すべてのアミノ酸が -10°回転する。
( Fig.11 に示したように、正の角度は時計回り、負の角度は 反時計回りである。)
(Fig.18) -10°回転。

Fig.18 に示したように、-10°回転においても、ある原子間距離は 短くなりすぎる。
酸素 149 と 窒素 214 間の距離は 2.698 Å となる。
このケースでは この部分のαへリックスが この回転によって きつくなりすぎてしまう。
(Fig.18') 最も短い原子間距離がさらに短くなる → この回転もブロックされる。
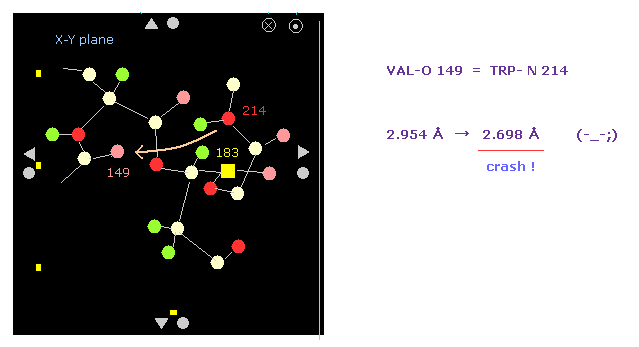
タンパク質画面においても、 O-149 と N-214 間の距離が さらに短くなることが分かる。
結果的に 最も短い原子間距離が -10°回転においても さらに短くなることが分かる。
これはつまり この回転も 立体障害によって ブロックされることが分かる。
つまり -48.1°の二面角が すべての障害物を避けた結果の 最も安定な状態であることが分かる。
これはつまり 1つ もしくは 2つの 際立った障害物が 各二面角を決定する キープレイヤーであることが分かる。
(Fig.19) 最も安定な二面角。

キーポイントは 最も短い原子間距離である。
なぜなら 例え 2,3つと言えども 際立って短い原子間距離が存在すれば、この回転は ブロックされ得るからである。
つまり、現在のタンパク質構造は すべての障害物を避けた結果であることを示している。
これが タンパク質構造を決定する 真の理由 と言える。
(Fig.20) ほぼすべての二面角は 固定されている。

プログラム実行後、 "0" (= Rotate all angles, yes ) を入力すると、Fig.20 の結果が表示される。
"CA-37" は プログラム原子番号 "37" (= CA ) の場所における回転を意味している。
"both-OK" は Fig.19 に示したように 両方向 (= ±10° ) の回転が ブロックされており この状態が 安定であることを意味している。
"20-OK (yes)" は 1方向の回転が +10°でブロック、もう1方向の回転が -20°でブロックされていることを意味している。
つまり このケースでも 両方向の回転が ほぼ ブロックされて 安定であることを意味している。
"one-No" は 1方向の回転が ブロックされており、もう1方向の回転が
ブロックされていないことを意味している。
これらの部位は タンパク質の 表面近くにあることが多く、 おそらく この回転は 他のタンパク質か何かによって ブロックされていると思われる。
ミオグロビンにおける C,CA 部位で 両方向がブロックされている部分は トータルで 192箇所あり、 この数は 17 (= 1 方向がブロックされていない箇所)よりも はるかに大きい。
この結果は 1、2 の障害物 (= 最も短い原子間距離 ) でさえ 各二面角 を決定する際の 重要な要因となっていることを示唆している。
(Fig.21) 回転が 両方でブロックされている。

タンパク質全体の構造は 二面角 (= ねじれ角 ) によって決まる。
各回転可能部位では アミノ酸は ある程度は 自由に回転できる (= 回転異性体 )。
この部位に示したように、2つの離れたアミノ酸部位の 衝突が これらの回転を ブロックし、 タンパク質全体の構造を決定している要因であると言える。
つまり タンパク質は 回転する固体のように振る舞っていると言える。
(Fig.22) C 部位における回転。
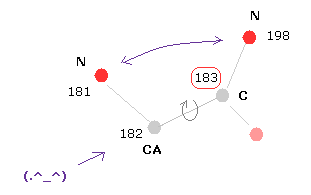
C 部位では、この C に近い 2つの窒素原子が 非常に重要である。
+10°方向回転によって この距離が さらに短くなり、これがブロックされる。
-10°回転では、この距離は 長くなるが、その代り 別の部分の原子同士が 互いに近づくため この回転はブロックされる。
このプログラムの計算は 最も短い原子間距離のみに注目している。
あるケースでは 元の N-N 長が -10°回転後も 最も短い距離のままのときもある。
これらのケースで この部位 N-N 長のみを除いて もし回転がブロックされた場合、これを -10-N-No と表示している。
ある部位では まれに 元の状態で 非常に短い ( 約 2.650 Å ) 原子間距離を含むケースがある。
この部位を除けば 回転がブロックされているとき、この部位を "+10-shortno" と表示している。
プログラム原子番号も表示されているので この部位を実際に回転させて これらの意味を確かめてほしい。
(Fig.23) アミノ酸計算部位の変更。

上のセクションでは Fig.12 に示すように ±8 に含まれるアミノ酸部位のみ計算した。
しかし アミノ酸番号が離れていても 実際の距離が近いケースもある。
そこで 上のプログラム内の 変数宣言を "int searchrange=20" のように変更する。
この変数は 計算するアミノ酸の範囲を意味している。
この値が 20 のとき、このプログラムは 回転部位を挟んだの両サイド ±20 アミノ酸以内の原子間距離を計算する。
( もしくは 下のプログラムを使うように。)
サンプルプログラム ( ami2.java. 計算範囲 ±20 )。
(Fig.24) 回転は ほぼすべてブロックされている (= both-OK ).
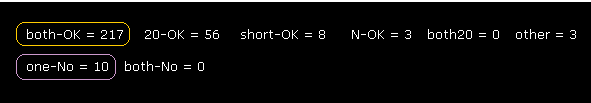
Fig.24 に示すように、計算部位を拡大すると、各二面角の回転が より顕著に ブロックされているのが分かる。
"both-OK" は 両方向の回転が ブロックされている という意味である。
( つまり ±10°の両方向の回転で 最も短い原子間距離が さらに短くなる。 = 両方向の回転がブロック。 )
両方向の回転が ブロックされた トータルの部位数 は 217 で、この数は 非ブロック部位 (= たった 10 ) の数より はるかに大きい。
(Fig.25) 2つの離れたアミノ酸部位が衝突。
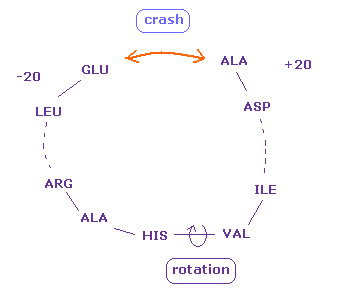
アミノ酸残基番号が離れていても 元の原子間距離が非常に短いときもある。
これらのケースでは そこから離れた部位の回転でも 2つの原子が Fig.25 に示したように衝突するケースもある。
結果的に Fig.20 の "192" (= ±8 の範囲 ) の数が Fig.24 で "217" に増加する。
これらの結果は タンパク質の構造は 固体のような性質を持つことを意味している。
つまり この固体の 一部分のみが衝突するだけで このコンフォーメーション変化は阻害されるということである。
非常に短い原子間距離が 少しあるだけで この部分は タンパク質構造において非常に重要な役割を果たしている。
(Fig.26) タンパク質の種類の変更。

次に カルモジュリンタンパク質について説明する。
上のテキストファイル ( もしくは PDB ウェブサイトから直接 ) を フォルダーにセーブする。
Fig.26 のように JAVA プログラム内を変更して 再コンパイルしてほしい。
( /* ---- */ を 1CLL から 1MBO に移動するように。 )
(Fig.27) カルモジュリンの回転制限結果。

Fig.27 に示したように、 ほとんどすべてのアミノ酸鎖回転が 両方向 (= ±10° ) でブロックされている。
54 (= 1方向が 10°、 もう1方向が 20°でブロックされた部位の総数 ) を 180 の値に追加すれば、 回転がブロックされた部位の総数は "234" にもなる。
この "234" の値は 非ブロック部位の総数 "24" に比して かなり 大きい。
このことは カルモジュリンのタンパク質構造は ±8 アミノ酸部分に含まれる 一部の際立った障害物によって決定されていることを示している。
( この構造は αへリックスを多く含む ミオグロビンに似ている。)
(Fig.28) "searchrange" の変更。

次に Fig.23 のように アミノ酸の検索範囲を ±8 から ±20 に変更して再コンパイルする。
( 変数宣言を "int searchrange = 20" に変更。 )
このケースでは ±20 アミノ酸内に含まれる 最も短い原子間距離を探索する。
(Fig.29) カルモジュリン結果 ( ±20 範囲 ).

Fig.29 に示したように 検索範囲を ±8 から ±20 に増やすと、回転が さらに ブロックされていることが分かる。
このことは ある部位では より離れたアミノ酸同士が 二面角を決定していることを示している。
これも重要な結果である。
つまり 元の安定なコンフォメーションは 近くから遠くまでの すべての際立った障害物を避けた結果であると言える。
この結果は タンパク質が 一種の固体であるかのように振る舞っていることを示している。
Fig.20, 24, 27, 29 に見られるように、ミオグロビンやカルモジュリンでは 各回転部位から ±8 の範囲に含まれるアミノ酸が ほぼすべてのコンフォーメーションを決定する際の 重要なファクターとなっていることが分かる。
なぜなら これらのタンパク質は たくさんの安定なαへリックスを含んでいるからである。
次に 光合成の一部に関わるタンパク質 (= PDB 2J96 ) に関して調べる。
上記のテキストファイル ( もしくは PDB サイトから直接 ) をフォルダーにセーブする。
Fig.26 のように JAVA プログラム内の部分を変更して 再コンパイルする。
(Fig.30) 2J96 回転制限結果。

Fig.30 に示したように、 ミオグロビンやカルモジュリンのケースのように ほとんどすべてのアミノ酸鎖回転が 両方向 (= ±10° ) でブロックされている。
2J96 は 二量体である。 このケースでは このプログラムは サブユニット A 内のアミノ酸のみ計算している。
また この計算では サブユニット A と B の衝突や、タンパク質と HETATM 原子の衝突は考慮していない。
もちろん、これらの衝突もすべて含めれば より多くの回転部位が ブロックされることは言うまでもない。
(Fig.31) アミノ酸の "searchrange" を "20" に変更。

次に アミノ酸の探索範囲を Fig.23 のように ±8 から ±20 に変更して コンパイルし直す。
Fig.30 と Fig.31 を比較すると、ある部分は アミノ酸残基番号が離れた部分によってブロックされていることが分かる。
しかし ほぼすべての回転部位が ±8 のアミノ酸によって 決定されている。
次に ヒドロキシラーゼタンパク質の1つについて調べる (= PDB 2PAH )。
上記のテキストファイル ( もしくは PDB サイトから直接 ) あるフォルダー内にセーブする。
Fig.26 のように JAVA プログラム内の 部分を変更して 再コンパイルする。
(Fig.32) 2PAH 回転制限結果。
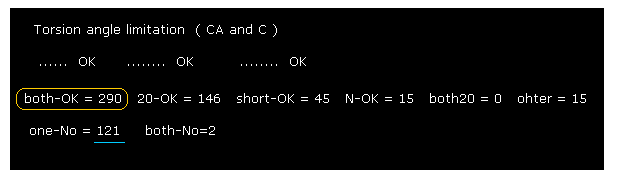
Fig.32 に示すように、 "290" の回転可能部位が 両方向 (= ±10°回転 ) にブロックされている。
しかし 2PAH のヒドロキシラーゼでは、 121 もの回転部位が ブロックされていない。
つまり この種の酵素は ミオグロビンやカルモジュリンよりも
柔軟であると言える。
(Fig.33) アミノ酸の "searchrange" を "20" に変更する。

次に Fig.23 のように、 アミノ酸の search-range を ±8 から ±20 に変更して 再コンパイルする。
Fig.32 と Fig.33 を比較すると、 Fig.33 では より多くの回転部位がブロックされていることが分かる。
( Fig.32 の "290" は Fig.33 では "403" に増加している。 ).
この結果は 2PAH のタンパク質において、 より遠くのアミノ酸同士が 各二面角を決定する際の 重要なキーファクターであることを示している。
次のタンパク質を searchrange などを変更して試してほしい。
1ROP.txt ( 転写制御 )
1CTS.txt ( クエン酸合成酵素 )
1TGH.txt ( 転写 / DNA )
(Fig.34) 何が 疎水性 (親水性) を決定するのか?

基本的に ロイシンやフェニルアラニンなどの疎水性アミノ酸は タンパク質内部に存在する。
一方 グルタミン酸やアスパラギンなどの親水性アミノ酸は タンパク質表面に存在して 水分子と接している。
その主要な理由の1つが 水素結合だと 彼らは主張している。
しかし 例えば なぜ " C-H ---- O " の組み合わせは 水素結合になれないのだろうか?
( " N-H ---- O " や " O-H ---- O " は 水素結合の一般的な形であるにも関わらず。 )
残念ながら 現在の量子力学は この重要な性質の肝心の部分を 曖昧にして答えてくれない。
(Fig.35) 炭素のすべての価電子 (= 結合状態 ) は動けない。

基本的に ある正電荷が近づいたとき、価電子のいくつかは この正電荷の方へ動いて この反発力をキャンセルしようとする。
しかし炭素の場合では、4つの価電子のすべては すでに 他の原子核に結合していて 動くことができない。
( 正電荷が強すぎて 共有結合を切断させるなどのケースは除いて。)
炭素の価電子の1つが 酸素の方へ動いたとしたら、それは 他の原子核が反対の方向へ 動くことを意味している。
しかし 共有結合は 非常に強いため、この現象は 起こりがたい。
(Fig.36) 酸素のフリーの価電子が 他の正の電荷方向へ移動する。

一方、酸素は6つの価電子を持ち、そのうち 4つは非結合の フリーの状態である。
これらの自由な電子は 常に 他の正電荷の原子核を探して そちら方向へ動こうとする。
この動きが 原子核間の反発力を キャンセルする。
(Fig.37) 酸素の電子の "up" と "down" の電子の引力。

基本的に 酸素の up と down の価電子の引きつけ力は非常に強い。
Fig.37 に示したように 電子と酸素原子核間の力が "F" のとき、 それに垂直な 引きつけ力は F sinθ になる。
θ に対する その微分は cosθ になる。
Fig.37 に示したように この微分 (= 力の増加率 ) は この θ が ゼロ近くのときに最も大きくなる。
他の原子核の反発力が強くなりすぎると、この θ は 90°に近くなる。
そのため この時は up と down の電子間反発力の増加のほうが 引きつけ力の増加よりも大きくなってしまう。
(Fig.38) フリーの "up" と "down" の N の電子が 他の原子核方向へ移動。

窒素 (= N ) 原子においても、 "up" と "down" の電子がフリーで 他の正電荷を探している状態である。
結果、 O-O や O-N 長は 2.5 Å と短くなることができ、 O-C 長は なれないことになる。
( もちろん C 近くで 強固な共有結合で繋がっている状態を除く。 )
このページで述べたように、酸素が この長さよりも水素に近づくとき、O と H 間の反発力は強くなり、これをブロックする。
(Fig.39) ミオグロビンの鉄付近の原子。

この PDB ファイル ( 1MBO ) (= oxymyoglobin ) を用いて、 鉄 (= FE ) 付近の原子は 必ず 窒素もしくは酸素になることがわかる。
Fig.39 では、 "PDBat" の条件で FE 原子 "1276" を選択し、"center" ボタンをクリックする (= 7 Å の距離で )。それから y-width を ± 4.0 Å にする。
テトラカルボニルニッケルは 有機金属化合物の1つである。
通常の化合物と異なり、 これは 炭素-金属 結合を含んでいる。
( もちろん、 3重結合のために、これらの化合物は不安定である。 )
(Fig.40) テトラカルボニルニッケル。

重要な点は この炭素は 4つの 単一結合を 形成していないという点である。
Fig.35 のように もし 4つの単一結合が形成されると この炭素は ニッケルの強い正の反発力に対抗できなくなる。
Fig.40 に示したように、炭素の 2つの余分な価電子が ニッケルの反発力をキャンセルする方向へ動くのは自然なことである。
このページに示したように、 炭素の4つの価電子間の反発力を考慮すれば、3重結合で 3つの電子が 単一の結合内に詰め込まれてしまうということは不可能に近い。
(Fig.41) 炭素は 酸素を避けて 他の C-H のほうへ近づく。

このプログラムを用いれば、 C-C 間の反発力が C-O 間よりも弱いことが分かる。
そのため 炭素原子 (= C ) は 水の酸素原子を避けるようにして 他の C-H 残基方向へ近づいていく。
Fig.35 (= C の価電子 ) と Fig.41 が 疎水性を示す 本当のメカニズムである。
サブユニット A と B のタンパク質間の C-C の長さは 約 4.0 Å である。
そのため C と C 間の小さな反発力のため、それらは この長さよりも互いに近づくことができないと言える。
この C-C 長では H2O 分子が その間に入っていくスペースがほとんどない。
( 水素原子も考慮して。 )
これはつまり 2つのタンパク質の疎水性部分は 接触面で いわゆる負の選択によって 互いにくっついていると言える。
(Fig.42) N --- H - N (= 窒素 ) 水素結合。
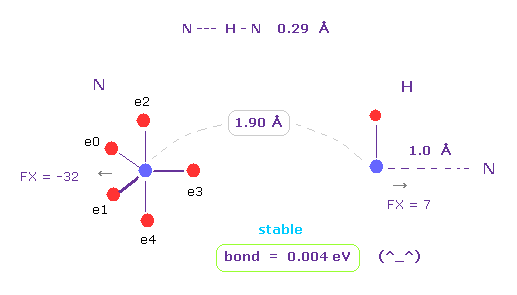
このページに示したように、 水素原子は 非常に弱い 反発力を持つ。
それは たった1つの負の電子と 1つの正の原子核を持つにすぎない。
そのため ある原子間距離においては、この結合エネルギーは 正になって 安定になりやすい。
この性質は 水素原子のみに 特徴的なものである。
(Fig.43) どうやって 原子は立体障害と共有結合を区別するのか?
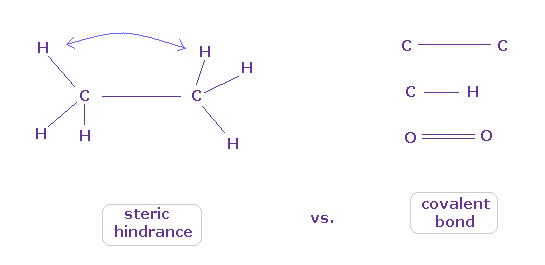
よく教科書で "エタンの6つの水素原子は 互いに避け合う配置をとる" とか "タンパク質の構造は その立体障害のために 非常に制限される " だとかの説明を見られるかもしれない。
これはつまり 各原子は 必ず 他の原子を避ける傾向があるということだろうか?
一方で 希ガス原子を除いて 様々な原子は 安定な共有結合を形成することができる。
各原子が 互いに"避け合う"のに、どうして それらは 安定で タイトな共有結合を形成することが可能なのだろうか?
実は これらの違いは それらの結合長に依存していると言っていい。
(Fig.44) C-C = 1.5400 Å は 釣り合いのとれた長さである。
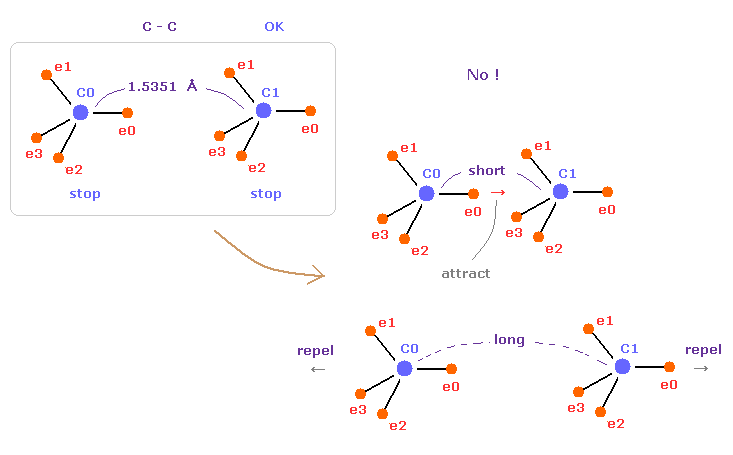
このページでは エタンの C-C 結合長 1.5351 Å が 両方の C 原子核の安定性にとって 必要不可欠なものであることを示した。
もし C-C 結合長が 1.5351 Å よりも短くなると、e0 と C1 間の引力が 強くなりすぎ、不安定になる (= 結合エネルギーは大きくなる )。
そして もし C-C 結合長が これよりも長くなると、2つの C 原子核間の反発力が優勢になり 不安定になる (= 結合エネルギーが 負の値になる。)。
この後者の例が 所謂 立体障害のメカニズムにあたる。
(Fig.45) "長い" か "短い" か の結合長が その性質を決定する。
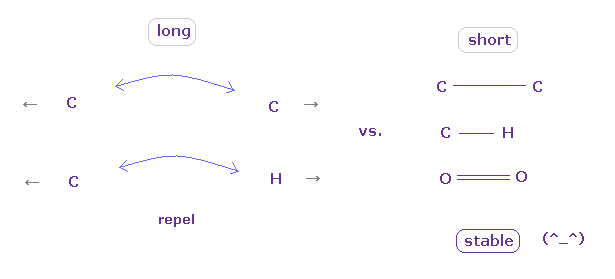
結論からして、安定な結合を形成するには、2つの原子が ある閾値の長さよりも 互いに 接近する必要があると言える。
その閾値の長さよりも 長いと、 電子間や核間の反発力 が 優勢になり、いわゆる 立体障害を引き起こす。
通常のタンパク質では、2つの原子間の ほぼすべての距離は 共有結合長よりも 長いため、それらは 立体障害を引き起こす。
(Fig.46) 回転は両方向でブロックされる。

このページで説明したとおり、2,3の 際立って短い原子間距離が存在するだけで、この回転は ほぼ ブロックされる。
もちろん この効果は Fig.43-Fig.45 に示すような立体障害によって起こる。
結果的に 各炭素原子が H2O などの 酸素原子を避けながら、その際に 水素結合と 回転のブロックという2つのメインの要因が タンパク質の構造を決定すると言える。
(Fig.46) アミノ酸

このプルグラムは
新しいアミノ酸鎖を設計できる。
Fig.26 のように プログラム内の指定の場所を変更するように
サンプル JAVA プログラム ( ami3.java タンパク質設計 )。
Fig.46 のように、 変数宣言を "int constr = 1" のように変更する。
"String sequence[]" は これから設計されるアミノ酸鎖配列である。
Fig.46 では 22 × ロイシンが作られる。.
変数 "resn" を アミノ酸の総数 (= "22" ) に変更するように。
"CAang" と "Cang" は CA と C すべての角度の初期値である。
CA と C の 二面角が -60° と -50°のとき、 このタンパク質は 典型的な αへリックスになる。
(Fig.47) αへリックスの水素結合 (= 全 22 アミノ酸 )。
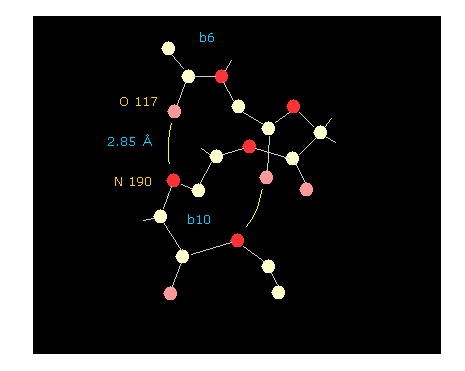
"hydrogen" と "chain" ボタンをクリックすると、水素原子なしの 主鎖のみ表示される。
ある 酸素 と 窒素 を続けてクリックすると、
その間の原子間距離が テキストボックス内に表示される。
Fig.47 に示すように、 残基 "6" の酸素と 残基 "10" の窒素が水素結合を形成し、この長さは 2.85 Å である。
もし 二面角をまとめて変更 ( "Change-d" ボタンを使う。 このページも参照のこと ) すると、この水素結合が 二面角に応じて どのように変化するかが分かる。一度試してみるといい。
(Fig.48) アラニンをフェニルアラニンに変更。
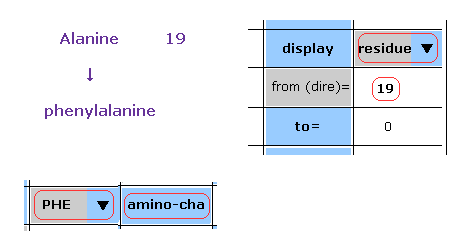
このプログラムでは、各アミノ酸の種類を変更できる。
例えば、残基 19 は アラニンである。
スクロールバー内から "residue" を選んで、 "19" を "from (dire)=" 横のテキストボックス内に入力する。
そして スクロールバー ( 7行目 ) 内 から "PHE" を選択して "amino-cha" ボタンをクリックする。
(Fig.49) アラニン → フェニルアラニン。
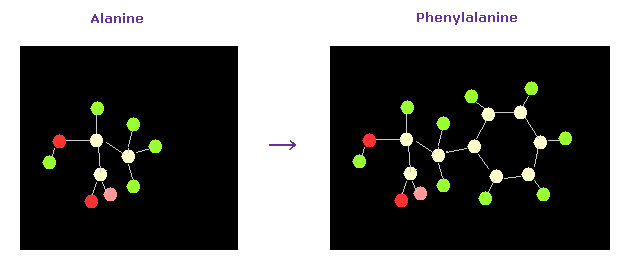
結果、指定のアミノ酸が変更された。

2013/9/1 updated This site is link free.