Exact Bohr's helium, lithium model

Home page

New Bohr's helium model with two perpendicular orbits perfectly agrees with experimental energies of all two-electron helium-like atoms and ions (= He, Li+, Be2+, B3+.. ).

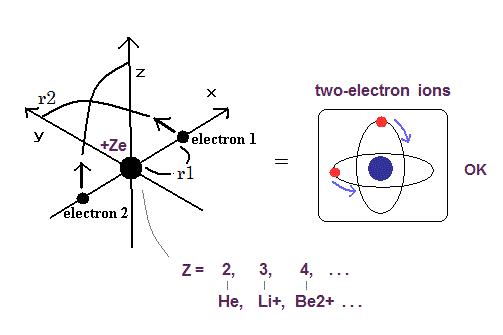
(Fig.1) Real Two-electron Atomic Model ( He, Li+, Be2+, B3+, C4+ ... )

Bohr's helium agrees with experimental energies.

Real Bohr's helium model with two perpendicular orbits perfectly agrees with all experimental energies of all two-electron atoms and ions.

New Bohr's helium with two orbits crossing each other perpendicularly to avoid destructive interference of de Broglie waves perfectly agrees with all experimental energies of all two-electron atoms and ions.

In the upper table-1, the predicted values are energies predicted by this real Bohr's helium model with two perpendicular orbits of just 1 × de Broglie wavelength (= total energy uniquely determines de Broglie wavelength of an orbit ).

Experimental total energy of each two-electron atom or ion is the sum of ionizations of energies of two most inner electrons.

The r1 (= MM = 10^-14 meter ) is the initial x-coordinate of the electron-1 which makes the electron-1 crosses y-axis perpendicularly after moving 1/4 orbit (= there is only one r1 satisfying this condition in each total energy ), which gives the most stable symmetrical two-electron orbits.

The old circular orbit is the wrong energy of the old Bohr's helium model with only one circular orbit.

Sample programs are
JAVA program to compute two-electron atoms
Simple C-program to computer two-electron atoms

This result shows this new Bohr helium model with two perpendicular orbits perfectly agrees with experimental energies, and can explain real Pauli principle based on de Broglie wave interference.

The sum of two innermost electrons' ionization energies (= red ) is ground state energy of two-electron atoms or ions.

Total energy of a two-electron atom (ion)

Total energy of a two-electron atom or ion is the sum of ionization energies of two most inner electrons.

In the upper table.2, the total energy of a two-electron atom or ion is the sum of ionization energies (= red number ) of two innermost electrons.

So the total energy of helium (= He ) is the sum of 1st (= 24.58738 eV ) and 2nd (= 54.41776 eV ) ionization energies equal to -79.0051 eV.

The total energy of lithium ion (= Li+ ) is the sum of 2nd (= 75.64009 eV ) and 3rd (= 122.45435 eV ) ionization energies equal to -198.094 eV.

Total energy of a three-electron atom (ion)

Total energy of a three-electron atom or ion is the sum of ionization energies of three most inner electrons.

The total energy of a three-electron atom or ion is the sum of ionization energies of three innermost electrons.

For example, the total energy of the 3-electron Beryllium ion (= Be+ = -389.826 eV ) is the sum of 2nd (= 18.21115 eV ), 3rd (= 153.89620 eV ) and 4th (= 217.71858 eV ) ionization energies.

This Bohr's model's prediction (= -198.984 eV ) perfectly agrees with experimental Li+ ion's energy of -198.093 eV

We use the same way as the helium energy calculation.

JAVA program to compute two-electron atoms
Simple C-program to computer two-electron atoms

After running one of the above programs (= by copying and pasting the source code ), we first choose two-electron lithium ion (= Li+ ) by inputting atomic number Z = 3.

Then, we input the electron-1's initial x-coordinate (= r1 ) in unit MM (= 10^-14 meter ) and the absolute value of the total energy (= eV ) of Li+ ion.

As shown in the above, when we input r1 = 1944.5 MM, and the energy = 198.984 eV, the electron-1 has moved its 1/4 orbit of just 0.250000 × de Broglie wavelength (= so one orbit is just an integer = 1.000000 × de Broglie wavelength, which is stable = Bohr's quantization condition ), and crosses the y-axis perpendicularly (= there is only one r1 this satisfies this condition in each chosen total energy E ).

↑ If we choose different total energy of Li+ (ex 194.0 eV ), the electron-1's 1/4 orbit becomes 0.253191 × de Broglie wavelength, which does Not satisfy one orbit being an integer (= 1.000000 ) times de Broglie wavelength. so this chosen -194.0 eV is wrong as Li+'s total energy in this program.

This energy value (= -198.984 eV ) predicted by this new Bohr's helium model perfectly agrees with the experimental Li+ ion's energy of -198.093 eV.

This result shows this Bohr's model with two perpendicular orbits is right.

This real Bohr's model's prediction (= -373.472 eV ) perfectly agrees with experimental Be2+ energy of -371.615 eV.

Also in the two-electron Beryllium ion (= Be2+ ), the prediction of this Bohr's helium with two perpendicular orbits (= -373.472 eV ) perfectly agrees with the experimental energy Be2+ ion (= -371.615 eV ).

As shown in the above table, when we choose 373.472 eV (= agreeing with the experimental energy ) as the total energy of Be2+. this program shows one orbital length becomes just an integer = 1.000000 × de Broglie wavelength = Bohr's quantization condition ).

If we choose any energies except for 373.472 eV, one orbit cannot satisfy the condition of an orbit being an integer (= 1.000000 ) times de Broglie wavelength, which is unstable due to destructive interference of de Broglie wave..

This real Bohr model's prediction (= -602.321 eV ) perfectly agrees with experimental B3+ energy if -599.60 eV.

Also in two-electron boron ion (= B3+ ), the energy value predicted by this real Bohr's model (= -602.231 eV ) agrees with experimental B3+ energy of -599.60 eV.

As shown in the above, when the total energy of B3+ is -602.321 eV, its orbital length becomes just an integer (= 1.000000 ) times de Broglie wavelength, which is the energy value predicted by this Bohr model.

Old Bohr's helium model with one circular orbit where two electrons are moving on the opposite sides of a nucleus gives wrong energy, causing destructive interference of de Broglie wave.

(Fig.2)   Old helium with only one circular orbit gives wrong energy (= -83.33 eV ), while real Bohr's helium with two perpendicular orbits ( -79.0037 eV ) agrees with experimental helium energy (= -79.005 eV ).

The old Bohr's helium model with only one circular orbit of 1 × de Broglie wavelength containing two electrons on the opposite side of nucleus gives wrong energy (= -83.33 eV ) different from the experimental helium energy (= -79.005 eV ) due to destructive interference of de Broglie wave.

↑ We can easily calculate the total energy of this old helium model where each electron is moving around the center of effective charge Z -1/4 (= Z is the real nuclear charge ) due to repulsion from the other electron in a circular orbit.

So by changing the nuclear charge Z of the ordinary hydrogen's energy (= -2.1.13,  this-lower,  this-p.5-(25) ) into Z -1/4, we can get the energy of this old helium model

Calculating energy of old helium model.

(Eq.1)   Centrifugal force = Coulomb force

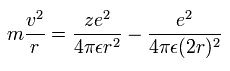
We can calculate this old helium energy in another way.

In Eq.1, The centrifugal force of an electron moving at a velocity of v in a circular orbit of radius r is equal to Coulomb force from nucleus (= with charge Z ) and the other electron (= charge is -e )

(Eq.2)

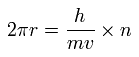
One orbit (= 2πr ) is 1 × de Broglie wavelength (= h/mv where h is Planck constant, m and v is the electron's mass and velocity ) in Bohr's quantization condition.

(Eq.3)  Total energy = kinetic + Coulomb energy

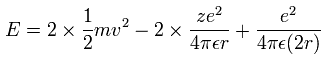
Eq.3 shows the total energy E of this old helium model is equal to kinetic energy of two electrons and all Coulomb electric potential energy among two electrons and a nucleus.

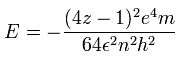
From Eq.1 ~ Eq.3, we can get the total energy E of this old helium model with a circular orbit, which gives wrong energy.

New Bohr's realistic model's prediction also agrees with experimental energies of all three-electron atoms and ions (= Li, Be+, B2+, C3+ .. ).

(Fig.3) Three-electron atomic model with two perpendicular inner n=1 orbits + one outer n=2 orbit

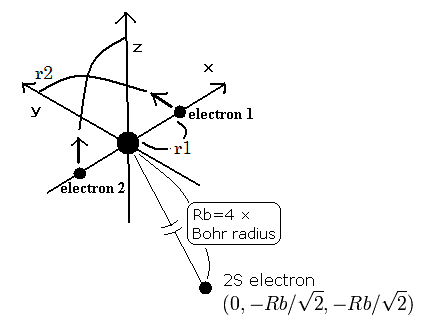
This new Bohr helium model with two perpendicular orbits can also perfectly explain any three-electron atomic or ions' energies.

In calculating three-electron atomic or ions' orbits, we fix only the outer 3rd-electron's coordinate in y-z position.

The distance Rb between the 3rd outer electron (= n= 2 ) and a nucleus is given by the ordinary Bohr's radius × 4 (= n = 2 orbit ) × 1/(Z-2) (= the outer electron experiences effective charge of Z-2 where Z nuclear charge is screened by two inner electrons ).

The total energy of this 3rd electron can approximately be obtained by the ordinary Bohr model hydrogen ( n = 2 energy level,  this-2.1.13,  this-lower,  this-p.3 ) with effective charge Z-2.

Like in the helium calculation, the electron-1 (or electron-2 ) starts from x-axis, and moves its 1/4 orbit to y-axis ( z-axis ) in the symmetrical orbits.

↑ Only the slowest 3rd outer electron's position is approximately fixed during this computation using the programs below.

JAVA program ( three-electron atoms ).
Simple C program.

↑ After running one of the above programs (= JAVA or simple C ), we input Z (= atomic number, Li = 3, Be+ = 4, .. ), initial x-coordinate r1 of the electron-1, and the total energy of the 3-electron atom or ion in the same way as the 2-electron atomic computation.

This real Bohr model prediction (= -203.033 eV ) perfectly agrees with experimental energy of the three-electron lithium (= Li ) of -203.480 eV

Bohr model agrees with 3-electron lithium's energy.

This real Bohr's 3-electron atomic model's prediction perfectly (= -203.033 eV ) agrees with the experimental lithium (= Li ) energy (= -203.480 eV ).

As shown in the above table.6, when the orbital length is just an integer (= 1.000000 ) times de Broglie wavelength (= satisfying Bohr's quantization condition ), the predicted lithium energy is -203.033 eV which perfectly agrees with the experimental lithium energy of -203.480 eV in this program.

This real Bohr model's prediction (= -388.787 eV ) perfectly agrees with experimental energy of actual three-electron Be+ ion of -389.826 eV

Bohr model agrees with 3-electron beryllium ion (= Be+ ) energy.

This real Bohr's 3-electron atomic model's prediction perfectly (= -388.787 eV ) agrees with the experimental beryllium ion (= Be+ ) energy (= -389.826 eV ).

As shown in the above table.6, when the orbital length is just an integer (= 1.000000 ) times de Broglie wavelength (= satisfying Bohr's quantization condition ), the predicted lithium energy is -388.787 eV which perfectly agrees with the experimental lithium energy of -389.826 eV.

As a result, this new Bohr's helium model with two perpendicular orbits can perfectly explain all energies of all 2-electron and 3-electron atoms and ions.

Various atoms and molecular model (= old version ).

Let's stop believing vague wave function "blindly" to develop "real" science.
Schrodinger wave function can NOT give the clear model of helium and other atoms.
( This is a main reason why the wave function gives only probability and many-world concept becomes dominant. )
So from the beginning, the quantum mechanical helium, which we can NOT understand, does NOT stand on the same stage as Bohr model.

(Atoms.  old version )
Bohr model Lithium (Li). Bohr model Beryllium (Be).
Bohr's Carbon - (visualization). Bohr's Oxygen - (visualization).
Bohr's Fluorine and Nitrogen. Bohr model Neon - (visualization).

(Molecules.  old version )   Proof of Virial Theorem.
Bohr's hydrogen molecule (H2). Bohr's hydrogen molecule ion (H2+)
True nature of CH4, H2O molecular bonds (13/3/6).
True nature of C-C and C=C molecular bonds. (13/3/18)

True atomic radius. (13/3/28)
Various two atomic combination calculator.(13/4/12)
Multi-atomic molecule calculator. (13/5/10)
Bohr's Covalent bonds (CH4,H2O,NH3). Bohr's C=C,O=O bonds.
Visualization of Bohr's water (H2O).

Feel free to link to this site.