Top page (correct Bohr model including the two-electron atoms).
Strange "Spin" is NOT a real thing.
Special relativity is wrong.
(Fig.1) If "Shut up and calculate !" state continues for more than 100 years ....

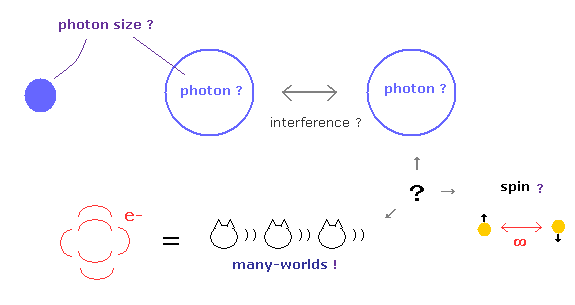
You may ask some questions such as " What are the shape and size of a photon ? ",
" How each spin particle feels spooky link ? ", " Electron in 1s orbital really crushes into nucleus ? ".
But they just repeat conventional words " Shut up and calculate ! ", and these abnormal questions and answers have continued for as much as 100 years !
Do you think it is natural that various serious problems are happening in various fields in these extremely long-term abnormal situations ?
(Fig.2) You won't be happy, unless you believe unreal string theory = abnormal state.
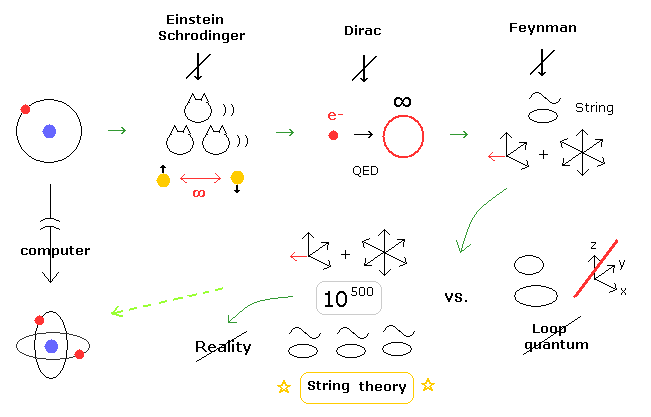
Actually, in the present physical worlds, heated disputes and distorted states continue about unrealistic 10-dimensional string theory.
For example, if you don't believe unreal string theory, you cannot succeed in the physical world.
( This situation is abnormal, as you feel. )
Even if we actually prove special relativity is wrong, they NEVER give up relativistic quantum field theories such as QED, standard model and general relativity (= black hole, expanding universe ).
Neglecting actual proof means these are not science, but just belief, I think.
And all people involved in physics education carry grave responsibility for teaching something related to relativity to students, hiding its fatal paradoxes.
(Fig.3) How antiparticles distinguish and adhere to their particles ??
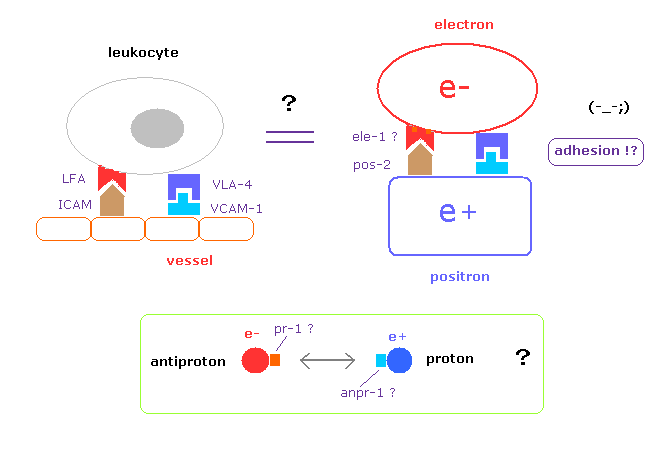
In real science, the instant we know the leukocytes adhere to blood vessels, we naturally try to investigate what adhesion factors ( LFA, ICAM-1 ) are related.
But they NEVER try to investigate these adhesion factors between electron and positron ( and proton and antiproton ), though as much as 80 years have passed since positron was discoverd.
As shown in this page, unstable antiparticles can be naturally replaced by electron, proton, and neutron captures.
And it is unnatural that very stable electron's energy (= mc2 ) is not negative.
"Not asking" for very long term means they admit these concepts are only mathematical things.
(Fig.4) Present biological technologies already reach the limits.
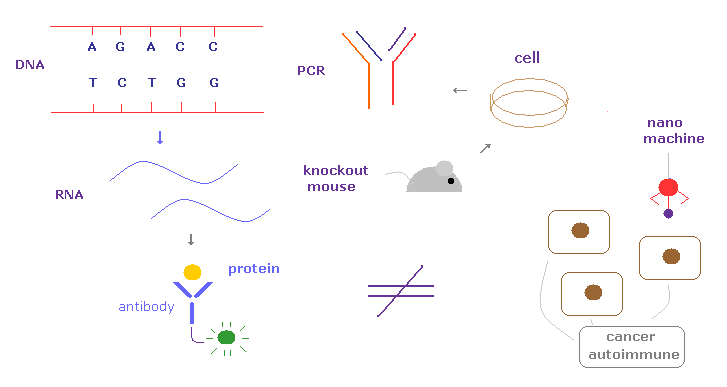
Unfortunately, the present biological technologies using DNA, RNA, cultured cells, protein interaction by antibodies have already reached their limits.
Actually, we cannot cure various serious diseases such as cancer, autoimmune disease, ALS, and dementia.
Different from antibiotics against bacteria, these serious diseases such as cancer, HIV, and autoimmune disease are generated from our own tissues.
So we need to distinguish and manipulate at nano ( electron ) levels to cure these diseases.
Unfortunately, the present biotechnology is too macro things to deal with these disease.
And we need to know and control various electron's motion patterns, giving up unuseful uncertainty principle and quantum chemistry.
(Fig.5) C-C = 1.5400 Å is an equilibrium length.
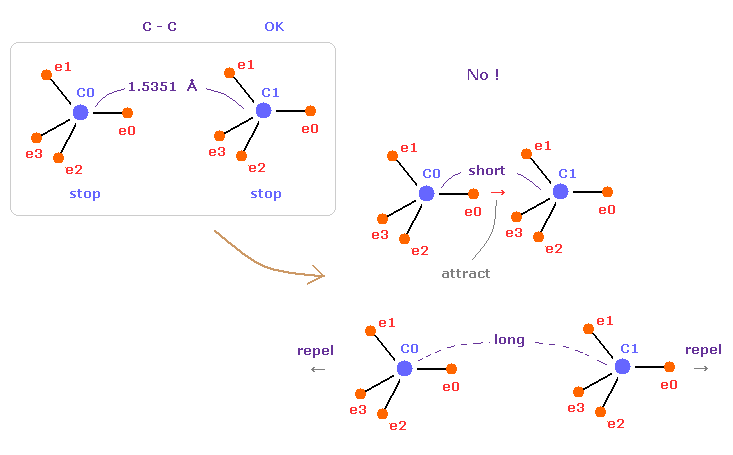
In this page, we show the reason why C-C bond length of ethane is 1.5351 angstrom, from the viewpoint of force balance.
In fact, this bond length is indispensable for the stability of both C nuclei.
If C-C bond length is shorter than 1.5351 Å, attractive force between e0 and C1 becomes too stronger.
And if C-C bond length is longer than this, repulsive force between two C nuclei becomes dominant.
As a result, these states are unstable.
This is the true mechanism of C-C bond length.
Sample JAVA program, or
Sample program (text).
Save this text editor as "twoato.java", and compile it, neglect note, "-Xlint : unchecked ---".
(Fig.6) Screen just after running ( C-C ).
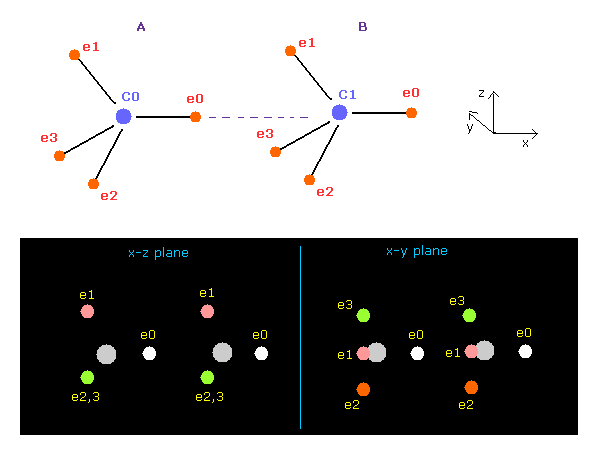
When you run the program above, the screen displays Fig.6 distribution.
This program can deal with various two atomic combinations such as hydrogen, carbon, oxygen, nitrogen, and fluorine if you choose them in the scroll bar.
Fig.6 state shows 8 valence electrons of two carbon (= C ) atoms are arranged like tetrahedron and their internuclear distance is the experimental value (= 15351 MM ), where 1 MM = 10-14 meter.
Central charge Z= 4.22, and nuc = 6415 are gotten based on carbon's 1-4 ionization energies and de Broglie wavelength "2.0", as shown in this page.
| eNo. | +X (MM) | +Y (MM) | +Z (MM) | nuc (MM) | CF | Waves |
|---|---|---|---|---|---|---|
| A ele 0 | 6415 | 0 | 0 | 6415 | 1673 | 2.000 |
| - ele 1 | -2138 | 0 | 6048 | 6415 | 2276 | 2.000 |
| - ele 2 | -2138 | -5237 | -3024 | 6415 | 2277 | 2.000 |
| - ele 3 | -2138 | 5237 | -3024 | 6415 | 2277 | 2.000 |
| B ele 0 | 6415 | 0 | 0 | 6415 | 1673 | 2.000 |
| - ele 1 | -2138 | 0 | 6048 | 6415 | 2276 | 2.000 |
| - ele 2 | -2138 | -5237 | -3024 | 6415 | 2277 | 2.000 |
| - ele 3 | -2138 | 5237 | -3024 | 6415 | 2277 | 2.000 |
| internuc (MM) | A nuc force | B nuc force | Difference | total V (eV) | Charge Z | nuc (MM) |
|---|---|---|---|---|---|---|
| C-C 15351 | FX = -340 | FX = -341 | = -1 | -596.7 | Z = 4.22 | 6415 |
You can choose which atomic ( A or B ) electrons' coordinates displayed in the textboxes on the screen, if you click "AB change" button.
Surprzingly, as shown in Table 1, when the internuclear distance of C-C is the experimental value (= 1.5351 Å ), the forces x component (FX) acting on A and B nuclei becomes -340 and -341, which keeps stable internuclear distance.
( Force unit 1000 = force between -e and +e, which are Bohr radius apart, as shown in this page.)
According to Virial theorem, the poterntial energies of free two C atoms becomes -148.025 × 4 = -592.1 eV.
So the binding energy of Table 1 becomes ( 596.7 - 592.1 ) × 0.5 = 2.3 eV, which is close to the experimental value of 3.5 eV (= 346 kl/mol )
| C-C (MM) | A nuc FX | B nuc FX | Difference |
|---|---|---|---|
| 12000 | -856 | -1703 | -847 |
| 13000 | -633 | -1013 | -380 |
| 14000 | -479 | -627 | -148 |
| 15000 | -370 | -399 | -29 |
| 15351 | -340 | -341 | -1 ← |
| 16000 | -292 | -258 | +34 |
| 17000 | -234 | -168 | +66 |
| 18000 | -191 | -109 | +82 |
| 19000 | -158 | -69 | +89 |
If you enter the value of C-C internuclear distance (MM) into the designated textbox and click "internuc" button, you can change bond length freely.
Table 2 shows the difference between force component FX acting on A and B nuclei.
When the internuclear distance becomes shorter, this difference becomes negative.
( This means internuclear distance becomes much shorter, and unstable. )
(Fig.7) C-C bond length is experimental value = 1.5351 Å
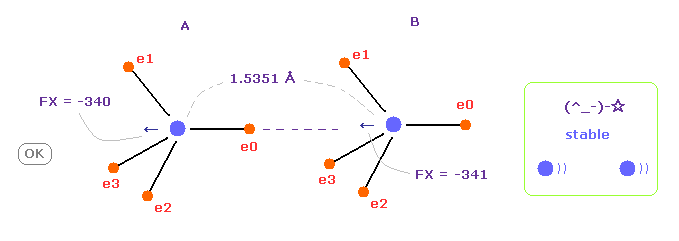
When C-C bond length is experimental value, forces acting on A and B nuclei are almost same.
( FX = -340 and -341 ).
This means C-C bond length is in equilibrium and stable.
And this result shows Coulomb and de Broglie relations are effective also in actual C-C bond.
(Fig.8) C-C bond length is shorter = 1.4000 Å
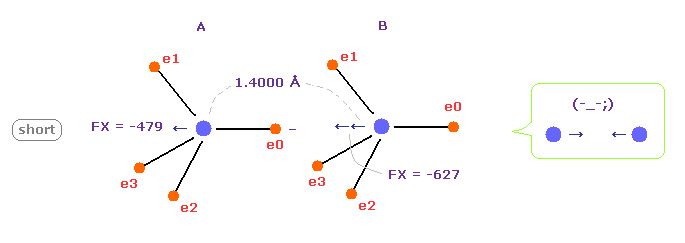
When C-C bond length becomes shorter (= 1.4000 Å ) than experimental value, B nucleus is attracted too strongly to electron e0 of A atom.
This means C-C bond length becomes unstable and tries to be much shorter in this case.
(Fig.9) C-C bond length is longer = 1.7000 Å
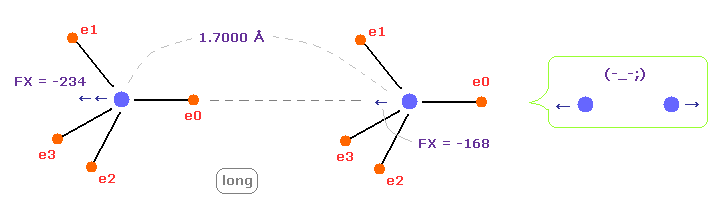
When C-C bond length becomes longer (= 1.7000 Å ) than experimental value, repulsive force between two nuclei becomes stronger.
This means C-C bond length becomes unstable also in this case.
As a result, when C-C bond length is experimental value, its distance is stable.
(Fig.10) Repeat upper and lower states.
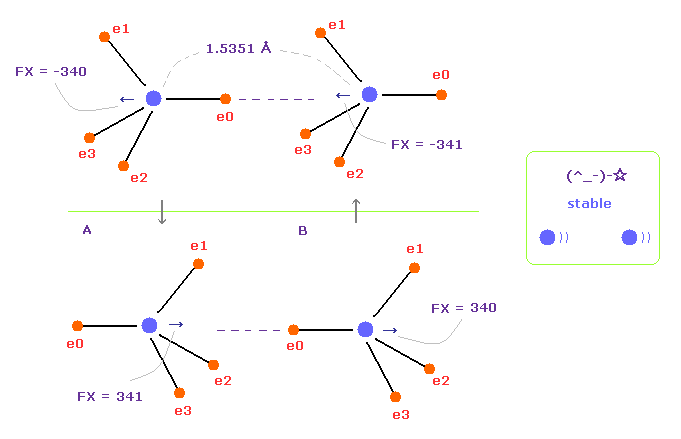
Overall forces of Fig.7 is toward minus x direction.
But valence electrons are moving around each nucleus, so upper and lower states of Fig.10 repeat.
Summing upper and lower states of Fig.10, total force acting on nuclei becomes almost zero.
In the program, input angle of "180" into the designated textbox, and click "x-y ang" button.
If so, all valence electrons of A atom rotates 180 degree in x-y plane.
And then click "AB change" button, and do the same rotation also in B atom.
This state is lower panel of Fig.10.
When C-C bond length is longer, the repulsive force between two nuclei is always stronger.
And C-C bond length is shorter, attractive force becomes always stronger.
(Fig.10') Tetrahedral structure is kept in C.
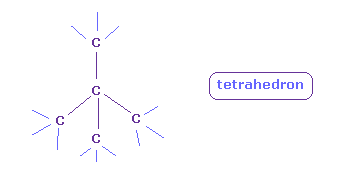
Basically, carbon (= C ) can keep its symmetric tetrahedral structure, because it has just four valence electrons.
In these tetrahedral structure, positive and negative particles are distributed equally around each C nucleus.
This point is different from oxygen ( H-O-H, O=O ) and fluorine ( H-F ).
So four valence electrons can keep their structure and we can consider "2" de Broglie wavelength only in each carbon atom.
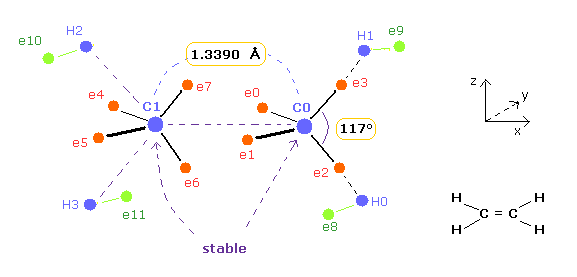
(Fig.11) Bond length and bond angle of C=C.
In this page, we can explain C=C bond length and angle of ethylene by classical orbits.
In this section, we think about these reasons only from the viewpoint of two carbon atoms.
After running this program, rotates both A and B atoms by -54.7 degree in x-z plane.
( Input -54.7 into textbox and click "x-z ang" button. )
In this state, ele 0,1 become parallel to z axis, and ele 2,3 become parallel to y axis.
(Fig.12) Bond length and bond angle of ethylene.

And then we move only ele 2,3 in A atom, and ele 0,1 in B atom symmetrically to make force (FX) acting on each nucleus close to zero.
And the distance between each electron and nucleus is supposed to be constant.
( Of course, these assumptions are only approximation, but we can grasp some tendency. )
| eNo. | +X (MM) | +Y (MM) | +Z (MM) | nuc (MM) | CF | Waves |
|---|---|---|---|---|---|---|
| A ele 0 | 3706 | 0 | -5235 | 6414 | 2162 | 1.976 |
| - ele 1 | 3700 | 0 | 5239 | 6413 | 2162 | 1.976 |
| - ele 2 | -3324 | -5487 | 0 | 6415 | 2272 | 2.023 |
| - ele 3 | -3324 | 5487 | 0 | 6415 | 2272 | 2.023 |
| B ele 0 | 3324 | 0 | -5487 | 6415 | 2272 | 2.023 |
| - ele 1 | 3324 | 0 | 5487 | 6415 | 2272 | 2.023 |
| - ele 2 | -3703 | -5237 | 0 | 6413 | 2162 | 1.976 |
| - ele 3 | -3703 | 5237 | 0 | 6413 | 2162 | 1.976 |
| internuc (MM) | A nuc FX | B nuc FX | total V (eV) | A e2-n-e3 | B e0-n-e1 |
|---|---|---|---|---|---|
| C=C 13390 | 0 | 0 | -594.36 | 117 deg | 117 deg |
As shown in Table 3, when the angle of e2-nuc-3 in A atom and e0-nuc-e1 in B atom are just 117 degree (= experimental value ), Force (= FX ) acting on each nucleus becomes just zero.
The repuslsive force in C=C bond is stronger than C-C, so bond angles of outer valence electrons need to to be wider.
| C=C bond | A e2 +X | - e2 +Y | - e2 +Z | A nuc FX | B nuc FX | A e2-nuc-e3 | B e0-nuc-e1 |
|---|---|---|---|---|---|---|---|
| 12000 | -3109 | -5612 | 0 | 0 | 0 | 122 deg | 122 deg |
| 12500 | -3201 | -5560 | 0 | 0 | 0 | 120 deg | 120 deg |
| 13000 | -3276 | -5516 | 0 | 0 | 0 | 118 deg | 118 deg |
| 13390 | -3324 | -5487 | 0 | 0 | 0 | 117 deg | 117 deg |
| 14000 | -3387 | -5449 | 0 | 0 | 0 | 116 deg | 116 deg |
| 15000 | -3459 | -5403 | 0 | 0 | 0 | 114 deg | 114 deg |
| 16000 | -3510 | -5370 | 0 | 0 | 0 | 113 deg | 113 deg |
As shown in Table 4, there is clear relationship between C=C bond length and outer bond angle.
Table 4 only shows coordinates of e2 in A atom.
Other electrons ( A e3, B e0,1 ) need to be arranged symmetrically to this e2.
Here new unit 1 MM = 10-14 meter is used.
(Fig.13) Bond length and bond angle of ethylene.
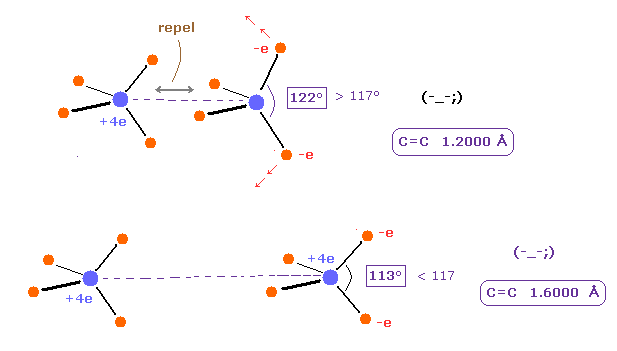
Basically, when C=C bond length becomes shorter, repulsive force between two C nuclei becomes stronger.
To cancel this repulsive force, bond angle of outer electrons ( A e2,3 and B e0,1 ) need to be wider.
Because if these angles are wider, attractive force outward becomes weaker.
On the other hand, when C=C bond length becomes longer, C=C repulsive force becomes weaker.
So attractive force outward needs to be stronger like Fig.13 lower panel.
This is the mechanism of C=C bond.
( Of course, in the actual bond, when e2-nuc-e3 angle is wider, e0-nuc-e1 angle becomes a little smaller. )
As shown in this page, we have succeed in expressing hydrogen molecule using Bohr's orbit.
In this page, we review hydrogen molecule using this program.
After running program, we choose "H" in both A,and B atom.
Internuclear distance of H2 is 0.7414 Å so input 7414 and click "internuc" button.
(Fig.14) H2 molecule.
In the program, we change x and z coodinates of "ele 0" electron symmetrically both in A and B atom.
"ele 1" means the coodinate after moving by the force acting on ele 0. See this page in detail.
We aim at the stability of both A and B nuclei ( FX = 0 ), and average de Broglie wave is "1.0000" ( ave = 1.0000 ).
| internuc (MM) | A-X (MM) | A-Z (MM) | B-X (MM) | B-Z (MM) | Force | aver waves | total V (eV) | bond energy |
|---|---|---|---|---|---|---|---|---|
| 6000 | 1870 | 4972 | -1870 | -4972 | 0 | 1.0000 | -60.664 | 3.120 |
| 6500 | 1145 | 4827 | -1145 | -4827 | 0 | 1.0000 | -62.204 | 3.890 |
| 7000 | 830 | 4755 | -830 | -4755 | 0 | 1.0000 | -62.893 | 4.234 |
| 7200 | 745 | 4739 | -745 | -4739 | 0 | 1.0000 | -63.014 | 4.295 |
| 7414 | 669 | 4729 | -669 | -4729 | 0 | 1.0000 | -63.056 | 4.316 |
| 7600 | 610 | 4724 | -610 | -4724 | 0 | 1.0000 | -63.047 | 4.311 |
| 7800 | 560 | 4721 | -560 | -4721 | 0 | 1.0000 | -63.010 | 4.293 |
| 8000 | 518 | 4720 | -518 | -4720 | 0 | 1.0000 | -62.952 | 4.264 |
| 9000 | 360 | 4741 | -360 | -4741 | 0 | 1.0000 | -62.365 | 3.971 |
Average binding energy of H2 is displayed in the last line (= "bin" ).
Total V of Table 5 means the average potential energy.
As shown in Table 5, when the bond length of H2 molecule is the experimental value of 0.7414 Å (= 7414 MM ), total V is the lowest, and binding energy becomes biggest (= 4.316 eV ).
This value is a little smaller than the experimental value of 4.746 eV.
But this result clearly shows H2 bond length is 0.7414 Å from the viewpoint of classical orbits.
| internuc (MM) | A-X (MM) | A-Z (MM) | B-X (MM) | B-Z (MM) | Force | aver waves | total V (eV) | bond energy |
|---|---|---|---|---|---|---|---|---|
| 6000 | 1665 | 4878 | -1665 | -4878 | 0 | 0.9933 | -61.787 | 3.681 |
| 6500 | 1059 | 4745.5 | -1059 | -4745.5 | 0 | 0.9933 | -63.224 | 4.400 |
| 7000 | 775 | 4684 | -775 | -4684 | 0 | 0.9933 | -63.802 | 4.689 |
| 7200 | 697 | 4671.5 | -697 | -4671.5 | 0 | 0.9933 | -63.8815 | 4.728 |
| 7414 | 629 | 4662.3 | -629 | -4662.3 | 0 | 0.9933 | -63.916 | 4.746 |
| 7600 | 577 | 4658 | -577 | -4658 | 0 | 0.9933 | -63.899 | 4.738 |
| 7800 | 530 | 4657 | -530 | -4657 | 0 | 0.9933 | -63.838 | 4.707 |
| 8000 | 488 | 4657 | -488 | -4657 | 0 | 0.9933 | -63.765 | 4.670 |
| 9000 | 340 | 4681.5 | -340 | -4681.5 | 0 | 0.9933 | -63.125 | 4.350 |
Next we aim at de Broglie wave of one orbit is 0.9933, like this page.
As shown in Table 6, when the bond length of H2 molecule is the experimental value of 0.7414 Å (= 7414 MM ), total V is the lowest, and binding energy becomes biggest (= 4.746 eV ).
The experimental value of binding energy is 4.746 eV.
This result is completely same as true H2 molecule, and this page.
So in this simplified way, de Broglie wave = 0.9933 is correct standard value.
And by both standards, bond length = 0.7414 Å of H2 proves to be most stable one.
(Fig.15) Two H atoms are completely dissociated.
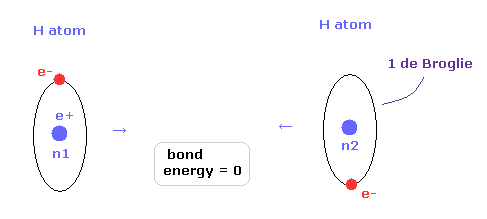
Next we think about the reason why H2 molecule becomes most stable when the internuclear distance of H2 is 7414 MM (= experimental value, 1 MM = 10-14 meter. ).
In Fig.15, two hydrogen atoms are completely dissociated, so the binding energy is just zero.
(Fig.16) Most stable H2 configuration.
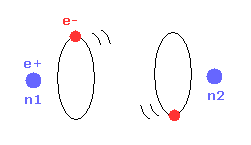
As the two nuclei come closer to each other, each electron can interact with two positive nuclei.
So, the bond energy becomes bigger, which means stable H2 molecule is formed.
(Fig.17) Repulsive force of two electrons.
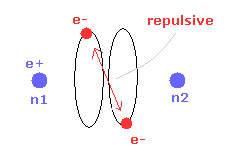
But when the two nuclei come closer to each other than the experimental value of 7414 MM, the repulsive force between two electrons are stronger.
As a result, "effective" central positive charge in it is smaller.
So under the common de Broglie wave's condition, this bond energy is smaller than the experimental value.
(Fig.18) When internuclear distance becomes shorter.
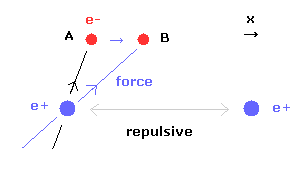
When the internuclear distance becomes shorter, the repulsive force between nuclei becomes stronger.
To cancel this repulsive force out, the two electrons need to move in the direction of the center.
As the electron 1 moves in the x direction ( A → B ), atrractive force of electron 1 becomes stronger in the x direction.
But in this case, the repulsive force between two electrons becomes stronger in Fig.17.
In this section, we investigate how strognly each atom ( C, N, O, F, Si, P, S, Cl ) can attract valence electron of another atom.
First, we investigate which is stronger, carbon (C) or silicon (Si).
C-Si bond length is 1.8500 Å, so after running this program, input 18500 into textbox and click "internuc" button.
(Fig.19) Force acting on e0 in C-Si bond.
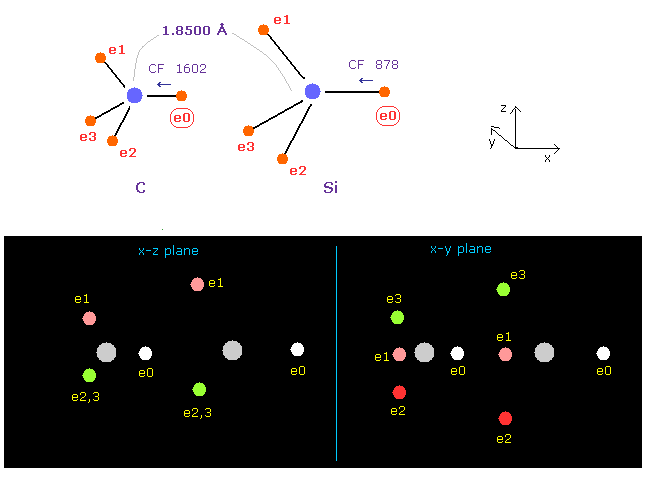
As shown in this page, the rotating electron radius of silicon is 1.1500 Å and its central charge is Z = 5.05, when we consider 1-4 ionization energies and "3" de Broglie wavelength.
Choose "Si" in the scroll bar and click "B atom" button.
We see the change of forces toward nucleus (= CF ) acting on e0 electron to compare electronegativities of them.
As shown in Fig.19, e0 of carbon (=A ) is attracted to its nucleus by the force CF 1602, and that of silicon is 878.
(Fig.20) Force acting on e0 in C-Si bond.
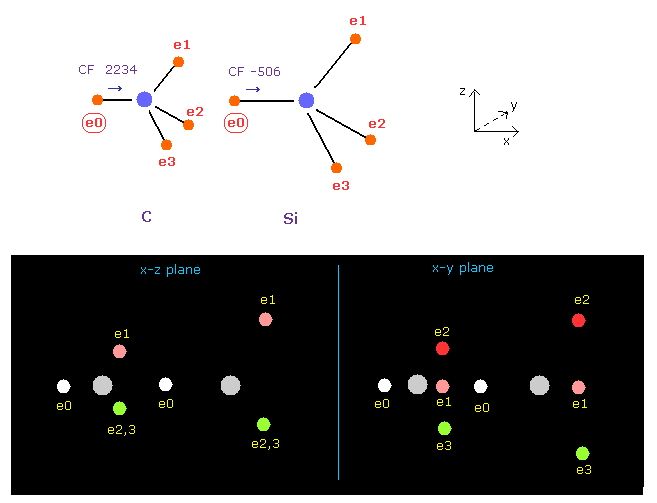
As I say in Fig.10, we need to think about two oscillating states.
Input the angle of 180 into textobox, and click "x-y ang" button in both A and B atoms to rotate them.
In Fig.20, the forces CF of e0 is 2234 in carbon, and -506 in silicon.
This indicates silicon tends to be easily ionized.
Actually silicon carbide ( SiC ), is rare crystal, and doesn't exist as a single molecule.
And this silicon carbide is semiconductor, which is different from diamond (= insulator )
(Fig.21) Carbon attracting power is stronger than silicon.

Fig.21 shows the ratio of force (= CF ) change to original force based on Fig.19 and Fig.20.
Even if this force change is larger, atoms with strong original force (= denominator ) doesn't leave its electron.
As shown in Fig.21, at a glance, e0 electron of silicon is strongly attracted to C nucleus.
This means attracting power of carbon is stronger than silicon.
Actually the electronegativitiy of carbon (= 2.55 ) is larger than that of silicon (= 1.90 ).
Next we investigate which attractive force is stronger, carbon or phosphorus.
After running this program, choose "P" in the scrollbar and click "B atom" button.
( Phosphorus Z and nuc is gotten in this page. )
(Fig.22) Carbon (C) - Phorphorus (P) bond
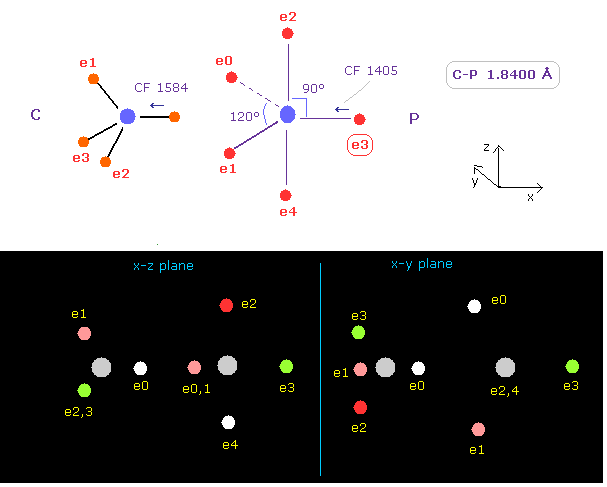
C - P bond length is about 1.8400 Å, so input 18400 into textbox, and click "internuc" button.
As shown in Fig.22, the force toward nucleus (= CF ) is 1584, and 1405
(Fig.23) C - P bond, part II.
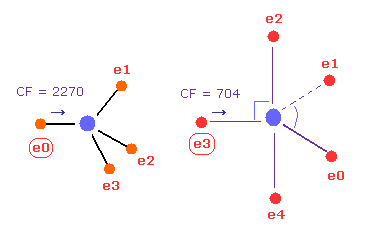
Then input the angle of 180 into textbox, and click "x-y ang" button in both A and B atoms.
In this state, the force CF is 2270 and 704, respectively.
(Fig.24) Carbon attracting power is stronger than phosphorus.
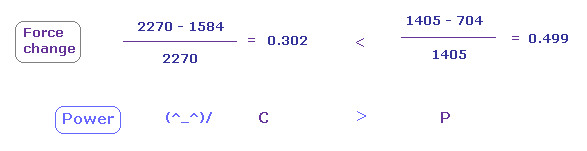
From Fig.22 and Fig.23, we compute each force change and ratio.
As shown in Fig.24, force change is larger in phosphorus.
( This means e3 electron of P is more attracted to C nucleus. )
So attracting power is stronger in carbon than phorphorus.
Actually, carbon electronegativity (= 2.55 ) is bigger than phosphorus (= 2.19 ).
(Fig.25) Carbon (C) - Sulfur (S) bond
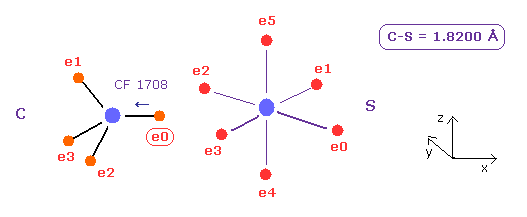
C - S bond length is about 1.8200 Å, so input 18200 into textbox, and click "internuc" button.
As shown in Fig.20, the force toward nucleus (= CF ) is 1708, in e0 of C atom.
(Fig.26) C - S bond, part II.
Then input the angle of 180 into textbox, and click "x-y ang" button in A atom (= carbon ).
And click "AB change" button, and change to B atom (= S ).
Input the angle of 45 into textbox, and "x-y ang" button in B atom.
Carbon and sulfur are rotated by the designated angles in x-y plane.
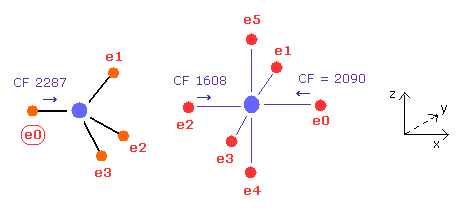
In this state, the force CF is 2287 in e0 of carbon, and 1608, 2090 in sulfur atom.
(Fig.27) Sulfur attracting power is stronger than carbon.
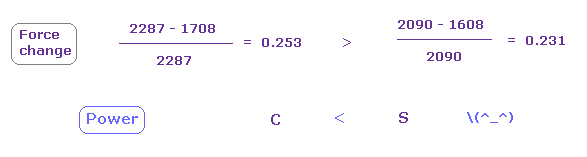
From Fig.25 and Fig.26, we compute each force change and ratio.
As shown in Fig.27, force change is a little larger in carbon.
So attracting power is a little stronger in sulfur than carbon.
Actually, sulfur electronegativity (= 2.58 ) is a little bigger than carbon (= 2.55 ).
( But they are almost same both in force and electronegativity. )
Next we investigate which attractive force is stronger, nitrogen or chlorine.
After running this program, choose "N" in the scrollbar and click "A atom" button.
And choose "Cl" in the scrollbar and click "B atom" button.
( Chlorine Z and nuc is gotten in this page. )
(Fig.28) Nitrogen (N) - Chlorine (Cl) bond
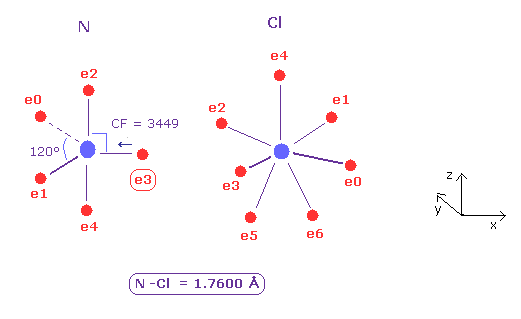
N - Cl bond length is about 1.7600 Å, so input 17600 into textbox, and click "internuc" button.
As shown in Fig.28, the force toward nucleus (= CF ) is 3449 and 2979 in N and Cl atoms, respectively.
(Fig.29) N - Cl bond, part II.
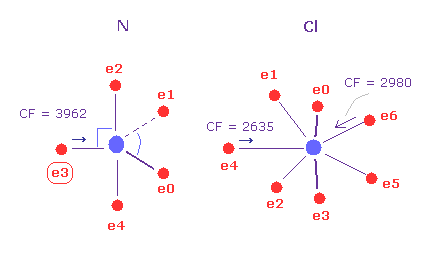
Then input the angle of 180 into textbox, and click "x-y ang" button in A atom (= nitrogen ).
And click "AB change" button, and change to B atom (= Cl ).
Input the angle of 90 into textbox, and "x-z ang" button in B atom.
Nitrogen and chlorine are rotated by the designated angles in each plane.
In this state, the force CF is 3962 in e3 of nitrogen, and 2980, 2635 in chlorine atom.
(Fig.30) Chlorine attracting power is stronger than nitrogen.
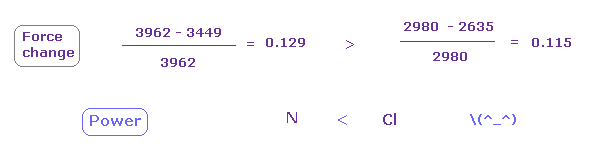
From Fig.28 and Fig.29, we compute each force change and ratio.
As shown in Fig.30, force change is a little larger in nitrogen.
So attracting power is a little stronger in chlorine than nitrogen.
Actually, chlorone electronegativity (= 3.16 ) is a little bigger than nitrogen (= 3.04 ).
(Fig.31) Fluorine (F) - Chlorine (Cl) bond
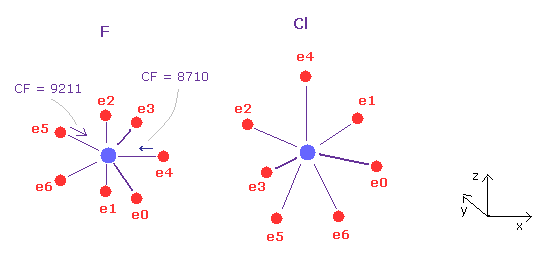
F - Cl bond length is 1.6283 Å, so input 16283 into textbox, and click "internuc" button.
As shown in Fig.31, the force toward nucleus (= CF ) is 8710 and 9211 in fluorine atom.
(Fig.32) F - Cl bond, part II.
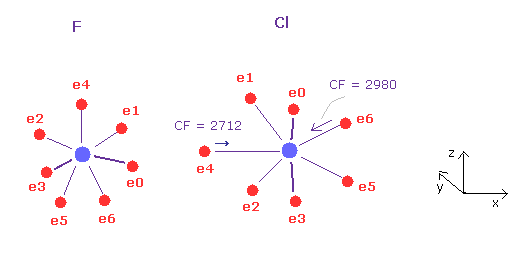
Next we click "A atom" button ( F in scrollbar ) to return to its original form.
Click "AB change" button to move into B atom, and input the angle of 90, click "x-z ang" button in B atom (= Cl ).
In this state, the force CF is 2712 and 2980 in chlorine.
(Fig.33) Fluorine attracting power is stronger than chlorine.

From Fig.31 and Fig.32, we compute each force change and ratio.
As shown in Fig.28, force change is larger in chlorine.
So attracting power is a stronger in fluorine than chlorine.
Actually, fluorone electronegativity (= 3.98 ) is bigger than chlorine (= 3.16 ).
Force change of numerator is larger in fluorine, but fluorine has the largest attracting power as shown in denominator (= 9211 )
As a result, we can explain the real meaning of electronegativity using classical orbits based on de Broglie waves.
(Fig.34) Force (CF) acting on C electron.
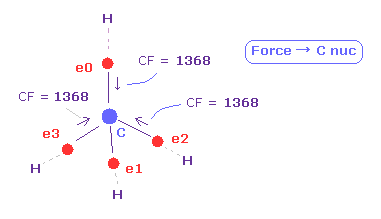
In this page, we investigate forces acting on four carbon valence electrons in methane-like molecules.
Force CF (= force component acting on each electron toward C nucleus ) of methane is 1368.
This value is proper.
(Fig.35) Force = 1000.
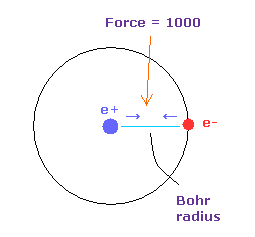
Force unit is shown in Fig.35.
The force between electron and nucleus in H atom ground state is supposed to be "1000".
So when the distance between electron and +e nucleus is Bohr radius, its force becomes 1000.
For example the force of 1468 is 1.468 times that in H atom ground state.
| C-H bond length | CF ( Z = -0.4500 Å ) | CF ( other ele 1-3 ) |
|---|---|---|
| 0.9000 Å | -1383 | +1382 |
| 0.9500 Å | -121 | +1377 |
| 1.0000 Å | +636 | +1374 |
| 1.0870 Å | +1368 | +1368 |
| 1.1500 Å | +1660 | +1367 |
Table 7 shows how force (= CF ) acting on carbon valence electron 0 changes depending on C-H bond length.
When C-H bond length is 1.0870 Å (= experimental value ), force CF is about 1400, which is good.
(Fig.36) Carbon electron (= e0 ) is attracted to H, instead of C !?
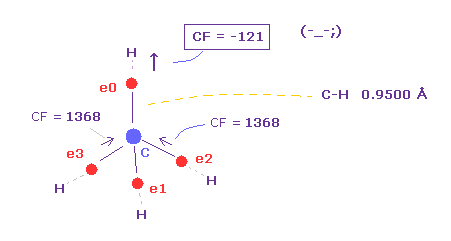
As you see in Table 7, when C-H bond length is shorter (= 0.9500 Å ), force toward C nucleus becomes negative ( CF = -121 ).
This means carbon valence electron e0 is attracted to hydrogen nucleus instead of C nucleus !
So in this case, electrons and H nucleus become unstable !
When C-H length is short like 0.9500 Å, de Broglie wave cannot be 1.000 to stop H nucleus.
Also in C-H = 1.0000 Å, CF = 636 is too small.
( As I said in Fig.35, even the force in simple hydrogen atom is as much as "1000". )
In conclusion, this stability of valence electrons and nuclei determines C-H bond length of methane, as I said in this page.
(Fig.37) Fluoromethane (= F-CH3 ).
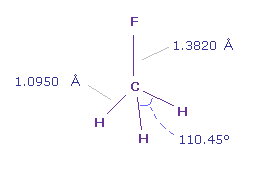
In fluoromethane, C-F bond length is 1.3820 Å and C-H bond length is 1.0950 Å.
(Fig.38) Force acting on four valence electrons are "balanced".
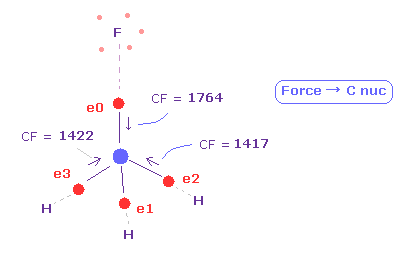
As shown in this page, we investigate forces acting on carbon valence electrons in fluoromethane.
Force "CF" of each electron means force component toward C nucleus acting on each valence electron.
( We can use this CF for judging force balance of 4 surrounding atoms. )
As shown in Fig.38, when F-C and H-C length is 1.3820 Å and 1.0950 Å, these forces are almost equal to each other.
CF = 1764 at F side, and CF = 1417 at H side.
(Fig.39) Force balance is broken.
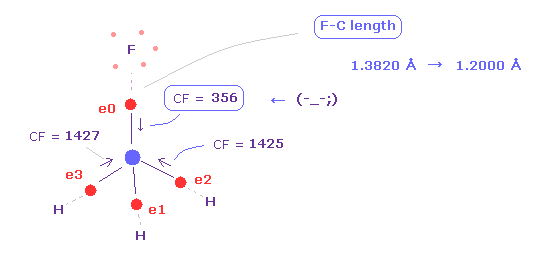
As you see in Fig.39, when F-C length is shorter (= 1.2000 Å ), carbon valence electron "0" is too attracted to fluorine nucleus.
So CF = 356 is too weak, comparing other CF = 1425.
( Of course, fluorine nucleus is also attracted to this electron 0 too much in this case. )
This means these particles become unstable in the same mechanism as CH4 above.
| F-C bond length | Force on e0 | Force on e1 | Force on e2 | Force on e3 |
|---|---|---|---|---|
| 1.1500 Å | -644 | +1425 | +1428 | +1428 |
| 1.2000 Å | +356 | +1423 | +1425 | +1427 |
| 1.2500 Å | +985 | +1423 | +1425 | +1427 |
| 1.3820 Å | +1764 | +1417 | +1417 | +1422 |
| 1.4500 Å | +1935 | +1415 | +1415 | +1420 |
As you see in Table 8, when the F-C bond length becomes shoter than the experimental value (= 1.3820 Å ), carbon's valence electron tends to be too much attracted to fluorine, and becomes unstable.
When F-C is 1.3820 Å. all four forces in e0-e3 are almost equal to each other.
This phenomenon is just the same as methane, and its factor determines the bond length.
After running this program, choose "C" (= carbon ) as "A atom".
And choose various atoms as "B atom", and investigate their influences on carbon electron "ele 0".
(Fig.40) Comparison of forces acting on C electron.
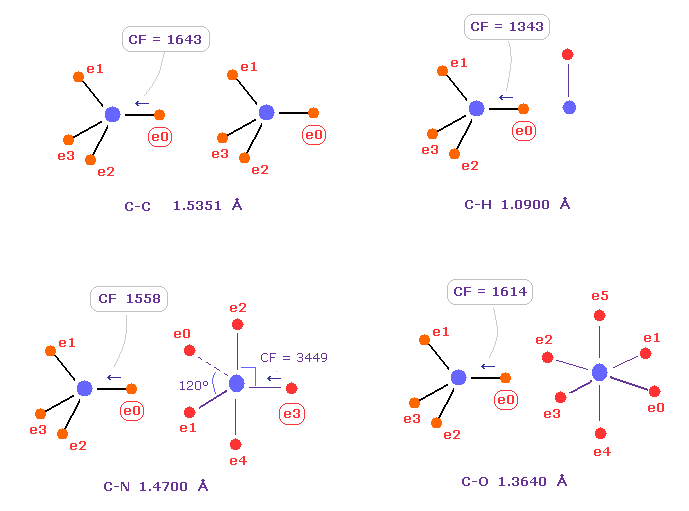
Fig.40 shows forces acting on carbon electron "e0" in C-C, C-H, C-N and C-O single bonds.
Considering carbon can keep tetrahedral structure in various bonds, it is natural forces acting on C electron are almost equal to each other.
Actually, these forces (= CF ) are 1643, 1343, 1558, 1614 in different C-C, C-H, C-N, C-O bonds, respectively.
( These bond lengths are average experimental values. C-O single bond is from acetic acid. )
| molecular bond | bond length | Force on e0 |
|---|---|---|
| C - H | 1.0900 Å | CF = 1343 |
| C - C | 1.5351 Å | CF = 1643 |
| C - N | 1.4700 Å | CF = 1558 |
| C - O | 1.3640 Å | CF = 1614 |
| C - F | 1.3500 Å | CF = 1605 |
| C - Si | 1.8500 Å | CF = 1602 |
| C - P | 1.8400 Å | CF = 1584 |
| C - S | 1.8200 Å | CF = 1708 |
| C - Cl | 1.7700 Å | CF = 1626 |
Table 9 shows forces (= CF ) acting on carbon electron "ele 0" in various bonds.
Surprisingly, in different bonds, these forces (= CF ) become almost same !
This means common mechanism is working, and carbon's tetrahedral structure is kept in various bonds.
(Fig.41) Various oxygen bond angle and length.
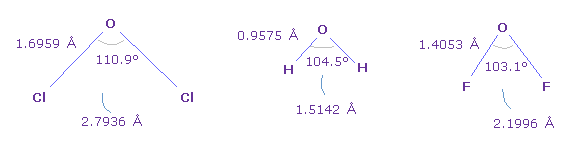
Fig.41 shows bond angles and length in various oxygen compounds.
Basically, Cl-O-Cl angle (= chlorine ) is the largest, and F-O-F angle (= fluorine ) is smallest.
( See also this page. )
As I said above, fluorine has the strongest attracting power, so electrons tend to be attracted to fluorine, which causes lower electron density at F side of O nucleus.
As a result, F-O-F angle becomes smaller.
But chlorine also has big attracting power, then why Cl-O-Cl angle is larger than H-O-H (= water ) ?
Here we think about these reasons from the viewpoint of pushing force of H, F, and Cl against O nucleus.
(Fig.42) Hyrogen's pusing force (= FX ) against O nucleus.
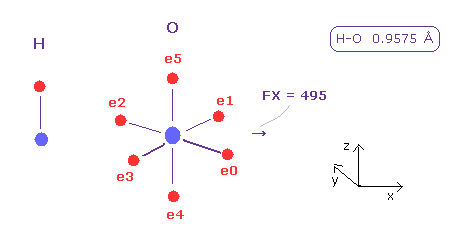
After running this program, choose "H" and "O" in the scrollbars and click "A atom" and "B atom" button.
And H-O bond length is 0.9575 Å, so input 9575 and click "internuc" botton.
Fig.42 shows x component of force acting on oxygen nucleus is FX = 495.
Of course, we need to move each electron to cancel these forces, but we can know some tendency about how strongly they push each other.
Hydrogen can come close to another nucleus keeping its own electron, because hydrogen orbit is short 1 × de Broglie wavelength.
(Fig.43) Fluorine's pusing force (= FX ) against O nucleus.
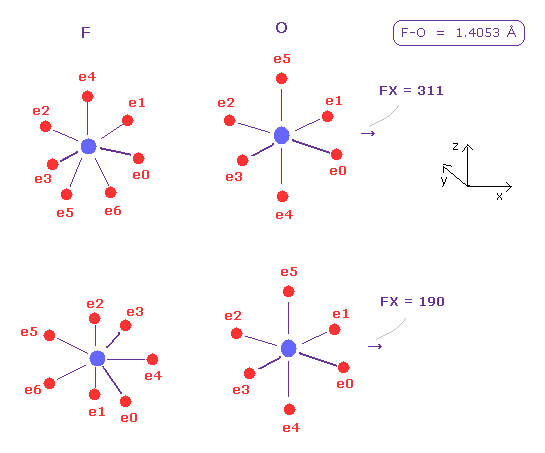
Next we choose "F" and click "A atom" button.
Internuclear distance of F-O is 1.4053 Å, so input 14053 and click "internuc" button.
In this state (= upper of Fig.43 ), x component of force acting on O nucleus is FX = 311.
This pusing power is smaller than hydrogen ( FX = 495 ), because fluorine has as much as seven valence electrons and its rotating radius is small.
And then input the angle of -90 and click "x-z ang" button to rotate fluorine.
Also in this state (= lower of Fig.43 ), FX = 190 is smaller.
As a result, for O nuclear stability, F-O-F angle needs to be smaller than H-O-H angle from the viewpoint of pusing power against O nucleus. (See Fig.41. )
(Fig.44) Chlorine's pusing force (= FX ) against O nucleus.
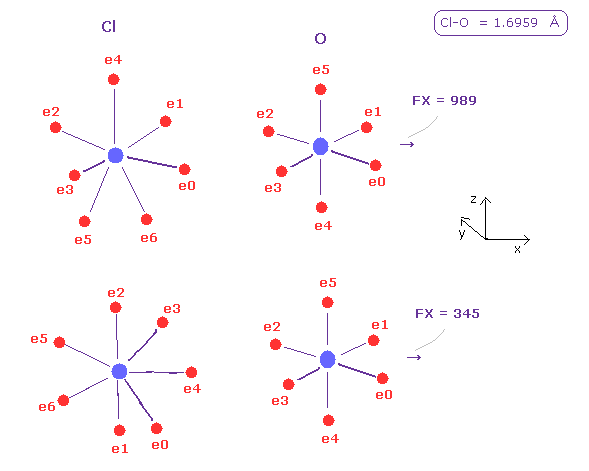
In the same way, do internuc=1.6959, and change A atom to chlorine ( Z = 8.26, nuc= 7640 ).
Average pusing force against O nucleus by chlorine is the biggest, ( 989 + 345 ) × 0.5 = 667.
Of course, chlorine valence electrons are farther away from Cl nucleus, so they can be more easily atracted to O nucleus than fluorine.
So these repulsive forces tend to be cancelled out.
But basically, due to its wide distribution of Cl valence electrons, chlorine has large repulsive power.
And Cl-O-Cl bond angle needs to be the largest for O nuclear stability in Fig.42.
(Fig.45) Why H-S-H bond angle is small ?
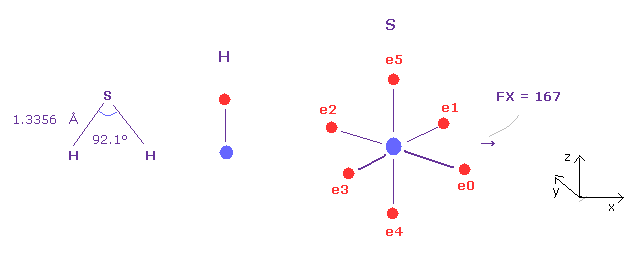
H-S-H bond angle (= 92.1 degree ) is smaller than H-O-H (= 104.5 degree ).
We can explain this reason from the viewpoint of pushing force.
Choose H and O as A and B atom, then change to Z = 7.18, nuc = 8622 in B atom to be sulfur.
And make internuclear distance 1.3356 Å (= 13356 MM ).
As shown in Fig.45, pusing force against S nucleus is FX = 167, which value is the smallest comparing Fig.42, Fig.43, and Fig.44.
So for the stability of S nucleus, H-S-H angle needs to be small, and can be close to 90 degree of octahedral structure.
(Fig.46) Various bond angle with carbon
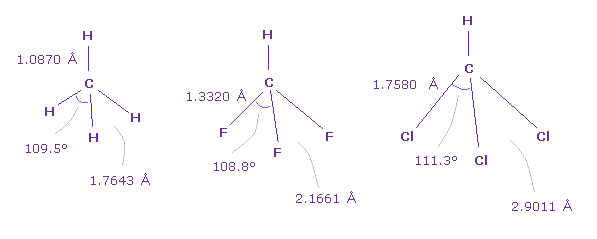
Actually, also in CH4 (=methane ), HCF3, HCCl3, F-C-F angle is smallest, and Cl-C-Cl angle is largest.
And F-F length (= 2.1661 Å ) of Fig.34 is very close to F-F length (= 2.1996 Å ) of Fig.42.
And Cl-Cl length (= 2.9011 Å ) of Fig.46 is also close to Cl-Cl length (= 2.7936 Å ) of Fig.42.
These results show the common mechanisms are working in various different molecules.
(Fig.47) Various bond angle with C=C.
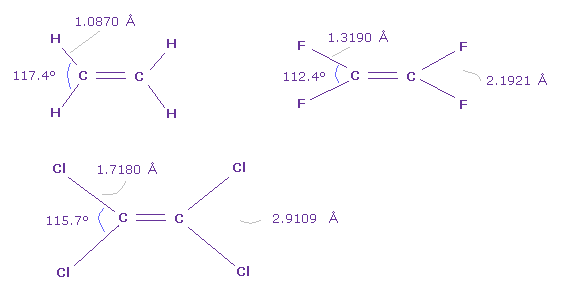
In Fig.47, H-C-H angle is largest and F-C-F angle is smallest.
But comparing Fig.46 and Fig.47, Cl-Cl lengths are almost same ( 2.9109 Å = 2.9011 Å ).
And considering the force balance of Fig.13, as bond angle is smaller, outer two valence electrons of carbon can attract C nucleus.
In molecules of Cl-O-H and F-O-H, these bond angle are smaller, 102.5 degree and 97.2 degree, respectively.
In these cases, hydrogen atom and chlorine, fluorine ( H-Cl, H-F ) tend to more attract each other than Cl-Cl or F-F.
(Fig.48) Hydrogen (H) - Carbon (C) bond.
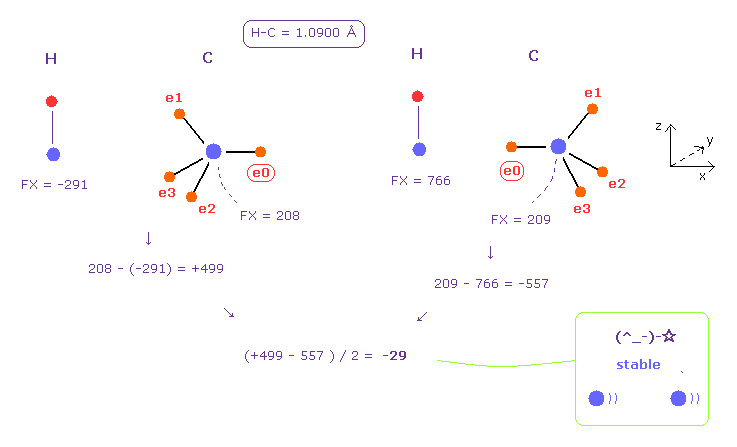
After running this program, we choose H and C atoms as A and B.
Basically, carbon's electrons are moving at two patterns.
The left of Fig.48 means repulsive force (= +499 ) between two nuclei.
The right is attractive force (= - 557 ).
( The right figure is gotten from rotating carbon by 180 degree in x-y plane. )
Summing them and divide it by two, we get the average force of -29, which is almost zero.
This means hydrogen electron doesn't need to came close to carbon nucleus.
( So hydrogen bond, C ---- H-C, is hard to be formed. )
(Fig.49) Hydrogen (H) - Nitrogen (N) bond.
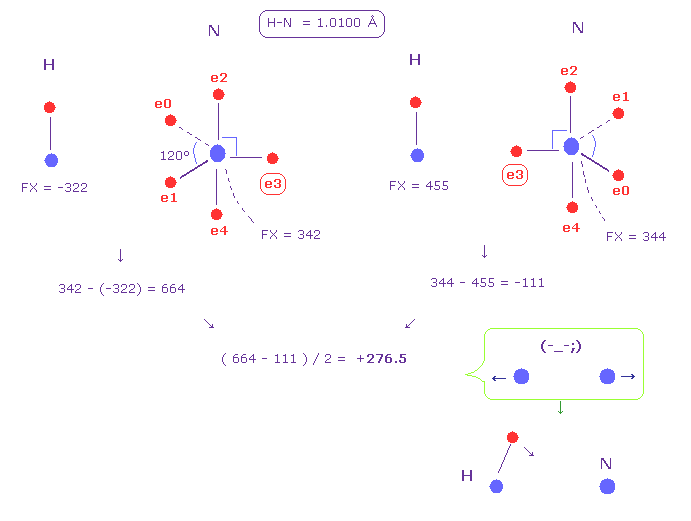
Fig.49 shows H-N bond.
Like Fig.48, we get the average force between two nuclei as +276.5 (= repulsive ).
Because in Fig.49, we suppose hydrogen's electron is fixed.
This result shows hydrogen electron needs to be attracted to another nucleus to cancel this force.
This causes positive hydrogen polarization, and hydrogen bond ( N ---- H-N ).
(Fig.50) Hydrogen (H) - Oxygen (O) bond.
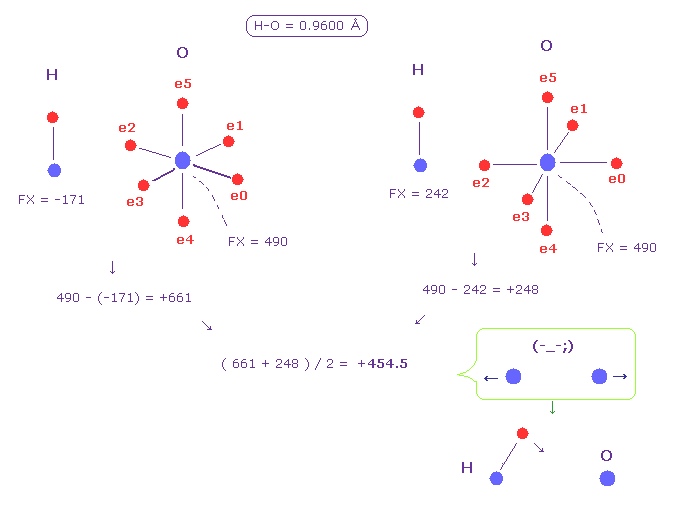
Fig.50 shows H-O bond.
Like Fig.48, we get the average force between two nuclei as +454.5 (= repulsive ).
This result shows hydrogen electron needs to be more attracted to another nucleus to cancel this force.
This causes positive hydrogen polarization, and hydrogen bond ( O ---- H-O ).
(Fig.51) Hydrogen (H) - Fluorine (F) bond.
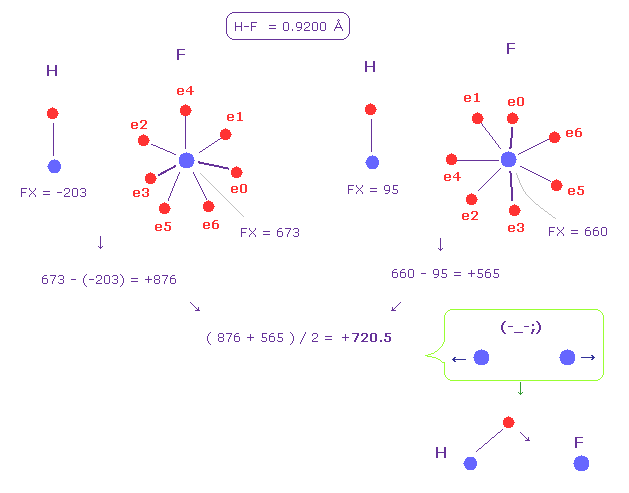
Fig.51 shows H-F bond.
Like Fig.50, we get the average force between two nuclei as +720.5 (= repulsive ).
This result shows hydrogen electron needs to be most attracted to another nucleus to cancel this force.
This causes almost ionization of hydrogen.
If you run the program above, and investigate H-F bond, hydrogen's de Broglie wave becomes too short due to strong fluorine's force.
So electron needs to come very close to fluorine nucleus.
Actually, hydrogen fluoride is crystal-like gas, cannot be a single H-F molecule.
| H - A atom | Charge Z | Radius | Bond length | Force-1 | Force-2 | Average force | A-Pauling |
|---|---|---|---|---|---|---|---|
| Silicon (Si) | 5.05 | 11500 | 14800 | +433 | -2000 | -783 | 1.90 |
| Phosphorus (P) | 6.12 | 9825 | 14400 | +476 | -670 | -97 | 2.19 |
| Carbon (C) | 4.22 | 6415 | 10900 | +499 | -557 | -29 | 2.55 |
| Sulfur (S) | 7.18 | 8622 | 13400 | +496 | -370 | +63 | 2.58 |
| Nitrogen (N) | 5.25 | 5331 | 10100 | +664 | -111 | +276 | 3.04 |
| Chlorine (Cl) | 8.26 | 7640 | 12700 | +635 | -60 | +287 | 3.16 |
| Oxygen (O) | 6.273 | 4596 | 9600 | +661 | +258 | +454 | 3.44 |
| Fluorine (F) | 7.3 | 4003 | 9200 | +876 | +565 | +720 | 3.98 |
Rotating radius of A atom's electron and bond length are unit 1 MM = 10-14 meter = 0.0001 Å.
Central charge Z and this radius of each atom is gotten in this page.
Force-1 is the force between two nuclei in pattern-1 ( for example, Fig.48, left ).
This value means difference between two FX. and if it is positive, it represents repulsive force.
Force -2 is that of pattern-2 ( for eample, Fig.48, right ).
Average force is gotten from summing them and dividing it by two.
As shown in Table 10, in H-C ( carbon ) bond, the force between two nuclei becomes almost zero.
Because hydrogen electronegativity (= 2.20 ) is close to carbon (= 2.55 ), and H-C bond is basically stable, and not ionized or polarized.
(Fig.52) H electron is attracted to F.
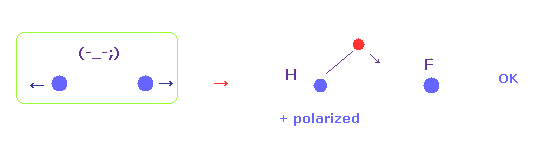
Silicon has very weak electronegativity, so silicon's electron is too attracted to H nucleus, which causes ionization.
As electronegativity becomes stronger, repulsive force between two nuclei becomes stronger.
( Because we fix hydrogen electron in all cases. )
So H electron needs to be attracted to another nucleus, as A atom's electronegativity is stronger.
( This causes positive polarization of hydrogen. )
Table 10 shows good correlation between average force and A atom electronegativity (= Pauling ).
(Fig.53) "Point" electrons (= e0 ) avoid each other.
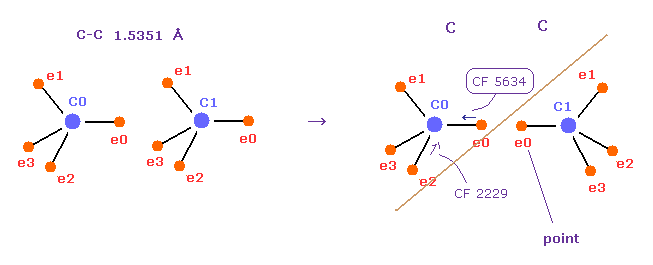
Basically, in C-C bond, carbon's valence electrons are moving periodically, avoiding valence electrons of another carbon.
Fig.53 shows carbon - carbon ( C-C ) bond,
Actually, in the right figure, CF (= force toward center ) rises suddenly from 2229 to 5634 by repulsitve force, if we try to make each point electron face each other.
(Fig.54) "Point" electrons of C-Cl bond can face each other more than C-C.
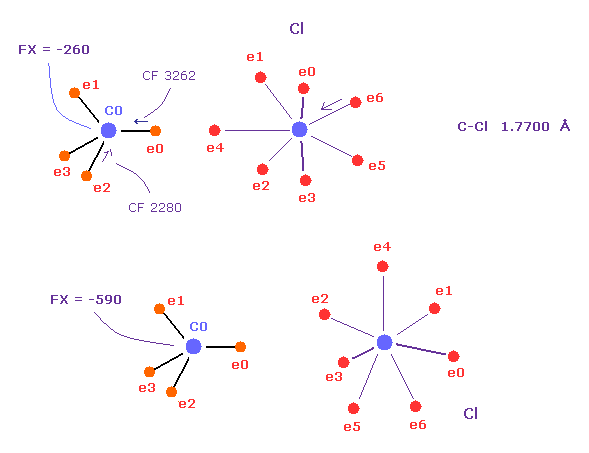
On the other hand, in C-Cl bond, point electrons of chlorine and carbon can face each other due to its long bond length (= 1.7700 Å ).
Actually, CF rises from 2280 to 3262, which is smaller than C-C.
If Cl doesn't point to carbon, carbon's nucleus is repelled too much by strong Cl positive nucleus.
( FX = -590 in lower figure ).
Because, seven valence electrons of chlorine are spreading widely.
But when Cl points to C nucleus, FX becomes small ( FX = -260 in upper figure ).
So to cancel strong repulsive force of Cl, they need to make point electrons face each other.
To do so, some long distance is needed.
(Fig.55) Force acting on C nucleus are similar.
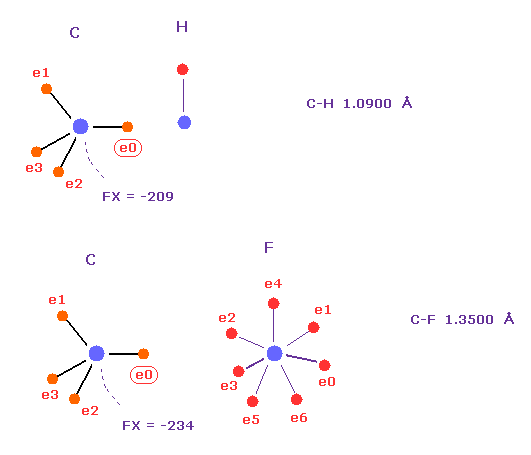
Force ( FX = -260 ) acting on carbon in C-Cl bond of Fig.54 is similar to those in C-H ( FX = -209 ) or C-F ( FX = -234) bonds.
Of course, we need to correct their positions a little, finding more stable states.
(Fig.56) Various bond angle with carbon.

Hydrogen, fluorine, and chlorine form methane like structures, so these similar FX are reasonable.
As I said, chlorine is very strong positively charged due to its widely spreading electrons.
So Cl-C-Cl bond angle is biggest in them.

2013/4/12 updated. Feel free to link to this site.