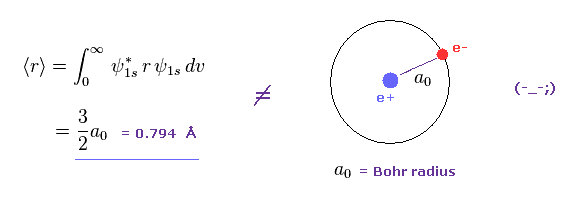
Top page (correct Bohr model including the two-electron atoms).
Strange "Spin" is NOT a real thing.
Special relativity is wrong.
(Fig.1) Orbital radius by quantum memcanical hydrogen ?
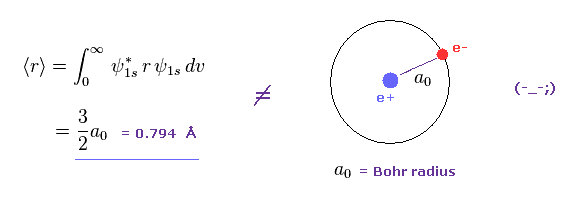
As shown in Fig.1, if we calculate average orbital radius of Schrodinger'd hydrogen, its value becomes about 1.5 × Bohr radius.
This result is different from that gotten from Virial theorem.
(Fig.2) Virial theorem of hydrogen → Bohr radius.
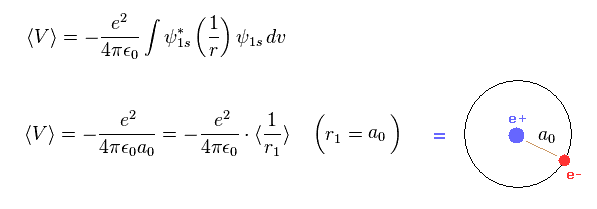
As shown in this page, Schrodinger's hydrogen also satisfies Virial theorem, and its radius is just Bohr radius like classical Bohr model.
This means what we call atomic radius of Hartree-Fock orbital is inconsistent with Virial theorem.
This inconsistency originates in unrealistic probability spreading of quantum mechanical model.
Also in 1s hydrogen wavefunction, the probability density at Bohr radius becomes maximum.
But their average value is different from Bohr radius.
(Fig.3) Difference between two atomic radii.

When two atoms of the same kind are bonded through a single bond in a neutral molecule, one half of that bond length is referred to as the covalent atomic radius.
For example, the internuclear distance of H2 molecule is 0.74 angstrom, so hydrogen atomic radius becomes 0.74 × 0.5 = 0.37 angstrom.
These covalent atomic radii are gotten from experiment, and have nothing to do with orbital radii by quantum mechanical methods.
Actually, as shown in Fig.3, orbital radius by quantum mechanical approach is completely different from the actual atomic radius.
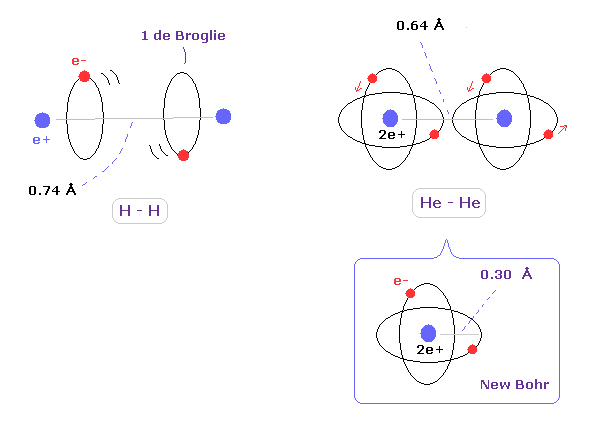
(Fig.4) Atomic radius of hydrogen and helium.
When we think about the relations between covalent atomic radius and experimental molecular bonds, the actual configurations of molecules are very important.
For example, in hydrogen molecule (H2), two orbits of hydrogen atom need to be almost parallel to each other, considering their energetically stable states.
So 2 × atomic radius is not equal to bond length in H2 molecule.
As shown in this page, we can get the correct energy states using classical orbits based on Coulomb and de Broglie relations in H2 molecule.
On the other hand, the quantum mechanical models cannot give clear and realistic atomic pictures at all.
In helium atom, the atomic orbital radius using new Bohr's helium (= 0.30 Å ) is almost same as experimental covalent atomic radius (= 0.32 Å ).
This agreement shows actual helium configuration.
(Fig.5) Ethane molecular model.
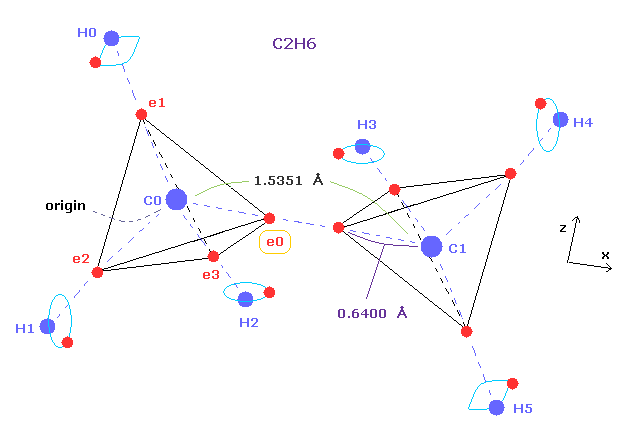
Single C-C bond length is 1.54 angstrom, so covalent atomic radius becomes 1.54 × 0.5 = 7.7 angstrom.
But as shown this page or this page, real rotating radius of carbon valence electron becomes 0.64 angstrom (= 0.6400 × 10-10 meter ), when we consider Coulomb and de Broglie wavelength.
This value 0.64 is a little smaller than 7.7.
So covalent atomic radius (= 0.77 ) itself does not mean real orbital radius (= 0.64 ).
In this page, we show Bohr orbit ( de Broglie wavelength ) based methods can give excellent atomic radius, which agrees with experimental results such as electronegativity.
(Fig.A-1) σ bond = two electrons are going back and forth between two H atoms ?

According to the quantum mechanics and Pauli exclusion principle, when two electrons of opposite spins enter one orbital, it becomes stable, they insist.
So in σ covalent bond, two electrons should belong to closed 1s orbitals in left or right H atoms, as one .
This means two electrons are always going back and forth as a pair between two H atoms ?
Unfortunately, each H nucleus has NO power to attract two nagetive electrons at the same time.
So this idea based on Pauli exclusion principle and closed orbital is unrealistic, and neglects basic Coulomb interaction.
(Fig.A-2) C-C bond = two electrons are going back and forth ?
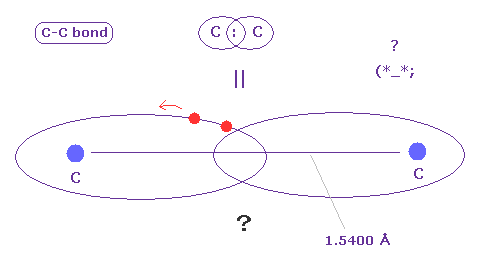
C-C bond is very long (= 1.5400 angstrom ).
In spite of this long bond length, two electrons must always form a pair to satisfy Pauli excluion principle ?
Considering realistic Coulomb interaction, it is quite natural that each electron belongs to each Carbon nucleus, not forming a pair. ( See Fig.7. )
The important point is that quantum mechanics cannot tell where electrons exist inside molecular bond.
They are like "black box".
So quantum mechanical molecular bonds, which cannot tell any concrete informations, are completely useless, when we think about larger molecules.
(Fig.A-3) An electron is spreading as sphere in QM ?
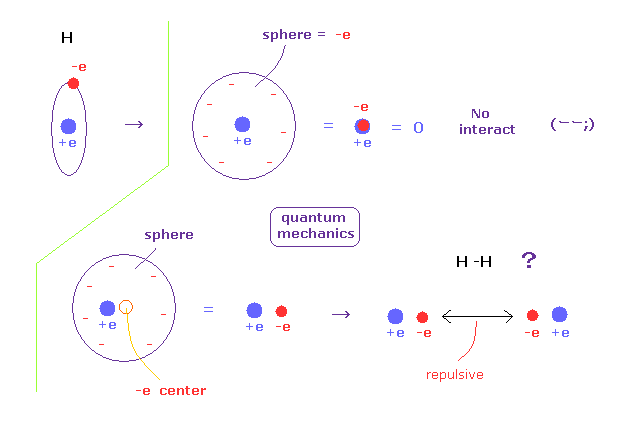
According to quantum mechanics, we cannot designate a single electron in hydrogen atom.
So a single elecctron of quantum mechanics is always spreading as wavefunction.
For example, when a single electron is spreading as sphere, we can consider that electron exists at the center of that sphere, from the viewpoint of potential energy.
If the electron is at the center, it just overlaps +e nucleus, and H atom completely becomes neutral.
So that H atom cannot interact with other atoms at all.
So an electron in H atom needs to be localized at some place like Bohr model, when it can interact with other atoms.
(Fig.A-4) H-H bond = two electrons are avoiding each other.
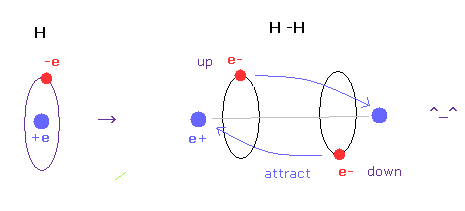
In hydrogen molecules, two electrons tend to be attracted to other nuclei.
But if we try to express this state using wavefunction sphere, they are repelling each other, as shown in Fig.A-3 lower figure.
On the other hand, if we use classical orbits, we can express H molecule naturally.
In this natural model, two electrons are avoiding each other (= up and down ), attracted to other positive nuclei, which can form covalent bond.
In conclusion, we need to use concrete localized electron in various molecules to express covalent bonds.
Electronegativity ( Pauling ) is the power of an atom in a molecule to attract nagative electrons to itself.
This electronegativity by Pauling is the average value gotten by comparing various experimental bond energies.
The electronegativity of hydrogen atom (H) is 2.20, and that of carbon (C) is 2.55.
Attracting powers of H and C atoms are almost same.
(Fig.6) "Force 1" acting on valence electron (= e0 ) in methane.
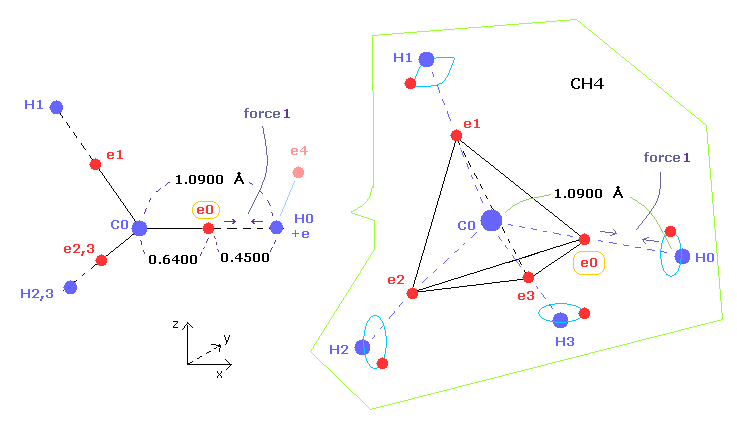
As shown in this page and this page (Fig.22), the rotating radius of four valence electrons of carbon is about 0.6400 × 10-10 meter, when we consider the total 1-4 ionization energies and "2" de Broglie wavelength orbit.
As a result, when valence electron e0 is closest to hydrogen nucleus, their distance becomes about 0.4500 angstrom, by 1.0900 (= C-H ) - 0.6400 .
At this point, ( Coulomb ) "force 1" is acting between a valence electron e0 of carbon and H0 nucleus.
(Fig.7) Periodic motion of ethane ( CH3-CH3 ).
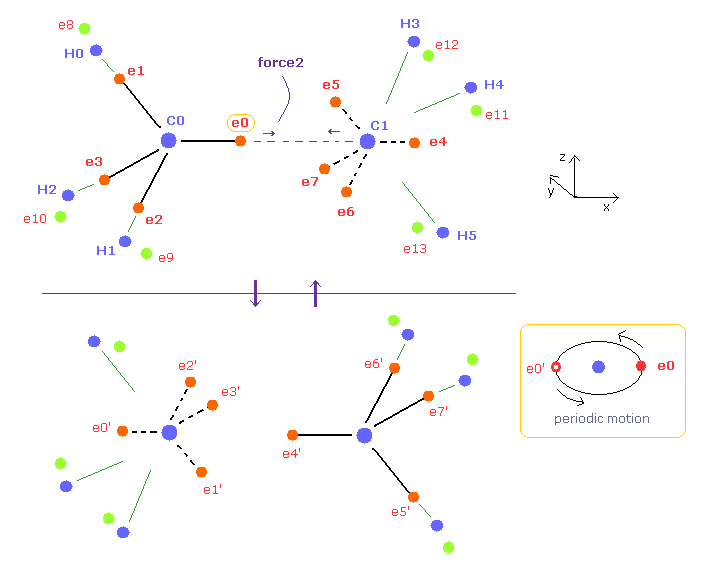
Four valence electrons of carbon are arranged as tetrahedral structure considering their symmetric distribution.
Each electron is actually moving around each centeral carbon nucleus, so Fig.7 upper and lower patterns are repeated periodically in ethane, if we try to know "real" motions in ethane. ( See also this page. )
(Fig.8) "Force 2" acting on valence electron (= e0 ) in ethane.
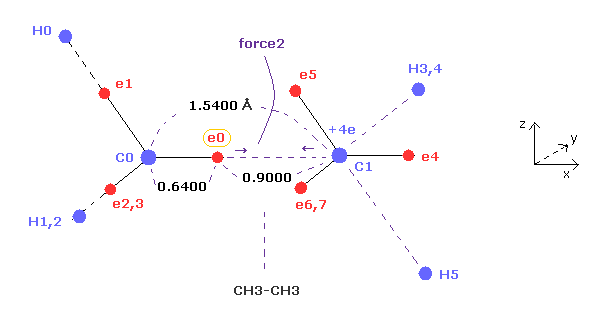
Fig.8 is the x-z cross-sectional view of ethane in Fig.7.
C-C bond length of ethane is about 1.5400 angstrom, and distance between valence electron e0 and C0 nucleus is about 0.6400 angstrom, when we consider "2" de Broglie wavelength orbit like methane.
As a result, the distance between e0 and another carbon nucleus C1 is about 0.9000 angstrom (= 1.5400 - 0.6400 ).
And central carbon nucleus (= C1 ) has about +4e positive charge ( +6e - 2e ), when two 1s negative charges are subtracted from +6e carbon nucleus.
"Force 2" is the force acting between this e0 electron and C1 nucleus.
(Fig.9) Coulomb forces 1, 2 in methane and ethane are almost same.
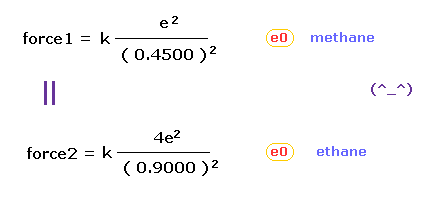
From Fig.6 (= methane ) and Fig.8 (= ethane ), we can know the forces acting between e0 valence electron and another nucleus ( H0 or C1 nucleus ).
Using Coulomb inverse square law, "force 1" in methane proves to be almost same as "force 2" in ethane !
This result agrees with almost same electronegativity of H and C atoms.
And the result of Fig.9 proves that both in methane and ethane, the idea of Coulomb relation and de Broglie wavelength are very important.
In this section, we review the methods of obtaining real atomic radius of carbon-like atoms (= C, Si .. ) based on Coulomb and de Broglie relations.
(Fig.10) Tetrahedral structure of carbon-like atoms.
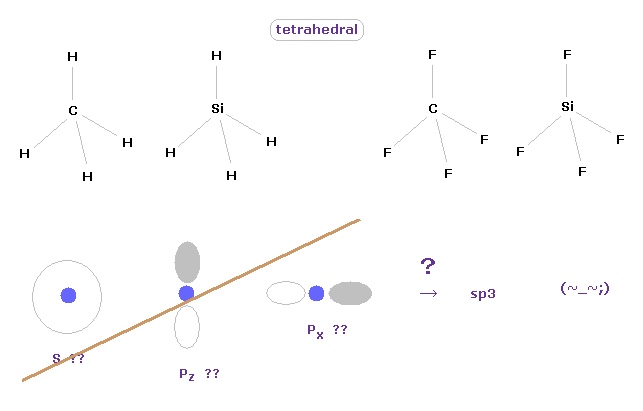
Considering symmetric structures of four valence electrons of carbon-like atoms, it is natural that those four electrons are distributed tetrahedrally around nucleus.
Actually, methane (= CH4 ), tetrafluoromethane (= CF4 ), silane (= SiH4 ), and siilicon tetrafluoride (= SiF4 ) are known to have tetrahedral structure.
This means the concepts of "s" and "p" ortbitals in quantum mechanics are completely useless, and NOT real.
They try to introduce the new concept of "sp3" orbitals, but this manipulation is very artificial, I think.
These unrealistic electron distributions such as "s", "p" and "d" prevent us from expressing various molecular bonds by real and clear picture.
(Fig.11) Valence electrons of carbon-like atoms.
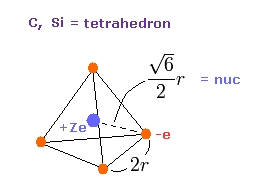
Here, using valence electrons' distribution of Fig.11, we compute "real" atomic radius and central positive charge Z.
The length of one side in tetrahedron ( Fig.11 ) is supposed to be"2r".
The total potential energy V is the sum of attractive V among +Ze nucleus and electrons, and repulsive V among four outer electrons.
(Eq.1) Total potenial energy V.
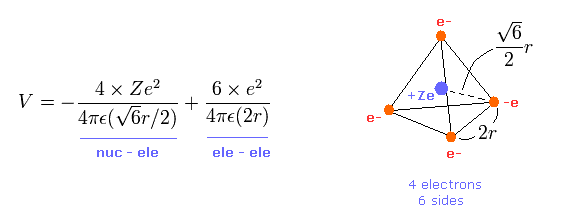
The first term of Eq.1 is potential energies between Ze nucleus and each electron.
And the second term of Eq.1 is the repulsive potential energies among four valence electrons.
Tetrahedron has six sides, so there are six interactions among electrons.
(Eq.2) Total kinetic energy T.
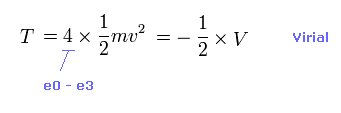
Total kinetic energy is the sum of kinetic energies in four valence electrons.
Using Virial theorem, this T can be gotten from total V. ( T = -1/2 V = -E. )
From the relation of Eq.2, we obtain the velocity "v" and de Broglie wavelength (= h/mv ) of each electron.
(Eq.3) Force F acting on each electron.
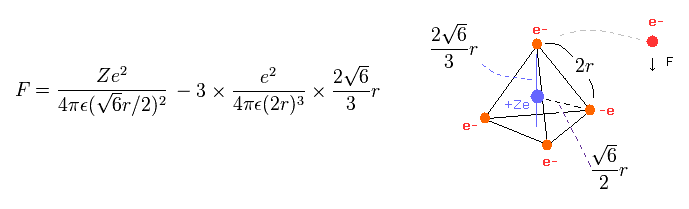
Eq.3 means force F acts on each electron.
The first term of Eq.3 is the attractive force by nucleus.
And the second term is repulsive forces from three other electrons.
Using the above velocity (v) ( of T ) and force F, we suppose the centrifugal force is equal to the force (F), as follows,
(Eq.4)
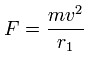
This r1 is "temporary" radius, which appears by this relation.
Using this r1, we can calculate the number of de Broglie's waves (= wn ) contained in one orbit, as follows,
(Eq.5)
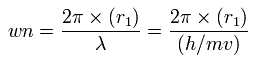
Sample JAVA program ( atomic radius ).
C language program ( atomic radius ).
In this program, first we choose the kind of atoms.
If you compute carbon like atoms (= C, Si ), input the valiue of "0", first.
Next input the central charge Z and total 1-4 ionization energies of all valence electrons.
From these inputted values, this program computes potential energies and force of tetrahedral carbon using Eq1 - Eq.5.
And using Virial theorem ( E = -T = 1/2 V ), this program calculate de Broglie wave in one orbit
In the screen, this de Broglie wave's number (= almost 2.0 ), and the distance between each valence electron and the central nucleus are shown.
| Atomic Name | 1st | 2nd | 3rd | 4th | 5th | 6th | 7th |
|---|---|---|---|---|---|---|---|
| Carbon (C) | 11.260 | 24.383 | 47.888 | 64.494 | - | - | - |
| Silicon (Si) | 8.151 | 16.346 | 33.493 | 45.142 | - | - | - |
For example, the sum of 1-4 ionization energies in carbon is 148.025 eV.
When Z = +4.0, this wn becomes 1.87 (almost 1.9) and rotating radius is almost 6000 MM. ( 1 MM = 10-14 meter. )
And when Z = +4.22, this wn becomes just 2.00 and rorating radius is almost 6400 MM.
This little difference between 4.0 and 4.22 is caused by the fact that two inner 1s electrons are apart from +6e carbon nucleus.
And this result agrees with those obtained from the program below, in which four valence electrons' motions are actually computed.
Sample JAVA program -- Visualization of carbon four valence electrons. ( central charge +4.22. )
After running the program above, and choose "1.0" or "2.0" de Broglie wave in the scrollbar, and click "orbit" button, you can understand when Z = 4.22, one orbit is just 2.0 de Broglie wavelength, and its rotating radius (= nuc ) is about 6400 MM (= 0.6400 × 10-10 meter. )
See also this page.
(Fig.12) Real atomic radius of carbon ( C ).
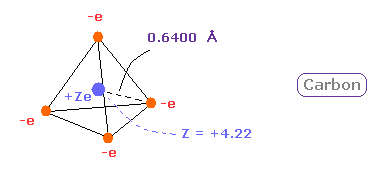
So we can define the real atomic radius of carbon as 0.6400 angstrom and the central positive charge as +4.22.
As I say later, these results agree with experimental results of bond length and electronegativity very well.
Next, the sum of 1-4 ionization energies in silicon ( Si ) is 103.132 eV.
Outer electrons of silicon is in n =3 ( three de Broglie wavelength ) orbits, so this value is smaller than n=2 carbon (= 148.025 ).
After running program above, choose "0" ( = carbon-like atoms ), in the same way.
And when Z = +5.05, de Broglie waves in one orbit becomes just 3.00 and rorating radius is almost 1.1500 angstrom.
(Fig.13) Real atomic radius of silicon ( Si ).
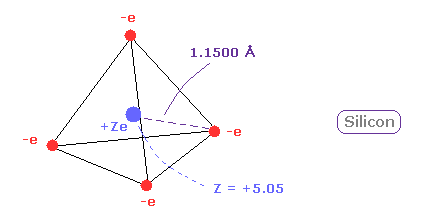
The atomic radius of silicon (Si) is bigger than that of carbon due to "3" de Broglie wavelength.
Actually, Si-H bond length is 1.4800 angstrom is much longer than C-H bond length (= 1.0900 angstrom ).
And due to wide distribution of 8 × n=2 middle electrons of silicon, central positive charge (= +5.05 ) is bigger than +4.
(Fig.14) Long atomic radius of silicon ( Si ) → unstable.
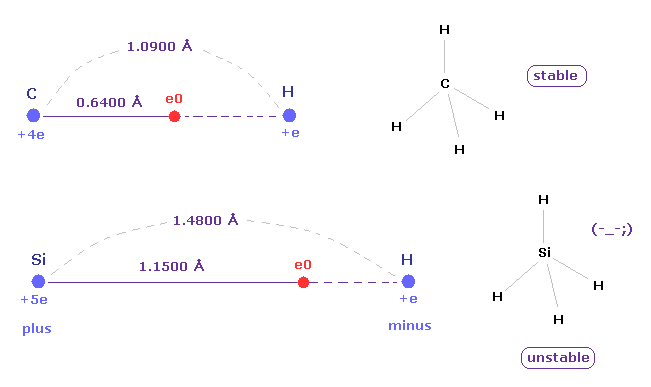
In silane (= SiH4 ), the hydrogen atoms have a partial negative charge and the silicon has a positive charge due to the difference between their electronegativity.
This property can be easily understood using new atomic radius based on de Broglie wavelength.
The distance between Si and its valence electron e0 is longer than that between e0 and H nucleus, which causes negative hydrogen atom.
And due to long distance of Si-H bond and the weak attracting power of silicon, silane (= SiH4 ) is much unstable than methane (= CH4 ).
Silane gas is easily pyrophoric, and it undergoes spontaneously combustion in air without the need for external ignition.
(Fig.15) New atomic radius can explain experimental Si-Si bond length.
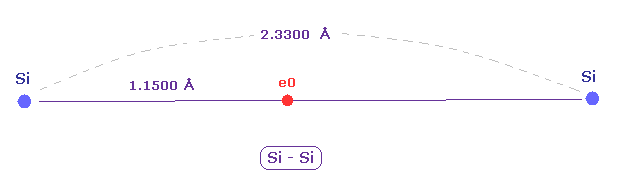
The experimental value of single Si-Si bond length is 2.3300 angstrom.
New atomic radius of silicon based on de Broglei wavelegnth is 1.1500 angstrom.
2 × 1.1500 = 2.3000 is near the experimental bond length of 2.3300 angstrom.
So these results almost agree with the actual values.
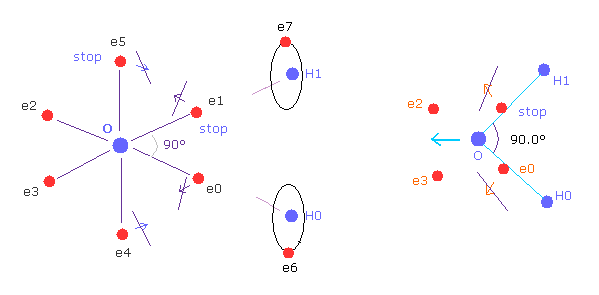
(Fig.16) Oxygen-like atom + hydrogen.
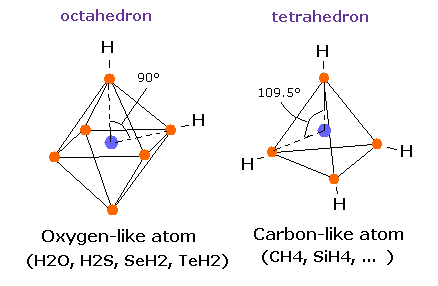
Oxygen -like atoms (= O, S, Se, Te ) has six valence electrons.
So it is natural that these six electrons are distributed octahedrally considering Coulomb repulsive forces among them.
Actually, H-S-H, H-Se-H, and H-Te-H angles are 92.1, 91.0, and 89.5 degrees, respectively. ( = almost 90 degrees).
In the case of oxygen, the hydrogen atom is closer to the oxygen atom than other oxygen-like atoms.
So, the repulsive force by hydrogen nuclei is so strong that the water (H2O) can not keep "octahedral" structure to make O nucleus stable.
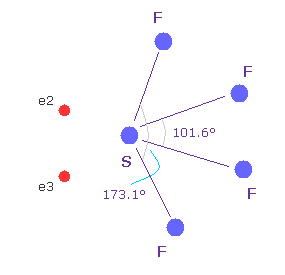
(Fig.17) Sulfur hexafluoride, SF6 = octahedron.

According to the quantum mechanics, sulfur (S) has six valence electrons like oxygen atom.
( 3s × 2 + 3p × 4 = 6. )
And stable sulfur hexafluoride is known to have just octahedral structure, in which F-S-F angle is just 90 degree.
This result clearly indicates, 3s2 3p4 state claimed by quantum mechanics is wrong and useless, and symmetric repulsive Coulomb force among six electrons is right.
(Fig.18) Oxygen-like atomic structrure.
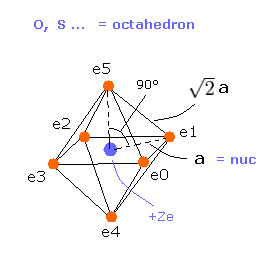
Here we compute real atomic radius of oxygen-like atoms using octahedral structure of Fig.18.
Considering Coulomb interactions among electrons and nucleus, total potenial energy V becomes
(Eq.6) Total potential energy.
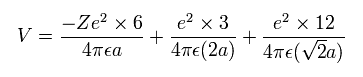
In Eq.6, the first term is attractive potential energy between +Ze nucleus and six electrons in Fig.18.
And the second and third terms are repulsive V among six valence electrons.
(Eq.7) Total kinetic energies.
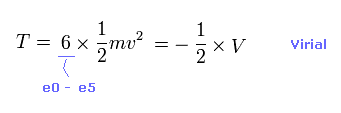
Using Virial theorem ( T = -1/2 V ), we can know total kinetic energy, each electron's velocity "v" and de Broglie wavelength (= h/mv ).
Total kinetic energy is the sum of six electrons.
(Eq.8) Force F acting on each electron.
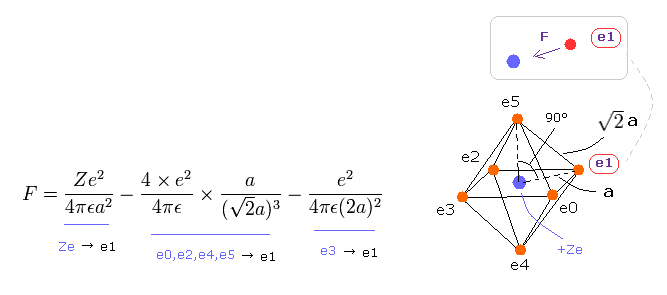
F of Eq.8 is the total attracting force acting on the electron "e1".
The first term of Eq.8 is the attracting force by +Ze nucleus.
The second term is repulsive force by e0, e2, e4 and e5, and the third term is the force by e3, as shown in Eq.8.
In the same way of carbon-like atoms, using Eq.4 and Eq.5, we obtain de Broglie waves in one orbit.
Sample JAVA program ( atomic radius ).
C language program ( atomic radius ).
If you compute oxygen like atoms (= O, S ), input the valiue of "1", first.
Next input the central charge Z and total 1-6 ionization energies of all valence electrons.
From these inputted values, this program compute potential energies and force of octahedral oxygen using Eq.6 - Eq.8 and Eq.4 - Eq.5.
On the screen, this de Broglie wave's number, and the distance between electron and nucleus are shown.
| Atomic Name | 1st | 2nd | 3rd | 4th | 5th | 6th | 7th |
|---|---|---|---|---|---|---|---|
| Oxygen (O) | 13.618 | 35.121 | 54.936 | 77.413 | 113.899 | 138.120 | - |
| Sulfur (S) | 10.360 | 23.338 | 34.790 | 47.222 | 72.595 | 88.053 | - |
The sum of 1-6 ionization energies in oxygen is 433.107 eV.
When Z = +6.0, this wn becomes 1.88 (almost 1.9) and rotating radius is almost 4300 MM. ( 1 MM = 10-14 meter. )
And when Z = +6.273, this wn becomes just 2.00 and rorating radius is almost 4600 MM.
(Fig.19) Real oxygen atomic radius.
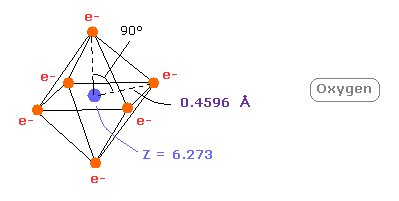
This small difference between 6.0 and 6.273 is caused by the fact two inner 1s electrons are apart from +8e oxygen nucleus.
( This influece is prominent especially in 5th and 6th ionization energies. )
These values agree with experimental phenomena.
(Fig.20) Coulomb forces 1, 2 in O-H and O-C bonds.
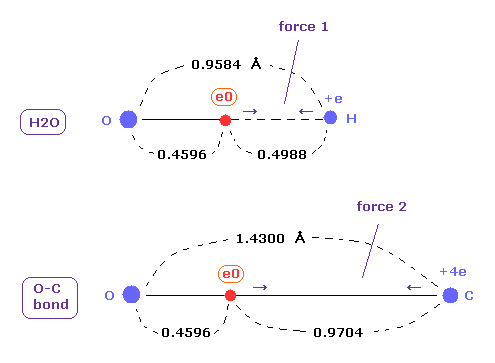
As is gotten above, real atomic radius of valence electron of oxygen is 0.4596 angstrom, when we consider 1-6 total ionization energies and their two de Broglie wavelength orbits.
O-H bond length of water is 0.9584 angstrom, and the average single O-C bond length is known to be 1.4300 angstrom.
Subtracting the atomic radius of 0.4596 from these bond lengths, we can know Coulomb forces 1,2 between electron and another nucleus.
(Fig.21) Coulomb forces 1, 2 in O-H and O-C bonds are almost same.
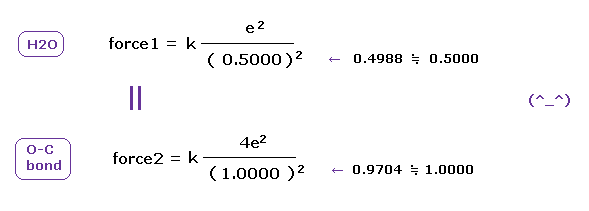
H nucleus is +e and, C nucleus is almost +4e (= +6e - 2e ), subtracting two inner 1s electrons from +6e nucleus.
As a result, Coulomb forces 1 and 2 between electron and another nucleus are almost same in O-H and O-C bonds.
Because the electronegativity of H (= 2.20 ) and C (= 2.55 ) atoms are almost same.
But due to strong attracting power of O atom, e0 of H2O is more attracted toward O nucleus than O-C bond in Fig.20. ( See Fig.21. )
These results demonstrate that valence electrons of oxygen in O-H and O-C bonds are moving obeying the common physical principle, and Coulomb and de Broglie relations are effective also in these cases.
(Fig.W-1) Electron distribution change in H2O
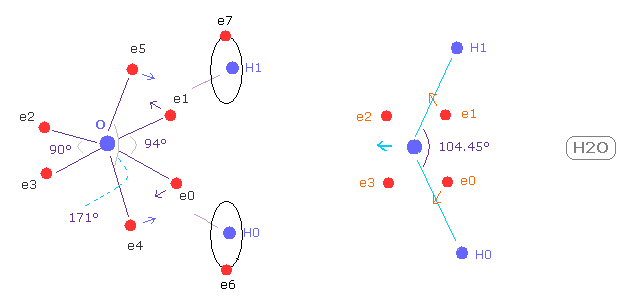
As shown in Fig.W-1, if H-O-H angle (= 104.45 degree ) is bigger than 90 degree of octahedral structure, e0 and e1 move outward, attracted to hydrogen nuclei.
As a result, e0 - O - e1 angle becomes wider than 90 degree.
Following this formal change, e4 - O -e5 angle becomes smaller than original 180 degree.
As a result, repulsive force by hydrogen nuclei is cancelled out by these configuration change.
( See this page. )
Because e4 and e5 pull O nucleus toward H atoms.
(Fig.W-2 ) Electron configuration change is blocked, when H-O-H is 90 degree.
On the other hand, if H-O-H angle is 90 degree, electron e0 and e1 cannot move outward, so e4 and e5 cannot move, either.
Because, O-e0 and O-el lines are on the same lines of O-H0 and O-H1 from the beginning.
So configuration change to cancel repulsive force of H nuclei does NOT happen.
Furthermore, this repulsive force by H nuclei becomes stronger when 90 degree than that of 104.45 degree, due to its sharp angle.
So the structual change to cancel these repulsive force of H nuclei is the reason of this angle.
(Fig.W-3) Sulfur tetrafluoride ( SF4 ).
Similar configuration change is seen in sulfur tetrafluoride (= SF4 ).
Sulfur (= S ) has six valence electrons like oxygen.
Due to the strong electronegativity of fluorine, sulfur's electrons are attracted toward fluorines and one side of electron density of S becomes weaker, which causes configuration change.
This mechanism is a little different from H2O above, but their configuration change is similar.
( The important difference between fluorine and hydrogen is seven valence electrons of F tend to repel electrons of other atoms, as the number of valence electrons in other atoms increases, while H tends to be attracted to them. )
(Fig.22) Real atomic radius of sulfur ( S ).

Next, the sum of 1-6 ionization energies in sulfur ( S ) is 276.358 eV.
Outer electrons of sulfur is in n =3 ( three de Broglie wavelength ) orbits, so this value is smaller than n=2 carbon (= 433.107 eV ).
After running program above, choose "1" ( = oxygen-like atoms ), in the same way.
And when Z = +7.18, de Broglie waves in one orbit becomes just 3.00 and rorating radius is almost 0.8622 angstrom.
As I said above, middle n=2 eight electrons are spreading more widely than n=1 electrons.
So effective central charge (= + 7.18 ) is bigger than +6.
(Fig.23) C-C and C-S bond length ( experimental values ).
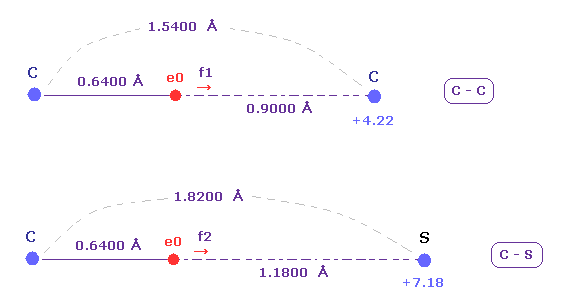
The exprimental values of C-C and C-S bond length are 1.5400 and 1.8200 angstrom, respectively.
The electronegativities ( Pauling ) of carbon (= 2.55 ) and sulfur (= 2.58 ) are almost same.
The electronegativity represents the power of attracting an electron of another nucleus.
So we investigate the forces acting on e0 (= carbon valence electron ), because this e0 is the target electron of ionization.
(Fig.24) Attracting powers of C and S are almost same.
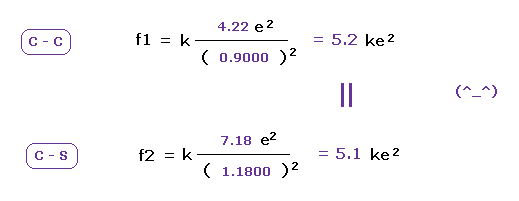
We compute the Coulomb forces ( f1 and f2 ) between e0 and another nucleus ( C or S ) in Fig.23 and Fig.24.
The results shows the powers of attracting electron are almost same in carbon and sulfur.
This means these classical orbits agree with almost same electronegativities in C and S atoms ( 2.55 and 2.58 ).
(Fig.25) BF3 = triangular.
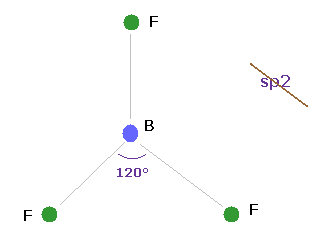
Boron (= B ) has three valence electrons.
If classical Coulomb force is always effective, the compounds of boron must be triangular.
Actually, boron trifluoride (= BF3 ) is known to be trigonal planar.
So the original "s" and "p" orbitals cannot be used also in boron-like atoms.
They try to introduce the new concept of sp2 hybrid orbitals temporarily, but this means original wavefunctions are completely unuseful in various molecules.
(Eq.9) Total potential energy V of boron - like atoms..
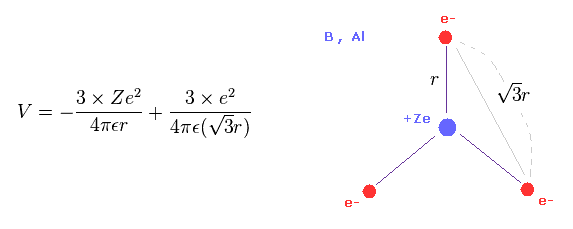
We suppose three valence electrons of boron-like atoms are distributed triangularly.
Considering Coulomb interactions among electrons and nucleus, total potenial energy V becomes like Eq.9.
In Eq.9, the first term is attractive potential energy between +Ze nucleus and three electrons.
And the second term is repulsive V among three valence electrons.
(Eq.10) Total kinetic energies.
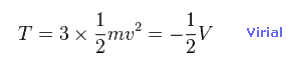
Using Virial theorem ( T = -1/2 V ), we can know the total kinetic energy and each electron's velocity.
Total kinetic energy is the sum of three electrons.
(Eq.11) Force F acting on each electron.
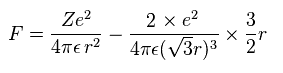
F of Eq.11 is the total attracting force acting on an electron.
The first term of Eq.11 is the attracting force by +Ze nucleus.
The second term is repulsive force by other two electrons.
In the same way of other atoms, using Eq.4 and Eq.5, we obtain de Broglie waves in one orbit.
Sample JAVA program ( atomic radius ).
C language program ( atomic radius ).
If you compute boron like atoms (= B, Al ), input the valiue of "2", first.
Next input the central charge Z and total 1-3 ionization energies of all valence electrons.
From these inputted values, this program compute potential energies and force of triangular boron using Eq.9 - Eq.11 and Eq.4 - Eq.5.
On the screen, this de Broglie wave's number, and the distance between electron and nucleus are shown.
| Atomic Name | 1st | 2nd | 3rd | 4th | 5th | 6th | 7th |
|---|---|---|---|---|---|---|---|
| Boron (B) | 8.298 | 25.155 | 37.931 | - | - | - | - |
| Aluminum (Al) | 5.986 | 18.828 | 28.448 | - | - | - | - |
The sum of 1-3 ionization energies in boron is 71.384 eV.
When Z = +3.22, this wn becomes 2.00 and rotating radius is 7996 MM. ( 1 MM = 10-14 meter. )
(Fig.26) Real boron atomic radius.
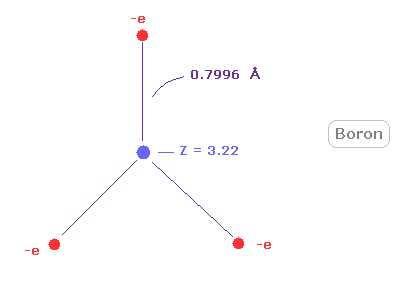
As shown in Fig.26, rotating radius of boron is very long (= about 0.8000 angstrom ) for its small central charge (= +3.22 ).
This very long atomic radius is related to small electronegativity of boron (= 2.04 ).
(Fig.27) Borane (= BH3 ) is very unstable.
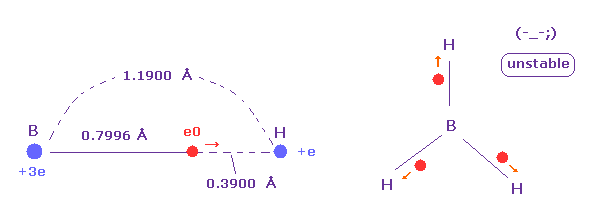
The borane is composed of one boron and three hydrogens.
But this borane molecule is very unstable.
Because as shown in Fig.27, valence electron "e0" of boron tend to be attracted to hydrogen nucleus due to its long radius.
On the other hand, B-H bond length is long and boron nucleus has weak attracting power ( Z = 3.0 ), hydrogen electron and nucleus cannot come close to boron nucleus.
In this process, hydrogen electron ( accompanied by its nucleus ) is repelled by e0 electron, and they are separated from each other.
(Fig.28) Unusual bond of Diborane (= B2H6 ).
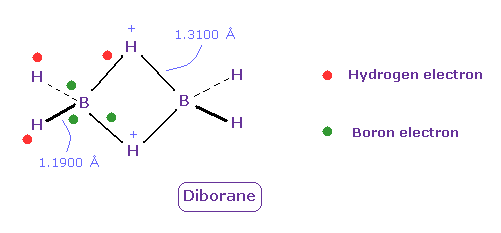
Diborane (= B2H6 ) is colorless gas, and ignite spontaneously in moist air at room temperature.
But this diborane is more stable than borane.
Boron tends to form unusual bonds such as electron-deficient.
In Fig.28, green ball is boron valence electrons, and red is hydrogen electron.
Boron's electrons tend to be attracted to two positive H nuclei of center, outer hydrogen's electrons also tend to be attracted toward ( slightly positive ) boron, and their bond strength becomes a little stronger.
( Unfortunately, quantum mechanics cannot give concrete mechanism of diborane. )
(Fig.29) Real atomic radius of aluminum ( Al ).
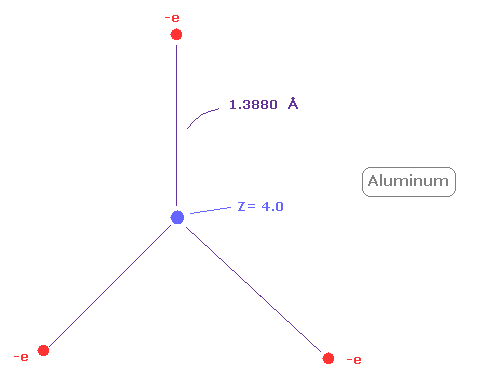
Next, the sum of 1-3 ionization energies in aluminum ( Al ) is 53.262 eV.
Outer electrons of aluminum is in n =3 ( three de Broglie wavelength ) orbits, so this value is smaller than n=2 boron (= 71.384 eV ).
After running program above, choose "2" ( = boron-like atoms ), in the same way.
And when Z = +4.0, de Broglie waves in one orbit becomes just 3.00, and rorating radius is almost 1.3880 angstrom.
As I said above, middle n=2 eight electrons are spreading more widely than n=1 electrons.
So effective central charge (= + 4.0 ) is bigger than +3.
(Fig.30) Weak electronegativity → aluminium hydride = crystal.
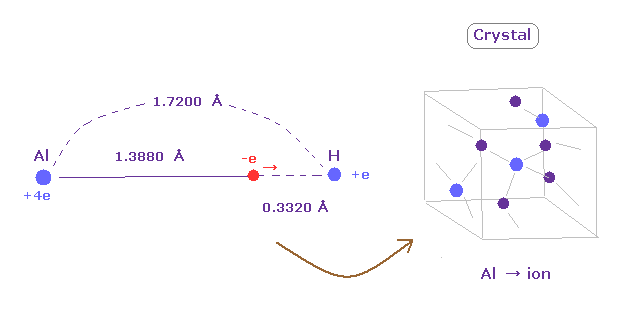
Aluminum (Al) has very long rotating radius (= 1.3880 angstrom ).
So its valence electrons easily leave aluminum, which means aluminium easily becomes ionized to be stable.
For example, in aluminium hydride, the distance between Al nucleus and its valence electron is much longer than that between H nucleus.
So alminum hydride becomes crystal and their valence electrons are moving around to make crystal's bonds strong.
( The electronegativity of alminum is 1.61, which is smaller than 2.20 of hydrogen. )
It can be said that diborane of Fig.28 is incomplete version of crystal.
(Fig.31) Distribution of five valence electrons in nitrogen (central charge = +5.25e)
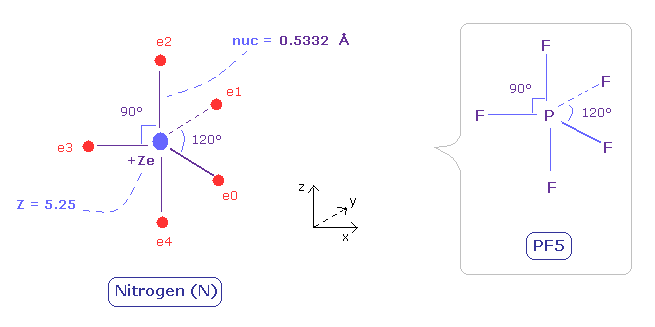
In the nitrogen atom, it is much more difficult to visualize the electrons' motions than carbon atom.
As the nitrogen has five valence electrons, it cannot be expressed as a regular polyhedrons like carbon (tetrahedron), oxygen (octahedron).
Phosphorus pentafluoride (PF5) is known to have structure like Fig.31.
( Phosohorus has five valence electrons like nitrogen. )
So we suppose five valence electrons of nitrogen are distributed like F of PF5.
Sample JAVA program (distribution of N electrons)
Here we use sample program above to seek symmetric distribution of nitrogen.
Also in the nitrogen atom (N), the two 1S electrons are a little apart from the +7e nucleus of N.
So the "effective" central charge of this figure is a little bigger than the +5e ( = +7e -2e ).
First, we use +5.25e, which is 0.25e+ bigger like the carbon case.
( This central charge Z can ne changed freely, input arbitrary value into the designated textbox. )
(Fig.31') Distribution of five valence electrons in nitrogen (central charge = +5.25e)
In this program, the nitrogen nucleus is gray.
Here we use the new units, ( 1 MM = 10-14 meter).
Each coordinate of electrons (+X (MM), +Y (MM), +Z (MM)) in the text box means "relative" positions from this nucleus.
"nuc (MM)" means the distance between the nucleus and each electron.
You can change "nuc" by entering the values into the designated text box, and press the Enter key.
(Fig.32) Forces acting on electron and nucleus.
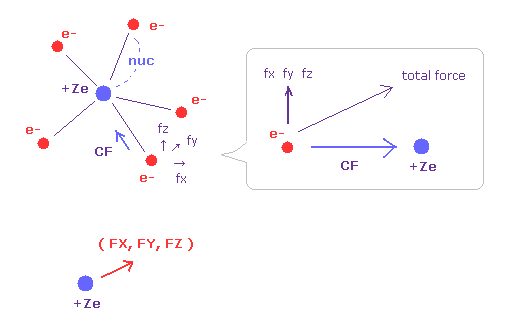
V (eV) and T (eV) mean the potential and kinetic energies of each electron.
CF means the force toward the nucleus acting on each electron.
(fx, fy, fz) mean the each component of the "remaining" force other than CF.
So when five valence electrons of nitrogen is symmetrically distributed around nucleus, these (fx, fy, fz) should be close to zero.
( FX, FY, FZ ) mean each component of the force acting on the nucleus.
For the stability, these FX, FY, FZ should be close to zero, too.
(Fig.33) Force = 1000.
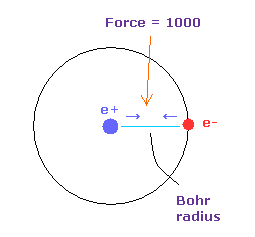
The unit of force: 1000 = the force between +e nucleus and an -e electron which are Bohr radius apart from each other.
"tV" is the total potential energy (eV).
Waves (wn) means the number of de Broglie's waves contained in one orbit of each electron.
| Atomic Name | 1st | 2nd | 3rd | 4th | 5th | 6th | 7th |
|---|---|---|---|---|---|---|---|
| Nitrogen (N) | 14.534 | 29.601 | 47.449 | 77.474 | 97.890 | - | - |
According to the Virial theorem, "average" total potential (V) and kinetic (T) energies satisfy the relation,
V = 2 × E = -2 × T
The total energy (E) of the five valence electrons of nitrogen is -266.948 eV (= the sum of the 1-5th ionization energies), so this potential energy (V) becomes 2 × -266.948 = -533.89 eV.
When the valence electrons are distributed "symmetrically" around the nucleus, the distances between electrons and nucleus (nuc) need to be the same in all valence electrons.
And the forces acting on electrons need to be toward the nucleus in the equlibrium state.
Based on total force (F) acting on each electron, we define "temporary" radius (r1) like Eq.4 and Eq.5, as follows,
(Eq.12)
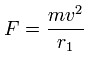
This means the centrifugal force is supposed to be equal to F.
"v" is the electron's velocity which value can be gotten from each kinetic energy.
And based on these values, we can find the values (wn) of de Broglie's waves, which is contained in one orbit of each electron, as follows,
(Eq.13)
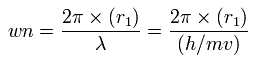
As shown in Table. 5, when the total potential energy (tV) of nitrogen valence electrons is - 534.05 eV, this wn (Waves) of each electron becomes almost 2.0.
| eNo. | +X (MM) | +Y (MM) | +Z (MM) | nuc (MM) | CF | fx | fy | fz | Waves |
|---|---|---|---|---|---|---|---|---|---|
| ele 0 | 2666 | -4617 | 0 | 5331 | 3904 | 0 | 0 | 0 | 1.998 |
| ele 1 | 2666 | 4617 | 0 | 5331 | 3904 | 0 | 0 | 0 | 1.998 |
| ele 2 | 0 | 0 | 5332 | 5332 | 3878 | 0 | 0 | 0 | 1.992 |
| ele 3 | -5332 | 0 | 0 | 5332 | 3904 | 0 | 0 | 0 | 1.998 |
| ele 4 | 0 | 0 | -5332 | 5332 | 3878 | 0 | 0 | 0 | 1.992 |
| nuc FX | nuc FY | nuc FZ | total V (eV) | Charge Z | Distance (MM) |
|---|---|---|---|---|---|
| 0 | 0 | 0 | -534.05 | Z = 5.25 | nuc= 5332 |
You can change the coordinates (+X, +Y, +Z), nuc (MM) and charge Z freely.
Table 5 shows that the all five valence electrons of nitrogen are moving on the orbits of "2" de Broglie's wavelength.
In this case, each component of the force acting on the nucleus becomes ( FX, FY, FZ ) = ( 0, 0, 0 ), which means stable nucleus.
Of cource, (fx, fy, fz) of each electron needs to be very small (= zero ) in the equilibrium state.
But nitogen with five electrons cannot be completely symmetric.
( In Fig.31 model, bond angles of 90 and 120 degree are mixed. )
(Fig.34) Real atomic radius of nitrogen.
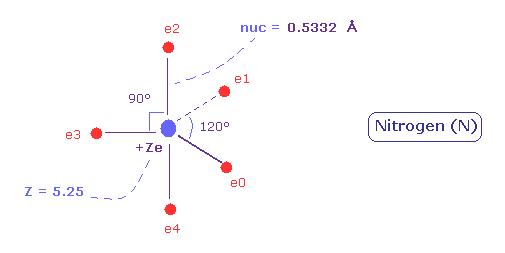
As a result, real atomic ( rotating ) radius of nitrogen valence electrons become 0.5332 angstrom.
And the central charge is +5.25.
( The small difference 0.25 is due to 1s electrons, which are apart from +7e nucleus. )
Next we think about the phosphorus (P) atom, which also has five valence electrons in n=3 orbital.
We can use the sample program above, also in this case.
| Atomic Name | 1st | 2nd | 3rd | 4th | 5th | 6th | 7th |
|---|---|---|---|---|---|---|---|
| Phosphorus (P) | 10.487 | 19.770 | 30.203 | 51.444 | 65.025 | - | - |
The sum of 1-5 ionization energy of phosphorus is 176.929 eV.
According to Virial theorem, the total potential energy V becomes 2 × 176.9 = -353.8 eV.
Input "6.12" into charge Z textbox, and "9825" into nuc textbox after running the program of nitrogen.
| eNo. | +X (MM) | +Y (MM) | +Z (MM) | nuc (MM) | CF | fx | fy | fz | Waves |
|---|---|---|---|---|---|---|---|---|---|
| ele 0 | 4912 | -8508 | 0 | 9825 | 1402 | 0 | 0 | 0 | 2.996 |
| ele 1 | 4912 | 8508 | 0 | 9825 | 1402 | 0 | 0 | 0 | 2.996 |
| ele 2 | 0 | 0 | 9825 | 9825 | 1394 | 0 | 0 | 0 | 2.988 |
| ele 3 | -9825 | 0 | 0 | 9825 | 1402 | 0 | 0 | 0 | 2.996 |
| ele 4 | 0 | 0 | -9825 | 9825 | 1394 | 0 | 0 | 0 | 2.988 |
| nuc FX | nuc FY | nuc FZ | total V (eV) | Charge Z | Distance (MM) |
|---|---|---|---|---|---|
| 0 | 0 | 0 | -353.58 | Z = 6.12 | nuc= 9825 |
When Z = 6.12 and the distance between each electron and P nucleus is 0.9825 angstrom ( 1 MM = 10-14 meter ), each electron orbit becomes almost "3" de Broglie wavelegth.
(Fig.35) Real atomic radius of phosphorus (P).
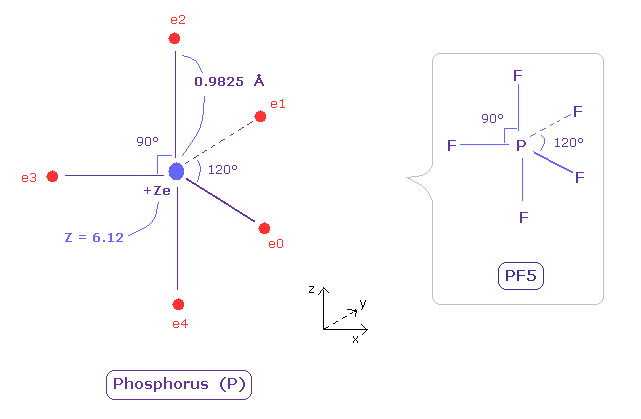
The radius of phosporus is longer than nitrogen.
So the electronegativity of phosphorus is weak (= 2.19 ).
And due to the widely spreading n=2 electrons, its effective central charge Z is +6.12, which is bigger than +5.
(Fig.36) Single P-P bond length.
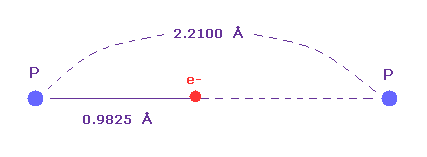
Single P-P bond length is known to be 2.2100 angtrom.
The atomic radius (= 0.9825 angstrom ) based on de Broglie wavelength is about an half of this single bond length.
So also in phosphorus atom, de Broglie and Coulomb relations prove to be effective.
(Fig.N-1) What angle between valence electrons ?
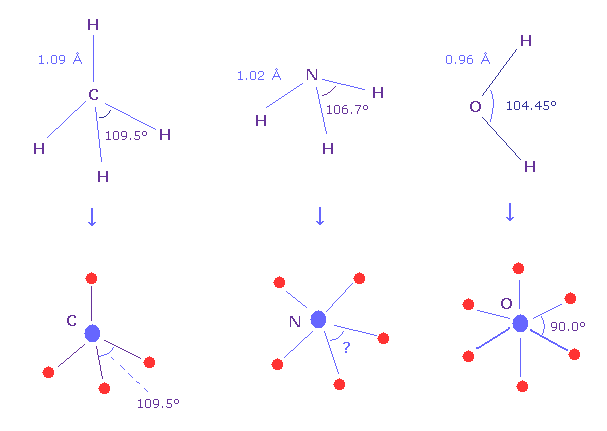
Methane molecule (= CH4 ) is just tetrahedral structure, so H-C-H bond angle is just 109.5 degree.
And H-O-H angle of water is 104.45 degree, which is a little different from 90.0 degree of octahedral structure.
H-N-H angle of ammonia (= NH3 ) is 106.7 degree, then what is the real angle between 5 valence electrons of nitrogen in molecules ?
(Fig.N-2) Angles between 5 and 6 valence electrons.
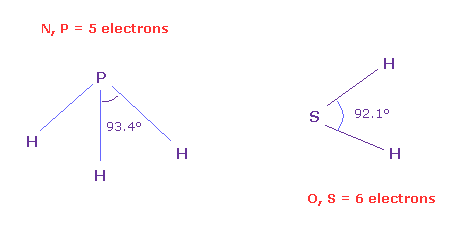
To know the real angles between valence electrons, we should investigate larger atoms of the same number of valence electrons.
Because as shown in this page, due to the short bond length (= 0.96 Å ) of H2O and the strong repulsive force by two H nuclei, the water cannot keep octahedral structure.
On the other hand, H-S bond length of SH2 is longer (= 1.34 Å ), so we can know more exact angle between 6 valence electrons, which is close to 90 degree (= 92.1 degree ).
And H-P bond length (= 1.42 Å ) is longer than H-N bond length (= 1.02 Å ).
So H-P-H bond angle of PH3 (= 93.4 degree ) is closer to the real angle between 5 valence electrons .
Actually the average angle among 5 valence electrons in Fig.31 nitorogen model is between 90 and 120 degree.
Also in the fluorine atom, it is difficult to visualize the electrons' motions.
As the fluorine has seven valence electrons, it cannot be expressed as a regular polyhedrons like carbon and oxygen.
We try to find as much "symmetrical" distribution as possible using the following sample program.
Sample JAVA program (distribution of F electrons)
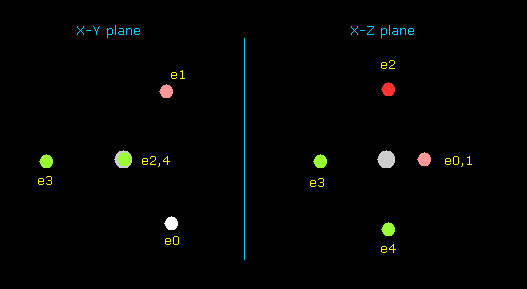
(Fig.37) Distribution of seven valence electrons in fluorine.
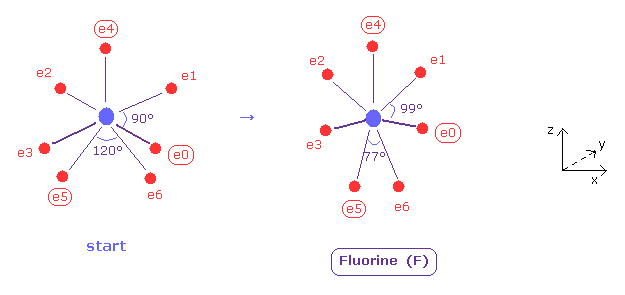
In this program, we start from the fluorine configuration of Fig.37 left.
Electrons e0, e1, e2 and e3 are symmetric to each other, and e5 and e6 are symmetric.
So we can change only coordinates of e0, e4, and e5, which determine other positions.
( In this starting positions, e0, e1, e2 and e3 are on x-y plane, and e4, e5 and e6 are on x-z plane. )
And we seek the distribution of seven valence electrons in which its potential energy becomes the lowest (= experimental value ).
(Fig.37') Distribution of seven valence electrons in fluorine (central charge = +7.3e)
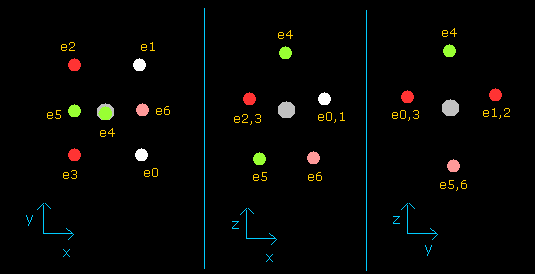
In this program, the fluorine nucleus is gray.
Here we use the new units, ( 1 MM = 10-14 meter).
Other manipurations and calculation methods are the same as the upper nitrogen.
| Atomic Name | 1st | 2nd | 3rd | 4th | 5th | 6th | 7th |
|---|---|---|---|---|---|---|---|
| Fluorine (F) | 17.423 | 34.971 | 62.708 | 87.140 | 114.243 | 157.165 | 185.186 |
According to the Virial theorem, "average" total potential (V) and kinetic (T) energies satisfy the relation,
V = -2 × T = 2 × E.
The total energy (E) of the seven valence electrons of fluorine is -658.836 eV (= the sum of 1-7 the ionization energies), so this potential energy (V) becomes 2 × -658.836 = -1317.67 eV.
As shown in Table 9, when the total potential energy (tV) of fluorine valence electrons is - 1317.71 eV, this wn (Waves) of each electron becomes almost 2.0.
| eNo. | +X (MM) | +Y (MM) | +Z (MM) | nuc (MM) | CF | fx | fy | fz | Waves |
|---|---|---|---|---|---|---|---|---|---|
| ele 0 | 2537 | -3045 | 563 | 4003 | 9147 | 9 | 22 | 78 | 1.990 |
| ele 1 | 2537 | 3045 | 563 | 4003 | 9147 | 9 | -22 | 78 | 1.990 |
| ele 2 | -2537 | 3045 | 563 | 4003 | 9147 | -9 | -22 | 78 | 1.990 |
| ele 3 | -2537 | -3045 | 563 | 4003 | 9162 | 0 | 0 | 0 | 1.991 |
| ele 4 | 0 | 0 | 4003 | 4003 | 9162 | 0 | 0 | 0 | 1.991 |
| ele 5 | -2500 | 0 | -3127 | 4003 | 9119 | 162 | 0 | -130 | 1.987 |
| ele 6 | 2500 | 0 | -3127 | 4003 | 9119 | -162 | 0 | -130 | 1.987 |
| nuc FX | nuc FY | nuc FZ | total V (eV) | Charge Z | Distance (MM) |
|---|---|---|---|---|---|
| 0 | 0 | 9 | -1317.71 | Z = 7.3 | nuc= 4003 |
You can change the coordinates (+X, +Y, +Z), nuc (MM) and charge Z freely.
If you try changing these values, you will know the de Broglie's waves ( Waves ) become almost 2.0, when the total potential energy is about -1317.71 eV.
This result shows that all seven valence electrons of fluorine are moving on the orbits of "2" de Broglie's wavelength.
In this case, each component of the force acting on the nucleus becomes ( FX, FY, FZ ) = ( 0, 0, 9 ), which values are almost zero and means stable nucleus.
Of cource, ( fx, fy, fz ) of each electron needs to be small in the equilibrium state.
( As I said, these values cannot be completely zero. )
(Fig.38) Real atomic radius of fluorine (= F ).
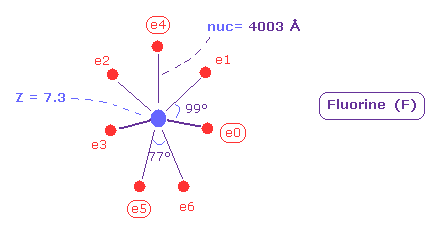
As shown in Fig.38, the atomic ( rotating ) radius of seven valence electrons of fluorine becomes 0.4003 angstrom (= 4003 MM ), which is very small.
And the central charge Z is 7.3.
(Fig.39) Strong electronegativity of F.
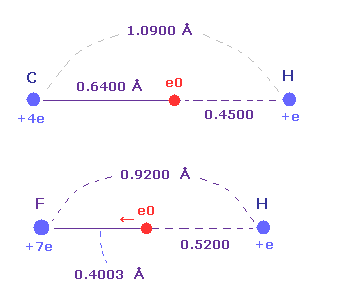
Actually, F-H bond length (= 0.9200 angstrom ) is shorter than C-H bond length (= 1.0900 angstrom ).
Furthermore, the distance between F nucleus and its valence electron e0 (= 0.4003 angstrom ) is shorter than that between H nucleus (= 0.5200 angstrom ), though its central charge Z is larger (= +7.0e ) than hydrogen (= +e ).
These structures appear as strong electronegativity of fluorine.
The electronegativities are F (= 3.98 ), H (= 2.20 ), and C (= 2.55).
So this result shows Coulomb and de Broglie relations are valid also in fluorine.
Next we think about chlorine (= Cl ) atom, which also has seven velence electrons in n = 3 energy levels.
| Atomic Name | 1st | 2nd | 3rd | 4th | 5th | 6th | 7th |
|---|---|---|---|---|---|---|---|
| Chlorine (Cl) | 12.968 | 23.813 | 39.610 | 53.465 | 67.800 | 97.030 | 114.196 |
The total ionization energies of seven valence electrons of chlorine is 408.88 eV.
So the total potential energy V becomes 2 × -408.88 = -817.76 eV.
After running the same program as fluorine, and input each coordinate of Table 9 (= fluorine ).
Then, when we input charge Z = 8.26 and nuc = 7640 into the designated textboxes, we can get the following values.
| eNo. | +X (MM) | +Y (MM) | +Z (MM) | nuc (MM) | CF | fx | fy | fz | Waves |
|---|---|---|---|---|---|---|---|---|---|
| ele 0 | 4841 | -5811 | 1074 | 7640 | 2972 | 2 | 6 | 21 | 2.990 |
| ele 1 | 4841 | 5811 | 1074 | 7640 | 2972 | 2 | -6 | 21 | 2.990 |
| ele 2 | -4841 | 5811 | 1074 | 7640 | 2972 | -2 | -6 | 21 | 2.990 |
| ele 3 | -4841 | -5811 | 1074 | 7640 | 2972 | -2 | 6 | 21 | 2.990 |
| ele 4 | 0 | 0 | 7640 | 7640 | 2975 | 0 | 0 | 0 | 2.993 |
| ele 5 | -4770 | 0 | -5967 | 7640 | 2965 | 44 | 0 | -35 | 2.986 |
| ele 6 | 4770 | 0 | -5967 | 7640 | 2965 | -44 | 0 | -35 | 2.986 |
| nuc FX | nuc FY | nuc FZ | total V (eV) | Charge Z | Distance (MM) |
|---|---|---|---|---|---|
| 0 | 0 | 0 | -817.19 | Z = 8.26 | nuc= 7640 |
As shonw in Table 11, when the distance between each electron and Cl nucleus is 0.7640 angstrom (= 7640 MM ), and its central charge Z = 8.26, each orbit becomes almost "3" de Broglie wavelength.
( The total V of -817.19 is almost same as experimental value of -817.76 eV. )
Due to widely spreading of n = 2 middle electrons, effective charge Z (= +8.26 ) is bigger than +7
(Fig.40) Real atomic radius of chlorine (= Cl ).
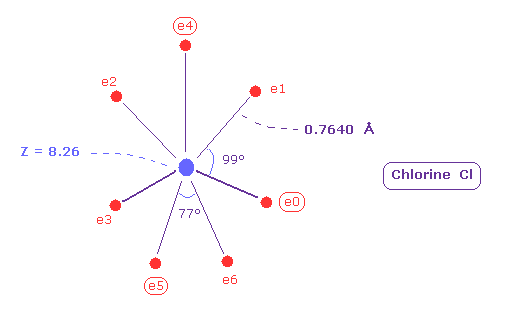
Comparing Fig.40 and Fig.38, the distribution of seven electrons are larger in chlorine than fluorine.
Actually the electronegativity of chlorine (= 3.26 ) is smaller than that of fluorine (= 3.98 ).
And the difference of spreading areas in Cl and F is related to moleculr bond angle.
(Fig.41) Fluoroform (= HCF3 ) and chloroform (= HCCl3 ) .
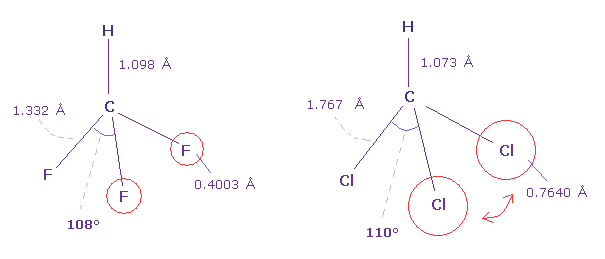
As shown in Fig.41, F-C-F angle (= 108.5 degree ) of fluoroform is a little smaller than basic tetrahedron (= 109.5 degree ).
Because the valence electrons around C nucleus tend to be attracted toward F, and electron density of F sides becomes lower .
But Cl-C-Cl angle of chloroform is a little bigger (= 110.4 degree ), though Cl has stronger electronegativity than carbon.
Because seven valence electrons of chlorine spread over larger area (= 0.7640 angstrom ) than fluorine (= 0.4003 angstrom ).
These repulsive interactions becomes slightly stronger in chloroform.
( Due to electron's wide distribution, positive chlorine nucleus exerts stronger repulstive force. )
(Fig.42) Electronegativity.
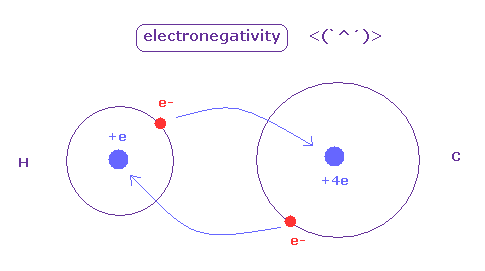
The electronegativity ( Pauling ) was gotten comparing various bond energies of various molecules composed of different pairs.
As the difference of eletronegativity between atoms becomes stronger, its bond includes more "ion" effects, which make that bond stronger.
Electronegativity represents the power of attracting an electron in each atom.
The hydrogen and carbon atoms have almost same electronegativity ( H = 2.20, C = 2.55 ).
The positive charge of C nucleus is bigger than H, but the electron orbit of H atom is one de Broglie wavelength, which is shorter.
So H atom can come close to another nucleus, keeping its own electron. ( It's related to why C-H bond of methane cannot be shorter than experimental value. )
As a result, they are almost same.
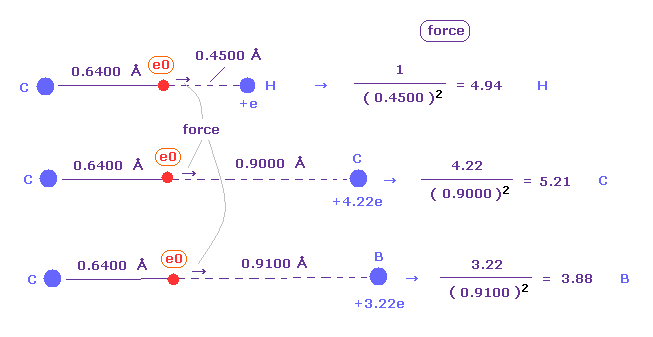
(Fig.43) "Force 1" acting on valence electron (= e0 ) in methane.

As is explained above, the rotating radius of four valence electrons of carbon is about 0.6400 × 10-10 meter, when we consider the total 1-4 ionization energies and "2" de Broglie wavelength orbit.
As a result, when valence electron e0 is closest to hydrogen nucleus, their distance becomes about 0.4500 angstrom, by 1.0900 (= C-H ) - 0.6400 .
At this point, ( Coulomb ) "force 1" is acting between a valence electron e0 of carbon and H0 nucleus.
(Fig.44) "Force 2" acting on valence electron (= e0 ) in ethane.

C-C bond length of ethane is about 1.5400 angstrom, and distance between valence electron e0 and C0 nucleus is about 0.6400 angstrom, when we consider "2" de Broglie wavelength orbit like methane.
As a result, the distance between e0 and another carbon nucleus C1 is about 0.9000 angstrom (= 1.5400 - 0.6400 ).
And central carbon nucleus (= C1 ) has about +4e positive charge ( +6e - 2e ), when two 1s negative charges are subtracted from +6e carbon nucleus.
"Force 2" is the force acting between this e0 electron and C1 nucleus.
(Fig.45) Coulomb forces 1, 2 in methane and ethane are almost same.
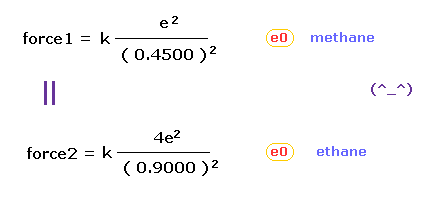
From Fig.43 (= methane ) and Fig.44 (= ethane ), we can know the forces acting between e0 valence electron and another nucleus ( H0 or C1 nucleus ).
Using Coulomb inverse square law, "force 1" in methane proves to be almost same as "force 2" in ethane.
This result agrees with almost same electronegativity of H and C atoms.
(Fig.46) Coulomb forces 1, 2 in O-H and O-C bonds.

As is gotten above, real atomic radius of valence electron of oxygen is 0.4596 angstrom, when we consider 1-6 total ionization energies and their two de Broglie wavelength orbits.
O-H bond length of water is 0.9584 angstrom, and the average single O-C bond length is known to be 1.4300 angstrom.
Subtracting the atomic radius of 0.4596 from these bond lengths, we can know Coulomb forces 1,2 between electron and another nucleus.
(Fig.47) Coulomb forces 1, 2 in O-H and O-C bonds are almost same.
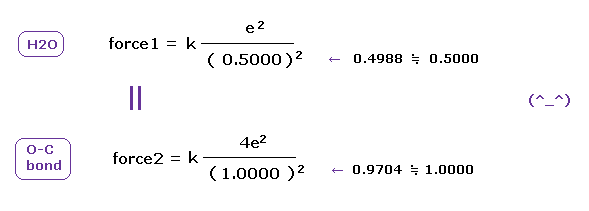
As shown in Fig.47, Coulomb forces 1 and 2 between electron and another nucleus are almost same in O-H and O-C bonds.
So also in bonds with oxygen, the electronegativity of H and C atoms are same using real atomic radius.
(Fig.48) Coulomb forces 1, 2 in N-H and N-C bonds.
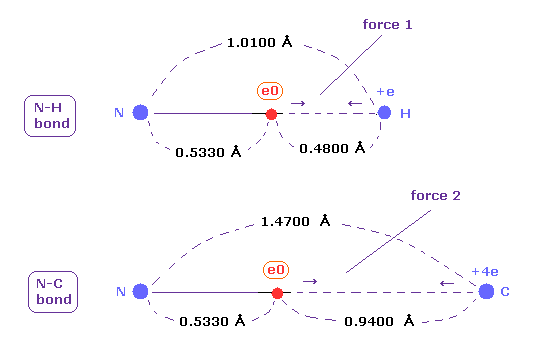
As is gotten above, real atomic radius of valence electron of nitrogen is 0.5330 angstrom, when we consider 1-5 total ionization energies and their two de Broglie wavelength orbits.
N-H bond length is 1.0100 angstrom, and the average single N-C bond length is known to be 1.4700 angstrom.
Subtracting the atomic radius of 0.5330 from these bond lengths, we can know Coulomb forces 1,2 between electron and another nucleus.
(Fig.49) Coulomb forces 1, 2 in N-H and N-C bonds are almost same.
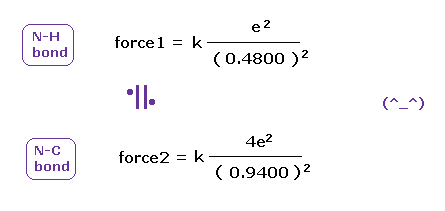
As shown in Fig.49, also in bonds with nitrogen, the electronegativity of H and C atoms are same using real atomic radius.
Basically the target electron of ionization is one closest to another nucleus (= "e0" ).
Hydrogen atom is composed of one nucleus and one electron.
When another outer electron "e0" is closest to H nucleus, H electron moves away from this "e0".
( This gap between H nucleus and electron causes attracting power. )
So a pair of one nucleus + one electron is one unit of ionization power.
C atom can be considered as having four pairs of a nucleus + an electron, so its power is four times stronger than H atom when their distances are the same.
| Atoms (= A ) | A-C bond ( Å ) | A-H bond ( Å ) | A-e0 ( Å ) | e0 - C nuc | e0 - H nuc | e0-C / e0-H |
|---|---|---|---|---|---|---|
| Carbon (C) | C-C 1.5400 | C-H 1.0900 | 0.6400 | 0.9000 / | 0.4500 | = 2.000 |
| Oxygen (O) | O-C 1.4300 | O-H 0.9584 | 0.4596 | 0.9700 / | 0.4980 | = 1.948 |
| Nitrogen (N) | N-C 1.4700 | N-H 1.0100 | 0.5330 | 0.9400 / | 0.4800 | = 1.958 |
| Boron (B) | B-C 1.5500 | B-H 1.1900 | 0.8000 | 0.7500 / | 0.3900 | = 1.923 |
| Fluorine (F) | F-C 1.3500 | F-H 0.9200 | 0.4000 | 0.9500 / | 0.5200 | = 1.827 |
| Silicon (Si) | Si-C 1.8500 | Si-H 1.4800 | 1.1500 | 0.7000 / | 0.3300 | = 2.121 |
| Phosphorus (P) | P-C 1.8400 | P-H 1.4400 | 0.9800 | 0.8600 / | 0.4600 | = 1.870 |
| Sulfur (S) | S-C 1.8200 | P-H 1.3400 | 0.8600 | 0.9600 / | 0.4800 | = 2.000 |
| Chlorine (Cl) | Cl-C 1.7700 | Cl-H 1.2700 | 0.7640 | 1.0060 / | 0.5060 | = 1.988 |
(Fig.50) Coulomb forces 1, 2 in A-H and A-C bonds are almost same.
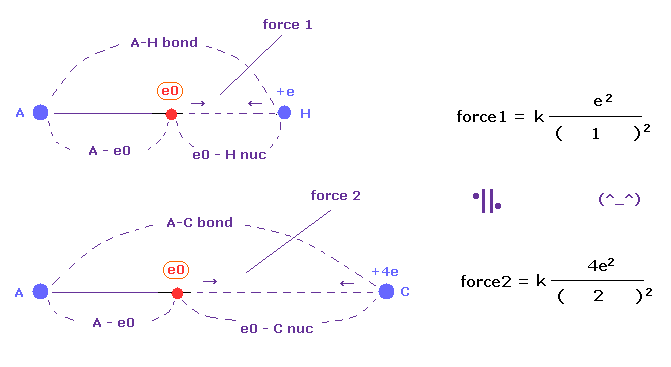
The electronegativity of H (= 2.20 ) and C (= 2.55 ) are almost same.
This means the powers of them attracting another electron are almost same.
In Fig.50, when the distance ratio of e0 - C nuc / e0 - H nuc is near "2.00", their attracting powers are equal, considering their nuclear charges.
As shown in Table 12, the power of H and C are almost same in various atoms, because e0 - C nuc / e0 - H nuc is near "2.00".
To be precise, electronegativity of carbon is a little stronger than hydrogen, so this ratio tends to be a little smaller than 2.00.
(Fig.51) Attracting force in H, C, B atoms.
Next we investigate the relations between the electronegativity and attracting force of each atom.
Fig.51 shows forces of attracting "e0" electron in H, C, and B atoms.
( "e0" belongs to left carbon in all cases. )
Of course, rotating radius (= 0.6400 Å ) of carbon based on de Broglie wave is used here.
Attracting power is biggest in carbon (= C ), and weakest in boron (= B ).
(Fig.52) Attracting force in H, C, B atoms.
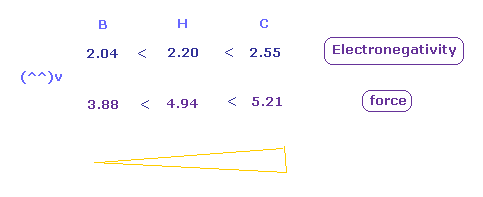
As shown in Fig.52, the electronegativities are strongest in carbon, and weakest in boron in the same way as force.
These results shows the real rotating radius based on Coulomb and de Broglie relations are correct also from the viewpoint of electronegativity.
| Atoms (= A ) | charge Z | C-A bond ( Å ) | "e0"-A length | Force | Electronegativity |
|---|---|---|---|---|---|
| Silicon (Si) | 5.04 | C-Si 1.8500 | 1.2100 | 3.44 | 1.90 |
| Boron (B) | 3.22 | C-B 1.5500 | 0.9100 | 3.88 | 2.04 |
| Phosphorus (P) | 6.12 | C-P 1.8400 | 1.2000 | 4.25 | 2.19 |
| Hydrogen (H) | 1.00 | C-H 1.0900 | 0.4500 | 4.94 | 2.20 |
| Carbon (C) | 4.22 | C-C 1.5400 | 0.9000 | 5.21 | 2.55 |
| Sulfur (S) | 7.18 | C-S 1.8200 | 1.1800 | 5.15 | 2.58 |
| Nitrogen (N) | 5.25 | C-N 1.4700 | 0.8300 | 7.62 | 3.04 |
| Chlorine (Cl) | 8.26 | C-Cl 1.7700 | 1.1300 | 6.47 | 3.16 |
| Oxygen (O) | 6.27 | C-O 1.4300 | 0.7900 | 10.05 | 3.44 |
| Fluorine (F) | 7.30 | C-F 1.3500 | 0.7100 | 14.48 | 3.98 |
As shown in Table 3, a close correlation is found between attracting force and electronegativity in each atom.
Generally, as the electronegativity is bigger, the force of attracting an electron is bigger.
Again, it is proved that de Broglie relation (= 1, 2, 3 wavelegnth ) and Coulomb force are effective in all atoms.

2013/3/28 updated. Feel free to link to this site.