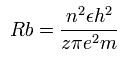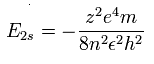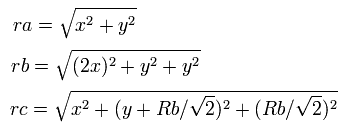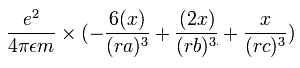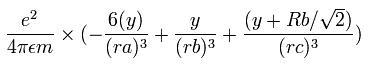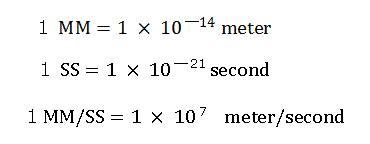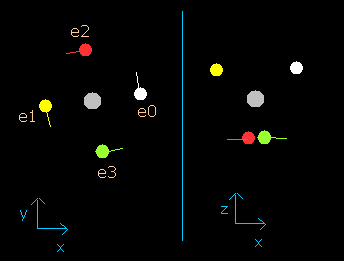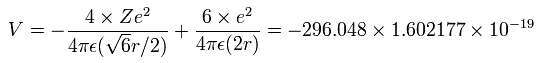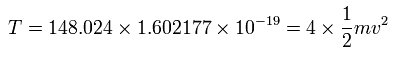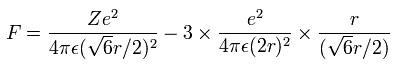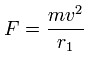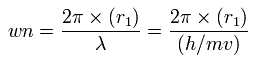New Bohr model Carbon (C)
Top page (correct Bohr model including the two-electron atoms).
Electron spin is an illusion !
Our new Bohr model has succeeded in calculating the Helium ionization energy more correctly than the quantum mechanical variational methods as shown in the Top page.
In this new successful Bohr model, the two electrons of the helium atom (He) are moving on the orbits of just one de Broglie's wavelength which are perpendicular to each other.
This model can explain the phenomena of Pauli exclusion principle correctly, because there is no space for the third electron to enter this new two-electron Bohr atom.
Surprisingly, this new atomic structure of the Bohr's helium can be applied to other two-electron atoms (ions ), Lithium ion (Li+), Beryllium (Be2+), Boron (B3+) and Carbon (C4+) ions, too.
(See this page.)
Furthermore, the ionization (ground state) energy of the three-electron atom lithium (Li) can be calculated correctly using the approximate "2S" Bohr orbit. (See this page.)
Bohr model Carbon ion (C 3+)
Here we try the three-electron Carbon ion (C3+).
Carbon ion (C3+) has two electrons in 1S orbital, and one electron in 2S orbital.
The two electrons of 1S state are attracted to the 6e+ nucleus strongly, so they are much closer to the nucleus than the 2S electron.
So approximately, we can suppose the 2S electron is moving around the 4e+ nucleus ( +6e - 2e = +4e ) on the circular orbit of the two de Broglie's wavelength.
(This means that we can use the equations of the hydrogen-like atom in 2S electron approximately.)
According to the Bohr hydrogen-like model, the radius (Rb) of the n × de Broglie's wavelength orbit is,
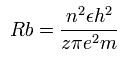
(when z =1 and n = 1, this Rb becomes "Bohr radius.")
In 2S electron of C3+, the positive charge of the nucleus (z) is supposed to be 4+ (see above), and n is 2.
So this Rb is 1 × Bohr radius ( = 0.5291 × 10-10 meter = 5291 MM ) .
(Here we use the new units, 1 MM = 10-14 meter, 1 SS = 10-22 second, 1 MM/SS = 108 m/s )
The energy levels of the hydrogen-like atom is known to be,
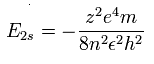
In the 2S electron of C3+, we substitute n=2 and z=4 into this equation.
So we suppose the carbon ion (C3+) model as follows,
Fig. 1. Carbon ion (C3+) model
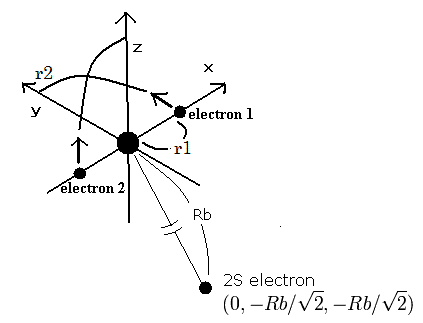
The two electrons of 1S state are avoiding 2S electron, so we fix the 2S electron at ( 0, - Rb / √2, - Rb / √2 ) as shown in Fig. 1.
(Fig. 1. shows the relative positions, But actually, this 2S electron is rotating around the nucleus slower than the 1S electrons.)
Like C4+ (see this page ), when the electron 1 is at (x, y, 0), the electron 2 is at ( -x, 0, y ).
So the distances among the particles are,
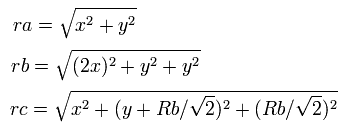
where ra is the distance between the electron 1 and the nucleus, rb is between the two 1S electrons, and rc is between the electron 1 and 2S electron, respectively.
The x component of the acceleration (m/sec2) of the electron 1 is,
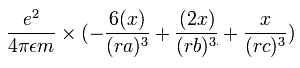
In the same way, the y component of the acceleration (m/sec2) of the electron 1 is,
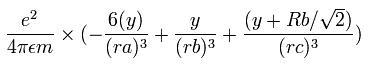
Then we compute the number of de Broglie's waves contained in one quarter of the 1S orbit like C4+
Sample JAVA program (C3+ ion)
Table. 1 shows the results in which the last VY ( y component of electron 1's velocity after moving one quarter of its orbit ) is the closest to zero in C3+.
Table.1. Results of r1 and WN in which last VY is zero (C3+).
| E (eV) | r1 (MM) | WN | WN x 4 |
|---|
| -930.0 | 944.0 | 0.25211 | 1.00844 |
| -935.0 | 939.0 | 0.25138 | 1.00552 |
| -940.0 | 933.5 | 0.25067 | 1.00268 |
| -944.7 | 928.5 | 0.25000 | 1.00000 |
| -950.0 | 923.0 | 0.24924 | 0.99696 |
| -955.0 | 917.5 | 0.24854 | 0.99416 |
| -960.0 | 912.5 | 0.24785 | 0.99140 |
This results shows that when the ground state energy of C3+ ion is -944.70 eV, the orbital length becomes just 1.00000 × de Broglie's wavelength.
The experimental value of the ground state energy of the carbon (C3+) ion is -64.49390 - 392.08700 - 489.99334 = -946.574 eV.
So the calculation error is only 1.87 eV ( 0.20 % ).
(This small error is probably caused by using the "approximate" orbit of the 2S electron.)
This means that it is almost correct to say that the three electrons of the carbon ion (C3+) are moving like Fig.1.
Visualization of Bohr model Carbon (C)
In the neutral carbon (C), how are four outer-shell electrons moving ?
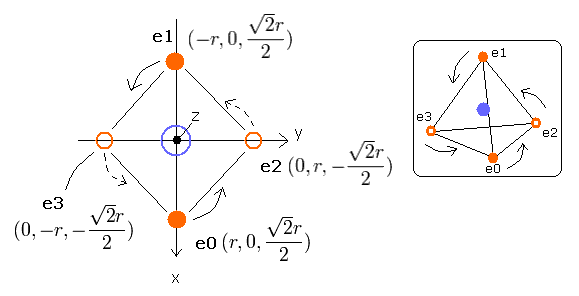
The neutral carbon has six electrons, in which two 1S electrons are very close to the nucleus (see above C3+ section), and four outer-shell electrons are thought to be arranged tetrahedrally.
So approximately we suppose these four electrons are moving around one +4e central nucleus (+6e-2e = +4e).
(Here, the total energy of the four valence electrons are supposed to be -148.024 eV = sum of 1-4 ionization energies.)
Fig. 2-1. Estimated Carbon atom. (Tetrahedron) Nucleus = (0,0,0)
Here, we use the next sample JAVA (version 1.5 (or 5.0)) program to visualize the four electrons' motions.
Sample JAVA program (C visualization)
This program is a little long. So if you copy and paste the above program source code into some text editor,
you can easily compile and run this.
In this program, class file name is cavis1, so save this text editor as "cavis1.java", and compile it.
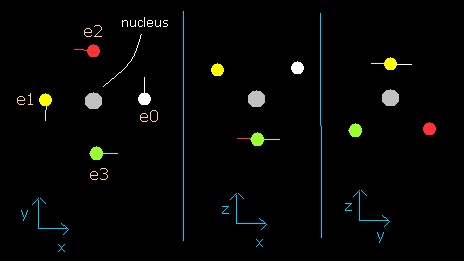
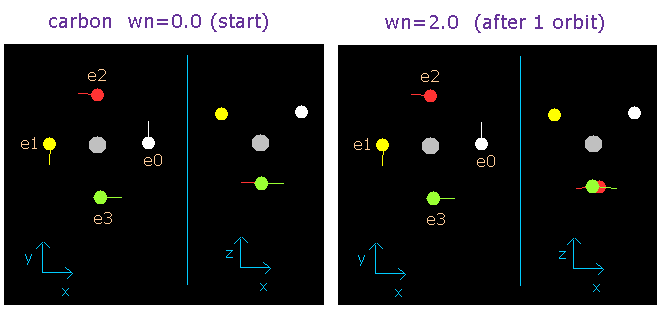
In this program, the carbon nucleus is shown as a gray circle. (See Fig.2-2.)
Four electrons are white (e0), yellow (e1), red (e2), and green (e3) circles.
The x, y and z axes are the same as Fig. 2-1.
The left, center and right figures are x-y, x-z, and y-z planes, respectively.
And the velocity vector of each eletron is shown as a line.
(Here, the initial velocity vectors of four electrons are e0=(0,1,0), e1=(0,-1,0), e2=(-1,0,0), and e3=(1,0,0).)
Fig. 2-2. C nucleus and four valence electrons in the program (wn=0)
Each coordinate of electrons (+X (MM), +Y (MM), +Z (MM)) in the text box means "relative" position from the nucleus.
Here we use the new units, as follows.
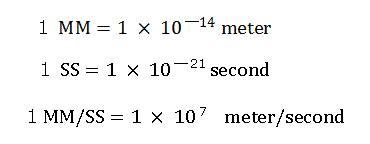
"nuc (MM)" means the distance between the nucleus and each electron.
"VX: VY: VZ" means the ratio of each component of the initial electron's velocity vector.
So, (VX: VY; VZ)=(100:100:0) is the same as (VX: VY: VZ)=(10:10:0).
When you choose the number (=wn) of de Broglie's waves (0.1 -- 2.0) in the scrollbar, and put "orbit" button, this program starts to compute the electron's orbit until de Broglie's waves contained in the orbit becomes wn.
About the detailed method, see Top page.
At short time intervals (1 SS), we calculate the Coulomb forces among electrons and nuclei, and change each velocity vector based on that result.
And we also compute the number of de Broglie's waves contained in the short segments at each electron.
(In this program, the total energy of the four valence electrons are supposed to be -148.024 eV = sum of 1-4 ionization energy.)
And this program outpus the last coordinate and velocity vector of each electron in both the text box and image area.
When you type the value (=r (MM) of Fig.2-1) in the textbox next to "radiu" button and click this button, the size (radius) of the four electrons' tetrahedron changes as shown in Fig.2-1.
First, we input the value "4890" as r (MM), and click "radiu" button.
(In this case, the value r of Fig.2-1. becomes 4890 (MM), and the first distance (=nuc) between nucleus and each electron becomes 5989 MM.)
And when we choose the value "0.5" in the scrollbar as the number of de Broglie's waves (wn), and click "orbit" button, the calculation starts and the image result becomes as follows,
Fig. 2-3. Carbon electrons at wn = 0.5
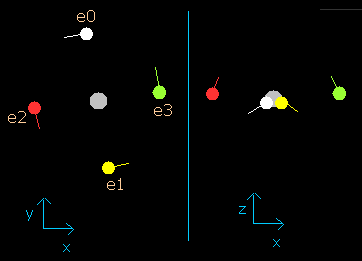
When the electrons have moved their orbits of 0.5 de Broglie's wavelength (wn=0.5), all four valence electrons of carbon are arranged near the x-y plane (Fig. 2-3, right panel).
And at this point (wn=0.5), the distance between nucleus and electron is about 5976 MM.
Next, click the "retur" button, which go back to the initial condition (wn=0).
And choose the value "0.9" in the scrollbar as the number of de Broglie's waves (wn), and click "orbit" button again. (Fig.2-4)
Fig. 2-4. Carbon electrons at wn = 0.9
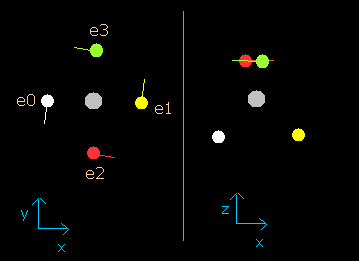
This result shows that when the electrons have moved their orbits of 0.9 (about 1.0) de Broglie's wavelength (wn=0.9), all four valence electrons of carbon are on the opposite side from their initial positions.
At this point (wn=0.9), the distance between mucleus and electron becomes the shortest. ( = 5921 MM).
Click the "retur" button again, choose the value "1.9", and click "orbit" button.
The result is, (Fig. 2-5)
Fig. 2-5. Carbon electrons at wn = 1.9 (=almost same as wn=0.0)
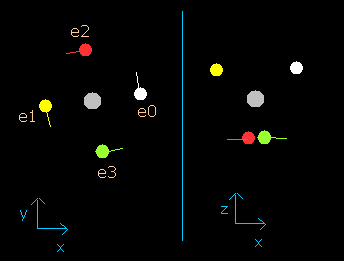
So this result proves that the all four electrons go back to almost original position when the the number of de Broglie's waves contained in their orbits becomes 1.9 (almost 2.0).
(Probably, these orbits are precessing or swaying a little.)
In the above program. we suppose the "central positive charge" is just +4.0e (= +6e (nucleus) -2e (two 1s electrons) = +4e)
But as shown in the above section, the two 1S electrons are about 930 MM apart from +6e carbon nucleus. (They don't stick to the nucleus.)
So, the "effective" positive charge which influences the four valence electrons are probably a little bigger than +4.0e.
Here, we try this orbital calculation again, supposing this central positive charge is +4.25e instead of +4.0e
Sample JAVA program. (central charge +4.25e instead of +4.0e)
This sample program is almost same as the above sample program except for the central positive charge (+4.0e --> +4.25e).
In this program, when the orbital length becomes just 2.0 de Broglie's wavelength, all four valence electrons of carbon can return to their original positions, as follows,
Fig. 2-6. Carbon electrons at wn = 0.0 and wn = 2.0 ("effective" charge = +4.25e)
This result is very important.
When the total energy of the four valence electrons is determined (=-148.024 eV), the average length (or radius) of one-round orbit is fixed.
(This means that if the total energy of electrons is determined, the average length and the number of de Broglie's waves contained in the one-round of the orbit is fixed "automatically".)
And this number proves to be 2.0 in the case of neutral carbon atom.
(So this result shows that the four valence electrons of carbon atom are moving on the orbits of 2.0 de Broglie's wavelength.)
In the above C3+ ion, we use the +4.0e central charge, because at the starting point of Fig.1, the error by this approximate methods is very small.
See also this page (the relation between inner 1S and 2S electrons).
When the central positive charge (Z) is just +4.0e (=+6e-2e), the number of de Broglie's waves (wn) contained in one orbit is 1.9.
But actually the two 1S electrons don't stick to the +6e nucleus, so if we suppose this charge (Z) is +4.25e (a little bigger than +4.0e), the de Broglie's wave becomes just 2.0, as shown above.
The effect of this +4.25e charge (not +4e) is included especially in the ionization energies of 3 or 4.
(As the valence electrons decrease, the remaining valence electrons come closer to the +6e nucleus.)
Here we try to prove this using the Virial theorem.
We suppose that the four valence electrons are arranged "tetrahedrally" around +Ze central charge, as follows,
Fig. 3. Carbon valence electrons ("effective" charge = +Ze)
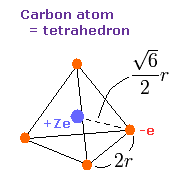
As shown in Fig. 3, the edge length of the tetrahedron is supposed to be 2r.
According to the Virial theorem, "average" total potential (V) and kinetic (T) energies satisfy the relation,
< V > = -2 × < T > , E = V + T
The total energy (E) of the four valence electrons is -148.024 eV, so this potential energy (V) becomes 2 × -148.024 = -296.048 eV.
When we calculate this potential energy (V) using Fig. 3 model, this V ( eV --> J ) becomes,
(by calculating the interactions between electron - nucleus and electron-electron,)
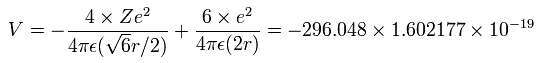
And the total kinetic energy (T) of the four electrons is 148.024 (eV), as follows,
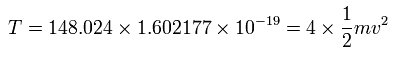
And by calculating the Coulomb forces among the particles of Fig.3, the force (F) acting on an electron (toward nucleus) becomes,
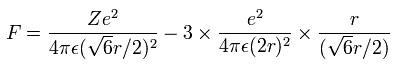
Using the above velocity (v) (of T) and F, we suppose the centrifugal force is equal to the force (F), as follows,
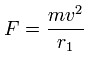
This r1 is "temporary" radius, which appears by this relation.
Using this r1, we can calculate the number of de Broglie's waves (wn) contained in one orbit, as follows,
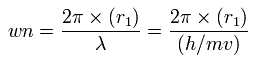
When Z = +4.0, this wn becomes 1.87 (almost 1.9).
And when Z = +4.25, this wn becomes just 2.02.
So we can prove this fact using the Virial theorem.
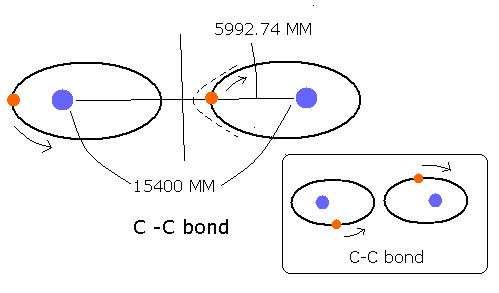
C-C bond (for example, of ethan CH3-CH3 ) is composed of two identical carbon atoms, which is different from H-C bond and H-O bond.
So if an electron is near one of the carbons' nuclei, the attractive Coulomb force of this carbon nucleus is always stronger than that of another carbon nucleus.
This means the electrons of C-C bond belong mainly to one of the carbon nuclei.
C-C bond length is 1.54 × 10-10 meter ( = 15400 MM ).
The half of this bond length is 15400 / 2 = 7700 MM.
The above longest distance 5993 MM is a good result, because it is near 7700 MM, and less than 7700 MM. (though it becomes a little longer by attractive Coulomb force of another carbon nucleus.)
(If the above longest distance is longer than 7700 MM, the electron will fly away to another carbon nucleus, which is inconsistent with the above explanation of C-C bond. So the longest distance must not be longer than 7700 MM. )
Fig. 4 Estimated C-C bond.

2010/7/28 updated. Feel free to link to this site.