Top page (correct Bohr model including the two-electron atoms)
Electron spin is an illusion !
In this top page, we calculate the reduced mass of the helium atom, which belongs to the three-body system.
And we use this reduced mass except when the center of mass is at the helium nucleus.
This method can give more accurate result than the quantum-mechanical variational method.
(Fig.1)

First, we explain the reduced mass of the two-body hydrogen atom.
Because the reduced mass of the helium atom is based on this hydrogen.
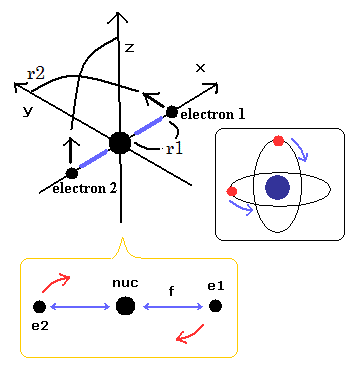
We suppose the particle 1 is a hydrogen nucleus, and the particle 2 is an electron.
We define as follows,
(Eq.1)
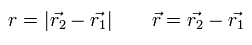
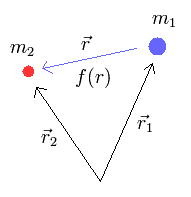
where r1 and r2 mean the position vectors of each particle.
When the force between the two particles is f(r), the equation of motion in the particle 1 is
(Eq.2)
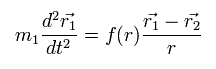
where m1 means the mass of the particle 1.
And the particle 2 satisfies
(Eq.3)
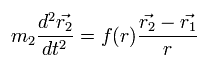
These relations satisfy the law of action and reaction.
Subtracting Eq.2 from Eq.3, we obtain
(Eq.4)
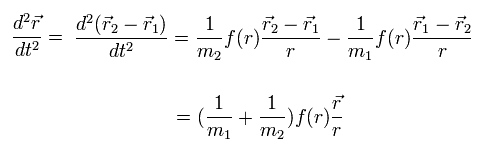
where Eq.1 is used.
If we use the reduced mass (μ) of
(Eq.5)
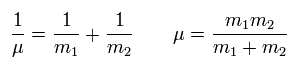
Eq.4 can be expressed as
(Eq.6)
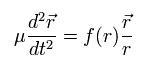
Eq.6 means that we need to use the reduced mass (μ), if we consider that the nucleus is at rest.
For the reduced mass to be effective, we need to confirm the nuclear kinetic energy is absorbed into another light particle with reduced mass.
The coordinate of the center of mass (R) is
(Eq.7)
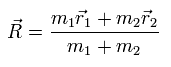
From Eq.1 and Eq.7,
(Eq.8)
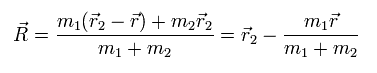
In the same way, we obtain
(Eq.9)
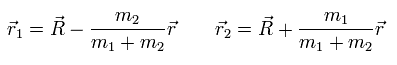
So the total kinetic energy of the two particles are
(Eq.10)
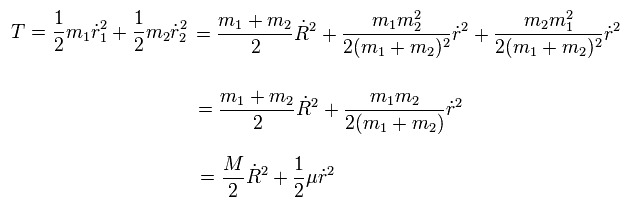
As shown in Eq.10, the total kinetic energy is the sum of the movement of the center of mass and the relative motion of the particles.
From Eq.6 and Eq.10 if we use the reduced mass, we can treat the nucleus as if it is at rest inside atoms with respect to the force and energy.
(Eq.11) Relation between redued mass and velocities.
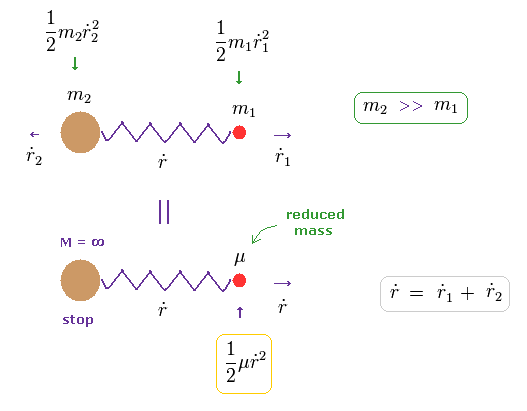
In Eq.10, when the total velocity of the center of mass (= R ) is zero, the total kinetic energy is expressed only by reduced mass (= μ ) and relative velocity (= dot r ).
( In Eq.11, total momentum is zero, because m2 and m1 are moving in the opposite directions. )
It seems that total momentum is not zero in Eq.11 below, because only mass μ is moving in one direction.
In fact, the mass of heavy m2 automatically becomes infinite, when the reduced mass μ is used.
So as this infinite mass × velocity2 (= 0 ) is not zero, total momentum including μ and m2 is conserved.
In the case of the three-body problem like the helium, it is a little complicated.
See also this page.
(Fig.2) Hydrogen and helium nuclei.
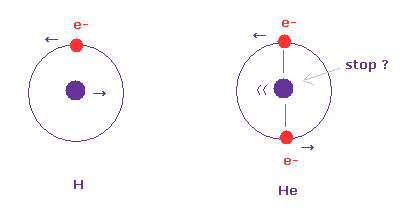
In case of hydrogen (= Fig.2 left ), nucleus is always moving due to two-body relation.
But in case of Fig.2 right ( two electrons are just opposite of nucleus ), its helium nucleus is stationary, because it's just in equilibrium between two electrons.
Of course, it is known that Fig.2 right helium model gives a little different value from actual ground state energy.
So how about the case when two electron's orbits are just perpendicular to each other ?
( Quantum mechanical vague wavefunction cannot distinguish these differences. This is also one of the reasons why quantum mechanics is wrong. )
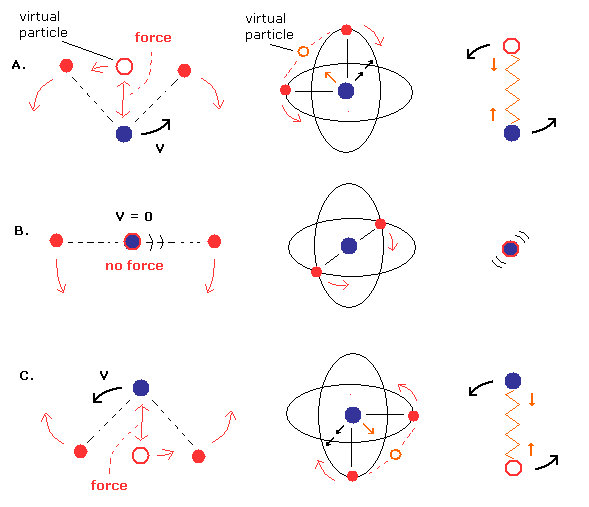
(Fig.3) Nucleus is "oscillating" instead of rotating. (= special case)
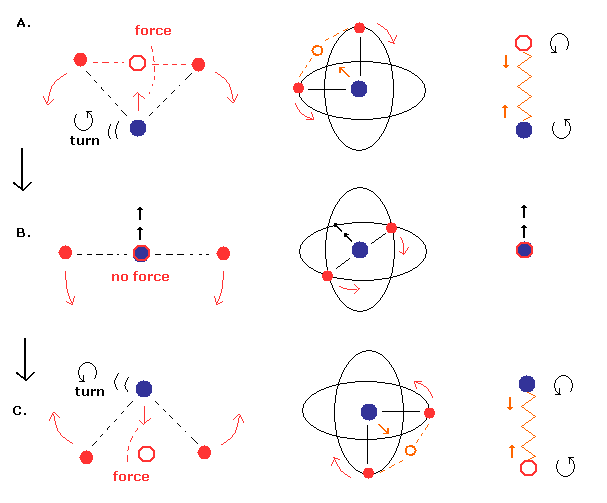
First we think about the very special case, in which the nucleus is oscillating like a spring. (= straight-line motion, Fig.3. )
Different from Fig.8 (= normal pattern ), the nuclear ( linear ) velocity becomes maximum, when the center of mass is at the nucleus ( Fig.3 middle ).
And in the upper (= A. ) and lower (= C.) panel of Fig.3, the nucleus turns back, so its velocity becomes zero at these points.
sample JAVA program (= the nucleus is oscillating like Fig.3)
C language program
If you copy and paste the above program source code into a text editor, you can easily compile and run this.
In this program, we first input the initial y-coordinate r2 (in MM) of electron 1 (see Fig.4), and the absolute value of the total energy E (in eV) of Helium.
From the inputted values, this program outputs the x component of electron 1 velocity in Fig.5, and WN (= 1/4 de Broglie's waves ). Here 1 SS = 1 × 10-23 second.
(Fig.4) Starting positions of Fig.3 model.
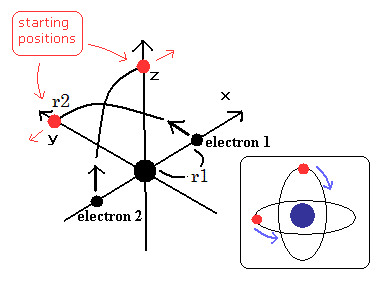
(Fig.5) Electrons have moved one quarter of their orbits.

We choose the positions of Fig.4 as the starting points.
Because in Fig,3 moving pattern, the helium nucleus stops when the electrons are at the positions of Fig.3 A and C.
So we use the usual electron mass (NOT reduced mass), when we calculate the initial velocity of Fig.4.
(After starting, we use the reduced mass.)
Table 1 shows the result of "nuclear oscillating model" of Fig.3. ( last VX = 0 )
| E (eV) | r2 (MM) | WN | WN x 4 |
|---|---|---|---|
| -79.0000 | 3137.0 | 0.250011 | 1.000044 |
| -79.0037 | 3137.5 | 0.250005 | 1.000020 |
| -79.0069 | 3136.5 | 0.250000 | 1.000000 |
| -79.0100 | 3136.0 | 0.249996 | 0.999984 |
| -79.0300 | 3135.5 | 0.249964 | 0.999856 |
As shown in Table 1, r2 is a little longer than r1 due to the repulsive force between electrons.
And the result of Table 1 is -79.0069 eV, which is a little different from -79.0037 eV of top page.
( Experimental value is -79.005 eV. )
But of course, this result is more accurate than latest quantum mechanical method (= -79.015 eV ).
Only the relativistic correction can not be explained in Fig.3 (= Table 1) model.
The nuclear linear motion in Fig.3 model is very "special" case, which doesn't occur naturally.
For example, the planets which attract each other usually rotate (not oscillate).
(Fig.6) Starting point = NOT reduced mass= Virtual particle stops.
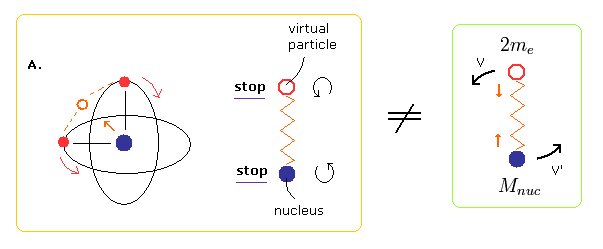
Unlike the two-body hydrogen atom, the oscillating motion of Fig.3 includes two points at which the nucleus stops (= A and C of Fig.3 ).
At these points of A and C of Fig.3, the virtual particle between the two electrons stops, too.
So if we choose A of Fig.3 as the starting point of the program, we should not use the reduced mass in calculating the initial electron's velocity.
Because using reduced mass means that the virtual particle and nucleus are behaving like hydrogen atom.
(Fig.7) Reduced mass of Helium atom.

At other points, the nucleus and virtual particle are moving (linearly) in Fig.3.
And the virtual particle is a single existence influencing the nuclear motion.
So in this case, we can use reduced mass in other moving positions.
The electron number is "2" in helium, so each electron is a half of the overall reduced mass,
(Eq.12)
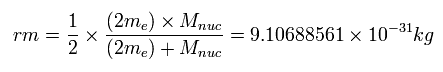
This correct discrimination between reduced mass and usual mass gives real and exact results of the helium ground state energy.
(Fig.8) Nucleus and virtual particle are "rotating".
Actually, when the virtual particle between two electrons is at the nucleus (= center of mass ), they stop temporarily (= Fig.8B, Fig.10 ).
Because Fig.8B and Fig.10 (= two electrons are at just opposite sides of their nucleus ) are most stable and "equilibrium" point, considering Coulomb repulsive force.
(Fig.9) Only "tangential" velocity is left at center of mass.
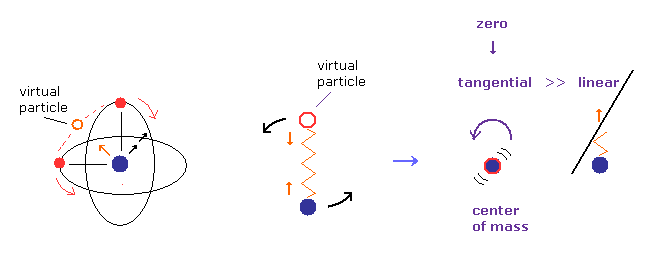
Considering the conservation of angular momentum, tangential ( rotating ) velocity of the nucleus becomes much bigger than the linear motion at Fig.8B, when it is closer to center of mass.
( Imagine rotating figure skater. )
So we can neglect linear motion of nucleus, when the center of mass is at origin.
Of course, when the rotating radius is zero, tangential velocity of nucleus also becomes close to zero.
So if we choose Fig.8 model, we should use usual mass ( not reduced mass ), when two electrons are just at opposite sides of nucleus.
(Fig.10) Most stable positions = NOT reduced mass.
In Fig.10, two electrons are just at the opposite sides of the nucleus.
But before and after that, due to the de Broglie's interference, two orbits have to be just perpendicular to each other.
( If they are not perpendicular, the opposite wave phases of them cancel each other out and let them unstable. )
This force is caused by the de Broglie wave's interference, and of course, due to the law of action and reaction, the nucleus is pushed in the opposite direction inside the helium.
The point is that when the center of the two electrons are just equal to the nucleus, they become most stable.
This is like the bottom of the curve.
So only at this equilibrium point (= Fig.10 ), the nucleus stops, and we have to use the usual mass in calculating the initial electron's velocity.
(Fig.11) Two electrons are moving (= reduced mass ).
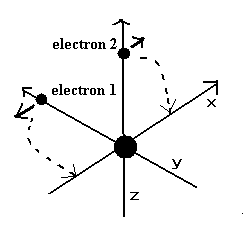
The instant two electrons start to move in the direction of Fig.11, their nucleus goes away from the center of mass.
So to stop the nucleus, we have to use reduced mass, as I explain in Eq.11
| E (eV) | r1 (MM) | WN | WN x 4 |
|---|---|---|---|
| -78.9900 | 3075.0 | 0.250022 | 1.000088 |
| -79.0000 | 3074.0 | 0.250006 | 1.000024 |
| -79.0037 | 3074.0 | 0.250000 | 1.000000 |
| -79.0100 | 3074.0 | 0.249990 | 0.999960 |
| -79.0300 | 3073.0 | 0.249958 | 0.999832 |
This result (= -79.0037 eV ) is just consistent with the experimental results ( except for the relativistic effect ).
This result clearly shows Fig.8-Fig.11 helium model is most accurate.
We use the following program. See also this page in detail.
In this program, we can choose the usual mass or reduced mass in the electron.
sample JAVA program 1 SS = 1 × 10-23
C language program
Table 3 shows the "Not reduced mass condition" results.
| E (eV) | r1 (MM) | WN | WN x 4 |
|---|---|---|---|
| -79.0037 | 3075.0 | 0.250071 | 1.000284 |
| -79.0300 | 3074.0 | 0.250030 | 1.000120 |
| -79.0485 | 3073.5 | 0.250000 | 1.000000 |
| -79.0600 | 3073.0 | 0.249982 | 0.999928 |
| -79.0800 | 3072.0 | 0.249950 | 0.999800 |
As shown in Table 3, if we don't use the reduced mass in the neutral helium atom, the calculation result becomes -79.0485 eV, which is a little different from the experimental value (-79.005147 eV).
(The error is -79.0485 - (-79.005147) = -0.04335 eV. Compare this with Table 2 result of 0.001447 eV.)
Of course, this result is also very close to the experimental value.
But we have to use the reduced mass to get most correct ground state energy in helium.
Table 4 shows the "All reduced mass condition" results.
| E (eV) | r1 (MM) | WN | WN x 4 |
|---|---|---|---|
| -79.0037 | 3075.0 | 0.250037 | 1.000148 |
| -79.0200 | 3074.5 | 0.250011 | 1.000044 |
| -79.0268 | 3074.0 | 0.250000 | 1.000000 |
| -79.0300 | 3074.0 | 0.249995 | 0.999980 |
| -79.0500 | 3073.0 | 0.249963 | 0.999852 |
In Table 4, we always use reduced mass, even when the center of two electrons is just equal to the nucleus.
This result is also a little different from the experimental result.
( Though it is almost the same. )
So we have to discriminate "reduced" or "usual" mass, depending on their positional relation, to get most accurate value.
(Fig.12) Electron pushes nucleus (= law of action and reaction ).
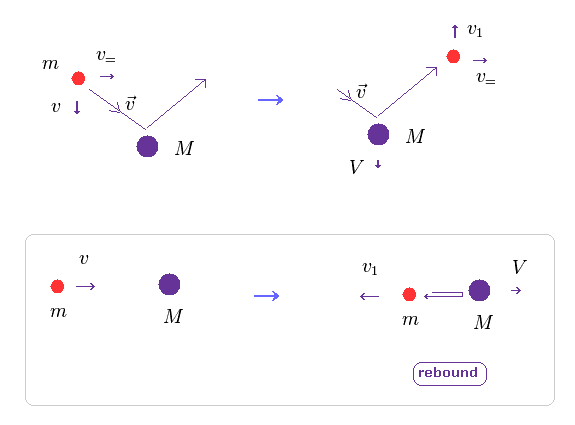
As I said above, when two electrons move in the orbitals perpendicular to each other, they are influenced by de Broglie wave's interference.
Of course, when the center of these two electrons goes away from the center of mass, helium nucleus are pushed by electrons due to law of action and reaction.
In Fig.12, only the direction of two particles' crashing is important (= v, Fig.12 lower ).
( The parallel component doesn't change. )
(Eq.13) Total energy conservation.
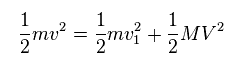
As shown in Eq.13, total ( kinetic ) energies are conserved before and after this collision.
In Eq.13, "m" is electron's mass, "M" is nuclear mass.
(Eq.14) Total momentum.
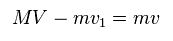
And total momentum is conserved, too.
From Eq.13 and Eq.14, we get each velocity of
(Eq.15) Each velocity.
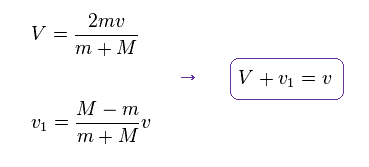
You can confirm this result by substituting Eq.15 into Eq.13 and Eq.14.
As shown in Eq.15, the relative velocity of Eq.11 is almost conserved.
(Eq.16)
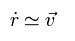
So if we get initial electron's velocity (= v ) using usual mass in Fig.10, that velocity can be used as it is, even in relative coordinate.
(Eq.17)
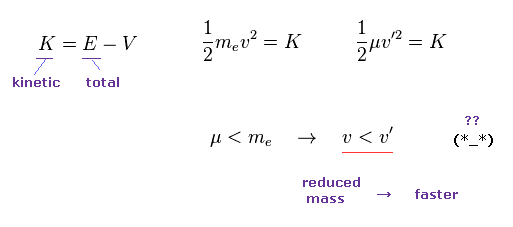
But if you use the initial velocity gotten by reduced mass (= μ ), this initial velocty becomes faster on the condition of the same kinetic energy K.
Because the reduced mass is smaller than usual mass.
So if you suddenly change initial velocity into one gotten by reduced mass, it means this electron suddenly becomes faster !
This is strange.
So the initial velocity by usual mass remains the same even in relative coordinate.
Total momentum is always conserved, even when only the initial nuclear velocity is zero.
Because as shown in Eq.11, nuclear mass becomes infinite, the moment we start to use reduced mass.

2013/9/30 updated. Feel free to link to this site.