Top page ( Quantum mechanics is wrong, electron spin is illusion ← 6/30/2024 )
Wrong spin theories.
Singlet, triplet are NOT "spin".
Spin-orbit coupling is wrong
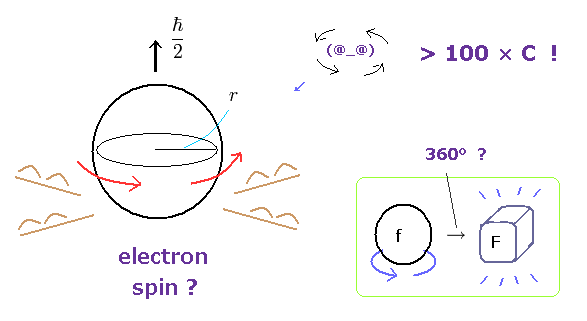
(Fig.1) Spinning speed is superluminal ! → electron spin is illusion.

Though ordinary textbooks treat the "spin" as if it was a real object, electron spin is completely unrealistic.
An electron is very light and tiny.
So by equating the angular momentum of the spinning sphere of the electron to 1/2 ħ, the sphere speed leads to more than one hundred times the speed of light. ( websites this p.5, this. )
Furthermore, fermions such as electrons cannot return to their original states by 360o rotation ! See this site.
At this point, you easily find electron spin does NOT exist in our real world.
There is No proof of spin in Pauli exclusion and ferromagnetism.
(Fig.2) Angular momentum is constant. → a tiny particle spins faster.
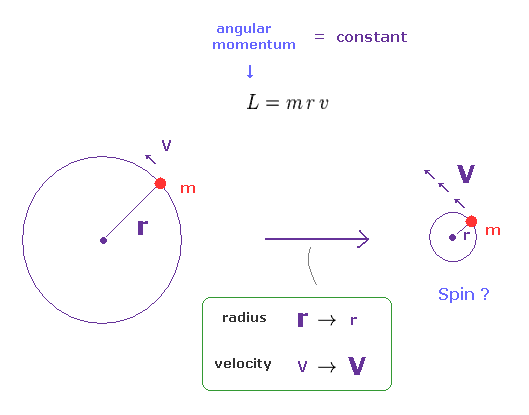
The angular momentum is given by L = mrv, where "m" is mass, "r" is radius, and "v" is tangential velocity.
When this angular momentum is constant, the rotational velocity becomes higher, as its radius becomes smaller
(Fig.3) In a tiny electron, the spinning speed becomes faster-than-light !
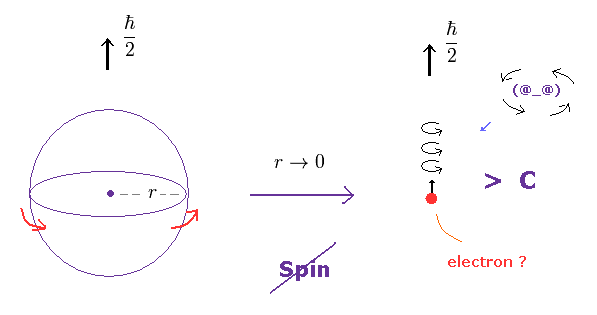
An eletron is known to be a point-like partice, which means its radius is extremely small.
But this electron has finite spin angular momentum of 1/2 ħ.
As a result, its rotational speed becomes almost infinite, of course, faster-than-light !
(Fig.3') Spinning speed is much faster than light.
So you easily find that the electrons spin is a completely unrealistic concept.
This is the main reason why Wolfgang Pauli resolutely objected to the existence of "spin" in 1920s, at first.
(Fig.4) Proton's spin OK. Electron spin is illusion !
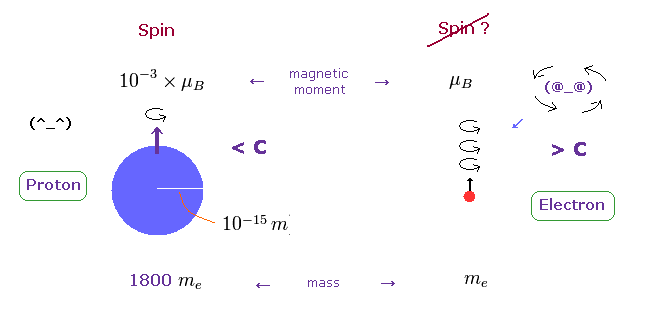
On the other hand, heavy proton with some size can produce "real" spin, NOT exceeding light speed.
So nuclear spin is real, and electron spin is an illusion, it's only circular orbit like Bohr model.
In fact, the magnetic moment of electron spin is about 1000 times bigger than that of proton !
This wide discrepancy indicates electron spin is rotating in circular orbit with some radius, NOT on its own axis.
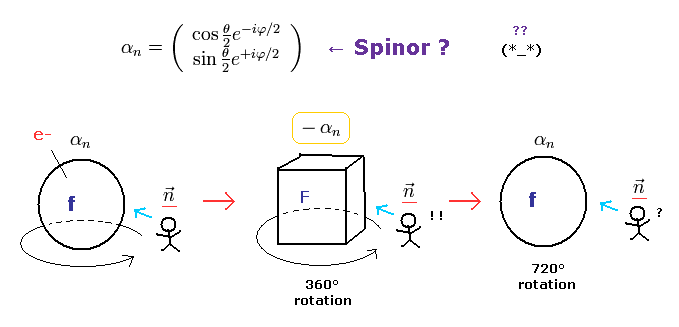
(Fig.5) Fermions return by two ( NOT one ) revolutions (= 720o ).
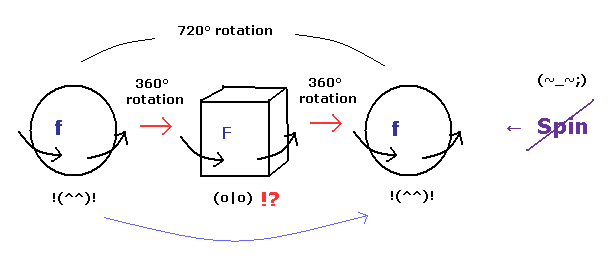
In the quantum mechanics, the spinor (= spinning electron) doesn't go back to its original configuration by one rotation ( 360o ).
It must be rotated twice (= 720o ) to be back, as shown on this site.
This is called "two-valued" or "orientation entanglement".
Surprisingly, the quantum theory says various fermions such as electrons, neutrons, and protons can't return after 360o rotation !
(Fig.6) Fermions must be rotated twice (= 720o ) to be back
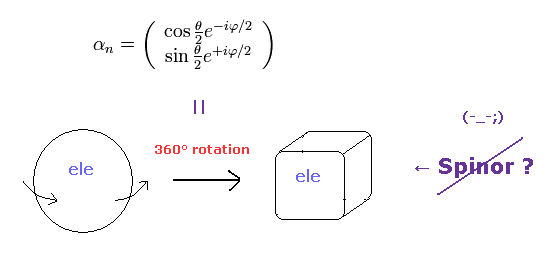
Considering spin angular momentum of 1/2ħ, the wavefunction of the spinor becomes like Fig.6.
The rotation of 360o ( θ = 0 → 360o ) changes this spinor ( from plus to minus ).
So the spinor, which represents fermions, is NOT a real object.
Surprisingly, they argue this strange phenomenon had been observed in actual experiments, as shown in this section.
Of course, it is natural that real object can return after one rotation.
The trick of these experiments exists in the wrong assumption of angular momentum.
(Fig.7) Spinor = tray or string ?? Impossible !
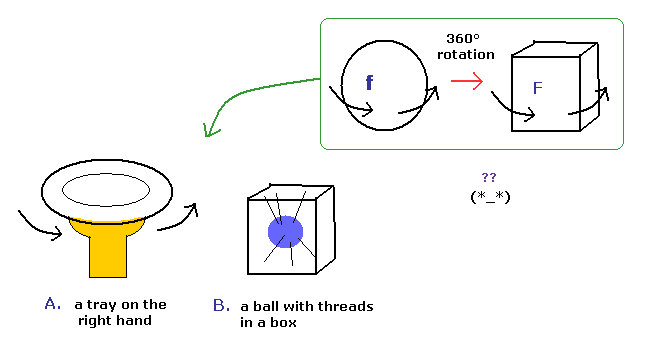
Various people tried to express this strange spinor using realistic things.
Fig.7A means one tray on the right hand, and Fig.7B means the ball with threads in a box.
But these models cannot describe the strange property of spinor rotation in all directions.
( If you try to do so, an arm or threads are twisted or entangled. )
So the spinor rotation itself cannot be expressed using real things.
(Fig.8) Bohr's orbit = Bohr magneton, Spin = Bohr magneton !
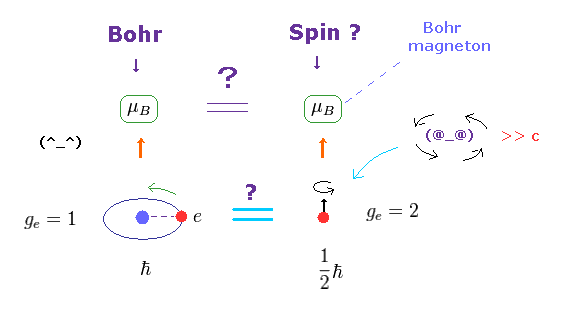
The magnetic moment of the magnitude of Bohr magneton (= μB ) was first obtained from Bohr's orbit, as shown on this site.
Surprisingly, the spin magnetic moment is the same as this Bohr magneton, as shown on this site and this site.
Though orbital motion and "spin" are completely different concepts, this fact is very strange.
The magnetic moment is given by g-factor × angular momentum.
In Bohr's orbit, g-factor = 1 and angular momentum = ħ
In electron spin, g-factor = 2 and angular momentum = 1/2ħ
So these are the same. Too good !
(Fig.9) Stern-Gerlach experiment = Bohr's orbit.
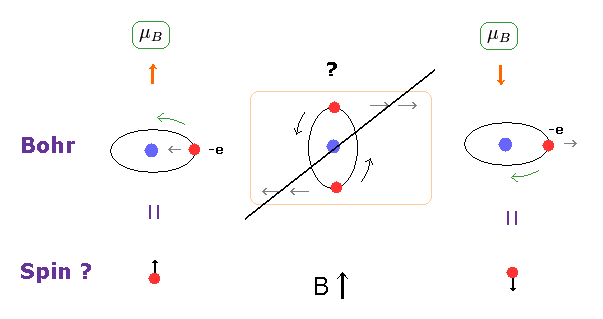
It is said that Stern-Gerlach experiment showed the existence of spin.
But Bohr's classical orbit can explain this phenomenon naturally, too.
As you see in Fig.9 middle, when the orbital plane is parallel to the magnetic field B, this plane tends to rotate.
So, also in Bohr's orbit, two split lines can be observed in Stern-Gerlach experiment.
As shown in Fig.8, the magnitudes of magnetic moment are Bohr magneton in both Bohr's orbit and electron spin.
The split intervals are the same in them. Too good to be true.
(Fig.10) Magnetic moment.
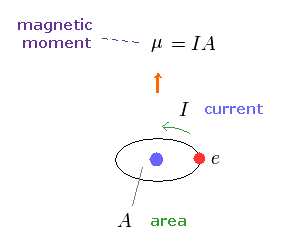
As shown on this site, the magnetic moment μ is given by the electric current I × the area (= A ) of this circuit.
This magnetic moment gives the same magnetic field of two magnetic poles, as shown on this site.
So this is called "magnetic dipole moment".
(Fig.11)
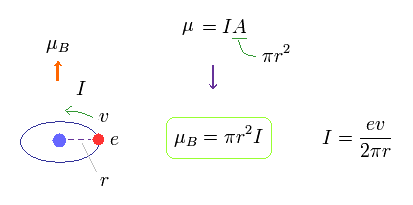
In Fig.11, one electric charge is orbiting around the nucleus at a velocity of "v".
This orbital radius is "r".
The electric current I means the amount of electric charges passing some point per second.
So I is given by ev/2πr.
The area of this circular loop is A = πr2, so the magnetic moment μB = IA = Iπr2.
(Eq.1) When the orbital length is 1 × de Broglie wavelength.
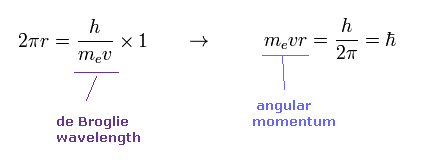
According to de Broglie relation, the wavelength of an electron is given by λ = h/mv.
Eq.1 shows the case in which the orbital length (= 2πr ) is just equal to this de Broglie wavelength.
In this case, the orbital angular momentum (= mvr ) becomes ħ.
From Fig.11 and Eq.1, the magnetic moment μB becomes
(Eq.2) Bohr magneton.
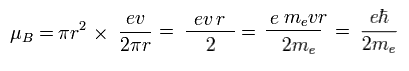
This value of magnetic moment is called "Bohr magneton".
Bohr magneton plays an important role as the unit of magnetic moment also in the current quantum mechanics.
So the quantization of de Broglie wavelength is the main mechanism, which causes the quantized magnetic moment.
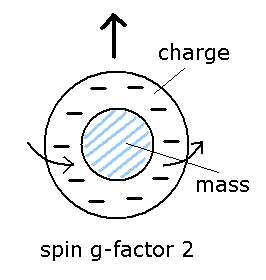
(Fig.12) Spin g factor = 2 ??
As I said in Fig.8, the spin angular momentum is 1/2ħ, so sping g-factor has to be "2" to give Bohr magneton ( 1 = 1/2 × 2, see Eq.3 ).
By the way, what does this spin g-factor really mean
In ordinary classical electromagnetism, g-factor is always "1".
So in g-factor "2", charge and mass must be separated like Fig.12.
(Eq.3) Spin magnetic moment = Bohr magneton
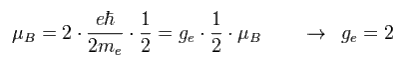
Then why this spin g-factor cannot be the values such as "2.3", "2.4", "2.7" ...
Do you think the value of just "2" is too good to be true ?
(Fig.13) Spin magnetic moment is too weak to explain sodium D-lines.
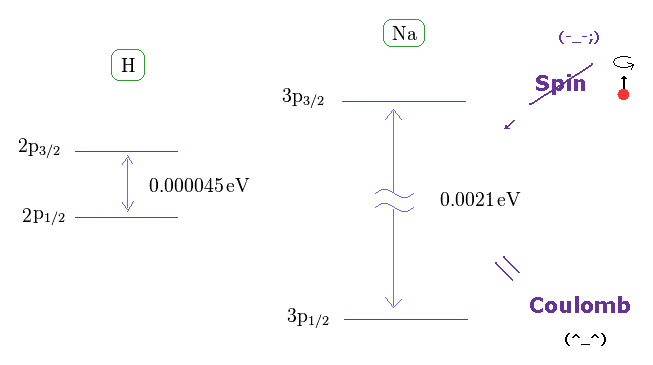
As shown on this site, hydrogen fine structure (= doublet ) between 2p3/2 and 2p1/2 is about 0.000045 eV.
On the other hand, the fine structure between 3p3/2 and 3p1/2 of sodium is as big as 0.0021 eV, as shown on this site.
If we assume hydrogen doublet is caused by spin-orbit interaction, sodium doublet cannot be explained by spin-orbit interaction. See also this page and this page.
It is known that Sommerfeld model and Dirac equation give exactly the same values in fine structure doublet.
Considering the same mechanism is working in both hydrogen and sodium D lines, the fine structure is caused by the Coulomb energy difference, when one electron can come closer to nucleus than another, like Sommerfeld model.
(Fig.14) Core charge of sodium is much bigger than Z = 1 !?
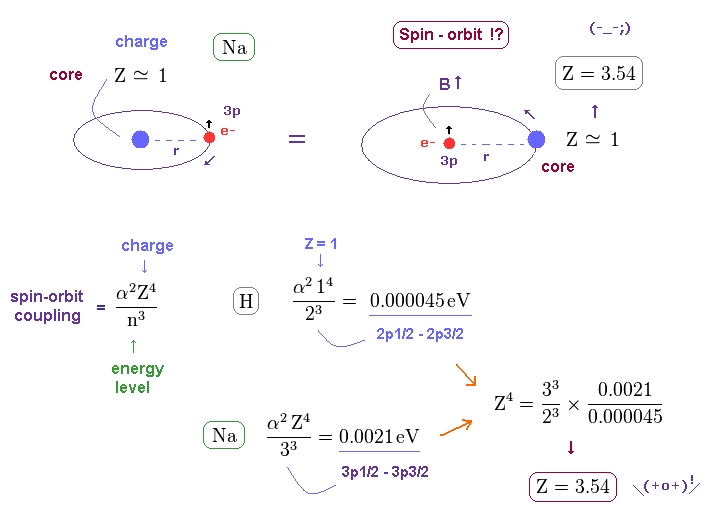
Approximately, we can consider the outer 3p ( or 3s ) electron of sodium is moving around Z = +1 central core charge.
( "Core" is the total charge of Na nucleus and all electrons contained in n = 1 and 2 orbits. )
From the viewpoint of this outer electron, the core charge is moving around in the opposite direction, which causes magnetic field at the point of the electron having "spin".
As a result, spin-orbit interaction is produced, they insist.
But the discrepancy between these H and Na spin-orbital interactions are too wide.
This means the effective central charge in sodium is much bigger than Z = 1 (= about Z = 3.54 in Na ), which is very unreasonable and unrealistic.
(Fig.15) Anomalous Zeeman effect of H atom ? ↓ = Bohr-Sommerfeld model.
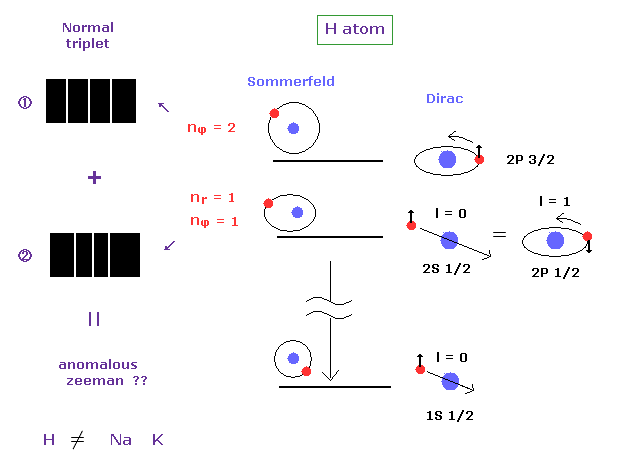
Anomalous Zeeman effect is mainly observed in alkali metals, which is inconsistent with actual energy interval, as I said above.
In fact, the spectrum of one-electron hydrogen is so simple that Bohr-Sommerfeld model can explain anomalous Zeeman effect in hydrogen.
(Fig.16) J Mehra's book.

On page 659 of the Historical Development of Quantum Theory v.1 part2 ( J. Mehra ).
--------------------------------
In 1922, Otto Oldenberg obtained the following results :
For weak fields, each component of Balmer Hα doublet was separated in a normal Zeeman triplet, but for strong fields, the Zeeman patterns of the doublet changed into the Zeeman pattern of a singlet line.
---------------------------------
So the anomalous Zeeman effect of hydrogne is so simple (= 2 × triplet lines ).
These doublets can be completely explained by Bohr-Sommerfeld model, Not depending on strange "spin".
(Fig.17) History of Zeeman effect.

According to the above book, anomalous Zeeman effects are often seen in multi-electron atoms such as Na, Cd, Mg..
In mercury (= Hg ), as much as 11 split lines were observed under magnetic fields in 1898.
The important point is that they didn't mention hydrogen atom, when they say about anomalous Zeeman effect. Instead they introduced convenient Paschen-Back effect in H and Li.
As a result, Heisenberg and Lande thought anomalous Zeeman effect is caused by core electrons, Not spin, at first.
And various atoms and metals do NOT obey Lande g-factor.
This fact made Russell and Saunders create new concepts such as jj coupling and jk coupling (= artificial ).
About the calculation of Lande g-factor, see this section.
(Fig.18) Triplet, Singlet of Magnesium (= Mg ) mean large "Coulomb" energy ( NOT spin ).
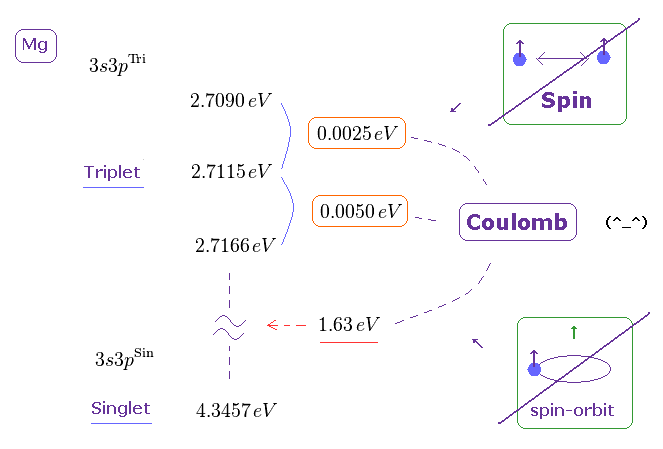
The current quantum theory insists that "triplet" and "singlet" states of the alkaline earths are caused by spin-spin and spin-orbit interactions.
But in fact, the energy intervals in singlet and triplet are much bigger than the magnetic energies among spins, as shown on this page
( The Story of Spin by S.Tomonaga says they are as big as those of electric origin. )
Because spin-spin magnetic dipole energy is too weak (= less than 1 × 10-4 eV ), which cannot reach singlet, triplet energy intervals. See this site (p.6) and this site (p.7).
(Fig.19) Spin-orbit coupling based on relativistic effect is too weak. ← illusion !
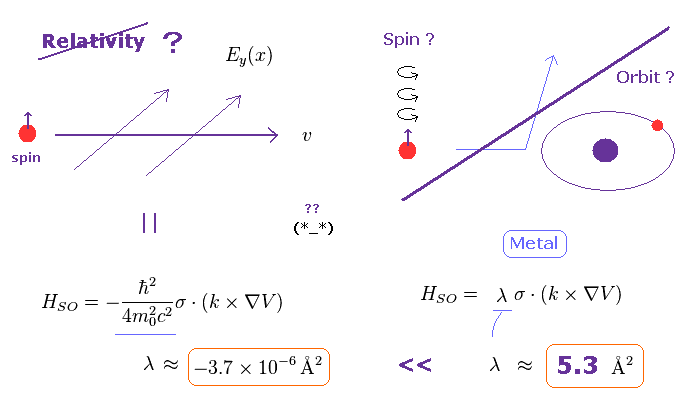
They insist spin orbit coupling is caused by relativistic effect (= see Wiki ).
But if so, the magnitude of theoretical spin orbit coupling becomes much smaller than the experimental values
( this site p.6 and this site ).
On this site ( p.2, left ), it is written
-----------------------------------
"For example, for GaAs one finds λ = 5.3 Å2.
Thus, the SO (= spin-orbit ) coupling in n-GaAs is by six orders of magnitude stronger than in vacuum ( λ = -3.7 × 10-6 Å2 ) and has the opposite sign.
This enhancement of SO coupling is critical for developing large extrinsic spin currents.
------------------------------------
This wide discrepancy between theoretical spin-orbit coupling and actual value shows the concept of spin-orbit coupling is completely false, as shown on this page.
(Fig.20) Spin magnetic moment is too weak for Pauli exclusion.
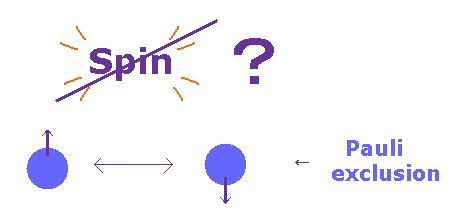
According to Pauli exclusion principle, two electrons cannot be the same state with respect to orbital and spin.
Ordinary textbooks say as if this phenomenon was caused by spin-spin interaction.
But the magnitude of Pauli exclusion principle is as much as 10 eV, which cannot be explained by very weak spin magnetic energy ( ~10-5 eV ).
(Fig.21) Repulsive force of Pauli exclusion principle is very strong (= about 11 eV in Li ).
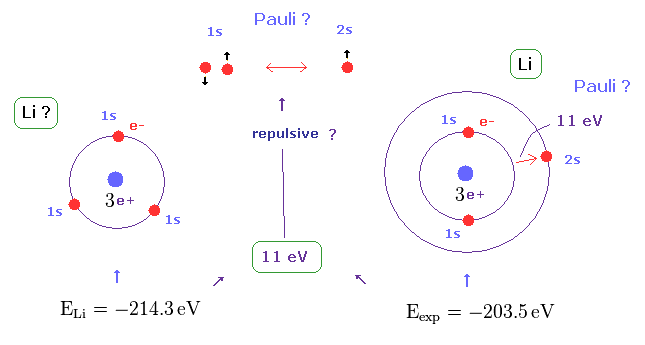
According to this book ( Quantum chemistry 6th edition, by Ira N. Levine, p 292 ), the ground state energy of lithium becomes lower than -214.3 eV, if all three electrons enter 1s orbitals.
On the other hand, the experimental value of ground state energy is -203.5 eV in which one of three electrons enters 2s ( NOT 1s ) orbital.
This means the third electron is expelled from 1s orbital by some force, though Coulomb attraction of force is strong enough.
This mysterious repulsive force of about 11 eV is due to Pauli exclusion principle, as shown in Fig.21.
(Fig.22) Spin-Spin interaction is too weak.
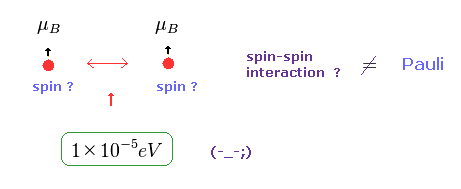
In Pauli exclusion principle, "spin" direction is crucial factor for deciding whether each electron enters the same orbital or not.
But magnetic dipole interaction of spin is basically too weak (= about fine structure level, 1 × 10-5 eV. ), which can NEVER reach as much as 11 eV.
This means we need other concepts to describe this strong repulsive force of Pauli exclusion.
If "spin" ( magnetic moment ) is too weak, there is only one thing left.
As shown on this page, de Broglie wave ( destructive ) interference is the main generator of this Pauli repulsive force.
(Fig.23) Origin of ferromagnetism = Spin ??
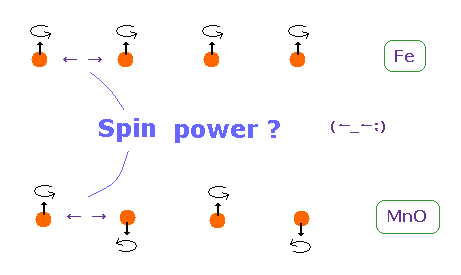
In ferromagnetism, they insist "spin" of each atom such as Fe tends to be parallel to each other.
On the other hand, in antiferromagnetism ( or diamagnetism ) such as MnO, each spin tends to be antiparallel to each other.
So the origin of (anti) ferromagnetism is "spin", as most textbooks say ??
In fact, spin magnetic ( dipole ) moment interaction is too weak to cause (anti) ferromagnetism.
(Fig.24) Origin of ferromagnetism = Exchange interaction "J" ??
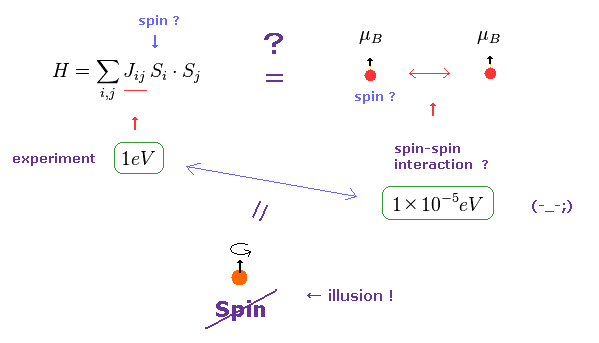
In the current quantum theory, they describe the force of (anti) ferromagnetism as coupling constant (= J ) in Heisenberg model.
The magnitude of coupling constant (= exchange interaction ) is as big as 1 eV, which is much stronger than spin magnetic dipole interaction (= 10-5 eV ).
Spin magnetic moment interaction is much too weak to account for most magnetic materials such as ferromagnet, as is referred to in various sites ( See
this (p.7),
this (p.5),
this (p.20),
this (p.7) ).
Spin dipole interaction is as small as 0.3 K as temperature expression, which is easily broken at room temperature.
( For example, iron can become ferromagnetism at 1043 K, which is much bigger than 0.3 K. )
(Fig.25) De Broglie wave interaction is the origin of ferromagnetism.

Spin - spin magnetic interaction is unrealistically too weak to describe magnetic materials.
Again, there is only one thing left.
Electron movement causing magnetic field is accompanied by de Broglie wave. ( See also this page. )
Like strong repulsive Pauli exclusion, it is quite natural that we think these synchronous de Broglie waves makes ferromagnetism stable at room temperature.
As shown in Davisson-Germer experiment, de Broglie wave interference has the power to change the direction of Coulomb force.
(Fig.26) Spin is too weak to explain molecular bonds.
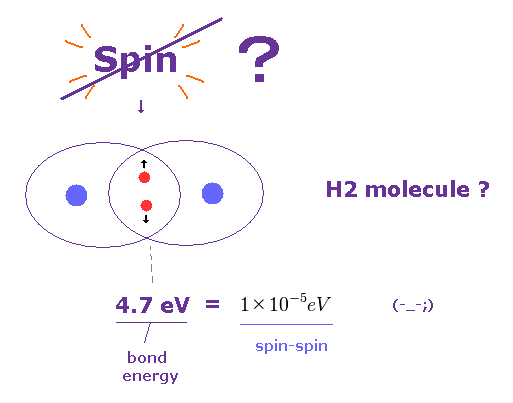
It is said that each molecular bond contains a pair of spin up and down electrons.
But the actual molecular bond strength is as much as 4.7 eV in H2 molecule, as shown on this site.
Again, spin-spin magnetic interaction (= 10-5 eV ) is too weak to explain these molecular bonds.
As long as we believe these wrong assumtions, true molecular bonds remains unknown, forever.
(Fig.27) "Spin" is fantasy ?

It is said spin high and low states are involved in Fe orbitals, as shown in this experiment.
But unfortunately, 3d electrons of iron (= Fe ) have nothing to do with unrealistic spin.
As shown on this site, six electrons in the iron 3d orbitals are split into several subsets.
"t2g" orbitals are basically nonbonding and at lower energy than the antibonding eg orbitals.
This experiment investigates how these states change using X rays, which can distinguish these energy levels, as shown in this Fig..
(Fig.28) "Spin" magnetic dipole energy is "too weak" !

As shown on this site (Fig.15.1), the energy difference between high and low spin states in iron is as large as 1 eV - 3 eV, which clearly originates in Coulomb energy ( NOT weak spin magnetic energy ).
Spin magnetic dipole-dipole interaction is only 1 × 10-4 eV, when their distance is about Bohr radius. See this site (p.6) and this site (p.7).
In Fe, this "spin" energy becomes very weak (= 1 × 10-5 eV ), which cannot reach 1 eV at all.
These kinds of experiments always depends on vague wavefunctions ( 3d ) and unreal Spin, which is inconsistent with the magnitude of actual energy.
Unless we use more concrete and realistic picture of each electron, true atomic bonding remains unknown and useless, forever.
(Fig.29) Current in coil changes the motions of atomic electrons.
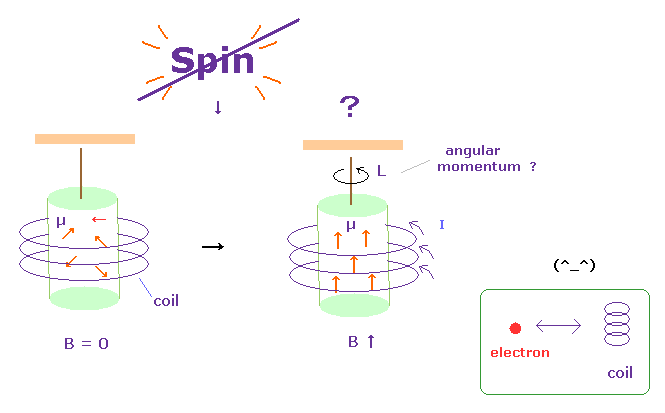
It is said that Einstein-de Haas effects showed "Spin" is "actual rotation".
But if spin is rotation, its spinning speed must be much faster than light speed, as I said above.
This is strange.
In Fig.29 left, the magnetic field B in the iron cylinder is zero, and the magnetic dipole moment vectors (= μ ) of its atoms are randomly oriented.
In Fig.29 right, when a magnetic field is set up along the cylinder's axis, the μ line up parallel to and the cylinder begins to rotate. See this site p.4 or
this.
They insist spin g-factor "2" can be observed in this experiment by measuring the action and reaction between electrons.
But as shown on this page, this experiment just showed the electric current inside coil influences atomic electrons through electromagnetic force (= action at a distance ).
So unrealistic spin has Nothing to do this experiment.
(Fig.30) Wavefunction and unrealistic spin are main obstructions.
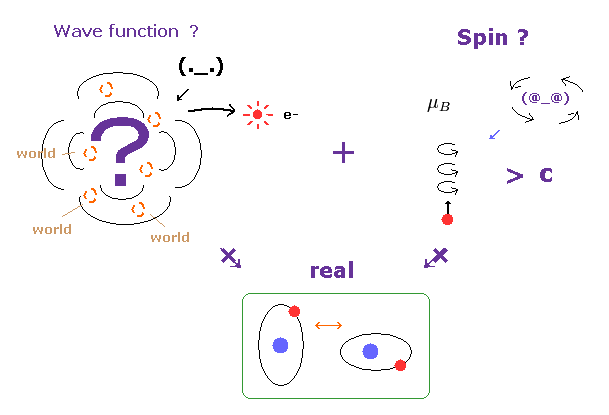
The wavefunction just gives vague probability density of a partcile.
So, it is impossible to describe concrete particle's motion using this vague wavefunction.
Under this strict situation, only unreal spin is left as a thing.
But as I said above, this spin ( magnetic moment ) diagrees with various important phenomena at all.
As a result, the current study based on quantum mechanics is chaotic and confusing.
Unless we admit concrete particle's motion, the microworld and biological mechanism remains unknown, forever.
(Fig.31) Interpretation of spectum lines is strange.
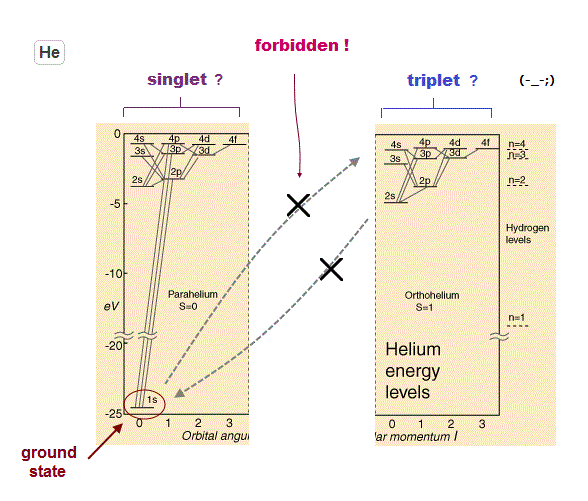
As shown on this site (p.5) and this site (p.3), the energy difference between "singlet" and "triplet" is caused by Coulomb force ( NOT by weak spin magnetic moment ).
Very conveniently, the selection rule prohibits transition between this singlet and triplet, as shown on this site (p.2).
Because if singlet and triplet are real, much more spectrum lines must be found.
But if this transition is prohibited, how an electron can go up to triplet states from singlet ground state ? This is inconsistent.
Though they argue very slow and weak transition may happen ( see this site ), the slow supply ( ground state → triplet ) cannot explain strong (= fast ) triplet-triplet transifion.
In the Nist data ( He, Mg ), only singlet-singlet, tiplet-triplet transitions can be seen ( "term" section ).
And they insist photon spin 1 allows specific transition ( S-P, P-D states ).
It is obvious that this selection rule was artificially introduced to conceal various inconsistent transition.
Actually, if you compare Mg and singly-ionized-Al+, the energy level of 3p2 ( triplet ) are completely different, though these two atoms have the same structure.
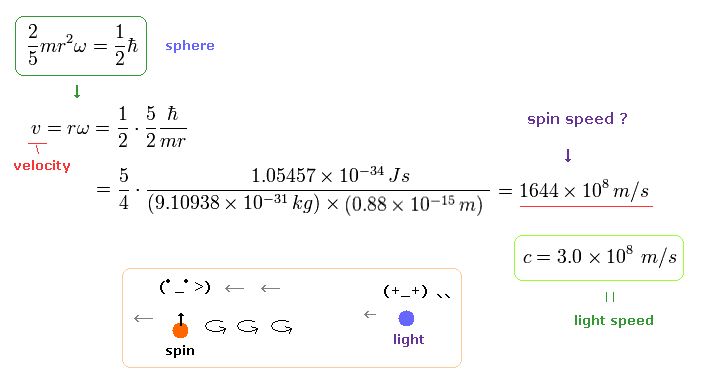
(Ap.1) Spinning speed of the sphere and spherical shell.
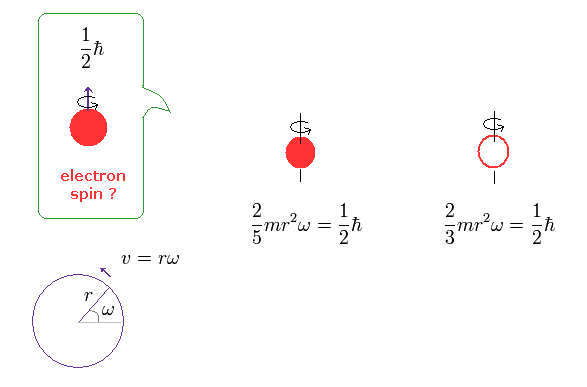
The angular momentum L is equal to the moment of inertia × angular frequency ω
The left of Ap.1 is solid sphere, and the right of Ap.1 is thin spherical shell, as shown on this site.
First, we calculate the spinning speed on the surface of the solid sphere (= rω ).
( Thin spherical shell case is 3/5 times solid sphere's speed. )
From Ap.1 left, the spinning speed (= rω ) on the spherical surface becomes much faster than light,
(Ap.2)

where m is the electron mass, and ħ is h/2π ( h = Plank's constant ).
This spinning speed is more than 100 times the speed of light (= 100 × c = 100 × 3.0 × 108 (m/s)) !
Here the electron radius (r) is supposed to be equal to proton's radius (= 0.88 × 10-15 m ).
But the actual electron size is much smaller than the proton.
As you see Ap.2, as the radius becomes smaller, its rotational velocity becomes faster.
So, the electron's spinning speed becomes much faster than light ! It's impossible.
(Ap.3) ↓ This can be confirmed by actual experiments ?
It is said that the strange spinor rotation was confirmed in actual experiments ( [4], [5] ).
But is it really so ?
These experiments used neutrons as fermions.
And even when they rotated a neutron by 360o, it couldn't return to its original state, they insist.
(Ap.4) One neutron is rotated, another remains as it is → interference.
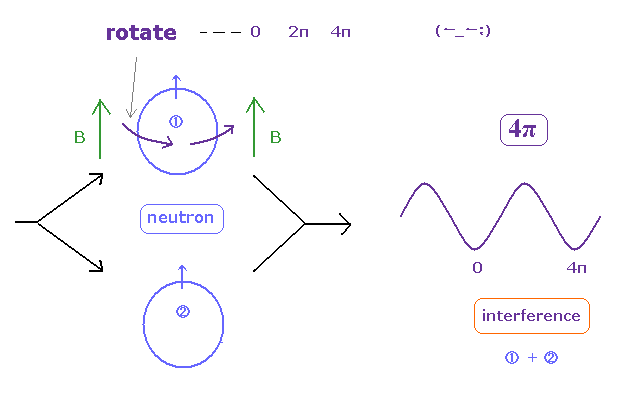
In these experiments, they split neutrons with the same phase into two paths.
One of them rotates (= precesses ) by an aribitrary angle under magnetic field, through Larmor precession.
Another neutron remains as it is.
Lastly, they mix and make these neutrons from two paths interfere with each other.
This experiment showed neutron cannot return by one rotation ( two rotations made them return. ), they insist.
(Ap.5) Torque on the magnetic moment (= neutron ).
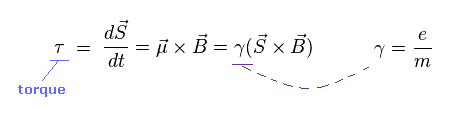
Neutron has neutral charge, but has weak magnetic moment.
According to Larmor precession, the external magnetic field (= B ) exerts a torque on the magnetic moment (= μ ).
"S" is angular momentum of neutron ( in this case, S = 1/2ħ ).
γ is the gyromagnetic ratio which gives the proportional constant between μ and S.
(Ap.6) Electron's magnetic moment = Bohr magneton.
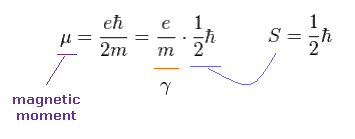
We simply think about electron's magnetic moment (= Bohr magneton ).
As shown in Ap.6, when spin angular momentum S is 1/2ħ, the gyromagnetic ratio γ becomes "e/m".
Here the magnetic field B is in the z direction.
Using cross pruduct, Ap.5 can be expressed as
(Ap.7) Larmor precession of neutron under magnetic field B.

From Ap.7, we obtain angular frequency ω of precession.
(Ap.8)
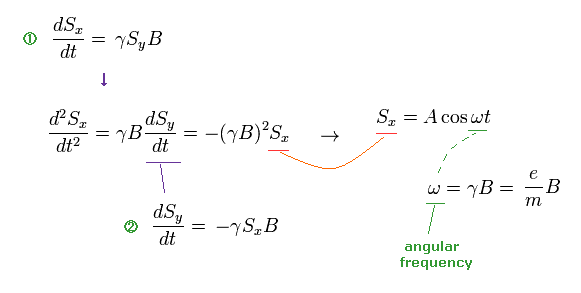
Based on the assumption of ω in Ap.8, they estimated the rotation angle of neutron.
So, if this assumption is different, the rotation angle becomes different, too. ( ← Important ! )
When we use the ordinary angular momentum (= ħ ) of Bohr's orbit, instead of spin 1/2ħ, the gyromagnetic ratio becomes half, as follows,
(Ap.9)
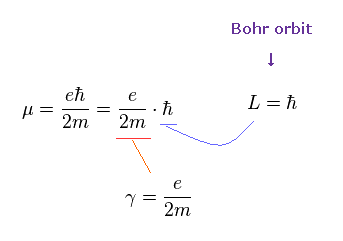
If γ becomes half, the angular frequency ω becomes half, too.
(Ap.10) If we assume Bohr's orbit instead of spin ..
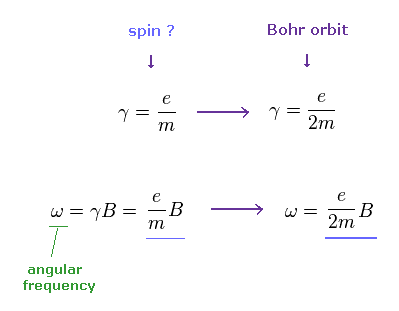
From Ap.10, if we assume Bohr's orbit (= ħ ), the precession angle becomes half of spin's case (= 1/2ħ ).
So, this experiment just showed a neutron returns by one rotation. It's natural.
(Ap.11) Bohr's orbit vs. spin.
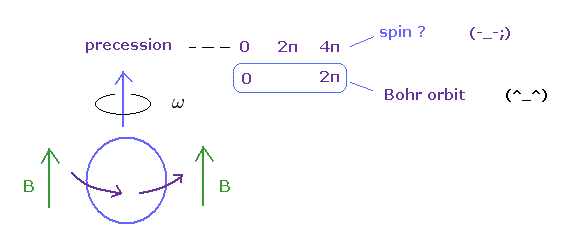
In gyroscope, as the angular momentum increases, the precession becomes slower.
Bearing in mind that the real objects return by 360o rotation, you find Bohr's angular momentum is true, and spin is illusion.
This strange nature of the "spinor" comes from the spin anglar momentum 1/2 ħ .
If the angular momentum is ħ like Bohr model, the wavefunction becomes,
(Ap.12)
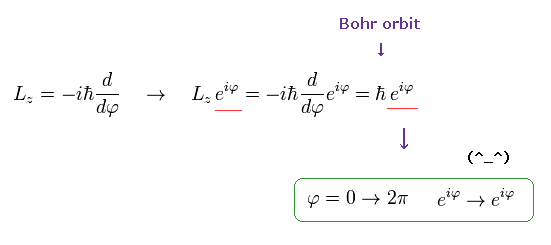
As shown here, this wavefunction ( eiφ) returns by 2π rotation.
But if the angular momentum is 1/2 ħ like "spinor" , the wavefunction becomes,
(Ap.13)
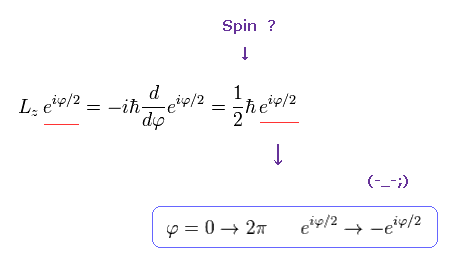
This wavefunction ( eiφ / 2 ) does NOT return by 2π rotation.
So, if we consider "real" atomic model, we must forget about the angular momentum 1/2 ħ.
(Ap.14) Angular momentum = ħ → 1 × de Broglie wavelength.
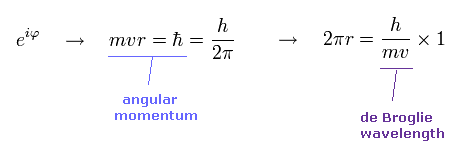
In Bohr model, the minimum angular momentum is ħ.
As shown in Ap.14, when the angular momentum is ħ, its orbital length becomes just 1 × de Broglie wavelength.
de Broglie relation is satisfied in all particles.
In proton, and neutron, spin + ( small ) rotation causes complicated g factor.
(Ap.15) 360o rotation makes "spinor" a different thing.

Here we explain the strange property of Ap.15.
We define the following unit vector using the polar coordinates,
(Ap.16)
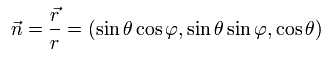
and Pauli matrices (= σ ) are
(Ap.17)
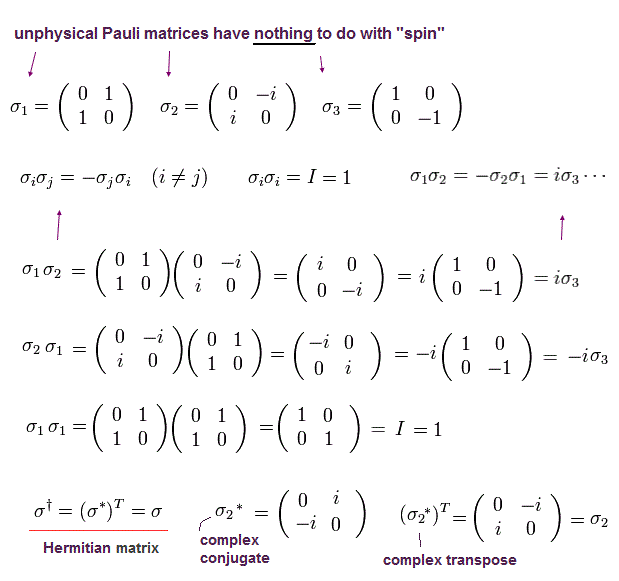
When the spin points to the direction of this unit vector, the spin operator (= S ) can be expressed as
(Ap.18)
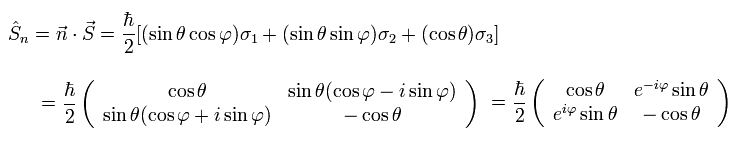
This is an inner product of vectors n and S.
So the eigenfunction expressing "spinor", which points to the direction of n is
(Ap.19)

because
(Ap.20)
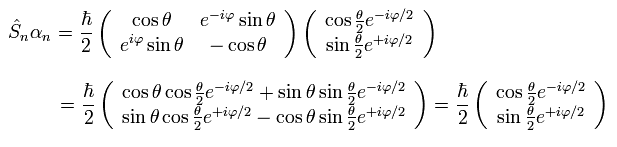
In Ap.20, we use
(Ap.21)
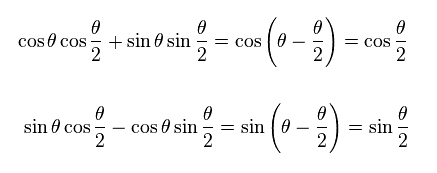
The spinor of Ap.15 and Ap.19 does NOT return by one revolution.
So the spinor itself is a completely unreal object.
It is said that the anomalous Zeeman effect is the evidence that "electron spin" really exists.
But one-electron atom hydrogen is known to show the normal Zeeman effect.
And lithium atom showed Paschen-Back effect, which spectral lines are much fewer than the sodium D line.
It is natural that we think the anomalous Zeeman effect is caused by the inner electrons rather than the "strange" spin. See anomalous Zeeman effect.
In the weak magnetic field (= z axis direction ), some of the lines of the sodium obey the Lande g-factor as follows,
(Ap.22)
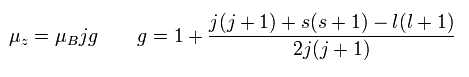
In Ap.22, μz is the z component of the total magnetic moment (μ) of the sodium.
μB is the Bohr magneton.
j (= ± 1/2, ± 3/2 ...) is the z component of the total angular momentum.
"g" is the Lande g-factor.
And s and l are the z components of spin and orbital angular momentums, respectively.
How can this Lande g-factor (g) be gotten?
(Ap.23) ↓ Anomalous Zeeman effect ?
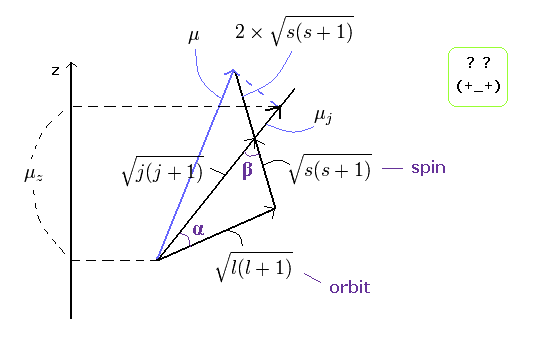
The total (j), angular (l) and spin (s) angular momentums satisfy the above "triangle" relation.
So the cosine formula become,
(Ap.24)
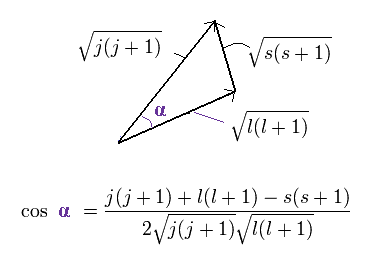
In the same way
(Ap.25)
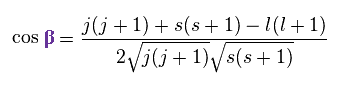
Each magnetic moment of the orbital (l) and the spin (s) becomes as follows, (using the spin g-factor 2)
(Ap.26)
Here, μj points to the direction of the total angular momentum of,
(Ap.27)
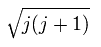
The projection of the above orbital and spin magnetic moments onto the axis of the μj is,
(Ap.28)
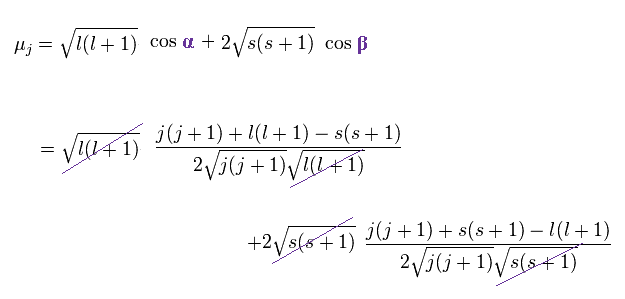
As a result,
(Ap.29)
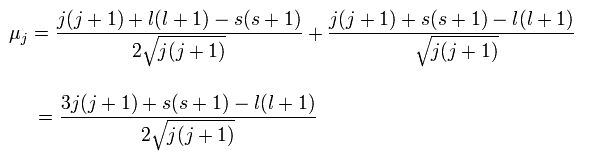
And the projection of this μj onto the z axis becomes
(Ap.30)
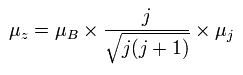
where the μB is the Bohr magneton, and then, the μz is the z component of the magnetic moment.
Substituting Ap.29 into μj of Ap.30,
(Ap.31)
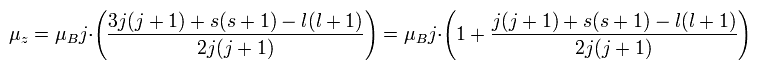
Finally, we can arrive at the Lande g-factor (g) of Ap.22.
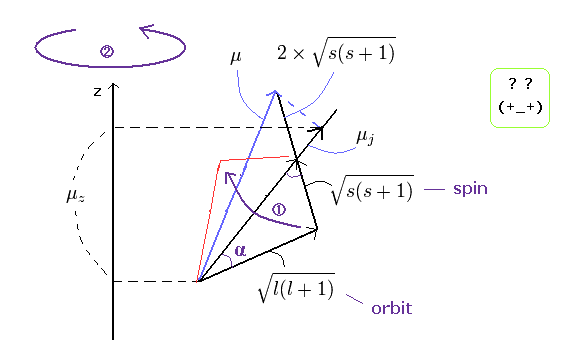
This means that in the weak magnetic field, two strange precessions are occurring ( see Ap.32 ).
Precession (1) ---- total magnetic moment μ precesses about total angular momentum ( direction of the μj)
Precession (2) ---- this μj precesses about z axis.
(Ap.32) Two "unnatural" precessions in anomalous Zeeman effect.
So the anomalous Zeeman effect is very complicated !
Here, if you look at these Precessions (1 and 2) carefully, you will notice something "strange".
Generally, things precess about the direction of some forces such as the magnetic field and gravity.
But the direction of total "angular" momentum (= the direction of μj) has no relation to the direction of forces.
( The direction of μj is neither the z axis direction (external magnetic field) nor the total "magnetic" moment direction (μ) as shown in the above figure.)
And moreover, this Precession (1) must be much faster than the Precession (2) by this calculational method.
So the Precession (1) is a very unnatural thing, and probably it is not occurring.
This Precession (1) was made intentionally to explain some of the sodium spectrum lines (like D line).
As you know, when the z components of orbital (l) and spin (s) angular momentums are 1 and 1/2, respectively, the z component (j) of the total angular momentum must be 1+1/2 = 3/2 even in this weak magnetic field.
But, due to this Precession (1), the z component of the spin (or orbital) angular momentum is changing with time. ( The s can be the value besides 1/2 ! ) .
For example, the case [ s (spin) = 1/2 + 0.05, l (orbital) = 1 - 0.05 ] is possible in the Lande's theory.
But the sum of them, j must be always 3/2 (= 1/2 + 0.05 + 1 - 0.05 = 3/2 ).
Do you think it is inconsistent?
To begin with, the value j=3/2 originates from the precondition [s (spin) =1/2, and l (orbital) = 1].
But the Lande's theory neglects this precondition, and say that j must be 3/2, but s and l must be changing with time.
This means that Lande g-factor includes the self-contradiction and it's one of the "mathematical" tricks.
It is said that the Larmor spin precession is related to the EPR (electron paramagnetic resonance), ESR (electron spin resonance), and NMR (nuclear magnetic resonance).
But as I said above, the spin itself can not be expressed by the real things.
This means that the Larmor spin precession is an illusion ?
As shown in Ap.5 and Ap.10, the angular frequency of the electron spin precession under the magnetic field (B) becomes
( Ap.33 )
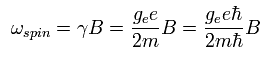
where ge is the spin g-factor (almost 2), and B is the magnetic field.
The Bohr magneton of the electron is
( Ap.34 )
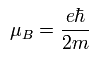
In the EPR (or NMR) resonance condition, the absorbing or emitting electromagnetic wave energy is equal to the energy difference between the spin up (S = +1/2) and spin down (S = -1/2) states.
(Ap.35) The energy of the absorbing (or emitting) electromagnetic waves.
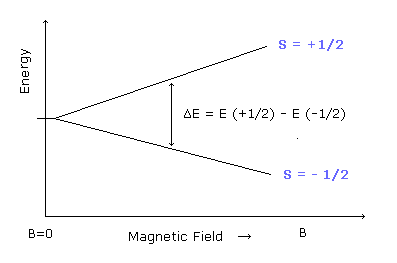
The energy difference between these two states can be expressed as
(Ap.36)
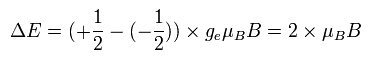
As I said above, the Bohr magneton is the common value in both the Bohr model and the electron spin.
So if we use the Bohr model instead of the "strange" electron spin, the energy difference becomes, (using angular momentum ± 1)
(Ap.37)
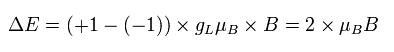
where gL is the orbital g factor (almost 1), which satisfies the following relation,
(Ap.38)
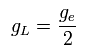
As a result, Aq.36 is equal to Aq.37.
So even if we use the Bohr model, we can explain the phenomena of EPR and NMR correctly.
This is due to the equation of 2 × 1/2 = 1 × 1 (= Bohr magneton ).
The quantum physicists try to explain these EPR and NMR resonance by the Larmor spin precession.
But is it really right ?
The energy difference of Ap.36 (or Ap.37 ) can be expressed using the spin precession angular frequency of Ap.33, as follows,
(Ap.39)
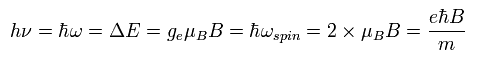
This is the reason why the physicists claim that the Larmor spin precession is related to the resonance.
But this interpretation includes a "strange" idea.
As I said above, the fermions such as electrons and neutrons can not return to their original states by one rotation.
So we should consider the angle of 4π ( not 2π ) as one cycle !
This means that the frequency (not angular frequency) becomes half of the original value.
This is inconsistent with the above interpretation.
In the Bohr model, the electron is rotating instead of "spin".
Under the magnetic field (B), the Lorentz force causes the circular movement of the angular frequency of
(Ap.40)
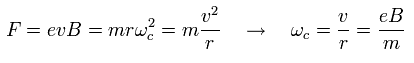
As a result, the resonance energy becomes
(Ap.41)
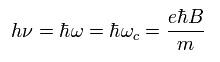
Ap.41 is equal to Ap.39.
So it is quite natural that the resonance is caused by the usual rotation instead of the "strange" spin.
The Bohr magneton is a "ideal" value.
If one electron can be split into the circular orbit equally, the Bohr magneton is correct. (Because the current density becomes uniform.)
But one electron can not be split, so the orbital g-factor is a little different from 1.
Various quantum number ( n = 1, 2, 3, ...) orbits contain the magnetic moment of the Bohr magneton.
For example, in the n=3 Bohr-Sommerfeld's orbit, the angular momentum (L) of the electron can be L = 1, 2, or 3.
The case of L=1 corresponds to the Bohr magneton ( magnetic moment = g-factor (1) × L (1) × Bohr magneton ).
In the n=3 energy level, the L=1 orbit becomes "ellipticall".
[1] G.E. Uhlenbeck and S.A. Goudsmit, Nature 117,264 (1926).
[2] Charles E. Burkhardt, Foundations of Quantum Physics (2008)
[3] J.C. Wesley and A. Rich, Phys. Rev. A4 1341-1363 (1971).
[4] H. Rauch et al., Phys. Lett. 54A, 425 (1975).
[5] S.A. Werner et al., Phys.Rev.Lett., 35 1053 (1975)

2014/5/10 updated. Feel free to link to this site.