Top page (correct Bohr model including the two-electron atoms).
Strange "Spin" is NOT a real thing.
Special relativity is wrong.
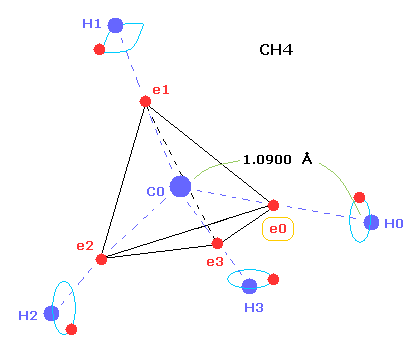
(Fig.1) C-H bond length of methane ( CH4 ).

As shown in this page, we can show why the C-H bond length of methane is 1.09 angstrom (= 1.09 × 10-10 meter ) using Bohr-orbit based molecular model.
Weak points of quantum mechanics and chemistry are that we cannot get away from fixed and complicated methods solving Schrodinger's equations themselves.
Furthermore, if we try to ask about the true natures of the Schrodinger's wavefunction and antisymmetric Pauli exclusion principle themselves, they just say "Shut up and calculate ! and give up thinking". ( These are inconsistent. )
These attitude of quantum mechanics is getting rid of people and students who have strong curiosity about the physics and true nature.
So as far as we don't improve these miserable situations, our science would NEVER develop from now and people with strong curiosity, who want to know the truth, tend to be away from physics itself. I think.
(Fig.2) If hydrogen becomes too close to carbon, methane ( CH4 ) is unstable
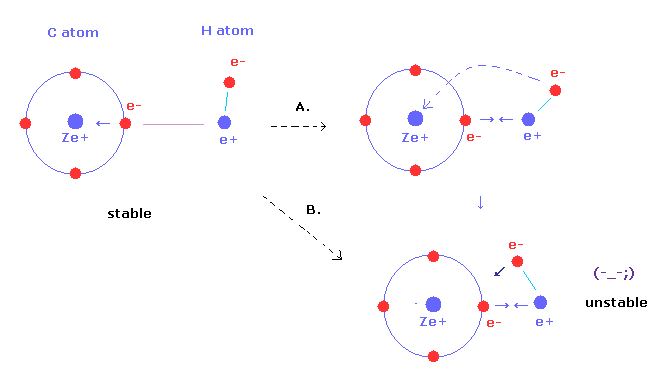
As C-H bond length of methane is shorter, these bonds become stronger.
But hydrogen nucleus of methane comes to be more attracted to valence electron of carbon atom.
Furthermore, carbon nuclear attracting force against H electron becomes stronger, too (= Fig.2B ).
As a result, hydrongen nuclei and electrons cannot keep their stable position.
(Fig.3) If C-H length becomes shoter.
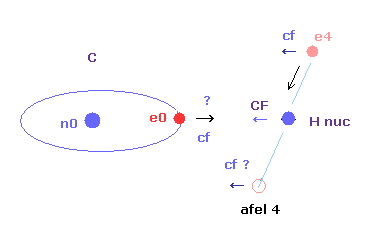
And as the carbon valence electron ( e0 ) also comes to be too strongly attracted to H nucleus, its orbit becomes too extended and unstable.
( This force "cf" acting on carbon electron e0 is a "key" player, as I say later. )
As a result, when C-H bond length of methane is shorter than the experimental value, both of electrons and nuclei cannot keep their stable positions ( or orbits ).
This is the reason why C-H bond length of methane cannot be shorter than the experimental value (= 1.09 × 10-10 meter ).
(Fig.4) Why C-C bond length of ethane is about 1.54 angstrom ?
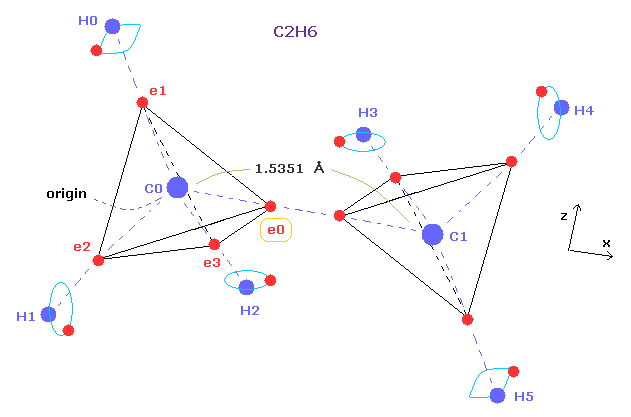
Comparing Fig.1 and Fig.4, you can notice both methane and ethane have almost common structure.
By replacing one H atom of methane by CH3, we can get the ethane from methane.
As I said above or in this page, forces between carbon electron ( e0 ) and H nucleus are key players in determining bond length of methane.
If the valence electrons of carbon in ethane also obey law of Coulomb force and de Broglie waves, force acting on carbon valence electron (= e0 ) should be almost same as that of methane.
(Fig.5) "Force 1" acting on valence electron (= e0 ) in methane.
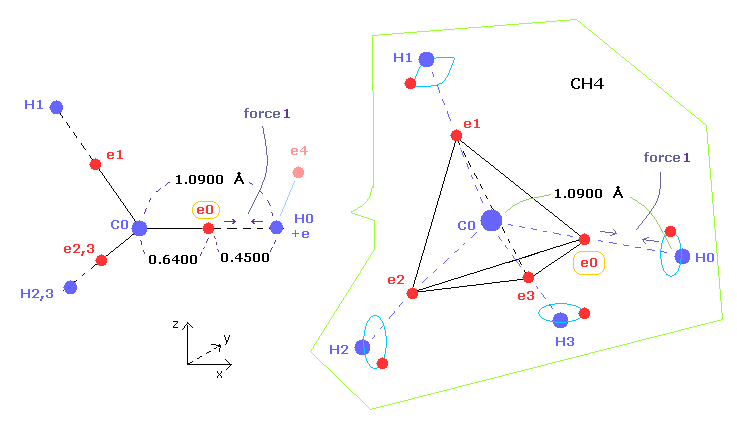
As shown in this page and this page (Fig.22), the rotating radius of four valence electrons of carbon is about 0.6400 × 10-10 meter (= 6400 MM ), when we consider the total 1-4 ionization energies and "2" de Broglie wavelength orbit.
( Here, new unit 1 MM = 1 × 10-14 meter is used. )
As a result, when valence electron e0 is closest to hydrogen nucleus, their distance becomes about 0.4500 angstrom (= 1.0900 - 0.6400 ).
At this point, ( Coulomb ) "force 1" is acting between e0 and H0 nucleus.
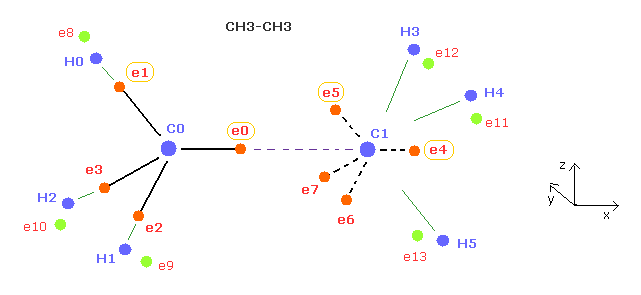
(Fig.6) Periodic motion of ethane ( CH3-CH3 ).
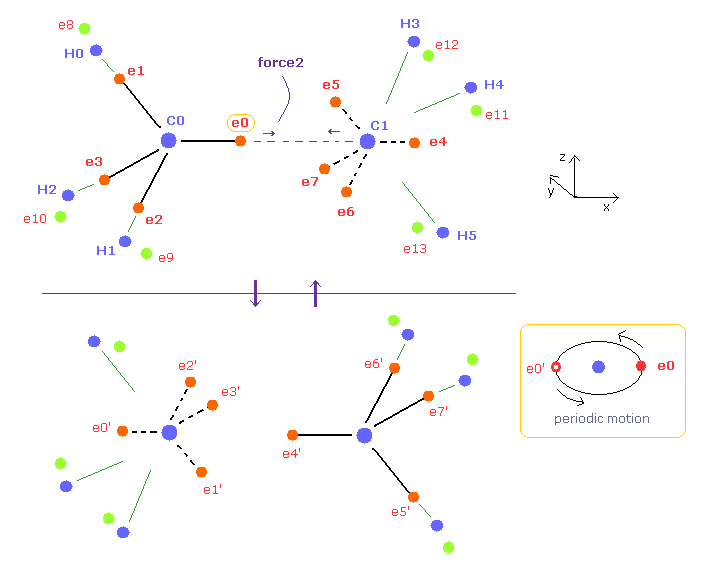
Four valence electrons of carbon are arranged as tetrahedral structure considering their symmetric distribution.
Each electron is actually moving around each centeral carbon nucleus, so Fig.6 upper and lower patterns are repeated periodically in ethane, if we try to know "real" motions in ethane.
(Fig.7) "Force 2" acting on valence electron (= e0 ) in ethane.
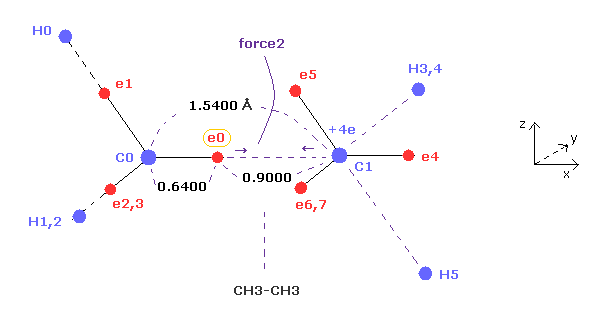
Fig.7 is the x-z cross-sectional view of Fig.6 upper figure.
C-C bond length of ethane is about 1.5400 angstrom, and distance between valence electron e0 and C0 nucleus is about 0.6400 angstrom, when we consider "2" de Broglie wavelength orbit like methane.
As a result, the distance between e0 and another carbon nucleus C1 is about 0.9000 angstrom (= 1.5400 - 0.6400 ).
And central carbon nucleus (= C1 ) has about +4e positive charge ( +6e - 2e ), when two 1s negative charges are subtracted from +6e carbon nucleus.
"Force 2" is the force acting between this e0 electron and C1 nucleus.
(Fig.8) Coulomb forces 1, 2 in methane and ethane are almost same.
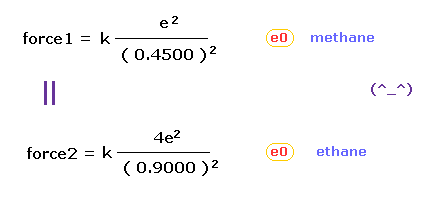
From Fig.5 (= methane ) and Fig.7 (= ethane ), we can know the forces acting between e0 valence electron and another nucleus ( H0 or C1 nucleus ).
Using Coulomb inverse square law, "force 1" in methane proves to be almost same as "force 2" in ethane !
This means the force acting on valence electron e0 is a key player also in determining bond length of ethane.
And the result of Fig.8 proves that both in methane and ethane, the idea of Coulomb relation and de Broglie wavelength are very important.
-----------------------------------------------------------------
(Fig.A-1) Coulomb forces 1, 2 in O-H and O-C bonds.
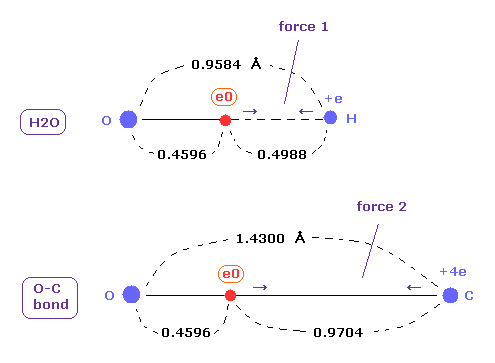
As shown in this page ( Eq.8 - Eq.12 ) or after running this program, you can find the rotating radius (= nuc ) of valence electron of oxygen is about 0.4596 angstrom, when we consider 1-6 total ionization energies and their two de Broglie wavelength orbits.
O-H bond length of water is 0.9584 angstrom, and the average single O-C bond length is known to be 1.4300 angstrom.
Subtracting the rotating radius of 0.4596 from these bond lengths, we can know Coulomb forces 1,2 between electron and another nucleus.
(Fig.A-2) Coulomb forces 1, 2 in O-H and O-C bonds are almost same.
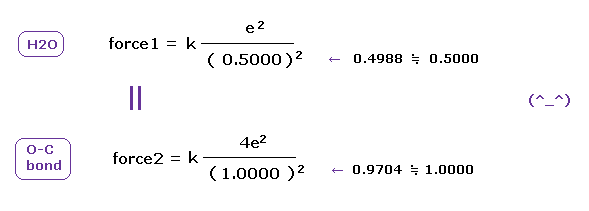
H nucleus is +e and, C nucleus is almost +4e (= +6e - 2e ), subtracting two inner 1s electrons from +6e nucleus.
As a result, Coulomb forces 1 and 2 between electron and another nucleus are almost same in O-H and O-C bonds !
( Of course, the forces between oxygen and electron are the same, too. )
These results demonstrate that valence electrons of oxygen in O-H and O-C bonds are moving obeying the common physical principle, and Coulomb and de Broglie relations are effective also in O-H and O-C bonds in molecules.
-------------------------------------------------------------------
(Fig.9) Bond length and bond angle are important for stability of ethylene.
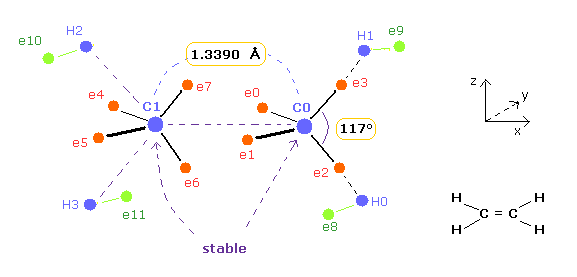
Experimental value of bond length of ethylene ( CH2=CH2 ) is 1.3390 angstrom.
And H-C-H angle of ethylene is 117 degree.
In the latter section, we show this bond length 1.3390 and bond angle 117 are necessary for stability of ethylene nuclei using classical orbits.
(Fig.10) Relation between bond length and bond angle in ethylene.
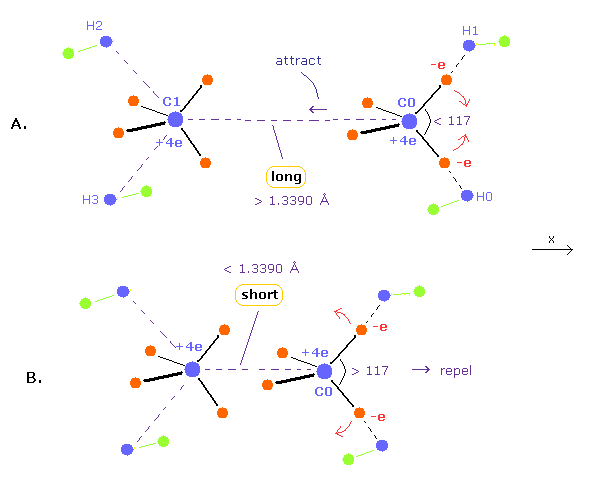
When bond length is longer than 1.3390 angstrom (= experimental value ), repulsive force by another carbon nucleus is weaker.
( This means C0 nucleus is attracted toward another C1 nucleus by its valence electrons, as shown in Fig.10A. )
To cancel this attractive force, H-C-H angle needs to be smaller than 117-degree.
When H-C-H angle is smaller, C0 is pulled in + x direction by other electrons, which can cancel above attractive force.
Conversely, when bond length is shorter than 1.3390 angstrom, repulsive force by another C nucleus is stronger.
As a result, H-C-H angle needs to be wider to make carbon nucleus stable. ( Fig.10B. )
Because, when H-C-H angle is bigger, the attractive force by valence electrons in + x direction is weaker.
In the latter section, using computer program, we show these relations correctly.
(Fig.11) Real motion of ethane ( CH3-CH3 ).

Considering symmetric structure, we can suppose four valence electrons of each carbon are distributed as tetrahedron, as shown in Fig.11.
Each electron is actually orbiting around each centeral carbon nucleus, so Fig.11 upper and lower patterns are repeated periodically in ethane.
(Fig.12) Average positions of outer electrons of carbon.
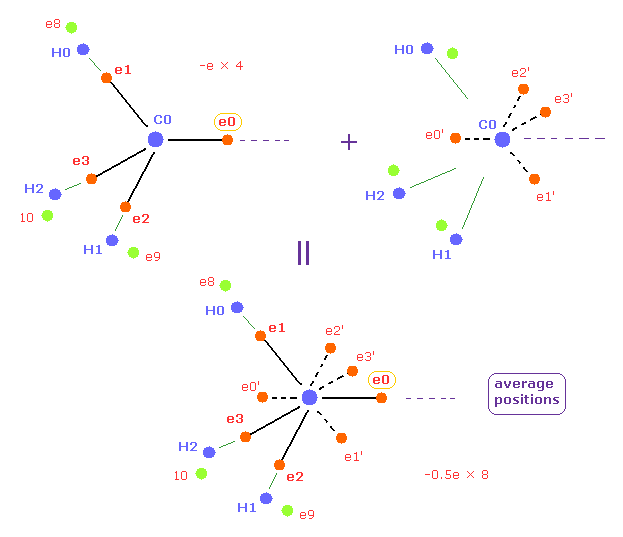
In this page, we use the average positions of four valence electrons of carbon in methane.
In this average distribution, we suppose four outer electrons are distributed as 8 half charge outer electrons like Fig.12.
( So total charges -e × 4 = -0.5e × 8 are the same. )
Each half charge is just at the opposite positions of carbon nucleus in Fig.12
(Fig.13) Symmetric average distributions of outer electrons in C0 and C1.
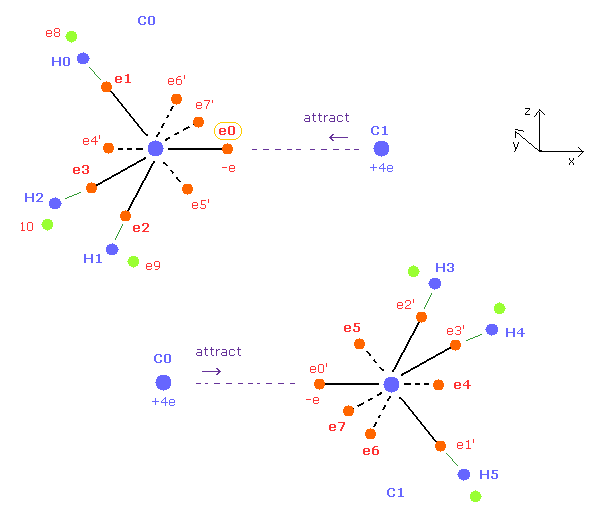
Both C0, C1 carbons of ethane in Fig.11 are symmetric with respect to each other.
So we use symmetric positions of e4,e5,e6,e7 instead of e0', e1', e2', e3' around C0 nucleus.
And C1 nucleus has the same average electron distribution as C0 nucleus.
So when C0 nucleus is attracted to electron 0', C1 nucleus is also attracted to electron 0.
( When you move the position of e0 in the x direction, its symmetric e0' is moved in the minus x direction in the same way. )
Of course, when we compute the interactions among electrons 0-7 themselves, we must use original charges, and not half charge.
Because e0 repels e0'. it is impossible.
Electrons e0', e1'... are only temporary electrons when we consider the average interactions between e0-7 and e8-13 and between e0-7 and each nucleus.
Sample JAVA program of ethane ( Virial theorem. )
The method used in this program is almost same as methane of this page.
(Fig.14) Ethane ( CH3-CH3 ) structure in the program.
After running program, you can only change the coordinates of electron 0, 1, 4, and 5 (= ele0, ele1, ele4, ele5 ) of Fig.14.
Electrons e2 and e3 are automatically arranged at symmetric positions based on e1 coordinate.
Electrons e6 and e7 are automatically arranged at symmetric positions based on e5 coordinate.
As I explain in Fig.13, for example, when you change the coordinate of e1 of carbon 0, symmetric e1' of carbon 1 is also changed.
( When you move e0 in x direction, e0' is moved in minus x direction in Fig.13 ).
Because we consider average and symmetric distribution of electrons.
In the same way, when you move e4 in x direction, e4' is moved in the minus x direction in Fig.13.
(Fig.15) Cross section ( x-z plane ) of Fig.14.
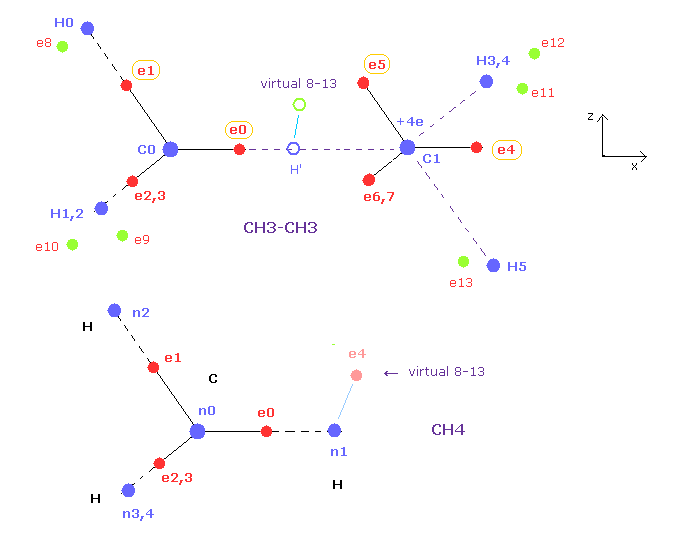
Fig.15 is cross section of ethane of Fig.14.
Electrons e0, e1, e4, e5 and nuclei C0, C1, H0, H5 are all in the x-z plane.
And x coordinates of e1, e2, e3 ( or e5, e6, e7 ) are all the same.
In the methane of this page, we can change only coordinate of e4 in hydrogen electrons.
This e4 belongs to x-z plane, so its position can be easily imagined.
In ethane, "virtual 8-13" electron corresponds to this "e4" of methane.
When you change the x or z coordinate of this virtual 8-13 electron relative to ( virtual ) H', all hydrogen electrons e8-e13 are automatically arranged symmetrically like methane.
Breaking all bonds ( 6 × C-H + C-C ) of ethane requires 2826.1 kJ/mol (= 29.29 eV)
So the ground state energy of ethane (8 carbon valence electrons + 6 hydrogen atoms) becomes -29.29 -148.024 × 2 -13.606 × 6 = -406.974 eV
(148.024 eV is the sum of 1-4th ionization energies of the carbon atom. )
According to the Virial theorem, the total potential energy (tV) becomes 2 × -406.974 = -813.948 eV.
The C-C and C-H bond lengths are 15351 MM, and 10940 MM, respectively. (1 MM = 10-14 meter).
And C-C-H angle is 111.7 degrees.
| eNo | +X (MM) | +Y (MM) | +Z (MM) | nuc | V | cforce | rforce | Waves |
|---|---|---|---|---|---|---|---|---|
| C0 ele 0 | 6549 | 0 | 0 | nuc 6549 | V -76.23 | cf 1505 | rf 0 | wn 2.026 |
| -- ele 1 | -2157 | 0 | 5990 | nuc 6366 | V -76.23 | cf 1531 | rf 0 | wn 1.991 |
| C1 ele 4 | 6303 | 0 | 0 | nuc 6303 | V -76.23 | cf 2432 | rf 0 | wn 1.975 |
| -- ele 5 | -2098 | 0 | 6098 | nuc 6448 | V -76.23 | cf 2229 | rf 0 | wn 2.008 |
| Virtual 8-13 | 468 | 0 | 4138 | - | - | - | - | - |
| C0 nuc | C1 nuc | H0 nuc | total V | avewave 0-3 | avewave 4-7 | 0,4 ave | avewave 8-10 |
|---|---|---|---|---|---|---|---|
| force = 0 | force = 0 | force = -1 | -817.22 eV | wave 2.0 | wave 2.0 | 2.0 | wave 1.0 |
In Table 1, we find each electron coordinate when the total forces acting on C0, C1, H0, and H3 nuclei become almost zero.
( In the program, "FX" is force in x direction, and "CF" is force toward center acting on nuclei. )
And the average de Broglie waves in ele0-3, ele4-7 orbits should be 2.0.
"0,4 ave" means the average de Broglie waves of e0 and e4 (= symmetric position of e0 ), and should be 2.0, too.
The average de Broglie waves in ele8-10, ele11-13 should be 1.0.
Try inputting each coordinate of Table 1 into textboxes after running program and confirm these values.
Total potential energy -817.22 is almost same as the experimental value of -813.9 eV.
The most important point is that force "cf" acting on ele 0 and ele 1 around C0 nucleus are almost same values.
( ele 0 is force cf 1505, and ele 1 is cf 1531. )
(Fig.16) Force = 1000.
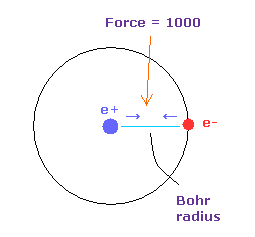
Like this page, the force between electron and nucleus in H atom ground state is supposed to be "1000".
So when the distance between electron and +e nucleus is Bohr radius, its force becomes 1000.
And "cf" is force acting on each electron toward central C nucleus.
(Fig.17) Forces acting on e0, e1 are almost same, when C-C length is experimental value.
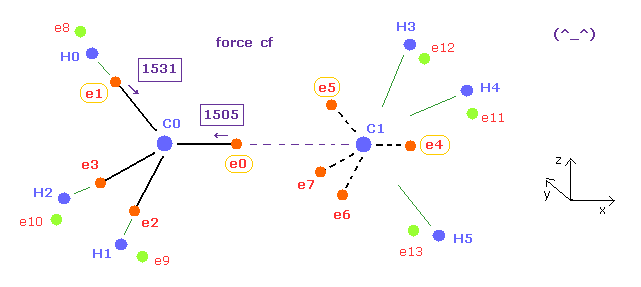
For the electrons around carbon to orbit with the same period, forces acting on them need to be almost same.
Fortunately, when the C-C length of ethane is experimental value (= 15351 MM ), these forces are almost equal to each other ( 1505 = 1531 ).
Here new unit, 1 MM = 1 × 10-14 meter, is used.
(Fig.18) Forces acting on e0, e1 in methane.
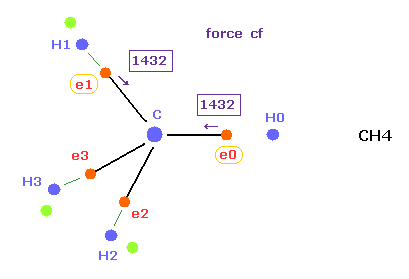
Comparing Fig.17 and Fig.18, force ( cf 1503 ) acting on e0 in ethane is almost same as e0 ( cf 1432 ) in methane.
So this result shows Coulomb and de Broglie relations are valid also in ethane molecule.
In the program, "afel" mean electrons after moving by the force, which meaning is the same as methane.
( In the program, only electrons 0, 4, 8, and 11 values are showed. )
Loooking the values of "cf" in ele 8 and afel 8, you can see hydrogen electron's motions ( e8-e13 ) are also stable in ethane.
( e8 cf = 254, and afel8 cf = -232, their signs are opposite and their absolute values are almost same. )
| eNo | +X (MM) | +Y (MM) | +Z (MM) | nuc | V | cforce | rforce | Waves |
|---|---|---|---|---|---|---|---|---|
| C0 ele 0 | 6579 | 0 | 0 | nuc 6579 | V -76.44 | cf 1191 | rf 0 | wn 2.032 |
| -- ele 1 | -2165 | 0 | 5980 | nuc 6359 | V -76.44 | cf 1551 | rf 0 | wn 1.990 |
| C1 ele 4 | 6273 | 0 | 0 | nuc 6273 | V -76.44 | cf 2455 | rf 0 | wn 1.970 |
| -- ele 5 | -2098 | 0 | 6109 | nuc 6459 | V -76.44 | cf 2191 | rf 0 | wn 2.010 |
| Virtual 8-13 | 456 | 0 | 4125 | - | - | - | - | - |
| C0 nuc | C1 nuc | H0 nuc | total V | avewave 0-3 | avewave 4-7 | 0,4 ave | avewave 8-10 |
|---|---|---|---|---|---|---|---|
| force = 0 | force = 0 | force = 0 | -820.0 eV | wave 2.0 | wave 2.0 | 2.0 | wave 1.0 |
Next, we choose "14500" in the scroll bar and click C-C (MM) button.
As shown in Table 2, when the C-C bond length becomes shorter than the experimental value, e0 tends to be attracted to another C1 nucleus.
As a result, force cf of e0 becomes too weaker than other electrons of carbon ( 1191 < 1551 )
This means the same rotating periods of four valence electrons are broken ( Fig.19 ).
(Fig.19) Forces acting on e0 becomes too small when C-C length is shorter.
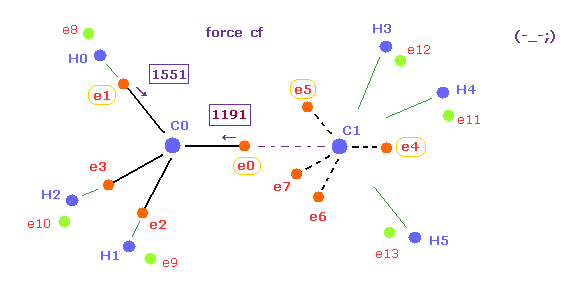
Fig.19 expresses the state when C-C legnth is shorter (= 14500 MM ) than the experimental value, as shown in Table 2.
Of course, 1191 of Fig.19 is completely different from 1430 of methane (= Fig.18 ).
| eNo | +X (MM) | +Y (MM) | +Z (MM) | nuc | V | cforce | rforce | Waves |
|---|---|---|---|---|---|---|---|---|
| C0 ele 0 | 6529 | 0 | 0 | nuc 6529 | V -76.04 | cf 1764 | rf 0 | wn 2.023 |
| -- ele 1 | -2162 | 0 | 5996 | nuc 6373 | V -76.04 | cf 1512 | rf 0 | wn 1.992 |
| C1 ele 4 | 6303 | 0 | 0 | nuc 6303 | V -76.04 | cf 2436 | rf 0 | wn 1.979 |
| -- ele 5 | -2120 | 0 | 6090 | nuc 6448 | V -76.04 | cf 2256 | rf 0 | wn 2.007 |
| Virtual 8-13 | 473 | 0 | 4145 | - | - | - | - | - |
| C0 nuc | C1 nuc | H0 nuc | total V | avewave 0-3 | avewave 4-7 | 0,4 ave | avewave 8-10 |
|---|---|---|---|---|---|---|---|
| force = 0 | force = 0 | force = 0 | -815.1 eV | wave 2.0 | wave 2.0 | 2.0 | wave 1.0 |
(Fig.20) Forces acting on e0 becomes too stronger when C-C length is longer.
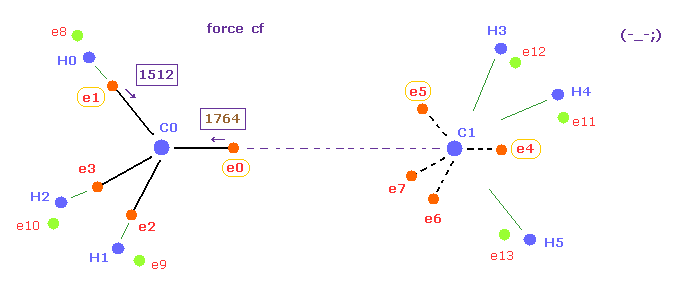
Next, we choose "16500" in the scroll bar and click C-C (MM) button.
As shown in Table 3, when the C-C bond length becomes longer than the experimental value, attractive force of C1 nucleus against e0 becomes weaker.
As a result, force "cf" of e0 toward C0 nucleus becomes too stronger than other electrons of carbon ( 1764 > 1512 )
So also in this case, the same rotating periods of four valence electrons are broken ( Fig.20 ).
Furthermore, total potential energy becomes higher than that of 15351 MM.
(Fig.21) How to make C nucleus stable ( FX = 0 ).
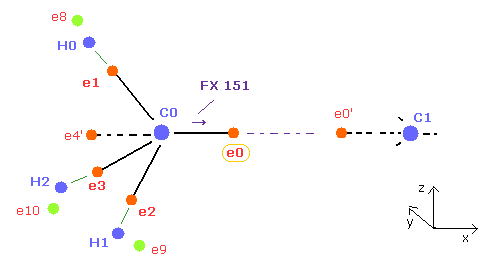
After running program, C0 and C1 nuclei are attracted to electrons 0 and 0' of another nucleus, so C0 nuc FX = 151 ( C1 nuc FX = -151 ).
Here "FX" means force acting on each C nucleus in x direction.
Because as I said in Fig.12 and Fig.13, we consider average distribution around C nucleus.
So when C0 nucleus tends to be attracted to e0' electron (= symmetric to e0 ), C1 nucleus is also attracted to e0 electron.
To make this FX = 151 close to zero, we need to move e0 in the x direction. ( e0' moves in minus x direction. )
Because when e0 moves in the x direction, the distance between e0 and C0 nucleus is longer, which weakens the force component of C0 in the x direction.
(Fig.22) How to make C nucleus stable ( FX = 0 ).
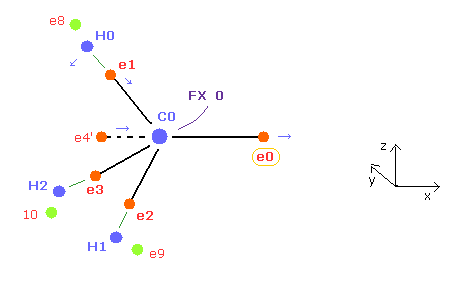
And e0 and e4' forms one orbit around C0 nucleus, e4' needs to come closer to C0 ( which means e4 comes closer to C1 symmetrically ) to keep the average "2" de Broglie wave of 0, 4 ( 0,4ave = 2.0 ).
And as e0 is more apart from C0, e1,e2, and e3 electrons tends to be closer to C0 nucleus.
( Of course, if e1-e3 become too close to C0, the same rotating periods of e1 and e0 are broken, so we need to make their distances between C0 nucleus almost same as possible. )
As C-C length becomes shorter, C-C-H angle becomes bigger.
So e1 electron tends to move in x and -z directions.
Considering all these effects and average de Broglie waves = 2.0, we can get the results of Table 1-3.
The distance between e0 and C0 nucleus is a littler longer (= about 6500MM ) due to attractive force of C1 nucleus than methane (= 6415 MM ).
(Fig.23) Classical orbits of ethylene ( CH2=CH2 ).

Breaking all bonds ( 4 × C-H + C=C ) of ethylene (=ethene) requires 2253.1 kJ/mol (= 23.35 eV)
So the ground state energy of ethylene ( 8 carbon valence electrons + 4 hydrogen atoms ) becomes -23.35 -148.024 × 2 -13.606 × 4 = -373.822 eV
According to the Virial theorem, the total potential energy (tV) becomes 2 × -373.822 = -747.644 eV.
The C=C and C-H bond lengths are 13390 MM, and 10870 MM, respectively. (1 MM = 10-14 meter).
And H-C-H angle of ethylene is 117 degree, which is important.
Sample JAVA program of ethylene ( Virial theorem )
(Fig.24) Ethylene ( CH2=CH2 ) model in the program
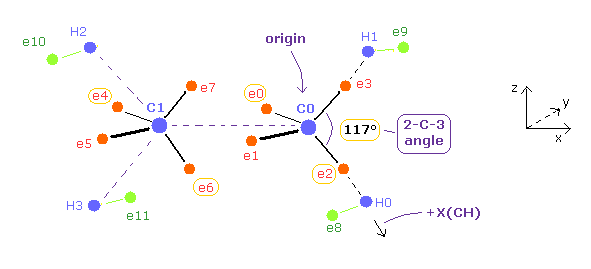
In this program, nuclei C0 (= origin ), C1, H0-H3 and electrons e2, e3, e6, e7 are on the same x-z plane.
Electrons e0, e1, e4 and e5 are on the x-y plane.
You can change the coordinates of ele 0, 2, 4, 6, and 8 in the textboxes.
+X(CH) of ele 8 means the coodinate in the direction of C0 → H0 ( see Fig.24 ).
Based on these inputted values, the coordinates of remaining electrons are automatically determined.
Like ethane, this program defines symmetric electrons of e0, e1, e2, and e3 with respect to C0 nucleus as e4', e5', e6' and e7', and uses average distributions.
( -e × 4 = -0.5e × 8 around each C nucleus. )
| eNo | +X (MM) | +Y (MM) | +Z (MM) | nuc | V | cforce | rforce | Waves |
|---|---|---|---|---|---|---|---|---|
| C0 ele 0 | -3703 | 5237 | 0 | nuc 6413 | V -76.56 | cf 2196 | rf 0 | wn 1.978 |
| C0 ele 2 | 3357 | 0 | -5465 | nuc 6413 | V -75.56 | cf 1430 | rf 0 | wn 2.021 |
| C1 ele 4 | -3703 | 5237 | 0 | nuc 6413 | V -75.56 | cf 2349 | rf 0 | wn 2.0 |
| C1 ele 6 | 3703 | 0 | -5237 | nuc 6413 | V -75.56 | cf 2189 | rf 0 | wn 2.0 |
| H0 ele8 | 496 | -3957 | 0 | nuc 3987 | V -35.62 | cf 270 | rf 1672 | wn 0.884 |
| C0 nuc | C1 nuc | H0 nuc | total V | e0-7 avewave | avewave 8 | nospilt wave | 2-C0-3 angle |
|---|---|---|---|---|---|---|---|
| force = 0 | force = 0 | force = 0 | -747.01 eV | wave 2.0 | wave 0.934 | wave 0.982 | 116 degree |
Different from ethane, e0 electron (= Fig.17 ), which orbit extremely extends into another nucleus, does not exist in etylene.
( Compare e0 of Fig.17 and Fig.23. )
So just after running program, C0 and C1 nuclei are repelled by each other.
C0 nuc FX is 161, so C0 nucleus is repelled into x direction in Fig.24 and Fig.25.
(Fig.25) H-C-H angle becomes 116 degree for the stability of C nucleus.
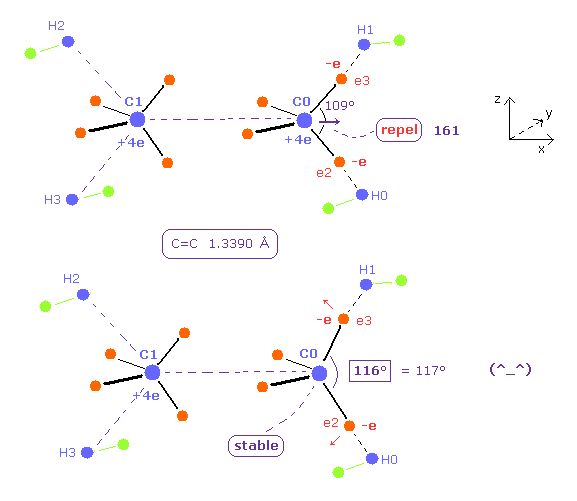
To cancel this repulsive force between carbon nuclei, we try changing only ele2 ( and ele8 ) coordinates, keeping other electrons tetrahedrally distributed.
Try inputting the red values of Table 4 on each textboxes after running the program.
As shown in Table 4, when the bond angle of ele2-C0-ele3 is 116 degree ( almost 117 ), the force acting on each nuclei becomes just zero.
This means the experimental values of bond length 13390 MM and H-C-H bond angle 117 degree can be explained by Bohr orbit based model.
As shown in Table 4, when the potential energy is the experimental value (= -747 eV ), the average de Broglie wave of hydrogen electron (= e8 ) becomes a little smaller than 1.0.
This is due to the less hydrogen atom in etylene than in ethane.
So in ethylene, instead of binding to other hydrogn nuclei, electrons tend to bind to C nuclei and oscillating fast.
( If we compute de Broglie waves of e8, not spilitting electrons 0-7 into half charge, its value becomes 0.982. )
| eNo | +X (MM) | +Y (MM) | +Z (MM) | nuc | V | cforce | rforce | Waves |
|---|---|---|---|---|---|---|---|---|
| C0 ele 0 | -3703 | 5237 | 0 | nuc 6413 | V -75.64 | cf 2181 | rf 0 | wn 1.963 |
| C0 ele 2 | 3107 | 0 | -5620 | nuc 6421 | V -75.64 | cf 1435 | rf 0 | wn 2.035 |
| C1 ele 4 | -3703 | 5237 | 0 | nuc 6413 | V -75.64 | cf 2353 | rf 0 | wn 2.0 |
| C1 ele 6 | 3703 | 0 | -5237 | nuc 6413 | V -75.64 | cf 2181 | rf 0 | wn 2.0 |
| H0 ele8 | 490 | -3980 | 0 | nuc 4010 | V -35.35 | cf 267 | rf 1655 | wn 0.883 |
| C0 nuc | C1 nuc | H0 nuc | total V | e0-7 avewave | avewave 8 | nospilt wave | 2-C0-3 angle |
|---|---|---|---|---|---|---|---|
| force = 0 | force = 0 | force = 0 | -746.52 eV | wave 2.0 | wave 0.934 | wave 0.985 | 122 degree |
Next we choose "12500" in the scroll bar and click C=C button.
And input the red values of Table 5 into each textboxes on the screen.
We aim at the same de Broglie wave ( e0-7 average = 2.0 and e8 wave = 0.934 ) as Table 4.
(Fig.26) H-C-H angle needs to be 122 degree for the stability of C nucleus.
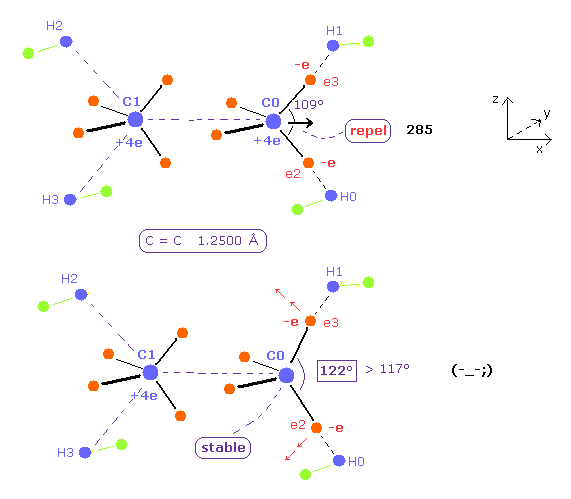
As the C=C internuclear distance is shorter, repulsive force by another C nucleus is stronger.
To cancel this repulsive force , H-C-H angle needs to be much wider than the experimental value.
When C=C length is 12500 MM, H-C-H angle needs to be 122 degree, which is greater than the actual value of 117 degree.
Furthermore, the total potential energy -746.52 eV is higher than Table 4 (= -747.01 eV ).
So the ethylene itself becomes unstable in this case.
| eNo | +X (MM) | +Y (MM) | +Z (MM) | nuc | V | cforce | rforce | Waves |
|---|---|---|---|---|---|---|---|---|
| C0 ele 0 | -3703 | 5237 | 0 | nuc 6413 | V -75.43 | cf 2215 | rf 0 | wn 1.992 |
| C0 ele 2 | 3572 | 0 | -5327 | nuc 6413 | V -75.43 | cf 1440 | rf 0 | wn 2.008 |
| C1 ele 4 | -3703 | 5237 | 0 | nuc 6413 | V -75.43 | cf 2345 | rf 0 | wn 2.0 |
| C1 ele 6 | 3703 | 0 | -5237 | nuc 6413 | V -75.43 | cf 2204 | rf 0 | wn 2.0 |
| H0 ele8 | 480 | -3945 | 0 | nuc 3974 | V -35.83 | cf 264 | rf 1685 | wn 0.885 |
| C0 nuc | C1 nuc | H0 nuc | total V | e0-7 avewave | avewave 8 | nospilt wave | 2-C0-3 angle |
|---|---|---|---|---|---|---|---|
| force = 0 | force = 0 | force = 0 | -746.82 eV | wave 2.0 | wave 0.934 | wave 0.979 | 112 degree |
Next we choose "14500" in the scroll bar and click C=C button.
And input the red values of Table 6 into each textboxes on the screen.
We aim at the same de Broglie wave ( e0-7 average = 2.0 and e8 wave = 0.934 ) as Table 4.
(Fig.27) H-C-H angle needs to be 112 degree for the stability of C nucleus.
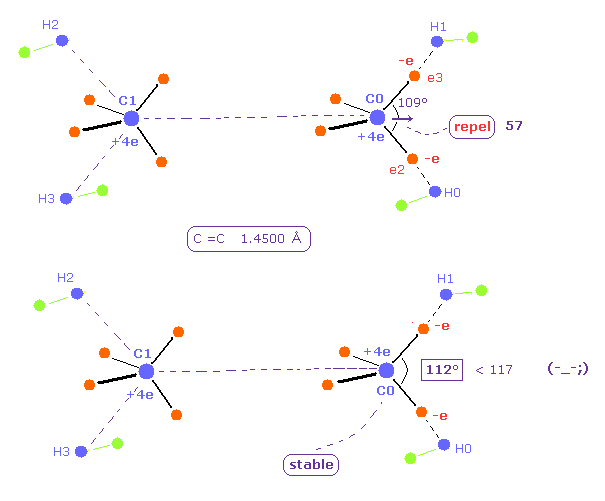
As the C=C internuclear distance is longer, repulsive force by another C nucleus is weaker.
So H-C-H angle does NOT need to be so bigger.
When C=C length is 14500 MM, H-C-H angle becomes 112 degree, which is smaller than the actual value of 117 degree.
Furthermore, the total potential energy -746.82 eV is higher than Table 4 (= -747.01 eV ).
Three positive nuclei of C1, H0, and H1 tend to be arranged into triangle (= H-C-H angle is about 120 degree. ).
So this 112 degree is inconsistent with this triangle distribution of nuclei.
| C = C bond | e2 +X | e2 +Y | e2 +Z | e8 CH | e8 +Y | V (eV) | Waves | H-C-H angle |
|---|---|---|---|---|---|---|---|---|
| 12000 | 2929 | 0 | -5730 | 476 | -4000 | V -745.72 | 0.934 | 125 degree |
| 12500 | 3107 | 0 | -5620 | 490 | -3980 | V -746.53 | 0.934 | 122 degree |
| 13390 | 3357 | 0 | -5465 | 496 | -3957 | V -747.01 | 0.934 | 116 degree |
| 14500 | 3572 | 0 | -5327 | 480 | -3945 | V -746.82 | 0.934 | 112 degree |
| 15000 | 3630 | 0 | -5278 | 473 | -3949 | V -746.55 | 0.934 | 110 degree |
| C0 nuc | C1 nuc | H0 nuc | e0-7 avewave | avewave 8 |
|---|---|---|---|---|
| force = 0 | force = 0 | force = 0 | wave 2.0 | wave 0.934 |
Table 7 shows the coodinates of ele2 and 8, in which de Broglie wave of e8 is 0.934 and each nucleus becomes stable.
Total potential energy V = -747 eV is experimental value, as I said above.
As you see in Table 7, when the C=C bond length is 13390 MM (= 1.3390 angstrom, experimental value ), potential energy becomes the lowest, and H-C-H angle (= 116 degree ) is closest to experimental value (= 117 degree ).
| C = C bond | e2 +X | e2 +Y | e2 +Z | e8 CH | e8 +Y | V (eV) | nosplit wave | H-C-H angle |
|---|---|---|---|---|---|---|---|---|
| 12000 | 2929 | 0 | -5734 | 471 | -3979 | V -746.40 | 0.982 | 125 degree |
| 12500 | 3107 | 0 | -5620 | 487 | -3969 | V -746.92 | 0.982 | 122 degree |
| 13390 | 3357 | 0 | -5465 | 496 | -3957 | V -747.01 | 0.982 | 116 degree |
| 14500 | 3572 | 0 | -5327 | 485 | -3958 | V -746.34 | 0.982 | 112 degree |
| 15000 | 3630 | 0 | -5278 | 473 | -3949 | V -746.05 | 0.982 | 110 degree |
| C0 nuc | C1 nuc | H0 nuc | e0-7 avewave | nosplit 8wave |
|---|---|---|---|---|
| force = 0 | force = 0 | force = 0 | wave 2.0 | wave 0.982 |
"Nospilit" de Broglie wave of electron 8 is computed, not splitting carbon electrons 0-7 into half charge.
Considering average electron distribution around C nuclei, we split 4 valence electrons into 8 symmetric electrons with half charge, as shown in Fig.12 and Fig.13 also in ethylene.
But in ethylene case, hydrogen electron is more influenced by carbon's nuclei and electrons due to less hydrogen atoms.
So we need to compute de Broglie wave, as they are.
Also in this condition of Table 8, when the C=C bond length is experimental value (= 13390 MM ), total potential energy becomes lowest, and H-C-H angle is closest to 117 degree.
These results demonstrate that classical orbits using usual Coulomb and de Broglie relations can explain molecular bonds ( including double bond ) correctly.
(Fig.28) "Mathematical" Schrodinger equation vs. "real" Bohr model.
Even though the science all over the world has developed greatly now,
we cannot know what the Schrodinger's wavefunctions really are, and just give up asking what they are.
Though the computing methods by the present quantum chemistry is incomplete and very problematic.
Furthermore, as shown in this page, even if we study about relativistic quantum field theory and string theory, we cannot know what mysterious Pauli exclusion principle really is.
These attitudes about the basic physics clearly obstruct the development of our science.
We cannot solve the Schrodinger's equation (+ complicated determinants ) especially in multi-electron atoms and molecules.
(Fig.29) 1 × de Broglie wavelength = hydrogen ground state.
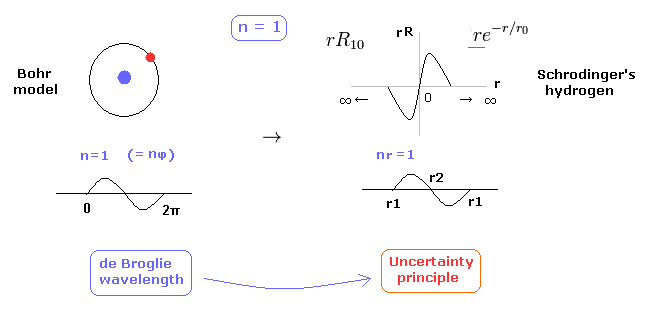
As shown in this page, Schrodinger's hydrogen also satisfies the condition of an integer times de Broglie wavelength.
This is the reason why Schrodinger's hydrogen gives completely the same results as Bohr model in all energy levels.
As shown in Fig.29, in the ground state of hydrogen atom, Bohr model consists of tangential de Broglie wave, and Schrodinger's model ( rR ) consists of "radial" de Broglie wave.
( It is easily understood also by seeing the probability graphs of |rR|2. )
(Fig.30) Unrealistic "s" states ( angular momentum zero )
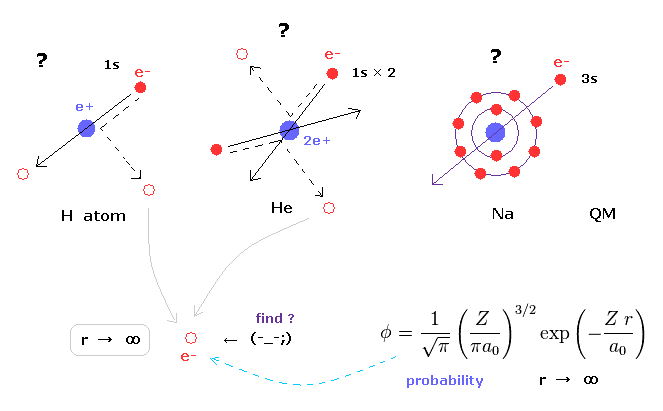
In various atoms and molecules such as helium and hydrogen molecule, Schrodinger's wavefunction ALWAYS spread to infinity.
And All energy levels of quantum mechanical models always contain unrealistic "s" state, which has no angular momentum.
Due to this unrealistic "s" state, we cannot visualize the actual electron distribution in multi-electron atoms and molecules.
For example, in sodium or potassium, how 3s or 4s electron can penetrate inner electrons avoiding their strong repulsive forces ?
This is clearly impossible.
So these "s" states clearly forbid developing much simpler methods, and keep us from imaging actual electron's distribution in various molecules.
In multi-electron molecules, molecular dynamics calculation (= MD ) is often used, because we cannot deal with these molecules by complicated wavefunctions.
But MD method do not use electrons themselves, they just rely on virtual forces.
So if we combine Bohr orbit based electron distritbuions to the theories like this, the present molecular computing would be much easier and develop more greatly.
And popular Density functional theory ( DFT ) is only approximation, which cannot tell us true natures of various molecules.
Unless we can develop easier and correct ways using clear orbits such as Bohr model, the present molecular methods and nanotechnology would NEVER develop in the furture.

2013/3/18 updated. Feel free to link to this site.