Entanglement is unreal, can send No information.
Quantum entanglement is a useless, unneeded concept that cannot send any information nor do any work.
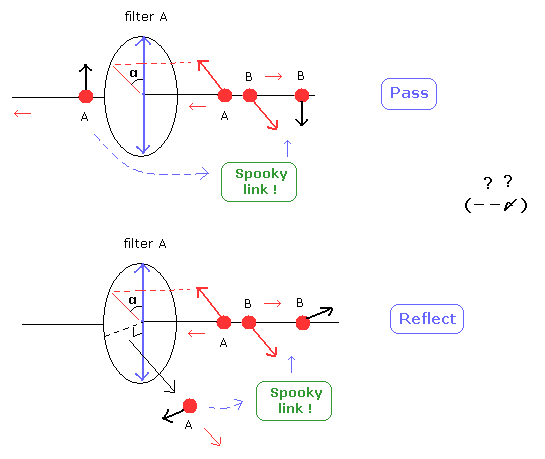
(Fig.1) Entanglement is meaningless = a box-A (or box-B ) contains a red (or blue ) ball. → when the box-A is opened to expose the red ball, the box-B has a blue ball. ← No spooky action.
Quantum entanglement is a meaningless concept.
Put a red or blue ball into each of two boxes. → When one box has a red ball, the other ball has a blue ball. ← entanglement is a meaningless concept.
Contrary to overhyped news, the quantum entanglement is a completely meaningless concept irrelevant to the faster-than-light spooky action.
In Fig.1, one of boxes-A and B contains a red ball, and the other box has a blue ball (= which box contains a red or blue ball is uncertain ).
When these boxes are sent to two distant positions A and B, a man in A opens the box-A and sees a red ball, it instantly (= by faster than light entanglement spooky action ? No ) determines that the other box-B (= still closed ) contains a blue ball.
↑ This meaningless natural concept (= No faster-than-light spooky action ) is quantum entanglement.
Quantum entanglement, teleportation are useless.
Only ordinary classical methods can send information.
Quantum entanglement and teleportation are useless.
↑ This meaningless quantum entanglement can Not send any information nor communicate, because the other man in B position cannot know what ball is contained in the distant box-A ( or the closed box-B ), unless the distant man in A sends the information of the ball inside the box-A to the man-B via the ordinary classical communication slower than light.
No faster-than-light spooky action
This-1st~2nd-paragraphs say
"Quantum entanglement does Not allow for faster-than-light communication."
"the measurement of the entangled particle is fundamentally random and unpredictable, and any attempt to transmit information using this method would require a classical communication channel (= ordinary phones or email ), which would be limited by the speed of light."
Only classical methods can send information.
Quantum entanglement is useless, cannot send any information. Only classical communication is useful, can send real information.
This-last-paragraph says -- Teleportation = classical
"It turns out entanglement alone is Not enough to send data. For example, quantum teleportation uses entanglement to transfer quantum states across long distances. However, teleportation requires sending a classical bit (= by ordinary classical communication ) in addition to the entangled qubits. So, while the entanglement operates instantaneously, the information transfer is limited by the speed of the classical information, "
This-p.14-last-paragraph says -- Entanglement = No information
"According to quantum mechanics, therefore, No information can be conveyed faster than
light by exploiting quantum entanglement. The signal that two particles really were entangled can only be ascertained once we use some other (= classical ) means of communication — limited
by the speed of light"
As a result, this meaningless quantum entanglement sending No information is completely useless for any technologies such as cryptography and quantum computers.
Quantum entanglement is unreal, useless.
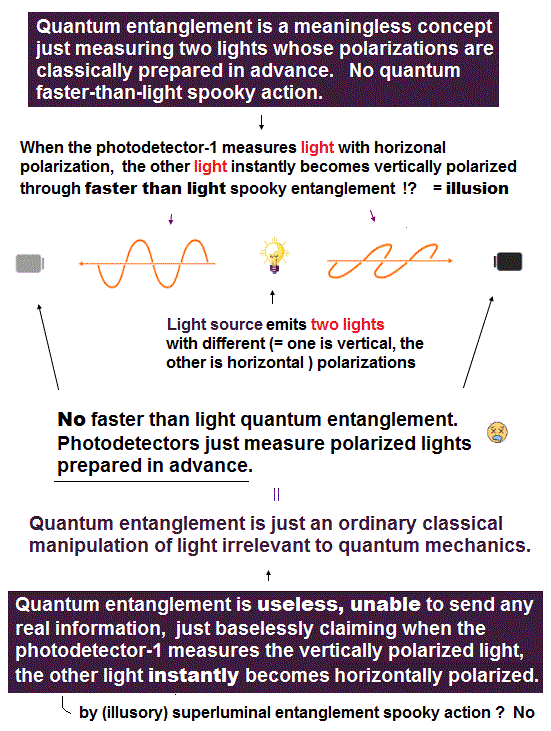
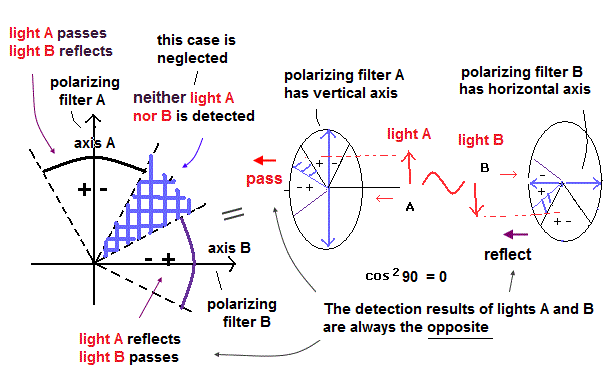
Quantum entanglement just preparing and measuring two classical polarized lights is irrelevant to faster than light spooky action.
(Fig.2) Entanglement means just preparing two lights with the same polarization in the case below, No quantum spooky action.
Entanglement = just prepare some classical light pair.
Just preparing and measuring two (classical) lights with the same polarization. ← quantum entanglement is a meaningless concept.
The quantum entanglement is a meaningless concept irrelevant to the faster-than-light spooky action, which is useless for any technologies and unable to send any real information.
In Fig.2, they artificially choose the light source (= called BBO crystal, this-p.5 this-p.2-left ) emitting two lights with same polarizations (= both lights have vertical-vertical VV or horizontal-horizontal HH polarizations ) in the opposite directions toward photodetectors-1 and 2.
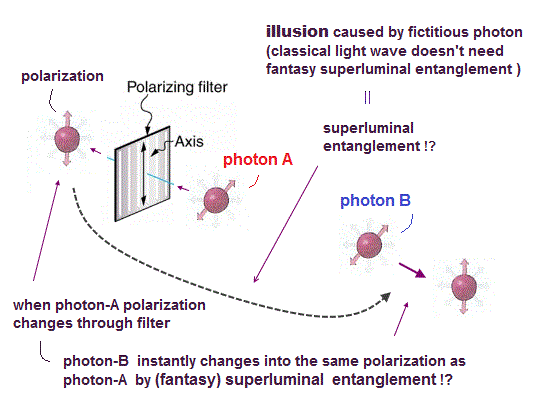
Measurement of one light instantly affects the other light's polarization ? ← entanglement is unreal.
After preparing a pair of classical lights with the same polarizations, when the photodetector-1 measures a vertically-polarized light, it instantly (= by faster-than-light spooky entanglement action ? No ) determines that the other light sent to the opposite photodetector-2 also has the vertical polarization ( this-p.7-2nd-paragraph ).
This-4th-paragraph says -- No faster than light
"if an experimenter measures one photon and it collapses into (= turns out to be ) horizontal polarization, then the other photon will instantly (= faster-than-light entanglement ? No ) do the same, no matter the distance."
↑ This is quite a natural thing irrelevant to quantum mechanics nor faster-than-light entanglement spooky action ( this-2nd-last-paragraph ).
Entanglement is just measurement, No spooky action.
Quantum mechanics unrealistically insists the measurement of one light instantly affects the other light's polarization by (illusory) faster than light entanglement spooky action.
Today's unrealistic quantum mechanics insists when the photodetector-A measures the vertically-polarized light, some spooky faster-than-light action makes the other distant light have the same vertical polarization instantly ( this-p.5-lower ). ← Nonsense.
This-5th~7th-paragraphs say -- Entanglement = just measurement
"The light source always produces pairs of photons with the same polarization. Alice and Bob do not know which polarization the pair has until they measure their photons. Let's say Alice measures vertical; Bob will measure vertical too. If Alice measures horizontal, so will Bob."
"nothing can travel faster than the speed of light, Alice apparently influenced Bob's photon instantaneously without interacting with it... If not instantaneously, the influence is at least superluminal, faster than the speed of light." ← self-contradiction, spooky entanglement is faster or not-faster than light ?
Each light is in unreal parallel universes ?
Unrealistic quantum mechanics claims there are (illusory) parallel universes or superposition containing photons with different polarizations until the measurement.
In addition to this unrealistic entanglement, they baselessly claim these two lights or photons are in the (unseen) superposition (= a dead-and-alive cat ) state containing two (illusory) parallel worlds ( this-3~4th-paragraphs ) of both lights having vertical polarization in one parallel universe and both lights having horizontal polarization in the other parallel universe until the measurement ( this-p.2-left-2nd-paragraph, this-2. ).
This-3rd-paragraph says
"the photon pairs actually will be in both states—horizontal and vertical polarization—at the same time. Until someone measures one, at which time both photons must chose one specific, and identical, state"
Faster-than-light entanglement is contradictory.
Faster-than-light spooky entanglement action disproves Einstein relativity, hence quantum mechanics is wrong, too.
↑ If this (illusory) faster than light spooky entanglement action (= EPR paradox ) was true ( this-2~4th-paragraphs ), Einstein relativity prohibiting any faster-than-light objects is wrong, which also disproves quantum mechanics heavily relying on Einstein relativity in (unphysical) relativistic quantum field theory and spin-orbit interaction.
This-2nd-last paragraph says Entangle = Not superluminal
"Importantly, there is also no conflict with special relativity, which forbids faster-than-light communication. The fact that measurements over vast distances are correlated does not imply that information is transmitted between the particles. Two parties far apart performing measurements on entangled particles cannot use the phenomenon to pass along information faster than the speed of light."
↑ We cannot send any information nor communicate by the quantum entanglement, which is a useless meaningless concept
Quantum entanglement or spooky action is illusion.
No superluminal action. Quantum entanglement is illusion, Not affecting other light's polarization.
(Fig.2') When one light is measured to have horizontal-polarization (= H ), it instantly (= by faster-than-light entanglement ? No ) determines the other light as vertically-polarized light (= V ).
Entanglement is just measuring prepared lights.
Just preparing and measuring two lights with the perpendicular polarizations has nothing to do with superluminal entanglement spooky action between these lights.
In Fig.2', they artificially choose the light source (= called BBO crystal type II ) emitting two lights with the different polarizations (= one light has vertical, the other light has horizontal polarizations ).
↑ So when one detector measures the vertically polarized light, it determines that the other light has horizontal polarization, instantly (= by faster-than-light spooky entanglement ? No ).
No entanglement, No quantum parallel universes.
Quantum mechanics baselessly insists that these two lights are in the (illusory) superposition containing two parallel universes where each light has vertical and horizontal polarizations simultaneously until the measurement (= so quantum superposition = a dead-and-alive cat state or parallel universes are unobservable ).
↑ They claim the moment one light is measured to have the vertical polarization, a quantum spooky faster-than-light entanglement action makes the other light have the horizontal polarization ( this-1~4th-paragraphs, this-3rd-paragraph ). ← nonsense.
This-3rd-paragraph says -- Entanglement illusion
"two entangled photons are polarized in perpendicular directions,..
Measure photon A to be vertically polarized, and photon B instantaneously (= by faster-than-light entanglement action ? No. ) becomes horizontally polarized "
As shown here, quantum entanglement (= just measuring artificially-prepared polarized lights ) is useless, unable to send any real information.
Quantum entanglement, teleportation are useless.
Entanglement or teleportation is just "measurement" of two classical lights with some artificially-prepared polarizations, which sends No real information, No practical application.
(Fig.3) Prepare two classical ( entangled ? ) light pairs → measurement (= BSM ) of two lights' polarizations → two distant lights' polarizations are entangled (= when one light is horizontally-polarized, the other distant light is also horizontally-polarized ) ? ← entanglement is a meaningless concept.
Just measuring classical lights, No entanglement
Quantum entanglement or teleportation is just the measurement of two classical polarized lights, irrelevant to faster-than-light spooky action.
In Fig.3, each light source A (and B) emits a pair of classical lights (= one light is horizontally-polarized, the other light is vertically-polarized ).
↑ Quantum mechanics baselessly argues this pair of two classical polarized lights are entangled via (illusory) faster-than-light spooky action. ← nonsense.
When the polarizations of two lights ② (= from source-1 ) and ③ (= from source-2 ) are measured to have the same vertical polarizations at the center photodetectors (= called Bell-state measurement or BSM, this-p.2 ), this measurement instantly determines (= by superluminal spooky entanglement ? No ) that two other lights ① and ④ have the same horizontal polarizations.
Quantum entanglement or teleportation are useless, cannot send any information without classical communication.
↑ This meaningless quantum entanglement or teleportation which is just the measurement of two classical lights, is unable to send any information faster than light (= ordinary classical communication is necessary to send real information slower than light ).
This-2nd-last-paragraph says -- Entanglement = No information
"This (= teleportation or entanglement ) does Not allow for faster than light communication, as Bob cannot extract this information without the result that Alice sends him, which is classical and can only be sent as fast as the speed of light."
Quantum swapping with two pairs of entangled lights is just classical manipulation irrelevant to quantum spooky action.
Fig.3 is called quantum swapping, which is said to be used for quantum repeater, which is impractical forever due to easily-lost fragile quantum information (= photons or weak light ).
Each atomic (or an ion's ) two energy levels are used as a (illusory) quantum computer's bit or a qubit's 0 or 1 state.
Quantum computers are useless, Not using entanglement nor superposition.
(Fig.4) Each atomic (or an ion's ) ground-state (= 0 ) and excited state (= 1) are often used as a (useless) quantum computer's bit or a qubit.
Each atomic two energy levels are used as a quantum computer's bit's (= a qubit's ) 0 or 1 value.
Each atomic (or an ion's ) ground-state (= 0 ) and the excited state (= 1 ) are often used as a (overhyped useless) quantum computer's bit (= qubit ) 0 or 1 states.
These qubit states (= an atomic energy states ) are controlled by by laser light.
Quantum computers are useless, irrelevant to quantum entanglement or superposition.
Today's error-prone quantum computers with only less than 100 qubits (= one qubit can take only 0 or 1 value ) are unable to calculate anything, still Not (quantum) computers.
They baselessly insist each atom (or an ion) can be in two different energy levels 0 and 1 at the same time by utilizing quantum superposition (= a dead and alive cat ) states or parallel universes (= unobservable, so No evidence, this-p.5 ).
↑ This superposition is just a classical intermediate state between two energy levels (= giving 0 or 1 bit state with the same probability, when measured ) irrelevant to quantum mechanics.
Quantum computers irrelevant to entanglement.
Quantum computer qubits do Not use (illusory) quantum superposition (= parallel universes ) nor faster-than-light entanglement.
(Fig.5) Whether two qubits are 00 or 11 states are uncertain = two qubits are in (illusory) superposition states of 00 and 11 → when one qubit is 0, the other qubit is 0 = superluminal quantum entanglement ? No.
Quantum entanglement is unnecessary.
Faster-than-light quantum entanglement is irrelevant to quantum computers.
Overhyped quantum computers are said to use ( illusory ) quantum entanglement and parallel-universe superposition for (illusory) faster calculations ( this-4~7th-paragraphs ), which is totally wrong.
This-p.1-left-last~right says -- No entanglement
"Typically entanglement is considered as crucial for
quantum computing. However, entanglement is just a
mathematical structure and its physical meaning is still the subject of intensive foundational debates" ← No evidence of (superluminal) entanglement related to quantum computers.
Just preparing two qubits with the same bit states has nothing to do with entanglement.
In Fig.5, there are two qubits (= one qubit, which is made of an atom or a superconducting circuit, can take only 0 or 1, which is still Not a computer ).
They unreasonably claim the qubit-1 can be in (illusory) quantum superposition where each qubit can be in 0 and 1 states simultaneously using two parallel universes (= which just means each qubit outputs 0 or 1 with 50%-50% chance, so irrelevant to quantum superposition or parallel universes ) illuminated by some laser light (= called Hadamard H gate ).
When one qubit is 0 (or 1 ), the other qubit is prepared to be 0 (or 1 ), which has nothing to do with entanglement.
When CNOT gate is applied to the qubit-1 in the (illusory) superposition of 0 and 1 states, it is said to create the new (illusory) superposition and entangled states of two qubits-1 and 2 being 00 and 11 states simultaneously called Bell state ( this-Figure 4 ) like a dead and alive cat.
No entanglement nor superposition in qubits.
Preparing and measuring two qubits being in the same bit states of 00 or 11 has nothing to do with superluminal spooky entanglement nor superposition.
↑ It means when the qubit-1 is measured to be in 0 state, the other qubit-2 instantly becomes 0 (= by the faster-than-light quantum spooky entanglement action ? No ).
↑ When qubit-1 is measured to be 1 bit state, qubit-2 is determined as "1" bit state, too (← this meaningless concept just preparing two qubits in the same bit state is quantum entanglement, this-coherence in qubits ).
This-9~10th-paragraphs say
Two of the Bell states give an equal superposition such that both of the qubits end up in the same state when measured, with a 50% chance that both will be in either the 0 or 1 state."
"If we measure the first qubit in the state 0, we know that the second qubit must be in 0 when we measure it. Even if these two qubits were on opposite ends of the globe and... While this is often taken to mean that entanglement violates locality,... No superluminal transmission of information is possible using entanglement"
↑ We cannot see the quantum superposition nor parallel universes (= so No evidence of quantum superposition nor quantum computer's speed-up ).
We can observe only one state of two qubits being 00 states or 11 states in the upper case ( this-p.2 ), which has nothing to do with quantum entanglement nor parallel universes.
Bell inequality is irrelevant to entanglement.
Loophole-free Bell inequality violation denying local realism is wrong, Not proving the faster-than-light quantum entanglement.
(Fig.6) Just preparing two atomic states (= one atom is +1 energy level, the other atom is -1 energy level ) does Not mean the faster-than-light spooky quantum entanglement.
No experimental evidence of the faster-than-light spooky entanglement.
Two lights emitted from two distant atoms are measured at the photodetectors in the middle. ← No entanglement.
The alleged loophole-free Bell inequality violation experiments did Not deny the realism nor prove the faster-than-light quantum entanglement spooky action.
In this experiment, they just prepared two distant atoms in nitrogen-vacancy (= NV ) center in diamond (= with No electron spin ) where one atom is in +1 energy level, and the other atom is in -1 energy level. ← That's all, useless, No faster-than-light quantum entanglement.
When the photodetectors in the center C measures a pair of the early-arriving light and the late-arriving light emitted from these two distant atoms, it means one atom (= A or B ) in NV-center in diamond is in +1 energy level (= emitting the early-arriving light ) and the other atom is in -1 energy level (= emitting the late-arriving light ).
↑ After they artificially preapared these two atomic energy levels in diamonds, when one atom was measured to be in the energy level of +1, it instantly (= by faster-than-light spooky entanglement ? No ) determined the other atom being in the energy level of -1.
Just preparing one atom being ms = 0 energy level and the other atom being ms = ±1 energy level is useless, irrelevant to quantum entanglement.
↑ This alleged loophole free Bell inequality violation paper ↓
p.3-right says "causing the NV centre to emit many photons when it is in the bright ms = 0 spin state, while it remains dark when it is in either of the ms = ±1 states" ← They just measured and distinguished lights (= or photons ) emitted from two different energy levels (= bright ms = 0 state and the dark ms = ±1) instead of seeing the (fictional) electron spin itself.
"First we entangle each spin with the emission time of a single photon ( time bin encoding). The two photons are then sent to location C, where they are overlapped on a beam-splitter and subsequently detected. If the photons are indistinguishable,..."
"the observation of one early and one late photon (= two photons or lights emitted from two different atomic energy levels arrived at the center photodetectors at different times, early and late ) in different output ports projects the spins at A and B into the maximally entangled state ψ= (|↑↓ − |↓↑) / where ms = 0 ≡ ↑, ms = −1 ≡ ↓"
↑ By measuring lights emitted from two distant atoms in NV center in diamond, they judged that one atom being ms = 0 energy level (= emitting the early-arriving classical light ) and the other atom being ms = ±1 (= emitting the late-arriving light ).
↑ They just treated this preparation of two atoms in diamonds being in different energy states as "(illusory) entanglement", which is useless, irrelevant to superluminal spooky action, and No practical application.
Extremely high error rates due to massive photon loss invalidate this loophole free entanglement results.
This-p.5-right-last-paragraph says -- massive photon loss
"We find a success probability per entanglement generation attempt of about 6.4 × 10−9" ← only one photon or light in 1000000000 attempts was detected at the center photodetectors due to massive photon loss, which extremely low success rate (= high error rates ) cannot prove anything such as loophole free entanglement.
This (= alleged loophole-free entanglement paper)-p.7-left-2nd-paragraph says "Strictly speaking, No Bell experiment can exclude the infinite number of conceivable local realist theories" ← there are still loopholes, which means they could Not prove the faster-than-light entanglement after all.
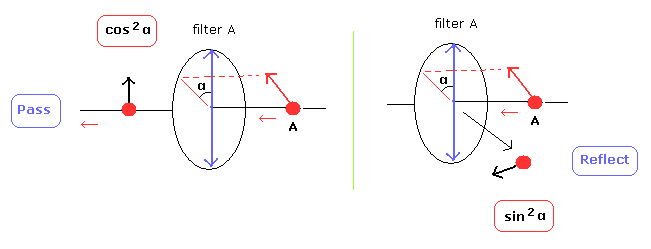
A photon is illusion, just classical light wave.
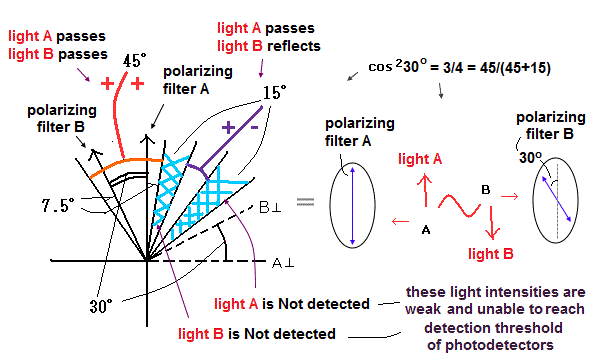
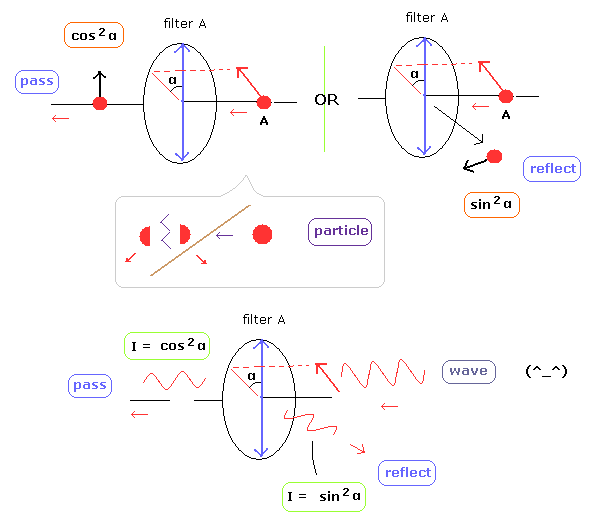
The probability of a fictional photon passing or reflecting from the polarizer obeys classical light's Malus law ?
(Fig.7) They baselessly claim the probability of a (fictional) photon passing (or reflected from ) the polarizer is cos2θ (or sin2θ ) where θ is the angle difference between the photon's (or light's ) polarization and the polarizer's axis.
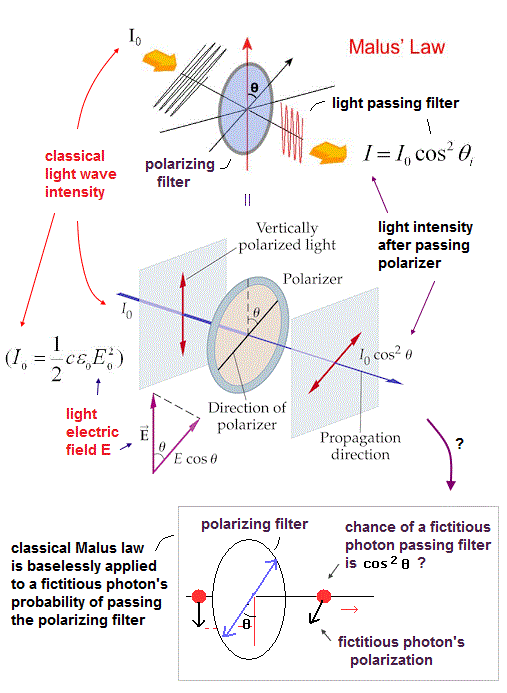
A photon is just classical light obeying Malus law.
Probability of a (fictional) photon passing the polarizer is cos2θ (= θ is the angle between the photon's polarization and the polarizer's axis ) like classical light's Malus law ?
It is known that the (classical) light's intensity (= I ) passing the polarizer becomes I cos2θ (= θ is the angle difference between the polarizer's axis and the light polarization ), and the light's intensity reflected from the polarizer is I sin2θ
↑ This classical Malus law is based on classical light which can be split by the polarizing fiters.
But the quantum entanglement experiments try to use this classical Malus law based on the splittable classical light for the unsplittable fictional photon case.
Probability of a (fictional) photon reflected from the polarizer is sin2θ ?
They baselessly insist the probability of the (fictional) photon ball passing the polarizer is cos2θ (= θ is the angle difference between the photon's polarization and the polarizer's axis, this-p.3 ), and the probability of the photon ball reflected from the polarizer is sin2θ ( this-p.2-last, this-p.1-3rd-paragraph, this-p.2 ).
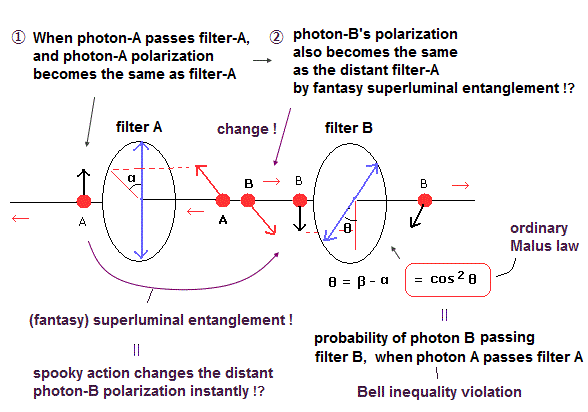
Quantum entanglement or spooky action is unreal.
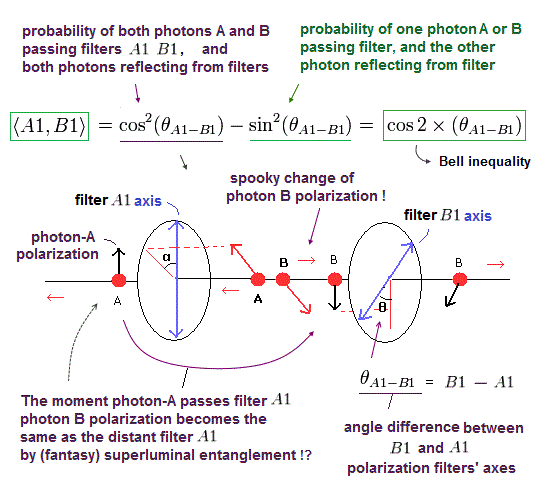
Quantum entanglement unrealistically claims the measurement of one light's polarization instantly affects the distant light polarization via the (illusory) faster than light spooky action, which violates Bell inequality.
(Fig.8) The probability of both distant lights (= photons ) passing their polarizers is cos2θ (= θ is the angle difference between two polarizers' axes ) due to faster than light spooky entanglement action ? ← No.
Faster-than-light quantum entanglement is unreal.
Quantum entanglement is based on fictional superluminal action changing the distant photon's polarization instantly.
As I said, the quantum entanglement is a meaningless useless concept just preparing a pair of things such as two boxes containing blue or red balls, and the vertically-horizontally-polarized lights...
In case of two polarized lights, they use some tricks treating classical light as a fictional photon to make it look like the faster-than-light spooky entanglement action obeying (classical) Malus law.
They unrealistically claim when two (classical) lights (= photons A and B ? ) with the same polarizations traveling in the opposite directions hit their polarizers, and the photon-A passes the polarizer-A, it instantly (= faster-than-light entanglement ? No. ) changes the distant photon-B's polarization into the same as the distant polarizer-A's axis (= polarization of the photon-A passing the polarizer-A ).
Superluminal action changes distant light polarization ?
Probability of both photons passing the polarizers is cos2θ (= θ is angle difference between two polarizers ) due to the (illusory) faster-than-light entanglement spooky action ? ← No
↑ It means the probability of both these distant photons-A and B passing their polarizers is cos2θ (= correctly 1/2cos2θ θ is the angle difference between axes of the polarizers-A and B ) according to the classical Malus law ( this-p.2-(1), this-p.4 ).
↑ The probability of one photon passing the polarizer and the other photon reflected from the polarizer is sin2θ.
This-p.3-1st-paragraph says
"If the first photon goes through a
polarizer at angle α, the other photon immediately becomes polarized in the
same direction (= by superluminal entanglement action ? No ). The second photon's probability of going through a polarizer at angle β is now given by
Malus's law, cos2 (α - β) ( this-p.5 )"
When the light or photon-A is reflected from the polarizer-A, it instantly (= faster than light entanglement ? No. ) makes the distant photon-B's polarization perpendicular to the distant polarizer-A's axis (= same as the polarization angle of the photon-A reflected from the polarizer-A ).
So the probability of both photons-A and B reflected from the polarizers is also 1/2cos2θ (= θ is the angle difference between two polarizers' axes ) according to the classical Malus law.
↑ The probability of both photons passing polarizers and both photons reflected from polarizers is cos2θ.
The probability of one photon passing and the other photon reflected from polarizers is sin2θ.
↑ These cases can violate Bell inequality (= Not due to superluminal entanglement but due to classical light ).
Bell inequality violation or entanglement can be explained by classical light wave.
This case of entangled polarized lights seemingly violating Bell inequality via the (illusory) faster-than-light action can be explained by the divisible classical light + photodetectors without the unrealistic faster-than-light entanglement action.
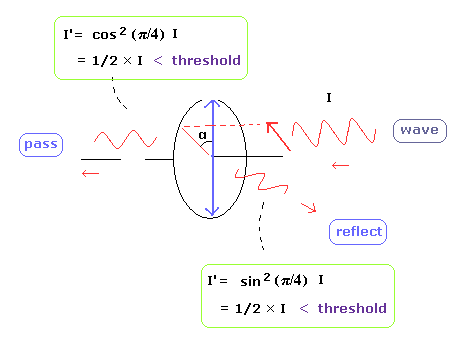
A photon is just a splittable classical light wave
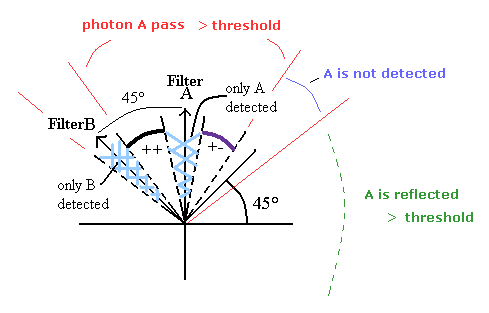
Classical light wave whose intensity surpasses some threshold is detected as a (illusory) photon at the photodetector.
(Fig.9) A (fictional) photon is just a splittable classical light whose light intensity surpassing the detection threshold of a photodetector, even after the light splits at a polarizer.
A photon is just classical light whose intensity surpassing the detection threshold of the photodetector.
When light intensity (= pass = Icos2θ, reflect = Isin2θ ) after splitting at a polarizer surpasses some threshold, this light is detected as a (fictional) photon at a photodetector.
The unrealistic faster-than-light quantum entanglement action is caused by wrongly treating a splittable classical light wave as a (fictional) unsplittable quantum photon ball.
According to Malus law. the classical light (= whose light intensity I ) splits into the pass side (= light intensity is I cos2θ where θ is angle difference between the light's polarization and the polarizer's axis ) and the reflect side (= light intensity is I sin2θ ) of the polarizer.
↑ When the θ is close to zero, the light intensity passing the polarizer (= I cos2θ ) is strong enough to be detected as a (fictional) photon by the photodetector.
↑ On the other hand, when the θ is close to 0, the light intensity reflected from the polarizer (= I sin2θ ) is too weak to reach the detection threshold of the photodetector (= Not detected as a photon ).
When classical light is almost equally split (= weakened ) by the polarizer, these equally-split light intensities are too weak to detect as a photon by photodetectors.
When the θ (= angle difference between light polarization and the polarizer's axis ) is close to 45o, the light is split (= weakened ) almost equally into the pass and reflect sides of the photodetector, so these equally-split light intensities cannot reach the photodetector's detection threshold, and No photons are detected either in the pass or reflect sides.
This is the trick of causing the illusory faster than light entangled polarized photons or lights.
Light weakened at a polarizer is Not detected as a photon.
When angle difference between the light's polarization and the polarizer is close to 45o, light intensity is equally split and too weak to detect as a (fictional) photon.
(Fig.10) When classical light's intensity is divided almost equally by the polarizer into the pass and reflect sides, No photons are detected.
Weak light intensity is not detected as a photon.
When classical light with 45o polarization is split (= weakened ) almost equally by the polarizer (= 0o axis ), this split light intensity is too weak to detect as a photon.
When the angle difference between the classical light polarization and the polarizer's axis is close to θ = 45o, the light is split almost equally into the "pass" and "reflect sides of the polarizer" due to classical Malus law ( I cos2 45o = I/2 ).
As a result, both light intensities passing and reflected from the polarizer become too weak to detect by the photodetector as a (fictional) photon.
Classical light, which is split equally by the polarizer and too weak to detect as a photon, is the trick of causing (illusory) superluminal quantum entanglement action.
This falsely treating the classical divisible light whose light intensity reaches the photodetector's detection threshold as a (fictional) photon is the trick of causing the illusory faster than light entanglement spooky action.
This-p.7 says -- Entanglement = classical
"Discriminator threshold (by which the low amplitude outputs pulses are discarded = Not detected as a photon )
We believe that the influence of these thresholds may been overlooked in the discussion on non-classical effects,
and in particular in EPR and Bell inequality discussion....
tunable, detection threshold in
photon counting, which can lead to a sample selection bias in the detected events, leading to an apparent violation of
Bell inequalities in a fully local realistic framework."
↑ The apparent violation of Bell inequality is caused by classical light whose intensity reaching the detection threshold of the photodetector treated as a (fictional) photon, Not by the faster-than-light quantum entanglement.
Classical light can explain Bell inequality violation.
When two polarizers-A and B have the same axis, the probability of two (illusory) photons-A and B passing (or reflected from ) the polarizers is 1 (= cos20o ), which violates Bell inequality, which can be explained by classical light. ← No evidence of entanglement
(Fig.11) When the axis angle difference between two polarizers-A and B is 0o, probability of both photons-A and B passing (or reflected from ) polarizers is cos2 0o = 1 (= 100% ), violating Bell inequality.
Entanglement = Bell inequaility violation is wrong.
When two polarizers have the same axis angle (= θ = 0o ), probability of two lights with the same polarization passing (or reflected ) from the polarizers is 1 = cos2 0o to violate Bell inequality even without quantum entanglement.
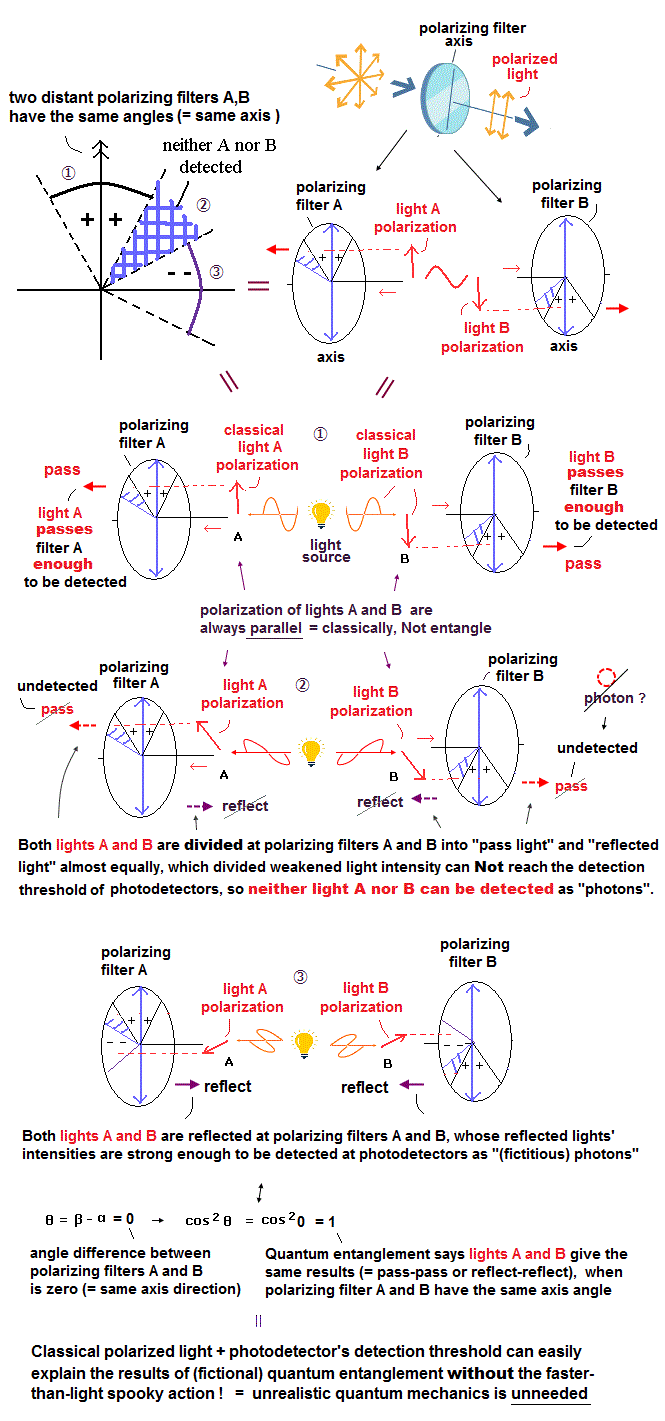
In fact, classical light wave without the faster-than-light spooky action can naturally explain the quantum entanglement results.
In case when the axis angle difference between two polarizers-A and B is 0o (= A and B have the same axis 0o ), the probability of both two photons-A and B passing the polarizers has to be "1 (= cos20o )" to violate Bell inequality.
Two lights-A and B with same polarizations (= two lights have the same parallel polarizations in random directions, this-p.4-(c) ) are emitted from the center light source in the opposite directions ( Alain Aspect used calcium laser as the source of entangled lights whose polarizations are parallel in random directions, this-p.2 ).
Light whose intensity is strong enough to surpass some threshold is detected as a (fictional) photon at a photodetector.
In Fig.11-① case, both the lights-A and B with the same 0o polarization hit the ( + + ) part (= close to polarizer's axis ) of their polarizers, hence, both these light intensities passing the polarizers (= almost I cos2 0o ) are strong enough to be detected as (fictional) photons by the photodetectors.
In Fig.11-③ case, both the lights-A and B with the same 90o polarization hit the ( - - ) part (= almost perpendicular to polarizers' axes ) of their polarizers, hence, both these light intensities reflected from the polarizers (= almost I sin2 90o = I = = I cos20o ) are strong enough to be detected as (fictional) photons by the photodetectors.
Light weakened by a polarizer is not detected as a photon.
When classical light is split almost equally by the polarizer, its split light intensity is too weak to detect as a (fictional) photon, which case is ignored, and violates Bell inequality even without entanglement.
In Fig.11-② case when both lights-A and B have the polarization close to 45o, both these lights are split almost equally into "pass" and "reflect" sides of the polarizers, which equally-split light intensities are too weak to be detected by the photodetectors (= No photons detected, so this case is Not used as the result ).
As a result, the probability of both (fictional) photons passing (or reflected from ) the polarizers (and detected as photons ) becomes 1 (= cos20o ), which can violate Bell inequality even without faster-than-light quantum entanglement.
So No evidence of quantum entanglement.
Classical light can violate Bell inequality without entanglement.
In case of the axes of two polarizers perpendicular to each other, when one photon passes, the other photon always reflects from the polarizer, which violates Bell inequality even without quantum entanglement.
(Fig.12) In case of the axis angle difference between two polarizers-A and B being 90o, when one light (= or photon ) passes the polarizer, the other light is always reflected from the polarizer, which violation of Bell inequality can be explained by classical light without spooky superluminal quantum entanglement.
When two polarizers A and B have perpendicular axes.
When the angle difference between two polarizers is 90o, the probability of both photons (= classical lights ) with the same polarization passing (or reflected from ) polarizers is 0 (= cos2 90o )
Classical light wave without the faster-than-light spooky action can naturally explain the quantum entanglement results violating Bell inequality like this.
In case when the axis angle difference between two polarizers-A and B is 90o (= polarizers-A and B have the perpendicular axes ), the probability of both two photons-A and B passing the polarizers has to be "0 (= cos2 90o )" to violate Bell inequality.
↑ It means when one photon is detected by the "pass" photodetector, the other photon is always detected by the "reflect" photodetector.
A fictional photon is just classical light wave whose light intensity surpasses the photodetector's detection threshold.
When two polarizers-A and B have perpendicular axes, one of two lights with the same polarization passes the polarizer, and the other light is reflected from the polarizer.
Both lights-A and B emitted from the source are supposed to have the same parallel polarizations in random directions = when one light is horizontally (or vertically or 45o .. ) polarized, the other light is also horizontally (or vertically or 45o .. ) polarized.
In Fig.12-① case, both the lights-A and B with the same 0o polarization hit the ( + - ) part (= close to polarizer-A' s axis, and perpendicular to polarizer-B's axis ) of their polarizers, hence, the light-A intensity passing the polarizer-A (= almost I cos2 0o = I ) and the light-B's intensity reflected from the polarizer-B (= almost I sin2 90o = I ) are strong enough to be detected as a (fictional) photon by the photodetectors.
In Fig.12-③ case, both the lights-A and B with the same 90o polarization hit the ( - + ) part of their polarizers, hence, the light-A's intensity reflected from the polarizer-A ( = almost I sin2 90o = I ) and the light intensity-B passing the polarizer-B (= almost I cos2 0o = I ) are strong enough to be detected as (fictional) photons by the photodetectors.
Too weak light not detected as a photon causes illusory entanglement.
When light is almost equally split by polarizers, its split light intensity is too weak to detect as a (fictional) photon, which is trick of causing illusory superluminal entanglement action or Bell inequality violation.
In Fig.12-② case when both lights-A and B have the polarization close to 45o, both these lights are split almost equally into "pass" and "reflect" sides of the polarizers, which equally-split light intensities are too weak to be detected by the photodetectors (= No photons detected, so this case is Not used as the experimental results of entanglement ).
As a result, the probability of both lights passing (or reflected from ) the polarizers becomes 0 (= cos2 90o ), which can violate Bell inequality even without faster-than-light spooky quantum entanglement action.
No evidence of entanglement. Classical light can violate Bell inequality.
When axis angle difference between two polarizers is 45o, the probability of both photons (= classical lights ) passing polarizers is 0.5, which violates Bell inequality without spooky entanglement action.
(Fig.13) Classical light without faster than light spooky action can explain quantum entanglement experiments.
Strong classical light after passing polarizers is detected as a photon.
When classical light's polarization points to almost 45o relative to polarizer's axis, this light intensity is split almost equally by the polarizer, and becomes too weak to detect as a photon (= this case is Not used ).
Also when the axis angle difference between two polarizers-A and B is 45o, classical light without faster-than-light spooky action can explain the quantum entanglement experiments violating Bell inequality.
Two lights-A and B have the same parallel (but random-directional ) polarizations.
In Fig.13-① case, both the lights-A and B with the same 0o polarization hit the blue shaded part. Only light-A's intensity passing the polarizer-A (= 0o axis ) is strong enough to detect as a photon by photodetector.
↑ The light-B is split almost equally by the photodetector (= axis 45o ), which split weakened light-B intensity is too weak to detect by the photodetector.
↑ This case of only one photon detected is discarded, Not used as the legitimate result of quantum entanglement experiments due to loss of photons.
In Fig.13-② case, both the lights-A and B with the same 30o polarization hit ( + + ) part of the polarizers. Light-A whose polarization (= 30o ) almost parallel to the polarizer-A's axis (= 0o ) can pass the polarizer-A, and its light intensity is strong enough to detect as a (fictional) photon by the photodetector.
↑ Light-B whose polarization (= 30o ) is also almost parallel to the polarizer-B's axis (= 45o ) can pass the polarizer-B, and its light intensity is strong enough to detect as a (fictional) photon by the photodetector.
Classical light can violate Bell inequality without entanglement.
Probability of both photons passing polarizers is cos2 45o = 1/2 when axis difference between two polarizers is 45o
In Fig.13-③ case, both the lights-A and B hit ( - + ) part of polarizers. Light-A whose polarization 60o is almost perpendicular to the polarizer-A's axis (= 0o ) is reflected from the polarizer-A and detected as a (fictional) photon by the photodetector.
And the light-B whose polarization (= 60o ) is almost parallel to the polarizer-B's axis (= 45o ) can pass the polarizer-B, which light intensity is also strong enough to detect as a (fictional) photon by the photodetector.
↑ As a result, the probability of one photon passing the polarizer and the other photon reflected from the polarizer is 0.5 (= cos2 45o ) which can violate Bell inequality without the (illusory) faster-than-light quantum entanglement.
Classical light can violate Bell inequality.
Quantum superluminal entanglement = Bell inequality violation is wrong. Classical light can explain it.
(Fig.14) Light-A hits polarizers-A1 (= axis 0o ) or A2 (= axis = 60o ), while light-B hits polarizers-B1 (= axis 30o ) or B2 (= axis 90o )
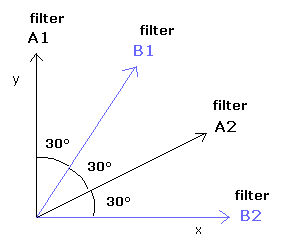
Bell inequality violation does Not need (unrealistic) quantum entanglement.
Here we explain the case of violating Bell inequality by using classical light wave without the (illusory faster-than-light ) quantum entanglement spooky action.
In Fig.14 using the lights-A and B with the same parallel (= but random ) polarization. Light-A hits polarizers-A1 (= axis 0o ) or polarizer-A2 (= axis = 60o ), while light-B hits polarizers-B1 (= axis 30o ) or B2 (= axis 90o ).
When the light is detected by the "pass (or reflect )" photodetector as a (fictional) photon, it is "+1 (or -1 )"
Classical light without entanglement can violate Bell inequality.
Textbooks are wrong. Classical light can violate Bell inequality even withoug superluminal quantum entanglement.
(Fig.15) Bell inequality violation (> 2 ) can Not deny realism nor prove (faster-than-light) quantum entanglement.
Bell inequality violation does Not prove the spooky quantum superluminal entanglement.
The standard claim that Bell inequality violation proved quantum entanglement is false.
According to the current ( wrong ) mainstream explanation, the faster-than-light spooky entanglement action was proved by experiments violating Bell inequality ( this-p.13, this-4th-paragraph ).
This-p.1-1st-paragraph says -- Entanglement violates Bell inequality ?
"systems that are prepared in a quantum- entangled state are predicted to
violate Bell’s inequality"
This-1st-paragraph says
"Experiments involve creating pairs of entangled photons and measuring their polarization along different axes. The observed correlations violate Bell’s inequalities ( this-p.7(or p.6)-2.3 )"
In fact, even classical light without (unrealistic) quantum entanglement can violate Bell inequality, so there is No exprimental evidence of quantum entanglement.
Classical light wave without quantum entanglement can violate Bell inequality > 2. ← No experimental evidence of quantum entanglement
Fig.15 shows Bell inequality (= CHSH = Clauser-Horne-Shimony-Holt ) where S is said to not exceed "2" when two lights (or two atoms ) satisfy (local) realism or no faster-than-light quantum entanglement, which is wrong.
↑ Even realistic classical light without (fantasy) superluminal quantum entanglement can violate Bell inequality, so No evidence of entanglement.
Classical light can violate Bell inequality.
Bell inequality violation based on classical polarized light without quantum entanglement.
The light-A hits the polarizer-A1, and light-B hits the polarizer-B1. When one light passes the polarizer (= +1 ), and the other light reflects from the polarizer (= -1 ), A1B1 become -1 (= +1 × -1 ).
When both these lights-A and B pass (= +1 × +1 = +1 ) or reflect from (= -1 × -1 = + 1 ) their polarizers, A1B1 become + 1
So the average A1B1 value means the average probability of both two lights passing and reflecting from the polarizers (= AB = + 1 ) minus the probability of one light passing and the other light reflected from the polarizer (= AB = -1 ).
As shown above, only when A1B1 (or A1B2, A2B1 .. ) are separable (= A1B1 → |A1| and |B1| ), or the results of A1 and B1 are independent of each other, Bell inequality S not exceeding 2 must be satisfied
S = A1(B1 - B2) + A2 (B1 + B2) = (B1-B2) + (B1+B2) = 2B1 ≤ 2, because A1, A2, B1, B2 ≤ 1 ( this-(9)-(11), this-p.10, this-p.2, this-p.10 ) ← No violation of Bell inequality.
Classical light can violate Bell inequality > 2 even without entanglement.
So when we artificially prepare two lights with the same (or perpendicular ) polarizations, A1B1 (or A1B2.. ) are inseparable (= probability of both lights passing or reflecting from each other is affected by the other light's polarizer's axis angle ), which can violate this Bell inequality even without quantum (superluminal) entanglement spooky action.
According to the (illusory faster-than-light) quantum entanglement theory, the average of A1B1 is equal to the cos2 θA1-B1 (= probability of both lights-A and B passing or reflected from polarizers ) - sin2 θA1-B1 (= probability of one light passing and the other light reflected from polarizers ) = cos 2θA1-B1 ( this-p.2-3, this-p.2-right, this-p.9-10 ).
↑ θA1-B1 is the angle difference between two polarizers A1 and B1.
Using this case of polarizers, we can show violation of Bell inequality ( S = 2.5 > 2 ) by realistic classical light wave without the (faster-than-light) quantum entanglement.
Bell inequality violation does Not need entanglement.
Bell inequality violation, which can be explained by artificially preparing two classical lights or atoms, does Not need (unreal) quantum superluminal entanglement.
As a result, there is No evidence of the faster-than-light quantum entanglement spooky action that can be naturally explained by realistic classical light wave (+ photodetector's threshold ).
Bell inequality is naturally violated even without the (faster-than-light) quantum entanglement, when two lights with correlated (= artificially-adjusted ) polarization (or two particles with the correlated states ) are artificially prepared.
↑ When two lights with the same polarization are prepared, one polarizer's axis angle affects (= is correlated with ) the probability of both lights passing or reflected from the polarizers, which does Not correspond to Bell inequality based on the assumption that each light measurement must be independent of each other.
Quantum entanglement is illusion in all things.
Bell inequality violation other than light is also caused by just artificially preparing two atoms with the same (or opposite ) energy levels, Not by quantum spooky (superluminal) entanglement.
In cases of two atomic entanglement without using light polarization, they just artificially prepared two atoms whose energy levels are the opposite ( or same ), and illuminate them by laser light with some phases.
↑ This Bell inequality violation in atomic (or ions' ) entanglement is caused just by artificial preparation of two atomic energy levels, Not by the (illusory superluminal ) quantum entanglement ( this-p.2-left prepared two Be+ ions having the same energy states of ↑↑ or ↓↓ with No faster than light spooky entanglement ).
Physicists often use the (unphysical) negative or imaginary amplitude (only) in papers, which means just some artificially-adjusted laser light or manipulation to artificially match the Bell inequality violation, which is irrelevant to the spooky faster-than-light entanglement ( this-p.6-11, this-p.1-Figure.1, p.2-(4). p.3-(6)(7) ).
↑ Just preparing two atoms being in the same energy levels (= ↑↑ ), and applying some laser to one atom to always give two atoms with the opposite states (= ↑↓ = A1B2 = -1 ) can naturally violates Bell inequality, when other laser manipulations are more likely to give two atoms with the same energy ( A1B1, A2B1, A2B2 > 0.4 ) levels (= A1B1 - A1B2 + A2B1 + A2B2 = 0.4 + 1 + 0.4 + 0.4 = 2.2 > 2 ) even without the quantum spooky superluminal entanglement.

Feel free to link to this site.