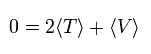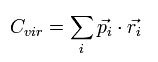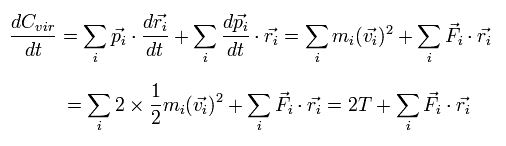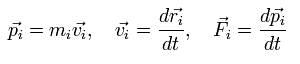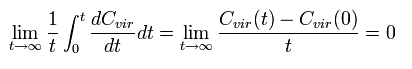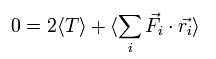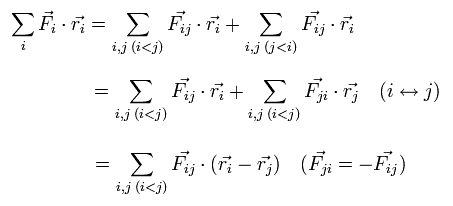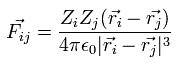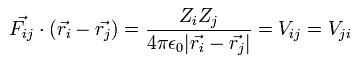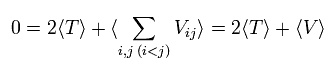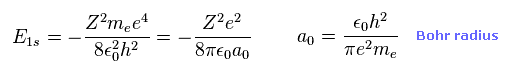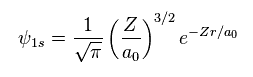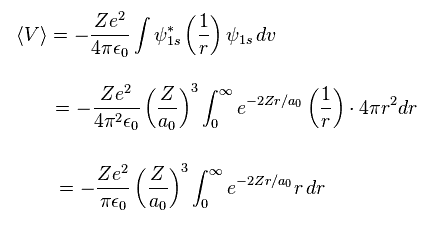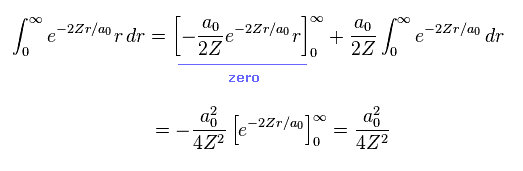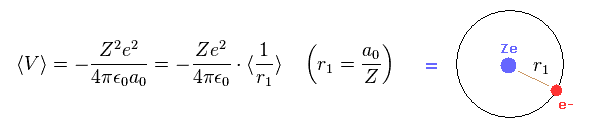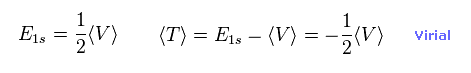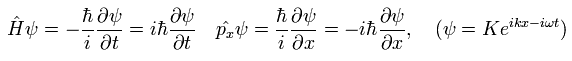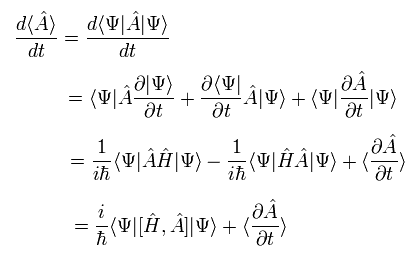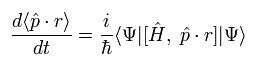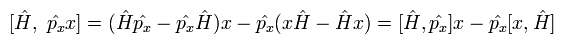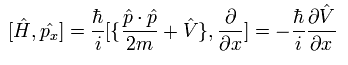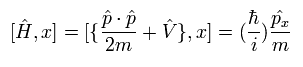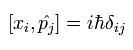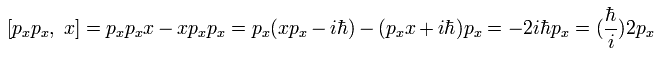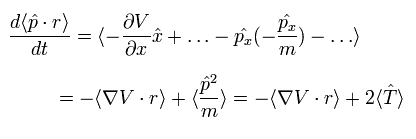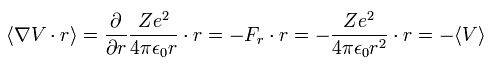Proof of Virial theorem in the multi-particle system.

Top page ( quantum mechanics is wrong ← 6/30/2024 )
Electron spin is an illusion ! ← 6/1/2024

• Proof of Virial theorem in many classical particles.
• Virial theorem in Schrodinger's hydrogen atom.
• Virial theorem in quantum mechanics.

Proof of Virial theorem in many classical particles.

The Virial theorem was suggested by Clausius in the nineteenth century.
This theorem is satisfied both in the classical mechanics and the quantum mechanics.
In the system of the multi-particles such as many nuclei and electrons, the average total kinetic energy (T) and the average total potential energy (V) satisfy the following relation, when the Coulomb forces are acting on each other.
(Eq.1)

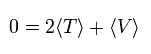
[ Virial theorem in many classical particles.]

First we prove this relation in the classical mechanical way.
If it can be proved, we can use this theorem in the various Bohr model molecules.
We define the scalar value (C_vir), as follows.
(Eq.2)

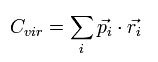
Eq.2 means the sum of the each particle's dot product of the momentum (p_i) and the position (r_i).
( p_i means the momentum vector of the i th particle. )
We can suppose the "arbitrary" particle's number (i = 1,2,3..) in Eq.2.
(We can use the Virial theorem in the system of many nuclei and electrons such as molecules.)

The time derivative of the Eq.2 is
(Eq.3)

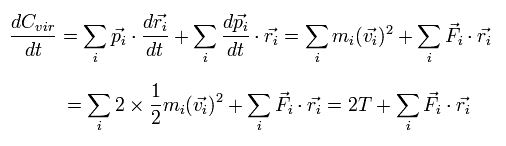
where we use the next relations,
(Eq.4)

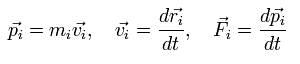
where m_i, v_i, and F_i are each particle's mass, velocity vector, and force vector, respectively.

For example, when the ith particle is a "static" heavy nucleus, the ith kinetic energy of Eq.3 becomes zero.
(Of course, in this case, the ith F and r don't need to be zero.)

Integrating both sides of Eq.3 from 0 to time t and divide it by t. Then take the limit as t → ∞
The left hand side of Eq.3 becomes
(Eq.5)

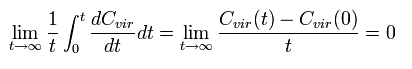
where the numerator is a "finite" value, and the denominator is a "infinite" value (t → ∞).
So the Eq.5 becomes zero !
( In the "bounded" motions, the value of C(t) becomes finite. It is quite natural.)

On the other hand, each term of the right hand side of Eq.3 becomes the time average values, as follows,
(Of course, the sum of them is zero like the left side.)
(Eq.6)

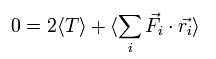
F_i means the total force exerted on the i th particle.
We can divide this F_i into the vectors of F_ij, which means the force of j th particle acting on i th particle.
So the dot product of the force (F) and position (r) vectors can be expressed as
(Eq.7)

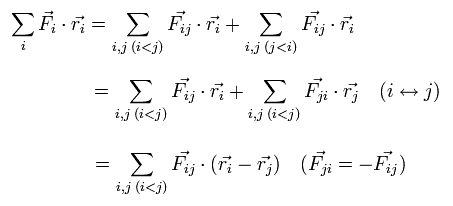
When the F_ij is the Coulomb force between ith and jth particles, F_ij can be expressed as
(Eq.8)

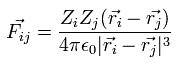
where Z_i means the charge of the ith particle.

Substituting Eq.8 into Eq.7,
(Eq.9)

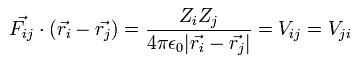
where V_ij means the Coulomb potential energy between the ith and jth particles.

Using Eq.9, Eq.7 and Eq.6, we can get the final Virial theorem as follows,
(Eq.10)

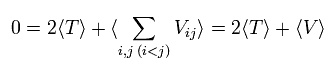
Virial theorem in Schrodinger's hydrogen atom

(Eq.11) Ground state energy of hydrogen-like atom.

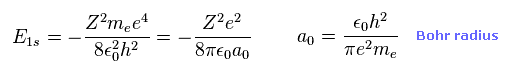
Here we prove Schrodinger's wavefunction of hydrogen atom satisfies Virial theorem ( E = 1/2 V ).
Eq.11 is the ground state energy ( n = 1 ) of hydrogen-like atom ( atomic number Z ).
Of course, this energy level is completely equal to Bohr model.
And a₀ is Bohr radius.

(Eq.12) Schrodinger's 1s wavefunction.

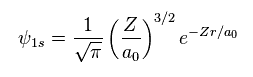
Schrodinger's 1s wavefunction is known to be Eq.12.
Using Eq.12, average potential energy V becomes
(Eq.13)

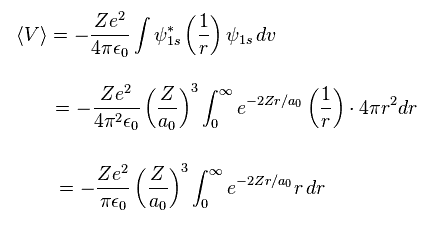
where
(Eq.14)

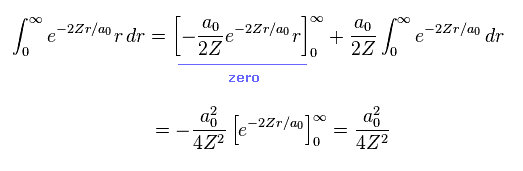
From Eq.13 and Eq.14, the potential energy V becomes
(Eq.15)

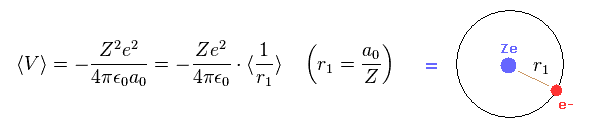
Eq.15 means the average probability density of 1s wavefunction (= Eq.12 ) is a₀/Z.
( Z is atomic number. In hydrognen, Z = 1. )
Of course, this result is the same as Bohr model hydrogen.

From Eq.11 and Eq.15, we can prove Schrodinger's hydrogen also satisfies Virial theorem,
(Eq.16)

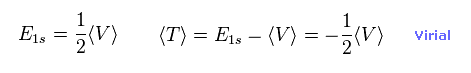
The result of Eq.16 is the main reason why quantum mechanical variational method gives similar results to Bohr model, as shown on this page.

Virial theorem in quantum mechanics.

Next we try to prove the Virial theorem in the quantum mechanics.
In 1927, P. Ehrenfest demonstrated the relationship between the quantum-mechanical wave and the motion of a classcial particle.
So the basic mechanisms of them are the same.
We use the following relations as the Hamiltonian (H) operator and the momentum (p) operator.
(Eq.17)

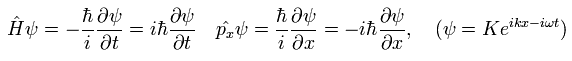
The total time derivative of the expectation value of an arbitrary operator A can be expressed as (using Eq.17),
(Eq.18)

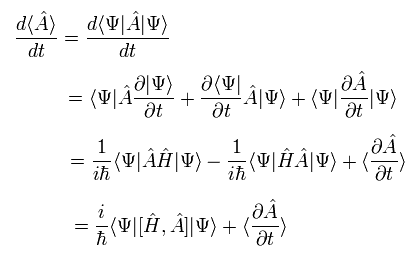
where we use the complex conjugate of the Hamiltonian, too.
As the operator A doesn't contain the time variable directly, the last term of Eq.18 vanishes.

Here we use the dot product of the momentum (p) and the position (r) as the operator A.
The result of Eq.18 is
(Eq.19)

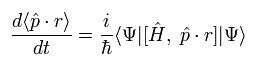
The commutator of Eq.19 can be expressed as
(Eq.20)

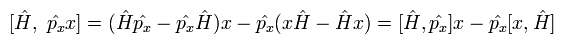
The commutator of the Hamiltonian and the momentum in Eq.20 becomes
(Eq.21)

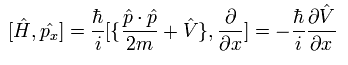
where V means the potential energy.

And the commutator of the Hamiltonian and the position operators in Eq.20 becomes
(Eq.22)

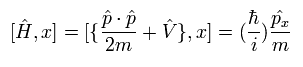
In Eq.22, we need to use the following commutation relations,
(Eq.23)

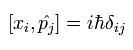
Using Eq.23, we calculate the commutator as follows,
(Eq.24)

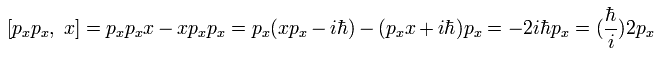
Using Eq.23 and Eq.24, we can get the result of Eq.22.

Substituting Eq.21 and Eq.22 into Eq.20, the result of Eq.19 becomes
(Eq.25)

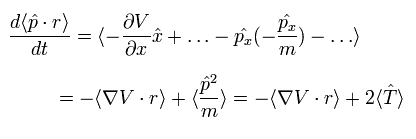
If we use the Coulomb potential as V, we can get the following value,
(Eq.26)

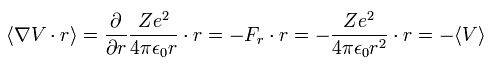
Like Eq.5, the left side of Eq.25 becomes zero in the stationary state.
As a result, we can get the Virial theorem also in the quantum mechanics.
(Eq.27)

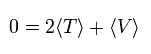
Some people say that the Schrodinger equation uses only the Coulomb potential, but it doesn't use the Coulomb force.
And they say it is the reason why the quantum mechanics is different from the classical mechanics.
But as shown in Eq.26, to get the Virial theorem of the quantum mechanics, we have to use the Coulomb force (F) in the calculation process.

2011/2/15 updated. Feel free to link to this site.