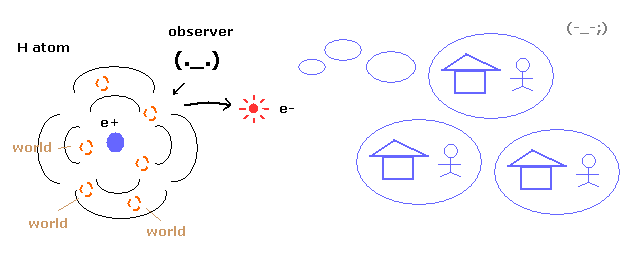
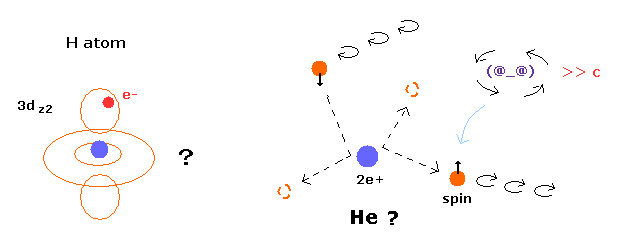
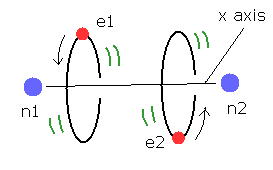
Top page (correct Bohr model including the two-electron atoms).
Strange "Spin" is NOT a real thing.
Special relativity is wrong.
(Fig.1) Superposition = unrealistic Many-worlds !

As you know, quantum mechanics cannot describe the electron's concrete motion at all.
It only shows the probability density of the electron in hydrogen atom.
So to explain wavefunction collapse, we need unrealistic many worlds.
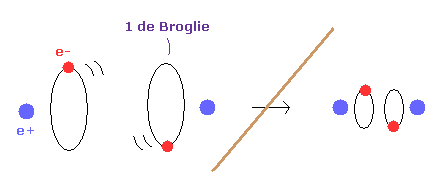
(Fig.2) 1 × de Broglie wavelength = hydrogen ground state.
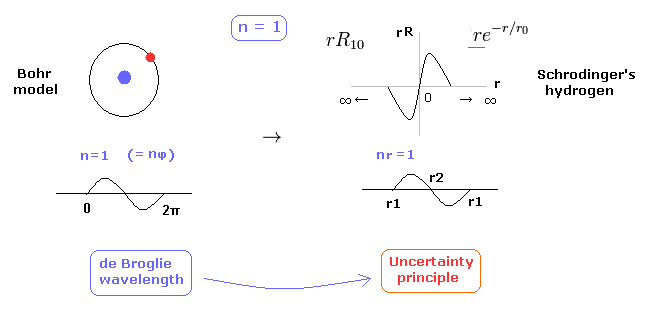
As shown in this page, Schrodinger's hydrogen also satisfies the condition of an integer times de Broglie wavelength.
This is the reason why Schrodinger's hydrogen gives completely the same results as Bohr model.
As shown in Fig.2, in the ground state of hydrogen atom, Bohr model consists of tangential de Broglie wave, and Schrodinger's model ( rR ) consists of "radial" de Broglie wave.
( It is easily understood also by seeing the probability graphs of |rR|2. )
Actually, the probability of ground state of hydrogen is the highest around Bohr radius.
The problem is that Schrodinger's radial wavefunction must be always from zero to infinity.
And the 1s de Broglie wave is linear, so the opposite phases of them overlap and cancel each other out.
(Fig.3) Schrodinger's wavefunctions always spread to infinity.
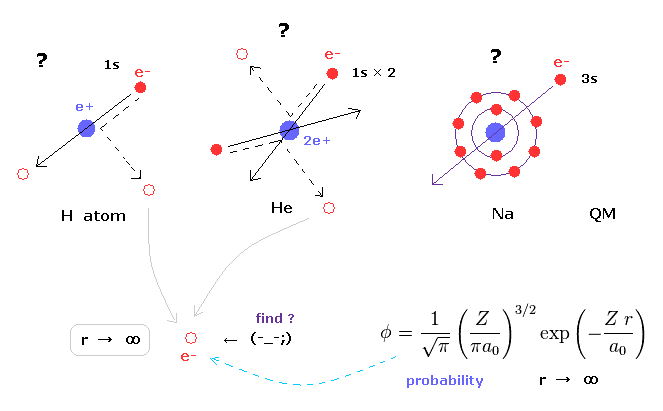
In various atoms and molecules such as helium and hydrogen molecule, Schrodinger's wavefunction ALWAYS spread to infinity.
This means we can find the bound-state electron near infinity even in very stable helium atom !
Of course, this is impossible, and quantum mechanics ( chemistry ) has NO ability to describe real states of various atoms and molecules.
Schrodinger's equation of helium atom cannot be solved, but variational functions of it are always spreading to infinity.
(Fig.4) Schrodinger's 2P "radial" wave function (angular momentum = 1).
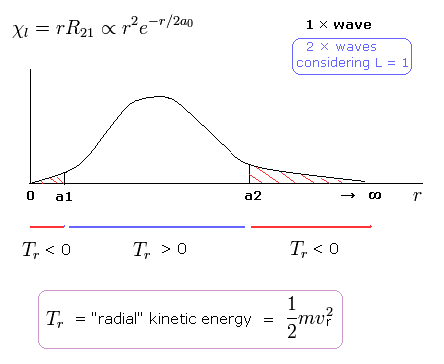
As shown in Fig.4, the 2P "radial" wave function ( χ = rR21 ) contains the regions of the minus kinetic energy ( r < a1, a2 < r ).
When the r is bigger than a2, the Coulomb potential energy becomes higher than some maximum value.
In this region, to keep the total energy (E < 0) constant, the "radial" kinetic energy must be minus !
Furthermore, in the region from 0 to a1 of Fig,4, the potential energy is lower than the total energy.
But the tangential kinetic energy increases much faster than others.
To cancel the increased tangential kinetic energy, radial kinetic energy has to be minus.
These unreasonable states clearly show Schrodinger's hydrogen atom is wrong.
(Fig.5) Quantum mecanical helium becomes chaotic and unstable.
In the quantum chemistry, if we use two 1s wavefunction of hydrogen atom, we can get the approximate gound state energy of helium.
But as you notice, 1s state has NO angular momentum.
In this state, two electrons of helium become chaotic and very unstable due to repulsive Coulomb force between them.
So the quantum mechanical helium is completely different from the actual helium atom.
(Fig.6) Quantum mechanical helium.
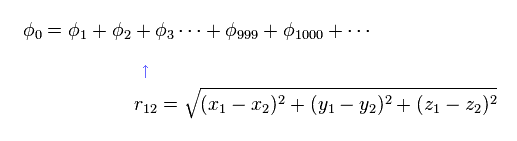
To get the exact ground state energy of helium (or hydrogen molecule ) using Schrodinger's equation, we have to use more than a thousand variational functions, as shown in Fig.6.
(Fig.7) Probability density of helium or H2 ?
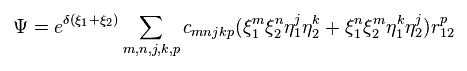
And these variational functions must include the variables (= r12 ) which express the distance between two electrons.
So, different from static hydrogen atom, the probability density at which we find electron 1 of helium (or H2 ) is always changing depending on the position of electron 2.
This variational functions of helium clearly shows the two electrons of helium are actually moving, even in the vague probability density waves.
(Fig.8) Reduced mass = electrons and nucleus are actually moving !
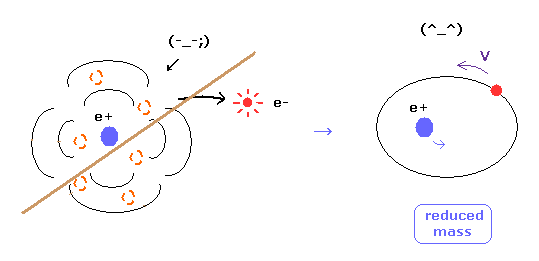
As you know, if we use the reduced mass of electron, we can get more exact values of the energy levels even in hydrogen atom.
This fact clearly shows that the electron and nucleus are actually moving interacting with each other.
Of course, as fractional charges of electron have not been found, we have to express real motions of the two electrons in helium atom.
As shown in this page, even pilot wave (Bohm) theory cannot explain two-electron helium at all, in quantum mechanics.
(Fig.9) Calculation results using reduced mass are more exact.
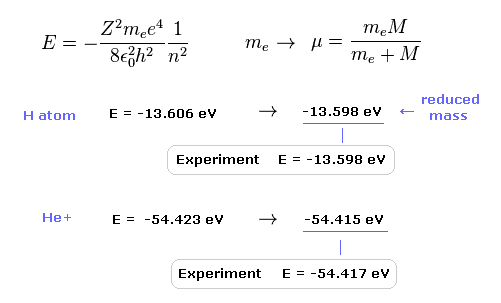
The experimental value of ground state hydrogen is -13.598 eV.
When we calculate this ground state energy using Schrodinger equation (or Bohr model ), it becomes -13.606 eV.
If we replace the usual electron mass by reduced mass considering nuclear motion, this calculation result becomes more exact (= -13.598 eV ).
This fact clearly shows the bound-state electron (and nucleus ) is actually moving.
Also in helium ion ( He+ ), if we use reduced mass, we can get more exact result (= -54.415 eV ) than the usual electron mass (= -54.423 eV ).
The experimental value of He+ is -54.417 eV.
(Fig.10) Two-electron Atomic Model ( He, Li+, Be2+, B3+, C4+ ... )
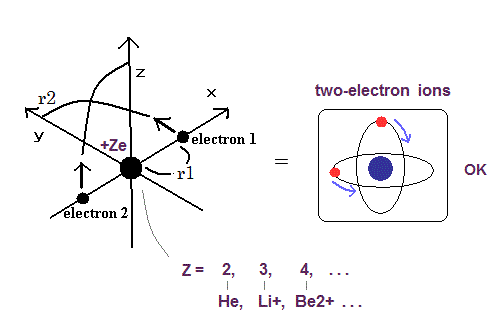
As shown in Top page, if the two de Broglie waves (= 1 × wavelength ) are overlapping each other, their opposite wave phases cancel each other due to destructive interference.
( These destructive interferences of electron's de Broglie waves were actually observed in Davisson and Germer experiments. )
So the two electrons's orbit have to be perpendicular to each other to avoid destructive inteference.
| Atoms | r1 (MM) | WN x 4 | Circular orbit | Result (eV) | Experiment | Error (eV) |
|---|---|---|---|---|---|---|
| He | 3074.0 | 1.000000 | -83.335 | -79.0037 | -79.0051 | 0.001 |
| Li+ | 1944.5 | 1.000000 | -205.78 | -198.984 | -198.093 | -0.89 |
| Be2+ | 1422.0 | 1.000000 | -382.66 | -373.470 | -371.615 | -1.85 |
| B3+ | 1121.0 | 1.000000 | -613.96 | -602.32 | -599.60 | -2.72 |
| C4+ | 925.0 | 1.000000 | -899.67 | -885.6 | -882.1 | -3.50 |
| N5+ | 788.0 | 1.000000 | -1239.8 | -1223.3 | -1219.1 | -4.20 |
| O6+ | 685.3 | 1.000000 | -1634.38 | -1615.44 | -1610.70 | -4.74 |
| F7+ | 607.3 | 1.000000 | -2083.3 | -2062.0 | -2057.0 | -5.00 |
| Ne8+ | 544.5 | 1.000000 | -2586.7 | -2563.0 | -2558.0 | -5.00 |
As shown in Table.1, these two-electron atomic model can completely explain actual energy states of various atoms.
The helium ground state energy ( -79.0037 eV ) is more exact than the latest quantum mechanical variational methods ( -79.015 eV ), because quantum mechanical helium cannot deal with nuclear motion ( reduced mass ) correctly.
About the computing methods and programs, see this page.
And this model can express three-electron atoms such as lithium correctly, too.
(Fig.11) New Bohr's helium (= A.) is not electrically polarized.
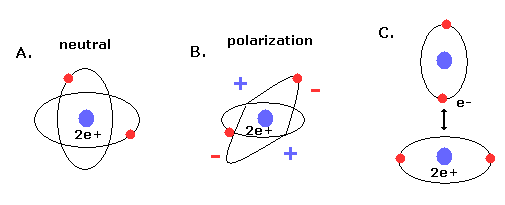
Furthermore, this helium model is just consistent with the fact that helium atom is most stable and doesn't form compounds with other atoms (or itself ).
Because when the two orbits are perpendicular to each other, the space around 2e+ nucleus becomes just neutral due to uniform distribution.
And of course, there is no space into which the third electron enter in Fig.10 helium, considering the stability of de Broglie waves (= Pauli exclusion principle ).
If the third electron enter them, destructive interferences of their de Broglie waves make them unstable.
(Fig.12) "Mathematical" Schrodinger equation vs. "real" Bohr model.
We cannot know what the Schrodinger's wavefunctions really are and just give up asking what they are.
Furthermore, as shown in this page, even if we study about relativistic quantum field theory and string theory, we cannot know what mysterious Pauli exclusion principle really is.
They just insist anticommutation of mathematical operators means Pauli exclusion principle.
So, as shown in this page, we cannot develop and try easier and useful methods in this very limited and vague conditions.
As this useless present quantum chemistry cannot be applied to various fields such as molecular biology and nanotechnology, their developments all stop now in the molecular levels. This is serious problem.
(Fig.13) Density functional theory = approximation.
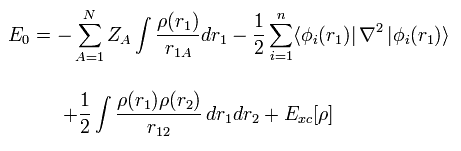
First, density functional theory (= DFT ), which is often used now, is only approximation, and NOT ab-initio method.
DFT is one of semi-empirical methods.
We can artificially choose various approximations such as LDA to match experimental results.
So popular DFT itself is NOT a true theory.
(Fig.14) Quantum mechanical hydrogen molecule ( H2 ) ?
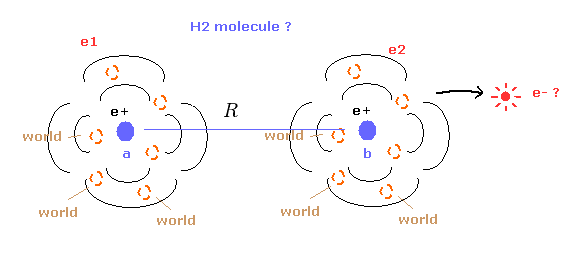
First we need to know the quantum mechanical approach about hydrogen molecule (H2).
Different from hydrogen atom, the wavefunction of H2 molecule itself does NOT mean real probability density of electrons.
So we cannot know the real states of two electrons from this quantum mechanical H2 molecule.
( Of course, we cannot apply this H2 structure to other molecules. )
(Eq.1) H2 molecule Hamiltonian.
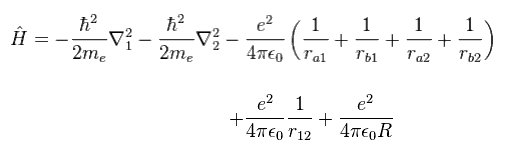
Eq.1 includes Coulomb interactions among two electrons ( 1 and 2 ) and two nuclei ( a and b ).
So this equation cannot be solved, and we have to rely on some approximation.
In quantum chemistry, Pauli exclusion principle is expressed using some determinant.
Because inside determinant, each wavefunction state must be different from each other.
(Eq.2) H2 wavefunction = determinant ?
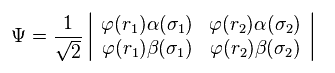
In Eq.2 φ represents the orbital wavefunction and α β represent spin states.
Of course, in multi-electron atoms or molecules, this determinant becomes much more complicated, as follows,
(Eq.3)
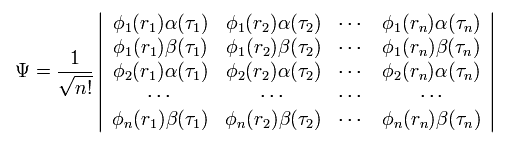
Due to these complicated mathematical expressions, we cannot apply the present quantum chemistry to various fields.
But the quantum mechanics is doing just "Shut up and caluclate !" about strange spin, we have NO other ways to express Pauli exclusion principle.
(Eq.4) Each wavefunction.
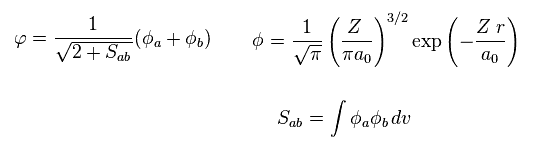
where a0 is Bohr radius.
The wavefunction of each electron contains the states belonging to nucleus a and b.
And we use 1s wavefunction of hydrogen-like atom.
( Z is atomic number. In hydrogen atom, Z = 1. )
Substituting Eq.4 into Eq.2,
(Eq.5)
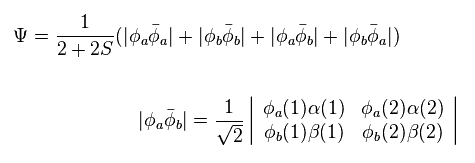
And using Eq.1 and Eq.5, we solve the following energy equation,
(Eq.6)
Even in most simple H2 molecule, this calculation is complicated.
The calculation result is
(Eq.7)
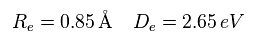
Re is the distance between two nuclei, and De is dissociation ( binding ) energy of H2 ( H2 → 2H ).
Eq.7 result is different from the experimental value of
(Eq.8) Experimental values of H2.
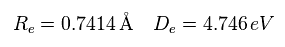
Both in valence bond (VB) and molecular orbital (MO) methods, we cannot get the exact values.
To get more exact values, we sometimes add fictional ion state ( H2 = H- - H+ ) to the original wavefunction.
(Eq.9)
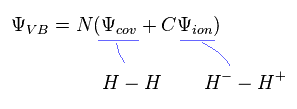
Even in this approach, calculation result is about 3.5 eV, which is different from the experimental values.
And of course, in the actual hydrogen molecule, this ion state does NOT happen.
So these artificial approaches are only for the calculation tools, and do NOT represent real states.
See also truth of variational method.
(Eq.10) Real hydrogen molecule ? = more than 100 terms.
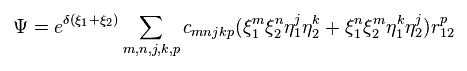
where δ and c are variational parameters.
To get the exact values, we have to use very complicated wavefunctions including variables such as r12.
" r12 " means the distance between two electrons, so the probability at which we find the electron 1 is changing depending on the position of electron 2.
So the probability density itself cannot be determined in H2 molecule or helium atom.
And we can artificially choose the number and kinds of terms in Eq.10, so they just try to find the wavefunction which gives exact values from infinite kinds of options.
Of course, we can NEVER apply complicated "mathematical" ( not physical ) terms of Eq.10 to other fields such as molecular biology or something.
And as I said above, this wavefunction always spreads to infinity, which is not real.
(Fig.15) Estimated H2 molecule.
Considering the internuclear distance ( 0.7414 × 10-10 m ) and Coulomb relations among two electrons and nuclei, it is natural that we think the actual electron's states of H2 molecule is like Fig.15.
Of course, Coulomb relations are most important concept also in quantum chemistry.
And another important concept which determines molecule's configuration is de Broglie wavelength.
Fig.15 is an "average" orbit to apply Virial theorm.
Considering interference of two de Broglie wave, actual H2 configuration becomes this.
(Fig.16) If de Broglie wavelength doesn't exist ?
If the concept of de Broglie wavelength doesn't exist, the electron's orbital radius of hydrogen atom can be smaller to zero.
As a result, internuclear distance of H2 molecule can be shorter as it likes, because the repulsive force between two nuclei can be cancelled out by arbitrary small electron's orbit.
So due to the concept of de Broglie wavelength, the internuclear distance ( 0.7414 × 10-10 m ) of H2 is kept.
(Eq.11) Schrodinger's wavefunction includes de Broglie wavelegnth.
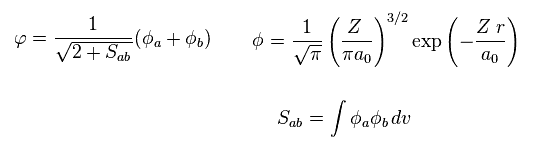
where a0 is Bohr radius.
Actually, also in the quantum chemistry, this concept of de Broglie wavelength is automatically used.
As shown in this page, Schrodinger's 1s wavefunction is 1 × de Broglie wavelength in the radial direction.
( They just changed the name of de Broglie wavelength to strange uncertainty principle. )
When we change the atomic number Z as a variational function, we can keep the condition of 1 × de Broglie wavelength in various interactions.
( For example, H atom → He+ ion, both ground states are 1 × de Broglie wavelength. )
(Fig.17) de Broglie wavelength and radius.
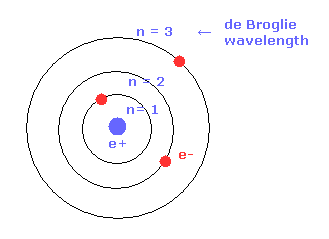
As shown in Bohr's orbit, as the number of de Broglie wavelength becomes larger, the electron's orbital radius becomes longer.
For example, the radius of 2 × de Broglie wavelegnth orbit is four times longer than that of 1 × de Broglie wavelength.
( n = 1 -- 1 × Bohr radius, n = 2 -- 4 × Bohr radius. )
This concept of Bohr radius is effective also in the quantum mechanics.
(Fig.18) de Broglie wavelength and charges.
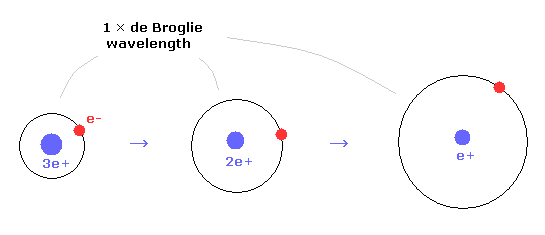
In 1 × de Broglie wavelegnth, as the central charges becomes smaller, the orbital radius becomes longer.
For example, the radius of helium ion is half of hydrogen atom.
Combining these ideas with Coulomb relation, we can explain molecular bond of H2 molecule.
(Fig.19) Two nuclei of H2+ molecule ion
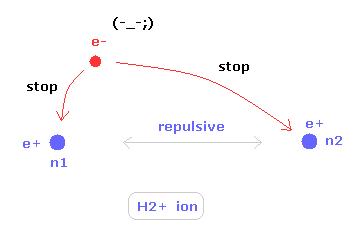
In some special condition, unstable hydrogen molecule ion (H2+) can exsit.
The hydrogen molecule ion has two positive nuclei and one negative electron.
To keep the two nuclei's positions stable, this only electron needs to move around more actively than hydrogen molecule.
So, H2+ molecule ion is completely different from helium atom, because the electron needs to keep two nuclei stable only by its movement.
Additional movement (= de Broglie wave ) is very important in molecules.
(Fig.20) Two nuclei of H2 molecule
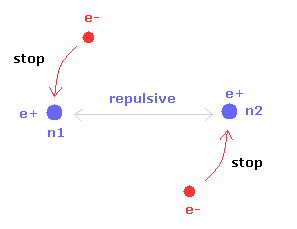
Different from H2+ molecule ion, H2 molecule has two electrons.
So each electron is moving to keep mainly one of the two nuclei stable.
If one of the two nuclei becomes stable, another nucleus is automatically stable due to the symmetric structure.
As a result, the electrons of H2 molecule don't need to move and shake like H2+ ion.
But of course, stable positions of nuclei and electron itself are different.
So this additional motion needs to be considered even in H2 molecule.
(Fig.21) H2 molecule.
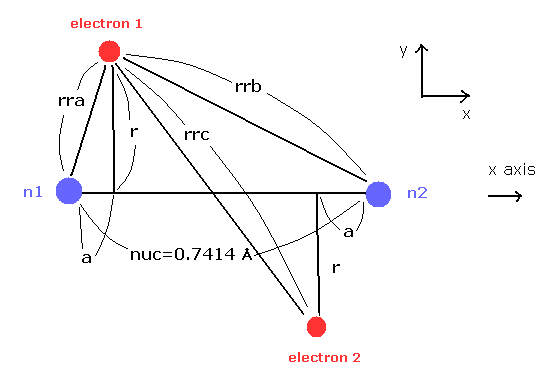
Here we calculate the number of de Broglie wave in one orbit using Fig.21 model and following programs.
Sample JAVA program of H2 molecule.
C language program of H2 molecule.
Here we use the new unit of 1 MM = 1 × 10-14 meter.
In this program, first we input the internuclear distance (= nuc in MM ) of H2.
And then input y-coordinate "r" (in MM) , and x-coordinate "a" ( in MM ) of electron 1.
(Fig.22) Various forces at ( a, r ).
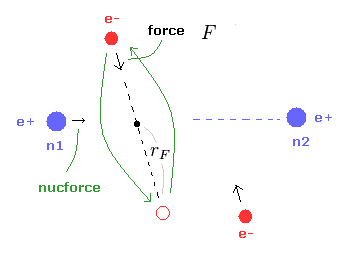
From the inputted values, this program outputs the total force acting on nucleus 1 (= nucforce ), and ( x, y ) components of forces acting on electron 1 (= elefx, elefy ) at the position of ( a, r ).
These forces are expressed as the ratio to the force between electron and nucleus of H atom's ground state.
(Fig.23) Force F acting on e1.
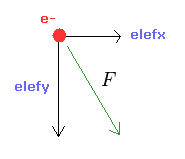
From the inputed values ( a, r, nuc ), we calculate the total potential energy V.
Using Virial theorem, we can get the total energy E = 1/2 V and kinetic energy T = -1/2 V.
From this kinetic energy, we obtain the electron's velocity (= v ) and de Broglie wavelength (= h/mv ).
(Eq.12) F = centrifugal force.
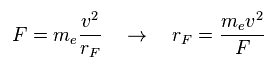
Here we suppose the force F is some centrifugal force.
From the relation of Eq.12, we can get the rotation radius (= rF ).
(Eq.13) de Broglie wave in one orbit.
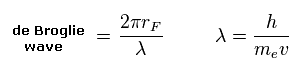
Using the de Broglie relation ( λ = h/mv ), we caluclate the number of de Broglie waves included in one orbit (= 2πrF ).
Using Virial theorem, we can get the binding energy of H2 atom at the position of ( a, r ).
(Fig.24) Another x coordinate of electron.
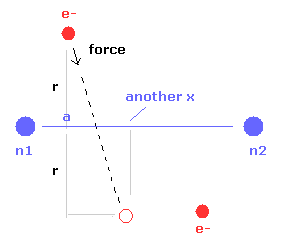
And this probram also outputs another x coordinate (in MM) of electron 1 in the direction of the force F, as shown in Fig.24.
This x coordinate becomes a indicator of the electron's shaking in the x direction.
First we think about the case when the binding energy (= 4.746 eV ) and the internuclear distance (= 0.7414 × 10-10m = 7414 MM ) are experimental values.
(Eq.14) Experimental values of H2.
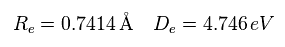
When the electron 1 is ( a = 624 MM, and r = 4660 MM ), the total forces acting on nucleus become zero.
( nucforce = 0. At this point, two nuclei are stable. )
(Fig.25) Experimental values.
At this point, de Broglie waves included in one orbit (= Eq.13) becomes 0.977.
This value is almost 1, but is a little different.
Because the electron's orbit is shaking in the x direction.
At the another x coodinate ( a, r ) = ( 972, 4660 ), this de Broglie wave becomes 1.009.
As a result, the average de Broglie waves become ( 0.977 + 1.009 ) / 2 = 0.993.
This value is closer to "1".
| nuc (MM) | r (MM) | a (MM) | Energy (eV) | another x | nucforce | waves | aver waves |
|---|---|---|---|---|---|---|---|
| 6000 | 4770 | 1470 | 4.341 | 1689 | 0.00 | 0.977 | 0.985 |
| 6500 | 4720 | 1030 | 4.546 | 1329 | 0.00 | 0.977 | 0.991 |
| 7000 | 4680 | 770 | 4.698 | 1105 | 0.00 | 0.977 | 0.993 |
| 7414 | 4660 | 624 | 4.746 | 972 | 0.00 | 0.977 | 0.993 |
| 8000 | 4650 | 480 | 4.705 | 830 | 0.00 | 0.977 | 0.992 |
| 8500 | 4640 | 390 | 4.689 | 728 | 0.00 | 0.977 | 0.990 |
| 9000 | 4642 | 325 | 4.602 | 645 | 0.00 | 0.977 | 0.989 |
As shown in Table 2, when we choose the common conditions of nucforce = 0 and de Broglie wave = 0.977, the binding energy at internuclear distance of nuc = 7414 MM (= experimental value ) becomes the largest.
So as I said, when we consider the stable nuclei and de Broglie wavelength, the most stable hydrogen configuration is determined.
The average de Broglie wave is also biggest at nuc = 7414 MM.
If we choose average waves = 0.993 as common condition instead of 0.977, binding energies other than nuc = 7414 become smaller than Table.2.
So the internuclear distance of 7414 MM is most stable.
( 1 MM =1 × 10-14 meter )
| nuc (MM) | r (MM) | a (MM) | Energy (eV) | elefx | elefy | nucforce | waves |
|---|---|---|---|---|---|---|---|
| 7414 | 4665 | 890 | 4.746 | 0.00 | 1.271 | 0.08 | 1.001 |
When the x component of force acting on electron is zero ( elefx = 0.00 ), de Broglie wave becomes just 1.001.
Try inputting nuc = 7414, r = 4665, a = 890 ( which is between 624 and 972 of Table 2 ).
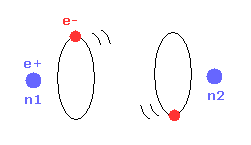
(Fig.26) Two H atoms are completely dissociated.
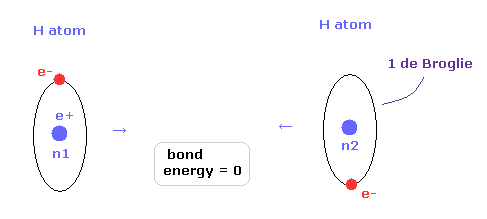
Next we think about the reason why H2 molecule becomes most stable when the internuclear distance of H2 is nuc = 7414 MM (= experimental value ).
In Fig.26, two hydrogen atoms are completely dissociated, so the binding energy is just zero.
(Fig.27) Most stable H2 configuration.
As the two nuclei come closer to each other, each electron can interact with two positive nuclei.
So, the bond energy becomes bigger, which means stable H2 molecule is formed.
(Fig.28) Repulsive force of two electrons.
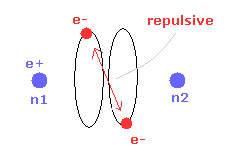
But when the two nuclei come closer to each other than the experimental value of 7414 MM, the repulsive force between two electrons are stronger.
As a result, "effective" central positive charge of Fig.18 is smaller.
So under the common de Broglie wave's condition, the radius "r" is larger, and bond energy is smaller than the experimental value. ( See Table 2. )
(Fig.29) When internuclear distance becomes shorter.
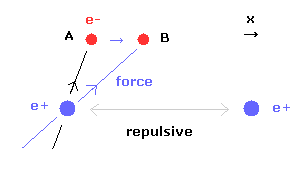
When the internuclear distance becomes shorter, the repulsive force between nuclei becomes stronger.
To cancel this repulsive force out, the two electrons need to move in the direction of the center.
As shown in Fig.29, as the electron 1 moves in the x direction ( A → B ), atrractive force of electron 1 becomes stronger in the x direction.
But in this case, the repulsive force between two electrons becomes stronger in Fig.28.
(Fig.30) "another x".

As I said, "another x" means another x coordinate, when the electron 1 has moved in the direction of force.
For example, when ( a, r, nuc ) = ( 624, 4660, 7414 ), another x becomes 972 (MM).
Then we calculate de Broglie wave and binding energy at the coodinate of ( anotherx, r ) in the same internuclear distance.
So in case of Fig.30, we calculate at ( a, r, nuc ) = ( 972, 4660, 7414 ).
And we get the average binding energy and average de Broglie waves of original "a" and "another x".
| nuc (MM) | r (MM) | a (MM) | AveEnergy (eV) | another x | nucforce | waves | aver waves |
|---|---|---|---|---|---|---|---|
| 6500 | 4744.3 | 1059 | 4.408 | 1351 | 0.00 | 0.9797 | 0.9933 |
| 7000 | 4684 | 775 | 4.689 | 1107 | 0.00 | 0.9773 | 0.9933 |
| 7200 | 4671 | 697 | 4.732 | 1037 | 0.00 | 0.9771 | 0.9933 |
| 7414 | 4662.3 | 629 | 4.746 | 972 | 0.00 | 0.9772 | 0.9933 |
| 7600 | 4658 | 577 | 4.738 | 922 | 0.00 | 0.9774 | 0.9933 |
| 8000 | 4657 | 488 | 4.671 | 831 | 0.00 | 0.9784 | 0.9933 |
| 8500 | 4665.3 | 402 | 4.532 | 739 | 0.00 | 0.9797 | 0.9933 |
In Table 4, the common conditions are the force acting on nucleus becomes zero ( nucforce = 0.00 ), and average de Broglie waves is 0.9933.
In these condition, like Table 3, the case of nuc = 7414 MM (= experimental value ) becomes the biggest in binding energy (= 4.746 eV ).
As a result, internuclear distance of 0.7414 × 10-10 meter proves to be most stable.
JAVA program of H2 molecule ( average waves ).
C language of H2 molecule ( average waves )
If you take the programs above, you can get the average binding energy and de Broglie waves in one orbit.
In the same way, you need to input the values of "nuc", "r", and "a" (MM) ( of Table 4 ), first.
(Fig.31) "a" = another x, when binding energy = 0.
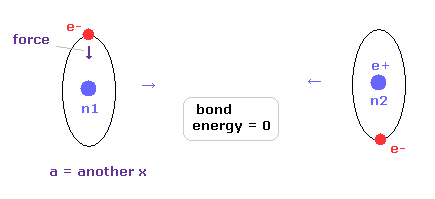
The reason why we have to consider "another x" is shown in Fig.31.
When the internuclear distance is very long, binding energy becomes zero.
In this case, each hydrogen atom becomes independent, and its orbit does NOT shake by another hydrogen nucleus.
So in Fig.31, original x coordinate "a" is just equal to "another x", and the calculation energy result is not true when we take the common consition of waves ( not average ) = 0.977 in Table 2.
(Fig.32) "a" is different from another x = orbit is shaking.
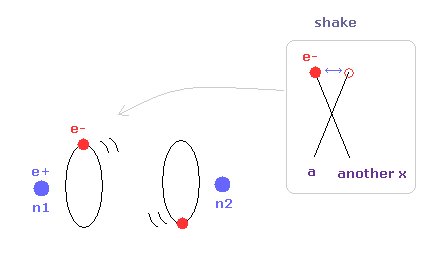
When the internuclear distance becomes shorter than Fig.31, the influence of another nucleus becomes stronger, and electron's orbit is shaking.
Especially in this case, average de Broglie waves is very important.
(Fig.33) "a" = another x, again.
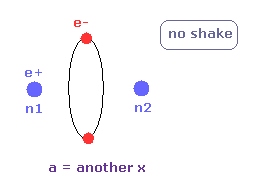
When the internuclear distance becomes much shorter, the electron's orbit does not shake.
Also in this case, "a" is just equal to "another x".
( Of course, two electrons cannot be in one 1 × de Broglie wavelegnth orbit. )
So in most stable configuration, the electron's orbit is shaking transversely.
(Fig.34) Two forces in one orbit are different.
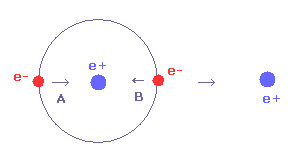
For example, in Fig.34, the force B is weaker than force A, though they are in the same one orbit.
Of course the potential energy is low in B, so the de Broglie wavelength becomes shorter due to Virial theorem.
So when we calculate in B ( using Eq.12 and Eq.13 ), de Broglie wave's number in one orbit becomes bigger than the average values.
So we need to take the average of A and B.
In this section, we visualize hydrogen molecule using this program or its text.
( See also this page. )
After running program, we choose "H" in both A,and B atom.
Internuclear distance of H2 is 0.7414 Å so input 7414 and click "internuc" button.
(Fig.35) H2 molecule.
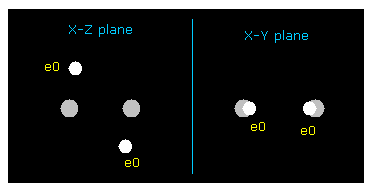
In the program, we change x and z coodinates of "ele 0" electron symmetrically both in A and B atom.
"ele 1" means the coodinate after moving by the force acting on ele 0.
We aim at the stability of both A and B nuclei ( FX = 0 ), and average de Broglie wave is "1.0000" ( ave = 1.0000 ).
| internuc (MM) | A-X (MM) | A-Z (MM) | B-X (MM) | B-Z (MM) | Force | aver waves | total V (eV) | bond energy |
|---|---|---|---|---|---|---|---|---|
| 6000 | 1870 | 4972 | -1870 | -4972 | 0 | 1.0000 | -60.664 | 3.120 |
| 6500 | 1145 | 4827 | -1145 | -4827 | 0 | 1.0000 | -62.204 | 3.890 |
| 7000 | 830 | 4755 | -830 | -4755 | 0 | 1.0000 | -62.893 | 4.234 |
| 7200 | 745 | 4739 | -745 | -4739 | 0 | 1.0000 | -63.014 | 4.295 |
| 7414 | 669 | 4729 | -669 | -4729 | 0 | 1.0000 | -63.056 | 4.316 |
| 7600 | 610 | 4724 | -610 | -4724 | 0 | 1.0000 | -63.047 | 4.311 |
| 7800 | 560 | 4721 | -560 | -4721 | 0 | 1.0000 | -63.010 | 4.293 |
| 8000 | 518 | 4720 | -518 | -4720 | 0 | 1.0000 | -62.952 | 4.264 |
| 9000 | 360 | 4741 | -360 | -4741 | 0 | 1.0000 | -62.365 | 3.971 |
Average binding energy of H2 is displayed in the last line (= "bin" ).
Total V of Table 5 means the average potential energy.
As shown in Table 5, when the bond length of H2 molecule is the experimental value of 0.7414 Å (= 7414 MM ), total V is the lowest, and binding energy becomes biggest (= 4.316 eV ).
This value is a little smaller than the experimental value of 4.746 eV.
But this result clearly shows H2 bond length is 0.7414 Å from the viewpoint of classical orbits.
| internuc (MM) | A-X (MM) | A-Z (MM) | B-X (MM) | B-Z (MM) | Force | aver waves | total V (eV) | bond energy |
|---|---|---|---|---|---|---|---|---|
| 6000 | 1665 | 4878 | -1665 | -4878 | 0 | 0.9933 | -61.787 | 3.681 |
| 6500 | 1059 | 4745.5 | -1059 | -4745.5 | 0 | 0.9933 | -63.224 | 4.400 |
| 7000 | 775 | 4684 | -775 | -4684 | 0 | 0.9933 | -63.802 | 4.689 |
| 7200 | 697 | 4671.5 | -697 | -4671.5 | 0 | 0.9933 | -63.8815 | 4.728 |
| 7414 | 629 | 4662.3 | -629 | -4662.3 | 0 | 0.9933 | -63.916 | 4.746 |
| 7600 | 577 | 4658 | -577 | -4658 | 0 | 0.9933 | -63.899 | 4.738 |
| 7800 | 530 | 4657 | -530 | -4657 | 0 | 0.9933 | -63.838 | 4.707 |
| 8000 | 488 | 4657 | -488 | -4657 | 0 | 0.9933 | -63.765 | 4.670 |
| 9000 | 340 | 4681.5 | -340 | -4681.5 | 0 | 0.9933 | -63.125 | 4.350 |
Next we aim at de Broglie wave of one orbit is 0.9933, like the upper section.
As shown in Table 6, when the bond length of H2 molecule is the experimental value of 0.7414 Å (= 7414 MM ), total V is the lowest, and binding energy becomes biggest (= 4.746 eV ).
The experimental value of binding energy is 4.746 eV.
This result is completely same as true H2 molecule.
So in this simplified way, de Broglie wave = 0.9933 is correct standard value.
And by both standards, bond length = 0.7414 Å of H2 proves to be most stable one.
In conclusion, Molecular configurations are determined by two important natures of Coulomb relation and de Broglie wavelength.
This is the essence of molecular bond.
(Eq.10) Quantum mechanical H2.
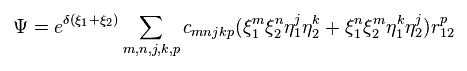
As you notice, new Bohr model hydrogen can give much clearer and easier H2 molecule than mathematical ( not physical ) terms of quantum mechanical H2 (= Eq.10 ).
So we can apply this new structure to other molecular bonds easily.
The most important point is that Bohr model has reality, and quantum mechanical model does NOT at all.
About the hydrogen molecule ion, see this page.

2013/2/7 updated. Feel free to link to this site.