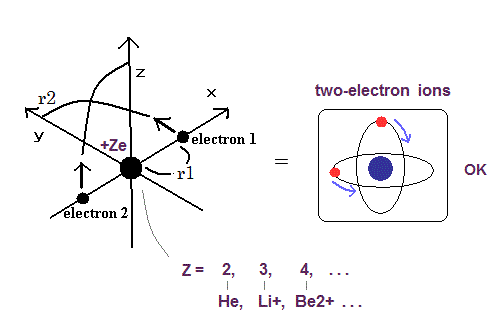
Top page (correct Bohr model including the two-electron atoms).
Lamb shift is an illusion !
Our new Bohr model has suceeded in calculating the Helium ionization energy more correctly than the quantum mechanical variational methods as shown in the Top page.
So next, we try Lithium atom (Li) and Lithium ion (Li+) by Bohr's theory.
Lithium belongs to the alkali metal group of chemical elements, and has the atomic number 3.
It is the lightest metal, and highly reactive and flammable (though more stable than the other alkali metals).
Lithium has a single valence electron ( its configuration, 1S × 2, 2S × 1 ) that is easily given up to form a cation. because of this, it is a good conductor of both heat and electricity, and used for the lithium (ion) batteries.
Naturally occurring lithium is composed of two stable isotopes, Li6 and Li7, the latter being the more abundant (92.5%).
The ionization energies of the lithium is 5.39 eV (1st), 75.64 eV (2nd), and 122.45 eV (3rd), respectively.
So the ground state energy of the lithium ion (Li+) is -75.64 - 122.45 = -198.09 eV.
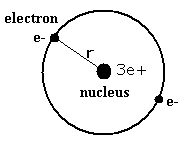
Lithium ion (Li+) has two electrons and one nucleus (3e+).
First, suppose we have one model (Fig. 1.) in which two electrons of the lithium ion are on the opposite sides of the nucleus and moving on the same circular orbit.
Fig. 1. One schematic model of lithum ion (Li+)

Equating the centrifugal force to the Coulomb force, we have
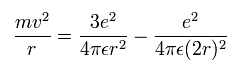
where r is the circular orbital radius (meter), m is the electron mass (me= 9.1093826 x 10-31 kg), e is the electron charge (= 1.60217653 × 10-19 C), and ε is the permittivity of vacuum (= 8.854187817 × 10-12 C2/Nm2).
The circular orbital length is supposed to be an integer times the wavelength of the electron, we have
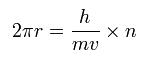
where h is Plank's constant (= 6.62606896 x 10-34 Js), and h/mv is the de Broglie's wavelength.
The total energy E of the lithium ion (Li+) is the sum of the kinetic and the Coulomb potential energy of the two electrons, so
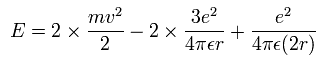
Solving the above three equations, the ground state energy (n=1) becomes -205.79 eV.
This value is lower than the experimental value -198.09 eV.
(The error is 7.7 eV. )
But as I said in the top page,
if the two electrons can be in one small orbit of one de Broglie's wavelength, this means that the ground state electron of the Bohr hydrogen-like model can come closer to the nucleus than the original orbit.
And in the orbit of Fig. 1., the two electrons are just at the opposite positions, so the wave phases of them may interfere with each other and vanish.
So here we suppose another model as shown in Fig. 2. in which two same-shaped orbital planes are perpendicular to each other.
As shown in the top page, we have succeeded in computing the two electron atom, helium ground state energy correctly using this model.
How about this two-electron lithium ion (Li+) ?
Fig. 2. Lithium ion model (Li+). Is it like helium atom (He) ?
In this model, the electron 1 moves on the X-Y plane, the electron 2 moves on the X-Z plane.
Electron 1 starts at (r1, 0, 0), while electron 2 starts at (-r1, 0, 0).
See the top page in detail.
Here we investigate how the electrons of the Li+ are moving by calculating the Coulomb force among the two electrons and the nucleus (3e+) at short time intervals.
The computer program (class filename: MathMethod) written in the JAVA language (version 1.5.0) to compute the electron orbit of the Li+ is shown in the link below.
The lithium nucleus is at the origin. The electron 1 initially at (r1, 0, 0) moves one quarter of its orbital to (0, r2, 0), while the electron 2 initially at (-r1, 0, 0) moves to (0, 0, r2).
Here we use new convenient units MM
( 1 MM = 1 × 10-14 meter ), SS ( 1 SS = 1 × 10-22 second ) and MM/SS ( 1 MM/SS = 1 × 10-14 meter/ 1 × 10-22 second = 1 × 108 meter/second ).
In this program, we first input the initial x-coordinate r1 (in MM) of the electron 1, and the absolute value of the total energy E (in eV) of the Li+. From the inputted value, we calculate the initial velocity of the electron. And at intervals of 1 SS we compute the Coulomb force among the two electrons and the nucleus. When the electron 1 is at (xx, yy, 0), the electron 2 is at (-xx, 0, yy) (in MM). Change MM to meter as follows; x (m) = xx × 10-14. y (m) = yy × 10-14. So the x component of the acceleration (m/sec2) of the electron 1 is,
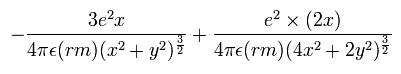
where the first term is by the Coulomb force between the nucleus and the electron 1, and the second term is by the force between the two electrons.
Considering the lithium nuclear mass (nucleus), we use here the reduced mass (rm =1/2 × (2me × nucleus)/(2me + nucleus) = 9.10794 × 10-31 kg) except when the center of mass is at the origin.
In the same way, the y component of the acceleration (m/sec2) is,
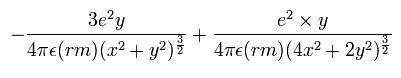
Change m/sec2 to MM/SS2 using the next relation,
1 MM/SS2 = 1 × 10-14 meter/ (1 × 10-22 second)2 = 1 × 1030 meter/(second)2
Based on that calculation value we change the velocity vector and the position of the electrons.
We suppose electron 1 moves only on the XY-plane, so the z component of the acceleration of the electron 1 is not considered. If we consider all components of the Coulomb force against the electrons, the electron's motion becomes as shown in Fig.1.
But in Fig.1., the two electrons are packed in one orbit of one de Broglie's wavelength.
We suppose de Broglie's waves are related to some limited spaces. Actually the two slit behavior of the electron is caused by this de Broglie's wave.
So if the two electrons's orbits come close to each other to some extent, the wave fields becomes condensed and block it.
We also calculate de Broglie's wavelength of the electron from the velocity (λ = h/mv) at intervals of 1 SS.
The number of that wave (λ in length) contained in that short movement section (the sum of them is WN) is,
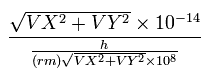
where (VX, VY) are the velocity of the electron 1 (in MM/SS), the numerator is the movement distance (in meter) for 1 SS. the denominator is de Broglie's wavelength (in meter).
Here, the estimated electron's orbit is divided into more than one hundred thousand short segments for the calculation.
When the electron 1 has moved one quarter of its orbit and its x-coordinate is zero, this program checked the y-component of the electron 1 velocity (last VY).
When the last VY is zero, two electrons are periodically moving around the nucleus on the same orbitals as shown in Fig.2.
So, only when -0.0001 < last VY < 0.0001 (MM/SS) is satisfied, the program displays the following values on the screen, r1, VY, preVY (VY 1 SS ago), and (mid)WN (the total number of de Broglie's waves contained in one quarter of the orbit).
Table. 1 shows the results in which the last VY is the closest to zero.
Fig. 3. graphs the results in Table.1.
| E (eV) | r1 (MM) | WN | WN x 4 |
|---|---|---|---|
| -185.0 | 2092.0 | 0.25928 | 1.03712 |
| -190.0 | 2036.5 | 0.25585 | 1.02340 |
| -195.0 | 1984.5 | 0.25255 | 1.01020 |
| -199.0 | 1944.5 | 0.25000 | 1.00000 |
| -205.0 | 1888.0 | 0.24631 | 0.98524 |
| -210.0 | 1843.0 | 0.24336 | 0.97344 |
| -215.0 | 1800.0 | 0.24051 | 0.96204 |
Fig. 3. Plots of the number of de Broglie's waves contained in one orbit at various energy levels of Li+.
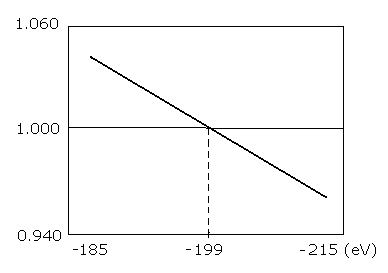
As shown in Table.1 and Fig.3., when the total energy of the Li+ (E) is -199.0 eV, WN × 4 is just 1.00000.
The experimental value is -198.09 eV. So this calculation result of -199.0 eV is almost consistent with the experimental value (-198.09 eV).
This means that also in the lithium ion (Li+), the orbital planes of the two electrons are perpendicular to each other like helium atom.
( The error is only 0.91 eV ( less than 0.5 % ). This error is probably caused by the fact that the lithium ion is more unstable than the helium atom, so the orbital planes are not completely as shown in Fig. 2.)
Next we try the litium atom (Li).
Lithium atom has two electrons in 1S orbital, and one electron in 2S orbital.
The two electrons of 1S state are attracted to the 3e+ nucleus strongly, so they are much closer to the nucleus than the 2S electron.
So approximately, we can suppose the 2S electron is moving around the e+ nucleus ( +3e - 2e = +e ) on the circular orbit of the two de Broglie's wavelength.
(This means that we can use the equations of the hydrogen atom in 2S electron approximately.)
According to the Bohr model, the radius (Rb) of the two de Broglie's wavelength orbit is 4 × Bohr radius, as follows,
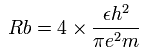
This Rb is 2.1167 × 10-10 meter ( = 21167 MM ) .
And the energy level of n =2 becomes, (using the energy levels of the hydrogen atom)
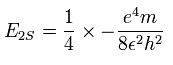
So we suppose the neutral lithium model as follows,
Fig. 4. Lithium atom (Li) model
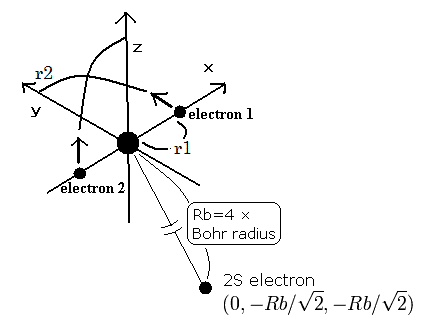
The two electrons of 1S state are avoiding 2S electron, so we fix the 2S electron at ( 0, - Rb / √2, - Rb / √2 ) as shown in Fig. 4.
(Fig. 4. shows the relative positions, But actually, this 2S electron is rotating around the nucleus slower than the 1S electrons.)
Like Li+, when the electron 1 is at (x, y, 0), the electron 2 is at ( -x, 0, y ).
So the distances among the particles are,
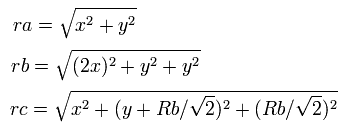
where ra is the distance between the electron 1 and the nucleus, rb is between the two 1S electrons, and rc is between the electron 1 and 2S electron, respectively.
The x component of the acceleration (m/sec2) of the electron 1 is,
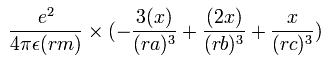
In the same way, the y component of the acceleration (m/sec2) of the electron 1 is,
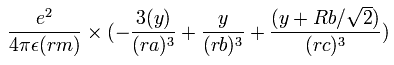
Then we compute the number of de Broglie's waves contained in one quarter of the 1S orbit like Li+
Sample JAVA program (Li atom)
Table. 2 shows the results in which the last VY is the closest to zero in Li.
| E (eV) | r1 (MM) | WN | WN x 4 |
|---|---|---|---|
| -190.00 | 2086.0 | 0.25860 | 1.03440 |
| -195.00 | 2031.0 | 0.25518 | 1.02072 |
| -200.00 | 1979.0 | 0.25190 | 1.00760 |
| -202.97 | 1949.0 | 0.25000 | 1.00000 |
| -205.00 | 1929.0 | 0.24874 | 0.99496 |
| -210.00 | 1882.0 | 0.24569 | 0.98276 |
| -215.00 | 1837.0 | 0.24276 | 0.97104 |
This results shows that when the ground state energy of Li atom is -202.97 eV, the orbital length becomes just 1.00000 × de Broglie's wavelength.
The experimental value of the ground state energy of the lithium (Li) atom is -203.48 eV.
So the calculation error is only 0.51 eV ( 0.25 % ).
(This small error is probably caused by using the "approximate" orbit of the 2S electron.)
This means that it is almost correct to say that the three electrons of the lithium atom are moving like Fig.4.
See also this page (relation between 1S and 2S electrons in Bohr model).
If we can express the lithium (Li) and lithium ion (Li+) correctly by the Bohr model, we can extend theses methods to other atoms such as Be (Beryllium), B (Boron) and C (Carbon)...

2010/7/15 updated. Feel free to link to this site.