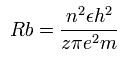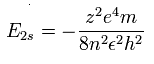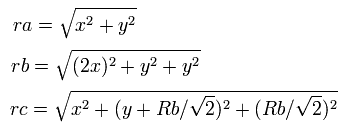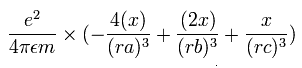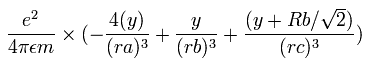New Bohr model Beryllium (Be)
Top page (correct Bohr model including the two-electron atoms).
Electron spin is an illusion !
Our new Bohr model has succeeded in calculating the Helium ionization energy more correctly than the quantum mechanical variational methods as shown in the Top page.
In this new successful Bohr model, the two electrons of the helium atom (He) are moving on the orbits of just one de Broglie's wavelength which are perpendicular to each other.
This model can explain the phenomena of Pauli exclusion principle correctly, because there is no space for the third electron to enter this new two-electron Bohr atom.
Surprisingly, this new atomic structure of the Bohr's helium can be applied to other two-electron atoms (ions ), Lithium ion (Li+), Beryllium (Be2+), Boron (B3+) and Carbon (C4+) ions, too.
(See this page.)
Furthermore, the ionization (ground state) energy of the three-electron atom lithium (Li) can be calculated correctly using the approximate "2S" Bohr orbit. (See this page.)
Bohr model Beryllium ion (Be+)
Here we try the three-electron beryllium ion (Be+).
Beryllium ion (Be+) has two electrons in 1S orbital, and one electron in 2S orbital.
The two electrons of 1S state are attracted to the 4e+ nucleus strongly, so they are much closer to the nucleus than the 2S electron.
So approximately, we can suppose the 2S electron is moving around the 2e+ nucleus ( +4e - 2e = +2e ) on the circular orbit of the two de Broglie's wavelength.
(This means that we can use the equations of the hydrogen-like atom in 2S electron approximately.)
According to the Bohr hydrogen-like model, the radius (Rb) of the n × de Broglie's wavelength orbit is,
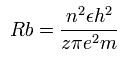
(when z = 1 and n = 1, Rb becomes "Bohr radius".)
In 2S electron of Be+, the positive charge of the nucleus (z) is supposed to be 2+ (see above), and n is 2.
So this Rb is 2 × Bohr radius ( = 1.0583 × 10-10 meter = 10583 MM ) .
(Here we use the new units, 1 MM = 10-14 meter, 1 SS = 10-22 second, 1 MM/SS = 108 m/s )
The energy levels of the hydrogen-like atom is known to be,
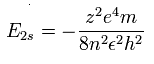
In the 2S electron of Be+, we substitute n=2 and z=2 into this equation.
So we suppose the beryllium ion (Be+) model as follows,
Fig. 1. Beryllium ion (Be+) model
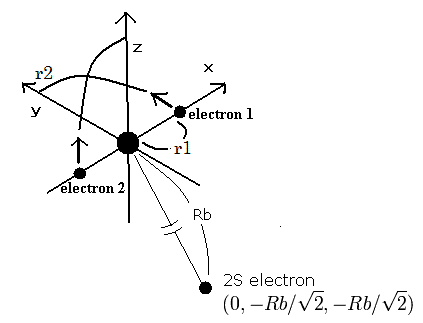
The two electrons of 1S state are avoiding 2S electron, so we fix the 2S electron at ( 0, - Rb / √2, - Rb / √2 ) as shown in Fig. 1.
(Fig. 1. shows the relative positions, But actually, this 2S electron is rotating around the nucleus slower than the 1S electrons.)
Like Be2+ (see this page ), when the electron 1 is at (x, y, 0), the electron 2 is at ( -x, 0, y ).
So the distances among the particles are,
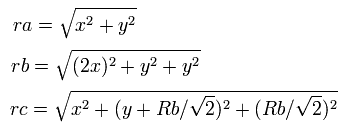
where ra is the distance between the electron 1 and the nucleus, rb is between the two 1S electrons, and rc is between the electron 1 and 2S electron, respectively.
The x component of the acceleration (m/sec2) of the electron 1 is,
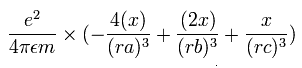
In the same way, the y component of the acceleration (m/sec2) of the electron 1 is,
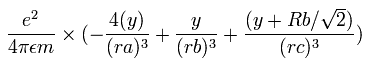
Then we compute the number of de Broglie's waves contained in one quarter of the 1S orbit like Be2+
Sample JAVA program (Be+ ion)
Table. 1 shows the results in which the last VY ( y component of electron 1's velocity after moving one quarter of its orbit ) is the closest to zero in Be+.
Table 1. Results of r1 and WN in which last VY is zero (Be+).
| E (eV) | r1 (MM) | WN | WN x 4 |
|---|
| -375.0 | 1482.5 | 0.25478 | 1.01948 |
| -380.0 | 1462.0 | 0.25302 | 1.01208 |
| -385.0 | 1442.0 | 0.25129 | 1.00516 |
| -388.82 | 1427.0 | 0.25000 | 1.00000 |
| -395.0 | 1403.5 | 0.24794 | 0.99176 |
| -400.0 | 1385.0 | 0.24632 | 0.98528 |
| -405.0 | 1367.0 | 0.24473 | 0.97892 |
This results shows that when the ground state energy of Be+ ion is -388.82 eV, the orbital length becomes just 1.00000 × de Broglie's wavelength.
The experimental value of the ground state energy of the beryllium (Be+) ion is -18.21116 - 153.89661 - 217.71865 = -389.826 eV.
So the calculation error is only 1.0 eV ( 0.25 % ).
(This small error is probably caused by using the "approximate" orbit of the 2S electron.)
This means that it is almost correct to say that the three electrons of the beryllium ion (Be+) are moving like Fig.1.
Bohr model Beryllium (Be)
In the neutral beryllium (Be), how are two 2S electrons moving ?
The neutral beryllium has four electrons, in which two 1S electrons are very close to the nucleus (see above Be+ section), and two 2S electrons are thought to be moving on the opposite sides of the nucleus.
The 2S electron's orbit is thought to be almost elliptical rather than circular.
When there is only one charged particle at the center like hydrogen-like atom, the orbit become elliptical or circular.
And the long and short axes of the ellipse can be just parallel to each other like Fig. 2.
Fig. 2. Orbits of hydrogen-like and non hydrogen-like atoms.
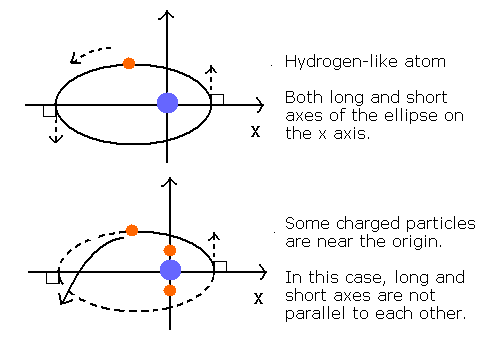
But when there are several charged particles at the center (for example, one nucleus + two 1S electrrons), the long and short axes of the orbit generally can not be parallel to each other.
So the whole orbit precesses about the nucleus like Fig. 3.
Fig. 3 Estimated Beryllium (Be) model.
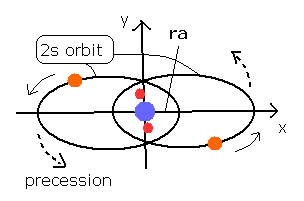
The 4e+ nucleus is at the origin, 1S electrons are approximately at (0, 0, ± 1430 MM ), and the 2S electron 1 starts at (ra, 0, 0) and moving on the X-Y plane.
Here we use the next JAVA sample program.
Sample JAVA program (Be)
In this program, we first input the initial x coordinate (ra) of the 2S electron 1.
Then, this 2S electron moves one round of the orbits of two de Broglie's wavelength.
And at this last point of the electron, this program outpus the following values on the screen,
last coordinate ( xxa, yya in MM ), last velocity ( VX,VY in MM/SS ), last distance between nucleus and electron 1,
inner product of last velocity and last coordinate (= VXA*xxa + VYA*yya ),
longest and shortest distances between the nucleus and points on the orbit.
When we input ra = 2286.40 (MM) (= 0.2286 × 10-10 meter), the last distance between nucleus and electron 1 becomes 2286.66, and the inner product of last velocity and last coordinate is close to zero.
This means that the electron can return to the first condition (distance = about 2286 MM), when the starting x-coordinate is 2286.40.
The shortest distance (2286.40) between the nucleus and the point on this 2S orbit proves to be almost same as the ra.
And the longest distance becomes 15578.72 MM.
Probably, estimated "real" orbits of the beryllium (Be) are like this.

2010/7/28 updated. Feel free to link to this site.