クロスオーバ・ネットワーク

クロスオーバ・ネットワークの要件

通常クロスオーバ・ネットワーク(チャンネル・デバイダを含む)で要求される性能は

遮断特性
ホーン・スピーカのシステムではスピーカ・ユニットの性格上遮断特性は非常に重要なファクタですが、 コーン・スピーカ主体の構成では逆に遮断特性では劣る -6 dB/octの1次フィルタで構成した方がつながりが自然でよいという意見も多く聞かれます。

再合成後の周波数特性
チャンネル・デバイダで分割した信号を再び加算したときに、周波数特性がフラットになるかどうかは、今から数十年前すでに山根式 vs 山中式という形でオーディオ雑誌上で議論されていたようで、今更と言われそうですが一応再確認させてもらいます。クロスオーバ・ポイントの位相から見るとButterworthのような-3dB交差ではフィルタ次数が奇数のハイパス/ローパスの位相差が90度または270度のときでないと、合成後クロスオーバ・ポイントでの 0 dBは実現できません。-6 dBでのクロスする場合は 0度(正相接続)または180度(逆相接続)で実現可能です。ここで注意が必要なのは周波数特性がフラットであってもほとんどの場合、伝達関数は1にならないことです。合成により伝達関数が1になるのは -6 dB/octの1次フィルタだけです。高次のフィルタでフラットになる場合、伝達関数はフェーズシフタの形になります。

群遅延(Group delay)
急峻な遮断特性を狙って高次のButterworthフィルタを使用するとクロスオーバ付近で群遅延が大きく変動します。これが遮断特性は必ずしも急峻であればよい。というわけではないことの理由です。群遅延が一定であれば、波形の再現ができます。群遅延一定という場合、分割後の各帯域の信号自体が群遅延一定な場合と、各帯域の信号は必ずしも一定ではないが、合成後の特性が群遅延一定になるという場合があります。前者の典型的な例がBesselフィルタで、後者の例は -6 dBの1次フィルタです。なおフィルタを使用すると、すべて要件を満たす特性をつくることも可能でが、低域のクロスオーバ・フィルタの実現にはDSPにもそれなりのリソースが要求されます。

1次 (6dB/oct) フィルタ

1次LPFの伝達関数は

H LPF ⁡ s = ω C s + ω C
Frequency Band Scale

1次HPFの伝達関数は

H HPF ⁡ s = s s + ω C

したがって 1次LPFとHPFを加算すれば伝達関数は1になり完全に元の波形が再現されます。一方、加算ではなく減算(位相反転して加算)をすると伝達関数はフェーズシフタとなって、波形は再現されませんが周波数特性はこちらもフラットになります。


3-Way 以上での周波数特性フラットの実現法

3-Way以上の場合一気に3分割(以上)してしまうと2-Wayでは伝達関数を1にすることができた -6 dB/octフィルタを使っても平坦な周波数特性は得られません。3-Way以上で周波数特性をフラットにするには、まず2分割した信号をまた2分割する。 つまり常に2分割づつというトーナメント方式(シードもOK)で分割していきます。

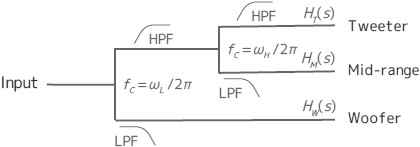
画像<tournament3Way.png>

ここで 3-Wayスピーカ・システムのウーファとミッドレンジのクロスオーバ角周波数をωLミッドレンジとトゥィータのクロスオーバ角周波数をωHとして

  1. ウーファとミッドレンジ＋トゥィータをカットオフ周波数 : fC = ωL / 2πで分割
    2. H W ⁡ s = ω L s + ω L , H M ⁡ s + H T ⁡ s = s s + ω L
    fCH/fCL Ratio = 10.00
    Frequency Band Scale

  2. 1のHPF側信号ををカットオフ周波数 : fC = ωH / 2πでミッドレンジとトゥィータに分割
    3. H M ⁡ s = s s + ω L × ω H s + ω H , H T ⁡ s = s s + ω L × s s + ω H

  3. 全帯域の信号すべてを加算すると
    4. H W ⁡ s + H M ⁡ s + H T ⁡ s = ω L s + ω L + s s + ω L ⁢ ω H s + ω H + s s + ω H = 1

最初にウーファとミッドレンジ＋トゥィータの分割ではなく、ウーファ＋ミッドレンジとトゥィータの分割から始めても、もちろん平坦な周波数特性は得られます。