What's New

台形波のフーリエ級数展開

周期\(2p\)の\(f(t)\)

\( \begin{eqnarray} f(t) = \begin{cases} 1 & ( 0 \lt t \lt q ) \\ \frac{ t-p+q }{ 2p-q } & ( q \lt t \lt p-q ) \\ 0 & ( p-q \lt t \lt p ) \end{cases} \end{eqnarray} \)

偶関数の台形波の第n高調波は

\( a_n = \frac{2}{p} \int_{0}^{p} f(t) \cos{ \frac{n \pi t}{p} } dt \)

\( \phantom{a_n} = \frac{2}{p} \int_{0}^{q} f(t) \cos{ \frac{n \pi t}{p} } dt + \frac{2}{p} \int_{q}^{p-q} f(t) \cos{ \frac{n \pi t}{p} } dt + \frac{2}{p} \int_{q-p}^{p} f(t) \cos{ \frac{n \pi t}{p} } dt \)

\( \phantom{a_n} = \frac{2}{p} \int_{0}^{q} \cos{ \frac{n \pi t}{p} } dt + \frac{2}{p} \int_{q}^{p-q} \frac{-t+p-q}{p-2q} \cos{ \frac{n \pi t}{p} } dt \)

\( \phantom{a_n} = \frac{2}{p} \left[ \frac{p}{n \pi} \sin{ \frac{n \pi t}{p} } \right]_0^q + \frac{2}{p(p-2q)} \left[- \frac{p}{n \pi} t \sin{ \frac{n \pi t}{p} }-(\frac{p}{n \pi})^2 \cos{ \frac{n \pi t}{p} }\right]_q^{p-q} + \frac{2(p-q)}{p(p-2q)} \left[ \frac{p}{n \pi} \sin{ \frac{n \pi t}{p} } \right]_q^{p-q} \)

\( \phantom{a_n} = \frac{2}{n \pi} \sin{ \frac{n \pi q}{p} } \)

\( \phantom{a_n \neq} - \frac{2}{(p-2q)n \pi} ((p-q) \sin{ \frac{n \pi (p-q)}{p} } + \frac{p}{n \pi} \cos{ \frac{n \pi (p-q)}{p} } + q \sin{ \frac{n \pi q}{p} } - \frac{p}{n \pi} \cos{ \frac{n \pi q}{p}}) \)

\( \phantom{a_n \neq} + \frac{p-q}{(p-2q) n \pi} ( \sin{ \frac{n \pi (p-q)}{p} } - \sin{ \frac{n \pi q}{p} }) \)

\( \phantom{a_n} = \frac{2}{n \pi} ( \sin{ \frac{n \pi q}{p} } - \frac{p}{(p-2q)n \pi} \cos{ \frac{n \pi (p-q)}{p} } + \frac{q}{p-2q} \sin{ \frac{n \pi q}{p} } + \frac{p}{(p-2q)n \pi} \cos{ \frac{n \pi q}{p}} - \frac{p-q}{p-2q} \sin{ \frac{n \pi q}{p} } ) \)

\( \phantom{a_n} = \frac {2p}{(p-2q)n^2 \pi ^2} (- \cos{ \frac{n \pi (p-q)}{p}} + \cos{ \frac{n \pi q}{p}}) \)

\(p=6q\) に設定すると

\[ a_n = \frac{3}{n^2 \pi ^2} ( - \cos{ \frac{5n \pi}{6}} + \cos{ \frac{n \pi}{6}}) \]

偶数次だけでなく 「第3高調波の相殺を考える」と同様、 奇数次の3の倍数 \((n=3 , 9 , 15 \ldots)\) の高調波もキャンセルされます。

また \(f(t)\) は偶関数なので、奇関数である \(\sin{}\) の項の係数はすべてゼロになります。

\[ b_n \equiv 0 \]


GNU Octaveでのフーリエ級数展開結果の検証

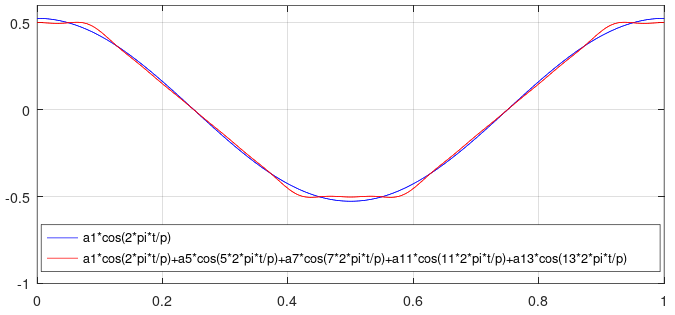
GNU Octaveでこのフーリエ級数展開の第13高調波までを加算し波形の確認をしてみました。

clear -all
function an = a(n)
  an = 3/(n*pi)^2*(-cos(5*n*pi/6)+cos(n*pi/6));
end
x = 0:0.001:1;
y1 = a(1)*cos(2*pi*x);
y5 = a(5)*cos(2*pi*5*x);
y7 = a(7)*cos(2*pi*7*x);
y11= a(11)*cos(2*pi*11*x);
y13 = a(13)*cos(2*pi*13*x);
plot(x,y1,'b;a1*cos(2*pi*t/p);')
hold on;
plot(x,y1+y5+y7+y11+y13,'r;a1*cos(2*pi*t/p)+a5*cos(5*2*pi*t/p)+a7*cos(7*2*pi*t/p)+a11*cos(11*2*pi*t/p)+a13*cos(13*2*pi*t/p);')
hold off;
axis([0,1,-1,0.6])
legend("location","south")
grid on


LTspiceでのFFT解析

FFT解析はGNU Octaveでも当然できますが、LTspiceなら電圧源で簡単に台形波を設定でき、窓関数の適応も簡単です。 なお post LPFとしてキルヒホッフの第一法則による連立方程式 の多重帰還型(MFB)LPF のコンデンサ容量を調整し、ほぼ \( 1V_{RMS} \) 出力が得られるように変更したフィルタをこの台形波電源に付加(負荷?)しました。

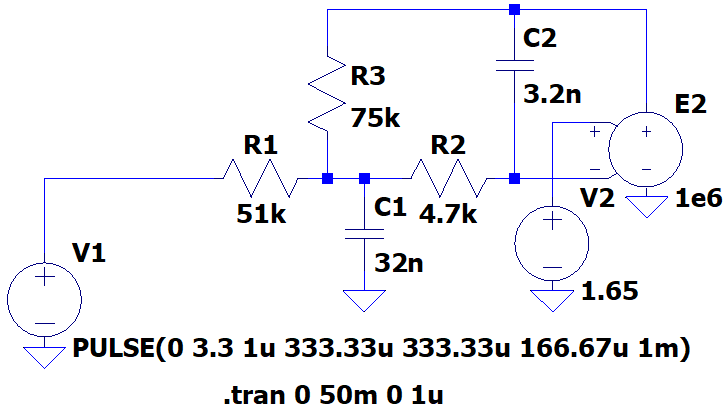
MFB LPF spec.

  • \( f_C = 865 \mathrm{H_Z}\)
  • \( Q = 0.688 \)
  • \( V_{OUT} = 2.85 \mathrm{V_{P-P}}(=1.01 \mathrm{V_{RMS}}) \)
    \((V_{IN} =3.3 \mathrm{V_{P-P}}, \ f=1 \mathrm{kHz})\)

高々2次のLPFなのですが、シミュレーションではきれいな正弦波が得られます。


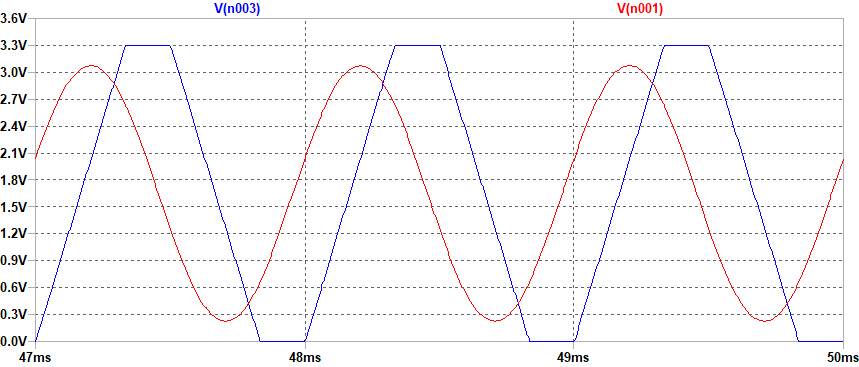
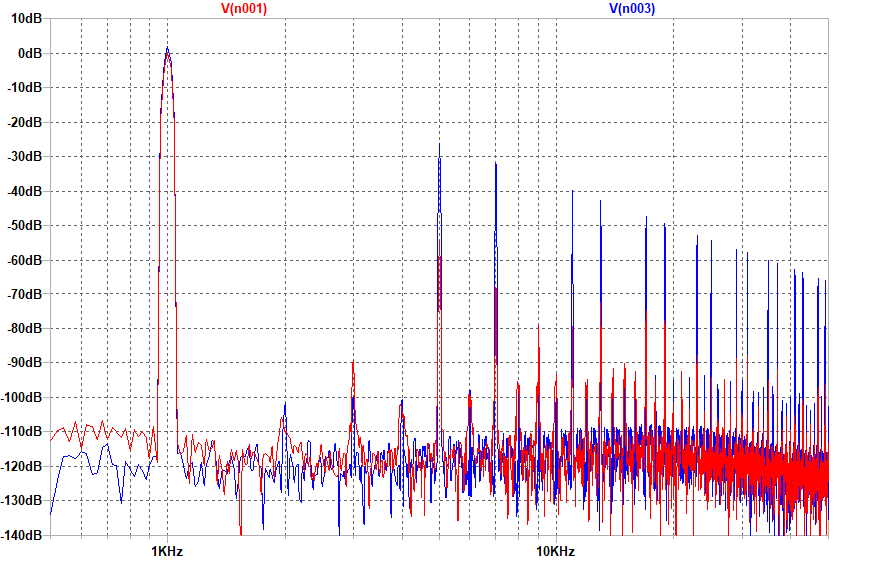
下はトランジェント・シミュレーション波形のFFT解析(Blackman窓使用)です。3,9,15次の高調波は偶数次の高調波と同等レベルにまで抑え込まれています。

台形波をつくる【設計 & シミュレーション編】

台形波をつくる回路を考えてみました。構成は以下の通りです。
U3の完全積分回路(三角波)
→ U1,U5,A1,A2のウインド・コンパレータ
→ A3,A4のRSフリップ・フロップ(方形波)
→ U3の完全積分回路(三角波)
→ U2,U6のオフセット付きの半波整流回路によるリミッタ回路(台形波)
→ U4の多重帰還型LPF(正弦波)

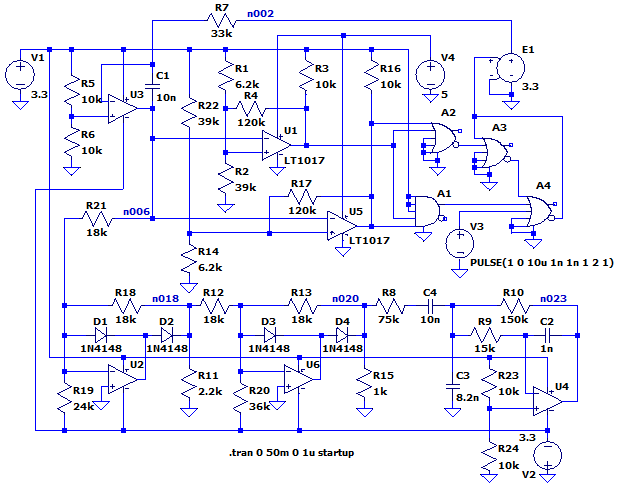
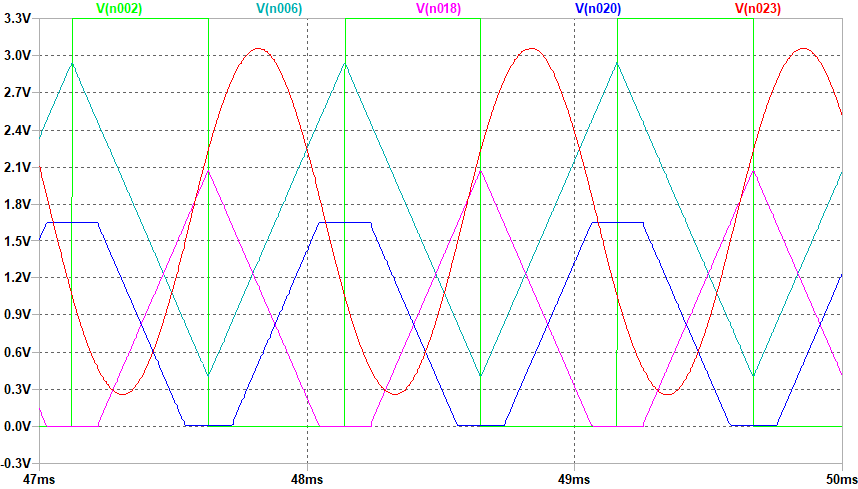
下のトランジェント・シミュレーション波形のように、上の回路からは、方形波(n002)、三角波(n006)、正弦波(n023)が同時に得られます。もうこれはファンクション・ジェネレータですね。

ちなみに、方形波、三角波、正弦波の3種類の波形だけのファンクション・ジェネレータなら、ICL8038やXR2206といったデバイスを使ったキットがインターネット上では極めて安価で手に入ります。



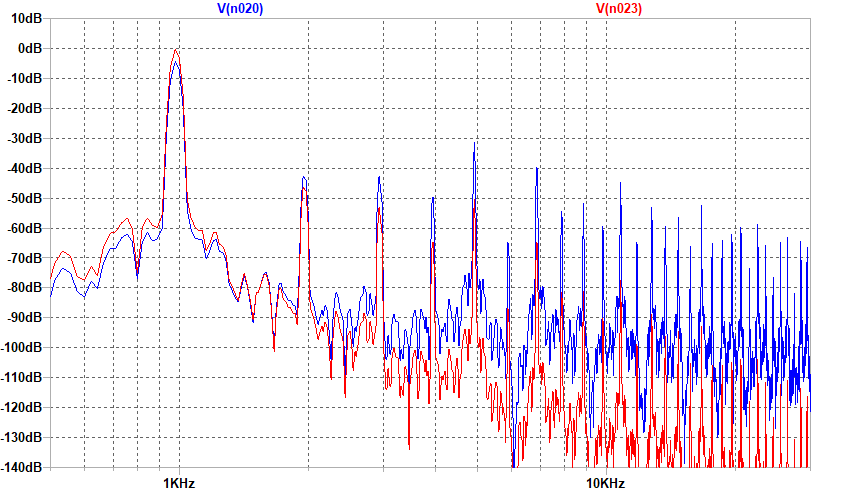
下はトランジェント・シミュレーション波形のFFT解析(Blackman窓使用)です。信号源そのものよりも 3,9,15次の高調波のレベルは大きめです。

台形波をつくる【制作 & 実測編】

下の写真は今回制作したファンクション・ジェネレータもどき回路の測定時のセッティングです。左下のオシロスコープのプローブに繋がれた基板が今回制作したボードです。

左上のスマホに表示されているのは、Raspberry PI Picoで使用したAndroidアプリScoppyのオシロスコープのモードです。オシロスコープ・モードでの信号経路は
オシロスコープ用プローブ(BNCコネクタ)→ フロントエンド回路 → Raspberry PI Pico (USB OTGケーブル)→ Androidスマホ
です。当初フロントエンド回路としてスイッチサイエンス マーケットプレイス(委託商品) -picoLABO の Raspberry Pi Pico オシロスコープ用アナログ基板の購入を検討しましたが、若干思うところあって自作に踏み切りました。 とはいえ自作にあたっては picoLABOのWeb上の回路図をかなり参考にさせていただきましたので、今回制作したRaspberry Pi Pico オシロスコープ用フロントエンド回路の公開は控えさせていただきます。

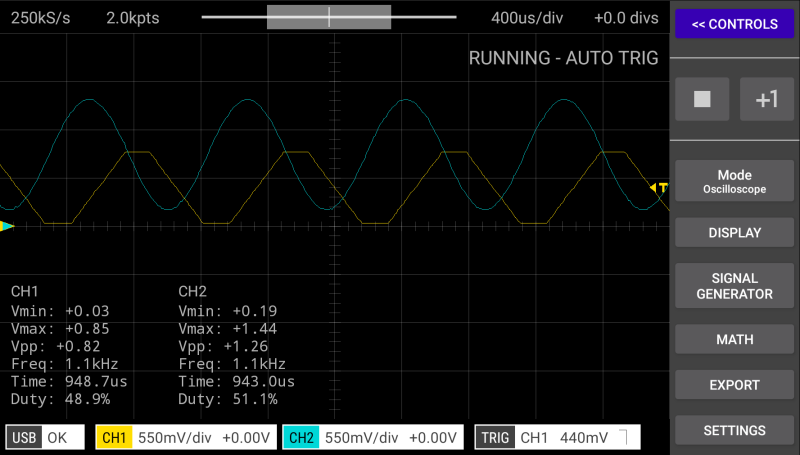
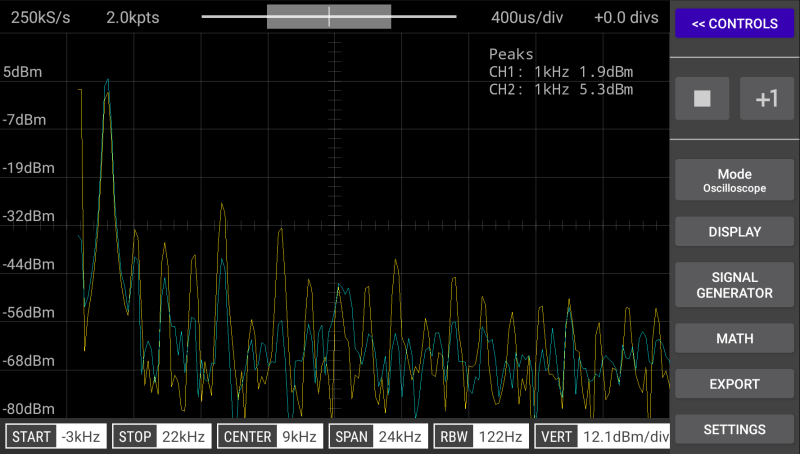
下の画像は今回制作したボードの ScoppyのMODE Oscilloscope / DISPLAY YT(Default) 波形とFFTのスクリーンショットです。概ねシミュレーションに近い結果が得られたのではないでしょうか。