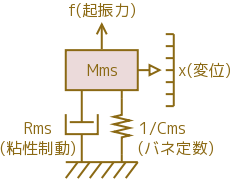
スピーカモデル

• T/S パラメータ
  | 
• 低域周波数シミュレーション

T/S パラメータ

基本パラメータ^*1

Sd [m²]

振動板投影面積

Mms [kg]

等価振動系質量,(m₀)
$M_{m\mathrm{s}}=M_{md}+M_a$
Mmd : スピーカの振動系質量(振動板、ボイスコイル、ボイスコイル・ボビン)
Ma   : 音響負荷

Cms [m/N]

等価コンプライアンス
スティフネス(ばね定数)の逆数

Rms [Nsec/m]

機械的損失(抵抗)

右図から以下の運動方程式が得られます

$f\left(x\right)=M_{m\mathrm{s}}\frac{d^{2}x}{d{t}^2}+R_{m\mathrm{s}}\frac{dx}{dt}+\frac{1}{C_{m\mathrm{s}}}x$

ラプラス変換して

$f\left(\mathrm{s}\right)=\left(M_{m\mathrm{s}}{\mathrm{s}}^2+R_{m\mathrm{s}}\mathrm{s}+\frac{1}{C_{m\mathrm{s}}}\right)x\left(\mathrm{s}\right)$

2次LPFの伝達関数が得られます

$\frac{x\left(\mathrm{s}\right)}{f\left(\mathrm{s}\right)}\left(=\frac{G}{{\mathrm{s}}^2+\frac{{\omega }_C}{Q}\mathrm{s}+{{\omega }_C}^2}\right)=\frac{\frac{1}{M_{m\mathrm{s}}}}{{\mathrm{s}}^2+\frac{R_{m\mathrm{s}}}{M_{m\mathrm{s}}}\mathrm{s}+\frac{1}{C_{m\mathrm{s}}{M}_{m\mathrm{s}}}}$

これは入力が力:fで、出力が振幅:xの伝達関数なのでHPFではありません。コーン型、ドーム型等のダイレクト・ラジエータ・タイプのスピーカの音圧は振動板の加速度に比例します。

Le [mH]

ボイスコイルのインダクタンス

Re [Ω]

ボイスコイルの直流抵抗

Bl [Tm]

フォースファクタ、動電変換の力係数
B [T] : 空隙磁束密度
l [m] : ボイスコイルの全長

小信号パラメータ^*2

Fs [Hz]

最低共振周波数
${\left(2\pi F_{\mathrm{s}}\right)}^2=\frac{1}{C_{m\mathrm{s}}{M}_{m\mathrm{s}}}$
$F_s=\frac{1}{2\pi \sqrt{C_{ms}{M}_{ms}}}$

Qms

機械的尖鋭度
$\frac{R_{m\mathrm{s}}}{M_{m\mathrm{s}}}=\frac{2\pi F_{\mathrm{s}}}{Q_{m\mathrm{s}}}$
$Q_{ms}=\frac{2\pi F_s{M}_{ms}}{R_{ms}}$

Qes

電気的尖鋭度
$Q_{es}=\frac{2\pi F_s{M}_{ms}{R}_e}{{\left(Bl\right)}^2}$

Qts

総合尖鋭度
$\left\{{\mathrm{s}}^2+\left(\frac{R_{m\mathrm{s}}}{M_{m\mathrm{s}}}+\frac{{\left(Bl\right)}^2}{M_{m\mathrm{s}}{R}_e}\right)\mathrm{s}+{\left(2\pi F_{\mathrm{s}}\right)}^2\right\}x\left(\mathrm{s}\right)=f\left(\mathrm{s}\right)$
$\frac{1}{Q_{t\mathrm{s}}}=\frac{1}{Q_{m\mathrm{s}}}+\frac{1}{Q_{e\mathrm{s}}}$
$Q_{ts}=\frac{Q_{ms}{Q}_{es}}{Q_{ms}+Q_{es}}$

Vas [m³]

等価コンプライアンス空気容量
$V_{a\mathrm{s}}=\rho c^2{{\mathrm{s}}_d}^2{C}_{m\mathrm{s}}$

大信号パラメータ^*3

Xmax

円錐の最大線形ピーク（または時々ピークツーピーク）偏位（mm）。 機械的な問題のために、ドライバーコーンの動きは大きな偏位、特にこのパラメーターを超える偏位では非線形になります。

Xmech

身体的損傷を与える前のドライバーの最大身体運動。 十分に大きい電気入力では、偏位運動はボイスコイルまたは運転者の他の可動部分に損傷を与えるであろう。 さらに、ボイスコイルを冷却するための配置（例えば、ポールピースの通気、 またはコイル自体の上方のボイスコイル形成体の開口部、両方とも空気流による熱放散を可能にする）は、それ自体、大きな円錐偏位で挙動を変える。

Pe

(最大入力)ドライバーの火力処理能力（ワット）。 この値は、製造業者などによって特徴付けるのが難しく、しばしば過大評価されています。 ボイスコイルが加熱されると、それはある程度寸法を変え、かなりの程度まで電気抵抗を変える。 後者は、ボイスコイルとパッシブクロスオーバーコンポーネント間の電気的関係を変化させ、 スピーカーシステムに設計されたスロープとクロスオーバーポイントを変化させます。

Vd

次式で計算されるピーク変位量
$V_d=S_d·X_{\mathit{max}}$

他のパラメータ^*4

未定係数法による強制振動の特殊解の求め方

$p\frac{d^{2}x}{d{t}^2}+q\frac{dx}{dt}+rx=k\sin \omega t$

$x=a\sin \omega t+b\cos \omega t$

$\frac{dx}{dt}=a\omega \cos \omega t-b\omega \sin \omega t$

$\frac{d^{2}x}{d{t}^2}=-a{\omega }^2\sin \omega t-b{\omega }^2\cos \omega t$

$\left(r-p{\omega }^2\right)a-q\omega b=k$

$q\omega a+\left(r-p{\omega }^2\right)b=0$

$\left[\begin{array}{cc}r-p{\omega }^2& -q\omega \\ q\omega & r-p{\omega }^2\end{array}\right]\left[\begin{array}{c}a\\ b\end{array}\right]=\left[\begin{array}{c}k\\ 0\end{array}\right]$

$a=\frac{k\left(r-p{\omega }^2\right)}{{\left(r-p{\omega }^2\right)}^2+{\left(q\omega \right)}^2}$

$b=\frac{-kq\omega }{{\left(r-p{\omega }^2\right)}^2+{\left(q\omega \right)}^2}$

$x=\frac{k\left(r-p{\omega }^2\right)}{{\left(r-p{\omega }^2\right)}^2+{\left(q\omega \right)}^2}\sin \omega t+\frac{-kq\omega }{{\left(r-p{\omega }^2\right)}^2+{\left(q\omega \right)}^2}\cos \omega t$

$\varphi ={\tan }^{-1}\frac{r-p{\omega }^2}{kq\omega }$

$x=\frac{k}{\sqrt{{\left(r-p{\omega }^2\right)}^2+{\left(q\omega \right)}^2}}\left(\sin \varphi \cos \omega t-\cos \varphi \sin \omega t\right)=\frac{-k}{\sqrt{{\left(r-p{\omega }^2\right)}^2+{\left(q\omega \right)}^2}}\cos \left(\omega t+\varphi \right)$

$\frac{dx}{dt}=\frac{k}{\sqrt{{\left(\frac{r}{\omega }-p\omega \right)}^2+q^2}}\sin \left(\omega t+\varphi \right)$

$p=M_{m\mathrm{s}}$ , $q=R_{m\mathrm{s}}$ , $r=\frac{1}{C_{m\mathrm{s}}}$ , $k=F$

$\frac{dx}{dt}=\frac{F}{\sqrt{{\left(\frac{1}{\omega C_{m\mathrm{s}}}-\omega M_{m\mathrm{s}}\right)}^2+{R_{m\mathrm{s}}}^2}}\sin \left(\omega t+\varphi \right)$

機械インピーダンス: Zm

Zmax [Ω]

$z_{\mathit{max}}={\left[z_e+z_{\mathit{em}}\right]}_{\mathit{max}}\simeq R_e+\frac{{\left(Bl\right)}^2}{{\left[z_a+z_m\right]}_{\mathit{min}}}$

$z_a+z_m=\sqrt{{R_{\mathit{ms}}}^2+{\left(\omega M_{\mathit{ms}}-\frac{1}{\omega C_{\mathit{ms}}}\right)}^2}$

${\left[z_a+z_m\right]}_{\mathit{min}}=R_{\mathit{ms}}$

$z_{\mathit{max}}=R_e\left(1+\frac{2\pi F_s{M}_{\mathit{ms}}}{R_{\mathit{ms}}}·\frac{{\left(Bl\right)}^2}{2\pi F_s{M}_{\mathit{ms}}{R}_e}\right)=R_e\left(1+\frac{Q_{\mathit{ms}}}{Q_{\mathit{es}}}\right)$

EBP (Efficiency Bandwidth Product)

大まかな指標尺度
$\mathit{EBP}=\frac{F_s}{Q_{\mathit{es}}}$
EBP < 50 : 密閉箱向きユニット
EBP > 100 : バスレフ箱向きユニット
50 < EBP < 100 : バスレフ/密閉箱向きユニット

Znom [Ω]

公称インピーダンス

η₀ [%]

${\eta }_0=\left(\frac{\rho ·B^2·l^2·{S_d}^2}{2·\pi ·c·{M_{\mathit{ms}}}^2·R_e}\right)\times 100\%$

$V_{a\mathrm{s}}=\rho c^2{{\mathrm{s}}_d}^2{C}_{m\mathrm{s}}$ , $F_s=\frac{1}{2\pi \sqrt{C_{ms}{M}_{ms}}}$ , $Q_{es}=\frac{2\pi F_s{M}_{ms}{R}_e}{{\left(Bl\right)}^2}$
から
${\eta }_0=\left(\frac{4·{\pi }^2·{F_s}^3·V_{\mathit{as}}}{c^3·Q_{\mathit{es}}}\right)\times 100\%$